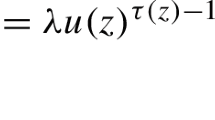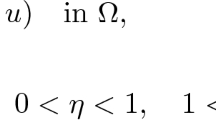Positive Solutions for Anisotropic Singular Dirichlet Problems

Abstract

We consider a Dirichlet problem driven by a (p(z), q(z))-Laplacian and a reaction involving the sum of a parametric singular term plus a superlinear perturbation. We prove a bifurcation-type result describing the changes in the set of positive solutions as the parameter $\lambda >0$ varies. Also we show that for every admissible parameter the problem has a smallest positive solution and obtain the monotonicity and continuity properties of the minimal solution map.

1 Introduction

In this paper, we study the following anisotropic singular Dirichlet problem

In this problem, $\Omega \subseteq \mathbb {R}^N$ is a bounded domain with a $C^2$-boundary $\partial \Omega$. If $\displaystyle E_1=\{r\in C(\overline{\Omega }): 1<\min _{\overline{\Omega }}r\}$, then for $r\in E_1$, by $\Delta _{r(z)}$ we denote the anisotropic r-Laplace differential operator defined by

$$\begin{aligned} \Delta _{r(z)}=\mathrm {div}\,\left( |Du|^{r(z)-2}Du\right) \; \text {for all } u\in W_0^{1,r(z)}(\Omega ). \end{aligned}$$

In contrast to the isotropic r-Laplacian (that is, $r(\cdot )$ is constant), the anisotropic one is nonhomogeneous. In ($\mathrm {P}_\lambda$) we have the sum of two such operators. So, even in the isotropic case, the differential operator of ($\mathrm {P}_\lambda$) is not homogeneous and this makes the study of ($\mathrm {P}_\lambda$) more difficult. In the reaction [right-hand side of ($\mathrm {P}_\lambda$)], we have the combined effects of two nonlinear terms of different nature. One is the parametric singular term $u\mapsto \lambda u^{-\eta (z)}$ with $\lambda >0$ being the parameter, with $\eta \in C(\overline{\Omega })$ and $\displaystyle 0<\eta _-=\min _{\overline{\Omega }}\eta \le \max _{\overline{\Omega }}\eta =\eta _+<1$. The other is a Carathéodory perturbation f(z, x) (that is, for all $x\in \mathbb {R}$, $z\mapsto f(z,x)$ is measurable and for a.a. $z\in \Omega$, $x\mapsto f(z,x)$ is continuous). We assume that for a.a. $z\in \Omega$, $f(z,\cdot )$ is $(p_+-1)$-superlinear ($\displaystyle p_+=\max _{\overline{\Omega }}p$), but need not satisfy the usual in such cases Ambrosetti–Rabinowitz condition (the AR-condition for short). We search for the existence of positive solutions, and our goal is to produce a precise description of the changes in the set of positive solutions as the parameter $\lambda$ varies in the open semiaxis $\mathring{\mathbb {R}}_+=(0,+\infty )$.

Anisotropic boundary value problems have been studied extensively in the last decade. We refer to the books of Diening–Harjulehto–Hästo–Růžička [4] and Rădulescu–Repovš [19] and the references therein. The study of singular anisotropic problems is lagging behind. Very few works on the subject can be found in the literature. We mention two recent ones by Byun–Ko [2] and Saoudi–Ghanmi [22] which are closely related to our work here. Both papers deal with equations driven by the Dirichlet anisotropic p-Laplacian and their hypotheses on the data are more restrictive (see hypothesis ($p_M$) in Byun–Ko [2] and hypotheses $(\text {H}_1)$–$(\text {H}_4)$ in Saoudi–Ghanmi [22]). In addition, our approach is different.

A main difficulty that we encounter when we deal with singular problems is that the corresponding energy (Euler) functional is not $C^1$, and so we cannot use the results of critical point theory directly on it. Therefore, we need to find a way to isolate the singularity and deal with $C^1$ functionals. For this reason, first we study an auxiliary purely singular problem for which we prove an existence and uniqueness result. Using this solution we are able to bypass the singularity and then, using variational tools from the critical point theory together with truncation and comparison techniques, we prove a bifurcation-type theorem describing the changes in the set of positive solutions of ($\mathrm {P}_\lambda$). According to our theorem, there exists a critical parameter $\lambda ^*>0$ such that

• for all $\lambda \in (0,\lambda ^*)$ problem ($\mathrm {P}_\lambda$) has at least two positive smooth solutions;

• for $\lambda =\lambda ^*$ problem ($\mathrm {P}_\lambda$) has at least one positive smooth solution;

• for all $\lambda >\lambda ^*$ problem ($\mathrm {P}_\lambda$) has no positive solutions.

Moreover, we show that for every admissible parameter $\lambda \in (0,\lambda ^*]$, problem ($\mathrm {P}_\lambda$) has a smallest positive solution $u_\lambda ^*$ (minimal or barrier solution) and we establish the monotonicity and continuity properties of the map $\lambda \mapsto u_\lambda ^*$.

For further details on the study of singular equations, we refer the reader to the papers [20, 21, 23].

2 Mathematical Background: Hypotheses

The study of problem ($\mathrm {P}_\lambda$) requires the use of Lebesgue and Sobolev spaces with variable exponents. A comprehensive presentation of the theory of these spaces can be found in the book of Diening–Harjuletho–Hästö–Růžička [4].

Let $M(\Omega )$ be the vector space of all measurable functions from $\Omega$ into $\mathbb {R}$. We identify two such functions which differ only on a Lebesgue-null set. Given $r\in E_1$, the anisotropic Lebesgue space $L^{r(z)}(\Omega )$ is defined by

$$\begin{aligned} L^{r(z)}(\Omega )=\left\{ u\in M(\Omega ): \int _\Omega |u|^{r(z)}\,\mathrm {d}z<\infty \right\} . \end{aligned}$$

We equip this space with the so-called Luxemburg norm defined by

$$\begin{aligned}\Vert u\Vert _{r(z)}=\inf \left[ \vartheta >0: \int _\Omega \left( \frac{|u(z)|}{\vartheta }\right) ^{r(z)}\,\mathrm {d}z\le 1\right] .\end{aligned}$$

Closely related to this norm is the modular function $\rho _r(\cdot )$ defined by

$$\begin{aligned} \rho _r(u)=\int _\Omega |u|^{r(z)}\,\mathrm {d}z\quad \text {for all } u\in L^{r(z)}(\Omega ). \end{aligned}$$

Evidently $\Vert \cdot \Vert _{r(z)}$ is the Minkowski functional of the set

$$\begin{aligned}C=\{u\in L^{r(z)}(\Omega ): \; \rho _r(u)\le 1\}.\end{aligned}$$

Also, we have the following proposition which illustrates the close relation between $\Vert \cdot \Vert _{r(z)}$ and $\rho _{r}(\cdot )$. Recall that, if $r\in E_1$, then $\displaystyle r_-=\min _{\overline{\Omega }}r$, $\displaystyle r_+=\max _{\overline{\Omega }}r$.

Proposition 2.1

If $r\in E_1$ and $\{u_n,u\}_{n\in \mathbb {N}}\subseteq L^{r(z)}(\Omega )$, then

• (a) $\Vert u\Vert _{r(z)}=\vartheta \Leftrightarrow \rho _r\left( \frac{u}{\vartheta }\right) =1$;

• (b) $\Vert u\Vert _{r(z)}<1$ (resp. $=1$, $>1$) $\Leftrightarrow \; \rho _r(u)<1$ (resp. $=1$, $>1$);

• (c) $\Vert u\Vert _{r(z)}\le 1\Rightarrow \Vert u\Vert _{r(z)}^{r_+}\le \rho _r(u)\le \Vert u\Vert _{r(z)}^{r_-}$; $\Vert u\Vert _{r(z)}\ge 1\Rightarrow \Vert u\Vert _{r(z)}^{r_-}\le \rho _r(u)\le \Vert u\Vert _{r(z)}^{r_+}$;

• (d) $\Vert u_n\Vert _{r(z)}\rightarrow 0$ (resp. $\rightarrow \infty$) $\Leftrightarrow \rho _r (u_n)\rightarrow 0$ (resp. $\rightarrow \infty$);

• (e) $\Vert u_n-u\Vert _{r(z)}\rightarrow 0 \Leftrightarrow \rho _r (u_n-u)\rightarrow 0$.

The space $L^{r(z)}(\Omega )$ ($r\in E_1$) is a Banach space which is separable, reflexive (in fact uniformly convex). Also, if $r'\in E_1$ is given by $r'(z)=\frac{r(z)}{r(z)-1}$ for all $z\in \overline{\Omega }$ (that is, $\frac{1}{r(z)}+\frac{1}{r'(z)}=1$ for all $z\in \overline{\Omega }$), then

$$\begin{aligned}L^{r(z)}(\Omega )^* = L^{r'(z)}(\Omega ).\end{aligned}$$

Moreover, we have the following version of Hölder’s inequality

$$\begin{aligned}\int _\Omega |uv|\,\mathrm {d}z\le \left( \frac{1}{r_-}+\frac{1}{r_-'}\right) \Vert u\Vert _{r(z)}\Vert v\Vert _{r'(z)}\quad \text {for all } u\in L^{r(z)}(\Omega ),\text { all } v\in L^{r'(z)}(\Omega ). \end{aligned}$$

We know that, if $q,r\in E_1$ and $q(z)\le r(z)$ for all $z\in \overline{\Omega }$, then

$$\begin{aligned}L^{r(z)}(\Omega )\hookrightarrow L^{q(z)}(\Omega )\hookrightarrow L^1(\Omega )\;\; \text {continuously}.\end{aligned}$$

Using the anisotropic Lebesgue spaces, we can define also anisotropic Sobolev spaces.

Given $r\in E_1$ we define

$$\begin{aligned}W^{1,r(z)}(\Omega )=\left\{ u\in L^{r(z)}(\Omega ): |Du|\in L^{r(z)}(\Omega )\right\} .\end{aligned}$$

We equip this space with the following norm:

$$\begin{aligned}\Vert u\Vert _{1,r(z)}=\Vert u\Vert _{r(z)}+\Vert Du\Vert _{r(z)}.\end{aligned}$$

Here $\Vert Du\Vert _{r(z)}=\Vert \,|Du|\,\Vert _{r(z)}$. Suppose that $r\in E_1 \cap C^{0,1}(\overline{\Omega })$ (that is, assume that the variable exponent is Lipschitz continuous). We define

$$\begin{aligned}W_0^{1,r(z)}(\Omega )=\overline{C_c^{\infty }(\Omega )}^{\Vert \cdot \Vert _{1,r(z)}}.\end{aligned}$$

Both spaces $W^{1,r(z)}(\Omega )$ and $W_0^{1,r(z)}(\Omega )$ are Banach spaces which are separable and reflexive (in fact uniformly convex), Moreover, for the space $W_0^{1,r(z)}(\Omega )$ the Poincaré inequality holds, namely

$$\begin{aligned} \Vert u\Vert _{r(z)}\le \widehat{c} \,\Vert Du\Vert _{r(z)}\quad \text {for some}\ \widehat{c}>0,\text { all } u\in W_0^{1,r(z)}(\Omega ). \end{aligned}$$

If $r\in E_1 \cap C^{0,1}(\overline{\Omega })$, then we define

$$\begin{aligned}r^*(z)={\left\{ \begin{array}{ll} \frac{N r(z)}{N-r(z)} &{} \text {if }r(z)<N\\ +\infty &{} \text {if }N\le r(z) \end{array}\right. }\quad \text {for all } z\in \overline{\Omega }. \end{aligned}$$

This is the variable critical Sobolev exponent corresponding to $r(\cdot )$. Suppose $q\in C(\overline{\Omega })$ and assume that

$$\begin{aligned}1\le q_- \le q(z)\le r^*(z)\quad \left( \text {resp. } 1\le q_-\le q(z) < r^*(z) \right) \; \text {for all } z\in \overline{\Omega }. \end{aligned}$$

Let $X=W^{1,r(z)}(\Omega )$ or $X=W_0^{1,r(z)}(\Omega )$. Then, we have that $X\hookrightarrow L^{q(z)}(\Omega )$ continuously (resp. $X\hookrightarrow L^{q(z)}(\Omega )$ compactly). This is the so-called anisotropic Sobolev embedding theorem. For $r\in E_1 \cap C^{0,1}(\overline{\Omega })$, we have

$$\begin{aligned}W_0^{1,r(z)}(\Omega )^* = W^{-1,r'(z)}(\Omega ).\end{aligned}$$

Consider the nonlinear operator $A_{r(z)}:W_0^{1,r(z)}(\Omega )\rightarrow W^{-1,r'(z)}(\Omega )$ defined by

$$\begin{aligned} \langle A_{r(z)}(u),h\rangle = \int _\Omega |Du|^{r(z)-2}(Du,Dh)_{\mathbb {R}^N}\,\mathrm {d}z\quad \text {for all } u,h\in W_0^{1,r(z)}(\Omega ). \end{aligned}$$

This operator has the following properties (see Gasiński–Papageorgiou [8], Proposition 2.5 and Rădulescu–Repovš [19], p. 40).

Proposition 2.2

The operator $A_{r(z)}(\cdot )$ is bounded (maps bounded sets to bounded sets), continuous, strictly monotone (hence maximal monotone too) and of type $(S)_+$, that is, it has the following property

"If $u_n \xrightarrow {w} u$ in $W_0^{1,r(z)}(\Omega )\,$ and $\,\displaystyle \limsup _{n\rightarrow \infty }\langle A_{r(z)}(u_n), u_n-u\rangle \le 0$,

then $u_n\rightarrow u$ in $W_0^{1,r(z)}(\Omega )$ as $n\rightarrow \infty$".

Another space that we will use (as a result of the anisotropic regularity theory) is the space $C_0^1(\overline{\Omega })=\{u\in C^1(\overline{\Omega }): u|_{\partial \Omega }=0\}$. This is an ordered Banach space with positive (order) cone $C_+=\{u\in C_0^1(\overline{\Omega }): u(z)\ge 0\; \text {for all }z\in \overline{\Omega }\}$. This cone has a nonempty interior given by

$$\begin{aligned} \mathrm {int}\, C_+=\left\{ u\in C_+: u(z)>0\; \text {for all } z\in \Omega , \left. \frac{\partial u}{\partial n}\right| _{\partial \Omega }<0\right\} , \end{aligned}$$

with $n(\cdot )$ being the outward unit normal on $\partial \Omega$.

Our hypotheses on the exponents involved in problem ($\mathrm {P}_\lambda$) are the following:

$\mathrm{H}_0$::

$p,q\in C^{0,1}(\overline{\Omega })$, $\eta \in C(\overline{\Omega })$, $q_-\le q_+<p_-\le p_+$ and $0<\eta (z)<1$ for all $z\in \overline{\Omega }$.

Consider $h_1,h_2\in M(\Omega )$. We write $h_1 \preceq h_2$ if and only if for every $K\subseteq \Omega$ compact we have $0<c_K\le h_2(z)-h_1(z)$ for a.a. $z\in K$. Note that if $h_1,h_2 \in C(\Omega )$ and $h_1(z)<h_2(z)$ for all $z\in \Omega$, then $h_1\preceq h_2$. Using this ordering notion and following the argument in the proof of Proposition 2.4 of Papageorgiou–Rădulescu–Repovš [17], we obtain the following strong comparison theorem for singular problems.

Proposition 2.3

If hypotheses $\mathrm {H}_0$ hold, $\widehat{\xi }\in L^\infty (\Omega )$, $\widehat{\xi }(z)\ge 0$ for a.a. $z\in \Omega$, $h_1,h_2\in L^\infty (\Omega )$, $h_1\preceq h_2$, $u\in W_0^{1,p(z)}(\Omega )$, $u\ge 0$, $u\ne 0$ and $v\in \mathrm {int}\, C_+$ satisfy

$$\begin{aligned}&-\Delta _{p(z)}u-\Delta _{q(z)}u+\widehat{\xi }(z)u^{p(z)-1}-\lambda u^{-\eta (z)}=h_1\quad \text {in } \Omega ,\\&-\Delta _{p(z)}v-\Delta _{q(z)}v+\widehat{\xi }(z)v^{p(z)-1}-\lambda v^{-\eta (z)}=h_2\quad \text {in }\Omega ,\quad \left. \frac{\partial v}{\partial n}\right| _{\partial \Omega }<0, \end{aligned}$$

then $v-u\in \mathrm {int}\, C_+$.

For every $u\in M(\Omega )$, we set $u^\pm =\max \{\pm u,0\}$. If $u\in W_0^{1,p(z)}(\Omega )$, then $u^\pm \in W_0^{1,r(z)}(\Omega )$, $u=u^+-u^-$, $|u|=u^+ +u^-$. Also, if $u,v\in M(\Omega )$ with $u(z)\le v(z)$ for a.a. $z\in \Omega$, then we introduce the following order intervals in $W_0^{1,p(z)}(\Omega )$:

$$\begin{aligned}&[u,v]=\left\{ h\in W_0^{1,p(z)}(\Omega ): u(z)\le h(z)\le v(z)\; \text {for a.a. } z\in \Omega \right\} ,\\&[u)=\left\{ h\in W_0^{1,p(z)}(\Omega ): u(z)\le h(z)\; \text {for a.a. } z\in \Omega \right\} ,\\&\mathrm {int}_{C_0^1(\overline{\Omega })}[u,v] = \text { the interior in } C_0^1(\overline{\Omega })\text { of } [u,v]\cap C_0^1(\overline{\Omega }). \end{aligned}$$

Throughout this work, by $\Vert \cdot \Vert$ we denote the norm $W_0^{1,p(z)}(\Omega )$. On account of the Poincaré inequality, we have

$$\begin{aligned} \Vert u\Vert =\Vert Du\Vert _{p(z)}\quad \text {for all } u\in W_0^{1,p(z)}(\Omega ). \end{aligned}$$

Suppose X is a Banach space and $\varphi \in C^1(X,\mathbb {R})$. We set

$$\begin{aligned} K_\varphi = \{u\in X: \varphi '(u)=0\}\quad \text {(the critical set of } \varphi \text {)}.\end{aligned}$$

We say that $\varphi (\cdot )$ satisfies the C-condition, if the following property holds:

"If $\{u_n\}_{n\in \mathbb {N}}\subseteq X$ is such that $\{\varphi (u_n)\}_{n\in \mathbb {N}}\subseteq \mathbb {R}$ is bounded and $(1+\Vert u_n\Vert _X)\varphi '(u_n)\rightarrow 0$ in $X^*$ as $n\rightarrow \infty$, then $\{u_n\}_{n\in \mathbb {N}}$ has a strongly convergent subsequence".

Now we will introduce our hypotheses on the perturbation f(z, x).

$\mathrm{H}_1$::

$f:\Omega \times \mathbb {R}\rightarrow \mathbb {R}$ is a Carathéodory function such that $f(z,0)=0$ for a.a. $z\in \Omega$ and

(i):

$f(z,x)\le a(z)[1+|x|^{r(z)-1}]$ for a.a. $z\in \Omega$, all $x\ge 0$, with $a\in L^\infty (\Omega )$, $a(z)\ge 0$ for a.a. $z\in \Omega$, $r\in C(\overline{\Omega })$, $p(z)<r(z)<p^*(z)$ for all $z\in \overline{\Omega }$;

(ii):

if $F(z,x)=\int _0^x f(z,s)\,\mathrm {d}s$, then $\displaystyle \lim _{x\rightarrow +\infty }\frac{F(z,x)}{x^{p_+}}=+\infty$ uniformly for a.a. $z\in \Omega$ and there exists $\tau \in C(\overline{\Omega })$ such that

$$\begin{aligned}&\tau (z) \in \left( (r_+-p_-)\max \left\{ \frac{N}{p_-},1\right\} , p^*(z)\right) \quad \text {for all } z\in \overline{\Omega }\\&0<\widehat{\delta }\le \liminf _{x\rightarrow +\infty }\frac{f(z,x)x-p_+F(z,x)}{x^{\tau (z)}}\; \text {uniformly for a.a. } z\in \Omega ; \end{aligned}$$

(iii):

$\displaystyle \lim _{x\rightarrow 0^+}\frac{f(z,x)}{x^{q(z)-1}}=0$ uniformly for a.a. $z\in \Omega$ and we have

$$\begin{aligned} 0\le f(z,x)\quad \text {for a.a. } z\in \Omega ,\text { all } x\ge 0; \end{aligned}$$

(iv):

for every $\rho >0$, we can find $\widehat{\xi }_\rho >0$ such that for a.a. $z\in \Omega$, the function

$$\begin{aligned}x\mapsto f(z,x)+\widehat{\xi }_\rho x^{p(z)-1}\end{aligned}$$

is nondecreasing on $[0,\rho ]$.

Remarks

Since our goal is to find positive solutions and all the above hypotheses concern the positive semiaxis $\mathbb {R}_+=[0,+\infty )$, without any loss of generality, we may assume that $f(z,x)=0$ for a.a. $z\in \Omega$, all $x\le 0$. Hypothesis $\mathrm {H}_1$(ii) says that for a.a. $z\in \Omega$, $f(z,\cdot )$ is $(p_+-1)$-superlinear. We do not use the AR-condition, which is common in the literature when dealing with superlinear problems (see, for example, Chang [3], p. 147). Hypothesis $\mathrm {H}_1$(ii) is less restrictive and incorporates in our framework also superlinear perturbations with "slower" growth as $x\rightarrow +\infty$. For example, consider the following function

$$\begin{aligned}f(z,x)= {\left\{ \begin{array}{ll} (x^+)^{\tau (z)-1}-(x^+)^{s(z)-1} &{} \text {if }x\le 1\\ x^{p_+-1}\ln x &{} \text {if }1<x \end{array}\right. }, \end{aligned}$$

where $\tau ,s\in C(\overline{\Omega })$ and $q(z)<\tau (z)\le s(z)$ for all $z\in \overline{\Omega }$. This function satisfies hypotheses $\mathrm {H}_1$ but fails to satisfy the AR-condition. Our hypotheses also incorporate the nonlinearity $f(z,x)=(x^+)^{r(z)-1}$ with $r\in C(\overline{\Omega })$ and $p(z)<r(z)$ for all $z\in \overline{\Omega }$. This is the perturbation used by Byun–Ko [2], where the equation is driven only by the p(z)-Laplacian with $p(\cdot )$ satisfying stronger conditions (see hypothesis ($p_M$) in [2]). Similarly, our hypotheses are more general than those used by Saoudi–Ghanmi [22] (see hypotheses ($\mathrm {H}_3$), ($\mathrm {H}_4$) in [22]), who also deal with equations driven by the p(z)-Laplacian only. The function f(z, x) given above lies outside the framework provided by the hypotheses in [22].

3 A Purely Singular Problem

As we already indicated in the Introduction, in order to handle the singular term, we will first consider a purely singular problem. The solution of this problem will allow us to bypass the singularity and deal with $C^1$-functionals.

So, in this section, we study the following purely singular problem

For this problem, we have the following existence and uniqueness result.

Proposition 3.1

If hypotheses $\mathrm {H}_0$ hold, then for every $\lambda >0$ problem ($\mathrm {Au}_\lambda$) has a unique positive solution $\overline{u}_\lambda \in \mathrm {int}\, C_+$ and the map $\mathring{\mathbb {R}}_+\ni \lambda \mapsto \overline{u}_\lambda$ is nondecreasing and $\Vert \overline{u}_\lambda \Vert _{C_0^1(\overline{\Omega })}\rightarrow 0$ as $\lambda \rightarrow 0^+$.

Proof

Given $\delta \in (0,1)$, first we solve the following approximation to problem ($\mathrm {Au}_\lambda$):

To solve this problem, we employ a fixed point argument. So, let $g\in C_0^1(\overline{\Omega })$ and consider the following Dirichlet problem

$$\begin{aligned} -\Delta _{p(z)} u(z)-\Delta _{q(z)}u(z)=\lambda [|g(z)|+\delta ]^{-\eta (z)}\;\; \text {in } \Omega ,\quad u\Big |_{\partial \Omega }=0. \end{aligned}$$

(3.1)

The operator $V=A_{p(z)}+A_{q(z)}: W_0^{1,p(z)}(\Omega )\rightarrow W^{-1,p'(z)}(\Omega )$ is maximal monotone (see Proposition 2.2) and coercive. So $V(\cdot )$ is surjective (see [15], p. 137). Since $\frac{\lambda }{[|g|+\delta ]^{\eta (\cdot )}}\in L^\infty (\Omega )$, we can find $v_\delta ^\lambda \in W_0^{1,p(z)}(\Omega )$ such that

$$\begin{aligned} V(v_\delta ^\lambda )=A_{p(z)}(v_\delta ^\lambda )+A_{q(z)}(v_\delta ^\lambda )=\lambda [|g|+\delta ]^{-\eta (\cdot )}. \end{aligned}$$

On account of the strict monotonicity of $V(\cdot )$ (see Proposition 2.2), this solution $v_\delta ^\lambda$ is unique. We have

$$\begin{aligned} \langle V(v_\delta ^\lambda ), -(v_\delta ^\lambda )^-\rangle =&\int _\Omega \frac{\lambda (-v_\delta ^\lambda )^-}{[|g|+\delta ]^{\eta (z)}}\,\mathrm {d}z\le 0\\&\Rightarrow \quad \rho _p\left( D(v_\delta ^\lambda )^-\right) \le 0\\&\Rightarrow \quad v_\delta ^\lambda \ge 0,\;\; v_\delta ^\lambda \ne 0\quad \text {(see Proposition }2.1\text {)}. \end{aligned}$$

From Theorem 4.1 of Fan–Zhao [6], we have that $v_\delta ^\lambda \in L^\infty (\Omega )$. Then Theorem 1.3 of Fan [5] implies that $v_\delta ^\lambda \in C_+\setminus \{0\}$. Finally, Proposition 4 of Papageorgiou–Qin–Rădulescu [14] says that $v_\delta ^\lambda \in \mathrm {int}\, C_+$.

We can define the solution map $\sigma _\delta ^\lambda : C_0^1(\overline{\Omega })\rightarrow C_0^1(\overline{\Omega })$ by setting

$$\begin{aligned} \sigma _\delta ^\lambda (g)=v_\delta ^\lambda \in \mathrm {int}\, C_+. \end{aligned}$$

We will show that this map is continuous. To this end, let $g_n\rightarrow g$ in $C_0^1(\overline{\Omega })$ and set $(v_\delta ^\lambda )_n=\sigma _\delta ^\lambda (g_n)$, for all $n\in \mathbb {N}$. We have

$$\begin{aligned} \langle V\left( (v_\delta ^\lambda )_n\right) , h\rangle = \int _\Omega \frac{\lambda h}{[|g_n|+\delta ]^{\eta (z)}}\,\mathrm {d}z\quad \text {for all } h\in W_0^{1,p(z)}(\Omega ). \end{aligned}$$

(3.2)

In (3.2) we use the test function $(v_\delta ^\lambda )_n\in W_0^{1,p(z)}(\Omega )$. We obtain

$$\begin{aligned}&\rho _p\left( D(v_\delta ^\lambda )_n\right) +\rho _q\left( D(v_\delta ^\lambda )_n\right) \le c_1\Vert (v_\delta ^\lambda )_n\Vert \quad \text {for some } c_1>0,\text { all}\ n\in \mathbb {N},\\&\qquad \Rightarrow \quad \left\{ (v_\delta ^\lambda )_n\right\} _{n\in \mathbb {N}}\subseteq W_0^{1,p(z)}(\Omega ) \;\; \text {is bounded (see Proposition } .2.1\text {)}. \end{aligned}$$

This implies that we can find $c_2>0$ such that

$$\begin{aligned}&(v_\delta ^\lambda )_n\in L^\infty (\Omega )\quad \text {and}\quad \Vert (v_\delta ^\lambda )_n\Vert _\infty \le c_2\;\; \text {for all } n\in \mathbb {N}\\&\text {(see}\ [6] \text { and } [8], \text { Proposition 3.1)}. \end{aligned}$$

Then Lemma 3.3 of Fukagai–Narukawa [7] says that there exist $\alpha \in (0,1)$ and $c_3>0$ such that

$$\begin{aligned} (v_\delta ^\lambda )_n\in C_0^{1,\alpha }(\overline{\Omega })=C^{1,\alpha }(\Omega )\cap C_0^1(\overline{\Omega }),\quad \Vert (v_\delta ^\lambda )_n\Vert _{C_0^{1,\alpha }(\Omega )}\le c_3,\quad \text {for all } n\in \mathbb {N}. \end{aligned}$$

Recall that $C_0^{1,\alpha }(\overline{\Omega })\hookrightarrow C_0^1(\overline{\Omega })$ compactly. So, by passing to a suitable subsequence if necessary, we may assume that

$$\begin{aligned} (v_\delta ^\lambda )_n\rightarrow v_\delta ^\lambda \; \; \text {in } C_0^1(\overline{\Omega })\text { as } n\rightarrow \infty . \end{aligned}$$

(3.3)

Then, if we pass to the limit as $n\rightarrow \infty$ in (3.2), we obtain

$$\begin{aligned} \langle V(v_\delta ^\lambda ), h\rangle =&\int _\Omega \frac{\lambda h}{[|g|+\delta ]^{\eta (z)}}\,\mathrm {d}z\quad \text {for all } h\in W_0^{1,p(z)}(\Omega ),\\&\Rightarrow \quad v_\delta ^\lambda = \sigma _\delta ^\lambda (g),\\&\Rightarrow \quad \sigma _\delta ^\lambda (\cdot )\text { is continuous.} \end{aligned}$$

Also for every $g\in C_0^1(\overline{\Omega })$ and with $v_\delta ^\lambda =\sigma _\delta ^\lambda (g)$, we have

$$\begin{aligned} \langle V(v_\delta ^\lambda ), h\rangle =&\int _\Omega \frac{\lambda h}{[|g|+\delta ]^{\eta (z)}}\,\mathrm {d}z \quad \text {for all } h\in W_0^{1,p(z)}(\Omega ), \nonumber \\&\Rightarrow \quad \rho _p(Dv_\delta ^\lambda )+\rho _q (Dv_\delta ^\lambda )\le \frac{1}{\delta ^{\eta _+}}\Vert v_\delta ^\lambda \Vert , \nonumber \\&\Rightarrow \quad \sigma _\delta ^\lambda (C_0^1(\overline{\Omega })) \subseteq W_0^{1,p(z)}(\Omega )\text { is bounded}\nonumber \\&\text {(see Proposition }2.1 \ \text {and recall that } 1<p_-). \end{aligned}$$

(3.4)

As above, using (3.4) and the anisotropic regularity theory, we infer that

$$\begin{aligned} \overline{\sigma _\delta ^\lambda (C_0^1(\overline{\Omega }))}^{\Vert \cdot \Vert _{C_0^1(\overline{\Omega })}}\subseteq C_0^1(\overline{\Omega })\text { is compact.} \end{aligned}$$

Then, the Schauder–Tychonov fixed point theorem (see [15], p. 298) implies that there exists $\overline{u}_\delta ^\lambda \in C_0^1(\overline{\Omega })$ such that

$$\begin{aligned}\sigma _\delta ^\lambda (\overline{u}_\delta ^\lambda )=\overline{u}_\delta ^\lambda \in \mathrm {int}\, C_+.\end{aligned}$$

This $\overline{u}_\delta ^\lambda \in \mathrm {int}\, C_+$ is a solution of the approximate problem ($\mathrm {Au}_\lambda ^\delta$). We show that this solution is unique. To this end, let $\overline{y}_\delta ^\lambda$ be another solution of ($\mathrm {Au}_\lambda ^\delta$). We have

$$\begin{aligned} 0\le & {} \langle V(\overline{u}_\delta ^\lambda )-V(\overline{y}_\delta ^\lambda ), \overline{u}_\delta ^\lambda - \overline{y}_\delta ^\lambda \rangle \\= & {} \int _\Omega \lambda \left[ \frac{1}{[\overline{u}_\delta ^\lambda +\delta ]^{\eta (z)}}- \frac{1}{[\overline{y}_\delta ^\lambda +\delta ]^{\eta (z)}}\right] (\overline{u}_\delta ^\lambda -\overline{y}_\delta ^\lambda )\,\mathrm {d}z\le 0\\&\Rightarrow \quad \overline{u}_\delta ^\lambda =\overline{y}_\delta ^\lambda . \end{aligned}$$

This proves the uniqueness of the solution $\overline{u}_\delta ^\lambda \in \mathrm {int}\, C_+$ of problem ($\mathrm {Au}_\lambda ^\delta$).

Claim: $0<\delta '<\delta \quad \Rightarrow \quad \overline{u}_\delta ^\lambda \le \overline{u}_{\delta '}^\lambda$.

We have

$$\begin{aligned} -\Delta _{p(z)} \overline{u}_{\delta '}^\lambda - \Delta _{q(z)}\overline{u}_{\delta '}^\lambda= & {} \lambda \left[ \overline{u}_{\delta '}^\lambda +\delta '\right] ^{-\eta (z)} \nonumber \\\ge & {} \lambda \left[ \overline{u}_{\delta '}^\lambda +\delta \right] ^{-\eta (z)}\quad \text {in } \Omega \text { (since } \delta '<\delta ). \end{aligned}$$

(3.5)

We introduce the Carathéodory function $e_\delta ^\lambda : \Omega \times \mathbb {R}\rightarrow \mathbb {R}$ defined by

$$\begin{aligned} e_\delta ^\lambda (z,x) = {\left\{ \begin{array}{ll} \lambda [x^+ + \delta ]^{-\eta (z)} &{} \quad \text {if } x\le \overline{u}_{\delta '}^\lambda (z)\\ \lambda [\overline{u}_{\delta '}^\lambda (z)+\delta ]^{-\eta (z)} &{} \quad \text {if } \overline{u}_{\delta '}^\lambda (z)<x \end{array}\right. }. \end{aligned}$$

(3.6)

We set $E_\delta ^\lambda (z,x)=\int _0^x e_\delta ^\lambda (z,s)\,\mathrm {d}s$ and consider the $C^1$-functional $\gamma _\lambda : W_0^{1,p(z)}(\Omega )\rightarrow \mathbb {R}$ defined by

$$\begin{aligned}&\gamma _\lambda (u) = \int _\Omega \frac{1}{p(z)}|Du|^{p(z)}\,\mathrm {d}z+\int _\Omega \frac{1}{q(z)}|Du|^{q(z)}\,\mathrm {d}z-\int _\Omega E_\delta ^\lambda (z,u)\,\mathrm {d}z\quad \\&\quad \text {for all } u\in W_0^{1,p(z)}(\Omega ). \end{aligned}$$

We have

$$\begin{aligned}&\gamma _\lambda (u)\ge \frac{1}{p_+}\rho _p(Du)-c_4\quad \text {for some }c_4>0,\text { all } u\in W_0^{1,p(z)}(\Omega )\text { (see }(3.6)),\\&\Rightarrow \quad \gamma _\lambda (\cdot )\text { is coercive (see Proposition } 2.1 \text { and recall the Poincar}\acute{\mathrm{e}}\text {'s inequality).} \end{aligned}$$

Also the anisotropic Sobolev embedding theorem implies that $\gamma _\lambda (\cdot )$ is sequentially weakly lower semicontinuous. So, by the Weierstrass–Tonelli theorem, we can find $\widetilde{u}_\delta ^\lambda \in W_0^{1,p(z)}(\Omega )$ such that

$$\begin{aligned}&\gamma _\lambda (\widetilde{u}_\delta ^\lambda ) = \min \left[ \gamma _\lambda (u): u\in W_0^{1,p(z)}(\Omega )\right] , \nonumber \\&\Rightarrow \quad \langle \gamma _\lambda ' (\widetilde{u}_\delta ^\lambda ), h \rangle =0\quad \text {for all } h\in W_0^{1,p(z)}(\Omega ),\nonumber \\&\Rightarrow \quad \langle A_{p(z)}(\widetilde{u}_\delta ^\lambda ), h\rangle + \langle A_{q(z)}(\widetilde{u}_\delta ^\lambda ), h\rangle =\int _\Omega e_\delta ^{\lambda }(z,\widetilde{u}_\delta ^\lambda )h\,\mathrm {d}z\quad \text {for all } h\in W_0^{1,p(z)}(\Omega ) \end{aligned}$$

(3.7)

In (3.7) we choose the test function $h=-(\widetilde{u}_\delta ^\lambda )^-\in W_0^{1,p(z)}(\Omega )$. We obtain

$$\begin{aligned}&\rho _p(D(\widetilde{u}_\delta ^\lambda )^-)+\rho _q(D(\widetilde{u}_\delta ^\lambda )^-)=0,\\&\qquad \Rightarrow \quad \widetilde{u}_\delta ^\lambda \ge 0,\;\; \widetilde{u}_\delta ^\lambda \ne 0. \end{aligned}$$

Next in (3.7) we choose $h=[\widetilde{u}_\delta ^\lambda -\overline{u}_{\delta '}^\lambda ]^+\in W_0^{1,p(z)}(\Omega )$. We have

$$\begin{aligned}&\langle A_{p(z)}(\widetilde{u}_\delta ^\lambda ), (\widetilde{u}_\delta ^\lambda -\overline{u}_{\delta '}^\lambda )^+\rangle + \langle A_{q(z)}(\widetilde{u}_\delta ^\lambda ), (\widetilde{u}_\delta ^\lambda -\overline{u}_{\delta '}^\lambda )^+\rangle \\&\quad =\quad \int _\Omega \lambda \left[ \overline{u}_{\delta '}^\lambda +\delta \right] ^{-\eta (z)}(\widetilde{u}_\delta ^\lambda -\overline{u}_{\delta '}^\lambda )^+\,\mathrm {d}z\quad \text {(see }(3.6))\\&\quad \le \quad \langle A_{p(z)}(\overline{u}_{\delta '}^\lambda ), (\widetilde{u}_\delta ^\lambda -\overline{u}_{\delta '}^\lambda )^+\rangle + \langle A_{q(z)}(\overline{u}_{\delta '}^\lambda ), (\widetilde{u}_\delta ^\lambda -\overline{u}_{\delta '}^\lambda )^+\rangle \quad \text {(see }(3.5)),\\&\qquad \Rightarrow \quad \widetilde{u}_\delta ^\lambda \le \overline{u}_{\delta '}^\lambda . \end{aligned}$$

So, we have proved that

$$\begin{aligned}&\widetilde{u}_\delta ^\lambda \in [0, \overline{u}_{\delta '}^\lambda ],\;\; \widetilde{u}_\delta ^\lambda \ne 0,\nonumber \\&\qquad \Rightarrow \quad \widetilde{u}_\delta ^\lambda = \overline{u}_{\delta }^\lambda \in \mathrm {int}\, C_+\quad \text {(see } (3.8), (3.6), (3.7)), \nonumber \\&\qquad \Rightarrow \quad \overline{u}_{\delta }^\lambda \le \overline{u}_{\delta '}^\lambda . \end{aligned}$$

(3.8)

This proves the claim.

Next we let $\delta \rightarrow 0^+$ to produce a solution of the auxiliary problem ($\mathrm {Au}_\lambda$). Let $\delta _n \rightarrow 0^+$ and set $\overline{u}_n^\lambda =\overline{u}_{\delta _n}^\lambda \in \mathrm {int}\, C_+$, for all $n\in \mathbb {N}$. We have

$$\begin{aligned}&0\le \overline{u}_1^\lambda \le \overline{u}_n^\lambda \quad \text {for all } n\in \mathbb {N}\text { (see the Claim)}, \end{aligned}$$

(3.9)

$$\begin{aligned}&\langle A_{p(z)}(\overline{u}_n^\lambda ), h\rangle + \langle A_{q(z)}(\overline{u}_n^\lambda ), h\rangle = \int _\Omega \lambda \left[ \overline{u}_n^\lambda +\delta _n\right] ^{-\eta (z)}h\,\mathrm {d}z \nonumber \\&\qquad \text {for all } h\in W_0^{1,p(z)}(\Omega ),\text { all }n\in \mathbb {N}. \end{aligned}$$

(3.10)

In (3.10) we use the test function $\overline{u}_n^\lambda \in W_0^{1,p(z)}(\Omega )$. We obtain

$$\begin{aligned} \rho _p(D\overline{u}_n^\lambda )+\rho _q(D\overline{u}_n^\lambda )\le&\int _\Omega \frac{\lambda \overline{u}_n^\lambda }{(\overline{u}_n^\lambda )^{\eta (z)}}\,\mathrm {d}z=\int _\Omega \lambda (\overline{u}_n^\lambda )^{1-\eta (z)}\,\mathrm {d}z \nonumber \\&\Rightarrow \quad \rho _p(D\overline{u}_n^\lambda )\le \lambda c_5\Vert \overline{u}_n^\lambda \Vert \quad \text {for some } c_5>0,\text { all } n\in \mathbb {N}\nonumber \\&\Rightarrow \quad \left\{ \overline{u}_n^\lambda \right\} _{n\in \mathbb {N}}\subseteq W_0^{1,p(z)}(\Omega ) \;\; \text {is bounded}\nonumber \\&\text {(see Proposition }2.1 \text { and recall that } 1<p_-). \end{aligned}$$

(3.11)

On account of (3.11), we may assume that

$$\begin{aligned}&\overline{u}_n^\lambda \xrightarrow {w} \overline{u}_\lambda \text { in } W_0^{1,p(z)}(\Omega ) \,\text { and }\, \nonumber \\&|D\overline{u}_n^\lambda |^{p(z)-2}D\overline{u}_n^\lambda +|D\overline{u}_n^\lambda |^{q(z)-2}D\overline{u}_n^\lambda \xrightarrow {w} \zeta \text { in } L^{p'(z)}(\Omega ,\mathbb {R}^N). \end{aligned}$$

(3.12)

From (3.9) we have

$$\begin{aligned}0\le \frac{1}{[\overline{u}_n^\lambda +\delta _n]^{\eta (z)}}\le \frac{1}{(\overline{u}_1^\lambda )^{\eta (z)}}.\end{aligned}$$

Then, for every $h\in C_c^\infty (\Omega )$, we have that $\overline{u}_1^\lambda (z)\ge c_h>0$ for all $z\in \mathrm {supp}\, h$ (recall that $\overline{u}_1^\lambda \in \mathrm {int}\, C_+$). Hence, for $h\in C_c^\infty (\Omega )$, we have

$$\begin{aligned} 0\le \frac{|h|}{[\overline{u}_n^\lambda + \delta _n]^{\eta (z)}}\le c_6(h)|h|\quad \text {for some } c_6(h)>0, \text { all } n\in \mathbb {N}. \end{aligned}$$

So, if in (3.10) we pass to the limit as $n\rightarrow \infty$ and use the dominated convergence theorem [see (3.12)], we obtain

$$\begin{aligned} \langle -\mathrm {div}\, \zeta , h\rangle =\int _\Omega \frac{h}{\overline{u}_\lambda ^{\eta (z)}}\,\mathrm {d}z\quad \text {for all } h\in C_c^\infty (\Omega ). \end{aligned}$$

(3.13)

The density of $C_c^\infty (\Omega )$ in $W_0^{1,p(z)}(\Omega )$ implies that (3.13) holds for all $h\in W_0^{1,p(z)}(\Omega )$ and so $-\mathrm {div}\,\zeta =\frac{1}{\overline{u}_\lambda ^{\eta (\cdot )}}$.

As above, we have

$$\begin{aligned} \left| \langle \frac{1}{[\overline{u}_n^\lambda + \delta _n]^{\eta (\cdot )}}-\frac{1}{\overline{u}_\lambda ^{\eta (\cdot )}}, h\rangle \right| \le \lambda \epsilon _n \Vert h\Vert \quad \text {for all } h\in C_c^\infty (\Omega ),\text { with } \epsilon _n\rightarrow 0^+. \end{aligned}$$

(3.14)

Exploiting the density of $C_c^{\infty }(\Omega )$ in $W_0^{1,p(z)}(\Omega )$, we infer that (3.14) holds for all $h\in W_0^{1,p(z)}(\Omega )$. It follows that

$$\begin{aligned} \frac{1}{[\overline{u}_n^\lambda + \delta _n]^{\eta (\cdot )}} \rightarrow \frac{1}{\overline{u}_\lambda ^{\eta (\cdot )}}\text { in } W^{-1,p'(z)}(\Omega ) \end{aligned}$$

(3.15)

From (3.11), (3.15) and Theorem 2.1 of Boccardo–Murat [1], we have that $D\overline{u}_n^\lambda (z)\rightarrow D\overline{u}_\lambda (z)$ for a.a. $z\in \Omega$. It follows that

$$\begin{aligned} \zeta = |D\overline{u}_\lambda |^{p(z)-2}D\overline{u}_\lambda + |D\overline{u}_\lambda |^{q(z)-2}D\overline{u}_\lambda \end{aligned}$$

and then

$$\begin{aligned} \langle A_{p(z)}(\overline{u}_\lambda ), h\rangle + \langle A_{q(z)}(\overline{u}_\lambda ), h\rangle = \int _\Omega \frac{\lambda h}{\overline{u}_\lambda ^{\eta (z)}}\quad \text {for all } h\in W_0^{1,p(z)}(\Omega ). \end{aligned}$$

Since $\overline{u}_1^\lambda \le \overline{u}_\lambda$ (see (3.9), (3.12)), we infer that $\overline{u}_\lambda$ is a positive solution of ($\mathrm {Au}_\lambda$). Then, from Theorem B.1 of Saoudi–Ghanmi [22] (see also Giacomoni–Schindler–Takáč [9], Theorem B.1), we have that $\overline{u}_\lambda \in \mathrm {int}\, C_+$. As before, we check that $\overline{u}_\lambda \in \mathrm {int}\, C_+$ is the unique positive solution of ($\mathrm {Au}_\lambda$).

Next we check that $\lambda \mapsto \overline{u}_\lambda$ is nondecreasing from $\mathring{\mathbb {R}}_+=(0,\infty )$ into $\mathrm {int}\, C_+$. So, let $0<\lambda <\lambda '$. We have

$$\begin{aligned}-\Delta _{p(z)}\overline{u}_{\lambda '}-\Delta _{q(z)}\overline{u}_{\lambda '} = \lambda ' \overline{u}_{\lambda '}^{-\eta (z)}\ge \lambda \overline{u}_{\lambda '}^{-\eta (z)}.\end{aligned}$$

We consider the Carathéodory function $\widehat{g}_\lambda : \Omega \times \mathring{\mathbb {R}}_+\rightarrow \mathring{\mathbb {R}}_+$ defined by

$$\begin{aligned} \widehat{g}_\lambda (z,x)={\left\{ \begin{array}{ll} \lambda x^{-\eta (z)} &{} \text {if } 0<x\le \overline{u}_{\lambda '}(z)\\ \lambda \overline{u}_{\lambda '}(z)^{-\eta (z)} &{} \text {if } \overline{u}_{\lambda '}(z)<x \end{array}\right. }. \end{aligned}$$

(3.16)

Note that from the proof of the Lemma of Lazer–McKenna [13], we have $\overline{u}_{\lambda '}(\cdot )^{-\eta (\cdot )}\in L^1(\Omega )$ (recall that $\overline{u}_{\lambda '}\in \mathrm {int}\,C_+$). We consider the following Dirichlet problem

$$\begin{aligned}-\Delta _{p(z)}u(z)-\Delta _{q(z)}u(z)=\widehat{g}_\lambda (z,u(z))\;\; \text {in }\Omega ,\quad u\Big |_{\partial \Omega }=0,\quad u>0.\end{aligned}$$

Reasoning as in the first part of the proof (using approximations of this problem), we show that it has a unique solution $\widetilde{u}_\lambda \in \mathrm {int}\, C_+$ and $\widetilde{u}_\lambda \le \overline{u}_{\lambda '}$. We conclude that $\widetilde{u}_\lambda = \overline{u}_\lambda$ [see (3.16)] and so $\overline{u}_\lambda \le \overline{u}_{\lambda '}$.

Finally let $\lambda _n \rightarrow 0^+$ and let $\overline{u}_n=\overline{u}_{\lambda _n}\in \mathrm {int}\, C_+$, $n\in \mathbb {N}$, be the unique solution of $(\mathrm {P}_{\lambda _n})$ produced earlier. We have

$$\begin{aligned}\langle A_{p(z)}(\overline{u}_n), h\rangle + \langle A_{q(z)}(\overline{u}_n), h\rangle = \int _\Omega \lambda _n \overline{u}_n^{-\eta (z)}h\,\mathrm {d}z\quad \text {for all } h\in W_0^{1,p(z)}(\Omega ),\text { all } n\in \mathbb {N}. \end{aligned}$$

Using the test function $h=\overline{u}_n\in W_0^{1,p(z)}(\Omega )$ we obtain

$$\begin{aligned}&\rho _p(D\overline{u}_n) + \rho _q(D\overline{u}_n) \le \lambda _n c_7\Vert u_n\Vert \;\; \text {for some } c_7>0,\text { all } n\in \mathbb {N}, \nonumber \\&\quad \Rightarrow \quad \overline{u}_n\rightarrow 0 \;\; \text {in } W_0^{1,p(z)}(\Omega )\text { (see Proposition }2.1). \end{aligned}$$

(3.17)

Then, the anisotropic regularity theory (see [22]), implies that $\{\overline{u}_n\}_{n\in \mathbb {N}}\subseteq C_0^1(\overline{\Omega })$ is relatively compact. Therefore $\overline{u}_n\rightarrow 0$ in $C_0^1(\overline{\Omega })$ [see (3.17)]. $\square$

4 Positive Solutions

We introduce the following two sets

$$\begin{aligned}&\mathscr {L}= \{\lambda >0: \; \text {problem }(\mathrm {P}_\lambda ) \text { has a positive solution}\},\\&S_\lambda = \text {set of positive solutions of problem} (\mathrm {P}_\lambda ). \end{aligned}$$

Proposition 4.1

If hypotheses $\mathrm {H}_0$, $\mathrm {H}_1$ hold, then $\mathscr {L}\ne \varnothing$ and for every $\lambda >0$, $S_\lambda \subseteq \mathrm {int}\, C_+$.

Proof

Hypotheses $\mathrm {H}_1$(i), (iii) imply that given $\epsilon >0$, we can find $c_8=c_8(\epsilon )>0$ such that for $\widehat{r}\in C(\overline{\Omega })$ with $\widehat{r}>r$, $\widehat{r}_->p_+$, we have

$$\begin{aligned}&f(z,x)\le \epsilon x^{q(z)-1}+c_8x^{\widehat{r}(z)-1}\;\; \text {for a.a. } z\in \Omega ,\text { all } x\ge 0,\nonumber \\&\quad \Rightarrow \quad F(z,x)\le \frac{\epsilon }{p(z)}x^{q(z)}+\frac{c_8}{r(z)}x^{\widehat{r}(z)}\;\; \text {for a.a. } z\in \Omega ,\text { all } x\ge 0. \end{aligned}$$

(4.1)

Let $\overline{u}_\lambda \in \mathrm {int}\, C_+$ be the unique solution of the auxiliary problem ($\mathrm {Au}_\lambda$). Recall that $\overline{u}_\lambda (\cdot )^{-\eta (\cdot )}\in L^1(\Omega )$. We introduce the Carathéodory function $k_\lambda : \Omega \times \mathbb {R}\rightarrow \mathbb {R}$ defined by

$$\begin{aligned} k_\lambda (z,x)={\left\{ \begin{array}{ll} \lambda \overline{u}_\lambda (z)^{-\eta (z)} + f(z,x^+) &{} \text {if } x\le \overline{u}_\lambda (z)\\ \lambda x^{-\eta (z)}+f(z,x) &{} \text {if } \overline{u}_\lambda (z)<x \end{array}\right. } \end{aligned}$$

(4.2)

We set $K_\lambda (z,x)=\int _0^x k_\lambda (z,s)\,\mathrm {d}s$ and consider the $C^1$-functional $\psi _\lambda : W_0^{1,p(z)}(\Omega )\rightarrow \mathbb {R}$ defined by

$$\begin{aligned} \psi _\lambda (u)= & {} \int _\Omega \frac{1}{p(z)}|Du|^{p(z)}\,\mathrm {d}z+\int _\Omega \frac{1}{q(z)}|Du|^{q(z)}\,\mathrm {d}z\\&-\int _\Omega K_\lambda (z,u)\,\mathrm {dz}, \quad \text {for all } u\in W_0^{1,p(z)}(\Omega ) \end{aligned}$$

Using (4.1) and (4.2), we have

$$\begin{aligned} \psi _\lambda (u)\ge & {} \frac{1}{p_+}\rho _p(Du)-\int _{\{0\le u\le \overline{u}_\lambda \}}\lambda u \overline{u}_\lambda ^{-\eta (z)}\,\mathrm {d}z-\nonumber \\&\int _{\{\overline{u}_\lambda <u\}}\frac{\lambda }{1-\eta (z)}\left[ u^{1-\eta (z)}- \overline{u}_\lambda ^{1-\eta (z)}\right] \,\mathrm {d}z-\frac{\epsilon }{q_-}\rho _q(u)-\frac{c_8}{\widehat{r}_-}\rho _{\widehat{r}}(u).\qquad \end{aligned}$$

(4.3)

Let $\widehat{d}(\cdot )=d(\cdot , \partial \Omega )$. From Lemma 14.16, p. 355, of Gilbarg–Trudinger [10], we know that we can find $\delta _0>0$ such that $\widehat{d}\in C^2(\Omega _{\delta _0})$ where $\Omega _{\delta _0} = \{z\in \overline{\Omega }: \widehat{d}(z)<\delta _0\}$. It follows that $\widehat{d}\in C_+\setminus \{0\}$. Since $\overline{u}_\lambda \in \mathrm {int}\, C_+$, on account of Proposition 4.1.22, p. 274, of Papageorgiou– Rădulescu–Repovš [15], we can find $c_9>0$ such that

$$\begin{aligned} c_9\widehat{d}\le \overline{u}_\lambda . \end{aligned}$$

(4.4)

Then we have

$$\begin{aligned} \int _\Omega \frac{|u|}{\overline{u}_\lambda ^{\eta (z)}}\,\mathrm {d}z= & {} \int _\Omega \overline{u}_\lambda ^{1-\eta (z)}\frac{|u|}{\overline{u}_\lambda }\,\mathrm {d}z \nonumber \\\le & {} c_{10} \int _\Omega \frac{|u|}{\widehat{d}}\,\mathrm {d}z \quad \text {for some } c_{10}>0\text { (see }(4.4)) \nonumber \\\le & {} c_{11}\Vert u\Vert \quad \text {for some } c_{11}>0, \end{aligned}$$

(4.5)

where in the last inequality, we have used the anisotropic Hardy inequality due to Harjuletho–Hästö–Koskenoja [11]. Returning to (4.3) and using (4.5), for all $u\in W_0^{1,p(z)}(\Omega )$ with $\Vert u\Vert =\rho <1$ we have

$$\begin{aligned} \psi _\lambda \ge \frac{1}{p_+} \rho ^{p_+} - c_{12}\rho ^{\widehat{r}_-}-c_{13}\left[ \lambda \rho + \epsilon \rho ^{q_-}\right] \quad \text {for some } c_{12},c_{13}>0. \end{aligned}$$

(4.6)

Since $p_+<\widehat{r}_-$, choosing $\rho \in (0,1)$ small, we have

$$\begin{aligned}\frac{1}{p_+}\rho ^{p_+}-c_{12}\rho ^{\widehat{r}_-}>0.\end{aligned}$$

Then choosing $\lambda >0$ and $\epsilon >0$ small, from (4.6) we see that

$$\begin{aligned} \psi _\lambda (u)\ge m_\lambda >0 \quad \text {for all } u\in W_0^{1,p(z)}(\Omega ), \Vert u\Vert =\rho . \end{aligned}$$

(4.7)

Let $v\in \mathrm {int}\,C_+$. Since $\overline{u}_\lambda \in \mathrm {int}\, C_+$, we can find $t\in (0,1)$ small such that $tv\le \overline{u}_\lambda$ (see [15], p. 274). We have

$$\begin{aligned}\psi _\lambda (tv)\le&\frac{t^{q_-}}{q_-}\left[ \rho _p(Dv)+\rho _q(Dv)\right] - \lambda t \int _\Omega \frac{v}{\overline{u}_\lambda ^{\eta (z)}}\,\mathrm {d}z\\&\qquad \quad \qquad \quad \text {(see } \text { and recall that } F\ge 0, q_-<p_-). \end{aligned}$$

We have seen above that $\frac{v}{\overline{u}_\lambda ^{\eta (\cdot )}}\in L^1(\Omega )$. Hence

$$\begin{aligned} \psi _\lambda (tv)\le c_{14}t^q-c_{15}t\quad \text {for some } c_{14},c_{15}>0. \end{aligned}$$

Since $q_->1$, choosing $t\in (0,1)$ even smaller if necessary, we have

$$\begin{aligned} \psi _\lambda (tv)<0 \quad \text {and}\quad \Vert tv\Vert \le \rho . \end{aligned}$$

(4.8)

Consider the closed ball

$$\begin{aligned}\overline{B}_\rho = \{u\in W_0^{1,p(z)}(\Omega ): \Vert u\Vert \le \rho \}.\end{aligned}$$

The reflexivity of $W_0^{1,p(z)}(\Omega )$ and the Eberlein–Smulian theorem imply that $\overline{B}_\rho$ is sequentially weakly compact. Also, using the anisotropic Sobolev embedding theorem, we check that $\psi _\lambda (\cdot )$ is sequentially weakly compact. So, we can find $u_\lambda \in W_0^{1,p(z)}(\Omega )$ such that

$$\begin{aligned} \psi _\lambda (u_\lambda ) =&\min \left[ \psi _\lambda (u): u\in \overline{B}_\rho \right] ,\nonumber \\&\Rightarrow \quad \psi _\lambda (u_\lambda )<0=\psi _\lambda (0)\quad \text {(see } (4.8)),\nonumber \\&\Rightarrow \quad u_\lambda \ne 0. \end{aligned}$$

(4.9)

From (4.7), we see that

$$\begin{aligned} 0<\Vert u_\lambda \Vert <\rho . \end{aligned}$$

(4.10)

Then, (4.9) and (4.10) imply that

$$\begin{aligned}&\psi _\lambda ' (u_\lambda ) = 0,\nonumber \\&\qquad \Rightarrow \quad \langle A_{p(z)} (u_\lambda ), h\rangle + \langle A_{q(z)} (u_\lambda ), h\rangle = \int _\Omega k_\lambda (z,u_\lambda )h\,\mathrm {d}z\quad \text {for all } h\in W_0^{1,p(z)}(\Omega ). \end{aligned}$$

(4.11)

In (4.11) we use the test function $h=(\overline{u}_\lambda - u_\lambda )^+\in W_0^{1,p(z)}(\Omega )$. Then

$$\begin{aligned}&\langle A_{p(z)} (u_\lambda ), (\overline{u}_\lambda - u_\lambda )^+\rangle + \langle A_{q(z)} (u_\lambda ), (\overline{u}_\lambda - u_\lambda )^+\rangle \nonumber \\&\quad =\; \int _\Omega \left[ \lambda \overline{u}_\lambda ^{-\eta (z)}+f(z,u_\lambda ^+)\right] (\overline{u}_\lambda - u_\lambda )^+\,\mathrm {d}z \quad \text {(see } .(4.2))\nonumber \\&\quad \ge \; \int _\Omega \lambda \overline{u}_\lambda ^{-\eta (z)}(\overline{u}_\lambda - u_\lambda )^+\,\mathrm {d}z\quad \text {(since }f\ge 0)\nonumber \\&\quad = \; \langle A_{p(z)} (\overline{u}_\lambda ), (\overline{u}_\lambda - u_\lambda )^+\rangle + \langle A_{q(z)} (\overline{u}_\lambda ), (\overline{u}_\lambda - u_\lambda )^+\rangle \quad \text {(see Proposition }3.1)\nonumber \\&\qquad \Rightarrow \quad \overline{u}_\lambda \le u_\lambda . \end{aligned}$$

(4.12)

Then (4.12), (4.2) and (4.11) imply that

$$\begin{aligned}&u_\lambda \in S_\lambda \quad (\lambda >0\text { small)},\\&\quad \Rightarrow \quad \mathscr {L}\ne \varnothing . \end{aligned}$$

Moreover, the anisotropic regularity theory (see Theorem B.1 of [22]) and the anisotropic maximum principle (see Proposition 4 of [14]) imply that $S_\lambda \subseteq \mathrm {int}\, C_+$ for all $\lambda \in \mathscr {L}$. $\square$

The next proposition shows that $\mathscr {L}$ is connected.

Proposition 4.2

If hypotheses $\mathrm {H}_0$, $\mathrm {H}_1$ hold, $\lambda \in \mathscr {L}$ and $\mu \in (0,\lambda )$, then $\mu \in \mathscr {L}$.

Proof

Since $\lambda \in \mathscr {L}$, we can find $u_\lambda \in S_\lambda \subseteq \mathrm {int}\, C_+$ (see Proposition 4.1). Recall that $u_\lambda ^{-\eta (\cdot )}\in L^1(\Omega )$. Also we have $\overline{u}_\mu \le \overline{u}_\lambda \le u_\lambda$ (see Proposition 3.1 and use the fact that $f\ge 0$). We introduce the Carathéodory function $\vartheta _\mu : \Omega \times \mathbb {R}\rightarrow \mathbb {R}$ defined by

$$\begin{aligned} \vartheta _\mu (z,x)={\left\{ \begin{array}{ll} \mu \overline{u}_\mu (z)^{-\eta (z)}+f(z,u_\mu (z)) &{} \quad \text {if }x<\overline{u}_\mu (z)\\ \mu x^{-\eta (z)}+f(z,x) &{} \quad \text {if } \overline{u}_\mu (z)\le x\le u_\lambda (z)\\ \mu u_\lambda (z)^{-\eta (z)}+f(z,u_\lambda (z)) &{} \quad \text {if } u_\lambda (z)<x \end{array}\right. }. \end{aligned}$$

(4.13)

We set $\Theta _\mu (z,x)=\int _0^x \vartheta _\mu (z,s)\,\mathrm {d}s$ and consider the $C^1$-functional $w_\mu : W_0^{1,p(z)}(\Omega )\rightarrow \mathbb {R}$ defined by

$$\begin{aligned}&w_\mu (u) = \int _\Omega \frac{1}{p(z)}|Du|^{p(z)}\,\mathrm {d}z + \int _\Omega \frac{1}{q(z)}|Du|^{q(z)}\,\mathrm {d}z - \int _\Omega \Theta _\mu (z,u)\,\mathrm {d}z\quad \\&\quad \text {for all } u\in W_0^{1,p(z)}(\Omega ). \end{aligned}$$

From (4.13), it is clear that $w_\mu (\cdot )$ is coercive. Also, it is sequentially weakly lower semicontinuous. So, we can find $u_\mu \in W_0^{1,p(z)}(\Omega )$ such that

$$\begin{aligned} w_\mu (u_\mu ) = \min \left[ w_\mu (u) : u\in W_0^{1,p(z)}(\Omega )\right] . \end{aligned}$$

(4.14)

From (4.14) we have

$$\begin{aligned} \langle A_{p(z)}(u_\mu ), h\rangle + \langle A_{q(z)}(u_\mu ), h\rangle = \int _\Omega \vartheta _\mu (z,u_\mu )h\,\mathrm {d}z\quad \text {for all } h\in W_0^{1,p(z)}(\Omega ). \end{aligned}$$

(4.15)

In (4.15) first we use the test function $h=(\overline{u}_\mu - u_\mu )^+\in W_0^{1,p(z)}(\Omega )$. Then

$$\begin{aligned}&\langle A_{p(z)} (u_\mu ), (\overline{u}_\mu - u_\mu )^+\rangle + \langle A_{q(z)} (u_\mu ), (\overline{u}_\mu - u_\mu )^+\rangle \\&\quad =\; \int _\Omega \left[ \mu \overline{u}_\mu ^{-\eta (z)}+f(z,\overline{u}_\mu )\right] (\overline{u}_\mu - u_\mu )^+\,\mathrm {d}z \quad \text {(see }(4.13))\\&\quad \ge \; \int _\Omega \mu \overline{u}_\mu ^{-\eta (z)}(\overline{u}_\mu - u_\mu )^+\,\mathrm {d}z\quad \text {(since } f\ge 0)\\&\quad = \; \langle A_{p(z)} (\overline{u}_\mu ), (\overline{u}_\mu - u_\mu )^+\rangle + \langle A_{q(z)} (\overline{u}_\mu ), (\overline{u}_\mu - u_\mu )^+\rangle \\&\qquad \Rightarrow \quad \overline{u}_\mu \le u_\mu . \end{aligned}$$

Next in (4.15) we choose $h=(u_\mu -u_\lambda )^+\in W_0^{1,p(z)}(\Omega )$. We have

$$\begin{aligned}&\langle A_{p(z)} (u_\mu ), (u_\mu -u_\lambda )^+\rangle + \langle A_{q(z)} (u_\mu ), (u_\mu -u_\lambda )^+\rangle \\&\quad =\; \int _\Omega \left[ \mu u_\lambda ^{-\eta (z)}+f(z, u_\lambda )\right] (u_\mu -u_\lambda )^+\,\mathrm {d}z \quad \text {(see }(4.13))\\&\quad \le \; \int _\Omega \left[ \lambda u_\lambda ^{-\eta (z)}+f(z,u_\lambda )\right] (u_\mu - u_\lambda )^+\,\mathrm {d}z\quad \text {(since }\mu <\lambda )\\&\quad = \; \langle A_{p(z)} (u_\lambda ), (u_\mu - u_\lambda )^+\rangle + \langle A_{q(z)} (u_\lambda ), (u_\mu - u_\lambda )^+\rangle \quad \text {(since } u_\lambda \in S_\lambda )\\&\qquad \Rightarrow \quad u_\mu \le u_\lambda . \end{aligned}$$

So, we have proved that

$$\begin{aligned} u_\mu \in [\overline{u}_\mu , u_\lambda ]. \end{aligned}$$

(4.16)

From (4.16), (4.13) and (4.15), we conclude that

$$\begin{aligned}&u_\mu \in S_\mu \subseteq \mathrm {int}\, C_+,\\&\qquad \Rightarrow \quad \mu \in \mathscr {L}. \end{aligned}$$

$\square$

A by-product of the above proof is the following weak monotonicity property for the solution multifunction $\lambda \mapsto S_\lambda$.

Corollary 4.3

If hypotheses $\mathrm {H}_0$, $\mathrm {H}_1$ hold, $\lambda \in \mathscr {L}$, $u_\lambda \in S_\lambda \subseteq \mathrm {int}\, C_+$ and $\mu \in (0,\lambda )$, then $\mu \in \mathscr {L}$ and we can find $u_\mu \in S_\mu \subseteq \mathrm {int}\, C_+$ such that $u_\mu \le u_\lambda$.

Using Proposition 2.3, we can improve the assertion of this corollary.

Proposition 4.4

If hypotheses $\mathrm {H}_0$, $\mathrm {H}_1$ hold, $\lambda \in \mathscr {L}$, $u_\lambda \in S_\lambda \subseteq \mathrm {int}\, C_+$ and $\mu \in (0,\lambda )$, then $\mu \in \mathscr {L}$ and we can find $u_\mu \in S_\mu \subseteq \mathrm {int}\, C_+$ such that

$$\begin{aligned}u_\lambda - u_\mu \in \mathrm {int}\, C_+.\end{aligned}$$

Proof

From Corollary 4.3, we already know that $\mu \in \mathscr {L}$ and there exists $u_\mu \in S_\mu \subseteq \mathrm {int}\, C_+$ such that

$$\begin{aligned} u_\mu \le u_\lambda . \end{aligned}$$

(4.17)

Let $\rho = \Vert u_\lambda \Vert _\infty$ and let $\widehat{\xi }_\rho >0$ be as postulated by hypothesis $\mathrm {H}_1$(iv). We have

$$\begin{aligned}&-\Delta _{p(z)}u_\mu -\Delta _{q(z)}u_\mu +\widehat{\xi }_\rho u_\mu ^{p(z)-1}-\lambda u_\mu ^{-\eta (z)} \nonumber \\&\quad = f(z,u_\mu ) +\widehat{\xi }_\rho u_\mu ^{p(z)-1}-(\lambda -\mu )u_\mu ^{-\eta (z)} \nonumber \\&\quad \le \; f(z,u_\lambda ) + \widehat{\xi }_\rho u_\lambda ^{p(z)-1} \quad \text {(see }(4.17), \text { hypothesis } \mathrm {H}_1\text {(iv) and use that } \mu <\lambda ) \nonumber \\&\quad = -\Delta _{p(z)}u_\lambda -\Delta _{q(z)}u_\lambda +\widehat{\xi }_\rho u_\lambda ^{p(z)-1}-\lambda u_\lambda ^{-\eta (z)}\quad \text {(since } u_\lambda \in S_\lambda ). \end{aligned}$$

(4.18)

Since $u_\mu \in \mathrm {int}\, C_+$, we have

$$\begin{aligned} 0\preceq (\lambda -\mu )u_\mu ^{-\eta (\cdot )}. \end{aligned}$$

So, from (4.18) and Proposition 2.3, it follows that

$$\begin{aligned}u_\lambda - u_\mu \in \mathrm {int}\, C_+.\end{aligned}$$

$\square$

Let $\lambda ^*= \sup \mathscr {L}$.

Proposition 4.5

If hypotheses $\mathrm {H}_0$, $\mathrm {H}_1$ hold, then $\lambda ^*<\infty$.

Proof

On account of hypotheses $\mathrm {H}_1$(i), (ii), (iii), we can find $\lambda _0>0$ such that

$$\begin{aligned} \lambda _0 x^{-\eta (z)}+f(z,x)\ge x^{p(z)-1} \quad \text {for a.a. } z\in \Omega , \text { all } x\ge 0. \end{aligned}$$

(4.19)

Let $\lambda >\lambda _0$ and suppose that $\lambda \in \mathscr {L}$. Then we can find $u_\lambda \in S_\lambda \subseteq \mathrm {int}\, C_+$. Consider an open set $\Omega _0\subseteq \Omega$ with $C^2$-boundary such that $\overline{\Omega }_0\subseteq \Omega$. We set $\displaystyle m_0=\min _{\overline{\Omega }_0}u_\lambda >0$ (since $u_\lambda \in \mathrm {int}\, C_+$). For $\delta >0$, set $m_0^\delta =m_0+\delta$, let $\rho = \Vert u_\lambda \Vert _\infty$ and let $\widehat{\xi }_\rho >0$ be as postulated by hypothesis $\mathrm {H}_1$(iv). We have

$$\begin{aligned}&-\Delta _{p(z)}m_0^\delta + \widehat{\xi }_\rho (m_0^\delta )^{p(z)-1}-\lambda (m_0^\delta )^{-\eta (z)}\\&\quad \le \; \widehat{\xi }_\rho m_0^{p(z)-1}+\chi (\delta )-\frac{\lambda }{m_0^{\eta (z)}+\delta ^{\eta (z)}}\\&\qquad \text {with } \chi (\delta )\rightarrow 0^+ \text { as } \delta \rightarrow 0^+\text { (recall that } 0<\eta (z)<1\text { for all } z\in \overline{\Omega })\\&\quad \le \; [\widehat{\xi }_\rho +1]m_0^{p(z)-1}+\chi (\delta ) + \frac{\lambda \delta ^{\eta (z)}}{m_0^{2\eta (z)}}-\frac{\lambda }{m_0^{\eta (z)}}\\&\quad =\; m_0^{p(z)-1}-\lambda _0 m_0^{-\eta (z)}+\widehat{\xi }_\rho m_0^{p(z)-1}+\widehat{\chi }(\delta )-\frac{\lambda -\lambda _0}{m_0^{\eta (z)}}\quad \text {with } \widehat{\chi }(\delta )\rightarrow 0^+\text { as } \delta \rightarrow 0^+\\&\quad \le \; f(z,m_0)+\widehat{\xi }_\rho m_0^{p(z)-1} \quad \text {for } \delta>0\text { small (see }(4.19) \text { and recall that } \lambda >\lambda _0)\\&\quad \le \; f(z,u_\lambda )+\widehat{\xi }_\rho u_\lambda ^{p(z)-1} \quad \text {(see hypothesis } \mathrm {H}_1\text {(iv))}\\&\quad =\; -\Delta _{p(z)} u_\lambda -\Delta _{q(z)}u_\lambda +\widehat{\xi }_\rho u_\lambda ^{p(z)-1} \;\; \text {in } \Omega _0. \end{aligned}$$

Invoking Proposition 6 of Papageorgiou–Rădulescu–Repovš [18], we infer that

$$\begin{aligned} m_0^\delta <u_\lambda (z)\;\; \text {for all } z\in \Omega _0,\text { all } \delta \in (0,1)\text { small,} \end{aligned}$$

a contradiction to the definition of $m_0$.

Therefore $\lambda \notin \mathscr {L}$ and so $\lambda ^*\le \lambda _0<\infty$. $\square$

Next we show that $\lambda \in (0,\lambda ^*)$ we have multiplicity of positive solutions for problem ($\mathrm {P}_\lambda$).

Proposition 4.6

If hypotheses $\mathrm {H}_0$, $\mathrm {H}_1$ hold and $\lambda \in (0,\lambda ^*)$, then problem ($\mathrm {P}_\lambda$) has at least two positive solutions

$$\begin{aligned} u_0, \widehat{u}\in \mathrm {int}\, C_+. \end{aligned}$$

Proof

Let $0<\mu<\lambda<\delta <\lambda ^*$. We know that $\mu ,\delta \in \mathscr {L}$ and on account of Proposition 4.4, we can find $u_\delta \in S_\delta \subseteq \mathrm {int}\, C_+$, $u_0 \in S_\lambda \subseteq \mathrm {int}\, C_+$ and $u_\mu \in S_\mu \subseteq \mathrm {int}\, C_+$ such that

$$\begin{aligned}&u_\delta -u_0\in \mathrm {int}\, C_+\;\; \text {and}\;\; u_0-u_\mu \in \mathrm {int}\, C_+\nonumber \\&\qquad \Rightarrow \quad u_0\in \mathrm {int}_{C_0^1{(\overline{\Omega })}}[u_\mu , u_\delta ]. \end{aligned}$$

(4.20)

Recall that $u_{\mu }(\cdot )^{-\eta (\cdot )}, u_\delta (\cdot )^{-\eta (\cdot )}\in L^1(\Omega )$. We introduce the Carathéodory function $\widehat{\beta }_\lambda :\Omega \times \mathbb {R}\rightarrow \mathbb {R}$ defined by

$$\begin{aligned} \widehat{\beta }_\lambda (z,x) = {\left\{ \begin{array}{ll} \lambda u_\mu (z)^{-\eta (z)}+f(z,u_\mu (z)) &{} \text {if } x<u_\mu (z)\\ \lambda x^{-\eta (z)}+f(z,x) &{} \text {if } u_\mu (z)\le x\le u_\delta (z)\\ \lambda u_\delta (z)^{-\eta (z)}+f(z,u_\delta (z)) &{} \text {if } u_\delta (z)<x \end{array}\right. }. \end{aligned}$$

(4.21)

We set $\widehat{B}_\lambda (z,x)=\int _0^x \widehat{\beta }_\lambda (z,s)\,\mathrm {d}s$ and consider the $C^1$-functional $\widehat{\zeta }_\lambda : W_0^{1,p(z)}(\Omega )\rightarrow \mathbb {R}$ defined by

$$\begin{aligned}&\widehat{\zeta }_\lambda (u)=\int _\Omega \frac{1}{p(z)}|Du|^{p(z)}\,\mathrm {d}z+\int _\Omega \frac{1}{q(z)}|Du|^{q(z)}\,\mathrm {d}z-\int _\Omega \widehat{B}_\lambda (z,u)\,\mathrm {d}z\quad \\&\quad \text {for all } u\in W_0^{1,p(z)}(\Omega ). \end{aligned}$$

We have

$$\begin{aligned}&\widehat{\zeta }_\lambda (u) \ge \frac{1}{p_+}\rho (Du)-c_{16}\quad \text {for some }c_{16}>0,\text { all } u\in W_0^{1,p(z)}(\Omega )\text { (see } (4.21)),\\&\qquad \Rightarrow \quad \widehat{\zeta }_\lambda (\cdot )\text { is coercive (see Proposition} \ 2.1). \end{aligned}$$

Also $\widehat{\zeta }_\lambda (\cdot )$ is sequentially weakly lower semicontinuous. Therefore, we can find $\widehat{u}_0\in W_0^{1,p(z)}(\Omega )$ such that

$$\begin{aligned} \widehat{\zeta }_\lambda (\widehat{u}_0)=\min \left[ \widehat{\zeta }_\lambda (u): u\in W_0^{1,p(z)}(\Omega )\right] . \end{aligned}$$

(4.22)

From (4.21) and the anisotropic regularity theory, we have

$$\begin{aligned} K_{\widehat{\zeta }_\lambda }\subseteq [u_\mu , u_\delta ]\cap \mathrm {int}\, C_+. \end{aligned}$$

(4.23)

From (4.22), (4.21) and (4.20), we see that

$$\begin{aligned}u_0,\widehat{u}_0\in K_{\widehat{\zeta }_\lambda }.\end{aligned}$$

If $u_0\ne \widehat{u}_0$, then we already have two positive smooth solutions of ($\mathrm {P}_\lambda$) and so we are done. Thus we may assume that

$$\begin{aligned} u_0=\widehat{u}_0. \end{aligned}$$

(4.24)

We consider the Carathéodory function $\beta _\lambda :\Omega \times \mathbb {R}\rightarrow \mathbb {R}$ defined by

$$\begin{aligned} \beta _\lambda (z,x)={\left\{ \begin{array}{ll} \lambda u_\mu (z)^{-\eta (z)}+f(z,u_\mu (z)) &{} \text {if } x\le u_\mu (z)\\ \lambda x^{-\eta (z)}+f(z,x) &{} \text {if } u_\mu (z)<x \end{array}\right. }. \end{aligned}$$

(4.25)

We set $B_\lambda (z,x)=\int _0^x \beta _\lambda (z,s)\,\mathrm {d}s$ and consider the $C^1$-functional $\zeta _\lambda : W_0^{1,p(z)}(\Omega )\rightarrow \mathbb {R}$ defined by

$$\begin{aligned}&\zeta _\lambda (u)=\int _\Omega \frac{1}{p(z)}|Du|^{p(z)}\,\mathrm {d}z+\int _\Omega \frac{1}{q(z)}|Du|^{q(z)}\,\mathrm {d}z-\int _\Omega B_\lambda (z,u)\,\mathrm {d}z\quad \\&\quad \text {for all } u\in W_0^{1,p(z)}(\Omega ). \end{aligned}$$

From (4.21) and (4.25), we see that

$$\begin{aligned} \zeta _\lambda \Big |_{[0,u_\delta ]} = \widehat{\zeta }_\lambda \Big |_{[0,u_\delta ]}. \end{aligned}$$

(4.26)

Combining (4.24), (4.22), (4.20) and (4.26), we see that

$$\begin{aligned}&u_0\text { is a local } C_0^1(\overline{\Omega })\text {-minimizer of } \zeta _\lambda (\cdot ),\nonumber \\&\qquad \Rightarrow \quad u_0\text { is a local } W_0^{1,p(z)}(\Omega )\text {-minimizer of } \zeta _\lambda (\cdot )\nonumber \\&\qquad \text {(see Gasi}\acute{\mathrm{n}}\text {ski-Papageorgiou [8], Proposition 3.3).} \end{aligned}$$

(4.27)

From (4.25), it follows that $K_{\zeta _\lambda }\subseteq [u_\mu )\cap \mathrm {int}\, C_+$. So, we may assume that $K_{\zeta _\lambda }$ is finite or otherwise we already have an infinity of positive smooth solutions of ($\mathrm {P}_\lambda$) and so we are done. Then, from (4.27) and using Theorem 5.7.6, p. 449, of [15], we can find $\rho \in (0,1)$ small such that

$$\begin{aligned} \zeta _\lambda (u_0)<\inf \left[ \zeta _\lambda (u): \Vert u-u_0\Vert =\rho \right] = m_\lambda . \end{aligned}$$

(4.28)

If $u\in \mathrm {int}\, C_+$, then on account of hypothesis $\mathrm {H}_1$(ii), we have

$$\begin{aligned} \zeta _\lambda (tv)\rightarrow -\infty \text { as } t\rightarrow +\infty . \end{aligned}$$

(4.29)

Moreover, Proposition 4.1, of Gasiński–Papageorgiou [8], implies that

$$\begin{aligned} \zeta _\lambda (\cdot )\text { satisfies the C-condition.} \end{aligned}$$

(4.30)

Then (4.28), (4.29) and (4.30) permit the use of the mountain pass theorem. So, we can find $\widehat{u}\in W_0^{1,p(z)}(\Omega )$ such that

$$\begin{aligned}&\widehat{u}\in K_{\zeta _\lambda }\subseteq [u_\mu )\cap \mathrm {int}\, C_+,\quad \zeta _\lambda (u_0)<m_\lambda \le \zeta _\lambda (\widehat{u}),\\&\qquad \Rightarrow \quad \widehat{u}\in \mathrm {int}\, C_+ \text { is a positive solution of }(\mathrm {P}_\lambda ), \widehat{u}\ne u_0. \end{aligned}$$

$\square$

We produce a lower bound for the elements of $S_\lambda$. This will be helpful in proving the admissibility of the critical parameter $\lambda ^*$ and also in producing the minimal positive solution for every $\lambda \in \mathscr {L}$ (see Sect. 5).

Proposition 4.7

If hypotheses $\mathrm {H}_0$, $\mathrm {H}_1$ hold and $\lambda \in \mathscr {L}$, then $\overline{u}_\lambda \le u$ for all $u\in S_\lambda$.

Proof

Let $u\in S_\lambda \subseteq \mathrm {int}\, C_+$ and consider the Carathéodory function $\sigma : \Omega \times \mathring{\mathbb {R}}_+\rightarrow \mathring{\mathbb {R}}_+$ defined by

$$\begin{aligned} \sigma (z,x)={\left\{ \begin{array}{ll} x^{-\eta (z)} &{} \text {if }0<x\le u(z)\\ u(z)^{-\eta (z)} &{} \text {if }u(z)<x \end{array}\right. }. \end{aligned}$$

(4.31)

We consider the following Dirichlet problem

As in the proof of Proposition 3.1, via approximations and fixed point theory, we show that problem ($\mathrm {Au}_\lambda '$) as a unique positive solution

$$\begin{aligned} \widetilde{u}_\lambda \in [0,u]\cap \mathrm {int}\, C_+\quad \text {(see } (4.31)). \end{aligned}$$

From Proposition 3.1, it follows that

$$\begin{aligned}&\widetilde{u}_\lambda = \overline{u}_\lambda ,\\&\quad \Rightarrow \quad \overline{u}_\lambda \le u\quad \text {for all } u\in S_\lambda . \end{aligned}$$

$\square$

Using this bound, we can prove the admissibility of $\lambda ^*$.

Proposition 4.8

If hypotheses $\mathrm {H}_0$, $\mathrm {H}_1$ hold, then $\lambda ^*\in \mathscr {L}$.

Proof

Let $\{\lambda _n\}_{n\in \mathbb {N}}\subseteq \mathscr {L}$ such that $\lambda _n \uparrow \lambda ^*$. From Proposition 3.1, we know that $\overline{u}_{\lambda _1}\le \overline{u}_{\lambda _n}$ for all $n\in \mathbb {N}$. Also let $\widetilde{u}_{n+1}\in S_{\lambda _{n+1}}\subseteq \mathrm {int}\, C_+$. On account of Proposition 4.7, we have $\overline{u}_{\lambda _1}\le \widetilde{u}_{n+1}$. Then we can introduce the Carathéodory function $\widehat{l}_n: \Omega \times \mathbb {R}\rightarrow \mathbb {R}$ defined by

$$\begin{aligned} \widehat{l}_n(z,x)={\left\{ \begin{array}{ll} \lambda _n \overline{u}_{\lambda _1}(z)^{-\eta (z)}+f(z,x^+) &{} \text {if } x<\overline{u}_{\lambda _1}(z)\\ \lambda _n x^{-\eta (z)}+f(z,x) &{} \text {if } \overline{u}_{\lambda _1}(z)\le x\le \widetilde{u}_{n+1}(z)\\ \lambda _n \widetilde{u}_{n+1}(z)+f(z,\widetilde{u}_{n+1}(z)) &{} \text {if } \widetilde{u}_{n+1}(z)<x \end{array}\right. }. \end{aligned}$$

(4.32)

We set $\widehat{L}_n(z,x)=\int _0^x \widehat{l}_n(z,s)\,\mathrm {d}s$ and consider the $C^1$-functional $\widehat{\chi }_n: W_0^{1,p(z)}(\Omega )\!\rightarrow \mathbb {R}$ defined by

$$\begin{aligned}&\widehat{\chi }_n (u)=\int _\Omega \frac{1}{p(z)}|Du|^{p(z)}\,\mathrm {d}z+\int _\Omega \frac{1}{q(z)}|Du|^{q(z)}\,\mathrm {d}z-\int _\Omega \widehat{L}_n (z,u)\,\mathrm {d}z\quad \\&\quad \text {for all } u\in W_0^{1,p(z)}(\Omega ). \end{aligned}$$

From (4.32), we see that $\widehat{\chi }_n(\cdot )$ is coercive. Also it is sequentially weakly lower semicontinuous. Hence we can find $u_n\in W_0^{1,p(z)}(\Omega )$ such that

$$\begin{aligned}&\widehat{\chi }_n(u_n) = \min \left[ \widehat{\chi }_n(u): u\in W_0^{1,p(z)}(\Omega )\right] ,\nonumber \\&\quad \Rightarrow \quad \langle \widehat{\chi }_n'(u_n), h\rangle =0\quad \text {for all } h\in W_0^{1,p(z)}(\Omega ). \end{aligned}$$

(4.33)

If in (4.33) we use first the test function $h=(\overline{u}_{\lambda _1}-u_n)^+\in W_0^{1,p(z)}(\Omega )$ and then the test function $h=(u_n-\widetilde{u}_{n+1})^+\in W_0^{1,p(z)}(\Omega )$, then using (4.32) we obtain

$$\begin{aligned}&u_n\in [\overline{u}_{\lambda _1},\widetilde{u}_{n+1}],\\&\qquad \Rightarrow \quad u_n\in S_{\lambda _n}\subseteq \mathrm {int}\, C_+\quad \text {(see } .(4.32)). \end{aligned}$$

Let $l_n:\Omega \times \mathbb {R}\rightarrow \mathbb {R}$ be the Carathéodory function defined by

$$\begin{aligned} l_n(z,x)={\left\{ \begin{array}{ll} \lambda _n \overline{u}_{\lambda _1}(z)^{-\eta (z)}+f(z,x^+) &{} \quad \text {if } x\le \overline{u}_{\lambda _1}(z)\\ \lambda _n x^{-\eta (z)}+f(z,x) &{} \quad \text {if } \overline{u}_{\lambda _1}(z)<x \end{array}\right. }. \end{aligned}$$

(4.34)

We set $L_n(z,x)=\int _0^x l_n(z,s)\,\mathrm {d}s$ and consider the $C^1$-functional $\chi _n: W_0^{1,p(z)}(\Omega )\!\rightarrow \mathbb {R}$ defined by

$$\begin{aligned}&\chi _n(u)=\int _\Omega \frac{1}{p(z)}|Du|^{p(z)}\,\mathrm {d}z+\int _\Omega \frac{1}{q(z)}|Du|^{q(z)}\,\mathrm {d}z-\int _\Omega L_n(z,u)\,\mathrm {d}z\quad \\&\quad \text {for all } u\in W_0^{1,p(z)}(\Omega ). \end{aligned}$$

From (4.32) and (4.34), we see that

$$\begin{aligned} \chi _n\Big |_{[0,\widetilde{u}_{n+1}]}=\widehat{\chi }_n\Big |_{[0,\widetilde{u}_{n+1}]},\qquad \chi _n'\Big |_{[0,\widetilde{u}_{n+1}]}=\widehat{\chi }_n'\Big |_{[0,\widetilde{u}_{n+1}]}. \end{aligned}$$

(4.35)

Also we have

$$\begin{aligned} \widehat{\chi }_n(u_n) \le \widehat{\chi _n}(\overline{u}_{\lambda _1})\le & {} \frac{1}{q_-}\left[ \rho _p(D \overline{u}_{\lambda _1}) +\rho _q (D\overline{u}_{\lambda _1})\right] -\int _\Omega \lambda _n \overline{u}_{\lambda _1}^{1-\eta (z)}\,\mathrm {d}z\quad \text {(since } f\ge 0)\\\le & {} \frac{1}{q_-}\left[ \rho _p(D \overline{u}_{\lambda _1}) +\rho _q (D\overline{u}_{\lambda _1})\right] -\int _\Omega \lambda _1 \overline{u}_{\lambda _1}^{1-\eta (z)}\,\mathrm {d}z \quad \text {(since } \lambda _1\le \lambda _n)\\\le & {} \frac{1}{q_-}\left[ \rho _p(D \overline{u}_{\lambda _1}) +\rho _q (D\overline{u}_{\lambda _1})\right] - \left[ \rho _p(D \overline{u}_{\lambda _1}) +\rho _q (D\overline{u}_{\lambda _1})\right] \\&\text {(see Proposition }3.1)\\< & {} 0 \quad \text {(since } 1<q_-). \end{aligned}$$

Then, from (4.35) we have

$$\begin{aligned} \chi _n'(u_n)=0\quad \text {and}\quad \chi _n(u_n)<0\;\text {for all } n\in \mathbb {N}. \end{aligned}$$

(4.36)

As in Proposition 4.1 of Gasiński–Papageorgiou [8], from (4.36) we deduce that

$$\begin{aligned}&u_n\rightarrow u_*\text { in } W_0^{1,p(z)}(\Omega ),\\&\Rightarrow \quad \langle A_{p(z)}(u_*),h\rangle + \langle A_{q(z)}(u_*),h\rangle = \int _\Omega \left[ \lambda ^* u_*^{-\eta (z)}+f(z,u_*)\right] h\,\mathrm {d}z\\&\quad \text {for all } h\in W_0^{1,p(z)}(\Omega ) \end{aligned}$$

and

$$\begin{aligned}\overline{u}_{\lambda _1}\le u_*.\end{aligned}$$

Therefore $u_*\in S_{\lambda ^*}\subseteq \mathrm {int}\, C_+$ and so $\lambda ^*\in \mathscr {L}$. $\square$

So, we have proved that

$$\begin{aligned}\mathscr {L}=(0,\lambda ^*].\end{aligned}$$

We can state the following bifurcation-type theorem about the positive solutions of problem ($\mathrm {P}_\lambda$).

Theorem 4.9

If hypotheses $\mathrm {H}_0$, $\mathrm {H}_1$ hold, then there exists $\lambda ^*>0$ such that

• (a) for all $\lambda \in (0,\lambda ^*)$ problem ($\mathrm {P}_\lambda$) has at least two positive solutions $u_0,\widehat{u}\in \mathrm {int}\, C_+$, $u_0\ne \widehat{u}$;

• (b) for $\lambda =\lambda ^*$ problem ($\mathrm {P}_\lambda$) has at least one positive solution $u_*\in \mathrm {int}\, C_+$;

• (c) for all $\lambda >\lambda ^*$ problem ($\mathrm {P}_\lambda$) has no positive solutions.

5 Minimal Positive Solution

In this section, we show that for every $\lambda \in \mathscr {L}=(0,\lambda ^*]$ problem ($\mathrm {P}_\lambda$) has a smallest positive solution $u_\lambda ^*\in \mathrm {int}\, C_+$ (minimal - or barrier - positive solution) and we prove the monotonicity and continuity properties of the map $\lambda \mapsto u_\lambda ^*$.

Proposition 5.1

If hypotheses $\mathrm {H}_0$, $\mathrm {H}_1$ hold and $\lambda \in \mathscr {L}=(0,\lambda ^*]$, then problem ($\mathrm {P}_\lambda$) has a smallest positive solution $u_\lambda ^*\in \mathrm {int}\, C_+$ (that is, $u_\lambda ^*\le u$ for all $u\in S_\lambda$).

Proof

From Papageorgiou–Rădulescu–Repovš [16] (see the proof of Proposition 7) we have that $S_\lambda$ is downward directed (that is, if $u_1,u_2\in S_\lambda$, then we can find $u\in S_\lambda$ such that $u\le u_1$, $u\le u_2$). Invoking Lemma 3.10, p. 178, of Hu–Papageorgiou [12], we can find a decreasing sequence $\{u_n\}_{n\in \mathbb {N}}\subseteq S_\lambda \subseteq \mathrm {int}\, C_+$ such that

$$\begin{aligned}\inf S_\lambda =\inf _{n\in \mathbb {N}} u_n.\end{aligned}$$

We have

$$\begin{aligned}&\overline{u}_\lambda \le u_n\le u_1\quad \text {for all } n\in \mathbb {N}\text { (see Proposition }4.7), \end{aligned}$$

(5.1)

$$\begin{aligned}&\langle A_{p(z)}(u_n), h\rangle + \langle A_{q(z)}(u_n), h\rangle = \int _\Omega \left[ \lambda u_n^{-\eta (z)}+f(z,u_n)\right] h\,\mathrm {d}z\quad \nonumber \\&\text {for all } h\in W_0^{1,p(z)}(\Omega ),\text { all } n\in \mathbb {N}. \end{aligned}$$

(5.2)

From (5.1) and (5.2), it follows that

$$\begin{aligned} \{u_n\}_{n\in \mathbb {N}} \subseteq W_0^{1,p(z)}(\Omega )\text { is bounded.} \end{aligned}$$

(5.3)

From (5.3) and Proposition 2.2 (in particular the $(S)_+$-property), we obtain

$$\begin{aligned}&u_n\rightarrow u_\lambda ^*\text { in } W_0^{1,p(z)}(\Omega ),\\&\qquad \Rightarrow \quad \langle A_{p(z)}(u_\lambda ^*), h\rangle + \langle A_{q(z)}(u_\lambda ^*), h\rangle \\&\quad = \int _\Omega \left[ \lambda (u_\lambda ^*)^{-\eta (z)}+f(z,u_\lambda ^*)\right] h\,\mathrm {d}z\quad \text {for all } h\in W_0^{1,p(z)}(\Omega ), \end{aligned}$$

and

$$\begin{aligned} \overline{u}_\lambda \le u_\lambda ^*. \end{aligned}$$

Therefore we conclude that

$$\begin{aligned} u_\lambda ^*\in S_\lambda \subseteq \mathrm {int}\, C_+\quad \text {and}\quad u_\lambda ^*=\inf S_\lambda . \end{aligned}$$

$\square$

We consider the map $\lambda \mapsto u_\lambda ^*$ from $\mathscr {L}=(0,\lambda ^*]$ into $\mathrm {int}\, C_+$. We will say that this map is strictly increasing if $0<\lambda <\lambda '\le \lambda ^*$, then $u_{\lambda '}^*-u_\lambda ^*\in \mathrm {int}\, C_+$.

Proposition 5.2

If hypotheses $\mathrm {H}_0$, $\mathrm {H}_1$ hold, then minimal solution map $\lambda \mapsto u_\lambda ^*$ is

• (a) strictly increasing;

• (b) left continuous.

Proof

• (a) Let $0<\lambda <\lambda '\le \lambda ^*$. From Proposition 4.4, we know that we can find $u_\lambda \in S_\lambda \subseteq \mathrm {int}\, C_+$ such that $u_{\lambda '}^*-u_\lambda \in \mathrm {int}\, C_+$. Since $u_\lambda ^*\le u_\lambda$, it follows that $u_{\lambda '}^*-u_\lambda ^*\in \mathrm {int}\, C_+$ and this proves that the minimal solution map is strictly increasing.

• (b) Let $\{\lambda _n\}_{n\in \mathbb {N}}\subseteq \mathscr {L}=(0,\lambda ^*]$ such that $\lambda _n\rightarrow \lambda ^-$. We have

  $$\begin{aligned}&u_{\lambda _1}^* \le u_{\lambda _n}^*\le u_\lambda ^*\quad \text {for all } n\in \mathbb {N}\text { (see (a))}, \end{aligned}$$

  (5.4)
  $$\begin{aligned}&\Rightarrow \quad \{u_{\lambda _n}^*\}_{n\in \mathbb {N}}\subseteq W_0^{1,p(z)}(\Omega ). \end{aligned}$$

  (5.5)

  From (5.4) and the anisotropic regularity theory (see [22]), we have that $\{u_{\lambda _n}^*\}_{n\in \mathbb {N}}\subseteq C_0^{1,\alpha }(\overline{\Omega })$ is bounded with $\alpha \in (0,1)$ and $C_0^{1,\alpha }(\overline{\Omega })=C^{1,\alpha }(\overline{\Omega })\cap C_0^1(\overline{\Omega })$. From the compact embedding of $C_0^{1,\alpha }(\overline{\Omega })$ into $C_0^1(\overline{\Omega })$, it follows that we may assume that at least for a subsequence we have

  $$\begin{aligned} u_{\lambda _n}^*\rightarrow \widetilde{u}_\lambda \text { in } C_0^1(\overline{\Omega }). \end{aligned}$$

  Suppose $\widetilde{u}_\lambda \ne u_\lambda ^*$. Then we can find $z_0\in \Omega$ such that

  $$\begin{aligned}&u_\lambda ^*(z_0)<\widetilde{u}_\lambda (z_0),\\&\qquad \Rightarrow \quad u_\lambda ^*(z_0)<u_{\lambda _n}^*(z_0)\quad \text {for all } n\ge n_0, \end{aligned}$$

  which contradicts (a). So, $\widetilde{u}_\lambda = u_\lambda ^*$ and by Urysohn’s criterion for the convergence of sequences, we infer that for the initial sequence we have

  $$\begin{aligned}&u_{\lambda _n}^*\rightarrow u_\lambda ^*\text { in } C_0^1(\overline{\Omega }),\\&\qquad \Rightarrow \quad \lambda \rightarrow u_\lambda ^*\text { is left continuous.} \end{aligned}$$

$\square$

So, we can state the following theorem for the minimal positive solutions of problem ($\mathrm {P}_\lambda$).

Theorem 5.3

If hypotheses $\mathrm {H}_0$, $\mathrm {H}_1$ hold, then for every $\lambda \in \mathscr {L}=(0,\lambda ^*]$ problem ($\mathrm {P}_\lambda$) has a smallest positive solution (minimal positive solution) $u_\lambda ^*\in \mathrm {int}\, C_+$ and the minimal solution map $\lambda \mapsto u_\lambda ^*$ from $\mathscr {L}$ into $\mathrm {int}\, C_+$ is strictly increasing and left continuous.