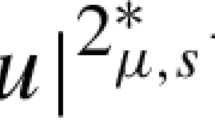Abstract
This paper is concerned with the following one-dimensional fractional Choquard equation
where \((-\Delta )^{1/2}\) denotes the 1/2-Laplacian opertor, \(I_{\mu }\) is the Riesz potential with \(0<\mu <1\), V is a continuous real function satisfying some mild assumptions and \(f\in {\mathcal {C}}(\mathbb {R},\mathbb {R})\) is a nonlinearity with exponential critical growth. The present paper has three typical features. Firstly, using a weaker assumption on f, we establish the energy inequality to recover the compactness. Second, without the strictly monotone condition and by establishing some new tricks, we obtain the existence of ground state solutions when \(\varepsilon \) is small enough. Finally, we take advantage of some refined analysis techniques to get over the difficulty carried by the nonlocality of the 1/2-Laplacian and prove the concentration of the ground state solutions when \(\varepsilon \rightarrow 0\). Our results extend and complement the results of Alves et al. (J Differ Equ 261:1933–1972, 2016) and Clemente et al. (Z Angew Math Phys 72:16, 2021].
Similar content being viewed by others
References
Ackermann, N.: On a periodic Schrödinger equation with nonlocal superlinear part. Math. Z. 248, 423–443 (2004)
Alves, C.O., Cassani, D., Tarsi, C., Yang, M.B.: Existence and concentration of ground state solutions for a critical nonlocal Schrödinger equation in \({\mathbb{R} }^{2}\). J. Differ. Equ. 261, 1933–1972 (2016)
Alves, C.O., Figueiredo, G.M.: Multiplicity of positive solutions for a class of quasilinear problems in \({\mathbb{R} }^{N}\) via penalization method. Adv. Nonlinear Stud. 5, 551–572 (2005)
Alves, C.O., do Ó, J. M., Miyagaki, O. H.: Concentration phenomena for fractional elliptic equations involving exponential critical growth. Adv. Nonlinear Stud. 16, 843–861 (2016)
Alves, C.O., Ledesma, C.T.: Multiplicity of solutions for a class of fractional elliptic problems with critical exponential growth and nonlocal Neumann condition. Commun. Pure. Appl. Anal. 20, 2065–2100 (2021)
Alves, C.O., Yang, M.: Multiplicity and concentration behavior of solutions for a quasilinear Choquard equation via penalization method. Proc. R. Soc. Edinburgh Sect. A 146, 23–58 (2016)
Ambrosio, V.: Multiplicity and concentration results for a fractional Choquard equation via penalization method. Potent. Anal. 50, 55–82 (2019)
Caffarelli, L., Silvestre, L.: An extension problems related to the fractional Laplacian. Commun. Partial Differ. Equ. 32, 1245–1260 (2007)
Chen, S., Tang, X.: On the planar Schrödinger equation with indefinite linear part and critical growth nonlinearity. Calc. Var. Partial Differ. Equa. 60, 95 (2021)
Chen, P., Tang X.: Ground states for a system of nonlinear Schrödinger equations with singular potentials. Discret. Contin. Dyn. Syst. https://doi.org/10.3934/dcds.2022088
Chen, P., Meng, L., Tang X.: Nonstationary homoclinic orbit for an infinite-dimensional fractional reaction-diffusion system. Discret. Contin. Dyn. Syst. Ser. B. https://doi.org/10.3934/dcdsb.2021279
Cingolani, S., Secchi, S., Squassina, M.: Semi-classical limit for Schrödinger equations with magnetic field and Hartree-type nonlinearities. Proc. R. Soc. Edinbur. Sect. A 140, 973–1009 (2010)
Clemente, R., de Albuquerque, J.C., Barboza, E.: Existence of solutions for a fractional Choquard-type equation in \({\mathbb{R}}\) with critical exponential growth. Z. Angew. Math. Phys. 72, 16 (2021)
Di Nezza, E., Palatucci, G., Valdinoci, E.: Hitchhiker’s guide to the fractional Sobolev spaces. Bull. Sci. Math. 136, 521–573 (2012)
do Ó, J. M., Miyagaki, O. H., Squassina, M.: Nonautonomous fractional problems with exponential growth,. Nonlinear Differ. Equ. Appl. 22, 1395–1410 (2015)
Ekeland, I.: On the variational principle. J. Math. Anal. Appl. 47, 324–353 (1974)
Floer, A., Weinstein, A.: Nonspreading wave pachets for the packets for the cubic Schrödinger with a bounded potential. J. Funct. Anal. 69, 397–408 (1986)
Frank, R., Lenzmann, E.: Uniqueness of non-linear ground states for fractional laplacians in \({\mathbb{R} }\). Acta Math. 210, 261–318 (2013)
Gao, Z., Tang, X., Chen, S.: On existence and concentration behavior of positive ground state solutions for a class of fractional Schrödinger-Choquard equations. Z. Angew. Math. Phys. 69, 122 (2018)
Giacomoni, J., Mishra, P.K., Sreenadh, K.: Fractional elliptic equations with critical exponential nonlinearity. Adv. Nonlinear Anal. 5, 57–74 (2016)
Iula, S., Maalaoui, A., Martinazzi, L.: A fractional Moser–Trudinger type inequality in one dimension and its critical points. Differ. Integral Equ. 29, 455–492 (2016)
Kozono, H., Sato, T., Wadade, H.: Upper bound of the best constant of a Trudinger–Moser inequality and its application to a Gagliardo–Nirenberg inequality. Indiana Univ. Math. J. 55, 1951–1974 (2006)
Laskin, N.: Fractional quantum mechanics and Lévy path integrals. Phys. Lett. A 268(4–6), 298–305 (2000)
Laskin, N.: Fractional Schrödinger equation. Phys. Rev. E 66, 056108 (2002)
Lieb, E.H.: Existence and uniqueness of the minimizing solution of Choquard’s nonlinear equation. Stud. Appl. Math. 57, 93–105 (1976)
Lin, G.H., Yu, J.S.: Homoclinic solutions of periodic discrete Schrödinger equations with local superquadratic conditions. SIAM J. Math. Anal. 54, 1966–2005 (2022)
Lions, P.L.: The Choquard equation and related questions. Nonlinear Anal. 4, 1063–1072 (1980)
Ma, L., Zhao, L.: Classification of positive solitary solutions of the nonlinear Choquard equation. Arch. Ration. Mech. Anal. 195, 455–467 (2010)
Mattner, L.: Strict definiteness of integrals via complete monotonicity of derivatives. Trans. Am. Math. Soc. 349, 3321–3342 (1997)
Molica Bisci, G., Rădulescu, V.D., Servadei, R.: Variational Methods for Nonlocal Fractional Problems. Encyclopedia of Mathematics and Its Applications, vol. 162. Cambridge University Press, Cambridge (2016)
Moroz, V., Van Schaftingen, J.: Groundstates of nonlinear Choquard equations: existence, qualitative properties and decay asymptotics. J. Funct. Anal. 265, 153–184 (2013)
Moroz, V., Van Schaftingen, J.: Existence of ground states for a class of nonlinear Choquard equations. Trans. Am. Math. Soc. 367, 6557–6579 (2015)
Moroz, V., Van Schaftingen, J.: A guide to the Choquard equation. J. Fixed Point Theory Appl. 19, 773–813 (2017)
Moser, J.: A new proof de Giorgi’s theorem concerning the regularity problem for elliptic differential equations. Commun. Pure Appl. Math. 13, 457–468 (1960)
Ozawa, T.: On critical cases of Sobolev’s inequalities. J. Funct. Anal. 127, 259–269 (1995)
Pekar, S.: Untersuchungüber die Elektronentheorie der Kristalle. Akademie Verlag, Berlin (1954)
Qin, D., Rădulescu, V.D., Tang, X.: Ground states and geometrically distinct solutions for periodic Choquard–Pekar equations. J. Differ. Equ. 275, 652–683 (2021)
Qin, D., Tang, X.: On the planar Choquard equation with indefinite potential and critical exponential growth. J. Differ. Equ. 285, 40–98 (2021)
Qin, D., Tang, X., Zhang, J.: Ground states for planar Hamiltonian elliptic systems with critical exponential growth. J. Differ. Equ. 308, 130–159 (2022)
Rabinowitz, P.: On a class of nonlinear Schrödinger equations. Z. Angew. Math. Phys. 43, 270–291 (1992)
Su, Y., Wang, L., Chen, H.B., Liu, S.L.: Multiplicity and concentration results for fractional Choquard equations: doubly critical case. Nonlinear Anal. 198, 37 (2020)
Takahashi, F.: Critical and subcritical fractional Trudinger+-Moser-type inequalities on \({\mathbb{R} }\). Adv. Nonlinear Anal. 8, 868–884 (2019)
Wei, J., Winter, M.: Strongly interacting bumps for the Schrödinger–Newton equations. J. Math. Phys. 50,(2009)
Willem, M.: Minimax Theorems, Progress in Nonlinear Differential Equations and Their Applications, vol. 24. Birkhäuser Boston Inc., Boston (1996)
Yang, Z.P., Zhao, F.K.: Multiplicity and concentration behaviour of solutions for a fractional Choquard equation with critical growth. Adv. Nonlinear Anal. 10, 732–774 (2021)
Zhang, L.M., Liao, F.F., Tang, X.H., Qin, D.D.: Ground states for singularly perturbed planar Choquard equation with critical exponential growth. J. Nonl. Mod. Anal. https://doi.org/10.12150/jnma.2023.1
Zhang, Y.P., Tang, X.H., Rădulescu, V.D.: Anisotropic Choquard problems with Stein–Weiss potential: nonlinear patterns and stationary waves. C. R. Math. Acad. Sci. Paris 359, 959–968 (2021)
Zhang, W., Yuan, S., Wen, L.: Existence and concentration of ground-states for fractional Choquard equation with indefinite potential. Adv. Nonlinear Anal. 11, 1552–1578 (2022)
Zhang, W., Zhang, J., Mi, H.: Ground states and multiple solutions for Hamiltonian elliptic system with gradient term. Adv. Nonlinear Anal. 10, 331–352 (2021)
Zhang, W., Zhang, J.: Multiplicity and concentration of positive solutions for fractional unbalanced double phase problems. J. Geom. Anal. 32, 235 (2022)
Zhang, J., Zhang, W.: Semiclassical states for coupled nonlinear Schrödinger system with competing potentials. J. Geom. Anal. 32, 114 (2022)
Zhang, J., Zhang, W., Rădulescu, V.D.: Double phase problems with competing potentials: concentration and multiplication of ground states. Math. Z. 301, 4037–4078 (2022)
Acknowledgements
The research of the first two authors is partially supported by the National Natural Science Foundation of China (No. 11971485) and the Fundamental Research Funds for the Central Universities of Central South University (No. 2021zzts0036). The research of Jian Zhang is supported by Natural Science Foundation of Hunan Province (2021JJ30189, 2022JJ30200), the Key project of Scientific Research Project of Department of Education of Hunan Province (21A0387). This paper has been completed while Shuai Yuan & Jian Zhang were visiting the University of Craiova (Romania) with the financial support of the China Scholarship Council (No. 202106370097, 201908430218). Shuai Yuan and Jian Zhang would like to thank the China Scholarship Council and the Embassy of the People’s Republic of China in Romania.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
To supplement the proof of Lemma 17, in this section we collect some preliminary facts. First of all, we denote the upper half-space in \(\mathbb {R}^{2}\) by \(\mathbb {R}_{+}^{2}=\{(x,y)\in \mathbb {R}^{2}:y>0\}\). Define the following:
The space \(X^{1}(\mathbb {R}_{+}^{2})\) is given by the completion of \(C_{0}^{\infty }(\overline{\mathbb {R}_{+}^{2}})\) with the norm \(\Vert \cdot \Vert ^{\varepsilon }\), that is
Moreover, we denote by \(\Vert \cdot \Vert \) the usual norm in \(X^{1}(\mathbb {R}_{+}^{2})\), that is
Note that the potential V is bounded from above and below, it is easy to verify that \(\Vert \cdot \Vert ^{\varepsilon }\) and \(\Vert \cdot \Vert \) are equivalent norms in \(X^{1}(\mathbb {R}_{+}^{2})\). Using the above definition, we see that if \(v\in X^{1}(\mathbb {R}_{+}^{2})\), then \(u(x)=v(x,0)\) belongs to \(H^{1/2}(\mathbb {R})\) and
Since \(H^{1/2}(\mathbb {R})\) is continuously embedding into \(L^{q}(\mathbb {R})\) for all \(q\ge 2\), c.f. [14, Theorem 6.9], it follows that \(X^{1}(\mathbb {R}_{+}^{2})\) is also continuously embedded into \(L^{q}(\mathbb {R})\) for all \(q\ge 2\). Moreover, the embeddings
are compact for any bounded measurable set \(A\subset \mathbb {R}\). See [18, Proposition 3.6] also [15, Remark 2.1].
Next, we will give a brief introduction with the technique used in the proof of Lemma 17, using the change of variable \(u(x)=v(\varepsilon x)\), it is easy to know that Problem (4) is equivalent to the problem
Hereafter, we will use the method due to Caffarelli and Silvestre in [8] to seek the solution of (47), more exactly, due to Frank and Lenzmann [18] for a whole line. In the seminal above papers, were developed a local interpretation of the fractional Laplacian given in \(\mathbb {R}\) by considering a Dirichlet to Neumann type operator in the domain \(\mathbb {R}_{+}^{2}=\{(x,t)\in \mathbb {R}^{2}:t>0\}\). For \(u\in H^{1/2}(\mathbb {R})\), the solution \(w\in X^{1}(\mathbb {R}_{+}^{2})\) of
is called \(1/2-\)harmonic extension \(w=E_{1/2}(u)\) of u and it is proved in [8] that
To get a solution for the nonlocal Problem (47), we can study the existence of solutions for the local problem defined on the upper half plane
where
We finally emphasize that u is the solution of (47), if and only if, \(u=v(x,0)\) for all \(x\in \mathbb {R}\), where v is some critical point of the corresponding energy functional of (48).
Rights and permissions
Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Yuan, S., Tang, X., Zhang, J. et al. Semiclassical States of Fractional Choquard Equations with Exponential Critical Growth. J Geom Anal 32, 290 (2022). https://doi.org/10.1007/s12220-022-01024-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s12220-022-01024-9
Keywords
- Fractional Choquard equation
- Semiclassical states
- Critical exponential growth
- Trudinger-Moser inequality