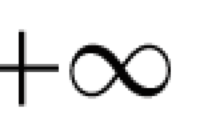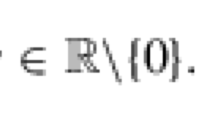Skip to main content
SpringerLink
Log in

Uniqueness of non-linear ground states for fractional Laplacians in \({\mathbb{R}}\)

  • Published:
Acta Mathematica

Abstract

We prove uniqueness of ground state solutions Q = Q(|x|) ≥ 0 of the non-linear equation

$$(-\Delta)^s Q+Q-Q^{\alpha+1}= 0 \quad {\rm in} \, \mathbb{R},$$

where 0 < s < 1 and 0 < α < 4s/(1−2s) for \({s<\frac{1}{2}}\) and 0 < α < ∞ for \({s\geq \frac{1}{2}}\). Here (−Δ)s denotes the fractional Laplacian in one dimension. In particular, we answer affirmatively an open question recently raised by Kenig–Martel–Robbiano and we generalize (by completely different techniques) the specific uniqueness result obtained by Amick and Toland for \({s=\frac{1}{2}}\) and α = 1 in [5] for the Benjamin–Ono equation.

As a technical key result in this paper, we show that the associated linearized operator L + = (−Δ)s+1−(α+1)Q α is non-degenerate; i.e., its kernel satisfies ker L + = span{Q′}. This result about L + proves a spectral assumption, which plays a central role for the stability of solitary waves and blowup analysis for non-linear dispersive PDEs with fractional Laplacians, such as the generalized Benjamin–Ono (BO) and Benjamin–Bona–Mahony (BBM) water wave equations.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Abdelouhab L., Bona J. L., Felland M., Saut J.-C.: Nonlocal models for nonlinear, dispersive waves. Phys. D, 40, 360–392 (1989)

    Article  MathSciNet  MATH  Google Scholar 

  2. Abramowitz, M. & Stegun, I. A., Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. National Bureau of Standards Applied Mathematics Series, 55. U.S. Government Printing Office, Washington, DC, 1972.

  3. Albert J.P., Bona J.L.: Total positivity and the stability of internal waves in stratified fluids of finite depth. IMA J. Appl. Math., 46, 1–19 (1991)

    Article  MathSciNet  MATH  Google Scholar 

  4. Albert J.P., Bona J.L., Saut J.-C.: Model equations for waves in stratified fluids. Proc. Roy. Soc. London Ser. A, 453, 1233–1260 (1997)

    Article  MathSciNet  MATH  Google Scholar 

  5. Amick C.J., Toland J.F.: Uniqueness and related analytic properties for the Benjamin–Ono equation—a nonlinear Neumann problem in the plane. Acta Math., 167, 107–126 (1991)

    Article  MathSciNet  MATH  Google Scholar 

  6. Bañuelos R., Kulczycki T.: The Cauchy process and the Steklov problem. J. Funct. Anal., 211, 355–423 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  7. Bennett D.P., Brown R.W., Stansfield S.E., Stroughair J.D., Bona J.L.: The stability of internal solitary waves. Math. Proc. Cambridge Philos. Soc., 94, 351–379 (1983)

    Article  MathSciNet  MATH  Google Scholar 

  8. Blumenthal R.M., Getoor R.K.: Some theorems on stable processes. Trans. Amer. Math. Soc., 95, 263–273 (1960)

    Article  MathSciNet  MATH  Google Scholar 

  9. Caffarelli L., Silvestre L.: An extension problem related to the fractional Laplacian. Comm. Partial Differential Equations, 32, 1245–1260 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  10. Carmona R., Masters W.C., Simon B.: Relativistic Schrödinger operators: asymptotic behavior of the eigenfunctions. J. Funct. Anal., 91, 117–142 (1990)

    Article  MathSciNet  MATH  Google Scholar 

  11. Chang S.-M., Gustafson S., Nakanishi K., Tsai T.-P.: Spectra of linearized operators for NLS solitary waves. SIAM J. Math. Anal., 39, 1070–1111 ((2007/08))

    Article  MathSciNet  Google Scholar 

  12. Chang S.-Y.A., González M.d.M.: Fractional Laplacian in conformal geometry. Adv. Math., 226, 1410–1432 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  13. Chen W., Li C., Ou B.: Classification of solutions for an integral equation. Comm. Pure Appl. Math., 59, 330–343 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  14. Elgart A., Schlein B.: Mean field dynamics of boson stars. Comm. Pure Appl. Math., 60, 500–545 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  15. Frank, R. L., Lenzmann, E. & Seiringer, R., Uniqueness of radial solutions for the fractional Laplacian. Preprint, 2013. arXiv:1302.2652 [math.AP].

    Google Scholar 

  16. Frank R. L., Seiringer R.: Non-linear ground state representations and sharp Hardy inequalities. J. Funct. Anal., 255, 3407–3430 (2008)

    Article  MathSciNet  Google Scholar 

  17. Fröhlich J., Lenzmann E.: Blowup for nonlinear wave equations describing boson stars. Comm. Pure Appl. Math., 60, 1691–1705 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  18. González M.d.M.: Gamma convergence of an energy functional related to the fractional Laplacian. Calc. Var. Partial Differential Equations, 36, 173–210 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  19. Graham C.R., Zworski M.: Scattering matrix in conformal geometry. Invent. Math., 152, 89–118 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  20. Kenig C.E., Martel Y., Robbiano L.: Local well-posedness and blow-up in the energy space for a class of L2 critical dispersion generalized Benjamin–Ono equations. Ann. Inst. H. Poincaré Anal. Non Linéaire, 28, 853–887 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  21. Kwong M. K.: Uniqueness of positive solutions of Δu−u + u p = 0 in R n. Arch. Ration. Mech. Anal., 105, 243–266 (1989)

    Article  Google Scholar 

  22. Li Y.A., Bona J.L.: Analyticity of solitary-wave solutions of model equations for long waves. SIAM J. Math. Anal., 27, 725–737 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  23. Li Y.Y.: Remark on some conformally invariant integral equations: the method of moving spheres. J. Eur. Math. Soc. (JEMS), 6, 153–180 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  24. Lieb E.H., Yau H.-T.: The Chandrasekhar theory of stellar collapse as the limit of quantum mechanics. Comm. Math. Phys., 112, 147–174 (1987)

    Article  MathSciNet  MATH  Google Scholar 

  25. Lin Z.: Instability of nonlinear dispersive solitary waves. J. Funct. Anal., 255, 1191–1224 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  26. Ma L., Zhao L.: Classification of positive solitary solutions of the nonlinear Choquard equation. Arch. Ration. Mech. Anal., 195, 455–467 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  27. Maehara R.: The Jordan curve theorem via the Brouwer fixed point theorem. Amer. Math. Monthly, 91, 641–643 (1984)

    Article  MathSciNet  MATH  Google Scholar 

  28. Majda A.J., McLaughlin D.W., Tabak E.G.: A one-dimensional model for dispersive wave turbulence. J. Nonlinear Sci., 7, 9–44 (1997)

    Article  MathSciNet  MATH  Google Scholar 

  29. Maz′ya, V.G., Sobolev Spaces. Springer Series in Soviet Mathematics. Springer, Berlin– Heidelberg, 1985.

  30. McLeod K.: Uniqueness of positive radial solutions of Δu + f(u) = 0 in R n. II. Trans. Amer. Math. Soc., 339, 495–505 (1993)

    MathSciNet  MATH  Google Scholar 

  31. McLeod K., Serrin J.: Uniqueness of positive radial solutions of Δu + f(u) = 0 in R n. Arch. Ration. Mech. Anal., 99, 115–145 (1987)

    Article  MathSciNet  MATH  Google Scholar 

  32. Reed, M. & Simon, B., Methods of Modern Mathematical Physics. IV. Analysis of Operators. Academic Press, New York, 1978.

  33. Weinstein M.I.: Modulational stability of ground states of nonlinear Schrödinger equations. SIAM J. Math. Anal., 16, 472–491 (1985)

    Article  MathSciNet  MATH  Google Scholar 

  34. Weinstein M.I.: Existence and dynamic stability of solitary wave solutions of equations arising in long wave propagation. Comm. Partial Differential Equations, 12, 1133–1173 (1987)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Author notes

  1. Rupert L. Frank

    Present address: Mathematics 253-37, Caltech, Pasadena, CA, 91125, U.S.A.

  2. Enno Lenzmann

    Present address: Department of Mathematics and Computer Sciences, University of Basel, Rheinsprung 21, CH-4051, Basel, Switzerland

Authors and Affiliations

  1. Department of Mathematics, Princeton University, Washington Road, Princeton, NJ, 08544, U.S.A.

    Rupert L. Frank

  2. Institute for Mathematical Sciences, University of Copenhagen, Universitetsparken 5, DK-2100, Copenhagen Ø, Denmark

    Enno Lenzmann

Authors
  1. Rupert L. Frank
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Enno Lenzmann
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Rupert L. Frank.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Frank, R.L., Lenzmann, E. Uniqueness of non-linear ground states for fractional Laplacians in \({\mathbb{R}}\) . Acta Math 210, 261–318 (2013). https://doi.org/10.1007/s11511-013-0095-9

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11511-013-0095-9

Keywords

Search

Navigation