Introduction

Binary Ti-Al alloys represent unique combinations of properties such as a low density, ductility, high strength and toughness, good oxidation resistance and biocompatibility. Among these alloys, γ-\(TiAl\) intermediate phase with a temperature dependent solubility range of 46 < Al < 66.5 (in at %) is characterised by different microstructures, of which \({Ti}_{3}Al+TiAl\) mixture exhibits the outstanding mechanical and corrosion properties that can be further improved by adding Nb, Ta, V, Cr, B and / or other refractory metals. Ti-Al based industrial alloys cover a broad range of applications from structural, aerospace and automotive, protective coating, catalytic chemistry to biomedical uses (Lasalmonie 2006; Wu 2006; Chunxiang et al. 2011). The Ti-Al phase diagram has been assessed several times by means of the CALPHAD (CALculation of PHAse Diagrams) method (Saunders and Miodownik 1998). The last re-assessment (Witusiewicz et al. 2008a) includes the most recent high temperature measurements and, by using new experimental data-driven optimization, the Ti-Al phase equilibria have been reassessed in terms of the equilibrium temperatures and the compositions. Investigation of complex Ti-based alloys, involves the knowledge of their thermodynamic and thermophysical properties. The phase diagrams of multicomponent systems, such as the Al-B-Nb-Ti (Witusiewicz et al. 2008b, 2009a, b), the Al-Nb-Ti-Ta (Bondar et al. 2011) and the Al-Cr-Nb-Ti (Liu et al. 2014) together with their binary and ternary subsystems have been assessed. On the other side, high chemical reactivity of liquid Ti-based alloys in contact with container materials and / or oxygen leads to scarcity of thermophysical properties data (Iida and Guthrie 2015). To overcome this lack, over the last few decades, the measurements using containerless methods have been performed on different classes of liquid metallic materials (Mohr and Fecht 2022a) including Ti-based alloys (Mohr and Fecht 2022b). Thermophysical properties data of metallic melts are input for simulation of solidification, which is the key step of liquid assisted industrial processes, involving the modelling of mass transport during liquid-solid phase transition and microstructural evolution at the interface. In order to predict accurately material’s microstructure, reliable thermophysical properties data including the surface tension and viscosity are necessary (Fecht et al. 2005; Mohr and Fecht 2022a).

There are a few datasets on the thermophysical properties of ternary Ti-Al based alloys obtained by container-based (Nowak et al. 2010) and containerless methods (Egry et al. 2007, 2010a; Wunderlich 2008; Mohr et al. 2020; Mohr et al. 2022b). To determine the surface tension of the 46Ti-46Al-8Nb and 46Ti-46Al-8Ta alloys (Nowak et al. 2010), the method combining the pinned and sessile drop measurements in one experiment has been used. The surface tension of these ternary alloys (Egry et al 2007, 2010a; Nowak et al. 2010; Zhou et al. 2011) including the Ti64 (Ti-6Al-4 V, in wt % or Ti-10.2Al-3.6 V, in at %) has also been measured on ground by the oscillating drop using electromagnetic levitation as a tool for containerless processing (Egry et al. 2010a). Recently, the surface tension determination of liquid Ti64 alloy, under microgravity conditions on board parabolic flights (PF) (Wunderlich 2008) and on board of the International Space Station (ISS) (Mohr et al. 2020, 2023) was also done. Temperature dependent surface tension datasets of the alloys investigated obey a linear law. The surface tension experimental datasets of the abovementioned alloys were used to validate the models (Egry et al. 2010b) and exhibit a good agreement among them as well as with the corresponding calculated values. The viscosity of the 46Ti-46Al-8Nb and 46Ti-46Al-8Ta alloys has been measured using the oscillating drop method in electromagnetic levitation during PF (Wunderlich et al. 2018a) and a comparison with model predicted values was done.

Concerning the quaternary alloys, the surface tension and viscosity datasets of liquid 48Ti-48Al-2Cr-2Nb alloy (Wunderlich et al. 2018a, b, 2021) were analysed with respect to the Ti-Al system formed by the principal alloying elements and estimating the effects of the other alloy components on these properties. The surface tension of liquid Ti-Al alloys was calculated by the Compound Formation Model (CFM) and Quasi Chemical Approximation (QCA) for regular solutions (Novakovic et al. 2012). In addition, to obtain more precise model predicted values, the analysis was also performed with respect to the Ti-Al-Nb and Ti-Al-Cr ternary subsystems. In this case, to describe the surface tension of ternary alloys, the Butler model (Egry et al. 2010b; Costa et al. 2014) was used. Subsequently, the surface tension predicted values were compared among them and with the literature data (Wunderlich et al. 2021, 2018a, b; Egry et al. 2010b; Zhou et al. 2011). Preliminary test of the models (Budai et al. 2007; Terzieff 2008; Iida and Guthrie 2015; Wunderlich et al. 2021) applied to calculate the viscosity isotherm of liquid Ti-Al alloys, indicated the Terzieff model (Terzieff 2008) as the most appropriate. A comparison of the literature data among them (Wunderlich et al. 2021, 2018a, b) and with respect to the viscosity isotherm was done.

Nowadays, due to partial or total lack of theoretical models, able to explain and predict the surface tension and viscosity of quaternary and / or higher order alloy systems, the theoretical evaluation of the corresponding properties values is quantitative. Future perspective of models development may be related to the creation of databases containing available experimental datasets and corresponding model predicted values with the possibility to apply directly different theoretical models. For elaboration of properties data including their reliable predictions, a Multivariate analysis (MVA) involving multiple independent variables (more than two) and the relationships among them with possibility to compare different tests seems to be a useful tool (Nawer et al. 2023). Further step in property data predictions has to include a wide use of Machine Learning and more advanced Deep Learning with a neural network architecture implementation.

Experimental Methods

Surface tension and viscosity of liquid Ti-Al-Cr-Nb alloy were measured by containerless methods aiming to prevent any contaminations with crucible or substrate material. The measurements were performed under microgravity conditions using the oscillating drop method in an electromagnetic levitation on board a parabolic flight (PF) airplane (Wunderlich et al. 2018a) and on board of the International Space Station (ISS) (Wunderlich et al. 2021, 2018b). The measurement methods applied to obtain the surface tension and viscosity together with the corresponding experimental datasets of binary and ternary Ti-based alloys were summarized in (Mohr and Fecht 2022b).

Parabolic Flight (PF)

Parabolic flights were used for the measurements of the surface tension and the viscosity of liquid Ti-48Al-2Cr-2Nb (in at %) alloy (Wunderlich et al. 2018a). Both properties were measured by the oscillating drop method in an electromagnetic levitation (OD-EML), over a wide range of temperatures from the undercooling of about 100 K to 200 K above the liquidus temperature of the alloy and the data obtained in different parabolas exhibited a good reproducibility. Knowing that oxygen is the major impurity having a strong tensioactive effects on the surface tension (Egry et al. 2010b) and it can increase significantly the viscosity (Higuchi et al. 2007) of metallic melts, the process of monitoring operating conditions during experiments is well assessed. Therefore, a water and oxygen partial pressure of < 1 ppb were provided and, prior to the measurements, the sample chamber was pumped to a pressure of 10–5 Pa. During parabolic flights offering 20 s of reduced gravity in a single parabola, a large undercooling of Ti-based alloys allows to process the alloy sample from heating and being a liquid to a solid form. Data analysis of the surface tension and viscosity shows the experimental errors of about 7 and 20%, respectively (Wunderlich et al. 2018a).

International Space Station (ISS)

An alternative to the oscillating drop method in an electromagnetic levitation on board a parabolic flight (PF) airplane is the same method on board of the International Space Station (ISS). As previously mentioned, parabolic flights offer 20 s of microgravity and serve as an important precursor for long-time duration ISS experiments, of about 20 min. Therefore, only the long microgravity times on board the ISS allow the precise measurements of properties (Mohr et al. 2023; Mohr and Fecht 2022c). Accordingly, the surface tension and viscosity of liquid Ti-48Al-2Cr-2Nb alloy (in at %) were also measured on board of the ISS (Wunderlich et al. 2018b, 2021). EML appears to be more versatile regarding the large variety of materials as well as its applicability under different gas atmospheres and in vacuum. In the case of the processing by OD-EML in microgravity, the surface tension and viscosity data exhibit the experimental errors of about ± 0.6 and ± 2%, respectively, (Mohr and Fecht 2022c).

Regarding containerless measurements, it is important to mention that, the surface tension can be measured by OD-EML on ground and under microgravity conditions, while the viscosity measurements can only be performed in microgravity. Indeed, under microgravity, the reduction of levitation / positioning forces, quantified by a factor of 1000 with respect to those on ground, leads from a turbulent to laminar flow transition and finally to laminar flow conditions, that make measurements of viscosity possible and reliable (Xiao et al. 2021). Therefore, the internal flow in liquid samples is a key feature of all containerless techniques and the viscosity is of fundamental importance to characterize the flow behaviour and ensure a clean experiment. However, it is practically impossible to measure the internal flow in levitated droplets directly. For that reason, to assess the internal flow in levitated droplets, Magnetohydrodynamic (MHD) modelling is used (Xiao et al. 2019). MHD makes possible to evaluate the state of the flow (laminar, unsteady, turbulent) and its effects on different measurements by using the experimental parameters and materials properties as input in the Navier–Stokes equations, that can be solved by commercial software, such as Computation Fluid Dynamics (CFD) Solver or ANSYS Fluent (Bracker et al. 2022). To characterise the internal flow, model predicted flow velocity in the droplet and the Reynolds number, calculated using its value, are the two decisive parameters for the assessment of experimental conditions (Baker et al. 2020). In EML measurements, the experimental results paired with models have been used to establish that the laminar to turbulent transition occurred at a Reynolds number of 600 (Hyers et al. 2003) and below its value of 600, the laminar flow is assumed. In the present work, the operating conditions of containerless measurements substantiate the laminar flow thus, the reliability of viscosity experimental datasets of the alloys investigated (Table 2). Speaking about measurements of thermophysical properties in microgravity conditions, an important issue related to the concept of data reliability is the evaluation of uncertainty. Until now, thanks to a large number of literature data on the thermophysical properties of pure liquid metals, such as for example gold, the uncertainty analysis was done aiming to evaluate facility performance (Nawer et al. 2023). In the future, the uncertainty analysis has to be used for reliability assessment of properties data of complex alloy systems.

Thermodynamic Modelling

The surface tension and viscosity of liquid Ti-Al-Cr-Nb alloys were analysed with respect to the Ti-Al, which is the principal binary subsystem, while in the case of the surface tension, the analysis was extended to the Ti-Al-Cr and Ti-Al-Nb subsystems, formed by the three major alloying elements. To this aim, the surface tension isotherms of liquid Ti-Al were calculated by the Compound Formation Model (CFM) in a weak interaction approximation (Novakovic et al. 2011a; Novakovic et al. 2012), Quasi Chemical Approximation (QCA) for regular solutions and Butler’s model (Butler 1932), while for the viscosity, Terzieff’s model (Terzieff 2008) was applied. In the following, only the equations used for the property calculations are described. The input data are given in Table 1. Detailed and rigorous mathematical formalisms are reported in the literature cited above.

Table 1 Thermodynamic data of the excess Gibbs free energies of liquid Al-Ti, Al-Nb, Nb-Ti, Al-Cr and Cr-Ti alloys described by the Redlich-Kister polynomials (with ν terms); the surface tension reference data of Al, Ti, Nb and Cr pure metals; the viscosity reference data of liquid Ti (linear temperature dependence) and Al (Arrhenius equation)
Full size table

Surface Tension

The surface tension data of the 48Ti-48Al-2Cr-2Nb alloy was analysed using two models, i.e. the Compound Formation Model (CFM) together with one of the models such as the QCA for regular solutions or Butler’s model assuming the same solution type, that describe the surface properties of alloy melts using the simplest non-ideal solution model known as the regular solution. The CFM is characterised by four interaction energy parameters, while the QCA for regular solutions and Butler’s model contain only one energy parameter. For a sake of simplicity, in all abovementioned models, the monolayer surface phase and the bulk phase are in equilibrium. Model predicted surface tension values of the binary and ternary subsystems of the Ti-Al-Nb-Cr with Ti and Al major alloy components were compared among them as well as with available literature data.

The interactions between atoms and molecules in Ti–Al melts are not strong in nature and, the TiAl has the most negative enthalpy of formation, and thus, it is an energetically favoured solution compound (or intermediate phase) of the Ti–Al system (Witusiewicz et al. 2008a). Therefore, the prevalence of TiAl-complexes (\({A}_{\mu }{B}_{\upsilon }\)) in the liquid phase with AB-stoichiometry (\(\mu\) = 1, \(\upsilon\) = 1) was postulated in the CFM in a weak interaction approximation model to obtain the surface tension isotherm of liquid Ti-Al alloys (Novakovic et al. 2012), as follows

$$\sigma ={\sigma }_{i}+\frac{{k}_{B}T}{\alpha }ln\frac{{C}_{i}^{s}}{{C}_{i}}+\frac{{k}_{B}T}{\alpha }ln\frac{{\gamma }_{i}^{s}}{{\gamma }_{i}}$$
(1)

where \({k}_{B}\), \(T\), \(\alpha\), \({\sigma }_{i}\), \({C}_{i}\), \({C}_{i}^{s}\), \({\gamma }_{i}\), \({\gamma }_{i}^{s}\) \((i=A,B)\) are Boltzmann’s constant, reference temperature, mean surface area, surface tension, atomic fraction, activity coefficient of the bulk and the surface phase of pure components \(A\) and \(B\), respectively.

The surface tension isotherm calculated by the QCA for regular solutions is very close or even overlapping with that obtained by Butler’s model and the two models are appropriate to describe the surface properties of weakly / moderate interacting systems. The difference between the CFM and QCA for regular solutions (or Butler’s) isotherms represents the contribution of short range ordering to an increase in the surface tension. The magnitude of difference of two surface tension isotherms is proportional to the intensity of atomic interactions in an alloy system. To evaluate the surface properties of ternary compound forming systems such as the Ti-Al-Cr or Ti-Al-Nb, the CFM together with either Butler’s or the QCA for regular solutions have to be applied (Egry et al. 2007; Costa et al. 2014; Mohr et al. 2020).

The QCA for regular solution used to calculate the surface tension of the binary systems is expressed by

$$\begin{aligned}\sigma =&\ {\sigma }_{i}+ \frac{{k}_{B}T(2-pZ)}{2\alpha }ln\frac{{C}_{i}^{s}}{{C}_{i}}+ \frac{Z{k}_{B}T}{2\alpha }\left[pln\frac{({\beta }^{s}-1+2{C}_{i}^{s})(1+\beta )}{(\beta -1+2{C}_{i})(1+{\beta }^{s})}\right.\\&\left.-qln\frac{(\beta -1+2{C}_{i})}{(1+\beta ){C}_{i}}\right]\end{aligned}$$
(2)

where \(Z\) is the coordination number, \(\beta\) and \({\beta }^{s}\) are auxiliary functions describing the energetics of the bulk and surface phase, respectively. \(p\) and \(q\) are the surface coordination fractions. For a closed-packed structure, the values of these parameters usually are taken as ½ and ¼, respectively.

Butler’s model is a simple thermodynamic model that has been developed to describe the surface properties of liquids. Similarly to the QCA for regular solutions, Butler’s model is appropriate for the calculations of the surface tension of alloy systems with weak and / or moderate interactions between the constituent atoms. As stated above, the surface phase is assumed to be a monolayer and it is in equilibrium with the bulk. Using the Butler model, the surface tension of liquid binary alloys can be calculated by

$$\sigma = {\sigma }_{i}+\frac{RT}{{S}_{i}}\mathrm{ln}\left(\frac{{C}_{i}^{s}}{{C}_{i}^{b}}\right)+\frac{1}{{S}_{i}}\left[{G}_{i}^{xs,s}\left(T,{C}_{i}^{s}\right)-{G}_{i}^{xs,b}\left(T,{C}_{i}^{b}\right)\right]\quad(i=A,B)$$
(3)

where \(R\), \({S}_{i}\), \({C}_{i}^{b}\), \({C}_{i}^{s}\), \({G}_{i}^{xs,b}\), \({G}_{i}^{xs,s}\) are gas constant, surface area, composition and partial excess Gibbs free energy of a component \(i\) in the bulk and surface phases, respectively. The last two mentioned are the functions of temperature and composition. From an energetic point of view, the partial excess Gibbs free energy \({G}_{i}^{xs,s}\) of the surface phase has the same functional form as that of \({G}_{i}^{xs,b}\) times a factor taking into account the reduced coordination. This factor is expressed as the ratio of the numbers of interactive contacts between neighbouring atoms in the two phases. The surface properties calculated by Butler’s model are very close or even overlapping with those obtained by the QCA for regular solutions. In the case of ternary alloys, a comparison of experimental data with model predicted surface tension values obtained by Butler’s exhibit a good agreement with measured values (Egry et al. 2007; Mohr et al. 2020). Regarding multicomponent alloy systems, an increase in numbers of components leads to more complex and cumbersome numerical solution of Butler’s equation. The three abovementioned models described by Eqs. (1)–(3) are detailed in (Egry et al 2010b; Novakovic et al. 2011a; Novakovic et al. 2012; Costa et al. 2014).

Viscosity

The viscosity data of the 48Ti-48Al-2Cr-2Nb alloy was evaluated with respect to the corresponding viscosity isotherm of liquid Ti-Al alloys calculated by Terzieff’s model (Terzieff 2008, 2009). It combines the energetics of a system in terms of thermodynamics (Iida et al. 1976) with the hard sphere approach (Protopapas et al. 1973). The viscosity is expressed as the ratio of the excess viscosity and additive viscosity, giving the relative viscosity of an alloy melt, as

$$\begin{aligned}{\eta }^{xs}\cdot {\left({\eta }_{id}\right)}^{-1} =&\;{\alpha \cdot c}_{A}{c}_{B}{\left( \overline{{\sigma }_{1}}-\overline{{\sigma }_{2}}\right)}^{2}\cdot {\left({c}_{A}{\tilde{\sigma }}_{1}^{2}-{c}_{B}{\tilde{\sigma }}_{2}^{2}\right)}^{-1}\\&+ \beta \cdot \left\{{\left[\left(1+{c}_{A}{c}_{B}{\left({m}_{1}^{0.5}-{m}_{2}^{0.5}\right)}^{2}\cdot {\left({c}_{A}{m}_{1}^{0.5}+{{c}_{B}m}_{2}^{0.5}\right)}^{-2}\right)\right]}^{0.5}-1\right\}\\&+ \gamma \cdot 2{H}_{mix}\cdot {\left(RT\right)}^{-1}+\delta \cdot 2{c}_{A}{c}_{B}\left|{V}_{1}{-V}_{2}\right|{\left({V}_{1}{+V}_{2}\right)}^{-1}\end{aligned}$$
(4)

with \({c}_{i}\), \({m}_{i}\), \({\tilde{\sigma }}_{i}\), \({V}_{i}\) \((i=A,B)\) atomic fraction, atomic mass, hard-sphere diameter and molar volume of a component \(i\), respectively. \({H}_{mix}\) and \(R\) are the enthalpy of mixing and gas constant, while \(\alpha\), \(\beta\), \(\gamma\), \(\delta\) parameters are statistical weights obtained by fitting to Eq. (4) a large number of experimental viscosity datasets at the equiatomic composition (Terzieff 2008). Based on the standard relation \(\eta \left(T\right)={\eta \left(T\right)}_{id}+{\eta \left(T\right)}^{xs}\), the viscosity of binary melts is calculated by

$$\eta \left(T\right)={\eta \left(T\right)}_{id}\cdot (1+{\eta \left(T\right)}^{xs})$$
(5)

where the viscosity of the ideal mixture is calculated by \({\eta }_{id}={c}_{A}{\eta }_{A}+{c}_{B}{\eta }_{B}\) with the viscosities of pure components, \({\eta }_{A}\) and \({\eta }_{B}\).

Results

Surface tension and viscosity of liquid 48Ti-48Al-2Cr-2Nb measured by the containerless methods were analysed from the experimental and theoretical point of view. For a comparison, the corresponding properties of liquid Ti-Al, Ti-Al-Nb, and Ti-Al-Ta alloys, obtained by the same methods were also taken into account. Within each class of alloys, the experimental datasets were compared among them as well as with the corresponding model predicted values.

Surface Tension Data

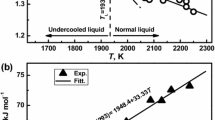
The surface tension of liquid 48Ti-48Al-2Cr-2Nb alloy was measured using the oscillating drop method in an electromagnetic processing device under microgravity conditions (Table 2). There are three experimental datasets: the first one obtained on board PF (Wunderlich et al. 2018a) and the other two on board the ISS (Wunderlich et al. 2018b, 2021). During PF, the surface tension measurements of the 48Ti-48Al-2Cr-2Nb were carried out over the temperature range of 1500–2000 K, indicating the melting temperature of T = 1775 K ± 3 K and thus, an undercooling of 275 K. The obtained temperature dependent datasets of four parabolas obeys a linear law. In the first experiment on board ISS, the surface tension data were obtained within the temperature range of 1525–1850 K as shown in Fig. 1 (Wunderlich et al. 2018b).

Table 2 Operating conditions of containerless experiments in microgravity together with the surface tension and viscosity data of liquid quaternary and ternary alloys of the Ti-Al-Cr-Nb system, obtained from these experiments
Full size table
Fig. 1
figure 1

Temperature dependent surface tension of liquid 48Ti-48Al-2Cr-2Nb alloy obtained by the oscillating drop method on board ISS (Wunderlich et al. 2018b)

Full size image

Similar surface tension behaviour of liquid 48Ti-48Al-2Cr-2Nb alloy was observed in the second ISS experiment, performed in the range of 1500–1850 K (Wunderlich et al. 2021). Both datasets show a linear temperature dependence. The ISS processing has longer measurement time to be completed and the surface tension datasets of the two experiments (Wunderlich et al. 2018b, 2021) differ up to 3% and result higher with respect to that obtained on board PF (Fig. 2). The maximum difference between the surface tensions of about 6% was found for the data (Wunderlich et al. 2018a) and (Wunderlich et al. 2021). The effects of metals such as Nb and Ta on the surface tension of Ti-Al based alloys was also investigated (Wunderlich et al. 2018a; Egry et al. 2010a; Zhou et al. 2011). It was found that the surface tensions of Ta and Nb-containing alloys are comparable to that of the 48Ti-48Al-2Cr-2Nb (Fig. 2) and together with significantly lower surface tension of 50Ti-50Al (Wessing and Brillo 2017) substantiate the obtained experimental values.

Fig. 2
figure 2

a Experimental surface tension data of liquid 48Ti-48Al-2Cr-2Nb alloy obtained by the OD-EML on the ISS (Wunderlich et al. 2021, 2018b) and on board PF (Wunderlich et al. 2018a). For a comparison, the Ti-Al surface tension isotherms (1- CFM; 2- QCA for regular solution, - the ideal solution model) calculated for T = 1973 K together with the literature data of different TiAl-based alloys (Egry et al. 2010a; Zhou et al. 2011; Wunderlich et al. 2018a) measured by containerless methods are shown. b a zoomed part of Fig. 2a: Surface tension isotherms of liquid Ti-Al alloys and the experimental data over a very narrow interval 0.48 < Ti, mole fraction < 0.60

Full size image

Surface Tension Isotherms

Among the binary subsystems of the Ti-Al-Cr-Nb, most of research has been focused on the thermodynamic and thermophysical properties of the Ti-Al system in the solid and liquid state. The assessed mixing properties of the liquid phases including the most recent re-assessments of the Ti-Al (Witusiewicz et al. 2008a) and Al-Cr (Hu et al. 2013) phase diagrams have been used to calculate the surface tension of liquid Ti-Al and Al-Cr alloys (Table 1). To this aim a variant of the compound formation model (CFM) for weakly interacting systems were applied. The surface tension of the other binary subsystems was calculated by the QCA for regular solution and Butler’s model. In the present calculations, Gibbs free energy of the Al-Ti (Witusiewicz et al. 2008a), Al-Cr (Hu et al. 2013), Al-Nb (Witusiewicz et al. 2009b) and Cr-Ti (Saunders 2003) liquid phases, the molar volumes (Iida and Guthrie 2015), structural data (Iida and Guthrie 2015) and the surface tension reference data of the pure components were taken as input (Table 1). To reduce the differences between the experimental and model predicted values, the surface tension reference data of liquid Al (Brillo and Kolland 2016) and Ti (Wessing and Brillo 2017), measured in electromagnetic levitation by the oscillating drop method, were used for the calculations of binary isotherms. Moreover, the availability of Nb and Cr surface tension data, obtained by similar containerless methods (Paradis et al. 2002; Chung et al. 1992), makes it possible to extend the analysis of 48Ti-48Al-2Cr-2Nb datasets with respect to the Ti-Al-Nb and Ti-Al-Cr ternary systems (Table 1). The iso-surface tension lines of liquid Ti-Al-Nb and Ti-Al-Cr alloys were obtained combining the surface tension values of their binaries. The effects of Cr and Nb on the surface tension of the 48Ti-48Al-2Cr-2Nb alloy were evaluated by comparison with the corresponding value of the 52Ti-48Al alloy having the same Al-content as the 48Ti-48Al-2Cr-2Nb (Fig. 2a, b). To distinguish the surface tension values of the 48Ti-48Al-2Cr-2Nb from those of the other TiAl-based alloys with similar compositions, an enlarged area around the equiatomic composition is shown in Fig. 2b. The surface tension of the 52Ti-48Al model alloy calculated by the CFM in weak interaction approximation (Eq. (1)) is \({\sigma }_{T=1973}^{CFM}\) = 0.997 N/m. The literature data of the 48Ti-48Al-2Cr-2Nb obtained on the ISS are \({\sigma }_{T=1973}^{ISS-exp3}\) = 1.235 N/m (Wunderlich et al. 2021) and \({\sigma }_{T=1973}^{ISS-exp2}\) = 1.189 N/m (Wunderlich et al. 2018b). The value measured on board PF is \({\sigma }_{T=1973}^{PF-exp1}\) = 1.124 N/m (Wunderlich et al. 2018a). Due to the presence of Cr and Nb minor components in the quaternary alloy (Fig. 2), the experimental datasets of the 48Ti-48Al-2Cr-2Nb differ from \({\sigma }_{T=1973}^{CFM}\) = 0.997 N/m up to 23%.

The model prediction of the surface tension by means of a ternary system assumes unchanged content of two principal alloy components and the cumulative sum of others. Based on this, a further comparison of the surface tension experimental data of the 48Ti-48Al-2Cr-2Nb (Wunderlich et al. 2018a, b, 2021) to the model predicted values with respect to the Ti-Al-Cr and Ti-Al-Nb systems was done. Therefore, taking into account Ti and Al-content and assuming the cumulative sums of Cr and Nb minor alloy components, the surface tension of the 48Ti-48Al-2Cr-2Nb was analysed with respect to those of the 48Ti-48Al-4Cr (Fig. 3) and 48Ti-48Al-4Nb model alloys (Fig. 4).

Fig. 3
figure 3

Iso-surface tension lines of liquid Ti-Al-Cr alloys calculated for T = 1973 K. In the Gibbs triangle the square symbol indicates the compositional locations of the 48Ti-48Al-4Cr model alloy that approximates the 48Ti-48Al-2Cr-2Nb (both in at %). The nearest iso-surface tension line shows the model predicted surface tension value of an alloy

Full size image
Fig. 4
figure 4

Iso-surface tension lines of liquid Ti-Al-Nb alloys calculated for T = 1973 K. In the Gibbs triangle the square symbol indicates the compositional locations of the 48Ti-48Al-4Nb model alloy that approximates the 48Ti-48Al-2Cr-2Nb and the triangle indicates the 46Ti-46Al-8Nb (all in at %). The nearest iso-surface tension line shows the model predicted surface tension value of an alloy

Full size image

Iso-surface tension lines of liquid Ti-Al-Cr alloys (Fig. 3) were calculated combining the surface tension values of Ti-Al (Novakovic et al. 2012) and Al-Cr (Novakovic 2011b) alloys obtained by the CFM in a weak interaction approximation (Eq. (1)) with those of Ti-Cr melts, calculated by Butler’s model (Eq. (3)) as the simplest one. In the case of the Ti-Cr, the surface isotherms calculated by QCA for regular solutions (Eq. (2)) and Butler’s model (Eq. (3)) overlap. The same is true for the corresponding surface tension isotherms of liquid Al-Nb and Ti-Nb alloys, regardless the Al-Nb is compound forming system (Okamoto 2014). Indeed, due to the lacking of thermodynamic properties data for the liquid Al-Nb phase and an extended composition range of Al-Nb alloys that for T = 1973 K representing undercooled melts (Fig. 4), the calculation of four interaction energy parameters (Novakovic et al. 2012, 2020) characterising the CFM was not possible. Therefore, the QCA for regular solutions and Butler’s model were applied. The calculations of the surface tension isotherms of liquid Nb-Ti alloys exhibit a difference up to 0.0001%. Accordingly, the iso-surface tension lines of liquid Ti-Al-Nb alloys were calculated combining the CFM surface tension values of Ti-Al melts with those of the Al-Nb and Ti-Nb obtained by Butler’s model (Fig. 4).

In both cases, the model predicted surface tensions indicate the values of about \(\sigma\) = 1.0 N/m (Figs. 3 and 4). The surface tensions of 48Ti-48Al-4Nb and 48Ti-48Al-Cr model alloys differ up to 23% from that of the 48Ti-48Al-2Cr-2Nb. On the other side, the surface tension of the 48Ti-48Al-4Nb is lower with respect to the 46Ti-46Al-8Nb experimental data (Wunderlich et al. 2021; Egry et al. 2010a) exhibiting differences between 8 and 14% (Fig. 2b). The estimated value of \(\sigma\) = 1.0 N/m can be considered as a lower limit value of the surface tension of liquid 48Ti-48Al-2Cr-2Nb alloy. It is interesting to observe that due to higher Nb-content in the 46Ti-46Al-8Nb, its calculated surface tension of \(\sigma\) = 1.026 N/m results to be slightly higher than those of the 48Ti-48Al-4Cr (Fig. 3) and 48Ti-48Al-4Nb (Fig. 4) model alloys.

Viscosity Data

The viscosity of liquid 48Ti-48Al-2Cr-2Nb alloy was measured using the oscillating drop method in an electromagnetic processing device under microgravity conditions (Table 2). There are three experimental datasets: the first one obtained on board PF (Wunderlich et al. 2018a) and the other two on board the ISS (Wunderlich et al. 2018b, 2021). During PF, the viscosity of liquid 48Ti-48Al-2Cr-2Nb was measured over the temperature range of 1823–200 < T / K < 1823 + 100 K (Wunderlich et al. 2018a), while on board the ISS, the measurements were performed within 1560 < T / K < 1820, as shown in Fig. 5 (Wunderlich et al. 2018b) and 1560 < T / K < 1820 (Wunderlich et al. 2021). The three viscosity datasets agree among them within an experimental error of about ± 12% and obey Arrhenius’s equation over an extended temperature interval including undercooled melts.

Fig. 5
figure 5

Temperature dependent viscosity of liquid 48Ti-48Al-2Cr-2Nb alloy obtained on board ISS (Mohr and Fecht 2022a; Wunderlich et al. 2021) and PF (Wunderlich et al. 2018a) by the oscillating drop method

Full size image

It is interesting to mention that the three viscosity datasets of the 48Ti-48Al-2Cr-2Nb, measured at T = 1800 K overlap, while for T = 1823 K the data (Wunderlich et al. 2018a, b) and (Wunderlich et al. 2021) differs about 2.5%. For a comparison the viscosity datasets of 50Ti-50Al (Wunderlich 2008), 46Ti-46Al-8Nb and 46Ti-46Al-8Ta alloys (Wunderlich et al. 2018a) are shown in Fig. 6. Due to the high viscosity values of liquid Ta (Ishikawa et al. 2013) and Nb (Paradis et al. 2002) with \({\eta }_{Ta}> {\eta }_{Nb}\), the corresponding viscosities of 46Ti-46Al-8Nb and 46Ti-46Al-8Ta alloys are significantly higher than those of the 48Ti-48Al-2Cr-2Nb.

Fig. 6
figure 6

Viscosity isotherm of liquid Ti-Al alloys calculated by Terzieff’s model for T = 1823 K together with experimental data of the 48Ti-48Al-2Cr-2Nb alloy (Wunderlich et al. 2021, 2018a, b). For a comparison, the viscosity data of liquid 50Ti-50Al, 46Ti-46Al-8Nb and 46Ti-46Al-8Ta (all in at %) are shown

Full size image

Viscosity Isotherm

Aiming to support theoretically the experimental data of the 48Ti-48Al-2Cr-2Nb alloy (Wunderlich et al. 2021, 2018a, b), the viscosity isotherm of liquid Ti-Al alloys was calculated by the Terzieff model (Terzieff 2008). The model predicted values were obtained using the viscosity reference data of liquid Al (Brooks et al. 2005) and Ti (Paradis et al. 2002) together with the enthalpy of mixing of Ti-Al liquid alloys (Witusiewicz et al. 2008a), molar volume of Al and Ti (Iida and Guthrie 2015) and hard sphere diameter of Al and Ti at the melting temperature (Protopapas et al. 1973) as input data. Temperature dependent hard spheres diameters were calculated as suggested in (Terzieff 2008). The viscosity isotherm was calculated for T = 1823 K and together with available viscosity data of the 48Ti-48Al-2Cr-2Nb is shown in Fig. 6.

The viscosity experimental data for T = 1823 K (Wunderlich et al. 2021, 2018a, b) exhibits maximum difference of about 18% with respect to the value calculated by Terzieff’s model, i.e. \({\eta }_{T=1823 K}^{50Ti-50Al}\) = 4.4 \(mPa\cdot s\) (Fig. 6). Taking into account the 52Ti-48Al model alloy and the presence of Cr and Nb in the 48Ti-48Al-2Cr-2Nb that increase its viscosity, the reported values of \({\eta }_{T=1823 K}^{PF-exp1}\) = 5.28, \({\eta }_{T=1823 K}^{ISS-exp2}\) = 5.30, and \({\eta }_{T=1823 K}^{ISS-exp3}\) = 4.92 (Wunderlich et al. 2018a, b, 2021) may be considered reasonable. The viscosity of liquid 48Ti-48Al-2Cr-2Nb alloy, processed by using containerless methods exhibits perfect agreement among them and a reasonable agreement with calculated data. The isotherm is also in agreement with the viscosity experimental data of the 46Ti-46Al-8Nb and 46Ti-46Al-8Ta (Wunderlich et al. 2018a) containing higher Ta and Nb-content.

Discussion

The reliability assessment of a property value refers to the consistency of results for the property in question. Speaking about multicomponent alloy systems such as the 48Ti-48Al-2Cr-2Nb, until now there are no models to describe precisely their surface tension and viscosity and only quantitative evaluation of these properties can be done (Mohr and Fecht 2022a, b). Therefore, it is possible to estimate a property value analysing a key binary and/or ternary subsystem formed by the major components of a multicomponent system of interest and taking into account the effects of the minority components on that property (Novakovic et al. 2022). Ti and Al are the major alloying elements in Ti-Al based alloys and hence the surface tension and viscosity values of the 48Ti-48Al-2Cr-2Nb alloy were compared to the model-based predictions for the Ti-Al. The effects of Cr and Nb minority alloying elements on the surface tension and viscosity of 48Ti-48Al-2Cr-2Nb alloy are comparable, at least to a first approximation, to that of liquid Ti itself. Therefore, for the calculations, Ti-content was taken as the sum of the amount of Ti present the alloy adding the content of minority alloying elements. Accordingly, the evaluation of the 48Ti-48Al-2Cr-2Nb surface tension takes into account the data reported (Wunderlich et al. 2021, 2018a, b). Most recent measurements of the 48Ti-48Al-2Cr-2Nb obtained on the ISS (Wunderlich et al. 2021), for T = 1973 K show the surface tension value \(\sigma\) = 1.235 N/m (Fig. 2). A comparison with previously reported surface tension data processed on board the ISS (\(\sigma\) = 1.189 N/m) (Wunderlich et al. 2018b) indicates a good agreement, and the data measured on board PF (\(\sigma\) = 1.124 N/m) (Wunderlich et al. 2018a) agrees within experimental error. Indeed, the two values measured on the ISS (Wunderlich et al. 2021, 2018a) differ about 2.8%, while a comparison of these data with that obtained on board PF (Wunderlich et al. 2018b) indicates a higher difference of about 6%. Higher surface tension value of the 48Ti-48Al-2Cr-2Nb (Wunderlich et al. 2021) may be explained by a longer processing time on the ISS with respect to that of PF. A reasonable agreement with the surface tension of the 52Ti-48Al model alloy can be observed (Fig. 2). So, the experimental data of the 48Ti-48Al-2Cr-2Nb (Wunderlich et al. 2018a, 2021) differs between 14 and 23.5%, respectively, from the surface tension of the 52Ti-48Al calculated by the CFM. Taking into account the experimental error, a higher difference is more reasonable due to the presence of Cr and Nb. In addition, a rough estimate of the surface tension of a multicomponent alloy can be done by the ideal mixture calculated using a weighted sum of the products formed by the surface tension reference data and the content of each alloy component in it. For the 48Ti-48Al-2Cr-2Nb alloy, at T = 1973 K, the ideal mixture value of \({\sigma }_{T=1973K}^{id. mixture}\) = 1.168 N/m was obtained. Keeping in mind that the Ti-Al-Cr-Nb is compound forming system, characterised by the exothermic reactions and therefore, its mixing properties exhibit negative deviations from Raoult's law implying positive deviations of its thermophysical properties (Egry et al. 2010b; Iida and Guthrie 2015). Based on this and taking into account positive deviations of the surface tension isotherms with respect to the ideal behaviour, observed for Ti-Al melts (Fig. 2), the surface tension of liquid 48Ti-48Al-2Cr-2Nb alloy has to be higher than the value calculated by the ideal mixture, i.e. \({\sigma }_{T=1973K}^{ISS-exp3}\) = 1.235 > \({\sigma }_{T=1973K}^{ISS-exp1}\)  = 1.189 > \({\sigma }_{T=1973K}^{id. mixture}\)  = 1.168 > \({\sigma }_{T=1973K}^{PF-exp1}\)  = 1.124 (all in N/m). Therefore, the surface tension of the 48Ti-48Al-2Cr-2Nb (Wunderlich et al. 2021, 2018b) equal to \(\sigma\) = 1.238 N/m and to \(\sigma\) = 1.189 N/m can be considered as its reference data. Similarly, the viscosity isotherm exhibits positive deviation from the ideal mixture and all literature datasets are higher than the corresponding values characterising the ideal behaviour (Fig. 6), i.e. \({\eta }_{T=1823K}^{ISS-exp2}\) = 5.30 > \({\eta }_{T=1823K}^{PF-exp1}\)  = 5.28 > \({\eta }_{T=1823K}^{ISS-exp3}\)  = 4.92 > \({\eta }_{T=1823K}^{52Ti-48Al}\)  = 4.43 > \({\eta }_{T=1823K}^{id. mixture}\)  = 2.90 (all in \(mPa\cdot s\)). Therefore, the viscosity values of \({\eta }_{T=1823 K}^{PF-exp1}\) = 5.28, \({\eta }_{T=1823 K}^{ISS-exp2}\) = 5.30, and \({\eta }_{T=1823 K}^{ISS-exp3}\) = 4.92 of the 48Ti-48Al-2Cr-2Nb (Wunderlich et al. 2018a, b, 2021) can be considered the reference data.

Conclusions

Reliability of the surface tension and / or viscosity experimental datasets of a complex alloy can be assessed comparing the property datasets with model predicted values. Accordingly, the surface tension and viscosity data of liquid 48Ti-48Al-2Cr-2Nb alloy obtained by the oscillating drop method in an electromagnetic processing device on board PF and on board the ISS were compared within each group of data and to the corresponding model predicted values. Both properties of the 48Ti-48Al-2Cr-2Nb alloy were evaluated with respect to the model-based predictions for liquid Ti-Al alloys and taking into accounts the effects of minority alloying elements on its surface tension and viscosity. To this aim, the CFM, QCA for regular solutions and Butler’s model were used to describe the surface tension of Ti-Al melts, while for the analysis of viscosity, Terzieff’s model was applied. The use of two or more models is useful for the constructing confidence intervals for predicted values that, combined with the experimental data obtained by different experimental methods, are necessary for data reliability assessment. Data analysis of the surface tension and viscosity of liquid 48Ti-48Al-2Cr-2Nb alloy indicates that the two datasets agree within experimental error and thus can be considered reliable.