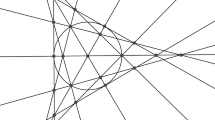
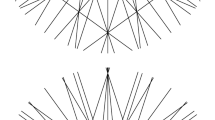
Abstract
In this paper, we construct an infinite series of line arrangements in characteristic two, each featuring only triple intersection points. This finding challenges the existing conjecture that suggests the existence of only a finite number of such arrangements, regardless of the characteristic. Leveraging the theory of matroids and employing computer algebra software, we rigorously examine the existence and non-existence across various characteristics of line arrangements with up to 19 lines maximizing the number of triple intersection points.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
A lot of theorems in Euclidean and projective geometry can be expressed as statements on unexpected incidences. This philosophy applies to very basic results in school geometry, e.g., the existence of the orthocenter of a triangle is a statement about three lines (the altitudes) intersecting in one point. The classical Pappus Theorem asserts in turn that some three points are collinear, see [20] for a beautiful and extended overview. This means that the three lines dual to these points intersect in a single point (dual to the line they are contained in).
A lot of interest and work on arrangements with triple points was sparked by one of the problems posed by Jackson in his collection [15]. In a poetic and pragmatic way, he asked if it is possible to plant nine trees so that in each row containing two of the trees, there must a third tree. The problem in a more formal way was posed by Sylvester [22] and became known as the orchard problem, see [2] for a nice modern account. The problem was solved by Gallai (Grünwald) in [13].
Sylvester-GallaiTheorem
Let \(\mathcal L\) be an arrangement of lines in the real projective plane which is not a pencil (i.e. not all lines intersect in a single point). Then there exists a point where exactly two lines from \(\mathcal L\) intersect (a double point of the arrangement).
An effective version of the orchard problem asks for a minimal number of double points in dependency on the number s of lines in the arrangement. This problem was solved only recently by Green and Tao [12].
From the statement of the Sylvester-Gallai Theorem it becomes immediately clear that incidences in an arrangement of lines depend in a strong way on the underlying field. For example, it follows directly, that the only arrangement with only triple points in the real projective plane is a set of three concurrent lines. Of course this trivial arrangement exists in any projective plane. In the complex projective plane there is the dual Hesse arrangement of 9 lines intersecting altogether in 12 points, see [17]. Urzua asks in [24, Question 3] if the dual Hesse arrangement is the only (nontrivial) complex line arrangement with only triple points? Possible approaches to this problem are discussed in [1, Section 4] in the context of the bounded negativity conjecture and Harbourne constants. The problems reappear slightly more generally in [6, Remark 6.13] and in a recent work by Hanumanthu and Harbourne [14, Question 11].
In positive characteristic there are two more examples. In characteristic 2, there is the Fano plane \(\P ^2(\mathbb F_2)\) consisting of 7 lines intersecting in exactly 7 triple points. In characteristic 3, there is an example of 9 lines intersecting in 12 points. This arrangement results from 13 lines in the projective plane \(\P ^2(\mathbb F_3)\) after removing one pencil of lines (all 4 lines passing through a fixed point). No further examples were known up to now. This motivated our research. Our first result is the existence of an infinite series of new examples in characteristic 2, which in particular shows that Conjecture 1.6 in [8] was slightly overoptimistic.
TheoremA
For any \(k\ge 2\) there exists an arrangement of
lines, which intersect in triple points only.
The number of the intersection points is of course
These arrangements are contained in finite projective planes over bigger and bigger fields of characteristic 2. Moreover, we found a sporadic arrangement with 19 lines over \(\mathbb F_{11}\) which intersects in triple points only.
A related path of research is motivated by the following problem. For an arrangement of lines \(\mathcal L\), we denote by \(t_3(\mathcal L)\) the number of points where exactly three lines from \(\mathcal L\) intersect.
Problem 1.1
Given a positive integer s determine the number
where the maximum is taken over all arrangements \(\mathcal L\) of s lines, with no restriction on the underlying field.
These numbers have been determined completely for \(s\le 11\) in [9].
There exists a non-trivial combinatorial upper bound on the numbers \(T_3(s)\) introduced by Schönheim in [21].
Proposition 1.2
(Schönheim) For \(s\ge 1\) let
where \(\varepsilon (s)=1\) if \(s\equiv 5\mod 6\) and \(\varepsilon (s)=0\) otherwise. Then
The second result concerns the values of \(T_3(s)\) for \(12\le s\le 19\).
TheoremB
We establish the following values for \(T_3(s)\) summarized in this table.
In particular we establish the (non)-existence of arrangements whose number of triple points is close to or matches the Schönheim bound.
-
i)
There does not exist an arrangement of 12 lines with 20 triple points.
-
i’)
There exists an arrangement of 12 lines with 19 triple points.
-
ii)
There does not exist an arrangement of 13 lines with 25 or 26 triple points.
-
ii’)
There exists an arrangement of 13 lines with 23 triple points.
-
iii)
There exists an arrangement of 14 lines with 28 triple points.
-
iv)
There exists an arrangement of 15 lines with 35 triple points.
-
v)
There exists an arrangement of 16 lines with 37 triple points.
-
vi)
There exists an arrangement of 17 lines with 40 triple points.
-
vii)
There exists an arrangement of 18 lines with 48 triple points.
-
viii)
There exists an arrangement of 19 lines with 57 triple points.
Our results mainly rest on two pillars. First we use an algorithm to compute the realization space of a matroid. In the language of arrangements, the algorithm checks whether a given geometric lattice is in fact the intersection of some line arrangement over some field. The details of this procedure are described in Sect. 2.1. Second, we benefit from the fact that the combinatorial structure of arrangements with only triple points is know as a Steiner triple system; a special type of a design which we discuss in Sect. 2.2. Subsequently, we prove Theorem A in Sect. 3 and turn to the proof of Theorem B in Sect. 4.
Recently, Golla proved several new restrictions on the existence of complex line arrangements with only triple points [11]. This in particular yields another proof of the fact that there are no line arrangements with 13 lines and only triple points in the complex case.
1.1 Open problems
We conclude the introduction with mentioning a few open problems. The question of whether there exists an arrangement with only triple points in a field of characteristic 0 with more than 9 lines remains open. Finally in the realm of Theorem B, let us mention that it remains open whether there exists arrangements with
-
13 lines and 24 triple points and
-
17 lines and at least 41 triple points.
2 Preliminaries
In this section we define the objects used throughout this note.
2.1 Matroids and their realizations
Let us start with a gentle introduction to the theory of matroids.
Definition 2.1
A matroid M is a pair \((E,\mathcal {B})\), where E is a finite ground set and \(\mathcal {B}\) is a non-empty set of subsets of E, called bases, such that for any two bases \(B,B' \in \mathcal {B}\) with some \(i \in B{\setminus } B'\) there exists \(j \in B'\) with \((B\setminus \{i\})\cup \{j\} \in \mathcal {B}\).
The size of M is the cardinality of the ground set E and the common size of all bases is called the rank of M. We say that the matroid M is simple if each pair of elements of E is contained in at least one basis.
Let \(M = (\{1,\dots , n\}, \mathcal {B})\) be a simple matroid of rank r. A realization of M over a given field \(\mathbb {K}\) is a matrix \(P \in \mathbb {K}^{r\times n}\) such that for all subsets \(X\subseteq \{1,\dots ,n\}\) of size r we have
where \(P_{X}\) is the \(r\times r\)-submatrix consisting of the columns indexed by X. The kernels of the linear forms given by the columns of P define an arrangement \(\mathcal {A}\) of n hyperplanes in \(\mathbb {K}^{r}\) whose intersection lattice isomorphic to the lattice of flats of matroid M.
The key question for this note is whether a given matroid admits such a realization, that is whether there exists an arrangement of hyperplanes over some field having that matroid as its intersection lattice. One can answer this question using computer algebra as we discuss now.
Observe that the condition (1) defines an ideal \(I'\) in the ring \(R' = R[d]\), where
given by
where \(P=(p_{ij}) \in R^{r \times n}\) is an \(r \times n\) matrix having the variables \(p_{ij}\) as entries. Now the realization space of the matroid M is an affine scheme, essentially described by
This leads to the following observation.
Proposition 2.2
[19, Thm. 6.8.9] The matroid M is realizable over some field if and only if \(1 \not \in I'\).
This condition can be refined by checking realizability over algebraically closed or finite fields using Gröbner bases. The details of this algorithm together with a tutorial on how to use it in OSCAR through several examples can be found in [7]. In particular, this article provides several speed-up techniques to make this computation practically feasible.
2.2 Steiner triple systems
The combinatorics underlying arrangements with only triple points is equivalent to Steiner triple systems, a particular type of block designs studied in coding and design theory.
Definition 2.3
A Steiner triple system (STS) is a finite set S together a set \(\mathcal {B}\) of 3-element subsets of S (called blocks) such that every pair of elements of S is contained in exactly one block. The order of the Steiner triple system is the cardinality of the set S.
An easy counting argument shows that Steiner triple systems of order n exists if and only if n is of the form \(6k+1\) or \(6k+3\) for some k. Moreover there is a complete catalog of Steiner triple systems up to permutation of the set S for the orders 7, 9, 13, 15, and 19 of which there are 1, 1, 2, 80, and 11, 084, 874, 829, respectively. See [4, Cha. 5] for an overview of Steiner triple systems.
Steiner triple systems are combinatorially equivalent to the intersection lattice of arrangements with only triple points as the blocks are then exactly the combinatorial data of the triple intersection points, that is the flats of rank 2 in the intersection lattice. In particular, we can use the available database of STSs and check whether the associated matroid is realizable in the sense described above. We did that for all STSs of order \(n\le 15\) and found that of these 84 designs exactly three are realizable as arrangements.
-
1.
The unique STS of order 7 is the Fano plane and therefore only realizable over fields of characteristic 2.
-
2.
The unique STS of order 9 is the matroid underlying the dual Hesse configuration and therefore realizable over a field \(\mathbb F\) if and only if there exists a solution to the equation \(x^2-x+1\) in \(\mathbb F\).
-
3.
Exactly one of the 80 STSs of order 15 is realizable. It is however only realizable over fields of characteristic 2, the smallest being \(\mathbb F_{16}\). Combinatorially it is the truncation of the projective space \(\mathbb {P}^3(\mathbb F_2)\). This is the basis of our general construction underlying Theorem A which we describe in the next section.
3 Arrangements with only triple points in characteristic 2
In this section, we show that truncated projective geometries over \(\mathbb F_2\) provide examples of line arrangements with only triple points. The general idea we present here was mentioned before vaguely in the coding theory literature, see for example [18]. To the best of our knowledge we give the first complete proof of this statement. By the way of illustrating the approach we begin with the simplest example and then pass to the general case.
Let \(X=\P ^3(\mathbb F_2)\) be the projective 3-space over \(\mathbb F_2\) considered as a subset of \(Y=\P ^3(\mathbb F_{2^4})\). Let Z be the union of planes in Y, which are generated by triples of non-collinear points in X.
Lemma 3.1
The set \(W:=Y\setminus Z\) is non-empty.
Proof
Here, we perform a very rough count of points. Any three non-collinear points in X span a plane in X and also a plane in Y, which contains the ”smaller” plane in X. A plane in X contains \(7=2^3-1\) points, as it is just a Fano plane. A plane in Y contains \(273=16^2+16+1\) points. There are \(15=2^4-1\) planes in X (by duality there are as many hyperplanes as there are points). They generate 15 planes in Y, which altogether contain no more than \(4 095= 15\cdot 273\) points. Since there are \(4 369=16^3+16^2+16+1\) points in Y, the claim follows. \(\square \)
Let us consider a projection \(\pi \) from a point \(P\in W\) to a hyperplane in Y. The crucial observation here is that P does not lie on any line passing through 2 or more points in X. Indeed, if it were contained in such a line (extended to Y), it would also be contained in one of the planes building the set Z in Lemma 3.1, but this would contradict its choice not in Z. Hence \(\pi \) restricted to X is injective. We may think of \(\pi \) as ”spreading” the 3-dimensional projective space X on the projective plane defined over the extension field \(\mathbb F_{2^4}/\mathbb F_2\).
Our next Lemma is a simple count of lines in X.
Lemma 3.2
There are 35 lines in \(\P ^3(\mathbb F_2)\).
Proof
As we already observed there are 15 points in \(\P ^3(\mathbb F_2)\). Every line is determined by a pair of distinct points and since there are 3 points on each line we have
as asserted. \(\square \)
Since collinearities remain unaltered under projections, there are 35 triples of collinear points in \(X'=\pi (X)\). In the dual projective plane \(H^*=\P ^2(\mathbb F_{2^4})^*\) these triples of collinear points become triples of lines meeting in a point. There are altogether 15 points in \(X'\), so they correspond to 15 lines in \(H^*\). These lines intersect by 3 in all points which are dual to the 35 lines determined by points in \(X'\). But then elementary combinatorics shows that there are no other intersection points among the 15 lines.
Corollary 3.3
There exists an arrangement of 15 lines in \(\P ^2(\mathbb F_{2^4})\) with 35 triple intersection points and no other intersection points.
The argument above is sharp with respect to the size of the field; we determined with OSCAR that this matroid is not realizable over \(\mathbb F_2\), \(\mathbb F_4\), and \(\mathbb F_8\).
In general for \(n\ge 3\), we consider the lines in the projective geometry \(\P ^n(\mathbb F_2)\). There are \(2^{n+1}-1\) such lines that intersect in \(\frac{1}{6}(2^{n+1}-1)(2^{n+1}-2)\) many points. Crucially every such intersection point is a triple point and there are no other intersection points.
The point of the argument below is that we can find the same configuration of lines in a projective plane of a field of characteristic two of larger size. So these are all line arrangements of size \(2^{n+1}-1\) with only triple points in larger and larger fields of characteristic two. Note that combinatorially the matroids are the truncations of the projective geometries \(\P ^n(\mathbb F_2)\) to rank 3.
The general result goes along the same lines, but we are not able to find the smallest possible m, such that the configuration of \(2^{n+1}-1\) lines with only triple intersection points exists in \(\mathbb F_{2^m}\). However, we are able to show:
Theorem 3.4
Take an integer \(k\ge 4\). Take \(m=3k-4\). Then there exists an arrangement of \(2^{k+1}-1\) lines in \(\P ^2(\mathbb F_{2^{m}})\) with \(\frac{(2^{k+1}-1)(2^k-1)}{3}\) triple intersection points and no other intersection points.
Proof
The idea of the proof, based on [18], is to take the configuration C of lines in \(\P ^k(\mathbb F_2)\). We embed this space into \(\P ^k(\mathbb F_{2^m})\) and project the configuration to \(\P ^{k-1}(\mathbb F_{2^m})\) from a point such that the collinearities are preserved. Then we repeat this process until we arrive at a configuration in \(\P ^2(\mathbb F_{2^m})\). As each line from C contains 3 points from \(\mathbb F_2\), the dual configuration is the desired one.
The condition on a projection to preserve collinearities in the configuration C is that the center of the projection does not lie on any plane containing at least two lines from C. So we check when it is possible to make such a choice.
The number \(n_3(C)\) of planes in \(\P ^k(\mathbb F_{2^m})\) containing at least two lines from C is at most
so
The number of points in \(\P ^k(\mathbb F_{2^m})\) on each such plane is \(p:=(2^m)^2+2^m+1.\)
We need to find a center of projection outside the planes in every \(\P ^j(\mathbb F_{2^m})\) for \(j=3,4,\dots ,k\). Thus, for each \(j=3,4,\cdots k\) the number of points in \(\P ^j(\mathbb F_{2^m})\), should be greater than \(p\cdot n_3(C)\).
This means, that we are able to find the desired center of projection if
This yields
which simplifies to
For \(m=3k-4\) this inequality is satisfied, because then we get
which is true for every \(k\ge 4\). \(\square \)
This construction in fact generalizes to every finite field \(\mathbb F_{q}\) which yields line arrangements over field extensions of \(\mathbb F_q\) with all intersection points of size \(q+1\).
Remark 3.5
Let \(k\ge 3\) be an integer, let \(q>2\) be (a power of) a prime number. A reasoning similar to the one above yields a configuration of \(q^{k+1}-1\) lines in \(\P ^2(\mathbb F_{q^{3k-5}})\) with \(\frac{(q^{k+1}-1)(q^k-1)}{(q-1)(q+1)}\) points which are \((q+1)\)-fold.
Proof
Now take as the set C all lines in \(\P ^k(\mathbb F_q)\). Embed \(\P ^k(\mathbb F_q)\) in \(\P ^k(\mathbb F_{q^{3k-5}})\). We have to ensure the existence of a suitable center of the collinearities-preserving projection from \(\P ^k(\mathbb F_{q^{3k-5}})\) to \(\P ^{k-1}(\mathbb F_{q^{3k-5}})\), then from \(\P ^{k-1}(\mathbb F_{q^{3k-5}})\) to \(\P ^{k-2}(\mathbb F_{q^{3k-5}})\) etc.
Again, the projection preserves collinearities in the lines from C if the center of the projection is not on any plane with at least two lines from C, thus again we get that the number of forbidden points is at most
After all but one projections, this number should be strictly less than the number of points in \(\P ^3(\mathbb F_{q^{3k-5}})\), so we get the inequality:
This is equivalent to:
Using the fact that \(q\ge 3\) and \(k\ge 3\) this is elementary (however tiresome) to show that this inequality holds. \(\square \)
4 Line arrangements with the maximal number of triple points
We begin with the following simple but useful observation.
Lemma 4.1
Let \(\mathcal A\) be a realizable Steiner triple system on s lines. Then
i.e., there exists an arrangement of \(s-1\) lines with the number of triple points attaining the Schönheim bound.
Proof
For s we have
hence \(s=6k+1\) or \(s=6k+3\) for a positive integer k (we omit the trivial case \(s=3\)).
It follows that for \(s=6k+1\) we have \(s-1=6k\) and
On the other hand in \(\mathcal A\) there are exactly \(\frac{s-1}{2}\) triple points on each line and \(6k^2+k\) triple points altogether. Let \(\mathcal B\) be an arrangement obtained from \(\mathcal A\) by removing one line. Then the number of triple points is
which shows that the bound in (3) is attained.
For \(s=6k+3\) we have \(s-1=6k+2\) and
In \(\mathcal A\) there are this time altogether \(6k^2+5k+1\) triple points and \(3k+1\) points on each line. Removing as above one line from \(\mathcal A\) we obtain an arrangement \(\mathcal B\) with
triple points. Again, the bound in (4) is attained. \(\square \)
Here we want to provide a computational proof of nonexistence (over any field) of configurations of 12 lines with 20 triple (and 6 double points) and 13 lines with 26 triple points.
Proof of Theorem B
For (i) note that a line arrangement with 12 lines and 20 triple points either has one additional quadruple point or 6 additional double points. Consulting the database of all matroids of rank 3 and 12 elements yields that there is no matroid of the former and exactly 5 matroids of the latter type. We checked that these five matroids are all not realizable over any field (four of these matroids even contain the non-Pappus matroid which immediately implies that they are not realizable). Thus, there is no line arrangement of 12 lines with 20 triple points over any field.
The arrangements announced in (i’) are well known, see for example [10] for a description of two such arrangements and their role the containment problem in commutative algebra.
As for (ii) the combinatorial structure of a line arrangement with 13 lines and 26 triple points is a Steiner triple system on 13 elements. As mentioned above, up to permutation of the elements, there are exactly two such designs [4]:
Limbos already checked that both matroids are not realizable over any field (“projectively embeddable” in their language) [18]. We confirmed this observation with our realization algorithm. Hence, there is no line arrangement with this underlying matroid.
Suppose there exists an arrangement with 13 lines and 25 triple points. There must be one line that contains at most 5 triple points, as we would have 26 triple points otherwise in total. Removing this line therefore yields and arrangement with 12 lines and at least 20 triple points By (i) such an arrangement does not exists and thus also the arrangement with 25 triple points can not exists.
The arrangement in (ii’) arises by removing three triple points from one of the STSs of order 13 and replacing them by three double intersection points each. Computations in OSCAR revealed that the resulting matroid is only realizable in a field of characteristic 7. One such arrangement with 13 lines and 23 triple points is defined via the following matrix in \(\mathbb F_7\).
The existence of an arrangement with 13 lines and 24 triple points remains open for now.
The Steiner triple system announced in (iv) exists in characteristic 2 by Corollary 3.3, hence also the arrangement in (iii) exists by Lemma 4.1.
(v) The existence of an arrangement of 16 lines with 37 triple points is claimed in [3, Theorem 2]. The authors use certain 15-division points on an elliptic curve to construct (after dualizing) an arrangement of 15 lines with 31 triple points and claim that the parameter \(\alpha \) in their construction can be chosen in such a way that six out of twelve double points of the configuration are collinear. However the value of \(\alpha \) is not specified and checking the construction directly requires knowledge of coordinates of 15-division points on a specific cubic. Our approach, motivated by [3] is much more explicit.
The matroid we want to realize geometrically is determined by the following triples (of lines intersecting in one point):
We checked with OSCAR that it can be realized over the reals by lines given by equations \(\alpha x+\beta y+\gamma z=0\) whose coefficients \((\alpha , \beta , \gamma )\) are given by the rows of the following matrix
where \(\varepsilon \) satisfies the equation \(4\varepsilon ^2-6\varepsilon +1=0\).
A nice realization of the same matroid over \(\mathbb F_{11}\) is given by the same token by the columns of the following matrix:
We now turn to the case of 17 lines in (vi). The existence of an arrangement with 40 triple points follows from the construction in [3]. It is not known whether there are arrangements with more than 40 triple points.
We describe an arrangement of 19 lines with only triple points in \(\mathbb F_{11}\) in Sect. 4.1. This proves the claimed statement in (viii). Hence also the arrangement in (vii) exists by Lemma 4.1. There also exists a combinatorially different arrangement of 18 lines with 48 triple points in characteristic zero described by Tombarkiewicz and Ziȩba in [23]. \(\square \)
4.1 Sporadic example
The automorphism group of a matroid \(M=([n],\mathcal {B})\) is the group of the permutations \(\sigma \in {{\,\textrm{Sym}\,}}([n])\) that preserve the bases \(\mathcal {B}\), that is \(B\in \mathcal {B}\) if and only if \(\sigma (B)\in \mathcal {B}\).
We observed that matroids underlying the line arrangements with only triple points all have a relatively large automorphism group. The matroid of the dual Hesse arrangement has an automorphism group of size 432. The matroids of the family of line arrangements in characteristic 2 in Sect. 3 have the automorphism group \(PSL_n(2)\) with
We therefore studied Steiner triple systems with a relatively large group of automorphisms. All Steiner triple systems of order 19 and 21 with a non-trivial automorphism group were computed in [5] and [16], respectively.
There are exactly 104 Steiner triple systems of order 19 with an automorphism group of order at least 9, and these are given in the appendix to [5]. We checked the realizability of the corresponding matroids and somewhat surprisingly, exactly one of those matroids is realizable. The matroid has an automorphism group of order 57 and it is only realizable over \(\mathbb F_{11}\). It is in fact a protectively unique arrangement and one realization is given by this matrix over \(\mathbb F_{11}\):
So this is a line arrangement over \(\mathbb F_{11}\) with 19 lines and 57 triple points. We verified that the automorphism group \(G_{57}\) acts transitively on the triple points, so we have a \(G_{57}\)-orbit of triple intersection points. Moreover, we found that there exists another Steiner triple system of order 19 with automorphism group \(G_{57}\) of order 57, but it cannot be realized over any field, which makes our sporadic example even more intriguing.
Subsequently, we consider realizability of all Steiner triple systems of order 21 with an automorphism group of size at least 7 enumerated in [16]. All corresponding matroids were however not realizable over any field.
References
Bauer, T., Di Rocco, S., Harbourne, B., Huizenga, J., Lundman, A., Pokora, P., Szemberg, T.: Bounded negativity and arrangements of lines. Int. Math. Res. Not. IMRN 2015(19), 9456–9471 (2015)
Burr, S.: Planting trees. In: Klarner, D.A. (ed.) The Mathematical Gardner, pp. 90–99. Springer, US, Boston, MA (1981)
Burr, S.A., Grünbaum, B., Sloane, N.J.A.: The orchard problem. Geomet. Dedic. 2, 397–424 (1974)
Colbourn, C. J., Dinitz, J. H.: editors. Handbook of combinatorial designs. Discrete Mathematics and its Applications (Boca Raton). Chapman & Hall/CRC, Boca Raton, FL, second edition, (2007)
Colbourn, C.J., Magliveras, S.S., Stinson, D.R.: Steiner triple systems of order \(19\) with nontrivial automorphism group. Math. Comp. 59(199), 283–295 (1992)
Cook, D., II., Harbourne, B., Migliore, J., Nagel, U.: Line arrangements and configurations of points with an unexpected geometric property. Compos. Math. 154(10), 2150–2194 (2018)
Corey, D., Kühne, L., Schröter, B.: Matroids in OSCAR. arXiv:2311.08792, (2023)
Dimca, A., Harbourne, B., Sticlaru, G.: On the bounded negativity conjecture and singular plane curves. Mosc. Math. J. 22(3), 427–450 (2022)
Dumnicki, M., Farnik, L., Główka, A., Lampa-Baczyńska, M., Malara, G., Szemberg, T., Szpond, J., Tutaj-Gasińska, H.: Line arrangements with the maximal number of triple points. Geom. Dedicata 180, 69–83 (2016)
Farnik, Ł, Kabat, J., Lampa-Baczyńska, M., Tutaj-Gasińska, H.: Containment problem and combinatorics. J. Algebraic Combin. 50(1), 39–47 (2019)
Golla, M.: On line arrangements with odd multiplicities. arXiv:2403.17260, (2024)
Green, B., Tao, T.: On sets defining few ordinary lines. Discr. Comput. Geom. 50(2), 409–468 (2013)
Grünwald, T.: Solution to problem 4065. Amer. Math. Monthly 51, 169–171 (1944)
Hanumanthu, K., Harbourne, B.: Real and complex supersolvable line arrangements in the projective plane. J. Algebraic Combin. 54(3), 767–785 (2021)
Jackson, J.: Rational amusement for winter evenings, or, A collection of above 200 curious and interesting puzzles and paradoxes relating to arithmetic, geometry, geography, & c.: with their solutions, and four plates, designed chiefly for young persons. London: Longman, Hurst, Rees, Orme and Brown, (1821)
Kaski, P.: Isomorph-free exhaustive generation of designs with prescribed groups of automorphisms. SIAM J. Discr. Math. 19(3), 664–690 (2005)
Lampa-Baczyńska, M., Wójcik, D.: On the dual Hesse arrangement. In: Analytic and algebraic geometry. 3, pp. 169–177. Wydawn. Uniw. Łódzkiego, Łódź (2019)
Limbos, M.: Projective embeddings of small Steiner triple systems. Ann. Discr. Math. 7, 151–173 (1980)
Oxley, J.: Matroid theory, volume 21 of Oxford Graduate Texts in Mathematics. Oxford University Press, Oxford, second edition, (2011)
Richter-Gebert, J.: Perspectives on projective geometry. Springer, Heidelberg, (2011). A guided tour through real and complex geometry
Schönheim, J.: On maximal systems of \(k\)-tuples. Studia Sci. Math. Hungar. 1, 363–368 (1966)
Sylvester, J.J.: Mathematical question 11851. Edu. Times 59, 98–99 (1893)
Tombarkiewicz, M., Ziȩba, M.: On Yoshinaga’s arrangement of lines and the containment problem. Bull. Math. Soc. Sci. Math. Roum. Nouv. Sér. 64(3), 207–215 (2021)
Urzúa, G.: Some open questions about line arrangements in the projective plane. Proyecciones 41(2), 517–536 (2022)
Acknowledgements
Our work was initiated during the Workshop on Complex and Symplectic Curve Configurations held in Nantes, France, in December 2022. We would like to thank the organizers for stimulating fruitful discussions and providing excellent working conditions. We would like also to thank Brian Harbourne for helpful comments on an earlier draft. We thank Piotr Pokora for a number of supporting remarks and suggestions while we were working on this project. Kühne was supported by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) – SFB-TRR 358/1 2023 – 491392403. Szemberg and Tutaj-Gasińska were partially supported by National Science Centre, Poland, grant 2019/35/B/ST1/00723.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kühne, L., Szemberg, T. & Tutaj-Gasińska, H. Line arrangements with many triple points. Rend. Circ. Mat. Palermo, II. Ser (2024). https://doi.org/10.1007/s12215-024-01047-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s12215-024-01047-x