1 Introduction

In the present note we focus on certain line arrangements in the projective plane over the real numbers. Our aim here is to show that almost whole family of Böröczky line arrangements is not free. Our result seems to be unraveled explicitly in the literature (according to our best knowledge), and we would like to fill this gap. Our result is actually much stronger since it allows to provide a complete characterization of free line arrangements having only double and triple points. Before we proceed to the core of the note, let us emphasize that there are some discrepancies in the literature around the notion of Böröczky arrangements of lines. For us Böröczky arrangements of lines are arrangements \({\mathcal {B}}_n\) defined in [3, Example 2] and they provide the maximal possible number of triple intersection points for arrangements defined over the real numbers. However, in [4, Proposition 2.1] the authors define four different classes of Böröczky arrangements of lines and for those Anzis and Tohǎneanu proved their supersolvability and thus the freeness. Fortunately, there is no contradiction in our claim since at the end of the day we consider different objects. Now we present key ingredients, we will follow mostly [10, 11].

Let \(\mathcal {A} = \{H_{1}, \ldots , H_{n} \}\) be an essential and central hyperplane arrangement in \(\mathbb {C}^{k}\), it means that \(H_{i} = V(\ell _{i})\) for homogeneous \(\ell _{i}\) and \(V(\ell _{1}, \ldots ,\ell _{n}) = 0 \in \mathbb {C}^{k}\). The central condition means here that \(\mathcal {A}\) also defines an arrangement in \(\mathbb {P}^{k-1}(\mathbb {C})\). The main combinatorial object associated to \(\mathcal {A}\) is the intersection lattice \(L_{\mathcal {A}}\), which consists of the intersections of elements of \(\mathcal {A}\), ordered by reverse inclusion. \(\mathbb {C}^{k}\) is the lattice element \(\widetilde{0}\) and the rank one elements of \(L_{\mathcal {A}}\) are the hyperplanes. We recall the following definition and we refer to [7] (p. 15, 32–44) for details.

Definition 1.1

The Möbius function \(\mu : L_{\mathcal {A}} \rightarrow {\mathbb {Z}}\) is defined by

$$\begin{aligned} \left\{ \begin{array}{ll} \mu (\widetilde{0}) = 1,\\ \mu (t) = -\sum _{s<t}\mu (s), &{} \quad {\text {if }}\widetilde{0} < t{\text {.}} \end{array} \right. \end{aligned}$$

Definition 1.2

The Poincaré and characteristic polynomials of \(\mathcal {A}\) are defined as

$$\begin{aligned} \pi (\mathcal {A},t) = \sum _{x \in L_{\mathcal {A}}} \mu (x) \cdot (-t)^{\text {rank}(x)}, \text { and } \chi (\mathcal {A},t) = t^{\text {rank}(\mathcal {A})}\pi \bigg (\mathcal {A},\frac{-1}{t}\bigg ). \end{aligned}$$

Here rank(x) is the codimension of element \(x \in L_{\mathcal {A}}\), and \(rank(\mathcal {A}) = max\{rank(x):x \in L_{\mathcal {A}}\}\).

Let \(\mathcal {A} = \bigcup _{i=1}^{n} H_{i} \subset \mathbb {C}^{k}\) be a central arrangement and for each \(i\in \{1,\ldots ,n\}\) we fix \(V(\ell _{i}) = H_{i} \in \mathcal {A}\), and define \(Q_{\mathcal {A}} = \prod _{i=1}^{n} \ell _{i} \in S = \mathbb {C}[x_{1}, \ldots ,x_{k}]\).

Definition 1.3

The module of \(\mathcal {A}\)-derivations is the submodule of \(\text {Der}_{\mathbb {C}}(S)\) consisting of vector fields tangent to \(\mathcal {A}\):

$$\begin{aligned} D(\mathcal {A}) = \{\theta \in \text {Der}_{\mathbb {C}}(S) | \theta (\ell _{i}) \in \langle \ell _{i} \rangle \text { for all } \ell _{i} \text { with } V(\ell _{i}) \in \mathcal {A} \}. \end{aligned}$$

Definition 1.4

An arrangement is free when \(D(\mathcal {A})\) is a free S-module. In this case, the degrees of the generators of \(D(\mathcal {A})\) are called the exponents of the arrangement.

In order to verify whether a certain arrangement is free, we can use the following famous result due to Saito [9, Theorem 1.8, statement ii)].

Theorem 1.5

\(\mathcal {A}\) is free iff there exist k elements

$$\begin{aligned} \theta _{i} = \sum _{j=1}^{k} f_{ij} \frac{\partial }{\partial x_{j}} \in D(\mathcal {A}) \end{aligned}$$

such that \(\det ([f_{ij}]) = c \cdot Q_{\mathcal {A}}\) for some \(c \ne 0\).

The famous open problem, due to Terao, tells us that the freeness is combinatorial in nature. For this conjecture, we can assume that the ground field is of characteristic zero.

Conjecture 1.6

Freeness of \(D(\mathcal {A})\) depends only on the intersection lattice \(L_{\mathcal {A}}\).

In the note we are going to use the following famous Terao Factorization Theorem [12].

Theorem 1.7

If \(D(\mathcal {A})\) is free, then

$$\begin{aligned} \pi (\mathcal {A},t) = \prod (1+ a_{i}t), \end{aligned}$$

where \(a_{i}\)’s are the exponents.

2 Böröczky’s construction

Let us recall briefly the main construction of Böröczky line arrangements [3].

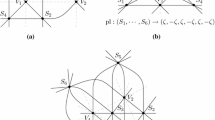
In general, if we want to obtain the arrangement \(\mathcal {B}_{n}\), which consists of n lines, we have to start with a regular 2n-gon inscribed in a circle O. Then we denote the vertices of this 2n-gon traced in clockwise order by \(P_{0},\ldots , P_{2n-1}\). In order to define the lines, we should note that we consider indices modulo 2n. Let \(\alpha \in \{0,1,\ldots ,n-1\}\). We get our n lines if in every \(\alpha \)-step we join \(P_{n - 4\alpha }\) with \(P_{2\alpha }\). Of course, it may happen that \(P_{n - 4\alpha }\) with \(P_{2\alpha }\) coincide – then we draw the tangent line to O at \(P_{2\alpha }\). As a result we obtain the arrangement \(\mathcal {B}_{n}\) which consists of n lines, \(n-3 +\varepsilon \) double points, and \(1 + \left\lfloor \frac{n(n-3)}{6} \right\rfloor \) triple points, where \(\varepsilon \) is equal to 0 if \(n = 0 \, \mathrm{mod}(3)\), or 2, otherwise. In Fig. 1. we depicted the case with \(n=12\).

Fig. 1
figure 1

Böröczky arrangement of 12 lines

Full size image

3 The Poincaré polynomials of line arrangements with only double and triple points

Let us restrict our attention to the following setting: we assume that our line arrangements have only double and triple points as the intersections and these are defined over the complex numbers.

This class of arrangements plays an important role in different branches of algebraic geometry and combinatorics. To mention just a few of the appearance, these can be found in Hirzebruch’s construction of surfaces which are ball-quotients [6], or around the so-called orchard problem and Dirac–Motzkin Conjecture [4].

Let us recall that for this class of line arrangements we have the following combinatorial equality, see [6, p. 114]

$$\begin{aligned} { |\mathcal {A}| \atopwithdelims ()2} = t_{2}(\mathcal {A}) + 3t_{3}(\mathcal {A}). \end{aligned}$$

Here \(|\mathcal {A}|\) denotes the number of lines, and \(t_{i}(\mathcal {A})\) denotes the number of i-fold points, i.e., points where i-lines meet, hence \(t_i=0\) for \(i\geqslant 4\). In our setting, it is easy to observe that \(\pi (\mathcal {A},t)\) has the following form

$$\begin{aligned} \pi (A,t) = 1+ |\mathcal {A}|t + (t_{2}(\mathcal {A}) + 2t_{3}(\mathcal {A}))t^{2} + (t_{2}(\mathcal {A}) + 2t_{3}(\mathcal {A}) + 1 - |\mathcal {A}|)t^{3}. \end{aligned}$$

4 Results

The first one tells us that for our particular class of line arrangements the Poincaré polynomial characterizes the combinatorics, which is not the case in general.

Proposition 4.1

Let \(\mathcal {A}, \mathcal {B}\) be two line arrangements having only double and triple points as the intersections. Suppose that \(\pi (\mathcal {A}, t) = \pi (\mathcal {B},t)\), then \(t_{2}(\mathcal {A}) = t_{2}(\mathcal {B})\) and \(t_{3}(\mathcal {A}) = t_{3}(\mathcal {B})\).

At the beginning, let us emphasize here that we can obtain an analogous result replacing triple points by arbitrary k-fold points with \(k\geqslant 3\).

Proof

Suppose that \(\pi (\mathcal {A},t) = \pi (\mathcal {B},t)\). This implies in particular that

$$\begin{aligned} |\mathcal {A}| = |\mathcal {B}| \end{aligned}$$

and

$$\begin{aligned} t_{2}(\mathcal {A}) + 2t_{3}(\mathcal {A}) = t_{2}(\mathcal {B}) + 2t_{3}(\mathcal {B}), \end{aligned}$$

which gives

$$\begin{aligned} t_{2}(\mathcal {A}) - t_{2}(\mathcal {B}) = 2(t_{3}(\mathcal {B}) - t_{3}(\mathcal {A})). \end{aligned}$$

Observe that

$$\begin{aligned} t_{2}(\mathcal {A}) + 3t_{3}(\mathcal {A}) = {|\mathcal {A}| \atopwithdelims ()2} = {|\mathcal {B}| \atopwithdelims ()2} = t_{2}(\mathcal {B}) + 3t_{3}(\mathcal {B}), \end{aligned}$$

and this gives

$$\begin{aligned} t_{2}(\mathcal {A}) - t_{2}(\mathcal {B}) = 3(t_{3}(\mathcal {B}) - t_{3}(\mathcal {A})). \end{aligned}$$

Since

$$\begin{aligned} 3(t_{3}(\mathcal {B}) - t_{3}(\mathcal {A})) = t_{2}(\mathcal {A}) - t_{2}(\mathcal {B}) = 2(t_{3}(\mathcal {B}) - t_{3}(\mathcal {A})), \end{aligned}$$

then this implies \(t_{3}(\mathcal {A}) = t_{3}(\mathcal {B})\) and we also have \(t_{2}(\mathcal {A}) = t_{2}(\mathcal {B})\), which completes the proof. \(\square \)

The main result of the note is the following classification result.

Theorem 4.2

Let \(\mathcal {A}\) be a line arrangement having only double and triple points as the intersections. Suppose that \(\mathcal {A}\) is free, then \(3 \leqslant |\mathcal {A}| \leqslant 9\).

Proof

Suppose that \(\mathcal {A}\) is free. Then by Terao’s result, the Poincaré polynomial \(\pi (\mathcal {A},t)\) splits into linear factors over the integers. Observe that

$$\begin{aligned} \pi (\mathcal {A},t) = (1+t)\cdot \bigg ( 1 + (|\mathcal {A}|-1)t + (t_{2}(\mathcal {A}) + 2t_{3}(\mathcal {A}) + 1 - \mathcal {A})t^{2}\bigg ), \end{aligned}$$

and the quadratic factor also splits into linear factors. This condition implies that

$$\begin{aligned} (|\mathcal {A}|-1)^{2} -4t_{2}(\mathcal {A}) - 8t_{3}(\mathcal {A}) +4|\mathcal {A}| - 4 \geqslant 0. \end{aligned}$$

Using the combinatorial equality

$$\begin{aligned} |\mathcal {A}|(|\mathcal {A}| - 1) = 2t_{2}(\mathcal {A}) + 6t_{3}(\mathcal {A}) \end{aligned}$$

one gets

$$\begin{aligned} 3|\mathcal {A}| - 3 \geqslant 2t_{2}(\mathcal {A}) + 2t_{3}(\mathcal {A}) \geqslant 2 | \mathcal {A}|, \end{aligned}$$

where the last right-hand side inequality comes from Hirzebruch’s inequality [6, p.132, Theorem]. This implies, in particular, that \(|\mathcal {A}| \geqslant 3\). Again, using the combinatorial equality one obtains

$$\begin{aligned} |\mathcal {A}| ( |\mathcal {A}| - 1) = 2t_{2}(\mathcal {A}) + 6t_{3}(\mathcal {A}) \leqslant 3(2t_{2}(\mathcal {A}) + 2t_{3}(\mathcal {A})) \leqslant 9|\mathcal {A}| - 9. \end{aligned}$$

This provides the condition \(|\mathcal {A}| \leqslant 9\), and finally we obtain \(3 \leqslant |\mathcal {A}| \leqslant 9\), which completes the proof. \(\square \)

Corollary 4.3

Except the cases \(n = 4,5,6\), Böröczky configurations of n lines are not free.

Proof

By the above result, it is enough to check the cases \(n \in \{4,5,6,7,8,9\}\). Since

$$\begin{aligned} \pi (\mathcal {A},t) = 1+ |\mathcal {A}|t + (t_{2}(\mathcal {A}) + 2t_{3}(\mathcal {A}))t^{2} + (t_{2}(\mathcal {A}) + 2t_{3}(\mathcal {A}) + 1 - |\mathcal {A}|)t^{3}, \end{aligned}$$

we obtain the following:

\(n = |\mathcal {A}|\)

\(t_{2}(\mathcal {A})\)

\(t_{3}(\mathcal {A})\)

\(\pi (\mathcal {A},t)\)

4

3

1

\(1 + 4t +5t^2 + 2t^3 = (t+1)^2(2t+1)\)

5

4

2

\(1 + 5t +8t^2 + 4t^3 = (t+1)(2t+1)^2\)

6

3

4

\(1 + 6t +11t^2 +6t^3 = (t+1)(2t+1)(3t+1)\)

7

6

5

\(1 + 7t +16t^2 + 10t^3 =(t+1)(10t^2+6t+1)\)

8

6

5

\(1 + 8t +21t^2 + 14t^3 =(t+1)(14t^2+7t+1)\)

9

6

10

\(1 + 9t + 26t^2 + 18t^3 =(t+1)(18t^2+8t+1)\)

It is easy to see that for \(n \in \{7,8,9\}\) we cannot factorize Poincaré polynomials into linear factors over the integers, so in these cases Böröczky arrangements are not free. When \(n=6\), then this arrangement is projectively equivalent to the well-known arrangement \(\mathcal {A}_{1}(6)\) (see  [5, p. 9]), which is known to be free. Now we focus on the remaining cases \(n \in \{4,5\}\) showing for them freeness explicitly. We will follow [2] and we compute the minimal free resolutions of the Milnor algebras. The formula (1.1) in [2] is crucial:

$$\begin{aligned} 0\rightarrow \oplus _{i=1,2}S(-a_i-(n-1))\rightarrow S^3(-n+1)\rightarrow S. \end{aligned}$$

If \(n=4\), then the defining equation has the form \(Q_{4}(x,y,z) = xy(y-x+z)(y+x-z)\). Denote by \(J_{\mathcal {B}_{4}}\) the Jacobian ideal generated by the partials of \(Q_{4}\), and by \(S/J_{\mathcal {B}_{4}}\) the Milnor algebra. Then the resolution of \(S/J_{\mathcal {B}_{4}}\) has the following form:

$$\begin{aligned} 0 \rightarrow S(-4) \oplus S(-5) \rightarrow S^{3}(-3) \rightarrow S, \end{aligned}$$

with the following relations:

$$\begin{aligned}&3x \cdot \partial _{x} Q_{4} - y \cdot \partial _{y} Q_{4} +(4x-z) \cdot \partial _{z} Q_{4} =0, \\&(4x^2-7xz) \cdot \partial _{x} Q_{4} +(13yz - 12xy) \cdot \partial _{y} Q_{4} +(16y^2-3z^2) \cdot \partial _{z} Q_{4} =0. \end{aligned}$$

This allows us to conclude that \(\mathcal {B}_{4}\) is free.

Now consider the case \(n=5\). As the coordinates of \(P_0,\ldots ,P_9\) (vertices of a regular 10-gon) in this case satisfy the condition \(\{P_0,\ldots ,P_9\} \subseteq \{(\pm (\frac{1}{4}\sqrt{5} \pm \frac{1}{4}),\pm \frac{1}{4}\sqrt{10 \pm 2\sqrt{5}})\}\), it is more convenient to change the coordinates and consider the following equivalent arrangement of lines given by

$$\begin{aligned} Q_{5}(x,y,z)= y(2y-x)(2y+3x)(x+2y-4z)(3x-2y-12z). \end{aligned}$$

The minimal resolution of \(S/J_{\mathcal {B}_{5}}\) has the following form:

$$\begin{aligned} 0 \rightarrow S(-6) \oplus S(-6) \rightarrow S^{3}(-4) \rightarrow S, \end{aligned}$$

with the following syzygies:

$$\begin{aligned}&(3x^2-20xy-20y^{2}+24xz) \cdot \partial _{x} Q_{5} + (24yz-12xy) \cdot \partial _{y} Q_{5} + (18xz+20yz-10xy\\&\quad -\,36z^2) \cdot \partial _{z} Q_{5} = 0, \\&(176xy+160y^2-288xz) \cdot \partial _{x} Q_{5} +(120xy +16y^2 -288yz) \cdot \partial _{y}Q_{5} +(15x^2+100xy\\&\quad -\,20y^2-240xz -224yz + 432z^2)\cdot \partial _{z} Q_{5} = 0, \end{aligned}$$

which tells us that \(\mathcal {B}_{5}\) is also free. \(\square \)

Remark 4.4

Observe that our simple criterion allows us, for instance, to conclude automatically that Rybnikov’s line arrangements [8] are not free.