Containment problem and combinatorics

Abstract

In this note, we consider two configurations of twelve lines with nineteen triple points (i.e. points where three lines meet). Both of them have the same arrangemental combinatorial features, which means that in both configurations nine of twelve lines have five triple points and one double point, and the remaining three lines have four triple points and three double points. Taking the ideal of the triple points of these configurations we discover that, quite surprisingly, for one of the configurations the containment $I^{(3)} \subset I^2$ holds, while for the other it does not. Hence, for ideals of points defined by arrangements of lines, the (non)containment of a symbolic power in an ordinary power is not determined alone by arrangemental combinatorial features of the configuration. Moreover, for the configuration with the non-containment $I^{(3)} \nsubseteq I^2$, we examine its parameter space, which turns out to be a rational curve, and thus establish the existence of a rational non-containment configuration of points. Such rational examples are very rare.

1 Introduction

The notion of the symbolic power of an ideal appears recently in many problems. Let $I\subset \mathbb {C}[\mathbb {P}^N]=\mathbb {C}[x_0,\dots ,x_N]$ be a homogeneous ideal. By m-th symbolic power of I, we mean $I^{(m)} = \mathbb {C}[\mathbb {P}^N] \cap \left( \bigcap _{\mathfrak {p} \in \mathop {\mathrm{Ass}}\nolimits (I)} (I^{m})_{\mathfrak {p}} \right) .$ For a radical ideal I, the Nagata-Zariski theorem says that $I^{(m)}$ is the ideal of all $f\in I$ which vanish to order at least m along the zero-set of I. The main question concerning the symbolic powers may be stated as follows. For which r and m does the containment

$$\begin{aligned} I^{(m)}\subset I^r \end{aligned}$$

hold? Or, more generally, when $M=(x_0,\ldots ,x_N)$, for which r, m and j do we have

$$\begin{aligned} I^{(m)} \subset M^jI^r? \end{aligned}$$

Ein, Lazarsfeld and Smith [11], and Hochster with Huneke [15] showed that, for any ideal $I \subset \mathbb {C}[\mathbb {P}^N]$, the containment $I^{(rN)} \subset I^r$ holds.

A few years ago Huneke asked if always $I^{(3)}\subset I^2$, afterwards Harbourne in [1] asked the following question. Let I be an ideal of points in $\mathbb {P}^N$. Does then the containment

$$\begin{aligned} I^{(rN-(N-1))} \subset I^r \end{aligned}$$

hold for all r? Lots of examples suggested that the answer is positive. For an ideal of points in $\mathbb {P}^2$ in particular, the question was if $I^{(2r-1)} \subset I^r$ holds. In the paper [10], the first counterexample for the case $r=2$, $N=2$ was presented. Since then, quite a few counterexamples appeared, see, e.g. [7, 14, 16,17,18,19] or are announced [2]. The case $r>2$ or $N>2$ is still open.

The first real—and rational—counterexamples (i.e. counterexamples where the coordinates of all points are real numbers) come from [7, 9] and [16]. They are modifications of Böröczky configuration of 12 lines. Böröczky configurations were introduced by Böröczky, they appeared in print probably for the first time in [6], and the construction of these configurations is described in the paper of Füredi and Palásti, see [13]. The non-existence of a rational counterexample among Böröczky configurations of 13, 14, 16, 18 and 24 lines is studied in [12]. Recently a new rational counterexample appeared, see [18].

In the paper of Bokowski and Pokora, [5], two non-isomorphic (and non-isomorphic to Böröczky configuration) examples of real configurations with 12 lines and 19 triple points are considered. They are named there $C_2$ and $C_7$.

In this paper, we consider the two configurations, $C_2$ and $C_7$. These configurations are realizable over the reals, and, what is interesting, they have the same arrangemental combinatorial features as Böröczky configuration of 12 lines. By “the same arrangemental combinatorial features”, we mean that both configurations have the same number of lines, the same number of triple and double points, and that their distribution on lines is the same. So here the 12 lines intersect in 19 triple points, 9 lines have 5 triple points and one double point on them; and 3 lines have 4 triple points and 3 double points. However, the incidence matrices of these configurations are not equivalent, i.e. it is not possible to pass from one matrix to the other by permutations of rows or columns, so the configurations do not have the same combinatorial data, cf. [4].

In this paper, we describe the parameter spaces of configurations $C_2$ and $C_7$. It turns out, that one of them, $C_2$, is “rigid”, this means that fixing some four out of 19 triple points (by a projective automorphism) to be (1:0:0), (0:1:0), (0:0:1), (1:1:1), the coordinates of other points can be computed, and these coordinates are non-rational. Moreover, for this configuration the containment $I_2^{(3)}\subset I_2^2$ holds, where $I_2$ is the radical ideal of the triple points of the configuration. The second configuration, namely $C_7$, turns out to have a one-dimensional projective space as a parameter space. Thus, we can take all the triple points of the configuration with rational coefficients. The radical ideal of these points, $I_7$, gives a new rational example of the non-containment $I_7^{(3)}\nsubseteq I_7^2$.

2 Configuration $C_2$

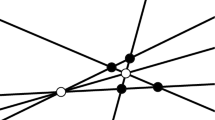
The real realization of the configuration $C_2$ is pictured in Fig. 1. Points $P_1$ and $P_2$ are “at infinity”.

Fig. 1

The real realization of the configuration $C_2$

By a projective automorphism, we may move any four general points of $\mathbb {P}^2$ into other four general points. Thus, we may assume (with the notation as in the picture) that $P_{1}=({1}{:}{0}{:}{0}), P_{2}=({0}{:}{1}{:}{0}), P_3=({0}{:}{0}{:}{1})$ and $P_4=({1}{:}{1}{:}{1})$. We take the following lines:

$$\begin{aligned} \begin{array}{ll} L_{1,3}: \ y=0,\\ L_{2,4}: \ x-z=0,\\ L_{1,4}: \ y-z=0,\\ L_{3,4}: \ x-y=0,\\ L_{2,3}: \ x=0, \end{array} \end{aligned}$$

where $L_{i,j}$, is the line passing through the points $P_{i}$ and $P_{j}$. Then we obtain the points

$$\begin{aligned} \begin{array}{ll} P_5= L_{1,3} \cap L_{2,4}=(1,0,1),\\ P_6= L_{1,4} \cap L_{2,3}=(0,1,1) \end{array} \end{aligned}$$

and the line

$$\begin{aligned} L_{5,6}: \ x+y-z=0. \end{aligned}$$

We need now to introduce a parameter to proceed with the construction. Thus, we take the point $P_7 = (0,1,a) \in L_{2,3}$. Since all points and lines in the configuration should be distinct, we assume that $a \ne 1$ and $a \ne 0$. We obtain the remaining lines and points in the following order:

$$\begin{aligned}&L_{1,7}:\ z-ay=0, \\&P_8= L_{1,7} \cap L_{2,4}=(a,1,a),\\&P_9= L_{1,7} \cap L_{5,6}=(a-1,1,a),\\&P_{10}= L_{1,7} \cap L_{3,4}=(1,1,a),\\&L_{2,9}:\ ax-(a-1)z=0, \\&P_{11}= L_{2,9} \cap L_{1,3}=(a-1,0,a),\\&P_{12}= L_{2,9} \cap L_{3,4}=(a-1,a-1,a),\\&P_{13}= L_{2,9} \cap L_{1,4}=(a-1,a,a), \\&L_{8,12}:\ a(2-a)x-ay+(a-1)^2z=0, \\&P_{14}= L_{8,12} \cap L_{1,3}=((a-1)^2,0,a(a-2)),\\&P_{15}= L_{8,12} \cap L_{5,6}=(a^2 -3a+1,-1,a(a-3)),\\&P_{16}= L_{8,12} \cap L_{1,4}=(a^2-3a+1,a(a-2),a(a-2)), \\&L_{10,11}:\ ax+a(a-2)y-(a-1)z=0, \\&P_{17}= L_{10,11} \cap L_{2,3}=(0,a-1,a(a-2)),\\&P_{18}= L_{10,11} \cap L_{2,4}=(a(2-a),1,a(2-a)), \\&L_{13,14}:\ a(a-2)x+(a-1)y-(a-1)^2 z=0, \\&L_{7,16}:\ a(a-1)(a-2)x-a(a^2-3a+1)y+ (a^2-3a +1) z=0, \\&P_{19}= L_{13,14} \cap L_{7,16}=(a^5 -5a^4 +7 a^3 -a^2 -3a +1, a^3 (a-2)^2, a^5 \\&\qquad \qquad -4a^4 +3a^3 +3a^2 -2a). \end{aligned}$$

Almost all points in the configuration are triple directly from the construction. Only for four of them, i.e. $P_{15}$, $P_{17}$, $P_{18}$ and $P_{19}$, we must verify this fact. We need to check the following incidences:

$$\begin{aligned} \begin{array}{ll} P_{15}= L_{8,12} \cap L_{5,6} \cap L_{10,11},\\ P_{17}= L_{10,11} \cap L_{2,3} \cap L_{13,14},\\ P_{18}= L_{10,11} \cap L_{2,4} \cap L_{7,16},\\ P_{19}= L_{13,14} \cap L_{7,16} \cap L_{5,6}. \end{array} \end{aligned}$$

By the determinant condition, we conclude that the lines $L_{8,12}$, $L_{5,6}$ and $L_{10,11}$ always meet at a point, but the remaining incidences occur under the algebraic condition

$$\begin{aligned} a^2 -2a -1=0. \end{aligned}$$

Thus, the configuration has no rational realization.

Then, implementing, e.g. in Singular [8], the ideal $I_2$ of all the triple points, we check that $I_2^{(3)}\subset I_2^2$. This inclusion may be explained also more theoretically. From [3], we have that if $\alpha (I^{(m)})\ge r\cdot \text {reg}I$ (where $\alpha (J)$ denotes the least degree of a nonzero form in a homogeneous ideal J), then the containment $I^{(m)}\subset I^r$ holds. It may be computed (e.g. with Singular) that reg $I_2=6$ and $\alpha (I^{(3)})=12$. Thus, $I_2^{(3)}\subset I_2^2$.

There is an interesting phenomenon that for ideal $I_{2}$ the inclusion $I_2^{(3)}\subset I_2^2$ is true, while for other configurations of 12 lines, Böröczky and $C_7$, with the same arrangemental combinatorial features, the inclusion does not occur, see the next section for $C_7$ and [16] for Böröczky. Thus, the arrangemental combinatoric features of the configuration do not determine the containment.

3 Configuration $C_7$

The real realization of the configuration $C_7$ is shown in Fig. 2 (the points $P_1, P_2, P_3$ are “at infinity”).

Fig. 2

The real realization of the configuration $C_7$

Here, using a projective automorphism, we may assume (with the notation as in the picture) that $P_1=(1,0,0), P_2=(-1,1,0), P_3=(1,1,0)$ and $P_4=(0,0,1)$. Then we have lines:

$$\begin{aligned} \begin{array}{ll} L_{2,4}:\ x+y=0,\\ L_{3,4}:\ x-y=0. \end{array} \end{aligned}$$

We need now to introduce the parameter to proceed with the construction, so take a point on the line $L_{3,4}$:

$$\begin{aligned} P_5=(a,a,1), \end{aligned}$$

where $a\ne 0$. We get the lines

$$\begin{aligned} \begin{array}{ll} L_{1,5}:\ y-az=0,\\ L_{2,5}:\ x+y-2az=0 \end{array} \end{aligned}$$

and the point

$$\begin{aligned} P_6=L_{2,4}\cap L_{1,5}=(-a,a,1) \end{aligned}$$

and then the line

$$\begin{aligned} L_{3,6}:\ x-y+2az=0. \end{aligned}$$

To continue, we need to choose another point. We take a point on the line $L_{2,5}$.

$$\begin{aligned} P_7=(b,-b+2a,1). \end{aligned}$$

We get the line

$$\begin{aligned} L_{4,7}:\ 2ax-bx-by=0. \end{aligned}$$

The condition for the lines $L_{4,7}, L_{2,5}, L_{3,6}$ to meet at $P_7$ is

$$\begin{aligned} ba=0. \end{aligned}$$

As $a\ne 0$, we have to take $b=0$. Thus, from now on:

$$\begin{aligned} P_7=(0,2a,1) \end{aligned}$$

and

$$\begin{aligned} L_{4,7}:\ 2ax=0. \end{aligned}$$

Again, we need a new parameter. Take a point on the line $L_{1,4}$

$$\begin{aligned} P_8=(c,c,1), \end{aligned}$$

where $a\ne c, c\ne 0$. Then

$$\begin{aligned}&L_{1,8}:\ y-cz=0, \\&P_9=L_{1,8}\cap L_{3,6}=(-2a+c,c,1),\\&P_{10}=L_{1,8}\cap L_{2,5}=(2a-c,c,1),\\&P_{11}=L_{1,8}\cap L_{2,4}=(-c,c,1). \end{aligned}$$

Now, choose the last parameter by taking a point, again on the line $L_{3,4}$

$$\begin{aligned} P_{12}=(d,d,1), \end{aligned}$$

with d different from 0, a and c. Then

$$\begin{aligned}&L_{1,12}:\ y-dz=0, \\&P_{13}=L_{1,12}\cap L_{3,6}=(-2a+d,d,1),\\&P_{14}=L_{1,12}\cap L_{2,5}=(2a-d,d,1),\\&P_{15}=L_{1,12}\cap L_{2,4}=(-d,d,1), \\&L_{10,15}:\ (c-d)x+(c-d-2a)y+2adz=0, \\&P_{16}=L_{4,7}\cap L_{9,12}=(0,4a^2d,-2a(-2a+c-d))\\&P_{17}=L_{10,15}\cap L_{1,5}=(2a^2-ac-ad,ac-ad,c-d), \\&L_{9,12}:\ (c-d)x+(2a-c+d)y-2adz=0, \\&P_{18}=L_{9,12}\cap L_{1,5}=(-2a^2+ac+ad, ac-ad,c-d), \\&L_{8,13}:\ (c-d)x-(2a+c-d)y+2acz=0,\\&L_{11,14}:\ (c-d)x+(2a+c-d)y-2acz=0, \end{aligned}$$

and finally

$$\begin{aligned} P_{19}=L_{8,13}\cap L_{11,14}=(0,4ac^2-4acd,4ac-4ad+2c^2-4cd+2d^2). \end{aligned}$$

Almost all points of the construction are triple without any additional conditions. Only $P_2$ and $P_3$ require an additional condition to be triple, namely:

$$\begin{aligned} 4a(a+c-d)=0. \end{aligned}$$

As $a\ne 0$, we get $a+c-d=0$. Thus, the parametrization space of this configuration is an affine plane and the configuration has a realization over $\mathbb {Q}$. It is not difficult to check (with help of, e.g. Singular) that the product of all twelve lines (which obviously is in $I_7^{(3)}$) does not belong to $I_7^2$. Thus, the triple points of this configuration give another rational example of the non-containment of the third symbolic power into the second ordinary power of an ideal.

For the convenience of the reader, we enclose the Singular script in Appendix.

Appendix

To check that the product of all twelve lines of the configuration $C_7$ does not belong to $I_7^2$, and thus $I_7^{(3)}\nsubseteq I_7^2$, the following Singular script may be used.