Adaptive Deprivation Scales in a Multi-National Context: The European Child Deprivation Indicators

Abstract

In 2018, EU Member States adopted a 17-item scale to measure child deprivation and monitor progress in their fight against child poverty. This indicator will be collected in future every three years via an ad hoc module of the European Union Statistics on Income and Living Conditions (EU-SILC). Previous research has shown how deprivation measures can be implemented more efficiently and with minimal information loss using adaptive testing, at least in the context of a single country. This paper examines the scope to implement the adaptive approach in a multi-national context with wide variations in deprivation levels and potentially in cultural preferences for consumption. The paper shows that the adaptive approach works effectively in this context. Time savings of around 40 per cent can be achieved with very minimal information losses both at the EU level and at the level of each individual country. Time savings are much greater in countries with lower deprivation. The adaptive approach may therefore offer particular advantages in a multi-national context as it can provide a consistent measure for all participating countries while targeting survey time and resources where they are most needed.

1 Introduction

Deprivation scales are non-monetary measures of poverty which capture household or individual consumption on a small set of indicative items or activities. These scales have been developed over more than 50 years (Townsend, 1979; Mack & Lansley, 1985; Callan et al., 1993; Nolan & Whelan, 1996; Gordon et al., 2000; Pantazis et al., 2006; Mack, 2018) and implemented in a wide range of national contexts in high-, middle- and low-income countries (Dickes et al., 2009; Gordon, 2006). They have also been adopted within official measures of poverty in many contexts, including by the European Union (EU). A scale to capture whole-population deprivation was adopted in 2009. It consisted at that time in nine items and was subsequently revised in 2017, now consisting of 13 items (Guio et al., 2016). In 2018, indicators of child deprivation were adopted at the EU level. They consist of 17 items (Guio et al., 2018).

The development of both EU deprivation scales followed the analytical framework developed in the context of the 1999 Poverty and Social Exclusion in the UK Survey (Gordon et al., 2000; Pantazis et al., 2006). A battery of tests assessing the suitability, validity, reliability and additivity of the items was used (see Guio et al., 2012, 2017). The items that successfully passed these tests were considered to be robust candidates for being aggregated into the deprivation measure. Among other tests, latent trait models, a cornerstone of modern testing theory, were used to assess the reliability of each deprivation item within the scale (Nunally, 1978; Nunally & Bernstein, 1996; Embretson, 1996; Embretson & Reise, 2000).

Latent trait models are a set of statistical models which describe the relationship between a person’s response to questionnaire items and an unobserved latent trait such as ability in a particular subject or, in this case, deprivation. Initially used in psychometric analyses and psychological testing, such models have been used for the measurement of deprivation for more than a decade (e.g. Martini & Vanin, 2013; Raileanu Szeles & Fusco, 2013; Fusco & Dickes, 2008; Cappellari & Jenkins, 2007). The fundamental insight from such models, also known as Item Response Theory (IRT), is that items in a scale are ordered by severity level (Deutsch et al., 2015; Guio & Pomati, 2016). In the context of deprivation scales, this means that, not only are some items lacked by more people than others, but more specifically that people tend to give up consumption of items in a predictable order as their resources fall. The ordering of items is estimated by fitting latent trait models.

This ordering of items provides the basis for adaptive testing where the set of items in a test asked of each individual is tailored to their initial responses. This enables tests to yield the most information for a given amount of time or survey resource (Embretson, 1996). Using the basis of deprivation scales in IRT, Bailey (2020) showed how adaptive testing could be applied to make them much more efficient. Rather than varying the items asked, the approach is simply to start questioning with the items where consumption tends to be given up first and stop if there is a strong indication from initial responses that the person will not lack any of the remaining items in the scale. When applied in the context of the UK’s child deprivation scale, Bailey (2020) shows that adaptive measures can yield time savings of around 50 per cent with very minimal information losses.

There are several potential benefits from adaptive deprivation scales. Most obviously, the time saving can mean a saving in survey costs or it can free up time which can be used to cover other topics. A reduction in time gives scope to introduce deprivation scales into a wider range of general purpose surveys where poverty is not the major focus, potentially deepening our insights into this key social problem. The main alternative currently is monetary poverty measures but these are notoriously prone to both error and bias, especially when based on only a few questions (Meyer & Sullivan, 2003; Moore et al., 2000). Adaptive approaches also offer a reduction in respondent burden and hence a likely improvement in data quality. In particular, the adaptive approach can remove the need to ask a long barrage of questions where many respondents will give the same negative answer to every single item, potentially causing irritation.

This last point could be a particular advantage in a context such as that of the EU where the scale has to cover countries facing very different national circumstances. Some countries have substantial deprivation with significant proportions of the population in more extreme deprivation. The scale needs to contain sufficient items to capture these cases. However, in the more affluent countries, only a very small fraction of the population may be deprived with few if any lacking items associated with extreme deprivation. In Sweden, for example, 88 per cent of households with children lack none of the 17 items in the EU scale whereas in Bulgaria, it is just 15 per cent. In Sweden, twelve items are lacked by less than 1 per cent whereas in Bulgaria, all 17 items are lacked by at least 26 per cent. (Figures from authors’ calculations, unweighted cases). This disparity can make richer nations more reluctant to adopt these scales, particular the items covering more extreme deprivation. The adaptive approach offers a potential solution here by enabling survey time and resources to be targeted where most needed yet still providing a measure which is directly comparable across all of the countries.

The aim of this paper is to broaden our understanding of adaptive deprivation scales by assessing whether the approach might be applied to the EU’s official child deprivation measure. In particular, we examine whether it performs sufficiently well both overall and within each individual country. The structure of the paper is as follows. In the next section, we introduce deprivation scales in general and the EU’s child deprivation indicator in particular. We explain the link between these scales and IRT, introducing the adaptive approach to deprivation scales developed in Bailey (2020) before discussing challenges in extending this to the EU context. The third section introduces the data source, the EU Statistics on Income and Living Conditions (EU-SILC), and provides details of the analytical approach. The fourth section summarises the findings while the last provides a concluding discussion.

2 Background

2.1 Deprivation Scales and Multi-Dimensional Poverty

Deprivation scales have a simplicity which belies their underlying methodological rigour. In the most common ‘enforced lack’ approach, people are asked whether they lack certain items or are unable to do certain activities. Where any lack is due to affordability, it is counted as a deprivation. Individuals are given an overall score based on the number of items lacked and counted as deprived where the score exceeds a threshold value.

These scales have their origin in the work of Peter Townsend and the surveys of poverty he conducted in the UK in the late 1960s (Townsend, 1979). Criticisms of his initial approach centred on the choice of items for inclusion in the measure which stemmed ultimately from Townsend’s personal judgement and the focus on whether households lacked items rather than lacking them through constrained resources (Piachaud, 1981). Developments by Mack and Lansley (1985) addressed both points: using popular opinion to determine the selection of items and focussing on lack arising from affordability. Further methodological developments were made through the increasing sophistication of the statistical checks on deprivation items, with recent scales being subject to checks not just on the grounds of item suitability (the popular support point) but also validity, reliability and additivity (Gordon et al., 2000; Pantazis et al., 2006).

Within the wider literature on the measurement of poverty, it has long been argued that poverty should be seen as multidimensional (Atkinson, 2003). There is, however, a lack of consensus about the best way to measure and combine these different dimensions. Following the approach of Alkire and Foster (2011), for example, dimensions must be specified, and rules developed to assess an individual’s level of deprivation on each dimension, and then to identify whether someone has sufficient deprivations to count as poor. The ‘union’ approach requires someone to be poor on just one dimension, the ‘intersection’ approach requires them to be poor on all, while counting approaches set the threshold somewhere in between, potentially also employing relative weights.

Multidimensionality in this context is often drawn very broadly. Alkire and Foster (2011: 477), for example, note that dimensions “might relate to health, education, work, living standards, or empowerment”. People can be deprived through very different combinations of deprivations so one might identify different types or groups among the poor. The global Multidimensional Poverty Index (MPI) (Alkire & Santos, 2010, 2014; Alkire et al., 2015), as well as numerous regional and national MPIs (see for example Alkire et al, 2021 for a recent development in Europe) use the family of mathematical measures proposed by Alkire and Foster (2011) and make a number of additional assumptions in terms of the number and type of dimensions, the choice of components in each, the thresholds used to identify deprivation in each component and in each dimension, and the weights in each dimension and between them. Critics (notably Ravallion [2011]) argue that the relative weighting of dimensions in multi-dimensional measures, whether left equal or made explicit, may differ substantially from perceptions of welfare for those in poverty.

Despite some superficial similarities, the consensual deprivation method, which has been followed to construct the EU deprivation indicators, departs from the MPI approach in many aspects. First, it focuses on a relatively narrow set of goods, services or activities. While it covers different aspects of consumption (food, clothing, housing, social activities, for example), the items are far less wide-ranging than the multidimensional scales. Second, the choice of the items included in the index is driven in part by popular views¹ but also in part by a set of empirical criteria which aim to ensure that the index fulfils construct validity and reliability requirements.² Third, the dimensional structure of the deprivation index is not pre-specified as it is in most MPIs but is derived from data analysis. Dimensional analysis is often conducted as part of the screening of items for these scales. For example, in constructing the EU’s child deprivation scale, Guio et al (2018) employ Hierarchical Omega Analysis to estimate the proportion of variation in the scale items accounted for by a single latent variable, concluding that the items form a unidimensional scale.

2.2 The EU’s Child Deprivation Scale

The EU included questions on material deprivation in its household surveys as early as 1994 through the European Community Household Panel (ECHP) and it continued these in the successor EU-SILC surveys (Nolan & Whelan, 2010). However, the questions took on a much greater significance from 2009 when the EU Member States agreed to include a material deprivation indicator in the portfolio of measures used to monitor poverty and social inclusion at the EU level and to monitor progress in each Member State. In 2010, the deprivation indicators gained further visibility when the severe material deprivation indicator formed part of the social inclusion target within the Europe 2020 strategy (European Council, 2010).

Reflecting their increased political importance, these indicators were further refined and developed. On the basis of the results of a Eurobarometer survey to identify which deprivation items are needed for people to have a decent life in the country where they live (see footnote 1. above), an ad hoc module was included in the 2009 EU-SILC surveys covering 50 items, including 17 for children. Analysis of this data by Guio et al. (2012) led to an update of the original whole-population deprivation scale (officially revised in 2017) and to a proposal for a child deprivation scale with 18 items: 13 on children’s consumption or activities and five on household deprivations (the latter already part of the whole-population scale). In both cases, items included had to cover “key aspects of living conditions which appear to be customary across the whole EU and from which some people are excluded due to a lack of resources” (Guio et al., 2012, p.11).

To further test the child deprivation scale, the 18 items were included in a second ad hoc module within the 2014 EU-SILC surveys and again subject to a barrage of tests (Guio et al., 2018). From this, a set of 17 items was selected (dropping one of the initial child items – ‘suitable place to do homework’). The five household items are collected annually as they form part of the whole-population scale. The 12 child items not covered by the whole-population deprivation scale will be collected from 2021 in 3-yearly modules. The whole set is as follows (with the short name used to refer to each in this paper shown in square brackets):

• 1. Child: Some new (not second-hand) clothes [clothes]

• 2. Child: Two pairs of properly fitting shoes [shoes]

• 3. Child: Fresh fruits and vegetables daily [fruit]

• 4. Child: Meat, chicken, fish or vegetarian equivalent daily [meat]

• 5. Child: Books at home suitable for the children’s age [books]

• 6. Child: Outdoor leisure equipment [outdoor]

• 7. Child: Indoor games [indoor]

• 8. Child: Regular leisure activities [activities]

• 9. Child: Celebrations on special occasions [celebration]

• 10. Child: Invitation of friends to play and eat from time to time [invitation]

• 11. Child: Participation in school trips and school events that cost money [school trip]

• 12. Child: Holiday [holiday]

• 13. Household: Arrears [arrears]

• 14. Household: Home adequately warm [warm]

• 15. Household: Access to a car for private use [car]

• 16. Household: Replace worn-out furniture [furniture]

• 17. Adults in the household: Access to internet [internet]

The EU child-specific deprivation score is created by simply summing the (unweighted) number of items lacked. The lack of three or more items is the standard threshold for identifying children as deprived (Guio et al., 2018). More complex weighted approaches have sometimes been adopted although Bailey (2020) argues that these are both theoretically inappropriate and empirically unnecessary (see also Guio et al., 2012). Further, Nájera Catalán (2019) provides the more general finding from numerical experimentation that the higher the reliability, the less important it is to weight the items.

2.3 Adaptive Deprivation Scales and IRT

IRT is set of statistical models which describe the relationship between a person’s response to an item of a questionnaire and an unobserved latent trait that the item intends to measure, such as knowledge or ability in a specific domain (Guio et al, 2018). The link between the development of deprivation scales and IRT has been recognised for some time (Martini & Vanin, 2013; Raileanu Szeles & Fusco, 2013; Fusco & Dickes, 2008; Cappellari & Jenkins, 2007; Guio & Pomati, 2016; Bailey, 2020). The main use of IRT here is to guide the selection of items for inclusion in the scales. Two-parameter latent trait models allow items to be assessed on two characteristics:

• Severity or difficulty measures the point on the distribution of the latent trait where people tend to give up consumption of an item, i.e. how poor they typically are when they lack this item;

• Discrimination measures how well an item differentiates between the deprived and the not-deprived, i.e. the extent to which consumption is driven solely by the latent trait, deprivation, or is influenced by other factors.

Ideally, a deprivation scale should include items with a range of severity levels in order to capture lower to higher severity situations. Items may be rejected where they have very high severity indicating that they are only lacked by people with the most extreme deprivation and therefore likely to be captured in only very small numbers by surveys. In terms of discrimination, items with high discrimination are desirable and low discrimination may be grounds for rejection as it suggests that lack may be driven by factors other than deprivation. Both criteria were applied at the country level in the construction of the EU’s child deprivation scales (Guio et al., 2012, 2018).

Bailey (2020) shows that this connection with IRT also provides a basis for adaptive testing. Items in deprivation scales are ordered, as captured by item severity. As household resources fall, people start to report the lack of items in a more-or-less predictable order. People with low levels of deprivation tend to lack similar items which are therefore more commonly lacked. People with higher levels of deprivation tend to lack those same items but also some of the more rarely-lacked ones. It follows that, if people do not lack the most commonly lacked items, it is unlikely – and possibly extremely unlikely – that they will lack the more rarely-lacked items.

The adaptive deprivation scale therefore works by asking a small initial set of the deprivation items with the lowest difficulty (most commonly lacked). On the basis of responses to those, the decision is made whether to halt questioning or continue. Questioning is halted when there is very good reason to expect that subsequent answers will all be negative (i.e. no further items will be lacked). Responses for the unasked questions are effectively set to negative i.e. it is assumed people do not lack those later items. If questioning continues, the next set of items is asked, again based on ordering by difficulty, with a further decision about whether to halt after that stage. There are potentially many different ways of structuring the test (algorithms) depending on the number of stages, the number of questions at each stage and the rules applied for deciding when to stop. We explore a large number of variations in this paper.

The adaptive approach produces a time saving which can be measured by the proportion of deprivation questions which do not have to be asked (i.e. the proportion of cases where questioning halts at a given stage multiplied by the proportion of questions unasked at that point). On the other hand, some information may be lost if people did actually lack some of the later items but were recorded as not lacking because questioning stopped. In general, information losses rise as time savings rise so the key question is whether there are algorithms which achieve sufficient time savings to justify the approach while also keeping information losses acceptably small. Different measures can be used to assess information losses by focussing on the impacts on the overall deprivation score, the classification of people into deprived or not, the average depth of deprivation or the numbers lacking individual items. All four approaches are used here as noted in the methods section below.

Bailey (2020) tests the adaptive approach using data for the UK’s official child deprivation scale for the years 2010/11–17/18. The full scale contains 21 items, nine based on household consumption and 12 for children. The analysis identifies one approach which yields time savings of around 50 per cent with very minimal information losses at the level of the overall scale or the measure of deprivation but with somewhat greater losses at the level of individual items. A more conservative approach could yield time savings of around 40 per cent and still capture 98 per cent of all items lacked as recorded by the full scale.

2.4 Challenges for an EU-Wide Adaptive Deprivation Scale

Two approaches might be taken to developing an adaptive scale for a multi-national context such as the EU. One would be to fit latent trait models for each country separately so the ordering of items reflected national consumption patterns. While it is likely to lead to greater efficiencies, it would add complexity in terms of the harmonisation of data collected which is a core goal of the EU-SILC. This could raise questions about the comparability of measures across countries which could in turn undermine acceptability. The approach in this paper is therefore to assess the feasibility of using a single algorithm for the whole EU, derived from one latent trait model fitted to all countries together. For comparison, it also examines whether separate adaptive scales for each country would perform significantly better than the EU-wide approach.

Although more complex in terms of data collection, the national approach might be preferable from an efficiency point of view for two reasons. First, despite EU-wide agreement on the items to be included in the scale, there may still be substantial variations between countries in the ordering of items. As resources fall, people in different countries may sacrifice different aspects of consumption earlier while preserving others, reflecting cultural preferences. As the ordering of items is key to adaptive testing, this may make it difficult if not impossible to find an approach which works effectively in all national contexts.

Second, the precise trade-off between time saved and information lost may vary, reflecting differences in item ordering but also the overall level of deprivation in each country. Using the standard threshold of lacking three or more items, child deprivation levels across the EU varied from less than 10 per cent in countries such as Sweden, Finland, Denmark, Luxembourg or Slovenia to more than 60 per cent in Bulgaria and Romania (Guio et al., 2018). In order to attract support, the adaptive approach has to prove effective not just for the set of EU countries as a whole but also for each country individually.

Previous research on the whole population deprivation indicators across the EU tends to support the idea that a single common algorithm could be feasible. Deutsch et al. (2015) and Guio and Pomati (2016) both compared the ordering of deprivation items between EU countries. Deutsch et al. (2015) used two methodologies: IRT and the concept of deprivation sequence which is an extension of the notion of “order of acquisition of durable goods” (p.724). Both approaches showed similar results when applied to EU countries. Overall, the order of curtailment found in the data does not differ substantially between EU Member states. Guio and Pomati (2016) extended this approach using both the cross-sectional and the longitudinal components of EU-SILC and reached similar conclusions.

For the original 18-item child-specific deprivation scale, Guio et al. (2012) and Guio et al. (2017) used IRT to test the severity and discrimination of all items and showed that the same list of items passed the tests in the EU countries. They also looked at the extent of multi-dimensionality when testing the reliability of the scale using hierarchical omega analysis. Across all EU countries, they find very similar levels of multidimensionality (i.e. the relationship between the hierarchical omega and the unidimensional omega is almost identical in each country). They also use hierarchical cluster analysis, reporting Beta as a measure of the internal homogeneity (lack of multi-dimensionality) of the scale for the EU as a whole and the individual countries. Here there is rather more variation between countries although they also note that the item ultimately dropped from the set of 18 is a significant factor in reducing homogeneity in a number of countries.

2.5 Research Questions

To focus the analysis which follows, we address three research questions:

• RQ1: When fitting latent trait models, is the ordering of items within individual countries similar to the ordering for the EU as a whole?

• RQ2: Are there adaptive algorithms which produce substantial time savings without serious information losses at the level of the EU as a whole and at the level of each individual country?

• RQ3: If we allow the algorithm to vary by country, how much improvement is there over a single EU-wide algorithm?

In the end, judgements about the success of an adaptive deprivation scale are subjective. It is the decision of data producers whether any time saving is sufficient to justify the corresponding information losses and whether any algorithm can attract sufficient support from across the participating countries. The purpose of this analysis is to reveal the scale of time savings and information losses under different conditions, and hence the trade-off between them in order than an informed decision can be made.

3 Data and Methods

3.1 Data

The data come from the ad hoc module on child deprivation conducted as part of the 2014 EU-SILC surveys (Eurostat, 2014). The paper covers the 27 member states of the EU as they are at the time of writing. Figures have been produced for the wider set of countries which provided child deprivation data in the 2014 survey and these are available on the github repository which hosts the code (https://github.com/nick-bailey/Adaptive-deprivation-EU-SILC); these also cover Iceland, Serbia, Switzerland and the UK. The sample is restricted to households with children. As the deprivation questions are asked at the household level, the analysis is on the basis of households rather than children because this is the level at which any time savings would be made. For the same reason, unweighted data are used throughout. Cases with any missing data on the 17 deprivation items were dropped but this affected only a very small percentage of cases (at most, 8.6 per cent in Ireland, with only six other countries above 3 per cent). With ‘school trips’, responses are missing where there are no school-age children but these are re-coded to ‘not deprived’ for this item.

Fifteen of the deprivation items have three response categories: have the item/do the activity; do not have/do – can’t afford; or do not have/do – other reasons. Only the second of these is counted as deprivation following the ‘enforced lack’ approach (Guio et al., 2012, 2018). One item (‘warm’) has only the first two options since it is assumed that affordability is the only reason for not keeping the home adequately warm in winter. The last item (‘arrears’) is constructed from responses to three related questions which ask about missed payments for mortgage/rent, utility bills and loans repayments. A response indicating any missed payments on any of these items is taken as a deprivation.

3.2 Latent trait Models

Following Bailey (2020), latent trait models are estimated using the standard two-parameter model which allows items to vary by severity/difficulty and discrimination. One model was estimated for all 27 countries together and this forms the basis for most of the results reported here. Item difficulties from this model are used to order items for the adaptive measures. One minor issue is that this effectively gives greater ‘weight’ to countries that have larger survey samples (e.g. Italy and Poland). We could make some adjustment (e.g. by randomly re-sampling within countries to balance numbers in relation to populations). In the end, countries with larger samples have more potential for time saving so it makes sense to leave this unadjusted. Separate latent trait models were also estimated for each country to assess how the ordering of items varies between countries and to explore the relative efficiency gains from a national rather than EU-wide approach (RQ3).

3.3 Adaptive Algorithms

Many different algorithms can be devised for the adaptive measures based on the number of stages of questioning, the number of questions asked at each stage and the rules for deciding when to stop. To keep things manageable, we focus on algorithms with questions asked in three groups, i.e. with two points at which we might stop. We ask an initial group of i items (i.e. the i items with lowest difficulties) and stop if the respondent lacks none of these. If they lack one or more of these i items, we then ask about the next j items, ordered by difficulty, and stop if the respondent lacked only one from these first two groups together. If they lack two or more, we ask the remaining questions. For shorthand, we refer to this as the “i + j” algorithm.

We explore every permutation where the first group contains three to ten items (i varies from 3 to 10), and the second group from three to ten (j varies from 3 to 10). There is a limit of 17 across the two groups as this is the maximal number of items and, in this case, there is no third group of questions. On the stopping rules, experimentation quickly showed that the most conservative approach (described here) was most appropriate; all others led to levels of information loss which would very likely be unacceptable.

Time savings are measured following the definition above (effectively the proportion of questions in the scale which we do not have to ask). Different measures are used to assess information losses. To begin with, we look at the proportion of cases which were measured as deprived on the full scale (lacking three or more items) but which would not be regarded as deprived on the adaptive scale (i.e. the proportion of deprived cases ‘missed’). This measure is used to select a subset of four algorithms which appear to perform particularly well but deliver slightly different combinations of time saving and information loss. Further measures of information loss are then used to evaluate these four algorithms in more detail. These are:

• the deprivation rate produced by the adaptive versus full scales;

• the correlation between deprivation scores on adaptive and full scales;

• the depth of deprivation for households with deprived children on adaptive and full scales; and

• the proportions lacking each individual item on adaptive and full scales.

We evaluate the algorithms at the level of the 27 countries as a group and at the level of each country separately.

3.4 Data Access and Reproducibility

The EU-SILC data (Eurostat, 2020) were obtained under license from Eurostat by following their standard procedures. The license conditions prevent onward sharing of the data but other researchers can obtain the same data in the same way. Dataset preparation and analysis were done using R v4.0.3 (R Core Team, 2013) using the ‘tidyverse’ suite of packages (Wickham et al., 2019) along with ‘ltm’ (Rizopoulos, 2006), all up-to-date at October 2020. The code are freely available from a github repository (https://github.com/nick-bailey/Adaptive-deprivation-EU-SILC) enabling all the analysis and figures to be reproduced.

4 Findings

4.1 The Varying National Contexts

Child deprivation levels vary enormously across the countries of the EU (Fig. 1); see Appendix for country names. The percentages shown here will differ slightly from those reported by Guio et al. (2018) as our analysis uses unweighted data and the unit of analysis is the household rather than the child as in the official EU indicator. In more affluent countries, few households with children lack even one item whereas in the poorest, a majority lack at least five items. Using the threshold of lacking three or more items, the proportion of households regarded as deprived varies from less than five per cent in Sweden, Finland and Denmark to more than 60 per cent in Romania and Bulgaria. Where deprivation rates are very low, the potential time savings from an adaptive scale are much greater as more households will lack none of the initial group of items, regardless of how many items that group has.

Fig. 1

Deprivation levels across the 27 countries. Note: EU-SILC 2014, unweighted data for households with children. Countries ordered by mean number of items lacked. Caption: Barchart shows proportion of households lacking different numbers of items from zero to ten or more. Each country shown separately along with average for EU-27

Of more importance for the adaptive approach, however, is the ordering of items within each country – our first research question. If the ordering varies too much, no single algorithm will be able to operate sufficiently well in every case and national algorithms will be needed. Figure 2 shows the ordering of items by severity/difficulty from the country-level latent trait models (y-axis) against the ordering from the EU-wide model (x-axis). We also show the rank correlation (Spearman’s rho). In 22 of the 27 countries, the correlation is above 0.5 indicating broad agreement but also some divergence. Finland is lowest (0.29) while four Central & East European countries were also below 0.5: Estonia, Czechia, Romania, Bulgaria.

Fig. 2

Item ordering by difficulty from EU-wide and country-specific latent trait models. Note: EU-SILC 2014, unweighted data for households with children. Countries ordered by mean number of items lacked. Caption: Scatterplot for each country showing rank order of item within country against rank order of item for EU-27. Also shows rank correlation coefficient in each case

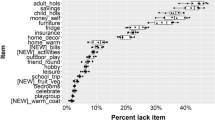
The EU ranking is as follows:

• 1. Furniture

• 2. Holiday

• 3. Activities

• 4. Arrears

• 5. Invitation

• 6. Outdoor

• 7. Celebrations

• 8. Clothes

• 9. Warm

• 10. School trip

• 11. Indoor

• 12. Meat

• 13. Books

• 14. Car

• 15. Internet

• 16. Fruit

• 17. Shoes

For the adaptive approach, it is the ordering of items with the lowest severity/difficulty which is most important since these are used in the first stage of data collection, when the most cases are affected. There we see rather more similarity. For example, there are only four countries that do not have three of the ‘top four’ items from EU-wide model in the ‘top four’ within their national model (Luxembourg, Estonia, Slovakia and Spain). In Slovakia, ‘arrears’ in particular seems different with a much higher difficulty on the national model than the EU-wide model; some other Central and East European countries are similar (see Czechia, Lithuania, Romania and Bulgaria for example). Overall, however, the picture is quite encouraging.

4.2 Selecting Adaptive Algorithms

Turning to the second research question, we start by examining how a wide range of adaptive algorithms perform at the EU-wide level in order to select four for further analysis. We measure information loss by the proportion of cases counted as deprived on the full scale (lacking 3 + items) which would not be counted as such on the adaptive scale. If we choose a higher deprivation threshold (lacking 6 + items, for example), the adaptive approach works progressively better (i.e. time savings are the same but information losses fall) so using the lower threshold is a relatively harsh test. Note also that all cases which are counted as ‘not deprived’ on the full scale will always be counted the same on the adaptive scale so focussing only on the deprived cases magnifies information losses.

Figure 3 summarises the results for the range of algorithms tested. Each line links results for algorithms which share the same number of items in the initial group (Group 1), with points denoting the differing number of items in the second group (Group 2). The algorithms cover the great majority of possible permutations with three groups and two stopping points. The Figure illustrates the core relationship that increases in time savings tend to come with rising information losses – the broad upward curve. There is not one solution which is obviously the ‘best’. Rather there is a choice to be made between the goals of maximising time saved and minimising information lost. There are however better and worse solutions: at any level of time saving, for example, there are solutions with more or less information loss. The latter are the algorithms lying along the bottom edge of the broad curve of points.

Fig. 3

Deprived cases missed versus time saved using a range of adaptive algorithms. Note: EU-SILC 2014, unweighted data for households with children. Caption: Scatterplot of time saving (x-axis) versus percent of deprived cases missed (y-axis). Details described in text

We select four algorithms for further evaluation. The “4 + 10” algorithm is the one which offers the highest time saving (45 per cent) while keeping information losses on this measure to 0.49 per cent (i.e. it misses just 0.49 per cent of cases regarded as deprived using the full scale). We add three more with progressively lower information losses but also lower time savings: “5 + 9”, “6 + 8” and “7 + 7”. These have time savings of 41, 38 and 35 per cent and information losses of 0.41, 0.28 and 0.24 per cent respectively. The fact that all of these cover the first 14 items indicates that the last three items rarely if ever determine whether someone is above or below the 3 + deprivation threshold; people who lack the last three items will almost always be regarded as deprived on the basis of the earlier 14 items.

Figure 4 shows time savings and information losses for the four selected algorithms at the level of each country. Not only are levels of missingness and savings different but the relationship between the two changes so it is not a consistent trade-off. In the majority of countries (N = 17), information losses change very little between algorithms. Algorithms with the smaller initial group (e.g. “4 + 10”) therefore perform better with time savings up to 15 per cent greater than the “7 + 7” algorithm. Most of these countries have zero or near zero information losses but there are three with losses around 1 per cent on all four algorithms (Finland, Belgium and Malta). Other countries show more or less of a trade-off but in most these cases (N = 7), the difference in information losses remains below 0.5 per cent. Three countries show more marked variations in information losses with Slovakia the most striking; Romania and Bulgaria are the other two.

Fig. 4

Deprived cases missed versus time saved using selected adaptive algorithms. Note: EU-SILC 2014, unweighted data for households with children. Countries ordered by mean number of items lacked. Caption: Scatterplots of time saved versus percent of deprived cases missed, one for each country plus EU as a whole. Details in text

4.3 Evaluating Adaptive Algorithms

We evaluate the selected algorithms using four further ways of assessing information losses: deprivation rates, correlations between full and adaptive scales, depth of deprivation and proportions lacking each item.

4.3.1 Deprivation Rates

Looking at the proportion of deprived cases missed by the adaptive approach exaggerates information losses because it ignores the fact that the adaptive approach provides a correct measure for all of those in the ‘not deprived’ category. A fairer test might be to compare deprivation rates using the adaptive and full scales (Fig. 5). In every country and for each of the four algorithms, deprivation rates are either identical or virtually indistinguishable. Only in the two countries with the highest levels of deprivation (Romania and Bulgaria) are the differences visible and, even then, only for the two algorithms which have higher information losses (‘4 + 10’; ‘5 + 9’). In Bulgaria, for example, the deprivation rate for the ‘5 + 9’ algorithm is 64.6 per cent compared with 65.4 per cent on the full scale. In more than half the comparisons, the difference is less than 0.05 per cent.

Fig. 5

Deprivation rates on full and adaptive scales. Note: EU-SILC 2014, unweighted data for households with children. Countries ordered by mean number of items lacked. Caption: Barcharts, one per country, showing deprivation rates for each of four algorithms plus the full scale

4.3.2 Correlations

The previous figure looks at differences using a single threshold (lacking 3 + items), reducing the deprivation scales to binary measures. We can also evaluate the adaptive approach using correlations between deprivation scores on full and adaptive scales. This is more appropriate where we are interested in relative levels of deprivation as would be the case, for example, when using the scale in regression models where we were examining how rising levels of deprivation relate to other phenomena. In these cases, the actual level or count matters less than the relationship between deprivation and those phenomena. If the adaptive and full scales correlate highly, the former can effectively substitute for the latter.

We can look at correlations for all cases but we can also focus on the non-zero cases (i.e. those with at least one deprivation on the full scale). The latter is a tougher test but perhaps appropriate given the predominance of households with no deprivations in most countries. Either way, correlations are extremely high. Finland has the lowest correlations but even here they are 0.99 for all cases and 0.98 for non-zero cases on the “4 + 10” algorithm and higher still on the others. For the EU-27, the correlation is 0.997 on that algorithm.

4.3.3 Depth of Deprivation

In addition to deprivation rates, policy makers are increasingly paying attention to the depth of deprivation: for households in deprivation, this is the average number of items lacked. This tends to rise with the deprivation rate, with the average depth ranging form four or five items for the ten countries with the lowest deprivation rates, up to eight items for Romania and ten for Bulgaria.

Using the adaptive scales, depth of deprivation is either identical or very nearly so in 20 countries; differences are less than 0.01. The depth of deprivation is marginally higher on the adaptive scale because it is the least-deprived households which tend to be missed. For four other countries, the difference is between 0.01 and 0.03. The highest difference is Bulgaria where it is 0.09 for the first algorithm, declining to 0.04 for the last. In proportional terms, this is still a very marginal difference.

4.3.4 Lacking Individual Items

The fourth and toughest test for the adaptive approach is to look at information losses at the level of individual items. In doing this, we should bear in mind that the primary intention in selecting deprivation items is to construct a scale which works as a whole, not to cover specific areas of consumption; the items are meant to be indicative not exhaustive. Nevertheless, there is sometimes interest in looking at the proportions lacking specific items.

We could show information losses in terms of the proportion of households lacking an item where the adaptive approach fails to identify this lack. However, this tends to highlight items which very few people lack because missing just a handful of these cases produces a high proportion. Instead we focus on the percentage of households missed by the adaptive approach (i.e. the difference between the percentage lacking an item on the full scale and the percentage lacking it on the adaptive scale). For simplicity, Fig. 6 shows this difference using the “5 + 9” algorithm. As all households are asked about the first five items, there is zero item missingness for those. For the other items, missingness is very low. In 11 of the 27 countries, item missingness is never above one percent while in 24 of the 27 countries, it is never above two per cent. One country (Romania) has two items with missingness of 2–3 per cent (car and internet). The outliers are Malta and Lithuania where the missingness for the item ‘warm’ is five and seven per cent respectively.

Fig. 6

Percent lacking item on full scales but not on adaptive scale. Note: EU-SILC 2014, unweighted data for households with children. Algorithm: “5 + 9”. Countries ordered by mean number of items lacked. Dashed line at 2 per cent purely to emphasise this threshold. Caption: Barchart, one per country, showing proportion of cases where lack of each item is missed

4.4 Country-Specific Models

To address the third research question, we construct adaptive scales for each country using country-specific latent trait models. We examine time saved versus information lost using these models and the same four algorithms used above, comparing these with the same algorithms applied to the EU-wide latent trait model (Fig. 7). Overall, country-specific models do not give consistently better results, contrary to expectations. In 11 countries, the country-specific model does better at every or almost every threshold, i.e. time savings are greater while information losses are the same or lower. Finland, Germany, Italy, Ireland and Romania would be examples. Time savings tend to be similar but information losses somewhat lower. Eight countries show minimal differences or slightly mixed results: Sweden, Czechia and Portugal would be examples. In the last eight countries, the EU-level model does better at all or almost all thresholds: Austria, Poland and Spain are examples.

Fig. 7

Country-level vs EU-level adaptive scales. Note: EU-SILC 2014, unweighted data for households with children. Countries ordered by mean number of items lacked. Caption: Scatterplots, one per country, showing time saving (x-axis) versus deprived cases missed (y-axis) for each of four algorithms and using the EU-wide LTM and the country-specific LTM

5 Further Issues Specific to EU-SILC

Up to now, we have examined the EU’s child deprivation scale as if it were a standalone module. However, as noted in the background section, the EU-SILC includes a whole-population scale collected annually and a child deprivation scale currently collected every three years, and the latter includes five items which are also part of the former. This would constrain any adaptive approach in practice since it would not be possible to omit one of the five whole-population items unless the adaptive approach were also applied to that scale. Such an extension would increase potential time savings but it would also increase the complexity of the task of designing a suitable algorithm. For this paper, we have ignored this constraint since we are more concerned with the general question of how the adaptive approach works in a multi-national context rather than the specifics of the EU-SILC.

Another possibility is raised by having both scales in the survey. If we assume that the whole-population scale is asked first, responses on those items could be used as the basis for initial screening for the 12 child-specific items: they can be used to identify cases where all of the child items could be skipped. This could be combined with the adaptive approach, the latter being used with the remaining child-specific items. In effect, this a new first stage in the adaptive approach. The whole-population items contain significant information about levels of child deprivation so this is likely to be very effective. To give one example, where households lack none of the whole-population items (40 per cent of cases at the EU level), they are extremely unlikely to lack any of the child items. These households account for just 0.4 per cent of all deprived cases. We do not pursue this approach further in this paper since it has limited wider relevance.

6 Discussion and Conclusions

Building on Bailey (2020), this paper extends our understanding about the potential to use adaptive testing methods to achieve more efficient measures of deprivation. It does this through the first examination of adaptive testing in a multi-national context, looking across the EU’s 27 countries with their very different standards of living and deprivation levels. While our focus has been on the deprivation scale, the questions raised in this paper and the method proposed would also be highly relevant for the efficient measurement of other social phenomena which concern a limited part of the sample and where data are collected through a battery of questions (housing deprivation, life satisfaction, health conditions etc.). In a general context where resources devoted to social statistics are limited and respondent burden needs to be minimised, surveys should avoid asking a large number of questions when the same information (or very nearly) can be collected with just a few.

The specific challenge examined here is to find an approach or algorithm for the EU’s new child deprivation scale which delivers sufficient time saving while minimising information losses, both for the EU-27 as a whole and at the level of each individual country. The paper identifies algorithms which yield time savings between 35 and 45 per cent with extremely low information losses. To take one algorithm as an illustration (“5 + 9”), the time saving is 41 per cent but the algorithm misses just 0.4 per cent of deprived cases for the EU as a whole and, for individual countries, there are just four where it misses more than 1 per cent of cases. The estimated deprivation rate is virtually identical to that based on the full measure for the EU as a whole (21.71 compared with 21.80 per cent). For individual countries, the deprivation rate on the adaptive measure is never more than 0.9 per cent lower and the biggest gap is for Bulgaria where the overall deprivation rate is 65 per cent. The correlation between full and adaptive scales is 0.997 for all 27 countries, and never less than 0.98 in any individual country. Even when we drill down to look at the 17 individual items separately in each of the 27 countries, there are just four cases where the adaptive measure is more than two per cent lower than the full measure.

The ability of the adaptive approach to work so well across the 27 countries covered here is quite surprising in some ways, given the extent of variation between them in overall levels of deprivation. It functions well because the ordering of items within countries is broadly similar, especially for the more commonly lacked items. In large part, this stems from the process used to construct the index which focussed on identifying items which were suitable, valid, reliable and additive in all the individual countries (Guio et al., 2018). However, the analysis also provides further reassurance about the coherence of the deprivation scale.

If an adaptive scale is used in future to collect information on child deprivation in EU countries, it will be important to regularly re-assess its efficiency. Indeed, if some items become strongly subsidised in some countries or consumption practices change, the ranking of items may change and consequently the algorithm would need to be adapted to remain efficient. We therefore advise that the full scale should be collected in every country periodically to check that the approach remains valid. This would need to be done for the periodic re-basing of items in the scales in any case.

While the results here represent a significant extension of the earlier work for the UK (Bailey, 2020), it remains an open question how far they can be extended to work effectively in more diverse international settings. For all its diversity in living standards, the 27 nations of EU fall within the same continent, with historical and contemporary links, not least in the shared political project of the EU itself. All except two would be regarded as ‘high income countries’. It remains to be seen how well an adaptive scale might cope with a much more diverse set, spanning low, middle and high income contexts. However, even if different deprivation scales are developed in each specific context, the methodology proposed in this paper could be used for each of them separately to achieve more efficient measures of deprivation.

Up to now, work on adaptive scales has focussed on information losses at the level of the whole population of a country. If there are significant differences in consumption preferences within the population, however, it is possible that information losses are higher in some groups than others. Adaptive scales would then systematically under-report deprivation for those groups, relative to the full scale, with potentially significant implications in terms of the focus of policy efforts. Obvious sources of variations in consumption include age, gender or ethnicity. Further research is needed to identify the scale of any such variations and their implications for adaptive measures.

It is not the task of this paper to recommend a single algorithm but rather to show the potential of the adaptive approach. The preferred algorithm will depend on the primary intended uses for the index and in particular whether the interest is in deprivation overall or the lack of individual items. It will also depend on the judgements of each individual country as to whether the balance of time savings and information losses is appropriate there. However, it is worth emphasising that the greatest potential time savings accrue in the richer countries since questioning halts in a larger proportion of households in these cases. This may help make the scales more acceptable in these countries despite the fact that so few households are regarded as severely deprived and very few lack the items which tend to indicate more severe deprivation. The ‘cost’ of the EU-wide scale could be reduced by 60–70 per cent in several of the most affluent countries with virtually no loss of information. In relation to the point just above, the adaptive approach might therefore have particular value for the development of consistent measures of deprivation indices across more diverse national contexts.

Appendix: Country labels and names

Label	Country
AT	Austria
BE	Belgium
BG	Bulgaria
CY	Cyprus
CZ	Czechia
DE	Germany
DK	Denmark
EE	Estonia
EL	Greece
ES	Spain
FI	Finland
FR	France
HR	Croatia
HU	Hungary
IE	Ireland
IT	Italy
LT	Lithuania
LU	Luxembourg
LV	Latvia
MT	Malta
NL	Netherlands
PL	Poland
PT	Portugal
RO	Romania
SE	Sweden
SI	Slovenia
SK	Slovakia