1 Introduction

Seismic data imaging is a key task of seismic data processing. It began with post-stack time migration (Bednar 2005), then pre-stack time and depth migration (e.g., Claerbout 1971; Claerbout and Doherty 1972; Gazdag 1978; Schneider 1978; Stolt 1978; Gazdag and Sguazzero 1984; Ma and Ji 1988; Hill 1990; Wu and Huang 1992; Ristow and Ruhl 1994; Popovici 1996; Stoffa et al. 1990), and reached reverse-time migration recently (e.g., Lailly 1983; Whitmore 1983; Baysal et al. 1983; Zhang et al. 2011). Currently, full-waveform inversion (FWI) represents the latest development of seismic data imaging and becomes a hotspot in this field. One reason is that it fills the resolution gap between tomography and migration, which is illustrated in Fig. 1. FWI is an optimization process that seeks an Earth model, e.g., P-wave velocity, to best fit the waveform of seismic record in a sense of the norm defined in the objective function. The concept and framework of FWI were proposed by Tarantola (1984), who is a French professor in geophysics. However, limited by the capacity of the computers in that time, Tarantola (1984) did not demonstrate FWI with numerical examples but derived the gradient of bulk modulus, density and source wavelets using functional analysis in the acoustic assumption. This derivation employed the adjoint-state method (Plessix 2006), and thus the gradient can be computed by backward propagating the adjoint source; it avoids formulating, storing and inverting the gigantic Jacobian matrix. Consequently, FWI became a feasible technique later.

Fig. 1
figure 1

Schematic illustration of the accuracy and resolution range of tomography, migration and full-waveform inversion. The solid black curve indicates the accuracy and resolution range of the results of tomography and migration (Claerbout 1985). There is a gap between 2 and 10 Hz, which can be filled by the results of full-waveform inversion with large-offset refractions and low-frequency signals (Biondi and Almomin 2013)

Full size image

Although the framework of conventional FWI was defined in the paper of Tarantola (1984), its title is “Inversion of seismic reflection data”; therefore, the author’s main objective is to invert reflection data. However, the conventional FWI proposed by Tarantola is ineffective for inverting reflection data. This will be analyzed fully in the subsequent section.

The second milestone of FWI was made by geophysicist Pratt (1999), who successfully applied FWI on an ultrasonic data set from a cross-hole geometry. Pratt used matrix algebra to reformulate the theory of FWI, which was derived with functional analysis by Tarantola (1984). It makes the theory of FWI more understandable. Pratt (1999) also pointed out the maximum resolution of FWI is the resolution of half wavelength, which is much higher than that of tomography, i.e., the width of the first Fresnel zone. Unfortunately, restricted by the speed and RAM size of computers at that time, Pratt solved the 2D acoustic wave equation in the frequency domain (Štekl and Pratt 1998). Compared to wavefield modeling in the time domain, there are two advantages in the frequency domain: firstly, factorization of the Helmholtz equation needs only once for multi-shot modeling; secondly, it is convenient to achieve attenuation by introducing velocity in complex numbers (Mueller 1983).

The third milestone of FWI was achieved by geophysicist Sirgue in BP (Sirgue et al. 2009), who successfully applied 3D frequency domain FWI on the oil field Valhall using 3D OBC data. It was the first time to demonstrate that FWI is capable of fixing background velocity and recovering the high-frequency structures with industry seismic data (see Fig. 14 of Virieux and Operto 2009). Since then, FWI has attracted wide attention and heavy research investments from both academia and industry. It is difficult to directly solve a 3D wave equation in the frequency domain. Sirgue achieved the frequency domain modeling indirectly by solving time-domain wave equations with finite-difference methods and applying discretized Fourier transform to extract a few interesting frequencies used for inversion (Sirgue et al. 2008). Afterward, Warner et al. (2013a) applied 3D time-domain anisotropic acoustic wave equation to FWI and successfully inverted the OBC data from the Tommeliten field in the North Sea. The inverted model reflects the gas-cloud boundary clearly and improves the accuracy and continuity of the anticline in the depth migration image significantly.

The open mark of the FWI workshop in SEG of that year (2013) is “Full-waveform inversion has emerged as the final and ultimate solution to the Earth resolution and imaging objective.” It emphasized that FWI is the final and ultimate solution of seismic data inversion and imaging. This point of view was questioned by some peers working on other seismic imaging methods, for instance, professor Weglein. He (2013) argued that acoustic FWI uses “wrong mathematic model” (acoustic wave equation), “wrong data” (pure pressure data) and “wrong method” (iterative methods) to invert a more complex Earth model. To some extent, Weglein’s argument about the early stage of FWI, i.e., the theory of Tarantola (1984) makes sense. The theory of Tarantola (1984) is based on the acoustic wave equation to invert P-wave velocity and density from pure pressure data using iterative methods. However, the Earth is not pure acoustic. Except for P-wave velocity and density, it includes S-wave velocity and other seismicity parameters. Consequently, acoustic wave equation cannot simulate wave propagation accurately. In addition, pure pressure data are insufficient for recovering P-wave, S-wave velocities and density simultaneously. Furthermore, gradient-based iterative methods could lead FWI to converge a local minimum due to the nonlinearity of FWI.

The main reasons for the successes on FWI achieved by Sirgue and Warner et al. include: firstly, fine-tuned inversion codes; secondly, good inversion strategies; thirdly, high-quality seismic data. Their inversion strategies are elaborated in their papers. Except for high signal-to-noise ratio, OBC/OBS data have some favorable features by FWI: firstly, although the Earth has elastic property, thanks to seawater filtering, the record by the hydrophones of OBC/OBS is similar to seismic data simulated by using acoustic wave equation; secondly, since the separation between OBC/OBS and air-guns, the offset of records can be very large, which helps to record transmitted (refractions and turning waves) seismic waves from a large depth; finally, the OBC/OBS data include rich low-frequency signals (< 3 Hz). These features help FWI to recover background velocity and mitigate cycle skipping.

Conventional FWI proposed by Tarantola (1984) fixes background velocity using refractions and turning waves mainly; therefore, conventional FWI needs these data in large offsets to repair the deep part of the model. A rule of thumb is that the maximum depth of background that FWI can fix is about a 1/5–1/3 of the maximum offset, which is the maximum penetration depth of turning waves (e.g., Zhou et al. (2015) pointed out that the maximum penetration depth is about 1.5 km for the turning waves in a record of an offset of 6 km from the Valhall field). FWI is a nonlinear problem, the reasons of which include: firstly, the wavefields in the wave equation have a nonlinear relationship with the model parameters; secondly, seismic signals oscillate around the zero value, the faster the oscillation (higher frequency), the stronger the nonlinearity. FWI is a large-scale inverse problem, which may contain millions of unknowns. In addition, the computational cost is high for solving wave equations numerically. Thereby, FWI currently is based on local-gradient methods, e.g., steepest-descent and conjugate-gradient methods. In order to avoid trapping in a local minimum due to nonlinearity, FWI usually begins from the lowest available frequency and then gradually increases the frequency. This strategy is called multi-scale proposed by Bunks et al. (1995). This also is the reason why FWI needs low frequencies.

In practice, due to large errors in the initial model, the time lag of the events in predicted data and observed data may be larger than half a period; even the lowest frequency still suffers cycle skipping. Consequently, solving cycle skipping turns into an important topic in FWI studies. Currently, the first category of proposed methods for cycle skipping is to introduce objective functions that have wider convex region; for example, the objective function based on penalizing the nonzero lags of cross-correlation or deconvolution [e.g., Adaptive Waveform Inversion—AWI (Warner and Guasch 2016; Guasch et al. 2019; van Leeuwen and Mulder 2010; Luo and Sava 2011; Zhu and Fomel 2016)], optimal transport distance functions (Métivier et al. 2016; Yang and Engquist 2018; Yang et al. 2018), Wavefield Reconstruction Inversion—RWI (van Leeuwen and Herrmann 2013; da Silva and Yao 2017), etc.

The second category of these methods aims to create lower-frequency signals through signal processing means, for instance, the envelope of seismic data (Wu et al. 2014; Chen et al. 2018a, b), the modulation of two close frequencies (Beat-tone, Hu 2014), downward frequency extrapolation (Warner et al. 2013b; Chen et al. 2019). The methods belonging to the third category utilize the travel time of seismic events to formulate the objective function, e.g., Jiao et al. (2015). Currently, the most widely used method for retraveling the travel-time information is dynamic time/image warping—DTW/DIW from the field of image processing (Hale 2013). Besides, there are some other methods, for example, intermediate data by Wang et al. (2016) and Yao et al. (2019b).

The most direct and efficient method for solving cycle skipping is to improve the acquisition systems for generating and recording lower-frequency signals. One successful example is the ultra-low-frequency marine seismic source, Wolfspar, designed by BP. It can produce the seismic signal as low as 1.6 Hz (Dellinger et al. 2016), which leads to their huge success of applying FWI on the Atlantis oil field in the Gulf of Mexico (Shen et al. 2017). BGP created an onshore controlled vibrator source, which can produce low frequencies as low as 1.5 Hz (Baeten et al. 2013). Unfortunately, so far not many successful FWI examples on land seismic data have been reported due to some complex factors, including low SNR, surface waves, near-surface heterogeneity and elastic effects (Mei and Tong 2015; Cheng et al. 2017; Sedova et al. 2019).

Multi-parameter inversion is another important research direction of FWI. The parameters include P-wave velocity, S-wave velocity, density, anisotropic parameters (ε, δ, γ) and attenuation factor Q. The biggest challenge in multi-parameter inversion is the cross-talk between different types of parameters; it means that the seismic data response generated by the perturbation of one type of parameter could be mapped back into the model perturbation of another type of parameter, for instance, the cross-talk between P-wave velocity and S-wave velocity. In mathematics, the cross-talk is a manifestation of ill-posedness of the inversion problem. The fundamental reason is that the number of independent data is less than the number of unknowns in the model. Except better inversion strategies, e.g., optimized parameterization (Tarantola 1986; Mora 1987; Zhou et al. 2015; Kazei and Alkhalifah 2019; Pan et al. 2019), the inversion system needs extra information to constrain inversion.

As described previously, the record in large offsets drives FWI to update the background velocity model. However, the data in large offsets exist two problems: firstly, low SNR, which is caused by energy attenuation through long wave paths; secondly, strong AVO effects, AVO in the real data follows the rule of elastic (not acoustic) waves on the interfaces (Aki and Richards 1981; Shuey 1985; Castagna et al. 1998; Wang 1999), which causes that predicted data generated by acoustic wave equation cannot match the waveform of recorded data accurately (da Silva et al. 2019). Besides, with current acquisition techniques, only reflections can reach the depth of targets. The three factors lead to the birth of an important branch of FWI—RWI (also called reflection full-waveform inversion—RFWI), which utilizes reflections to recover the background velocity under the framework of FWI. In the rest of this paper, we will review the principle, algorithm and examples of RWI.

2 The weaknesses of conventional FWI for inverting reflection data

Conventional FWI is an optimization problem. In the case of the simplest wave equation, i.e., isotropic acoustic wave equation, the objective function of conventional FWI is the square of L2-norm of data difference expressed as:

$$\phi = \frac{1}{2}\left\| {{\text{D}}u\left( v \right) - d} \right\|_{2}^{2} ,$$
(1)

which is constrained by the wave equation,

$$\left( {\frac{1}{{v^{2} }}\frac{{\partial^{2} }}{{\partial t^{2} }} - \nabla^{2} } \right)u = s,$$
(2)

where d denotes the observed seismic data, including refractions and reflections, u represents the simulated seismic wavefield from the velocity model v, s is the source wavelet, D denotes the receiver operator for extracting out the predicted data from u at the receivers’ location, D is a pulse function or identity matrix for a single-channel recording system. If a receiver is formed by a group of detectors, D is a stack of multi-pulse functions, and thus the non-diagonal elements may not be zero. The expression of the gradient of (1) can be found in the papers of Tarantola (1984), Pratt (1999) and Virieux and Operto (2009).

If conventional FWI applies to pure reflections starting with a smooth velocity model, which does not contain interfaces (this is common in real applications), then as illustrated in Fig. 2, the processes of forward and backward propagation generate only transmitted waves in the first iteration. Consequently, the gradient generated with zero-lag cross-correlation builds interfaces but does not contain components for background velocity update. This is because the waves in the forward and backward propagations only meet at the interfaces. In the later iterations, the wave paths of the source and residual wavefields are overlapped on and above the interfaces; therefore, the gradient contains the components for both interface and background update. Based on this observation, Mora (1989) proposed “Inversion = migration + tomography,” which means RWI possesses two functionalities, i.e., migration and tomography. Note that Mora did not mean that migration plus tomography is equivalent to inversion. Migration aims for building interfaces, while tomography is for background velocity update.

Fig. 2
figure 2

Behavior of conventional FWI for pure reflection data using a smooth starting model. a At the first iteration, only transmitted energy exists in both the source and residual wavefields. Cross-correlating these builds interface and does not update velocity. b At subsequent iterations, reflected energy exists in both wavefields. Cross-correlation can now update the velocity model, but the magnitude of this tomographic effect varies as R2, whereas updates to the reflectivity vary as R. Usually, R is much smaller than 1 (Yao and Wu 2017)

Full size image

As depicted in Fig. 2b, in general, the reflectivity of rock interfaces is much smaller than 1, usually less than 0.05. As a result, the gradient at interfaces is one order of magnitude higher than that above the interfaces, which causes FWI based on gradient methods mainly updates interfaces rather than the background velocity model. This is one of the weaknesses of conventional FWI for inverting pure reflection data.

On the contrary, the transmission coefficient is close to 1, for instance, the transmission coefficient is 0.95 if the reflection coefficient is 0.05. As a result, the magnitude of the gradient formed by transmitted waves is relatively uniform along the wave paths; conventional FWI with transmitted waves is good at fixing background velocity as well as rebuilds the interfaces with reflections.

FWI produces a model that contains interfaces after the first iteration. The predicted reflection data from the model fit the observed reflection data in a least-squares sense. Conventional FWI is based on a trace-by-trace comparison. Consequently, if the events in predicted data arrive later than the corresponding events in observed data, then inversion increases velocity; otherwise, inversion decreases velocity. In the case that the velocity of the current model is greater than the actual velocity, the events in predicted data are intercepted by the events in observed data (Fig. 3), and the travel time of the events between the intercept points (indicating small offsets) in predicted data is larger than that in observed data. The travel time outside the intercept points (indicating large offsets) in predicted data is smaller than that in observed data. In the rest iterations, the data between the intercept points drive inversion to increase background velocity for reducing travel time. However, the data outside the intercept points push inversion to decrease background velocity for raising travel time. Consequently, the two parts of data contradict each other, which leads to inversion stuck into a local minimum. The whole inversion then mainly updates the interfaces, which is equivalent to impedance inversion rather than fixing background velocity. This is the significance of FWI inverting reflection-dominated data (Wang and Rao 2009; Lazaratos et al. 2011; Plessix and Li 2013; Routh et al. 2016; Yao et al. 2018b). The contradiction and trapping in a local minimum are the second weakness of conventional FWI for inverting reflection data.

Fig. 3
figure 3

The move direction of predicted data in conventional FWI. After the first iteration, the reflector that fits the observed data in a least-squares sense is built. In the subsequent iterations, the section of the event between the two intercept points indicates the update direction of the background velocity is opposite to the rest section of the event. Consequently, the inversion is stuck in a local minimum

Full size image

3 Reflection-waveform inversion

Conventional FWI inverting pure reflection data have two weaknesses: firstly, the migration component in the gradient is much stronger than the tomography component; secondly, inversion traps in a local minimum. Thus, the inversion mainly rebuilds the interfaces rather than fixes background velocity. Modifying the algorithm of conventional FWI for fixing background velocity using reflection data is the aim of reflection-waveform inversion (RWI). In order to solve the two weaknesses, studies of RWI mainly focus on the three topics: (1) separation of tomography and migration components; (2) optimizing the objective functions; (3) improving the stability of inversion by incorporating constraints.

3.1 Separation of tomography and migration components

The tomography and migration components in the gradient of conventional FWI are mixed. If the source wavefield shares the same wave path with the residual wavefield, then zero-lag cross-correlation produces the tomography component. If the tomography component is formed from transmitted waves, then its sensitivity kernel has a shape of banana (e.g., Fig. 4a, Fig. 1a of Xu et al. 2012, or Fig. 5b of Virieux and Operto 2009). If the tomography component is formed from reflection waves, then the kernel is like “rabbit ears” (e.g., Fig. 4b, Fig. 1d of Xu et al. 2012). As the tomography component updates the model along the whole wave path, the tomography component is key for updating background velocity. As illustrated in Fig. 5b of Virieux and Opetro (2009), the resolution of the tomography component to the model is the width of the first Fresnel zone. This is because that other order Fresnel zones will be canceled out and then only the first Fresnel zones will remain if many sensitivity kernels are stacked together.

Fig. 4
figure 4

The sensitivity kernels of a transmitted waves and b reflected waves in conventional FWI. The sensitivity kernel of transmitted waves has a shape of banana because the velocity usually increases with the increase in depth. On the contrary, the sensitivity kernel of reflected waves includes the oval-shaped migration component and the rabbit-ear-like tomographic component. The dashed gray line represents the interface. The blue curves indicate the ray paths of the transmitted and reflected waves. The blue and green crosses “×” represent the location of the source and the receiver, respectively

Full size image
Fig. 5
figure 5

A vertical seismic record profile. a A three-layer velocity model. A 25 Hz Ricker wavelet is used as the source signature. The black circle on the surface indicates the source location; the dashed vertical line represents the distribution of the receiver array. b shows the vertical profile, in which all the down-going events tilt toward right while all the up-going events tilt toward left

Full size image

If the source wavefield travels in a different direction to the residual wavefield, then zero-lag cross-correlation generates the migration component. This situation only happens to reflections at the interfaces. The sensitivity kernel of the migration component has a shape of an ellipse, e.g., Fig. 4b, Fig. 1b of Xu et al. (2012). Multiple ellipse-shaped sensitivity kernels stack together to form the interfaces of the model.

As can be seen from Fig. 2, the migration component is much stronger than the tomography component in the gradient formed from reflections. In order to emphasize the tomographic function of FWI, it is necessary to separate the tomography component in the gradient from its migration component. Currently, the separation methods can be divided into three categories: (1) up/down wavefield separation; (2) scattering angle filtering; (3) born-based modeling.

3.1.1 Up/down wavefield separation

The gradient of the FWI system formed by Eqs. 1 and 2 can be expressed as:

$$g\left( {\mathbf{x}} \right) = - \frac{2}{{v^{3} }}\int\limits_{0}^{T_{max}} {\vec{U}\left( {{\mathbf{x}},t} \right)\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftarrow}$}}{U} \left( {{\mathbf{x}},t} \right){\text{d}}t} ,$$
(3)

where \(\vec{U}\left( {{\mathbf{x}},t} \right)\) and \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftarrow}$}}{U} \left( {{\mathbf{x}},t} \right)\) represent the first-order time derivative of the source and residual wavefields, respectively, at the location of x and the time of t.

If the source and residual wavefields are decomposed into upward and downward wavefields, then the migration and tomography components can be expressed as:

$$g_{\text{mig}} \left( {\mathbf{x}} \right) = - \frac{2}{{v^{3} }}\int\limits_{0}^{{T_{max} }} {\left( {\vec{U}_{\text{U}} \left( {{\mathbf{x}},t} \right)\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftarrow}$}}{U}_{\text{D}} \left( {{\mathbf{x}},t} \right) + \vec{U}_{\text{D}} \left( {{\mathbf{x}},t} \right)\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftarrow}$}}{U}_{\text{U}} \left( {{\mathbf{x}},t} \right)} \right){\text{d}}t} ,$$
(4)

and

$$g_{\text{tomo}} \left( {\mathbf{x}} \right) = - \frac{2}{{v^{3} }}\int\limits_{0}^{{T_{max} }} {\left( {\vec{U}_{\text{U}} \left( {{\mathbf{x}},t} \right)\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftarrow}$}}{U}_{\text{U}} \left( {{\mathbf{x}},t} \right) + \vec{U}_{\text{D}} \left( {{\mathbf{x}},t} \right)\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftarrow}$}}{U}_{\text{D}} \left( {{\mathbf{x}},t} \right)} \right){\text{d}}t} ,$$
(5)

where the subscripts U and D represent the upward and downward wavefields, respectively. As can be seen from Fig. 5, the separation of the upward and downward wavefields can be achieved using Fourier transform along the time and depth directions, in which the part of \(\omega k_{z} \ge 0\) corresponds the downward wavefield while the part of \(\omega k_{z} < 0\) is the upward wavefield (Hu and McMechan 1987). However, Fourier transform along the time and depth axes is prohibited in the time-domain FWI. Liu et al. (2011) derived an image condition that removes the background noise in the RTM image effectively and efficiently. This imaging condition only carries out 1D Fourier transform along the depth axis. The background noise in the RTM image is the tomography component in the FWI gradient, while the rest part is the migration component. Wang et al. (2013) utilized this imaging condition to separate the two components, which can be expressed as

$$g_{\text{mig}} \left( {\mathbf{x}} \right) = - \frac{2}{{v^{3} }}\int\limits_{0}^{{T_{max} }} {\left( {\vec{U}_{ + }^{ * } \left( {{\mathbf{x}},t} \right)\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftarrow}$}}{U}_{ - } \left( {{\mathbf{x}},t} \right) + \vec{U}_{ - }^{ * } \left( {{\mathbf{x}},t} \right)\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftarrow}$}}{U}_{ + } \left( {{\mathbf{x}},t} \right)} \right){\text{d}}t}$$
(6)

and

$$g_{\text{tomo}} \left( \mathbf{x} \right) = - \frac{2}{{v^{3} }}\int\limits_{0}^{{T_{max} }} {\left( {\vec{U}_{ + }^{ * } \left( {{\mathbf{x}},t} \right)\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftarrow}$}}{U}_{ + } \left( {{\mathbf{x}},t} \right) + \vec{U}_{ - }^{ * } \left( {{\mathbf{x}},t} \right)\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftarrow}$}}{U}_{ - } \left( {{\mathbf{x}},t} \right)} \right){\text{d}}t} ,$$
(7)

where the superscript * represents complex conjugate, \(U_{ + } \left( {{\mathbf{x}},t} \right)\) and \(U_{ - } \left( {{\mathbf{x}},t} \right)\) can be computed by taking inverse Fourier transformation of

$$U_{ + } \left( {k_{z} ,t} \right) = \left\{ {\begin{array}{*{20}l} {U\left( {k_{z} ,t} \right),} \hfill & {\quad k_{z} \ge 0} \hfill \\ {0,} \hfill & {\quad k_{z} < 0} \hfill \\ \end{array} } \right.,$$
(8)

and

$$U_{ - } \left( {k_{z} ,t} \right) = \left\{ {\begin{array}{*{20}l} {0,} \hfill & {\quad k_{z} \ge 0} \hfill \\ {U\left( {k_{z} ,t} \right),} \hfill & {\quad k_{z} < 0} \hfill \\ \end{array} } \right..$$
(9)

Equations 8 and 9 imply that \(U_{ + } \left( {{\mathbf{x}},t} \right)\) and \(U_{ - } \left( {{\mathbf{x}},t} \right)\) can be computed using Hilbert transform alternatively (Liu et al. 2011; Fei et al. 2015; Chi et al. 2017; Lian et al. 2018). The mechanism of Eqs. 6 and 7 for the separation of the incident and reflection waves is based on the assumption that the incident wave travels downwards, while the reflection wave propagates upwards (Fig. 5). However, if the strata have a large dipping angle (e.g., Figure 12 of Liu et al. 2011), this method fails to separate the wavefields. Consequently, the tomography component contains the migration component, vice versa. Since the migration component usually is much stronger than the tomography component, this leakage does not affect the result of RTM very much, but the leakage in the tomography component could lead to RWI updating background velocity along the wrong direction significantly. Wang et al. (2018) from CGG demonstrated that the leakage can cause inversion to update the model toward the wrong direction at the steep flanks of salt bodies. In order to mitigate this issue, Irabor and Warner (2016) proposed to split the wavefield into two parts, one of which travels along the vertical axis and the other of which propagates along the horizontal axis, and then applied Eqs. 6 and 7 to separate the two parts into the upward and downward waves. In the isotropic acoustic media, the vertical and horizontal waves can be simulated by using the equation system,

$$\left\{ {\begin{array}{*{20}c} {\frac{1}{{v^{2} }}\frac{{\partial^{2} u_{x} }}{{\partial t^{2} }} - \frac{{\partial^{2} u}}{{\partial x^{2} }} = \frac{s}{2}} \\ {\frac{1}{{v^{2} }}\frac{{\partial^{2} u_{z} }}{{\partial t^{2} }} - \frac{{\partial^{2} u}}{{\partial z^{2} }} = \frac{s}{2}} \\ \end{array} } \right.,$$
(10)

where uz and ux represent the vertical and horizontal wavefields.

3.1.2 Scattering angle filtering

The migration component is generated when the source wavefield meets the residual wavefield around the interfaces; the tomography component is formed when the waves meet on the wave path. As illustrated in Fig. 6, the two types of components can be separated according to the scattering angle between the source and residual waves: if the scattering angle is close to 180°, the cross-correlation of the two wavefields forms the tomography component; otherwise, the migration component is generated. Thus, the scattering angle can be used as an indicator to separate the two components. Three methods have been proposed for scattering angle filtering. The first filtering method is based on the time-lag gather (Khalil et al. 2013; Alkhalifah 2014). The gradient in Eq. 3 with time lag can be expressed as:

$$g\left( {{\mathbf{x}},\tau } \right) = - \frac{2}{{v^{3} }}\int\limits_{0}^{{T_{max} }} {U_{\text{S}} \left( {{\mathbf{x}},t - \tau } \right)U_{\text{R}} \left( {{\mathbf{x}},t + \tau } \right){\text{d}}t} ,$$
(11)

where US and UR represent the first-order time derivative of the source and residual wavefields, respectively, and τ denotes the time lag. In isotropic media, the wavenumber, frequency and velocity have a relationship of

$$\left| {{\mathbf{k}}_{\text{S}} } \right| = \left| {{\mathbf{k}}_{\text{R}} } \right| = \frac{\omega }{{v\left( {\mathbf{x}} \right)}},$$
(12)

where ks and kR represent the wavenumbers of the source and residual wavefields, ω denotes frequency and v(x) is the velocity at the location of x. As depicted in Fig. 7, the relationship of the wavenumber of the gradient, the scattering angle, frequency and velocity can be expressed as

$$\frac{{\left| {\mathbf{k}} \right|^{2} }}{{\omega^{2} }} = \frac{4}{{v^{2} \left( {\mathbf{x}} \right)}}\cos^{2} \left( {\frac{\alpha }{2}} \right).$$
(13)

The counterpart of Eq. 13 for the gradient with time lag shown in Eq. 11 can be expressed as

$$\frac{{\left| {\mathbf{k}} \right|^{2} }}{{\omega_{\tau }^{2} }} = \frac{4}{{v^{2} \left( {\mathbf{x}} \right)}}\cos^{2} \left( {\frac{\alpha }{2}} \right),$$
(14)

where \(\omega_{\tau }\) represents the frequency of the time-lag gather. Using the variable replacement

$$\xi = \frac{\tau }{2}v\left( {\mathbf{x}} \right),$$
(15)

Equation 14 can be expressed as

$$\frac{{\left| {\mathbf{k}} \right|^{2} }}{{\psi^{2} }} = \cos^{2} \left( {\frac{\alpha }{2}} \right),$$
(16)

where ψ represents the counterpart of ξ in the Fourier domain. As can be seen from Eq. 16, the scattering angle is independent of velocity; thus, we can achieve the scattering angle filtering using Eq. 16 to any velocity model (Khalil et al. 2013; Alkhalifah 2014).

Fig. 6
figure 6

The gradient formed by the reflection from a pair of “source-receiver” configuration. The interface of the two-layer model is at a depth of 4 km. The blue and green “×” indicate the location of the source and the receiver, respectively. The solid blue line represents the path of the incident wavefield in the source wavefield, while the dashed blue line is for the reflection. The green lines are the counterpart in the residual wavefield. α represents the angle between the source and residual wavefields at the interface; β is for their angle at the rest of the wave path

Full size image
Fig. 7
figure 7

Schematic illustration of the relationship between the wavenumbers of source and residual wavefields and the gradient. kS, kR and k represent the wavenumber of the source and residual wavefields and the gradient. α is the angle between the source and residual wavefields

Full size image

As can be seen from Fig. 8, the scattering angle filtering based on the time-lag gather includes five steps: (1) forming the gradient with time lag using Eq. 11, and stacking the gradient of all shots; (2) applying coordinate transform on the stacked gather using Eq. 15; (3) taking Fourier transform along all axes; (4) calculating the scattering angle using Eq. 16 and performing scattering angle filtering; (5) taking inverse Fourier transform along all wavenumber axes, and then stacking all frequencies to produce the migration and tomography components. One simple angle filtering function can be found in Fig. 2d of Yao et al. (2018a).

Fig. 8
figure 8

The transform between data domains in the scattering angle filtering process based on time-shift gathers

Full size image

The analysis above shows that the scattering angle filtering based on the time-lag gather has limitation: firstly, assuming the velocity is isotropic; secondly, relatively large memory and computation cost is caused due to generating the time-lag gather and high-dimension Fourier transform; Thirdly, the coordinate transform needs resampling, and thus simple interpolation, e.g., spline interpolation, could introduce alias. To improve the efficiency, Wu and Alkhalifah (2017) demonstrated that the separation can be achieved using spatial Fourier transform and simple extra computation if the inversion is carried out in the Frequency domain and the scattering angle is assumed independent on velocity.

The second method of scattering angle filtering is achieved in the plane-wave domain. The key point of scattering angle filtering is to compute the angle between the source and residual wavefields. A natural thought for the angle measurement is in the plane-wave domain. Thus, Yao et al. (2018a) proposed to Fourier transform the source and residual wavefields into the wavenumber domain and then achieve the scattering angle filtering by measuring the angle of the elements in the wavefields. The gradient expressed in Eq. 3 in the wavenumber domain becomes a convolution form,

$$\begin{aligned} \tilde{g}\left( {\mathbf{k}} \right) & = - \frac{2}{{v^{3} }}\sum\limits_{t} {\tilde{U}_{\text{S}} \left( {{\mathbf{k}}_{\text{S}} ,t} \right) * \tilde{U}_{\text{R}} \left( {{\mathbf{k}}_{\text{R}} ,t} \right)} \\ & = - \frac{2}{{v^{3} }}\sum\limits_{t} {\sum\limits_{i} {\sum\limits_{j} {\tilde{U}_{\text{S}} \left( {{\mathbf{k}}_{{{\text{S}}i}} ,t} \right)\tilde{U}_{\text{R}} \left( {{\mathbf{k}}_{{{\text{R}}j}} ,t} \right)} } } , \\ \end{aligned}$$
(17)

where i and j are the indexes of the first-order time derivative of the source and residual wavefields in the wavenumber domain, respectively, and * represents convolution. The process of convolution is illustrated in Fig. 9. Each element of wavefields in the wavenumber domain represents a plane-wave with a particular wavelength and a dipping angle; therefore, the angle between a pair of plane waves can be computed easily using the equation,

$$\cos \alpha = \frac{{{\mathbf{k}}_{\text{S}} \cdot {\mathbf{k}}_{\text{R}} }}{{\left| {{\mathbf{k}}_{\text{S}} } \right|\left| {{\mathbf{k}}_{\text{R}} } \right|}} .$$
(18)

The filtered gradient then can be expressed as

$$\hat{g}\left( {\mathbf{k}} \right) = - \frac{2}{{v^{3} }}\sum\limits_{t} {\sum\limits_{i} {\sum\limits_{j} {f\left( \alpha \right)\tilde{U}_{\text{S}} \left( {{\mathbf{k}}_{{{\text{S}}i}} ,t} \right)\tilde{U}_{\text{R}} \left( {{\mathbf{k}}_{{{\text{R}}j}} ,t} \right)} } } ,$$
(19)

where f(α) is the filtering function, the choice of which can be found in Yao et al. (2019a).

Fig. 9
figure 9

Sketch of the wavenumber mapping in the convolution process to form the gradient in the plane-wave domain

Full size image

As can be seen from the derivation above, scattering angle filtering in the plane-wave domain does not assume an isotropic or homogenous media; therefore, it is an effective algorithm. However, the convolution process has large computation cost.

The third method of scattering angle filtering is non-stationary smoothing proposed by Yao et al. (2019a). Equation 13 can be rewritten as

$$\left| {\mathbf{k}} \right| = \frac{2\omega }{v}\cos \frac{\alpha }{2}.$$
(20)

Equation 20 implies that for a fixed velocity and frequency, the wavenumber of the gradient, i.e., the inverse of wavelength, equals the cosine of half the scattering angle; in the other words, the wavenumber depends on the scattering angle monotonically. As illustrated in Fig. 10, after determined the maximum scattering angle of the migration component and the minimum scattering angle of the tomography component, they are distributed in different rings. Thus, scattering angle filtering can be achieved using non-stationary smoothing. If the minimum scattering angle αmin is fixed, the maximum wavenumber of the tomography component can be computed using the equation,

$$k_{\text{tomo\_max}} = \frac{2\omega }{v}\cos \frac{{\alpha_{min} }}{2}.$$
(21)

Thereby, we can design a smoother to filter out the wavenumber larger than \(k_{\text{tomo\_max}}\). A simple choice of the smoother is to design a Gaussian function, the standard deviation of which is

$$\sigma = \sqrt {\frac{ - \log \left( \beta \right)}{{2\pi^{2} k_{\text{tomo\_ max}}^{2} }}} ,$$
(22)

where β is the preset value of the Gaussian function at \(k_{\text{tomo\_max}}\) in the Fourier domain, e.g., 0.3. Then, the tomography component at one element of the gradient for this frequency can be computed by multiplying the Gaussian function with the gradient and then stacking the results. In the multiplication, the center of the Gaussian function is coincident with this element. Yao et al. (2019a) pointed out that this method is very suitable for frequency domain FWI. For time-domain FWI, we can divide the seismic data into several frequency bands, each of which uses one reference frequency to compute \(k_{\text{tomo\_max}}\); then, this band is smoothed with this reference frequency.

Fig. 10
figure 10

Schematic diagram for the relationship between opening angles and wavenumber distribution. \(\alpha_{\text{tomo\_min}}\) indicates the minimum opening angle for the tomographic component, while \(\alpha_{\text{mig\_max}}\) indicates the maximum opening angle for the migration component. kS and kR are the wavenumber of the source and residual wavefields, respectively. They sit on the dashed circle. The tomographic component sits inside the inner dark-gray-filled circle while the migration component locates inside the outer light-gray ring. The transition zone is the middle-gray ring between them (Yao et al. 2019a)

Full size image

Compared to the scattering angle filtering in the plane-wave domain, this method has much smaller computation cost. However, similar to the method based on the time-lag gather, this method assumes an isotropic model. In addition, as Gaussian functions have a relative wide transition zone, partial energy of the tomography component can be removed unnecessarily.

3.1.3 Born modeling

Another widely used method for separating the migration and tomography components is Born modeling (Xu et al. 2012; Wu and Alkhalifah 2015; Sun et al. 2017; Yao and Wu 2017). As can be seen from Fig. 6, the zero-lag cross-correlation of the incident waves of the source wavefield and the reflected waves of the residual wavefield forms one branch of the tomography component; the other branch is generated by the reflected waves of the source wavefield and the incident waves of the residual wavefield. Thus, if the reflected waves are separated from the incident waves, then the tomography and migration components can be isolated. Born modeling is a simple and effective method to separate reflected waves from incident waves. Born modeling for the isotropic wave equation can be expressed as

$$\left\{ {\begin{array}{*{20}l} {\left[ {\frac{1}{{v_{b}^{2} }}\frac{{\partial^{2} }}{{\partial t^{2} }} - \nabla^{2} } \right]u_{b} = s} \hfill \\ {\left[ {\frac{1}{{v_{b}^{2} }}\frac{{\partial^{2} }}{{\partial t^{2} }} - \nabla^{2} } \right]u_{\delta } = - m_{\delta } \frac{{\partial^{2} }}{{\partial t^{2} }}u_{b} } \hfill \\ \end{array} } \right.,$$
(23)

where ub and uδ represent the incident and scattering wavefields, vb and mδ denote background velocity and model perturbation, respectively. As illustrated in Fig. 6, the forward scattering waves of the source and residual wavefields travel in different directions; therefore, they have no contribution to the gradient. However, the backward scattering waves, i.e., mainly the reflected waves, contribute to the tomography component by cross-correlating with the incident waves of the other wavefield.

Compared to other methods, the Born modeling method can be applied to anisotropic media and arbitrarily complex media; therefore, it becomes the most widely used method for the separation. However, it cannot simulate higher-order scattering waves.

3.2 Objective functions of reflection-waveform inversion

The objective functions of reflection-waveform inversion can be divided into two main categories: the objective functions based on waveform and the objective functions based on travel time. The objective functions based on waveform can be expressed as

$$\phi = \frac{1}{2}\left\| {\text{D}u_{\delta } \left( {v_{b} ,m_{\delta } } \right) - d} \right\|_{2}^{2} ,$$
(24)

where d represents the observed reflection data, uδ denotes the predicted reflection wavefields, D is the receiver operator that is used for extracting the predicted data at the receiver position from uδ, vb represents background velocity, mδ is the reflector that generates reflections. Once we have an objective function, e.g., Eq. 24, combining it with a wave equation, e.g., Eqs. 2 or 23, can form an inversion system. Currently, restricted by the huge computation cost, FWI is based on local-gradient methods, e.g., steepest-descent methods and conjugate-gradient methods. As a result, computing the gradient is a key step. The formula of the gradient can be derived using the adjoint-state method (Plessix 2006) or the matrix algebra (Pratt 1999).

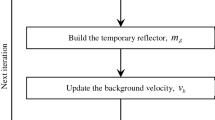
Currently, RWI is achieved mainly by alternatively updating vb and mδ. Its flowchart is shown in Fig. 11: firstly, setting reflectors mδ as zero; secondly, building temporary reflectors mδ with 3–5 iterations; thirdly, updating background velocity vb with a few iterations; the three steps form a big loop. In order to avoid the weakness of RWI illustrated in Fig. 3, one commonly used method is to build reflectors mδ with short-offset data. As can be seen from Fig. 12, the predicted data by the reflectors mδ can fit the observed data in these short offsets while the large-offset residuals contain the information for background velocity update.

Fig. 11
figure 11

The flowchart of reflection-waveform inversion in an alternating scheme

Full size image
Fig. 12
figure 12

Data offset selection for reflection-waveform inversion, the small offset data are used for building the temporal reflector mδ, while the large-offset data are applied for updating the background velocity vb

Full size image

The main objective of RWI is for fixing background velocity. Since the background velocity affects the travel time of seismic events much more than amplitudes, the travel-time information in the seismic data is more sensitive to the error of background velocity than amplitudes. Consequently, RWI can be achieved by using the objective functions based on travel time:

$$\phi = \frac{1}{2}\left\| {\Delta \tau } \right\|_{2}^{2} ,$$
(25)

where Δτ represents the travel-time differences between the reflection events in the observed and predicted data. For a shot gather containing multiple reflection events, cross-correlation with a sliding window can be used to compute the local travel-time difference, Δτ (Hale 2009). Hale (2013) pointed out that dynamic time/image warping (DTW/DIW) is more stable than cross-correlation for multiple events, especially in case of fast travel-time variation. When computing the gradient of the objective function in Eq. 25 with respect to background velocity, there are two choices: the first is based on connective function that gives the relationship between the travel-time difference Δτ and predicted data (Luo and Schuster 1991; Chi et al. 2015); the other is to combine instantaneous phase and phase-only FWI, in which DTW/DIW can be used to compute travel-time difference Δτ, Δτ multiplied by frequency is a stable means to calculate the instantaneous phase (Jiao et al. 2015; Sun et al. 2017).

Compared to the objective functions based on waveform, the objective functions based on travel time can mitigate the influence of amplitudes on inversion; therefore, the influence of the physics that cannot be predicted by acoustic wave equations, e.g., s-waves and attenuation, can be mitigated. However, if the initial model is relatively accurate, the objective functions based on waveform can give a more accurate result than the objective functions based on travel time, as the latter gives up the dynamic information in the data (Chi et al. 2015).

In addition, since the objective functions based on travel time are convex, they are immune to cycle skipping, for instance, Fig. 7d of Chi et al. (2016). However, this good feature is true only if the travel time is computed correctly. In case of large errors in the initial model, wrong pairs of events can be selected from the predicted and observed data to compute the travel-time difference.

The second step of RWI builds temporary reflectors mδ at a wrong depth to fit the data in short offsets; therefore, the likelihood of cycle skipping in large offsets using waveform-based objective functions is reduced significantly compared to conventional FWI. An example is illustrated in Fig. 13, which shows the width of the convex region in the waveform-based objective function is several times wider than that of conventional FWI. Wang et al. (2018) pointed out the likelihood can be further reduced by splitting the long-offset seismic data gather into two parts and then inverting them separately.

Fig. 13
figure 13

The waveform-based objective function of RWI. a The two-layer velocity model used for the test. The 10 Hz Ricker wavelet used as the source signature is located in the middle of the surface of the model; the receiver array is evenly distributed on the surface of the model. b The waveform-based objective function calculated by using Eq. 22. The dashed curve represents the functional value calculated by changing the velocity of the first layer but fixing the depth of the interface. The solid curve indicates the functional value by changing both the velocity of the first layer and the depth of the interface. The depth is determined by keeping the normal incident two-way travel time from the source to the interface as that of the true model. The dashed curve approximately represents the situation of conventional FWI, while the solid curve illustrates the situation of RWI, the flowchart of which is shown in Fig. 10. The predicted data are scaled by a factor so that they have the same L2 norm as the observed data for the central trace. In this example, the convex zone around the global minimum for the solid curve is 3.75 times as wide as that of the dashed curve

Full size image

Except the two types of objective functions of RWI based on pure reflection data, Zhou et al. (2015) proposed a joint inversion of reflection and transmission data:

$$\phi = \frac{1}{2}\left\| {W^{d} \left( {d_{\text{obs}}^{\text{div}} - d_{\text{pred}}^{\text{div}} } \right)} \right\|_{2}^{2} + \frac{1}{2}\left\| {W^{r} \left( {d_{\text{obs}}^{\text{refl}} - d_{\text{pred}}^{\text{refl}} } \right)} \right\|_{2}^{2} ,$$
(26)

where the superscripts div and refl represent the transmission and reflection data, the subscripts obs and pred denote observed and predicted data, Wd and Wr are the weighting of transmission and reflection data. The objection function is a function of reflectors, i.e., the impedance perturbation in Zhou et al. (2015), and background velocity. Zhou et al. (2015) updated reflectors and background velocity alternatively, where reflectors are built of reflections while the background velocity is updated with both reflection and transmission data. Different from Yao and Wu (2017), Zhou et al. (2015) did not reset the reflectors to zero in each inversion loop.

Similar to Zhou et al. (2015), Wu and Alkhalifah (2015) formed the objective function with both transmission and reflection data:

$$\phi = \frac{1}{2}\left\| {d_{\text{pred}}^{\text{div}} + d_{\text{pred}}^{\text{refl}} - d_{\text{obs}} } \right\|_{2}^{2} .$$
(27)

The inversion system is constrained by a Born wave equation, such as Eq. 23. Wu and Alkhalifah (2015) did not update reflectors and background velocity alternatively but simultaneously, i.e., the update direction is formed by weighted velocity and reflector gradients. In the early stage of inversion, the weighting to the velocity gradient is small; therefore, the velocity update is smooth, i.e., background velocity update. The weighting to the velocity gradient is then increased gradually as the inversion progress, which means inversion adds more and more high-frequency components into the velocity model.

3.3 Constraints in reflection-waveform inversion

Generally, RWI decomposes the Earth model into a background velocity model vb and a reflector model mδ; therefore, compared to conventional single-parameter FWI, the number of unknown parameters in the system of RWI is doubled. In addition, conventional FWI utilized all seismic records including refractions, but RWI uses much fewer data. The two factors lead to that RWI is more ill-posed than conventional single-parameter FWI. One manifestation of the ill-posedness is that an inverted background velocity model is full of artifacts but still fits the observed data, for example, Fig. 7a of Yao et al. (2019c).

In order to mitigate the ill-posedness, the inversion system has to incorporate extra information about the velocity model. Since the inversion uses all information from seismic data, the extra information only comes from non-seismic sources, for example, geology, well-logs or other geophysical methods. So far, the research on adding extra information has been studied inadequately. Recently, Yao et al. (2019c) introduced structural-oriented smoothing to constrain RWI. The constraint is a piece of geologic information: the rock properties vary slowly in one stratum but can be fast in different strata. This geological information can be realized by smoothing along strata. This smoothing can be achieved by using anisotropic smoothing. There are two commonly used methods for the anisotropic smoothing: the first is solving an anisotropic diffusion equation (Fehmers and Höcker 2003); the second is solving an anisotropic smoothing system (Hale 2011). In inversion, the anisotropic smoothing can be applied to the gradient of background velocity acting as preconditioning (Lewis et al. 2014; Lee and Pyun 2018); or the smoothing can be used on the background velocity. The latter is called shaping, which directly manipulates the model to possess a particular feature (Fomel 2007). The shaping process can be added as the last step in a loop of RWI (Yao et al. 2019c).

Figure 14 shows an example using the constraint of structural-oriented smoothing. The orientation of strata is picked up from the reflector model mδ automatically, e.g., Fig. 14c. Solving the anisotropic diffusion equation achieves the smoothness in a stratum but keeps the variation between strata. As can be seen from Fig. 14e, the ill-posedness of the inversion system leads to many artificial anomalies in the inversion result. These anomalies break the geological empirical law, i.e., slow variation of rock properties in a stratum. As a result, structural smoothing can suppress the artificial anomalies and force the velocity of the inversion result varies slowly along the structure. The constrained result follows the background trend of the true model (Fig. 14f).

Fig. 14
figure 14

Application of reflection-waveform inversion to the Marmousi Model. a The true velocity of Marmousi model. b The initial model of background velocity for inversion. The recorded data set is comprised of 128 shots in a uniform spacing of 100 m generated by using a 10 Hz Ricker wavelet. c The reflector model generated in the first loop of inversion. The blue arrows indicate the orientation of strata. d The response of spikes from structural smoothing by solving an anisotropic diffusion equation in a time of 400 s. e The inversion result without structural smoothing. f The inversion result with structural smoothing. g and h shows the results of conventional FWI starting from e and f, respectively (Yao et al. 2019c)

Full size image

4 Conclusions and future perspective

So far, the concept and theory of RWI have become mature. There are many successful applications on marine seismic data (Sun et al. 2017; Wang et al. 2018). The preprocesses of seismic data include de-multiples and de-ghost. These ensure the input data satisfy Born approximation and mitigate the nonlinearity of the inversion system caused by multiples. The separation of tomography and migration components is achieved using Born modeling. Both waveform-based (Wang et al. 2018) and travel time-based (Sun et al. 2017) objective functions succeeded to recover background velocity. Similar to conventional FWI, the industry is trying to apply RWI on land seismic data. However, there exist many difficulties including: firstly, low signal-to-noise ratio in land seismic data, it is often hard to observe hyperbolic-shape events in raw data; secondly, near-surface complexities, including severe heterogeneity, undulate topography and weather layer, which cause modeling kernels to simulate wavefields incorrectly; thirdly, current FWI commonly uses acoustic wave equations as the modeling kernel, and thus there exists large waveform discrepancy between the predicted data and the observed land data that contain strong elastic effects.

Based on the analysis above, except separation between the migration and tomography components, objective functions and inversion constraints described in previous sections, RWI includes other study topics: firstly, seismic data preprocesses, which aims to remove all energy unable to be modeled by the modeling kernel in the data, as well as the residuals not generated by the parameters of inversion; secondly, multi-parameter inversion, including P-wave velocity, S-wave velocity, anisotropic parameters and attenuation factor Q. RWI based on elastic wave equations has been explored preliminarily (e.g., Guo and Alkhalifah 2017; Li et al. 2019; Ren et al. 2019).

In a more general scope, for the past thirty years, especially the last decade, the research on FWI has made significant progress on the theory of FWI and many successful applications have been achieved in the industry. However, FWI has not reached the expectation of the industry. The reasons may include:

Gigantic computation cost FWI is achieved using local or global search methods to find the optimal solution so that the inversion solves wave equations numerically in hundreds of times. Mitigating this problem, except the advance of computer hardware, optimization on inversion algorithms, numerical wavefield modeling and computer codes are important research directions. Among them, improving the inversion and modeling algorithms are the key directions because computer code optimization, for example, load balance between processes, CPU vectorization, cache reuse and GPU acceleration (e.g., Wang et al. 2019), can only speed up the inversion in tens of times or less generally.

Insufficient information restricted by the technology and space of acquisition, the acquired seismic data are incomplete in spatial coverage and frequencies. Petroleum exploration and exploitation do not only require P-wave velocity but also other seismic properties, such as density and S-wave velocity and anisotropic parameters. Currently, in successful applications, FWI usually produces only P-wave velocity, in which the density is constrained by using Gardener’s relation, and the anisotropic parameters are preset. If FWI is used for multi-parameter inversion, then it turns into a severe under-determined problem. Consequently, the inversion results are still far different from the true models but fit the recorded data nicely. This is caused by insufficient information in the seismic data. Mathematic theory pointed out that the solution for an under-determined problem is to introduce more constraint information, which includes mathematic regularization and extra information. Common mathematic regularization includes Tikhonov, total variation and so on. The extra information includes seismic and non-seismic information. “two wide and one high” (i.e., broad frequency band, wide azimuth and high shot and receiver density) acquisition and multi-component acquisition can provide more seismic information for inversion. Theoretic tests show that the ill-posedness of multi-parameter inversion cannot be fully removed with a better acquisition. Extra non-seismic information, including well-logs, geologic laws, is an important information supplement. Thus, merging the multi-source information into FWI is an important research direction.

Incomplete theory Currently, the theory of FWI is still under the framework of Tarantola’s theory proposed in 1984. It includes localized gradient methods and Born approximation. FWI is a nonlinear problem; therefore, localized gradient methods have limitations. The Born approximation is used to compute the gradient. Many geologic bodies missed in the starting model cannot be represented using Born approximation, because Born approximation is valid only for weak scattering caused by small volume and magnitude. Global inversion is a way to solve this problem because it does not need to compute a gradient. But its gigantic computation cost forbids its use. Except the incomplete inversion theory, the forward modeling theory is also incomplete. The existing wave equations cannot describe the propagation of wavefields in the real world accurately. Thus, exploring the inversion and modeling theories is also an important research direction.

Unsophisticated acquisition technology Professor Teng Jiwen, who is a fellow of Chinese Academy of Sciences, pointed out that geophysics is a science of observation essentially; therefore, reliable information, or incompleteness and erroneous of information cannot be remedied by using any mathematic tricks or image processes. In the past several years, the significant advances of FWI in real data applications are mainly because of the progress in acquisition technology. In the applications on the salt models of the Gulf of Mexico, OBN acquisition and marine controlled source, i.e., Wolfspar, ensure the maximum offset exceeds 25 km and the valid signal lower than 2 Hz. However, there is a lack of breakthroughs in land acquisition, for instance low signal-to-noise ratio in the data and inconsistency of different shots. The quality of land data may be the main reason for restricting successful applications of FWI on land data. Consequently, developing acquisition technology is a key research direction for FWI as well as for other seismic methods.