1 Introduction

A high-resolution velocity model is key to migration methods and reservoir estimation. Traveltime tomography has been widely used in velocity model reconstruction, but it is based on the high-frequency assumption and has low resolution. Thanks to the considerable progress of computation ability, FWI has become a potential method to reveal detailed information by iteratively updating subsurface model parameters, the misfit between observed data and synthetic data minimized using a gradient-based method (Virieux and Operto 2009). Tarantola (1984) proposed the adjoint state method to estimate the gradient of misfit by a zero-lag correlation between the source wavefield and the residual wavefield, which avoids explicitly calculating the Jacobi matrix. Bunks et al. (1995) developed a multi-scale inversion strategy. Over the past decade, a lot of research has been conducted to solve FWI problems, such as the “cycle skipping” problem (Shin and Cha 2008; Van Leeuwen and Mulder 2010; Ma and Hale 2013; Métivier et al. 2016) and expensive computational costs (Ben-Hadj-Ali et al. 2011).

The needs of 3D seismic techniques have been increasing recently as more 3D wide-azimuth surveys have been carried out; however, the processing demands prohibitive computation costs. Ben-Hadj-Ali et al. (2008) and Sirgue et al. (2008) developed 3D FWI and provided preliminary insights on the feasibility and advance of 3D FWI in the time domain and frequency domain, respectively, based on some synthetic tests. Further 3D tests on field data sets were presented (Plessix and Perkins 2010; Warner et al. 2013; Raknes et al. 2015). In order to reduce computation, the simultaneous-shot technique provides a trade-off between computational efficiency and imaging quality, introducing cross-talk noises (Ben-Hadj-Ali et al. 2011). Vigh and Starr (2008) studied 3D prestack plane-wave FWI that reduced the amount of computation. Since the Compute Unified Device Architecture (CUDA) programming language was employed in computational science, graphics processing units (GPUs) have been widely applied to 3D data in exploration geophysics. It is presented that GPU runtimes are roughly one-tenth to one-twentieth of corresponding multi-core CPU-based implementations (Weiss and Shragge 2013). For example, 3D Laplace-domain full-waveform inversion on a single GPU card was verified to be accurate when used to invert a long-wavelength velocity model, and the peak speedup of GPU parallelization is 24.6 times (Shin et al. 2014). Liu et al. (2015) achieved a good acceleration ratio up to 19.5 using 3D simplified hybrid-domain FWI on GPU. The time-domain FWI is less memory-demanding but time-consuming; hence, intensive computation time still remains a distinct weakness of 3D time-domain FWI (Jiang and Zhu 2018). When tens of iterations and hundreds of shots are performed to characterize subsurface velocity structures, an efficient wavefield numerical modeling algorithm is the core of accelerating time-domain FWI (Vigh and Starr 2008).

During the process of FWI, forward propagation of the source wavefield and backward propagation of the residual wavefield occupy the largest portion of operation time. Therefore, the numerical simulation algorithm is the key to promoting efficiency. The variable-grid technique changes grid size in different areas aiming at near-surface low-velocity zone and complicated small-scale anomalies in deeper layers. The advantage of this method is that the improvement in efficiency, the reduction of memory requirements and the promotion of precision can be achieved simultaneously. Irregular spatial grid size was firstly proposed by Moczo (1989). Jastram and Behle (1992) modeled on a grid of varying spacing in depth based on a two-dimensional acoustic wave equation. Jastram and Tessmer (1994) developed it into elastic cases. Zhu et al. (2007) and Sun et al. (2008) proved that the variable-grid method in depth promotes the accuracy and efficiency of finite-difference forward modeling, and error was evaluated and reduced by changing the difference operator. Huang et al. (2015) combined the coordinate transformation for the irregular surface and a mapping staggered-grid finite-difference forward modeling method using the dual-variable-grid size in time and space. Zhang et al. (2018) used a discrete fracture model (DFM) to reflect the shape and distribution of the fractures in the flow model and to simulate reservoir production with different fracture parameters. Fan et al. (2015) applied a rotated grid system to the transition region for high-order finite-difference modeling that is capable of doubling the grid spacing without artificial reflections. Fan et al. (2018) further developed a discontinuous-grid finite-difference scheme for frequency-domain 2D scalar wave modeling. However, the fine-to-coarse spacing ratio of both modeling methods (Fan et al. 2015, 2018) is restricted to a power of two. To double the grid size, a transition zone in the coarse-grid area is indispensable. The modeling algorithms and strategies mentioned above showed good performance on models with a shallow low-velocity layer and a complex subsurface geological body, such as gas clouds and small-scale low-velocity inclusions.

Variable-grid modeling techniques have been used in migration and waveform inversion. Ha and Shin (2012) used an axis transformation technique to improve the Laplace-domain FWI efficiency, in which two transformation functions are proposed. Li et al. (2014) applied a dual-variable-grid forward modeling algorithm with high precision and efficiency to reverse time migration, which improves the accuracy in fractured reservoirs and irregular surface imaging. The dual-variable-grid method in time and space was applied to encoding FWI, and a multi-scale strategy was realized by reducing the global grid scale and fine grid scale (Qu et al. 2015). Frequency-domain FWI based on a variable-grid finite-difference method was also implemented to prove its feasibility and effectiveness by numerical tests (Li et al. 2016). However, a conventional grid discretization strategy always finely resamples a specified zone whose edge creates artificial reflections because the grid size in this zone is several times smaller than the global ones. Such an artificial error is difficult to remove from the calculated wavefield. In addition, all the above attempts are limited to 2D cases while the enormous computation cost, the biggest problem in 3D FWI, urgently needs to be reduced. Up to the present, variable-grid methods have not been used in 3D FWI on GPU devices to test their feasibility, efficiency and accuracy.

In this paper, we propose a 3D optimized variable-grid FWI on a single GPU card and 3D numerical tests are operated to verify the validity and efficiency of the method. Based on the dispersion relation, grid sizes adapt to local velocity and depth, which not only simulates wavefields with higher accuracy but also accelerates the calculation during the implementation of FWI. With the obvious reduction of computing time, the proposed FWI method inverts for the velocity model successfully. In the following sections, we will firstly review the FWI theory. Then we will introduce our grid discretization strategy, deriving a new wave equation used in adaptive variable-grid FWI. The GPU implementation workflow of this method is also detailed in the next part. After that, 3D numerical test results are shown using simple models to demonstrate the efficiency and accuracy of the proposed modeling method. In the next part, a complex 3D model, the 3D SEG/EAGE overthrust model, is used to show that application of this method to FWI is feasible. From the inverted results and computing time comparison, variable-grid FWI shows higher computational efficiency and has better convergence. In the last section, conclusions will be presented.

2 Theory

2.1 Adaptive variable-grid modeling

Time-domain 3D FWI is challenging due to the large amount of calculation. Conventional FWI usually uses a fixed regular grid while modeling the forward wavefield and the backward propagating residual wavefield. In most cases, the fixed global grid size is not fine enough in the near-surface low-velocity zone. Besides, in deeper layers with higher velocity, the model is oversampled and the calculation cost is increased without increasing accuracy. To improve this situation, we applied adaptive variable-grid modeling to FWI, which achieves higher efficiency without losing accuracy. In this section, we will focus on presenting the theory and strategy of adaptive variable-grid modeling.

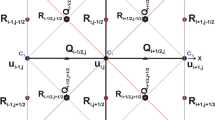
The 3D time-domain acoustic wave equation with constant density with regular-grid discretization can be written as

$$\frac{1}{{v^{2} ({\mathbf{x}})}}\frac{{\partial^{2} u}}{{\partial t^{2} }} = \left[ {\frac{{\partial^{2} u}}{{\partial x^{2} }} + \frac{{\partial^{2} u}}{{\partial y^{2} }} + \frac{{\partial^{2} u}}{{\partial z^{2} }}} \right] + f_{s} (t)$$
(1)

where v(x) is the velocity, fs(t) is the source, and u is the pressure field; x, y, z are the position in the regular-grid coordinate.

As shown in Fig. 1a, the spatial sampling intervals dx, dy, dz are fixed in the direction of x, y, z. When the near-surface velocity is low or low-velocity targets exist in the deeper zone, such coarse-grid discretization will lead to inaccurate forward and backward wavefields due to dispersion phenomenon. On the other hand, if we use fixed fine grids, the large computing and memory storage problem will be more severe especially for the implementation of FWI. Moreover, conventional variable-grid methods are fixed local grid refinement methods, which can only refine a specified area. The abrupt change of grid size in the transitional zone from fine grid to coarse-grid results in artificial reflections.

Fig. 1
figure 1

Physical coordinate with traditional (a) and adaptive variable-grid discretization strategy (b)

Full size image

Here, we use a new grid discretization strategy to resample velocity models in the z direction, based on dispersion relation written as

$$\lambda_{\min } = \frac{{v_{\min } }}{{f_{\max } }}$$
(2)

where λmin denotes the minimum wavelength, vmin represents the minimum velocity in the model, and fmax represents the maximum frequency of the source signal. Usually, the maximum frequency of the Ricker wavelet is three times the wavelet dominant frequency. So we refine the z-axis using the following equation:

$${\text{d}}z = \frac{v(z)}{{nf_{\text{d}} }}$$
(3)

where v(z) denotes the velocity in depth z. To ensure dispersion never occurs, we use the minimum velocity among all grid points in that depth to replace v(z). fd represents the dominant frequency of the Ricker wavelet. n is the number of grid points per wavelength, which is set as ten in this work to ensure the wavefields are adequately resampled. The horizontal grid size dx and dy is fixed and equals to the regular-grid size, while the vertical grid size dz adapts to the local velocity and automatically changes with depth. This is because the main velocity changing direction is along the depth direction, especially for background velocity models.

Using the dispersion relation mentioned above, we can calculate theoretical dz on each grid point according to its local velocity. With the theoretical grid intervals obtained, we take trial steps from z = 0 to get the first adaptive-grid depth like the five blue rectangles in Fig. 2. When the trial step length is equal to z (the first red square in Fig. 2), we will get the first feasible grid point z1. Then we restart the attempt with a new trial step until we get the next square and z2. We repeat the process to the maximum depth, and we obtain the depth of each optimal grid point zi; in other words, we get the new grid discretization with the adaptive variable grid. Note that the process of taking trial steps is necessary, because if we simply use theoretical dz as grid size and the local velocity is decreasing, it is not fine enough to assure that modeling is dispersion free. After that, we smooth zi to prevent spurious reflections. In this way, the regular physical coordinate is transformed into a new physical coordinate with variable vertical grid intervals.

Fig. 2
figure 2

Variable-grid discretization strategy to obtain transformed \(z_{\text{vg}}\)

Full size image

The resampled physical coordinate is shown in Fig. 1b. From this grid discretization graph, we can see that the lateral grid size is never changed. The vertical grid size increases gradually from shallow layers with low velocity to deep layers with high velocity. In general cases, the vertical grid size at the bottom of velocity models amounts up to several times the fine grid size. The new discretization strategy enables the grid size to increase gradually according to depth and velocity, instead of a violent change in the transitional zone that usually amounts to several times the fine grid size. That is the reason why our method has higher accuracy than the conventional variable-grid method.

Therefore, we have two coordinate systems and their transformation relation can be written as:

$$\begin{aligned} x_{\text{vg}} & = x \\ y_{\text{vg}} & = y \\ z_{\text{vg}} & = \varphi (z) \\ \end{aligned}$$
(4)

where xvg, yvg, and zvg are the new variable-grid location in the transformed coordinate system; φ(z) is the mapping from the original depth to the new depth after spatial resampling. Compared with a fixed axis transformation function proposed by Ha and Shin (2012), this function φ(z) is capable of varying according to different velocity models. The new axis transformation function φ(z) is changeable under different geological circumstances. Moreover, errors originating from large grids in deep layers are also avoided. In this method, the coordinate only changes in depth while the lateral grid size is fixed. Therefore, the x, y position of grid points is identical to the original ones. Here, we will focus on the formula derivation in the direction of z.

We can get the first-order and second-order derivatives of zvg with respect to the original physical coordinate variables z using a finite-difference method:

$$\frac{{\partial z_{\text{vg}} }}{\partial z} = \varphi^{\prime } (z)$$
(5)

According to the derivation of inverse functions, we derive the derivatives of z, with respect to zvg:

$$\frac{\partial z}{{\partial z_{\text{vg}} }} = \frac{1}{{\varphi^{\prime } (z)}}$$
(6)
$$\frac{{\partial z^{2} }}{{\partial z_{\text{vg}}^{2} }} = \frac{{\partial \left( {\frac{1}{{\varphi^{\prime } (z)}}} \right)}}{\partial z}\frac{\partial z}{{\partial z_{\text{vg}} }} = \frac{{ - \varphi^{\prime \prime } (z)}}{{[\varphi^{\prime } (z)]^{2} }}\frac{1}{{\varphi^{\prime } (z)}} = - \frac{{\varphi^{\prime \prime } (z)}}{{[\varphi^{\prime } (z)]^{3} }}$$
(7)

Based on Eq. 1, we derive the acoustic wave equation in the new coordinate system. The first-order derivative of the replacement is written as:

$$\frac{\partial u}{{\partial z_{\text{vg}} }} = \frac{\partial u}{\partial x}\frac{\partial x}{{\partial z_{\text{vg}} }} + \frac{\partial u}{\partial y}\frac{\partial y}{{\partial z_{\text{vg}} }} + \frac{\partial u}{\partial z}\frac{\partial z}{{\partial z_{\text{vg}} }} = \frac{\partial u}{\partial z}\frac{\partial z}{{\partial z_{\text{vg}} }}$$
(8)

Also, we can derive the second derivative:

$$\begin{aligned} \frac{{\partial^{2} u}}{{\partial z_{\text{vg}}^{2} }} & = \frac{{\partial \frac{\partial u}{{\partial z_{\text{vg}} }}}}{\partial x}\frac{\partial x}{{\partial z_{\text{vg}} }} + \frac{{\partial \frac{\partial u}{{\partial z_{\text{vg}} }}}}{\partial y}\frac{\partial y}{{\partial z_{\text{vg}} }} + \frac{{\partial \frac{\partial u}{{\partial z_{\text{vg}} }}}}{\partial z}\frac{\partial z}{{\partial z_{\text{vg}} }} \\ & = \left( {\frac{{\partial^{2} u}}{{\partial z^{2} }}\frac{\partial z}{{\partial z_{\text{vg}} }} + \frac{{\partial \frac{\partial z}{{\partial z_{\text{vg}} }}}}{\partial z}\frac{\partial u}{\partial z}} \right)\frac{\partial z}{{\partial z_{\text{vg}} }} \\ & = \frac{{\partial^{2} u}}{{\partial z^{2} }}\left( {\frac{\partial z}{{\partial z_{\text{vg}} }}} \right)^{2} + \frac{\partial u}{\partial z}\frac{{\partial^{2} z}}{{\partial z_{\text{vg}}^{2} }} \\ & = \frac{{\partial^{2} u}}{{\partial z^{2} }}\left( {\frac{1}{{\varphi^{\prime }(z)}}} \right)^{2} - \frac{\partial u}{\partial z}\frac{{\varphi ^{\prime \prime }(z)}}{{[\varphi^{\prime}(z)]^{3} }} \\ \end{aligned}$$
(9)

To sum up, we can rewrite Eq. 1 as follows:

$$\begin{aligned} \frac{1}{{v^{2} ({\mathbf{x}})}}\frac{{\partial^{2} u}}{{\partial t^{2} }} & = \frac{{\partial^{2} u}}{{\partial x_{\text{vg}}^{2} }} + \frac{{\partial^{2} u}}{{\partial y_{\text{vg}}^{2} }} + \frac{{\partial^{2} u}}{{\partial z_{\text{vg}}^{2} }} \\ & = \left[ {\frac{{\partial^{2} u}}{{\partial x^{2} }} + \frac{{\partial^{2} u}}{{\partial y^{2} }} + \frac{{\partial^{2} u}}{{\partial z^{2} }}\left( {\frac{1}{{\varphi^{\prime}(z)}}} \right)^{2} - \frac{\partial u}{\partial z}\frac{{\varphi^{\prime \prime } (z)}}{{[\varphi^{\prime } (z)]^{3} }}} \right] + f_{s} (t) \\ \end{aligned}$$
(10)

Equation 10 is the modified wave equation for variable-grid modeling. One term added to Eq. 1 increases the computation complexity for one grid point. Nevertheless, this small amount of extra calculation can be neglected compared with the large reduction of the calculated number of grid points. For 3D time-domain acoustic modeling, we adopt an 8th-order finite-difference operator. For the boundary condition, we applied an absorbing boundary condition suggested by Clayton and Engquist (1977) to minimize artificial reflected waves from the edges of the computation domain.

2.2 Full-waveform inversion based on GPU acceleration

As the most intensive and time-consuming step, full wavefield simulation is accelerated using the proposed grid discretization strategy. A GPU device has higher performance than CPU devices in accelerating the calculation for the data-parallel tasks in that it has several hundred or more thread processors (Jiang and Zhu 2018; Yang et al. 2015). The large computation cost is a challenging problem of 3D full-waveform simulation with the performance of a number of shots. Therefore, it is beneficial to apply GPU parallelization techniques in the procedural steps. To further increase efficiency, we use the CUDA-C language for GPU programming on a workstation with a single GPU card. The GPU card used in this paper is the NVIDIA Quadro P5000, which has 2560 processors, and 16 GB of GDDR5X memory. It uses PCI-E to connect with an Intel Xeon E5-2630 v4 CPU running at 2.20-GHz with 256 GB RAM memory. To illustrate the performance increase in GPU implementation, we test the efficiency of the CUDA-C code and CPU code based on several 3D models with different grid numbers (Table 1).

Table 1 Computing time and speedup of modeling on GPU
Full size table

We parallelize key computation modules of 3D FWI, mainly including forward modeling, backward propagating residual wavefield, estimating descent direction and searching step length. Each step above is calculated in a GPU kernel function. Resampling the velocity model is not as computationally intensive as the other steps, and hence it is implemented on the CPU, including obtaining φ(z) and calculating corresponding derivatives. Moreover, linear interpolation is applied to transform the wavefield snapshots and inversion results to the original regular-grid coordinate. The inverse transformation of the inverted velocity model works at the final step rather than after each full wavefield simulation in each shot loop. The working flowchart of the variable-grid FWI is shown in Fig. 3, in which the calculation modules with a gray background are implemented on the GPU.

Fig. 3
figure 3

Flowchart of adaptive variable-grid FWI

Full size image

FWI estimates subsurface model parameters by minimizing the least-squares distance between the synthetic and observed data. The L2 norm difference objective function is defined as (Tarantola 1984),

$$E({\mathbf{m}}) = \frac{1}{2}\sum\limits_{\text{s,r}}^{{}} {\int_{0}^{{t_{\max } }} {[u({\mathbf{x}}_{\text{r}} ,t;{\mathbf{x}}_{\text{s}} ) - u_{0} ({\mathbf{x}}_{\text{r}} ,t;{\mathbf{x}}_{\text{s}} )]^{2} } {\text{d}}t}$$
(11)

where u(xr, t; xs) is synthetic data; u0(xr, t; xs) is observed data recorded at time t; xs and xr are the locations of sources and receivers; and tmax is the largest calculated time.

FWI is a large-scale nonlinear optimization problem, and we generally use a gradient-based local optimization method to minimize the objective function and update the model parameters iteratively. Starting with an initial model m0, the model is updated iteratively as follows:

$${\mathbf{m}}_{k + 1} = {\mathbf{m}}_{k} + \alpha_{k} {\mathbf{d}}_{k}$$
(12)

where mk is the updated model at the kth iteration; αk is the step length obtained by parabolic interpolation to minimize the objective function in the descent direction dk.

In practice, the gradient of the objective function E(m) with respect to the model parameter is derived through the adjoint state method (Plessix 2006; Fichtner and Trampert 2011). It is formulated as the correlation of the source wavefield forward propagated from the source with the adjoint wavefield back propagated from the residual at the receivers (Tarantola 1984), which is expressed as:

$$\nabla E_{{\mathbf{m}}} = \frac{2}{{v^{3} ({\mathbf{x}})}}\sum\limits_{\text{s,r}}^{{}} {\int_{0}^{{t_{\max } }} {\frac{{\partial^{2} u({\mathbf{x}}_{\text{r}} ,t;{\mathbf{x}}_{\text{s}} )}}{{\partial t^{2} }}} u_{\text{res}} ({\mathbf{x}}_{\text{r}} ,t;{\mathbf{x}}_{\text{s}} ){\text{d}}t}$$
(13)

where ures is the back propagated residual wavefield, and v(x) is velocity.

In this work, we use a nonlinear conjugate gradient method to determine the descent direction. The descent direction is defined as:

$$d_{k} = \left\{ {\begin{array}{*{20}l} { - \nabla E(m_{0} ),} \hfill & {k = 0} \hfill \\ { - \nabla E(m_{0} ) + \beta_{k} d_{k - 1} ,} \hfill & {k \ge 1} \hfill \\ \end{array} } \right.$$
(14)

where βk is a correction coefficient modifying dk into an optimal direction, and dk−1 is the descent direction in the previous iteration. Here, we use a hybrid scheme combining the Hestenes–Stiefel method and the Dai–Yuan method (Hager and Zhang 2006)

$$\beta_{k} = \max (0,\min (\beta_{k}^{\text{HS}} ,\beta_{k}^{\text{DY}} ))$$
(15)

where \(\beta_{k}^{\text{HS}}\) is calculated by the Hestenes–Stiefel method, and \(\beta_{k}^{\text{DY}}\) is estimated by the Dai–Yuan method.

In this paper, we use the L2 norm difference objective function minimized by a nonlinear conjugate gradient method based on the theory mentioned above. Based on a local minimization algorithm, the traditional FWI has a high risk of converging to local minima. To mitigate the “cycle skipping” problem caused by L2 norm misfit, a multi-scale strategy is applied to lead the updated model to a better result.

3 3D numerical examples

3.1 Accuracy and efficiency tests

To validate the feasibility of the adaptive variable-grid algorithm, we designed 3D velocity models. Velocity changes with depth linearly from 1500 to 3500 m/s (Fig. 4). The model covers 3 × 3 km2 laterally and is 3 km deep. The original regular-grid size is 10 m in three directions. We use the regular-grid finite-difference method and variable-grid finite-difference method to simulate wavefields, respectively. The sketches of both grid discretization strategies are shown in Fig. 5. It is shown that the grid number at depth decreases from 300 to 150 points, one-half of the original grid points. Besides, the velocity in deep layers is resampled using coarse grids, while near-surface layers are resampled using fine grids. The grid size increases from shallow layers to deep layers automatically. The source is a Ricker wavelet with a dominant frequency of 10 Hz. One source is added to the top surface in the middle.

Fig. 4
figure 4

Velocity model

Full size image
Fig. 5
figure 5

Regular (a) and adaptive grid (b) discretization strategy

Full size image

We used both grid discretization methods to generate wavefields whose snapshot slices in three directions are extracted and shown in Fig. 6. The interpolated variable-grid wavefields are almost identical with regular-grid wavefields as can be seen by comparing Fig. 6a and b, c and d, e and f. The difference between them is less than 1% of the regular-grid wavefields (Fig. 7), which validates that the new strategy of adaptive variable-grid discretization is accurate and credible.

Fig. 6
figure 6

Wavefield snapshot slices using regular-grid discretization at a top surface, cx = 1500 m, ey = 1500 m, and using variable-grid discretization at b top surface, dx = 1500 m, fy = 1500 m

Full size image
Fig. 7
figure 7

The difference between wavefield snapshots using the two grid discretization strategy at a top surface, bx = 1500 m, cy = 1500 m

Full size image

According to the dispersion relation, the resampling interval depends on the velocity of each layer and seismic wavelet maximum frequency. To test the efficiency of the variable-grid finite-difference modeling method, we created several models with different ranges of velocities and record operation time of FWI based on both regular and variable-grid strategies. Table 2 presents some important modeling parameters. Among the series of tests, we treat test 1 as a standard, with 10-Hz dominant frequency, velocity ranging from 1500 m/s to 6000 m/s and 10-m original grid size. The computing time reduces to 50% of the regular-grid method. Therefore, the corresponding efficiency of the proposed variable-grid modeling method is twice as that of conventional modeling method. Then, the Ricker wavelet is set to 5 Hz and 20 Hz in tests 2 and 3 to find out the influence of the wavelet dominant frequency on efficiency improvement. In addition, the maximum velocity is changed to 3500 m/s in test 4, resulting in a slight decrease in efficiency improvement. The situation is similar when the original grid size is increased to 20 m in test 5. After several tests with different wavelet dominant frequencies, velocity range and original grid size, it is concluded that our adaptive variable-grid FWI displays obvious efficiency improvement compared with the conventional modeling method. In Fig. 8, we compare the normalized computing time of these tests, which shows that the computing time can decrease to less than 60% of the conventional method under most geological situations. Overall, the efficiency improvement ratio is about two in common geological conditions. Meanwhile, the accuracy loss is less than 1%, which can be completely tolerated if we apply the proposed accelerated modeling method to FWI.

Table 2 Efficiency comparison between variable-grid and conventional modeling
Full size table
Fig. 8
figure 8

Computing time comparison of variable-grid modeling and regular-grid modeling

Full size image

3.2 3D application on the SEG/EAGE overthrust model

In this numerical test, a part of the 3D SEG/EAGE overthrust model is considered (Fig. 9). Due to limited available computer resources, our application is carried out on a shallow left part of the whole overthrust model. It is discretized on a 280 × 45 × 110 grid with a grid spacing h = 20 m, which corresponds to a physical domain of 5.6 km × 0.9 km × 2.2 km. The minimum and maximum velocities in this overthrust model are 2000 m/s and 5500 m/s, respectively. We use fixed spread surface acquisition in which 28 × 5=140 sources are modeled every 200 m in both \(x\) and \(y\) directions. Receivers are regularly located each 20 m in the \(x\) direction and 40 m in the \(y\) direction. The acquisition geometry covers most of the underground area. A recording time of 2 s is used for the modeling. We use a time interval of 0.8 ms, resulting in 2500 time steps, to satisfy the stability condition.

Fig. 9
figure 9

True velocity model (Horizontal slice locates at z = 1 km. Inline section locates at y = 0.5 km. Crossline section locates at x = 2.2 km)

Full size image

The starting model for inversion is obtained by smoothing the true velocity model with a Gaussian function (Fig. 10). Slices of the exact model and initial model at constant \(x\) = 2.2 km and \(y\) = 0.5 km are presented. The constant depth slice at \(z\) = 1 km is chosen to show the lateral variation of the thrusted region as well as a channel complex, to demonstrate the horizontal accuracy of the 3D waveform inversion. The detailed channel information is removed by smoothing the exact model. In order to mitigate the local minima problem, the inversion is implemented using a multi-scale strategy, starting at the peak frequency of 3.5 Hz and sequentially stepping up to 7 Hz and then 15 Hz. For each scale, we compute 14 iterations.

Fig. 10
figure 10

Initial velocity model (Horizontal slice locates at z = 1 km. Inline section locates at y = 0.5 km. Crossline section locates at x = 2.2 km)

Full size image

The purpose of this experiment is to focus on the accuracy and efficiency of the proposed 3D variable-grid full-waveform inversion (VGFWI) compared with traditional full-waveform inversion. For this reason, the same acquisition geometry and workflow are implemented based on the regular-grid finite-difference modeling and the proposed variable-grid finite-difference modeling, respectively. After resampling the velocity model based on Eq. 3, we simulate the source wavefield and the residual wavefield using the new modified wave Eq. 10.

With a Ricker wavelet of 3.5-Hz dominant frequency, the velocity model is resampled to 54 grids in the depth direction, less than half of the original grid number (Table 3). The efficiency is double the traditional FWI with fixed square grids. Sequentially, the vertical resampled velocity model is decreased to 72 grids in depth, two-thirds of the original 110 grids, when the peak frequency is 7 Hz. However, as we invert for 13-Hz results, the new grid discretization strategy does not help to reduce computing time dramatically to ensure the wavefield is adequately sampled so that dispersion never occurs. In Fig. 11, we compared the computing time of one iteration in particular, which shows that the overall computing time is reduced to less than two-thirds of the conventional FWI. Generally, the efficiency is almost twice that of traditional waveform inversion while updating background velocity with a low-dominant-frequency Ricker wavelet.

Table 3 Efficiency comparison between variable-grid and conventional FWI
Full size table
Fig. 11
figure 11

Computing time comparison of variable-grid FWI and conventional FWI

Full size image

The inversion results using three-model scales are shown in Figs. 12 and 13, based on conventional FWI and variable-grid FWI (VGFWI), respectively. As shown in two sets of inverted velocity models, the large-scale layered structure is well characterized using both methods. From the inline section at y = 0.5 km, it is observed that high-velocity layers inverted by VGFWI are obviously closer to true velocity compared with traditional FWI, which indicates that the proposed method converges faster. Depth slices at z = 1 km show that variable-grid FWI also retains the accuracy of regular-grid FWI when reconstructing the target channel. The edges of channels are described with slightly higher resolution, and their velocities are retrieved closer to the exact model. Then, we extract vertical profiles from the shown inline section (y = 0.9 km) at x = 1 km and x = 2.7 km (Fig. 14). The inverted curves using VGFWI are nearly identical with curves using FWI and true curves in the shallow region less than 1 km. Some deviations exist at depth due to relatively weak illumination and an insufficient number of iterations. Still, the whole inversion results of VGFWI achieve slightly higher agreement with true velocity than conventional FWI.

Fig. 12
figure 12

Inverted velocity models using traditional FWI. a 14th iteration; b 28th iteration; c 42nd iteration (The horizontal slice is at z = 1 km. The inline section is at y = 0.5 km. The crossline section is at x = 2.2 km)

Full size image
Fig. 13
figure 13

Inverted velocity models using proposed variable-grid FWI. a 14th iteration; b 28th iteration; c 42nd iteration (The horizontal slice is at z = 1 km. The inline section is located at y = 0.5 km. The crossline section is at x = 2.2 km)

Full size image
Fig. 14
figure 14

Comparison between vertical profiles extracted from the true (black line), the starting (green line), conventional FWI (blue line), and variable-grid FWI (VGFWI) (red line). The three profile series are located at ay = 0.9 km, x = 1 km, by = 0.9 km, x = 2.7 km

Full size image

In general, the proposed adaptive variable-grid FWI is capable of introducing higher efficiency for waveform inversion. According to inversion results, such as sections and profiles, the accelerated FWI can achieve the same level of calculation precision as conventional FWI. If we compare inversion results more carefully, VGFWI shows slightly better agreement with the true model. Ha and Shin (2012) mentioned that the accumulated large-grid error could make the inversion using the transformed axis converge to a larger value. However, our method can control grid size in deep layers with milder z-axis variation according to the dispersion relation. Besides, the variable-grid method we proposed is free of dispersion. The grid size is sufficient for accurate modeling and inversion. That is the reason why the inversion results using the proposed method are not worse than conventional FWI. As for the slightly faster convergence rate, from our point of view, FWI is an inverse problem with nonlinearity and non-uniqueness, which lead to multiple solutions. The adaptive-grid velocity model has fewer grids especially for deep layers, so the inverse problem has less unknown variables mathematically. In this way, the complexity of the inverse problem is actually reduced, which makes it easier to converge.

In our method, only the vertical grid size changes because the main velocity change direction is with depth under common geological circumstances. However, when lateral change is dominant, multi-direction variable-grid modeling also needs to be developed to further improve efficiency. Another alternative development will be to try multiple grid time-space dual-variable methods, which will further decrease computation and involve multi-scale strategies by reducing grid scale through iterations.

4 Conclusions

Full-waveform inversion in 3D cases is known to be limited by the problem of expensive computation when hundreds of shots and tens of iterations are required. The process of wavefield propagation is the most computationally intensive step in the implementation of FWI. To alleviate this problem, we proposed an adaptive variable-grid finite-difference modeling method by deriving a new modified acoustic wave equation. This grid discretization strategy is based on a dispersion relation, which improves modeling efficiency without losing accuracy. Then we apply this efficient wavefield simulation method to 3D full-waveform inversion on GPU devices. In this way, 3D FWI is dramatically accelerated without precision loss.

We have presented several applications on both simple and complex examples to give insight into the feasibility of our approach. Some preliminary tests on linear models have shown that the modeling method is adequately accurate with an error less than 1%. Moreover, the efficiency is increased to about twice that of the regular-grid finite-difference method under common geological conditions. After that, we have shown the 3D applications of variable-grid full-waveform inversion on part of the SEG/EAGE overthrust model. Owing to the proposed modeling method and CUDA-C language programming, the computing time is significantly reduced especially for large-scale background velocity inversion. In addition, cross sections, depth slices and profiles demonstrate that VGFWI is a cost-effective and quality-assured approach for 3D acoustic FWI.