1 Introduction

Subsurface fractures contribute to providing pathways for fluid flow and increasing the permeability of reservoirs. The key parameters of great interest for fractured reservoir exploration are the distribution and orientation of fracture systems, which play an important role in optimizing production from naturally fractured reservoirs (Sayers 2009; Far et al. 2014; Den Boer and Sayers 2018).

The seismic fracture prediction can be classified into two basic types: One is the seismic fracture qualitative prediction, which is mainly based on the discontinuity of fractures and uses the prestack seismic diffraction wave imaging approach or poststack geometric seismic attributes (such as curvature, coherence, and discontinuity) to qualitatively describe macroscale fractures, such as faults. The other is the seismic fracture quantitative prediction, which is mainly based on seismic azimuthal anisotropy (such as reflection amplitude, velocity, and attenuation) to predict mesoscale fractures, including obtaining fracture density and direction by ellipse fitting using azimuthal anisotropy attributes and quantitatively inverting fracture parameters using azimuthal prestack seismic data (Liu et al. 2015; Chen et al. 2016; Liu et al. 2018; Yuan et al. 2019).

Fracture detection utilizing seismic anisotropy has been an active field in the past decades. Hydrocarbon reservoirs with vertically aligned fractures can be described by horizontally transverse isotropic (HTI) media caused by a single set of rotationally invariant fractures in isotropic background rock. The amplitude and velocity of seismic waves propagating in HTI media usually exhibit significant azimuthal anisotropy. Reflection amplitude is superior to seismic velocities in characterizing fractured reservoirs due to its higher vertical resolution and sensitivity to the properties of a reservoir (Far et al. 2013). Much work has been done in deriving linear P-wave reflection coefficients in HTI media (Rüger 1998; Pšencík and Martins 2001; Shaw and Sen 2006; Chen et al. 2014a; Pan et al. 2018a) and directly characterizing fractured zones using azimuthal P-wave reflectivity data (Mallick et al. 1998; Gray and Todorovic-Marinic 2004; Bachrach et al. 2009; Mahmoudian et al. 2015; Wang et al. 2019).

In recent years, amplitude variation with angle and azimuth (AVAZ) inversion combining with the linear slip theory (Schoenberg and Douma 1988; Schoenberg and Sayers 1995) used for modeling fractures embedded in isotropic host rock is widely applied to predict fractured reservoirs. Based on the rock physics model, Chen et al. (2014a) proposed the AVAZ inversion method to estimate elastic and fracture weakness parameters. Pan et al. (2019) presented Bayesian AVAZ direct inversion for fluid indicator and fracture weakness in an oil-bearing fractured reservoir. AVAZ inversion is an ill condition; a large number of unknown parameters and the cross talk between the elastic and fracture parameters inevitably make several-term AVAZ inversion unstable (Downton et al. 2006; Bachrach 2015). One tentative approach to reduce the number of unknown parameters is to implement azimuthal seismic amplitude difference inversion for fracture weakness estimation (Chen et al. 2017a; Pan et al. 2017; Xue et al. 2017). In addition, Downton and Roure (2011, 2015) rewrote azimuthal P-wave reflectivity in terms of Fourier coefficients (FCs) and proposed an azimuthal Fourier coefficient elastic inversion for fracture parameters estimation. Barone and Sen (2018) implemented the application of real seismic data targeting the Haynesville Shale using a Fourier azimuthal amplitude variation fracture characterization method. Nevertheless, the suitability and reliability of AVAZ inversion in the presence of noise are still controversial. Moreover, it is a challenging task to extract reasonable space variant wavelets of each incident angle at different azimuths used for AVAZ inversion. This can be addressed by azimuthal elastic impedance (EI) extended from the concept of EI (Connolly 1999; Whitcombe 2002; Wang et al. 2006; Yin et al. 2013; Zong et al. 2013, 2016; Mozayan et al. 2018). In the last decades, there were abundant studies on the application of azimuthal EI in anisotropic inversion (Martins 2006; Chen et al. 2014b, 2017b; Pan et al. 2018b; Pan and Zhang 2019).

Our study is the extension of Downton and Roure (2015) research, which stabilizes the inversion process by treating the fracture weakness separately from the elastic parameters using FCs. Different from traditional fracture weakness inversion using azimuthal reflection amplitude or azimuthal EI or azimuthal reflection amplitude FCs, in this paper, a novel azimuthal EI-based FC variation with angle inversion method is proposed. The normalized azimuthal EI equation in HTI media is rewritten by using the Fourier series expansion method, the azimuth of the symmetry axis is estimated without 90° ambiguity using FCs, and FCs with the highest sensitivity to fracture weakness are chosen to estimate fracture weakness, which is constrained utilizing the Cauchy sparse regularization and the low-frequency regularization in a Bayesian framework. The influence of the azimuth of the symmetry axis on fracture weakness inversion is analyzed, and the proposed approach is demonstrated on both synthetic and real data.

2 Method and theory

2.1 Fourier coefficients of normalized azimuthal EI in logarithm domain

The P-wave reflection coefficient in HTI media is given by (Pan et al. 2017):

$$R_{PP} \left( {\theta ,\phi } \right) = \frac{1}{2}A\left( \theta \right)\frac{\alpha }{{\overline{\alpha } }} + \frac{1}{2}B\left( \theta \right)\frac{\beta }{{\overline{\beta } }} + \frac{1}{2}C\left( \theta \right)\frac{\rho }{{\overline{\rho } }} + \frac{1}{2}D\left( {\theta ,\phi } \right)\Delta_{{\Delta_{\text{N}} }} + \frac{1}{2}E\left( {\theta ,\phi } \right)\Delta_{{\Delta_{\text{T}} }}$$
(1)

with

$$\begin{aligned} A\left( \theta \right) & = \sec^{2} \theta , \\ B\left( \theta \right) & = - 8g\sin^{2} \theta , \\ C\left( \theta \right) & = 1 - 4g\sin^{2} \theta , \\ D\left( {\theta ,\phi } \right) & = - 2g\left[ {\left( {\cos^{2} \varphi \sin^{2} \theta + \sin^{2} \varphi \cos^{2} \varphi \sin^{2} \theta \tan^{2} \theta } \right)\left( {1 - 2g} \right)} \right. \\ & \quad \left. { + \cos^{4} \varphi \sin^{2} \theta \tan^{2} \theta \left( {1 - g} \right)} \right], \\ E\left( {\theta ,\phi } \right) & = 2g\cos^{2} \varphi \sin^{2} \theta \left( {1 - \sin^{2} \varphi \tan^{2} \theta } \right), \\ \end{aligned}$$

where \(\alpha\), \(\beta\), and \(\rho\) represent P-wave velocity, S-wave velocity, and density of the background isotropic medium, respectively. The superscript – represents the average of elastic parameters. \(g = {{\overline{\beta }^{2} } \mathord{\left/ {\vphantom {{\overline{\beta }^{2} } {\overline{\alpha }^{2} }}} \right. \kern-0pt} {\overline{\alpha }^{2} }}\) is the ratio of the squared vertical S- and P-wave velocities in the background isotropic medium, and \(\Delta_{\text{N}}\) and \(\Delta_{\text{T}}\) are the normal and tangential fracture weakness of layers. If the HTI model is induced by penny-shaped cracks, \(\Delta_{\text{T}}\) gives a direct estimate of the crack density and the ratio \({{\Delta_{\text{N}} } \mathord{\left/ {\vphantom {{\Delta_{\text{N}} } {\Delta_{\text{T}} }}} \right. \kern-0pt} {\Delta_{\text{T}} }}\) is a sensitive indicator of fluid saturation (Bakulin et al. 2000). \(\Delta_{{\Delta_{\text{N}} }}\) represents the difference in normal weakness between the upper and lower layers, and \(\Delta_{{\Delta_{\text{T}} }}\) represents the difference in tangential weakness between the upper and lower layers. \(\theta\) is the incident angle, and \(\varphi = \phi - \phi_{\text{sym}}\) is the angle between the observed azimuth \(\phi\) and azimuth \(\phi_{\text{sym}}\) of the symmetry axis.

Pan et al. (2017) further derived the normalized azimuthal EI equation as follows:

$${\text{EI}}\left( {\phi ,\theta } \right) = {\text{EI}}_{0} \left( {\frac{\alpha }{{\overline{\alpha } }}} \right)^{A\left( \theta \right)} \left( {\frac{\beta }{{\overline{\beta } }}} \right)^{B\left( \theta \right)} \left( {\frac{\rho }{{\overline{\rho } }}} \right)^{C\left( \theta \right)} \exp \left[ {D\left( {\theta ,\phi } \right)\Delta_{\text{N}} + E\left( {\theta ,\phi } \right)\Delta_{\text{T}} } \right],$$
(2)

where the subscript zero represents the constant medium properties of elastic parameters. The dimensionality dependence on the incident angle \(\theta\) is addressed by the introduction of \({\text{EI}}_{0} = \overline{\alpha } \overline{\rho }\) (Whitcombe 2002).

Taking logarithms on both sides of Eq. (2) yields:

$$L_{\text{EI}} \left( {\phi ,\theta } \right) = A\left( \theta \right)L_{P} + B\left( \theta \right)L_{S} + C\left( \theta \right)L_{\rho } + D\left( {\theta ,\phi } \right)\Delta_{\text{N}} + E\left( {\theta ,\phi } \right)\Delta_{\text{T}}$$
(3)

with

$$L_{\text{EI}} \left( {\phi ,\theta } \right) = \ln \frac{{{\text{EI}}\left( {\phi ,\theta } \right)}}{{{\text{EI}}_{0} }},L_{P} = \ln \frac{\alpha }{{\overline{\alpha } }},L_{S} = \ln \frac{\beta }{{\overline{\beta } }},L_{\rho } = \ln \frac{\rho }{{\overline{\rho } }}.$$

Equation (3) is the basis of conventional EI variation with angle and azimuth inversion for elastic and fracture weakness parameters. However, the robustness of inverting fracture weakness from azimuthal EI is still controversial due to the coupling between elastic and fracture weakness parameters.

Downton and Roure (2011, 2015) rewrote the azimuthal P-wave reflection coefficient using FCs. We can also describe the normalized azimuthal EI in logarithm domain in terms of FCs and rearrange Eq. (3) as follows:

$$L_{\text{EI}} \left( {\phi ,\theta } \right) = r_{0} \left( \theta \right) + r_{2} \left( \theta \right)\cos \left[ {2\left( {\phi - \phi_{\text{sym}} } \right)} \right] + r_{4} \left( \theta \right)\cos \left[ {4\left( {\phi - \phi_{\text{sym}} } \right)} \right]$$
(4)
$$r_{0} \left( \theta \right) = A\left( \theta \right)L_{P} + B\left( \theta \right)L_{S} + C\left( \theta \right)L_{\rho } + F\left( \theta \right)\Delta_{\text{N}} + G\left( \theta \right)\Delta_{\text{T}}$$
(5)
$$r_{2} \left( \theta \right) = H\left( \theta \right)\Delta_{\text{N}} + I\left( \theta \right)\Delta_{\text{T}}$$
(6)
$$r_{4} \left( \theta \right) = J\left( \theta \right)\Delta_{\text{N}} + K\left( \theta \right)\Delta_{\text{T}}$$
(7)

with

$$\begin{aligned} F\left( \theta \right) & = g\left( {2g - 1} \right)\sin^{2} \theta + g\left( {\frac{5}{4}g - 1} \right)\sin^{2} \theta \tan^{2} \theta ,G\left( \theta \right) = g\sin^{2} \theta - \frac{1}{4}g\sin^{2} \theta \tan^{2} \theta , \\ H\left( \theta \right) & = g\left( {2g - 1} \right)\sin^{2} \theta + g\left( {g - 1} \right)\sin^{2} \theta \tan^{2} \theta ,I\left( \theta \right) = g\sin^{2} \theta , \\ J\left( \theta \right) & = - \frac{1}{4}g^{2} \sin^{2} \theta \tan^{2} \theta ,K\left( \theta \right) = - \frac{1}{4}g\sin^{2} \theta \tan^{2} \theta , \\ \end{aligned}$$

where \(r_{0} \left( \theta \right)\) represents the DC component FC, which involves the three-term AVO expression with the addition of fracture weakness terms, \(r_{2} \left( \theta \right)\) and \(r_{4} \left( \theta \right)\) represent the second and fourth FCs, respectively, which are only related to fracture weaknesses and independent of elastic parameters, and the phase of the second and fourth FCs is related to azimuth of the symmetry axis.

Equation (4) can be further written as the weighted sum of cosine and sine waves by:

$$L_{\text{EI}} \left( {\phi ,\theta } \right) = a_{0} \left( \theta \right) + a_{2} \left( \theta \right)\cos \left( {2\phi } \right) + b_{2} \left( \theta \right)\sin \left( {2\phi } \right) + a_{4} \left( \theta \right)\cos \left( {4\phi } \right) + b_{4} \left( \theta \right)\sin \left( {4\phi } \right)$$
(8)
$$a_{0} \left( \theta \right) = A\left( \theta \right)L_{P} + B\left( \theta \right)L_{S} + C\left( \theta \right)L_{\rho } + F\left( \theta \right)\Delta_{\text{N}} + G\left( \theta \right)\Delta_{\text{T}}$$
(9)
$$a_{2} \left( \theta \right) = H\left( \theta \right)\cos \left( {2\phi_{\text{sym}} } \right)\Delta_{\text{N}} + I\left( \theta \right)\cos \left( {2\phi_{\text{sym}} } \right)\Delta_{\text{T}}$$
(10)
$$b_{2} \left( \theta \right) = H\left( \theta \right)\sin \left( {2\phi_{\text{sym}} } \right)\Delta_{\text{N}} + I\left( \theta \right)\sin \left( {2\phi_{\text{sym}} } \right)\Delta_{\text{T}}$$
(11)
$$a_{4} \left( \theta \right) = J\left( \theta \right)\cos \left( {4\phi_{\text{sym}} } \right)\Delta_{\text{N}} + K\left( \theta \right)\cos \left( {4\phi_{\text{sym}} } \right)\Delta_{\text{T}}$$
(12)
$$b_{4} \left( \theta \right) = J\left( \theta \right)\sin \left( {4\phi_{\text{sym}} } \right)\Delta_{\text{N}} + K\left( \theta \right)\sin \left( {4\phi_{\text{sym}} } \right)\Delta_{\text{T}} ,$$
(13)

where \(a_{n} \left( \theta \right)\) and \(b_{n} \left( \theta \right)\) (n = 0, 2, 4) represent the nth FCs, respectively. For the case of X regularly sampled data, a discrete Fourier transform (DFT) can be used to calculate \(a_{n} \left( \theta \right)\) and \(b_{n} \left( \theta \right)\):

$$a_{n} \left( \theta \right) = \frac{1}{\pi }\sum\limits_{k = 1}^{X} {L_{\text{EI}_{k}} \left( {\phi ,\theta } \right)} \cos \left( {n\phi } \right){\text{d}}\phi$$
(14)
$$b_{n} \left( \theta \right) = \frac{1}{\pi }\sum\limits_{k = 1}^{X} {L_{\text{EI}_{k}} \left( {\phi ,\theta } \right)} \sin \left( {n\phi } \right){\text{d}}\phi .$$
(15)

Note that Nyquist criterion must be met so that \(a_{n} \left( \theta \right)\) and \(b_{n} \left( \theta \right)\) can be obtained by DFT. In order to estimate \(a_{ 2} \left( \theta \right)\) and \(b_{ 2} \left( \theta \right)\), the data must be sampled no coarser than 45°. In order to estimate \(a_{ 4} \left( \theta \right)\) and \(b_{ 4} \left( \theta \right)\), the data must be sampled no coarser than 22.5°.

2.2 Sensitivity analysis of the FCs

The second and fourth FCs are related to fracture weaknesses and independent of elastic parameters; we use the isotropic medium model parameters given by Rüger and Tsvankin (1997) and change the normal and tangential weaknesses, respectively, to analyze the sensitivity of the second and fourth FCs to normal and tangential weaknesses. The P-wave velocity, S-wave velocity, and density of the isotropic medium model are 4.500 km/s, 2.530 km/s, and 2.800 g/cm3, respectively. The normal and tangential weaknesses increase from 0 to 0.2, respectively, in increments of 0.05. We use Eqs. (6) and (7) to calculate the second and fourth FCs. Figure 1a, b shows the second FC \(r_{ 2} \left( \theta \right)\) variation with the normal and tangential fracture weaknesses. Figure 2a, b shows the fourth FC \(r_{4} \left( \theta \right)\) variation with the normal and tangential fracture weaknesses. It can be seen that when the incident angle is less than 30°, \(r_{4} \left( \theta \right)\) hardly changes with normal and tangential weaknesses, and \(r_{ 2} \left( \theta \right)\) changes significantly with normal and tangential weaknesses. Compared with \(r_{4} \left( \theta \right)\), \(r_{ 2} \left( \theta \right)\) is more sensitive to normal and tangential weaknesses.

Fig. 1
figure 1

Second FC \(r_{ 2} \left( \theta \right)\) variation with the normal and tangential fracture weaknesses, in which a shows \(r_{ 2} \left( \theta \right)\) in the case of changing normal weakness, and b shows \(r_{ 2} \left( \theta \right)\) in the case of changing tangential weakness

Full size image
Fig. 2
figure 2

Fourth FC \(r_{4} \left( \theta \right)\) variation with the normal and tangential fracture weaknesses, in which a shows \(r_{4} \left( \theta \right)\) in the case of changing normal weakness, and b shows \(r_{4} \left( \theta \right)\) in the case of changing tangential weakness

Full size image

Since \(a_{ 2} \left( \theta \right) = r_{ 2} \left( \theta \right)\cos 2\phi_{\text{sym}}\) and \(b_{ 2} \left( \theta \right) = r_{ 2} \left( \theta \right)\sin 2\phi_{\text{sym}}\), \(a_{ 2} \left( \theta \right)\) is a scaled version of \(r_{ 2} \left( \theta \right)\) by the scalar \(\cos 2\phi_{\text{sym}}\) and \(b_{ 2} \left( \theta \right)\) is a scaled version of \(r_{ 2} \left( \theta \right)\) by the scalar \(\sin 2\phi_{\text{sym}}\). In the case when one of \(a_{ 2} \left( \theta \right)\) and \(b_{ 2} \left( \theta \right)\) is zero, the other one is \(r_{ 2} \left( \theta \right)\) or \(- r_{ 2} \left( \theta \right)\). As shown in Figs. 1a, b and 3a, b, both \(r_{ 2} \left( \theta \right)\) and \(- r_{ 2} \left( \theta \right)\) are sensitive to fracture weaknesses. As a result, there is always one in \(a_{ 2} \left( \theta \right)\) and \(b_{ 2} \left( \theta \right)\) which is sensitive to fracture weaknesses. In the case when \(a_{ 2} \left( \theta \right)\) and \(b_{ 2} \left( \theta \right)\) are the same, both are \({{\sqrt 2 r_{ 2} \left( \theta \right)} \mathord{\left/ {\vphantom {{\sqrt 2 r_{ 2} \left( \theta \right)} 2}} \right. \kern-0pt} 2}\) or \({{ - \sqrt 2 r_{ 2} \left( \theta \right)} \mathord{\left/ {\vphantom {{ - \sqrt 2 r_{ 2} \left( \theta \right)} 2}} \right. \kern-0pt} 2}\). As shown in Fig. 3c–f, \({{\sqrt 2 r_{ 2} \left( \theta \right)} \mathord{\left/ {\vphantom {{\sqrt 2 r_{ 2} \left( \theta \right)} 2}} \right. \kern-0pt} 2}\) and \({{ - \sqrt 2 r_{ 2} \left( \theta \right)} \mathord{\left/ {\vphantom {{ - \sqrt 2 r_{ 2} \left( \theta \right)} 2}} \right. \kern-0pt} 2}\) are both sensitive to fracture weaknesses, so both \(a_{ 2} \left( \theta \right)\) and \(b_{ 2} \left( \theta \right)\) are sensitive to fracture weaknesses. In other cases, at least one of \(a_{ 2} \left( \theta \right)\) and \(b_{ 2} \left( \theta \right)\) is sensitive to fracture weaknesses, and its sensitivity to fracture weaknesses is greater than the sensitivity of \({{\sqrt 2 r_{ 2} \left( \theta \right)} \mathord{\left/ {\vphantom {{\sqrt 2 r_{ 2} \left( \theta \right)} 2}} \right. \kern-0pt} 2}\) or \({{ - \sqrt 2 r_{ 2} \left( \theta \right)} \mathord{\left/ {\vphantom {{ - \sqrt 2 r_{ 2} \left( \theta \right)} 2}} \right. \kern-0pt} 2}\) to fracture weaknesses. Consequently, no matter how \(\phi_{\text{sym}}\) changes, at least one of \(a_{ 2} \left( \theta \right)\) and \(b_{ 2} \left( \theta \right)\) is sensitive to fracture weaknesses, which indicates that \(a_{ 2} \left( \theta \right)\) and \(b_{ 2} \left( \theta \right)\) can be simultaneously combined to invert for fracture weaknesses.

Fig. 3
figure 3

Different scaled \(r_{2} \left( \theta \right)\) variation with the normal and tangential fracture weaknesses, in which a shows \(- r_{2} \left( \theta \right)\) in the case of changing normal weakness, b shows \(- r_{2} \left( \theta \right)\) in the case of changing tangential weakness, c shows \(\sqrt 2 r_{2} \left( \theta \right)/2\) in the case of changing normal weakness, d shows \(\sqrt 2 r_{2} \left( \theta \right)/2\) in the case of changing tangential weakness, e shows \(- \sqrt 2 r_{2} \left( \theta \right)/2\) in the case of changing normal weakness, and f shows \(- \sqrt 2 r_{2} \left( \theta \right)/2\) in the case of changing tangential weakness

Full size image

2.3 Resolving the 90° ambiguity in the azimuth estimation of the symmetry axis

According to Eqs. (10) and (11), \(a_{ 2} \left( \theta \right)\) and \(b_{ 2} \left( \theta \right)\) are functions of \(\phi_{\text{sym}}\). In order to estimate fracture weaknesses from \(a_{ 2} \left( \theta \right)\) and \(b_{ 2} \left( \theta \right)\), \(\phi_{\text{sym}}\) should be estimated first, which can be obtained by:

$$\phi_{\text{sym}} = \frac{1}{n}\arctan \left[ {\frac{{b_{n} \left( \theta \right)}}{{a_{n} \left( \theta \right)}}} \right],\quad \left( {n = 2,4} \right).$$
(16)

Since the signs of \(r_{ 2} \left( \theta \right)\) and \(r_{4} \left( \theta \right)\) cannot be determined, there is a 90° ambiguity in \(\phi_{\text{sym}}\) estimate using \(a_{ 2} \left( \theta \right)\) and \(b_{ 2} \left( \theta \right)\), and there is a 45° ambiguity in \(\phi_{\text{sym}}\) estimate using \(a_{4} \left( \theta \right)\) and \(b_{4} \left( \theta \right)\); we propose an approach to resolve the ambiguity. Firstly, \(\phi_{\text{sym}}\) is directly calculated from \(a_{ 2} \left( \theta \right)\) and \(b_{ 2} \left( \theta \right)\) by:

$$\phi_{\text{sym}} = \frac{1}{2}\arctan \left[ {\frac{{b_{2} \left( \theta \right)}}{{a_{2} \left( \theta \right)}}} \right].$$
(17)

Since \(a_{ 2} \left( \theta \right) = r_{ 2} \left( \theta \right)\cos 2\phi_{\text{sym}}\), \(b_{ 2} \left( \theta \right) = r_{ 2} \left( \theta \right)\sin 2\phi_{\text{sym}}\), for the case of \(r_{ 2} \left( \theta \right) > 0\), if the sign of \(a_{ 2} \left( \theta \right)\) is the same as the sign of \(\cos 2\phi_{\text{sym}}\), and the sign of \(b_{ 2} \left( \theta \right)\) is the same as the sign of \(\sin 2\phi_{\text{sym}}\), the estimated \(\phi_{\text{sym}}\) is correct, otherwise the estimated \(\phi_{\text{sym}} = \phi_{\text{sym}} + 90^\circ\). For the case of \(r_{ 2} \left( \theta \right) < 0\), if the sign of \(a_{ 2} \left( \theta \right)\) is opposite to the sign of \(\cos 2\phi_{\text{sym}}\), and the sign of \(b_{ 2} \left( \theta \right)\) is opposite to the sign of \(\sin 2\phi_{\text{sym}}\), the estimated \(\phi_{\text{sym}}\) is correct, otherwise the estimated \(\phi_{\text{sym}} = \phi_{\text{sym}} + 90^\circ\).

For fluid-filled cracks (Bakulin et al. 2000), the relationship between the fracture weaknesses and the crack density \(e\) is given as:

$$\Delta_{\text{N}} = 0$$
(18)
$$\Delta_{\text{T}} = \frac{16e}{{3\left( {3 - 2g} \right)}}.$$
(19)

Combining Eqs. (6), (18), and (19) gives:

$$r_{2} \left( \theta \right) = \frac{{16g\sin^{2} \theta }}{{3\left( {3 - 2g} \right)}}e.$$
(20)

Therefore, for fluid-filled cracks, there is always \(r_{ 2} \left( \theta \right) > 0\).

For dry (gas-filled) cracks:

$$\Delta_{\text{N}} = \frac{4e}{{3g\left( {1 - g} \right)}}$$
(21)
$$\Delta_{\text{T}} = \frac{16e}{{3\left( {3 - 2g} \right)}}.$$
(22)

Combining Eqs. (6), (21), and (22) gives:

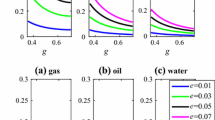
$$r_{2} \left( \theta \right) = \left[ {H\left( \theta \right)\frac{4}{{3g\left( {1 - g} \right)}} + I\left( \theta \right)\frac{16}{{3\left( {3 - 2g} \right)}}} \right]e.$$
(23)

Thus, for dry (gas-filled) cracks, \(r_{ 2} \left( \theta \right)\) is related to the incident angle, crack density, and the ratio \(g\), and since the crack density e is always positive, the sign of \(r_{ 2} \left( \theta \right)\) is only related to \(\theta\) and \(g\). As shown in Fig. 4a–d, for the case of different incident angles, \(r_{ 2} \left( \theta \right)\) increases with the ratio \(g\) and changes sign with increasing \(g\), and the slope of \(r_{ 2} \left( \theta \right)\) gradually increases with crack density. However, the change of the crack density does not change the corresponding ratio \(g\) for \(r_{ 2} \left( \theta \right)\) changing sign, while the change of the incident angle changes the corresponding ratio \(g\) for \(r_{ 2} \left( \theta \right)\) changing sign, and the corresponding ratio \(g\) for \(r_{ 2} \left( \theta \right)\) changing sign becomes larger with increasing incident angle. Note that for the case of incident angle \(\theta \le 30\) (in Fig. 4a–c), if \(g > 0.4\), there is always \(r_{ 2} \left( \theta \right) > 0\). For the case of incident angle \(\theta > 30^\circ\) (in Fig. 4d), if \(g < 0.4\), there is always \(r_{ 2} \left( \theta \right) < 0\).

Fig. 4
figure 4

Second FC \(r_{2} \left( \theta \right)\) variation with crack density and ratio \(g\) at different incident angles for dry (gas-filled) cracks, a\(\theta = 10^\circ\), b\(\theta = 20^\circ\), c\(\theta = 30^\circ\), and d\(\theta = 40^\circ\)

Full size image

To judge the sign of \(r_{ 2} \left( \theta \right)\) using the above method requires knowing fracture infill (content) in advance, but fracture infill is usually unknown, so anisotropic rock physical model (Zhang et al. 2013; Chen et al. 2014a; Pan et al. 2017) can be used to estimate fracture weaknesses, then calculate \(r_{ 2} \left( \theta \right)\), and judge its sign to further resolve ambiguity.

2.4 Azimuthal EI-based FC variation with angle inversion for fracture weakness

For each incident angle, the normalized azimuthal EI in logarithm domain can be decomposed into a series of FCs, the second and fourth FCs are only related to fracture weakness and independent of elastic parameters, and the previous analysis suggests that we use second FCs to estimate fracture weakness. In the case of M incident angle and N time sample, combining Eqs. (10) and (11), we can get the following matrix expression:

$$\left[ {\begin{array}{*{20}c} {{\mathbf{a}}_{2} \left( {\theta_{1} } \right)} \\ {{\mathbf{b}}_{2} \left( {\theta_{1} } \right)} \\ \vdots \\ {{\mathbf{a}}_{2} \left( {\theta_{M} } \right)} \\ {{\mathbf{b}}_{2} \left( {\theta_{M} } \right)} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {{\mathbf{H}}\left( {\theta_{1} } \right)\cos \left( {2\phi_{\text{sym}} } \right)} & {{\mathbf{I}}\left( {\theta_{1} } \right)\cos \left( {2\phi_{\text{sym}} } \right)} \\ {{\mathbf{H}}\left( {\theta_{1} } \right)\sin \left( {2\phi_{\text{sym}} } \right)} & {{\mathbf{I}}\left( {\theta_{1} } \right)\sin \left( {2\phi_{\text{sym}} } \right)} \\ \vdots & \vdots \\ {{\mathbf{H}}\left( {\theta_{M} } \right)\cos \left( {2\phi_{\text{sym}} } \right)} & {{\mathbf{I}}\left( {\theta_{M} } \right)\cos \left( {2\phi_{\text{sym}} } \right)} \\ {{\mathbf{H}}\left( {\theta_{M} } \right)\sin \left( {2\phi_{\text{sym}} } \right)} & {{\mathbf{I}}\left( {\theta_{M} } \right)\sin \left( {2\phi_{\text{sym}} } \right)} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {{\varvec{\Delta}}_{{\mathbf{N}}} } \\ {{\varvec{\Delta}}_{{\mathbf{T}}} } \\ \end{array} } \right]$$
(24)

with

$$\begin{aligned} & {\mathbf{a}}_{2} \left( {\theta_{m} } \right) = \left[ {a_{2}^{1} \left( {\theta_{m} } \right), \ldots ,a_{2}^{N} \left( {\theta_{m} } \right)} \right]^{\text{T}} ,{\mathbf{b}}_{2} \left( {\theta_{m} } \right) = \left[ {b_{2}^{1} \left( {\theta_{m} } \right), \ldots ,b_{2}^{N} \left( {\theta_{m} } \right)} \right]^{\text{T}} , \\ & {\mathbf{H}}\left( {\theta_{m} } \right) = \text{diag} \left[ {H^{1} \left( {\theta_{m} } \right), \ldots ,H^{N} \left( {\theta_{m} } \right)} \right],{\mathbf{I}}\left( {\theta_{m} } \right) = \text{diag} \left[ {I^{1} \left( {\theta_{m} } \right), \ldots ,I^{N} \left( {\theta_{m} } \right)} \right] , \\ & {\varvec{\Delta}}_{{\mathbf{N}}} = \left[ {\Delta_{\text{N}}^{1} , \ldots ,\Delta_{\text{N}}^{N} } \right]^{T} ,{\varvec{\Delta}}_{{\mathbf{T}}} = \left[ {\Delta_{\text{T}}^{1} , \ldots ,\Delta_{\text{T}}^{N} } \right]^{\text{T}} . \\ \end{aligned}$$

Here, the superscript \({\text{T}}\) denotes the transpose of a matrix, and the symbol \(\text{diag}\) denotes a diagonal matrix; the subscripts m represents the mth angle of incidence.

Equation (24) can be expressed in matrix form as:

$${\mathbf{d}}_{NM \times 1} = {\mathbf{G}}_{NM \times 2N} {\mathbf{m}}_{2N \times 1}$$
(25)

with

$${\mathbf{d}} = \left[ {\begin{array}{*{20}c} {{\mathbf{a}}_{2} \left( {\theta_{1} } \right)} \\ {{\mathbf{b}}_{2} \left( {\theta_{1} } \right)} \\ \vdots \\ {{\mathbf{a}}_{2} \left( {\theta_{M} } \right)} \\ {{\mathbf{b}}_{2} \left( {\theta_{M} } \right)} \\ \end{array} } \right],{\mathbf{m}} = \left[ {\begin{array}{*{20}c} {{\varvec{\Delta}}_{{\mathbf{N}}} } \\ {{\varvec{\Delta}}_{{\mathbf{T}}} } \\ \end{array} } \right],{\mathbf{G}} = \left[ {\begin{array}{*{20}c} {{\mathbf{H}}\left( {\theta_{1} } \right)\cos \left( {2\phi_{\text{sym}} } \right)} & {{\mathbf{I}}\left( {\theta_{1} } \right)\cos \left( {2\phi_{\text{sym}} } \right)} \\ {{\mathbf{H}}\left( {\theta_{1} } \right)\sin \left( {2\phi_{\text{sym}} } \right)} & {{\mathbf{I}}\left( {\theta_{1} } \right)\sin \left( {2\phi_{\text{sym}} } \right)} \\ \vdots & \vdots \\ {{\mathbf{H}}\left( {\theta_{M} } \right)\cos \left( {2\phi_{\text{sym}} } \right)} & {{\mathbf{I}}\left( {\theta_{M} } \right)\cos \left( {2\phi_{\text{sym}} } \right)} \\ {{\mathbf{H}}\left( {\theta_{M} } \right)\sin \left( {2\phi_{\text{sym}} } \right)} & {{\mathbf{I}}\left( {\theta_{M} } \right)\sin \left( {2\phi_{\text{sym}} } \right)} \\ \end{array} } \right].$$

Based on Bayesian theory (Buland and More 2003), the posterior probability density function of the model parameters can be expressed as:

$$p\left( {{\mathbf{m}}\left| {\mathbf{d}} \right.} \right) = \frac{{p\left( {\mathbf{m}} \right)p\left( {{\mathbf{d}}\left| {\mathbf{m}} \right.} \right)}}{{\int {p\left( {{\mathbf{d}}\left| {\mathbf{m}} \right.} \right){\text{d}}{\mathbf{m}}} }} \propto p\left( {\mathbf{m}} \right)p\left( {{\mathbf{d}}\left| {\mathbf{m}} \right.} \right).$$
(26)

We assume that the likelihood function \(p\left( {{\mathbf{d}}\left| {\mathbf{m}} \right.} \right)\) obeys a Gaussian probability distribution, which is given by:

$$p\left( {{\mathbf{d}}\left| {\mathbf{m}} \right.} \right) = \frac{1}{{\sqrt {2\pi } \sigma_{n} }}\exp \left[ {\frac{{ - \left( {{\mathbf{d}} - {\mathbf{Gm}}} \right)^{\text{T}} \left( {{\mathbf{d}} - {\mathbf{Gm}}} \right)}}{{2\sigma_{n}^{2} }}} \right],$$
(27)

where \(\sigma_{n}^{2}\) is the variance of noise. Cauchy probability distribution can suppress random noise and produce a sparse solution with high vertical resolution (Downton 2005; Chen et al. 2017b; Yuan et al. 2018); we assume that the prior probability distribution \(p\left( {\mathbf{m}} \right)\) obeys Cauchy probability distribution as follows:

$$p\left( {\mathbf{m}} \right) = \frac{1}{{\left( {\pi \sigma_{m} } \right)^{2N} }}\prod\limits_{i = 1}^{2N} {\left[ {\frac{1}{{1 + {{{\mathbf{m}}_{i}^{2} } \mathord{\left/ {\vphantom {{{\mathbf{m}}_{i}^{2} } {\sigma_{m}^{2} }}} \right. \kern-0pt} {\sigma_{m}^{2} }}}}} \right]} ,$$
(28)

where \(\sigma_{m}^{2}\) is the variance of model parameters. Combining Eqs. (26), (27), and (28), we can get the initial objective function for the MAP solution inversion, which is expressed as:

$$F\left( {\mathbf{m}} \right) = \left( {{\mathbf{d}} - {\mathbf{Gm}}} \right)^{\text{T}} \left( {{\mathbf{d}} - {\mathbf{Gm}}} \right) + 2\sigma_{n}^{2} \sum\limits_{i = 1}^{2N} {\ln \left( {1 + {{{\mathbf{m}}_{i}^{2} } \mathord{\left/ {\vphantom {{{\mathbf{m}}_{i}^{2} } {\sigma_{m}^{2} }}} \right. \kern-0pt} {\sigma_{m}^{2} }}} \right)} .$$
(29)

We combine the low-frequency information constraint obtained from well logs; the final objective function is obtained as follows:

$$\begin{aligned} F\left( {\mathbf{m}} \right) & = \left( {{\mathbf{d}} - {\mathbf{Gm}}} \right)^{\text{T}} \left( {{\mathbf{d}} - {\mathbf{Gm}}} \right) + 2\sigma_{n}^{2} \sum\limits_{i = 1}^{2N} {\ln \left( {1 + {{{\mathbf{m}}_{i}^{2} } \mathord{\left/ {\vphantom {{{\mathbf{m}}_{i}^{2} } {\sigma_{m}^{2} }}} \right. \kern-0pt} {\sigma_{m}^{2} }}} \right)} \\ & \quad + \lambda_{{\Delta_{\text{N}} }} \left( {{\varvec{\Delta}}_{{\mathbf{N}}} - {\varvec{\Delta}}_{{{\mathbf{N0}}}} } \right)^{\text{T}} \left( {{\varvec{\Delta}}_{{\mathbf{N}}} - {\varvec{\Delta}}_{{{\mathbf{N0}}}} } \right) + \lambda_{{\Delta_{T} }} \left( {{\varvec{\Delta}}_{{\mathbf{T}}} - {\varvec{\Delta}}_{{{\mathbf{T0}}}} } \right)^{\text{T}} \left( {{\varvec{\Delta}}_{{\mathbf{T}}} - {\varvec{\Delta}}_{{{\mathbf{T0}}}} } \right), \\ \end{aligned}$$
(30)

where \(\lambda_{{\Delta_{\text{N}} }}\) and \(\lambda_{{\Delta_{\text{T}} }}\) are weighting factors for the normal and tangential fracture weaknesses, respectively. \({\varvec{\Delta}}_{{{\mathbf{N0}}}}\) and \({\varvec{\Delta}}_{{{\mathbf{T0}}}}\) represent initial models for the normal and tangential fracture weaknesses, which can be obtained by using the estimation results from the anisotropic rock physics model (Zhang et al. 2013; Chen et al. 2014a; Pan et al. 2017). The iteratively reweighted least squares (IRLS) method is employed to solve Eq. (30) for estimating the normal and tangential fracture weaknesses.

2.5 Workflow of azimuthal EI-based FC variation with angle inversion for fracture weakness

A workflow of azimuthal EI-based FC variation with angle inversion is proposed to estimate fracture weaknesses; we conclude the whole process as follows:

  1. 1.

    The constrained sparse spike inversion (CSSI) for azimuthal EI datasets from azimuthal angle stacks. The inputs include azimuthal angle stacks, azimuthal seismic wavelets, and low-frequency azimuthal EI models of each incident angle. Since azimuth \(\phi_{\text{sym}}\) of the symmetry axis is unknown, low-frequency azimuthal EI models are obtained by interpolating isotropic EI calculated from well log data.

  2. 2.

    The prediction for \(a_{ 2} \left( \theta \right)\) and \(b_{ 2} \left( \theta \right)\) from all estimated azimuthal EI datasets and estimation for \(\phi_{\text{sym}}\) from \(a_{ 2} \left( \theta \right)\) and \(b_{ 2} \left( \theta \right)\). The ambiguity in \(\phi_{\text{sym}}\) estimate is resolved by judging the sign of \(r_{ 2} \left( \theta \right)\), which is obtained by combining fracture weaknesses from the anisotropic rock physics model (Zhang et al. 2013; Chen et al. 2014a; Pan et al. 2017) and elastic parameters from well log. Note that for the case of regularly sampled azimuthal EI datasets, \(a_{ 2} \left( \theta \right)\) and \(b_{ 2} \left( \theta \right)\) can be calculated using a DFT shown in Eqs. (14) and (15). For the more complex case of irregularly sampled EI datasets in azimuth, a least squares inversion may be performed by using Eq. (8).

  3. 3.

    The estimation for fracture weaknesses using the extracted \(a_{ 2} \left( \theta \right)\), \(b_{ 2} \left( \theta \right)\), and \(\phi_{\text{sym}}\) iteratively, which is constrained utilizing the Cauchy sparse regularization and the low-frequency regularization in a Bayesian framework (Pan and Zhang 2019).

3 Examples

3.1 Synthetic examples

In order to validate the proposed approach, a five-layer medium model is established (as indicated in Table 1), in which the first, third, and fifth layers are isotropic medium, and the second and fourth layers are HTI medium resulting from dry cracks; the model parameters are given by Rüger and Tsvankin (1997). Note that the fracture symmetry axis azimuths of the second and fourth layers are assumed to be 60° and 120°, respectively. Thomsen anisotropy parameters are given in Table 1; the normal and tangential weaknesses are obtained using the approximation given by Bakulin et al. (2000):

$$\Delta_{\text{N}} = \frac{2g}{1 - g}\varepsilon^{\left( V \right)}$$
(31)
$$\Delta_{\text{T}} = 2\gamma .$$
(32)
Table 1 Elastic and anisotropic parameters of the five-layer model (Rüger and Tsvankin 1997)
Full size table

Synthetic data are generated from model parameters given in Table 1 convolved with a 35 Hz Ricker wavelet, including four azimuthal angle gathers (the given azimuths are 0°, 45°, 90°, and 135°, respectively), and the incident angle ranges from 5° to 35°. Firstly, angle gathers for each azimuth are stacked to obtain azimuthal angle stacks, including three average incident angles (small incident angle 10°, stacked by 5°–15°; middle incident angle 20°, stacked by 15°–25°; large incident angle 30°, stacked by 25°–35°); for each azimuth, the azimuthal EI datasets are obtained from azimuthal angle stacks and used to calculate \(a_{ 2} \left( \theta \right)\) and \(b_{ 2} \left( \theta \right)\). Since \(a_{ 2} \left( \theta \right)\) and \(b_{ 2} \left( \theta \right)\) are related to \(\phi_{\text{sym}}\) and the ratio \(g\), the ratio \(g\) can be calculated from a constant or slowly varying prior known background model (Buland and More 2003). In order to analyze the effect of \(\phi_{\text{sym}}\) on fracture weakness inversion, we combine \(a_{ 2} \left( \theta \right)\), \(b_{ 2} \left( \theta \right)\), and different \(\phi_{\text{sym}}\) (the azimuth deviation \(\Delta \phi_{\text{sym}}\) of the symmetry axis is 0°, 15°, 30°, 45°, 60°, 75°, and 90°, respectively) to estimate fracture weaknesses. Figure 5a shows the synthetic azimuthal angle gathers without noise; Fig. 6 shows the inversion results of fracture weaknesses in different \(\Delta \phi_{\text{sym}}\) cases, the black curve represents the true models, and the dashed lines of different colors, respectively, represent the inversion results in the case of different \(\Delta \phi_{\text{sym}}\). It can be seen that when \(\Delta \phi_{\text{sym}}\) is 0°, the inversion results are completely consistent with the true models. When \(\Delta \phi_{\text{sym}}\) is 15°, the inversion results are slightly deviated from the true models. When \(\Delta \phi_{\text{sym}}\) is 30°, the inversion results are more deviated from the true models, but they are basically consistent with the true model trends. As \(\Delta \phi_{\text{sym}}\) continues to increase (\(\Delta \phi_{\text{sym}}\) is 45°, 60°, 75°, and 90°, respectively), the inversion results are gradually opposite to the true model trends and are no longer reliable, which indicates that fracture weakness inversion results obtained by the proposed approach is reliable when \(\Delta \phi_{\text{sym}}\) is less than 30°.

Fig. 5
figure 5

Synthetic azimuthal angle gathers, in which a shows the case of no noise, b shows the case of S/N = 5, (c) shows the case of S/N = 2

Full size image
Fig. 6
figure 6

Comparisons between the inversion results of fracture weaknesses (dashed lines in different colors) using different \(\phi_{\text{sym}}\) (\(\Delta \phi_{\text{sym}}\) is 0°, 15°, 30°, 45°, 60°, 75°, and 90°, respectively) and the true models (black line) for the case of no noise

Full size image

\(\phi_{\text{sym}}\) should be estimated before fracture weakness inversion from \(a_{ 2} \left( \theta \right)\) and \(b_{ 2} \left( \theta \right)\); we propose a stable approach to estimate \(\phi_{\text{sym}}\) without ambiguity and also use the above model to validate the proposed approach. Figure 7a shows the directly estimated \(\phi_{\text{sym}}\), and Fig. 7b shows the corrected \(\phi_{\text{sym}}\) using the proposed approach. Note that the directly estimated \(\phi_{\text{sym}}\) of the second layer (pink rectangle) and fourth layer (green rectangle) is 150° and 30°, respectively, both having a 90° ambiguity, while the relevant corrected \(\phi_{\text{sym}}\) is 60° and 120°, respectively, which indicates that the 90° ambiguity is successfully resolved using the proposed approach. It is noted that in the proposed approach, the sign of \(r_{ 2} \left( \theta \right)\) should be determined first. Here, \(r_{ 2} \left( \theta \right)\) is calculated by smoothing model parameters for 100 times. In order to show the performance of the proposed approach in synthetic noisy data, white Gaussian noise with different signal-to-noise (S/N) ratios is added to the resulting synthetics; the relevant synthetic noisy results are shown in Fig. 5b, c, respectively. The relevant directly estimated \(\phi_{\text{sym}}\) is shown in Figs. 8a and 9a, respectively, and the relevant corrected \(\phi_{\text{sym}}\) is shown in Figs. 8b and 9b, respectively. As can be seen from Fig. 8a, b, for the case of S/N = 5, in the second layer, the \(\phi_{\text{sym}}\) directly estimated at small, middle, and large incident angles is approximately 135°, 143°, and 149°, respectively, and the relevant corrected \(\phi_{\text{sym}}\) is approximately 45°, 53°, and 59°, respectively. In the fourth layer, the \(\phi_{\text{sym}}\) directly estimated at small, middle, and large incident angles is approximately 173°, 27°, and 28°, respectively, and the relevant corrected \(\phi_{\text{sym}}\) is approximately 173°, 117°, and 118°, respectively. As can be seen from Fig. 9a, b, for the case of S/N = 2, in the second layer, the \(\phi_{\text{sym}}\) directly estimated at small, middle, and large incident angles is approximately 25°, 141°, and 151°, respectively, and the relevant corrected \(\phi_{\text{sym}}\) is approximately 25°, 51°, and 61°, respectively. In the fourth layer, \(\phi_{\text{sym}}\) directly estimated at small, middle, and large incident angles is approximately 171°, 23°, and 35°, respectively, and the relevant corrected \(\phi_{\text{sym}}\) is approximately 171°, 113°, and 125°, respectively. It can be seen that \(\phi_{\text{sym}}\) directly estimated at small incident angles is unreliable, and \(\phi_{\text{sym}}\) directly estimated at middle and large incident angles is more stable and reliable but has a 90° ambiguity, while the 90° ambiguity is successfully resolved using the proposed approach. It indicates that \(\phi_{\text{sym}}\) can be estimated by using seismic data at middle and large incident angles. If there are multiple \(\phi_{\text{sym}}\) estimated at middle and large incident angles, the average of multiple \(\phi_{\text{sym}}\) can be a more stable and reliable result.

Fig. 7
figure 7

Comparisons between the directly estimated \(\phi_{\text{sym}}\) and the relevant corrected \(\phi_{\text{sym}}\) at different incident angles (circle lines in different colors) for the case of no noise. a The directly estimated \(\phi_{\text{sym}}\), and b the relevant corrected \(\phi_{\text{sym}}\). Note that the true \(\phi_{\text{sym}}\) of the second layer (pink rectangle) and the fourth layer (green rectangle) is 60° and 120°, respectively

Full size image
Fig. 8
figure 8

Same as Fig. 7 but for the case of S/N = 5

Full size image
Fig. 9
figure 9

Same as Fig. 8 but for the case of S/N = 2

Full size image

The fracture weakness can be obtained by combining \(a_{ 2} \left( \theta \right)\), \(b_{ 2} \left( \theta \right)\), and the estimated \(\phi_{\text{sym}}\). The above model is also used to validate the proposed fracture weakness inversion approach. Here, the average of \(\phi_{\text{sym}}\) estimated at middle and large incident angles is taken as the final \(\phi_{\text{sym}}\) for fracture weakness inversion. Figure 10a–c shows the comparisons between the inversion results (red) and the true models (black) of the normal and tangential weaknesses. Here, the initial models (green) of fracture weaknesses are the smooth results of true models. It can be seen that the inversion results are basically consistent with the true models in the case of no noise. In the case of S/N being 5 and 2, the inversion results still show good consistency with the true models, which further verifies the robustness of the proposed approach.

Fig. 10
figure 10

Comparisons between the inversion results (red) and the true models (black) of the normal and tangential weaknesses, in which a shows the case of no noise, b shows the case of S/N = 5, and c shows the case of S/N = 2. The green curve represents the initial models

Full size image

3.2 Field data example

A 2D line through single well acquired in western China is used to further verify the stability of the proposed approach. Noise and multiples must be carefully removed to get the true-amplitude-processed gathers before inversion. When sorting azimuths, we should ensure sufficient coverage and S/N at each azimuth division. Here, the data were sorted into four azimuth sectors, including 0° (stacked by − 22.5°–22.5°), 45° (stacked by 22.5°–67.5°), 90° (stacked by 67.5°–112.5°), and 135° (stacked by 112.5°–157.5°). For each divided azimuth, seismic data is stacked over the incident angle to obtain three angle stacks, including small angle 10° (stacked by 5°–15°), middle angle 20° (stacked by 15°–25°), and large angle 30° (stacked by 25°–35°). We first implement CSSI for azimuthal EI datasets from azimuthal angle stacks. Figure 11a–c shows the azimuthal angle stacks at different incident angles. Figure 12a–c shows the corresponding azimuthal EI inversion results.

Fig. 11
figure 11

Azimuthal angle stacks at small, middle, and large incident angles, in which a shows an average angle of 10° (small incident angle), b shows an average angle of 20° (middle incident angle), and c shows an average angle of 30° (large incident angle). The red curve represents the P-wave impedance at the well location

Full size image
Fig. 12
figure 12

Inverted azimuthal EI data at small, middle, and large incident angles, in which a shows an average angle of 10° (small incident angle), b shows an average angle of 20° (middle incident angle), and c shows an average angle of 30° (large incident angle). The red curve represents the P-wave impedance at the well location

Full size image

We next implement DFT for \(a_{ 2} \left( \theta \right)\) and \(b_{ 2} \left( \theta \right)\) from all estimated azimuthal EI datasets and estimation for \(\phi_{\text{sym}}\) from \(a_{ 2} \left( \theta \right)\) and \(b_{ 2} \left( \theta \right)\). Under the HTI medium assumption, the fast P-wave orientation is usually parallel to the fracture strike and perpendicular to the fracture symmetry axis (Delbecq et al. 2013). Since there is fast P-wave orientation data in the work area, we use the fast P-wave orientation to rotate 90° to calculate \(\phi_{\text{sym}}\), which is used as the true \(\phi_{\text{sym}}\) for comparison with the \(\phi_{\text{sym}}\) estimated by the proposed approach. Figure 13a shows the true \(\phi_{\text{sym}}\) calculated from the fast P-wave orientation. Figure 13b–d shows the estimated \(\phi_{\text{sym}}\) at different incident angles. It can be seen that the estimated \(\phi_{\text{sym}}\) at small incident angle is the worst and the estimated \(\phi_{\text{sym}}\) at middle and large incident angles is relatively better. The estimated \(\phi_{\text{sym}}\) near the well location is better than that away from the well location, which may be caused due to the unreasonable fracture weakness models away from the well location. The average of estimated \(\phi_{\text{sym}}\) at middle and large incident angles is taken as the final estimated \(\phi_{\text{sym}}\). Figure 14a shows the final estimated \(\phi_{\text{sym}}\), and Fig. 14b shows the absolute values of the error between the final estimated \(\phi_{\text{sym}}\) and true \(\phi_{\text{sym}}\). It can be seen that most of the final estimated \(\phi_{\text{sym}}\) is basically consistent with true values, and most of the absolute values of the error between the final estimated \(\phi_{\text{sym}}\) and true \(\phi_{\text{sym}}\) are less than 30°.

Fig. 13
figure 13

Comparisons between the true \(\phi_{\text{sym}}\) (calculated from fast P-wave azimuth) and the estimated \(\phi_{\text{sym}}\) at different incident angles, in which a shows the true \(\phi_{\text{sym}}\), b shows the estimated \(\phi_{\text{sym}}\) at small incident angle (\(\theta = 10^\circ\)), c shows the estimated \(\phi_{\text{sym}}\) at middle incident angle (\(\theta = 20^\circ\)), and d shows the estimated \(\phi_{\text{sym}}\) at large incident angle (\(\theta = 30^\circ\)). The red line shows the well location

Full size image
Fig. 14
figure 14

Final estimated \(\phi_{\text{sym}}\) and the absolute value of the error between the estimated and true \(\phi_{\text{sym}}\), a the final estimated \(\phi_{\text{sym}}\) (the average of the estimated \(\phi_{\text{sym}}\) at middle and large incident angles, and b the absolute value of the error between the final estimated and true \(\phi_{\text{sym}}\)

Full size image

Finally, combining \(a_{ 2} \left( \theta \right)\) and \(b_{ 2} \left( \theta \right)\), the fracture weakness inversion is performed using true \(\phi_{\text{sym}}\) and the final estimated \(\phi_{\text{sym}}\), respectively. Figure 15a, b shows the inversion results of fracture weakness obtained using true \(\phi_{\text{sym}}\); Fig. 16a, b shows the inversion results of fracture weakness obtained using the final estimated \(\phi_{\text{sym}}\). It can be seen that the inversion results near the well location are basically the same in both cases, and there are some differences in the inversion results away from the well location, which may be caused due to the error in the \(\phi_{\text{sym}}\) estimation. As a whole, the inversion results in both cases are basically the same. We plot the well logs for comparison with the inversion results, which show good agreement with the observation in wells. The large values of the inverted normal and tangential weaknesses near the well are consistent with the fractured zones in the reservoir. Therefore, the application of field data further verifies the validity and feasibility of the proposed approach.

Fig. 15
figure 15

Inversion results of fracture weakness obtained using the true \(\phi_{\text{sym}}\), a the inverted normal weakness and b the inverted tangential weakness

Full size image
Fig. 16
figure 16

Inversion results of fracture weakness obtained using the final estimated \(\phi_{\text{sym}}\), a the inverted normal weakness and b the inverted tangential weakness

Full size image

4 Conclusions

Fractured reservoirs with a set of vertical fractures are equivalent to HTI medium under long-wavelength assumptions. A logarithmic normalized azimuthal EI equation is rewritten in terms of FCs; a novel azimuthal EI-based FC variation with angle inversion is proposed to estimate fracture weakness. Finally, the synthetic and real data are used to verify the feasibility and rationality of the proposed approach, and the following conclusions are obtained:

  1. 1.

    The approach based on reflection amplitude for estimating azimuth of the symmetry axis has a 90° ambiguity. In this paper, the ambiguity is eliminated by judging the sign of the second FC \(r_{ 2} \left( \theta \right)\). If fracture infill is known, for example, for fluid-filled cracks, there is always \(r_{ 2} \left( \theta \right) > 0\). If the cracks are dry (gas-filled), in this case it becomes complicated to determine the sign of \(r_{ 2} \left( \theta \right)\), which is related to incident angle and the ratio \(g\). For the case of \(\theta \le 30^\circ\), if \(g > 0.4\), there is always \(r_{ 2} \left( \theta \right) > 0\). For the case of \(\theta > 30^\circ\), if \(g < 0.4\), there is always \(r_{ 2} \left( \theta \right) < 0\). While fracture infill is usually unknown, anisotropic rock physical model can be used to estimate fracture weakness, then calculate \(r_{ 2} \left( \theta \right)\), and judge its sign to further resolve ambiguity. In addition, the analysis shows that seismic data at middle and large incident angles should be used to estimate \(\phi_{\text{sym}}\). In the case that there are multiple \(\phi_{\text{sym}}\) estimated at middle and large incident angles, the average of multiple \(\phi_{\text{sym}}\) can be a more stable and reliable estimate, which contributes to reducing the uncertainty of the \(\phi_{\text{sym}}\) estimate.

  2. 2.

    The sensitivity analysis of the FCs to fracture weaknesses shows that the second FC is more sensitive to fracture weaknesses than the fourth FC; the second FCs obtained from azimuthal EI data can be simultaneously combined to estimate fracture weaknesses. However, azimuth of the symmetry axis should be estimated prior to the fracture weakness inversion, and the fracture weakness inversion is affected by the estimated azimuth of the symmetry axis. Tests on the synthetic and real data show that the inversion results of fracture weaknesses obtained by the proposed approach are stable and reliable when azimuth of the symmetry axis deviates less than 30°.

  3. 3.

    The proposed approach for estimating azimuth of the symmetry axis and fracture weaknesses depends on the constructed anisotropic rock physical model. The correctness of the model affects the accuracy of the azimuth of the symmetry axis and fracture weakness estimation, so questions remain about the reliability of this inversion, and more work needs to be done to improve the reliability of fracture prediction.