1 Introduction

The concept of a poroelastic material was introduced by Biot (1955) in order to describe the mechanical behavior of water-saturated soil. Biot’s material consists of a combination of a deformable solid and a fluid, the solid constituting a porous skeleton whose innumerable tiny cavities are interconnected and filled with the fluid. Apart from water-saturated soil, the class of poroelastic materials includes other materials such as polyurethane foam and sound-absorbing materials, osseous tissue, and so on.

Due to many applications in the fields of geophysics, plasma physics and related topics, increasing attention is being devoted to the interaction between fluid such as water and thermo elastic solids, which is the domain of the theory of poro-thermoelasticity. The field of poro-thermoelasticity has a wide range of applications especially in studying the effect of using waste materials on disintegration of asphalt concrete mixture (ACM).

Asphalt concrete pavements are made of asphalt concrete mixtures (ACMs) consisting of graded aggregates, asphalt binders, and air voids. Due to the complexity of internal composition, mechanical characteristics of ACM exhibit extremely non-linear constitutive behavior with respect to loading time, loading rate, and temperature. The experimental observations suggest that the total deformation behavior has recoverable and irrecoverable parts, which could occur simultaneously and are time-dependent functions of stress levels, strain rates, and temperature (Krishnan and Rajagopal 2003). Time-dependent properties of ACM are not only one of the main sources of pavement rutting (e.g., permanent deformation), but also plays a critical role in fatigue and low-temperature cracking, roughness, and corrugation.

Coupled thermal and poromechanical processes play an important role in a number of problems of interest in geomechanics such as stability of boreholes and hydraulic fracturing in geothermal reservoirs or high temperature petroleum-bearing formations. This is due to that fact that when rocks are heated/cooled, the bulk solid as well as the pore fluid tends to undergo expansion/contraction. A volumetric expansion can result in significant pressurization of the pore fluid depending on the degree of containment and the thermal and hydraulic properties of the fluid as well as the solid. The net effect is a coupling of thermal and poromechanical processes. A few analytical procedures have been developed and used to solve geomechanics problems of interest involving coupled thermal and poromechanical problems (Delaney 1982; Wang and Papamichos 1994; Li et al. 1998; Ghassemi and Diek 2002; Ghassemi and Zhang 2004). However, many problems formulated within the framework of poro-thermoelasticity are not amenable to analytical treatment and need to be solved numerically.

The coupled rock deformation and liquid flow and various factors that affect it need to be studied both theoretically and experimentally. Implementation of theoretical rheologies in numerical models enables scientific interpretation of field measurements and provides a powerful means for understanding and predicting phenomena related to the internal earth processes. This is of paramount significance to the development of renewable geothermal energy resources as well as the prediction of natural hazards. However, the traditional isotropic elastic, plastic, and viscous rheological models are inadequate to study Earth and its tectonics. This is especially true at transform plate boundaries, where deformation-enhanced weakening is thought to be responsible for localization of strain (Simakin and Ghassemi 2005). Therefore, there is strong scientific and industrial interest in developing new mechanical models of liquid saturated rocks such as poro-viscoelasticity with damage mechanics that can include the effects of fluid phase pressurization and transport.

Porous materials make their appearance in a wide variety of settings, natural, and artificial, and in diverse technological applications. As a consequence a number of problems arise dealing with, among other issues, statics and strength, fluid flow and heat conduction, and dynamics. In connection with the latter, we note that problems of this kind are encountered in the prediction of the behavior of sound-absorbing materials and in the area of exploration geophysics, the steadily growing literature bearing witness to the importance of the subject. The existence and uniqueness of the generalized solutions for the boundary value problems in elasticity of initially stressed bodies with voids (porous materials) are proved (Marin 2008).

The field of poro-thermoelasticity has a wide range of applications especially in studying the effect of using waste materials on disintegration of asphalt concrete mixture (Pecker and Deresiewiez 1973). The problem of a fluid-saturated porous material has been studied for many years. A short list of papers pertinent to the present study includes Biot (1956a, b), Biot and Willis (1957), Deresiewicz and Skalak (1963), Nur and Byerlee (1971), Sherief and Hussein (2012), Youssef (2007).

Mathematical modeling is the process of constructing mathematical objects whose behavior or properties correspond in some way to a particular real-world system. The term real-world system could refer to a physical system, a financial system, a social system, an ecological system, or essentially any other system whose behavior can be observed. In this description, a mathematical object could be a system of equations, a stochastic process, a geometric or algebraic structure, an algorithm or any other mathematical apparatus like a fractional derivative, integral or fractional system of equations. Fractional calculus and fractional differential equations serve as mathematical objects describing many real-world systems.

Fractional calculus has been used successfully to modify many existing models of physical processes. One can state that the whole theory of fractional derivatives and integrals was established in the second half of the 19th century. The first application of fractional derivatives was given by Abel, who applied fractional calculus in the solution of an integral equation that arises in the formulation of the tautochrone problem. The generalization of the concept of derivatives and integrals to a non-integer order has been subjected to several approaches and some various alternative definitions of fractional derivatives appeared elsewhere (Gorenflo and Mainardi 1997; Miller and Ross 1993; Samko et al. 1993; Oldham and Spanier 1974). In the last few years, fractional calculus has been applied successfully in various areas to modify many existing models of physical processes, e.g., chemistry, biology, modeling and identification, electronics, wave propagation, and viscoelasticity (Rossikhin and Shitikova 1967; Bagley and Torvik 1986). Fractional order models often work well, particularly for dielectrics and viscoelastic materials over extended ranges of time and frequency (Lakes 1999; Grimnes and Martinsen 2000). In heat transfer and electrochemistry, for example, the half-order fractional integral is the natural integral operator connecting the applied gradients (thermal or material) with the diffusion of ions with heat (Gorenflo et al. 2002). One can refer to Podlubny (1999) for a survey of applications of fractional calculus.

Ezzat (2010, 2011a, b, c) was the first writer who established a new formula of heat conduction law by using the new Taylor-Riemann series expansion of time-fractional order α developed by Jumarie (2010) as follows:

$$q(x,t)\; + \;\frac{{\tau^{\upsilon } }}{\upsilon !}\,\frac{{\partial^{\upsilon } q}}{{\partial \,t^{\upsilon } }} = - k\,\nabla T,\quad 0\, < \,\upsilon \le 1$$
(1)

where q the heat flux vector and \(\tau\) is the relaxation time.

Sherief et al. (2010) introduced a fractional formula of heat conduction and proved a uniqueness theorem and derived a reciprocity relation and a variational principle. El-Karamany and Ezzat (2011) introduced two general models of fractional heat conduction law for a non-homogeneous anisotropic elastic solid. Uniqueness and reciprocal theorems are proved and the convolutional variational principle is established and used to prove a uniqueness theorem with no restriction on the elasticity or thermal conductivity tensors except symmetry conditions. Ezzat and El-Karamany (2011a, b, c) introduced a new mathematical model for electro-thermoelasticity equations using the methodology of fractional calculus. The model is applied to one-dimensional problems to investigate the thermal behavior in thermoelectric solids. The verification process was done by comparison of model predictions with the previous work and shows good agreement is achieved. Abbas (2014, 2015) solved some problems on fractional order theory of thermoelasticity for a functional graded material. Some applications of fractional calculus to various problems in continuum mechanics are reviewed in the literature (Ezzat et al. 2012a, b; 2013a, b; 2014a, b, c, d; 2015).

In the current work, a modified law of heat conduction including fractional order of the time derivative is constructed and replaces the conventional Fourier’s law in poro-thermoelasticity. The resulting non-dimensional coupled equations for poroelastic half-space saturated with fluid are considered. The general solution in the Laplace transform domain is obtained and applied in a certain asphalt material which is thermally shocked on its bounding plane. The inversion of the Laplace transform will be obtained numerically and the numerical values of the temperature, displacement, and stress will be illustrated graphically.

2 Derivation of fractional heat conduction equation in poro-thermoelasticity

Much effort has been devoted recently for determining conditions which guarantee that the assumption of local thermal equilibrium (LTE) is accurate when modeling heat transfer in porous media. When it is accurate, then the thermal field is well approximated by a single thermal energy equation. In other circumstances, the local thermal non-equilibrium (LTNE) prevails, and it is necessary to employ two energy equations, one for each phase (Nouri-Borujerdi et al. 2007). Fourie and Du Plessis (2003) showed that the intrinsic volume-averaged equilibrium temperature of the solid phase is equal to that of the fluid phase everywhere though that their values may differ locally.

The conventional poro-thermoelasticity is based on the principles of the classical theory of heat conductivity, specifically on classical Fourier’s law, in which relates the heat flux vector q to the temperature gradient (Nowinski 1978)

$$q_{{i{\text{s}}}} (x_{i} ,t) = - k_{\text{s}} \theta_{{{\text{s}},i}}$$
(2)
$$q_{{i{\text{f}}}} (x_{i} ,t) = - k_{\text{f}} \theta_{{{\text{f}},i}}$$
(3)

The energy equation in terms of the heat conduction vectors \(q_{{i{\text{s}}}}\) and \(q_{{i{\text{f}}}}\) are

$$\frac{\partial }{\partial t}\left( {F_{11} \,\theta_{\text{s}} + T_{\text{o}} R_{11} \,e_{\text{s}} + T_{\text{o}} R_{21} \,e_{\text{f}} } \right) = - \nabla q_{{i{\text{s}}}} + \rho_{1} \,Q_{\text{s}} - \kappa \left( {\theta_{\text{s}} - \,\theta_{\text{f}} } \right)$$
(4)
$$\frac{\partial }{\partial t}\left( {F_{22} \,\theta_{\text{f}} + T_{\text{o}} R_{12} \,e_{\text{s}} + T_{\text{o}} R_{22} \,e_{\text{f}} } \right) = - \nabla q_{{i{\text{f}}}} + \rho_{2} \,Q_{\text{f}} + \kappa \left( {\theta_{\text{s}} - \,\theta_{\text{f}} } \right)$$
(5)

Although Fourier’s law of heat conduction is well tested for most practical problems, it fails to describe the transient temperature field in situations involving short times, high frequencies, and small wavelengths (Lebon et al. 2008). To eliminate these anomalies, Cattaneo (1948) and Vernotte (1958) proposed a damped version of Fourier’s law by introducing a heat flux relaxation term, by taking Taylor’s series to expand \(q_{{i{\text{s}}}} (x_{i} ,\,t + \tau_{\text{s}} )\), \(q_{{i{\text{f}}}} (x_{i} ,\,t + \tau_{\text{f}} )\) and retaining terms up to the first order in \(\tau_{\text{s}}\) and \(\tau_{\text{f}}\). The first well-known generalization of such a type (Sherief and Hussein 2012)

$$q_{{i{\text{s}}}} + \tau_{\text{s}} \dot{q}_{{i{\text{s}}}} = - k_{\text{s}} \theta_{{{\text{s}},i}}$$
(6)
$$q_{{i{\text{f}}}} + \tau_{\text{f}} \dot{q}_{{i{\text{f}}}} = - k_{\text{f}} \theta_{{{\text{f}},i}}$$
(7)

leads to the hyperbolic-type heat transport equation in the theory of poro-thermoelasticity

$$\begin{aligned} & k_{\text{s}} \theta_{{{\text{s}},ii}} + \left( {1 + \tau_{\text{s}} \frac{\partial }{\partial t}} \right)\left[ {\rho_{1} \,Q_{\text{s}} - \kappa \left( {\theta_{\text{s}} - \,\theta_{\text{f}} } \right)} \right] \\ & \quad = \frac{\partial }{\partial t}\left( {1 + \tau_{\text{s}} \frac{\partial }{\partial t}} \right)\left( {F_{11} \,\theta_{\text{s}} + T_{\text{o}} R_{11} \,e_{\text{s}} + T_{\text{o}} R_{21} \,e_{\text{f}} } \right) \\ \end{aligned}$$
(8)
$$\begin{aligned} & k_{\text{f}} \theta_{{{\text{f}},ii}} + \left( {1 + \tau_{\text{f}} \,\frac{\partial }{\partial t}} \right)\left[ {\rho_{2} \,Q_{\text{f}} + \kappa \left( {\theta_{\text{s}} - \,\theta_{\text{f}} } \right)} \right] \\ & \quad = \frac{\partial }{\partial t}\left( {1 + \tau_{\text{f}} \,\frac{\partial }{\partial t}} \right)\left( {F_{22} \,\theta_{\text{f}} + T_{\text{o}} R_{12} \,e_{\text{s}} + T_{\text{o}} R_{22} \,e_{\text{f}} } \right). \\ \end{aligned}$$
(9)

In the present work, the new fractional Taylor-Riemann series of time-fractional order \(\upsilon\) is adopted to expand \(q_{{i{\text{s}}}} (x_{i} ,\,t + \tau_{\text{s}} )\), \(q_{{i{\text{f}}}} (x_{i} ,\,t + \tau_{\text{f}} )\) and retaining terms up to order \(\upsilon\) in the thermal relaxation times \(\tau_{\text{s}}\) and \(\tau_{\text{f}}\), we get

$$q_{{i{\text{s}}}} (x_{i} ,t + \tau_{\text{s}} ) = q_{{i{\text{s}}}} (x_{i} ,t) + \frac{{\tau_{\text{s}}^{\upsilon } }}{\upsilon !}\frac{{\partial^{\upsilon } q_{{i{\text{s}}}} }}{{\partial t^{\upsilon } }},\quad 0\, < \,\upsilon \le 1$$
(10)
$$q_{{i{\text{f}}}} (x_{i} ,t + \tau_{\text{f}} ) = q_{{i{\text{f}}}} (x_{i} ,t) + \frac{{\tau_{\text{f}}^{\upsilon } }}{\upsilon !}\frac{{\partial^{\upsilon } q_{{i{\text{f}}}} }}{{\partial t^{\upsilon } }},\quad 0 \,<\, \upsilon \le 1$$
(11)

From a mathematical viewpoint, Fourier’s laws (2) and (3) in poro-thermoelasticity theory of generalized fractional heat conduction are given by

$$q_{{i{\text{s}}}} (x_{i} ,t) + \frac{{\tau_{\text{s} }^{\upsilon } }}{\upsilon !}\frac{{\partial^{\upsilon } q_{{i{\text{s}}}} }}{{\partial t^{\upsilon } }} = - k_{\text{s}} \theta_{{{\text{s}},i}} ,\quad 0 \,<\, \upsilon \le 1$$
(12)
$$q_{{i{\text{f}}}} (x_{i} ,t) + \frac{{\tau_{\text{f}}^{\upsilon } }}{\upsilon !}\frac{{\partial^{\upsilon } q_{{i{\text{f}}}} }}{{\partial t^{\upsilon } }} = - k_{\text{f}} \theta_{{{\text{f}},i}} ,\quad 0 \,<\, \upsilon \le 1.$$
(13)

Taking the partial time derivative of fraction order \(\upsilon\) of Eqs. (4) and (5), we get (Tarasov 2008)

$$\begin{aligned} & \frac{{\partial^{\upsilon + 1} }}{{\partial t^{\upsilon + 1} }}\left( {F_{11} \,\theta_{\text{s}} + T_{\text{o}} R_{11} \,e_{\text{s}} + T_{\text{o}} R_{21} \,e_{\text{f}} } \right) \\ & \quad { = } - \nabla \left( {\frac{{\partial^{\upsilon } q_{{i{\text{s}}}} }}{{\partial t^{\upsilon } }}} \right) + \frac{{\partial^{\upsilon } }}{{\partial t^{\upsilon } }}\left[ {\rho_{1} \,Q_{\text{s}} - \kappa \left( {\theta_{\text{s}} - \,\theta_{\text{f}} } \right)} \right] \\ \end{aligned}$$
(14)
$$\begin{aligned} & \frac{{\partial^{\upsilon + 1} }}{{\partial t^{\upsilon + 1} }}\left( {F_{22} \,\theta_{\text{f}} + T_{\text{o}} R_{12} \,e_{\text{s}} + T_{\text{o}} R_{22} \,e_{\text{f}} } \right) \\ & \quad = - \nabla \left( {\frac{{\partial^{\upsilon } q_{{i{\text{f}}}} }}{{\partial t^{\upsilon } }}} \right) + \frac{{\partial^{\upsilon } }}{{\partial t^{\upsilon } }}\left[ {\rho_{2} \,Q_{\text{f}} + \kappa \left( {\theta_{\text{s}} - \,\theta_{\text{f}} } \right)} \right] \\ \end{aligned}.$$
(15)

Multiplying Eqs. (14) and (15) by \(\frac{{\tau_{\text{s}}^{\upsilon } }}{\upsilon !}\) and \(\frac{{\tau_{\text{f}}^{\upsilon } }}{\upsilon !}\) and adding to Eqs. (4) and (5), respectively, we have

$$\begin{aligned} & k_{\text{s}} \theta_{{{\text{s}},ii}} + \left( {1 + \frac{{\tau_{\text{s}}^{\upsilon } }}{\upsilon !}\,\frac{{\partial^{\upsilon } }}{{\partial t^{\upsilon } }}} \right)\left[ {\rho_{1} \,Q_{\text{s}} - \kappa \left( {\theta_{\text{s}} - \,\theta_{\text{f}} } \right)} \right] \\ & \quad = \frac{\partial }{\partial t}\left( {1 + \frac{{\tau_{\text{s}}^{\upsilon } }}{\upsilon !}\,\frac{{\partial^{\upsilon } }}{{\partial t^{\upsilon } }}} \right)\left( {F_{11} \,\theta_{\text{s}} + T_{\text{o}} R_{11} \,e_{\text{s}} + T_{\text{o}} R_{21} \,e_{\text{f}} } \right) \\ \end{aligned}$$
(16)
$$\begin{aligned} & k_{\text{f}} \theta_{{{\text{f}},ii}} + \left( {1 + \frac{{\tau_{\text{s}}^{\upsilon } }}{\upsilon !}\,\frac{{\partial^{\upsilon } }}{{\partial t^{\upsilon } }}} \right)\left[ {\rho_{2} \,Q_{\text{f}} + \kappa \left( {\theta_{\text{s}} - \,\theta_{f} } \right)} \right] \\ & \quad = \frac{\partial }{\partial t}\left( {1 + \frac{{\tau_{\text{s}}^{\upsilon } }}{\upsilon !}\,\frac{{\partial^{\upsilon } }}{{\partial t^{\upsilon } }}} \right)\left( {F_{22} \,\theta_{\text{f}} + T_{\text{o}} R_{12} \,e_{\text{s}} + T_{\text{o}} R_{22} \,e_{\text{f}} } \right) \\ \end{aligned}$$
(17)

Equations (16) and (17) are the generalized energy equations of poro-thermoelasticity with fractional derivatives and taking into account the relaxation times \(\tau_{\text{s}}\) and \(\tau_{\text{f}}\). Some theories of heat conduction law follow as limit cases for different values of the parameters \(\tau_{\text{s}},\) \(\tau_{\text{f}}\) , and \(\upsilon\).

Taking into consideration

$$\frac{{\partial ^{\upsilon } }}{{\partial {\mkern 1mu} t^{\upsilon } }}f(y,t) = \left\{ {\begin{array}{ll} {f(y,t) - f(y,0)} & {\upsilon \to 0} \\ {I^{{\upsilon - 1}} {\mkern 1mu} \frac{{\partial {\mkern 1mu} f(y,t)}}{{\partial {\mkern 1mu} t}}} & {0 < \upsilon < 1} \\ {\frac{{\partial {\mkern 1mu} f(y,t)}}{{\partial {\mkern 1mu} t}}} & {\upsilon = 1,} \\ \end{array} } \right.$$

where the notion \(I^{\upsilon }\) is the Riemann–Liouville fractional integral introduced as a natural generalization of the well-known n-fold repeated integral \(I^{n} f(t)\) written in a convolution-type form (Mainardi and Gorenflo 2000)

$$\left. \begin{gathered} I^{\upsilon } f(t) = \int\limits_{0}^{t} {\frac{{(t - \varsigma )^{{\upsilon - 1}} }}{{\Gamma (\upsilon - 1)}}f(\varsigma )d\varsigma } \hfill \\ I^{0} f(t) = f(t) \hfill \\ \end{gathered} \right\}\upsilon > 0$$

In the limit as \(\upsilon\) tends to 1, Eqs. (16) and (17) reduce to the well-known Cattaneo-Vernotte (1948) law used by Lord and Shulman (1967) to derive the equation of the generalized theory of poro-thermoelasticity with one relaxation time. It is known that the classical entropy derived using this law instead of monotonically increasing behaves in an oscillatory way (Lebon et al. 2008; Jou et al. 1988). Strictly speaking, this result is not incompatible with Clausius’ formulation of the second law, which states that the entropy of the final equilibrium state must be higher than the entropy of the initial equilibrium state. However, the non-monotonic behavior of the entropy is in contradiction with the local equilibrium formulation of the second law, which requires that the entropy production must be positive everywhere at any time (Lebon et al. 2008). During the last two decades, this became the subject of many research papers and resulted in the introduction of what is known now as extended irreversible thermodynamics. A review can be found in Jou et al. (1988).

2.1 Limiting cases

  1. 1.

    The heat Eqs. (16) and (17) for the two-phase system in the limiting case \(\upsilon = 0\) transforms to the work of Biot (1984) in the context of coupled thermoelasticity (Biot 1956b).

  2. 2.

    The heat Eqs. (16) and (17) for the two-phase system in the limiting case \(\upsilon = 1\) transforms to the work of Sherief and Hussein (2012) in the context generalized thermoelasticity with one relaxation time (Lord and Shulman 1967).

3 Mathematical models

The linear governing equations of isotropic, generalized poro-thermoelasticity in the absence of body forces and heat sources are as follows:

  1. (i)

    Equations of motion

    $$\mu u_{{i{\text{s}},jj}} + \left[ {(\lambda + \mu )\,e_{\text{s}} + Ge_{\text{f}} - R_{11} \theta_{\text{s}} - R_{12} \theta_{\text{f}} } \right]_{i} = \rho_{11} {\ddot{u}}_{{{\text{s}}i}} + \rho_{12} {\ddot{u}}_{{{\text{f}}i}}$$
    (18)
    $$\left[ {Ge_{\text{s}} + Re_{\text{f}} - R_{21} \theta_{\text{s}} - R_{22} \theta_{\text{f}} } \right]_{i} = \rho_{12} \,{\ddot{u}}_{{i{\text{s}}}} + \rho_{22} \,{\ddot{u}}_{{i{\text{f}}}}$$
    (19)
  2. (ii)

    Fractional heat equation

    $$\begin{aligned} & k_{\text{s}} \theta_{{{\text{s}},ii}} - \kappa \left( {1 + \frac{{\tau_{\text{s}}^{\upsilon } }}{\upsilon !}\,\frac{{\partial^{\upsilon } }}{{\partial t^{\upsilon } }}} \right)\left( {\theta_{\text{s}} - \,\theta_{\text{f}} } \right) \\ & \quad = \frac{\partial }{\partial t}\left( {1 + \frac{{\tau_{\text{s}}^{\upsilon } }}{\upsilon !}\,\frac{{\partial^{\upsilon } }}{{\partial t^{\upsilon } }}} \right)\left( {F_{11} \,\theta_{\text{s}} + T_{\text{o}} R_{11} \,e_{\text{s}} + T_{\text{o}} R_{21} \,e_{\text{f}} } \right) \\ \end{aligned}$$
    (20)
    $$\begin{aligned} & k_{\text{f}} \theta_{{{\text{f}},ii}} + \kappa \left( {1 + \frac{{\tau_{\text{s}}^{\upsilon } }}{\upsilon !}\,\frac{{\partial^{\upsilon } }}{{\partial t^{\upsilon } }}} \right)\left( {\theta_{\text{s}} - \,\theta_{\text{f}} } \right) \\ & \quad = \frac{\partial }{\partial t}\left( {1 + \frac{{\tau_{\text{s}}^{\upsilon } }}{\upsilon !}\,\frac{{\partial^{\upsilon } }}{{\partial t^{\upsilon } }}} \right)\left( {F_{22} \,\theta_{\text{f}} + T_{\text{o}} R_{12} \,e_{\text{s}} + T_{\text{o}} R_{22} \,e_{\text{f}} } \right) \\ \end{aligned}$$
    (21)
  3. (iii)

    Constitutive equations

    $$\sigma_{ij} = 2\mu e_{ij} + \lambda e_{\text{s}} \delta_{ij} + \left( {Ge_{\text{f}} - R_{11} \,\theta_{\text{s}} - R_{12} \,\theta_{\text{f}} } \right)\,\delta_{ij}$$
    (22)
    $$\sigma = Re_{\text{f}} + Ge_{\text{s}} - R_{21} \theta_{\text{s}} - R_{22} \theta_{\text{f}}$$
    (23)
    $$e_{ij} = \frac{1}{2}\left( {u_{{i{\text{s}},j}} + u_{{j{\text{s}},i}} } \right),\quad e_{\text{s}} = e_{ii} = u_{{i{\text{s}},i}}$$
    (24)
    $$e_{\text{f}} = u_{{i{\text{f}},i}}$$
    (25)

4 Formulation of the problem

We shall consider a homogeneous isotropic thermo-poroelastic medium occupying the region \(x \ge 0\), where the x-axis is taken perpendicular to the bounding plane of half-space pointing inwards, subjected to traction-free time-dependent heating. The initial conditions of the problem are taken to be quiescent.

For the one-dimensional problems, all the considered functions will depend only on the space variables x and t. The displacement components take the form:

$$u_{{x{\text{s}}}} = u_{\text{s}} (x,t),\quad u_{{y{\text{s}}}} = u_{{z{\text{s}}}} = 0,\quad u_{{x{\text{f}}}} = u_{\text{f}} (x,t),\quad u_{{y{\text{f}}}} = u_{{z{\text{f}}}} = 0$$

Let us introduce the following non-dimensional variables

$$\begin{aligned} & \left( {x^{{\prime }} ,\;u_{\text{s}}^{{\prime }} ,\;u_{\text{f}}^{{\prime }} } \right) = c_{1} \eta \left( {x,\;u_{\text{s}} ,\;u_{\text{f}} } \right), \\ & \left( {t^{\prime},\;\tau_{\text{s}}^{{\prime }} ,\;\tau_{\text{s}}^{{\prime }} } \right) = c_{1}^{2} \eta \left( {t,\;\tau_{\text{s}} ,\;\tau_{\text{s}} } \right), \\ & c_{1} = \sqrt {M/\rho_{11} } , \\ & \left( {\sigma_{ij}^{{\prime }} ,\;\sigma^{{\prime }} } \right) = \left( {\sigma_{ij} ,\;\sigma } \right)/M, \\ & \left( {\theta_{\text{s}}^{{\prime }} ,\;\theta_{\text{f}}^{{\prime }} } \right) = R_{11} \left( {\theta_{\text{s}} ,\;\theta_{\text{f}} } \right)/M, \\ & \eta = F_{11} /k_{\text{s}} , \\ & \left( {q_{\text{s}}^{{\prime }} ,\;q_{\text{f}}^{{\prime }} } \right) = R_{11} M\left( {k_{\text{s}} q_{\text{s}}^{{\prime }} ,\;k_{\text{f}} q_{\text{f}}^{{\prime }} } \right)/c_{1} \eta , \\ & M = \lambda + 2\mu \\ \end{aligned}$$

In terms of these non-dimensional variables, Eqs. (18)–(25) take the following form (dropping primes for convenience):

$$\frac{{\partial^{2} u_{\text{s}} }}{{\partial x^{2} }} + a_{1} \frac{{\partial^{2} u_{\text{f}} }}{{\partial x^{2} }} - \frac{{\partial \theta_{\text{s}} }}{\partial x} - A_{1} \frac{{\partial \theta_{\text{f}} }}{\partial x} = \frac{{\partial^{2} u_{\text{s}} }}{{\partial t^{2} }} + b_{1} \frac{{\partial^{2} u_{\text{f}} }}{{\partial t^{2} }}$$
(26)
$$a_{1} \frac{{\partial^{2} u_{\text{s}} }}{{\partial x^{2} }} + a_{2} \frac{{\partial^{2} u_{\text{f}} }}{{\partial x^{2} }} - A_{2} \frac{{\partial \theta_{\text{s}} }}{\partial x} - A_{3} \frac{{\partial \theta_{\text{f}} }}{\partial x} = b_{1} \frac{{\partial^{2} u_{\text{s}} }}{{\partial t^{2} }} + b_{2} \frac{{\partial^{2} u_{\text{f}} }}{{\partial t^{2} }}$$
(27)
$$\frac{{\partial^{2} \theta_{\text{s}} }}{{\partial x^{2} }} = \left( {\frac{\partial }{\partial t} + \frac{{\tau_{\text{s}}^{\upsilon } }}{\upsilon !}\,\frac{{\partial^{\upsilon + 1} }}{{\partial t^{\upsilon + 1} }}} \right)\left( {\theta_{\text{s}} + \varepsilon_{2} \frac{\partial }{\partial x}\left[ {u_{\text{s}} + A_{2} u_{\text{f}} } \right]} \right) + \varepsilon_{1} \left( {1 + \frac{{\tau_{\text{s}}^{\upsilon } }}{\upsilon !}\,\frac{{\partial^{\upsilon } }}{{\partial t^{\upsilon } }}} \right)\left( {\theta_{\text{s}} - \theta_{\text{f}} } \right)$$
(28)
$$\frac{{\partial^{2} \theta_{\text{f}} }}{{\partial x^{2} }} = \left( {\frac{\partial }{\partial t} + \frac{{\tau_{\text{s}}^{\upsilon } }}{\upsilon !}\,\frac{{\partial^{\upsilon + 1} }}{{\partial t^{\upsilon + 1} }}} \right)\left( {F\theta_{\text{f}} + \omega \varepsilon_{2} \frac{\partial }{\partial x}\left[ {A_{1} u_{\text{s}} + A_{3} u_{\text{f}} } \right]} \right) - \omega \varepsilon_{1} \left( {1 + \frac{{\tau_{\text{s}}^{\upsilon } }}{\upsilon !}\,\frac{{\partial^{\upsilon } }}{{\partial t^{\upsilon } }}} \right)\left( {\theta_{\text{s}} - \theta_{\text{f}} } \right)$$
(29)
$$\sigma_{xx} = \frac{{\partial u_{\text{s}} }}{\partial x} + a_{1} \frac{{\partial u_{\text{f}} }}{\partial x} - \theta_{\text{s}} - A_{1} \theta_{\text{f}}$$
(30a)
$$\sigma_{yy} = \sigma_{zz} = a_{3} \frac{{\partial u_{\text{s}} }}{\partial x} + a_{1} \frac{{\partial u_{\text{f}} }}{\partial x} - \theta_{\text{s}} - A_{1} \theta_{\text{f}}$$
(30b)
$$\sigma_{xy} = \sigma_{xz} = \sigma_{zy} = 0$$
(30c)
$$\sigma = a_{2} \frac{{\partial u_{\text{f}} }}{\partial x} + a_{1} \frac{{\partial u_{\text{s}} }}{\partial x} - A_{3} \theta_{\text{f}} - A_{2} \theta_{\text{s}}$$
(30d)
$$q_{\text{s}} + \frac{{\tau_{\text{s}}^{\upsilon } }}{\upsilon !}\frac{{\partial^{\upsilon } q_{\text{s}} }}{{\partial t^{\upsilon } }} = - \frac{{\partial \theta_{\text{s}} }}{\partial x},\quad 0\, <\, \upsilon \le 1$$
(31a)
$$q_{\text{f}} + \frac{{\tau_{\text{f}}^{\upsilon } }}{\upsilon !}\frac{{\partial^{\upsilon } q_{\text{f}} }}{{\partial t^{\upsilon } }} = - \frac{{\partial \theta_{\text{f}} }}{\partial x},\quad 0 \,< \,\upsilon \le 1$$
(31b)

The boundary conditions can be expressed as

$$\sigma_{xx} (0,t) = \sigma (0,t) = 0$$
(32a)
$$q_{\text{s}} (0,t) + B_{\text{s}} \theta_{\text{s}} (0,t) = f(t)$$
(32b)
$$q_{\text{f}} (0,t) + B_{\text{f}} \theta_{\text{f}} (0,t) = f(t),$$
(32c)

where \(B_{\text{s}}\) and \(B_{\text{f}}\) are the Biot’s numbers and \(f(t)\) represents the magnitude of surface heating.

5 The analytical solutions in the Laplace transform domain

Performing the Laplace transform defined by the relation

$$\bar{g}(s) = \int\limits_{0}^{\infty } {\text{e}^{ - st} g(t)\;\text{d} t}$$

of both sides Eqs. (26)–(32), with the homogeneous initial conditions

$$D^{2} \bar{u}_{\text{s}} + a_{1} D^{2} \bar{u}_{\text{f}} - D\bar{\theta }_{\text{s}} - A_{1} D\bar{\theta }_{\text{f}} = s^{2} \left( {\bar{u}_{\text{s}} + b_{1} u_{\text{f}} } \right)$$
(33)
$$a_{1} D^{2} \bar{u}_{\text{s}} + a_{2} D^{2} \bar{u}_{\text{f}} - A_{2} D\bar{\theta }_{\text{s}} - A_{3} D\bar{\theta }_{\text{f}} = s^{2} \left( {b_{1} \bar{u}_{\text{s}} + b_{2} u_{\text{f}} } \right)$$
(34)
$$D^{2} \bar{\theta }_{\text{s}} = s\left( {1 + \frac{{\tau_{\text{s}}^{\upsilon } }}{\upsilon !}\,s^{\upsilon } } \right)\left( {\bar{\theta }_{\text{s}} + \varepsilon_{2} D\left[ {\bar{u}_{\text{s}} + A_{2} \bar{u}_{\text{f}} } \right]} \right) + \varepsilon_{1} \left( {1 + \frac{{\tau_{\text{s}}^{\upsilon } }}{\upsilon !}\,s^{\upsilon } } \right)\left( {\bar{\theta }_{\text{s}} - \bar{\theta }_{\text{f}} } \right)$$
(35)
$$D^{2} \bar{\theta }_{\text{f}} = s\left( {1 + \frac{{\tau_{\text{s}}^{\upsilon } }}{\upsilon !}\,s^{\upsilon } } \right)\left( {F\bar{\theta }_{\text{f}} + \omega \varepsilon_{2} D\left[ {A_{1} \bar{u}_{\text{s}} + A_{3} \bar{u}_{\text{f}} } \right]} \right) + \omega \varepsilon_{1} \left( {1 + \frac{{\tau_{\text{s}}^{\upsilon } }}{\upsilon !}\,s^{\upsilon } } \right)\left( {\bar{\theta }_{\text{s}} - \bar{\theta }_{\text{f}} } \right)$$
(36)
$$\bar{\sigma }_{xx} = D\bar{u}_{\text{s}} + a_{1} D\bar{u}_{\text{f}} - \bar{\theta }_{\text{s}} - A_{1} \bar{\theta }_{\text{f}}$$
(37a)
$$\bar{\sigma }_{yy} = \bar{\sigma }_{zz} = a_{3} D\bar{u}_{\text{s}} + a_{1} D\bar{u}_{\text{f}} - \bar{\theta }_{\text{s}} - A_{1} \bar{\theta }_{\text{f}}$$
(37b)
$$\bar{\sigma }_{xy} = \bar{\sigma }_{xz} = \bar{\sigma }_{zy} = 0$$
(37c)
$$\bar{\sigma } = a_{2} D\bar{u}_{\text{f}} + a_{1} D\bar{u}_{\text{s}} - A_{3} \bar{\theta }_{\text{f}} - A_{2} \bar{\theta }_{\text{s}}$$
(37d)
$$\left( {1 + \frac{{\tau_{\text{s}}^{\upsilon } }}{\upsilon !}s^{\upsilon } } \right)\bar{q}_{\text{s}} = - D\bar{\theta }_{\text{s}} ,\quad 0 \,<\, \upsilon \le 1$$
(38a)
$$\left( {1 + \frac{{\tau_{\text{s}}^{\upsilon } }}{\upsilon !}s^{\upsilon } } \right)\bar{q}_{\text{f}} = - D\bar{\theta }_{\text{f}} ,\quad 0 \,<\, \upsilon \le 1$$
(38b)
$$\bar{\sigma }_{xx} (0,t) = \bar{\sigma }(0,t) = 0$$
(39a)
$$\left( {1 + \frac{{\tau_{\text{s}}^{\upsilon } }}{\upsilon !}s^{\upsilon } } \right)\;\left[ {f(t) - B_{\text{s}} \theta_{\text{s}} (0,t)} \right] = - D\bar{\theta }_{\text{s}} ,\quad \quad 0 \,<\, \upsilon \le 1$$
(39b)
$$\left( {1 + \frac{{\tau_{\text{f}}^{\upsilon } }}{\upsilon !}s^{\upsilon } } \right)\;\left[ {f(t) - B_{\text{f}} \theta_{\text{f}} (0,t)} \right] = - D\bar{\theta }_{\text{f}} ,\quad \quad 0\, <\, \upsilon \le 1$$
(39c)

Eliminating \(\bar{u}_{\text{s}}\), \(\bar{u}_{\text{f}}\), and \(\bar{\theta }_{\text{f}}\) between Eqs. (33) and (36), we obtain the following equation satisfied by \(\bar{\theta }_{\text{s}}\):

$$\left( {D^{8} \; + \;\ell_{1} D^{6} \; + \;\ell_{2} D^{4} \; + \;\ell_{3} D^{2} \; + \;\ell_{4} } \right)\,\bar{\theta }_{\text{s}} = 0.$$
(40a)

In a similar manner, we can get the following Eqs. for \(\bar{u}_{\text{s}}\), \(\bar{u}_{\text{f}}\), and \(\bar{\theta }_{\text{f}}\) which satisfy Eq. (40) as follows:

$$\left( {D^{8} +\ell_{1} D^{6} +\ell_{2} D^{4} +\ell_{3} D^{2} +\ell_{4} } \right)\,\bar{u}_{\text{s}} = 0$$
(40b)
$$\left( {D^{8} +\ell_{1} D^{6} +\ell_{2} D^{4} +\ell_{3} D^{2} +\ell_{4} } \right)\,\bar{u}_{\text{f}} = 0$$
(40c)
$$\left( {D^{8} +\ell_{1} D^{6} +\ell_{2} D^{4} +\ell_{3} D^{2} +\ell_{4} } \right)\,\bar{\theta }_{\text{f}} = 0,$$
(40d)

where \(\ell_{i} ,\;i = 1,\;2,\;3,\;4\) are the parameters depending on s.

Equation (40a) can be factorized as

$$\left( {D^{2} - k_{1}^{2} } \right)\left( {D^{2} - k_{2}^{2} } \right)\left( {D^{2} - k_{3}^{2} } \right)\left( {D^{2} - k_{4}^{2} } \right)\bar{\theta }_{\text{s}} = 0,$$
(41)

where \(k_{m} ,\;\;m = 1,\;2,\;3,\;4\) are the roots of the characteristic equation of the system (40) which takes the form

$$k^{8} +\ell_{1} k^{6} +\ell_{2} k^{4} +\ell_{3} k^{2} +\ell_{4} = 0.$$
(42)

We can consider the general solutions of Eqs. (40), according to the bounded state of functions at infinity, in the following forms

$$\left( {\bar{u}_{\text{s}} ,\;\bar{u}_{\text{f}} ,\;\bar{\theta }_{\text{s}} ,\;\bar{\theta }_{\text{s}} } \right) = \sum\limits_{m\, = \,1}^{4} {\left( {L_{m} ,\;M_{m} ,\;N_{m} ,\;H_{m} } \right)} \;\text{e}^{{ - k_{m} x}},$$
(43)

where L m , M m , N m , and H m are the parameters that depend on s.

Hence, the velocity for the fluid is given by

$$\bar{v}_{\text{f}} (x,s) = \sum\limits_{m\, = \,1}^{4} {sM_{m} } (s)\;\text{e}^{{ - k_{m} x}}.$$
(44)

Thus, the skin friction function \(\tau_{\text{w}}\) (shear stress on the bounding plane surface of half-space) takes the expression (Ezzat 1994; Ezzat and Abd-Elaal 1997)

$$\tau_{\text{w}} (s) = - \;\left. {\frac{{\partial \bar{v}_{\text{f}} (x,s)}}{\partial x}} \right|_{x = 0} = \sum\limits_{m\, = \,1}^{4} {s\,k_{m} (s)\,M_{m} } (s).$$
(45)

Putting

$$ M_{m} = g_{m1} \,L_{m} ,N_{m} = g_{m2} \,L_{m} ,\;H_{m} = g_{m3} \,L_{m} $$
(46)

Hence, from Eqs. (43) and (33)–(35), one can obtain the following relations:

$$g_{m1} = \left[ {k_{m} r_{m3} \left( {A_{1} A_{2} - A_{3} } \right) - A_{1} r_{m2} Z_{3} - A_{2} r_{m1} Z_{4} + A_{3} r_{m1} Z_{3} + r_{m2} Z_{4} } \right]/\varLambda ,$$
$$g_{m2} = \left[ {k_{m} \left( {A_{1} (r_{m2} Z_{2} - r_{m3} Z_{1} ) - A_{3} (r_{m1} Z_{2} + r_{m2} r_{m3} )} \right) + Z_{4} (r_{m1} Z_{1} + r_{m2}^{2} )} \right]/k_{m} \varLambda ,$$
$$g_{m3} = \left[ {k_{m} \left( {A_{2} (r_{m1} Z_{2} + r_{m2} r_{m3} ) - r_{m2} Z_{2} + r_{m3} Z_{1} } \right) - Z_{3} (r_{m1} Z_{1} + r_{m2}^{2} )} \right]/k_{m} \varLambda .$$

where all constants are given in the “Appendix.”

From conditions (37) and Eqs. (37a, 37d), (43) and (44), we obtain a linear system of equations whose solution (numerically) gives the parameters L m , m = 1, 2, 3, 4.

This completes the solution in the Laplace transform domain.

6 Numerical results and discussion

The method, which is based on a Fourier series expansion proposed by Honig and Hirdes (1984) and is developed in detail in some literature (Ezzat et al. 1999; Sherief et al. 2010), is adopted to invert the Laplace transform in Eqs. (43). Numerical code has been prepared using the Fortran 77 programming language.

The asphaltic material saturated with water was chosen for the purpose of numerical evaluations. The basic data for this two-phase system are shown in Table 1 (Sherief and Hussein 2012).

Table 1 Value of the constants
Full size table

The computations were carried out for the functions \(f(t)\) where

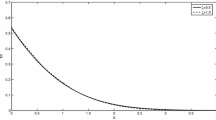
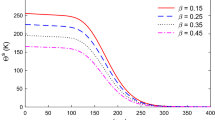
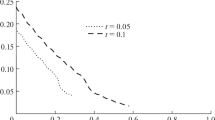
$$f(t) = \left\{ {\begin{array}{ll} {\sin \left( {\frac{{\pi t}}{{a_{{\text{o}}} }}} \right)} & {0 \le \;t\; \le \;a_{{\text{o}}} } \\ 0 & {{\text{otherwise}}} \\ \end{array} } \right. \quad {\text{or }} \quad \bar{f}(s) = \frac{{\pi a_{{\text{o}}} \left( {s\; + \;{\text{e}}^{{ - a_{{\text{o}}} s}} } \right)}}{{a_{{\text{o}}}^{2} s^{2} \; + \;\pi ^{2} }}$$

The temperature, stress, and displacement as well as the velocity of the fluid and the skin friction values for the two phases were calculated by using the numerical method of the inversion of the Laplace transform. The FORTRAN programming language was used on a personal computer. The precision maintained was five digits for the numerical program. The roots of the characteristic Eq. (42) were obtained analytically using the Mathematika 6.0 software. The system of linear equations resulting from applying the boundary conditions was solved numerically using the LU decomposition method. The results are displayed graphically at different positions of x as shown in Figs. 1, 2, 3, 4, 5, 6. In these figures, the solid line represents the solution obtained in the frame of the dynamic coupled theory (\(\upsilon = 0\)) (Biot 1955), and the dotted lines represent the solution obtained in the frame of the generalized thermoelasticity with thermal relaxation time \(\left( {\upsilon = 1.0,\;\;\tau_{\text{o}} = 0.02} \right)\) (Sherief and Hussein 2012), while the dashed lines represent the solution obtained in the frame of generalized thermoelasticity with fractional heat transfer \(\left( {0\, < \,\upsilon\, < \,1,\;\;\tau_{\text{o}} = 0.02} \right)\) (Ezzat 2012).

Fig. 1
figure 1

Temperature distribution for the solid phase for different theories. (DCT: Dynamic coupled theory, L-S: Lord-Shulman theory, F-T: Fractional heat transfer model)

Full size image
Fig. 2
figure 2

Temperature distribution for the fluid phase for different theories

Full size image
Fig. 3
figure 3

Normal stress distribution for the solid phase for different theories

Full size image
Fig. 4
figure 4

Pressure for the fluid phase for different theories

Full size image
Fig. 5
figure 5

Displacement distribution for the solid phase for different theories

Full size image
Fig. 6
figure 6

Velocity distribution for the fluid phase

Full size image

The important phenomenon observed in all figures is that the solution of any of the considered functions in the fractional theory is restricted in a bounded region. Beyond this region, the variations of these distributions do not take place. This means that the solutions according the generalized fractional thermoelasticity theory exhibit the behavior of finite speeds of wave propagation.

In the frame of the fractional theory, Figs. 1 and 2 indicate the variation in temperature in the elastic body and fluid for different values of fractional order \(\upsilon = 0.0,\;\;1.0,\,\;0.5\). We notice that the temperature fields have been affected by the fractional order \(\upsilon\) and the thermal waves cut the x-axis more rapidly when υ decreases. In the fractional theory of generalized poro-thermoelasticity, we observed that the thermal waves are continuous functions, smooth and reach steady state depending on the value of fractional \(\upsilon\), which means that the particles transport the heat to the other particles easily and this makes the decreasing rate of the temperature greater than the other ones.

Figures 3, 4, 5, 6 display the stress and displacement distributions in the elastic body and fluid, with distance x for different values of fractional order \(\upsilon = 0.0,\;\;1.0,\;0.5\). We observe that the stress and displacement fields have the same behavior as the temperature and the absolute value of the maximum stress decreases. We note here that some of these figures show broken lines indicating discontinuities of the solutions. These discontinuities indicate the locations of the wave fronts of the shock waves resulting from the sudden heating of the surface.

7 Conclusions

  • The main goal of this work is to introduce a new mathematical model for Fourier law of heat conduction with time-derivative fractional order α (Fractional model). According to this new theory, we have to construct a new classification for materials according to their fractional parameter where this parameter becomes a new indicator of its ability to conduct heat.

  • For the fractional model of thermoelasticity \(0\,<\,\upsilon\, < \,1\), the solution seems to behave like the generalized theory of generalized thermoelasticity (Lord-Shulman theory). This result is very important that the new theory may preserve the advantage of the generalized theory that the velocity of waves is finite.

  • As was mentioned in (Povstenko 2011) “From numerical calculations, it is difficult to say whether the solution for \(\upsilon\) approaching 1 has a jump at the wave front or it is continuous with very fast changes. This aspect invites further investigation.”

  • The present model avoids the negative temperature defect of the Lord-Shulman model.

  • The result provides a motivation to investigate thermoelastic materials as a new class of applicable materials.