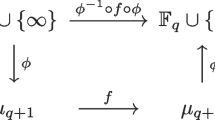Complete characterization of a class of permutation trinomials in characteristic five

Abstract

In this paper, we address an open problem posed by Bai and Xia in [2]. We study polynomials of the form $f(x)=x^{4q+1}+\lambda _1x^{5q}+\lambda _2x^{q+4}$ over the finite field ${\mathbb F}_{5^{k}}$, which are not quasi-multiplicative equivalent to any of the known permutation polynomials in the literature. We find necessary and sufficient conditions on $\lambda _1, \lambda _2 \in {\mathbb F}_{5^{k}}$ so that f(x) is a permutation monomial, binomial, or trinomial of ${\mathbb F}_{5^{2k}}$.

1 Introduction

Let ${\mathbb F}_q$ be a finite field with q elements, where q is a prime power. A polynomial $g(x)\in {\mathbb F}_q[x]$ is called a permutation polynomial (PP) over ${\mathbb F}_q$ if g(x) is a bijection of ${\mathbb F}_q$. Due to their simple algebraic structure and extraordinary properties, there has been a great interest in permutation polynomials with a few terms, such as binomials or trinomials. Permutation polynomials are also very important in terms of their applications in areas such as cryptography, coding theory and combinatorial designs. As far as we know, the studies on permutation polynomials go back to the work done by Dickson and Hermite (see, [13, 17]). As an introduction, the books on finite fields (see, [28] and [29, Chapter 8]) could be very helpful for the interested reader to get into the topic. Furthermore, the survey papers (see, [19, 21, 31, 39]) could also be useful as they consist of many of the recent results on permutation polynomials over finite fields. We refer the interested reader to [6, 7, 15, 20, 25, 26, 30] and the references therein for more results on permutation polynomials over finite fields.

In [2], Bai and Xia proved that the polynomial $g(x) = x^{(p-1)q+1}+x^{pq}-x^{q+p-1}$ over the finite field ${\mathbb F}_{q^2}$, where $p = 3$ or 5 and $q = p^k$ with k being a positive integer, is a permutation trinomial for ${\mathbb F}_{q^2}$ if and only if k is even. Later, in [14] Gupta and Rai investigated the trinomial $f(x)=x^{4q+1}+\alpha x^{5q}+x^{q+4}$ over the finite field ${\mathbb F}_{5^{2k}}$, where $\alpha \in {\mathbb F}_{5^k}^*$ with k being a positive integer. They proved that the trinomial f(x) permutes ${\mathbb F}_{5^{2k}}$ if and only if $\alpha =-1$ and k is even. In this paper, our aim is to determine the permutation properties of the more general trinomial $f(x)=x^{(p-1)q+1}+\lambda _1x^{pq}+\lambda _2x^{q+p-1}\in {\mathbb F}_q[x]$ over ${\mathbb F}_{q^2}$, where ${\mathbb F}_q$ is of characteristic 5. Our results include the ones in [2, 14]. Note that while proving our main result (see Theorem 2) in the absolutely irreducible case, we use a bound (see [23, Theorem 5.28]) which is derived from the well-known Hasse-Weil bound for function fields. For the characterization of some planar functions and related structures, like exceptional polynomials and APN permutations, the theory of algebraic curves over finite fields and in particular, Hasse-Weil type inequalities become a very useful instrument. In recent years, there have been very interesting studies on these topics through the Hasse-Weil approach (see for instance, [4, 8, 11, 18, 34] and the references therein).

The paper is organized as follows. Section 2 contains background material that is used in the rest of the paper. Sections 3 and 4 contain our main results, where we prove necessary and sufficient conditions on $\lambda _1, \lambda _2 \in {\mathbb F}_{5^{k}}$ so that f(x) permutes ${\mathbb F}_{5^{2k}}$. Finally, Section 5 investigates the quasi-multiplicative equivalence of the polynomial f(x) with the existing permutation trinomials in odd or arbitrary characteristic.

2 Preliminaries

In order to determine whether a polynomial that can be written in the form $f(x) = x^rh\left( x^{(q^n-1)/d}\right)$ permutes ${\mathbb F}_{q^n}$ or not, mostly a well known criterion due to Wan and Lidl [37], Park and Lee [32], Akbary and Wang [1], Wang [38] and Zieve [42] is being used, which is given in the following lemma.

Lemma 1

[1, 32, 37, 38, 42] Let $h\left( x\right) \in {\mathbb F}_{q^n}[x]$ and d, r be positive integers with d dividing $q^n-1$. Then $f\left( x\right) = x^rh\left( x^{\left( q^n-1\right) /d}\right)$ permutes ${\mathbb F}_{q^n}$ if and only if the following conditions hold:

• (i) $\gcd \left( r,\left( q^n-1\right) /d\right) = 1$,

• (ii) $x^rh\left( x\right) ^{\left( q^n-1\right) /d}$ permutes $\mu _{d}$, where $\mu _d=\{\theta \in {\mathbb F}_{q^n}^*\mid \theta ^d=1\}$.

In this paper, we plan to apply Lemma 1 over the finite field ${\mathbb F}_{q^2}$ with $d=q+1$ and $r=5$, using

$$\begin{aligned} h(x) = \lambda _1 x^5 + x^4 +\lambda _2 x,\qquad \text {with}\lambda _1,\lambda _2\in {\mathbb F}_q. \end{aligned}$$

(1)

Condition (i) of Lemma 1 holds as $\gcd (r,(q^n-1)/d)=\gcd (r,q-1)=\gcd (5,5^k-1)=1$. Instead of finding the conditions for which $g(x)=x^rh(x)^{q-1}$ permutes $\mu _{q+1}$, we will use the following idea throughout the paper:

Let $z\in \mathbb {F}_{q^2}\setminus \mathbb {F}_{q}$ be an arbitrary element. For any $x\in \mathbb {F}_q$, let $\Phi :{\mathbb F}_q\cup \{\infty \}\longrightarrow \mu _{q+1}$ be the map defined by $\displaystyle \Phi \left( x\right) =\frac{x+z}{x+z^q}$, where $\Phi \left( \infty \right) =1$. It is not so hard to observe that $\Phi$ is one to one from $\mathbb {F}_q \cup \{\infty \}$ to $\mu _{q+1}$ and thus onto since the number of elements on both sides are equal. Then we obtain that $\displaystyle \Phi ^{-1}\left( x\right) = \frac{xz^q-z}{1-x}$, for any $x\ne 1$ with $\Phi ^{-1}\left( 1\right) =\infty$. In this setting, we have $g(x)=x^rh(x)^{q-1}$ is one to one on $\mu _{q+1}$ and therefore permutes $\mu _{q+1}$ if and only if the map $\left( \Phi ^{-1} \circ g \circ \Phi \right)$ is one to one on $\mathbb {F}_q\cup \{\infty \}$. In our situation, $g(1)=(\lambda _1+\lambda _2+1)^{q-1}=1$ when $h(1)\ne 0$. Then $\infty$ is a fixed-point of the map $\left( \Phi ^{-1}\circ g \circ \Phi \right)$, and it suffices to investigate its action on ${\mathbb F}_q$. We note that an analogous idea has been used in a few more studies before, see for instance [3, 6, 22].

This situation can be easily summarized in the diagram below:

(2)

Moreover, we will make a suitable choice of the element $z\in \mathbb {F}_{q^2}\setminus \mathbb {F}_{q}$ that results in simpler computations.

3 The trinomial h(x) of degree 5 in arbitrary characteristic

As a preliminary step to apply Lemma 1, we investigate for which $\lambda _1,\lambda _2\in {\mathbb F}_q$ the polynomial $h(x)=\lambda _1x^5+x^4+\lambda _2x\in {\mathbb F}_q[x]$ does not have any roots in $\mu _{q+1}$ without restrictions on the characteristic.

If $h(1)=0$ or $h(-1)=0$, then h(x) has a root in $\mu _{q+1}$ trivially. Therefore we characterize all such polynomials in the next proposition under the assumptions $h(1)\ne 0$ and $h(-1)\ne 0$. For this we first need to prove some lemmas.

Lemma 2

The polynomial h(x) has a root in $\mu _{q+1}\setminus \{1,-1\}$ if and only if there exists $A\in {\mathbb F}_q$ such that $m(x)=x^2+Ax+1$ is irreducible over ${\mathbb F}_q$ and m(x) divides h(x).

Proof

The set $\mu _{q+1}\setminus \{1,-1\}$ contains exactly the elements $\theta \in {\mathbb F}_{q^2}\setminus {\mathbb F}_q$ with $\theta ^{q+1}=1$.

Let $\theta \in {\mathbb F}_{q^2}\setminus {\mathbb F}_q$ be such that $h(\theta )=0$ and $\theta ^{q+1}=1$. As h(x) is a polynomial over ${\mathbb F}_q$, $\theta ^q$ is another root of h(x). Then $m(x)=(x-\theta )(x-\theta ^q)=x^2-(\theta +\theta ^q)+\theta ^{q+1}=x^2+Ax+1$ divides h(x). Moreover m(x) is the minimal polynomial of $\theta$ over ${\mathbb F}_q$ and hence irreducible.

For the converse, assume that an irreducible polynomial $m(x)=x^2+Ax+1$ divides h(x). The roots $\theta _1$ and $\theta _2$ of $m(x)=(x-\theta _1)(x-\theta _2)$ are roots of h(x) as well. As m(x) is irreducible, the roots lie in ${\mathbb F}_{q^2}\setminus {\mathbb F}_q$ and they are conjugates, i.e., $\theta _2=\theta _1^q$. From the constant coefficient of m(x) we find $1=\theta _1\theta _2=\theta _1^{q+1}$.

Lemma 3

The polynomial $h(x)=\lambda _1x^5+x^4+\lambda _2 x\in {\mathbb F}_q[x]$ is divisible by $m(x)=x^2+Ax+1$ with $A\in {\mathbb F}_q$ if and only if $\lambda _2\ne 0$ and

$$\begin{aligned} s(\lambda _1,\lambda _2)=\lambda _1^3 - \lambda _1^2\lambda _2 - \lambda _1\lambda _2^2 + \lambda _2^3 - \lambda _2=0. \end{aligned}$$

(3)

Proof

Let $h_1(x)=\lambda _1x^4+x^3+\lambda _2$ such that $h(x)=xh_1(x)$. If h(x) is divisible by m(x), then m(x) must be a factor of $h_1(x)$. If we divide $h_1(x)$ by $m(x)=x^2+Ax+1$, the remainder is

$$\begin{aligned} \left( -A^3\lambda _1 + A^2 + 2A\lambda _1 - 1\right) x - A^2\lambda _1 + A + \lambda _1 + \lambda _2=c_1x+c_0. \end{aligned}$$

(4)

The polynomial $h_1(x)$ is divisible by m(x) if and only if both $c_0$ and $c_1$ are zero. Direct calculation shows that

$$\begin{aligned} s(\lambda _1,\lambda _2)=&\left( -A^2\lambda _1^2 + A^2\lambda _1\lambda _2 - A\lambda _2 + \lambda _1^2 + 3\lambda _1\lambda _2 + \lambda _2^2\right) c_0\nonumber \\&+\left( A\lambda _1^2 - A\lambda _1\lambda _2 + \lambda _2\right) c_1. \end{aligned}$$

(5)

Hence $s(\lambda _1,\lambda _2)$ vanishes when $h_1(x)$ is divisible by m(x). When $\lambda _2=0$, condition (3) reduces to $\lambda _1^3=0$. Then $h_1(x)=x^3$, which contradicts divisibility by m(x).

For the converse, assume that $\lambda _2\ne 0$ and define

$$\begin{aligned} h_{1,1}(x)&=x^2 + \frac{\lambda _1^2 - \lambda _2^2}{\lambda _2}x + 1 \end{aligned}$$

(6)

$$\begin{aligned} \text {and}\qquad h_{1,2}(x)&=\lambda _1x^2 + (-\lambda _1^2 + \lambda _2^2)x + \lambda _2. \end{aligned}$$

(7)

Direct calculation shows that

$$\begin{aligned} h_1(x)-h_{1,1}(x)h_{1,2}(x)= \left( \frac{(\lambda _1+\lambda _2)x^2-x^3}{\lambda _2}\right) s(\lambda _1,\lambda _2). \end{aligned}$$

(8)

Hence the condition in (3) implies that the polynomial $h_{1,1}(x)$ in (6) is a factor of h(x). $\square$

Combining Lemma 2 and Lemma 3, we obtain the following characterization of the roots of h(x) in $\mu _{q+1}\setminus \{1,-1\}$.

Proposition 1

The polynomial $h(x)=\lambda _1x^5+x^4+\lambda _2 x\in {\mathbb F}_q[x]$ has a root in $\mu _{q+1}\setminus \{1,-1\}$ if and only if all the following conditions hold:

• (i) $\lambda _2\ne 0$,

• (ii) $s(\lambda _1,\lambda _2)=\lambda _1^3 - \lambda _1^2\lambda _2 - \lambda _1\lambda _2^2 + \lambda _2^3 - \lambda _2=0$,

• (iii)

  • (a) $\lambda _1/\lambda _2-3$ is not a square in ${\mathbb F}_q$ when q is odd,

  • (b) $\lambda _1\ne \lambda _2$ and $\textrm{Tr}\left( \dfrac{\lambda _2}{\lambda _1^2-\lambda _2^2}\right) =1$ when q is even.

Proof

By Lemma 3, conditions (i) and (ii) are equivalent to h(x) having a factor $m(x)=x^2+Ax+1$. From the proof of Lemma 3 it follows that $m(x)=h_{1,1}(x)$ given in (6). If m(x) was a multiple of $h_{1,2}(x)$, then $\lambda _1=\lambda _2$, which by (ii) implies $-\lambda _2=0$, contradicting (i). In order to apply Lemma 2, we have to investigate when $h_{1,1}(x)$ is irreducible. For odd characteristic, this is the case if and only if the discriminant D of $h_{1,1}(x)$ is not a square in ${\mathbb F}_q$. Direct calculation yields

$$\begin{aligned} D=\lambda _1/\lambda _2-3 +\left( \frac{\lambda _1+\lambda _2}{\lambda _2^2}\right) s(\lambda _1,\lambda _2)=\lambda _1/\lambda _2-3. \end{aligned}$$

(9)

For the last equality, we have used condition (ii). In even characteristic, $m(x)=x^2+Ax+1$ is irreducible if and only if $A\ne 0$ and $\textrm{Tr}(1/A)=1$. Applying this criterion to $m(x)=h_{1,1}(x)$ yields the conditions in case (b) of (iii). We are left to investigate whether the second factor $h_{1,2}(x)$ in (7) has a root in $\mu _{q+1}\setminus \{1,-1\}$. If that is the case, we get $\lambda _1=\lambda _2$. Then $s(\lambda _2,\lambda _2)=-\lambda _2=0$, a contradiction to condition (i). $\square$

Note that necessity of condition (ii) was shown in [14, Lemma 3.1] for the polynomial $h_1(x)$ of degree four in the case of characteristic five.

4 PPs over finite fields of characteristic five

With this preparation, we study the action of $g(x)=x^5h(x)^{q-1}$ on the set $\mu _{q+1}$, using the idea of diagram (2). Assuming that h(x) has no roots in $\mu _{q+1}$ and using the relation $x^{q+1}=1$ for $x\in \mu _{q+1}$, we have

$$\begin{aligned} g(x)&=x^5\dfrac{h(x)^q}{h(x)}&=\dfrac{x^5(\lambda _1x^{5q}+x^{4q}+\lambda _2x^q)}{\lambda _1x^5+x^4+\lambda _2x}&=\dfrac{x^5\left( \lambda _1\dfrac{1}{x^5}+\dfrac{1}{x^4}+\lambda _2\dfrac{1}{x}\right) }{\lambda _1x^5+x^4+\lambda _2x}\\ & &=\dfrac{\lambda _1+x+\lambda _2x^4}{\lambda _1x^5+x^4+\lambda _2x}. \end{aligned}$$

Let z be an arbitrary element in ${\mathbb F}_{q^2}\setminus {\mathbb F}_q$ and let $\displaystyle \Phi \left( x\right) =\frac{x+z}{x+z^q}$ and $\displaystyle \Phi ^{-1}\left( x\right) = \frac{xz^q-z}{1-x}$, for any $x\ne 1$. We obtain

$$\begin{aligned} (g\circ \Phi )(x)=\dfrac{\lambda _2(x+z)^4(x+z^q)+(x+z)(x+z^q)^4+\lambda _1(x+z^q)^5}{\lambda _1(x+z)^5+(x+z)^4(x+z^q)+\lambda _2(x+z)(x+z^q)^4} \end{aligned}$$

(10)

Let $\Delta (z,x)=\lambda _2(x+z)^4(x+z^q)+(x+z)(x+z^q)^4+\lambda _1(x+z^q)^5$, then we have

$$\begin{aligned} \Delta (z^q,x)=\lambda _2(x+z^q)^4(x+z)+(x+z^q)(x+z)^4+\lambda _1(x+z)^5. \end{aligned}$$

Then we get

$$\begin{aligned} (\Phi ^{-1}\circ g\circ \Phi )=\dfrac{\Delta (z,x)z^q-z\Delta (z^q,x)}{\Delta (z^q,x)-\Delta (z,x)}. \end{aligned}$$

Choosing $z^q=-z$, i.e., z is the square root of a non-square in ${\mathbb F}_q$, we get that the denominator is

$$\begin{aligned} \Delta (z^q,x)-\Delta (z,x)=(-\lambda _2+1)(zx^4+z^3x^2)+(2\lambda _1+2\lambda _2-2)z^5. \end{aligned}$$

(11)

Similarly, computing the numerator we get

$$\begin{aligned} \Delta (z,x)z^q-z\Delta (z^q,x)=-2z(\lambda _1+\lambda _2+1)x^5+(\lambda _2+1)z^3x^3+(\lambda _2+1)z^5x. \end{aligned}$$

(12)

The following theorem is our main result.

Theorem 2

Let ${\mathbb F}_q$ be a finite field, where $q=5^k$. Let $h(x)=\lambda _1x^5+x^4+\lambda _2x$ with $\lambda _1,\lambda _2\in {\mathbb F}_q$ and assume that $h(1)=\lambda _1+\lambda _2+1\ne 0$, $h(-1)=-\lambda _1-\lambda _2+1\ne 0$. Then $f(x)=x^5h(x^{q-1})=\lambda _1x^{5q}+x^{4q+1}+\lambda _2x^{q+4}$ is a permutation polynomial of ${\mathbb F}_{q^2}$ if and only if one of the following holds:

• (i) $\lambda _1=0$, $\lambda _2\ne \pm 1$ and k is even,

• (ii) $\lambda _1=1$, $\lambda _2= -1$ and k is even,

• (iii) $\lambda _1=-1$, $\lambda _2= 1$ and k is even,

• (iv) $(\lambda _1,\lambda _2)=(2,1)$ or $(\lambda _1,\lambda _2)=(3,-1)$ for $q=5$.

Proof

By Lemma 1, we have to show that $g(x)=x^5 h(x)^{q-1}$ permutes the set $\mu _{q+1}$. We apply the idea shown in diagram (2) and hence show that $(\Phi ^{-1}\circ g\circ \Phi )$ permutes ${\mathbb F}_q$. For this, we consider the curve defined by

$$\begin{aligned} \mathcal {C}(x,y)=\dfrac{(\Phi ^{-1}\circ g\circ \Phi )(x)-(\Phi ^{-1}\circ g\circ \Phi )(y)}{x-y} \end{aligned}$$

(13)

and show that is has no rational points off the line $x=y$ over ${\mathbb F}_q$.

We first assume that $-\lambda _2+1\ne 0$, that is, $\lambda _2\ne 1$ and consider the map $(\Phi ^{-1}\circ g \circ \Phi )(x)$ which is given by

$$\begin{aligned} 2\frac{\lambda _1 + \lambda _2 + 1}{\lambda _2 - 1} \left( \frac{\quad x^5 + \dfrac{2\lambda _2 + 2}{\lambda _1 + \lambda _2 + 1}z^2x^3 + \dfrac{2\lambda _2 + 2}{\lambda _1 + \lambda _2 + 1}z^4x\quad }{x^4 + z^2x^2 + \dfrac{3\lambda _1 + 3\lambda _2 + 2}{\lambda _2 - 1}z^4}\right) . \end{aligned}$$

(14)

We investigate whether this map in injective on ${\mathbb F}_q$. Recall that h(x) may not have any root in $\mu _{q+1}$. In particular, $h(1)=\lambda _1 + \lambda _2+1\ne 0$, i.e., the prefactor in (14) is non-zero. Moreover, we have assumed $\lambda _2\ne 1$, i.e., the prefactor does not have a pole, and we can ignore it.

The denominator of the expression in brackets in (14) is the quartic polynomial

$$\begin{aligned} x^4 + z^2x^2 + \dfrac{3\lambda _1 + 3\lambda _2 + 2}{\lambda _2 - 1}z^4, \end{aligned}$$

(15)

and we investigate when it has a root in ${\mathbb F}_q$. First note that the constant coefficient is non-zero, since $h(-1)=-\lambda _1-\lambda _2+1\ne 0$. Using the substitution $t=x^2$, we obtain a quadratic polynomial for t with discriminant

$$\begin{aligned} D_1 = \dfrac{3\lambda _1 - \lambda _2 + 1}{\lambda _2 - 1} z^4. \end{aligned}$$

(16)

When $D_1$ is not a square in ${\mathbb F}_q$, then there is no solution for t in ${\mathbb F}_q$, and hence (14) has no pole in ${\mathbb F}_q$. Note that $z^4$ is a square in ${\mathbb F}_q$, and hence it is sufficient that $\dfrac{3\lambda _1 - \lambda _2 + 1}{\lambda _2 - 1}$ is a non-square in ${\mathbb F}_q$.

Next assume that $D_1$ is a square in ${\mathbb F}_q$, i.e., $D_1=\delta ^2 z^4$ for some $\delta \in {\mathbb F}_q$. Then (15) factors as

$$\begin{aligned} \Bigl (x^2-2(1+\delta )z^2\Bigr )\Bigl (x^2-2(1-\delta )z^2\Bigr ). \end{aligned}$$

(17)

Hence, (15) has a root in ${\mathbb F}_q$ when $D_1$ is a square in ${\mathbb F}_q$ and additionally $2(1+\delta )z^2$ or $2(1-\delta )z^2$ is a square in ${\mathbb F}_q$. As $z^2$ is a non-square in ${\mathbb F}_q$, the second part is equivalent to $2(1+\delta )$ or $2(1-\delta )$ being a non-square.

First consider the special case that $D_1=0$, i.e., $\lambda _2=3\lambda _1+1$. Then (17) has a root in ${\mathbb F}_q$ if and only if $2z^2$ is a square in ${\mathbb F}_q$, which is equivalent to $q=5^k$ with k odd. The roots are $\pm \sqrt{2}z$. For these values of x, the numerator of (14) is nonzero, i.e., (14) has a pole. That implies that we do not get a permutation polynomial when $\lambda _2=3\lambda _1+1\ne 1$ and $q=5^k$, k odd.

When $D_1$ is a non-zero square, we have roots of (15) with

$$\begin{aligned} x^2 = 2(1\pm \delta )z^2. \end{aligned}$$

(18)

Recall that the constant coefficient of (15) is non-zero, and hence $x\ne 0$. In order to obtain a permutation polynomial, (14) must not have a pole in ${\mathbb F}_q$, i.e., it is necessary that the numerator of (14) vanishes as well for the roots (18) that lie in ${\mathbb F}_q$. We fix one root x and compute for the fixed choice of the sign in the factor $1\pm \delta$:

$$\begin{aligned} 0&= x^5 + \dfrac{2\lambda _2 + 2}{\lambda _1 + \lambda _2 + 1}z^2x^3 + \dfrac{2\lambda _2 + 2}{\lambda _1 + \lambda _2 + 1}z^4x\nonumber \\&=x\left( x^4+ \dfrac{2\lambda _2 + 2}{\lambda _1 + \lambda _2 + 1}z^2x^2 + \dfrac{2\lambda _2 + 2}{\lambda _1 + \lambda _2 + 1}z^4\right) \nonumber \\&=x\left( 4(1\pm \delta )^2z^4+ \dfrac{2\lambda _2 + 2}{\lambda _1 + \lambda _2 + 1}2(1\pm \delta )z^4 + \dfrac{2\lambda _2 + 2}{\lambda _1 + \lambda _2 + 1}z^4\right) \nonumber \\&=xz^4\left( 4(1\pm \delta )^2+ \bigl (4(1\pm \delta )+2\bigr )\dfrac{\lambda _2 + 1}{\lambda _1 + \lambda _2 + 1}\right) . \end{aligned}$$

(19)

Using that both x and z are non-zero, this reduces to the condition

$$\begin{aligned} \left( 4(1\pm \delta )^2+ \bigl (4(1\pm \delta )+2\bigr )\dfrac{\lambda _2 + 1}{\lambda _1 + \lambda _2 + 1}\right) =0. \end{aligned}$$

(20)

From (16) we get the condition

$$\begin{aligned} \delta ^2=\dfrac{3\lambda _1 - \lambda _2 + 1}{\lambda _2 - 1}. \end{aligned}$$

(21)

For either choice of the sign in the factor $1\pm \delta$, combining (20) and (21) implies that $\lambda _1=0$ or $s(\lambda _1,\lambda _2)=0$. This can be shown computing an elimination ideal in Magma. These cases are treated below, yielding reduced equations for $\mathcal {C}(x,y)$ in (31) and (36).

In summary, excluding the last two cases, (14) does not have a pole if and only if one of the following conditions holds:

$$\begin{aligned}&\text {(i)}\quad&\dfrac{3\lambda _1 - \lambda _2 + 1}{\lambda _2 - 1}~\text {is a non-square in}~{\mathbb F}_q,\end{aligned}$$

(22)

$$\begin{aligned}&\text {(ii)}&\lambda _2=3\lambda _1+1~\text {and}~q=5^k, k~\text {even},\end{aligned}$$

(23)

$$\begin{aligned}&\text {(iii)}&\dfrac{3\lambda _1 - \lambda _2 + 1}{\lambda _2 - 1}=\delta ^2 ~\text {with}~\delta \in {\mathbb F}_q\nonumber \\ & \text {and}~2(1+\delta ), 2(1-\delta )~\text {are both squares in}~{\mathbb F}_q.\qquad \qquad \qquad \qquad \end{aligned}$$

(24)

In the calculations with the possible factorizations of the curve (26) below, we check every possible outcome in terms of these conditions and we verify that they all satisfy one of the conditions above. Therefore, we do not add these conditions in the statement of the theorem.

Returning to the curve (13), consider the normalized denominator and numerator in (11) and (12) to obtain

$$\begin{aligned} \dfrac{\ \dfrac{x^5+A_1x^3+A_0x}{x^4+B_1x^2+B_0}-\dfrac{y^5+A_1y^3+A_0y}{y^4+B_1y^2+B_0}\ }{x-y}. \end{aligned}$$

(25)

Simplifying this expression and considering the numerator, we obtain the following curve defined by a polynomial

$$\begin{aligned} \mathcal {C}(x,y):=&x^4y^4+B_1(x^4y^2+x^2y^4)+B_0(x^4+y^4)+(B_1-A_1)x^3y^3\nonumber \\&+(B_0-A_0)(x^3y+xy^3) +(B_0+A_1B_1-A_0)x^2y^2\nonumber \\&+A_1B_0(x^2+y^2) +(A_1B_0-A_0B_1)xy+A_0B_0, \end{aligned}$$

(26)

where we have used

$$\begin{aligned} A_0&=\dfrac{-(\lambda _2+1)}{2(\lambda _1+\lambda _2+1)}z^4,&A_1&=\dfrac{-(\lambda _2+1)}{2(\lambda _1+\lambda _2+1)}z^2,\nonumber \\ B_0&=\dfrac{(2\lambda _1+2\lambda _2-2)}{-\lambda _2+1}z^4,&\qquad B_1&=z^2. \end{aligned}$$

(27)

Recall that we have chosen $z\in {\mathbb F}_{q^2}\setminus {\mathbb F}_q$ such that $z^2\in {\mathbb F}_q$.

First assume that the curve in (26) is absolutely irreducible. Note that the underlying idea here is first of all estimating the number of ${\mathbb F}_q$-rational points of the curve $\mathcal {C}(x,y)$ in (26). For this purpose, one can use Hasse-Weil type bounds (see for instance [33, Theorem 5.2.3] for the Hasse-Weil bound given in terms of algebraic function fields, [24] for the Lang-Weil bound). In this paper we use [23, Theorem 5.28] which involves a bound obtained from the Hasse-Weil bound. Let $\widetilde{\mathcal {C}}(X,Y,Z)\in {\mathbb F}_q[X,Y,Z]$ be the homogeneous polynomial defined as

$$\begin{aligned} \widetilde{\mathcal {C}}(X,Y,Z)=Z^8\mathcal {C}\left( \dfrac{X}{Z},\dfrac{Y}{Z}\right) . \end{aligned}$$

Homogenization of $\mathcal {C}(x,y)$ in (26) by substituting $\left( \dfrac{X}{Z},\dfrac{Y}{Z}\right)$ yields a homogeneous polynomial of degree $d=8$. Let $\mathbb {P}^2({\mathbb F}_q)$ denote the projective space consisting of projective coordinates (X : Y : Z). Let $N=|\{(x,y)\in {\mathbb F}_q\times {\mathbb F}_q\mid \mathcal {C}(x,y)=0\}|$ be the number of affine ${\mathbb F}_q$-rational points of $\mathcal {C}$. Let $V=|\{(X:Y:Z)\in \mathbb {P}^2({\mathbb F}_q)\mid \widetilde{\mathcal {C}}(X,Y,Z)=0\}|$ be the number of projective ${\mathbb F}_q$-rational points of $\widetilde{\mathcal {C}}$. Let $V_0$ and $V_1$ be the numbers of projective ${\mathbb F}_q$-rational points of $\widetilde{\mathcal {C}}$ corresponding to the cases $z=0$ and $z\ne 0$ respectively. Namely,

$$\begin{aligned} V_0&=|\{(X:Y:0)\in \mathbb {P}^2({\mathbb F}_q)\mid \widetilde{\mathcal {C}}(X,Y,0)=0\}|\\ \text {and}\qquad V_1&=|\{(X:Y:1)\in \mathbb {P}^2({\mathbb F}_q)\mid \widetilde{\mathcal {C}}(X,Y,1)=0\}|. \end{aligned}$$

It follows from the definitions that $N=V_1$ and $V=V_0+V_1$. Moreover it follows from (26) that $\widetilde{\mathcal {C}}(X,Y,0)=X^4Y^4$. This implies $V_0=|\{(1:0:0),(0:1:0)\}|=2$. Using [23, Theorem 5.28] we get

$$\begin{aligned} |V - q | \le (d-1)(d-2)q^{1/2}+c(d)= 42q^{1/2}+ 197, \end{aligned}$$

(28)

where $c(d)=\frac{1}{2}d(d-1)^2+1$ and $d=8$. The arguments above imply that

$$\begin{aligned} V=N+2. \end{aligned}$$

(29)

Combining (28) and (29) we conclude that

$$\begin{aligned} |N-q|=|(V-q)-2|\le |V-q|+2\le 42q^{1/2}+199. \end{aligned}$$

Note that

$$\begin{aligned} |\{(x,y)\in {\mathbb F}_q^2\mid \mathcal {C}(x,y)=0~\text {and}~x=y\}|\le 8 \end{aligned}$$

as $\mathcal {C}(x,x)$ is a polynomial of degree 8 in ${\mathbb F}_q[x]$. Therefore, if $q-42q^{1/2}-199>8$, then $\mathcal {C}(x,y)$ has an affine point off the line $x=y$. We note that $q-42q^{1/2}-199>8$ for any $q=5^k$ with $k\ge 5$. As a result, we deduce that f(x) is not a permutation polynomial of ${\mathbb F}_{q^2}$ if $\mathcal {C}(x,y)$ is absolutely irreducible and $q\ge 5^k$. In characteristic 5, it remains to consider $q\in \{5,25,125,625\}$. Using MAGMA [9], we obtained the following:

• 1. Over ${\mathbb F}_5$, f(x) permutes ${\mathbb F}_{25}$ when $(\lambda _1,\lambda _2)=(2,1)$ and $(\lambda _1,\lambda _2)=(3,-1)$.

• 2. Over ${\mathbb F}_{25}$, f(x) permutes ${\mathbb F}_{625}$ when $(\lambda _1,\lambda _2)=(-1,1)$, $(\lambda _1,\lambda _2)=(1,-1)$ and $(\lambda _1,\lambda _2)=(0,\zeta )$ where $\zeta \in {\mathbb F}_{25}\setminus \{1,-1\}$.

• 3. Over ${\mathbb F}_{125}$, f(x) is not a PP of ${\mathbb F}_{5^6}$ for any $(\lambda _1,\lambda _2)\in {\mathbb F}_{125}^2\setminus \{(0,0)\}$.

• 4. Over ${\mathbb F}_{625}$, the situation is similar to ${\mathbb F}_{25}$, with $\zeta \in {\mathbb F}_{625}\setminus \{1,-1\}$.

Hence, except the first item corresponding to item (iv) of Theorem 2 where $\mathcal {C}(x,y)$ is absolutely irreducible, all the remaining cases are covered by items (i)–(iii) of Theorem 2.

In order to obtain a permutation polynomial for $q\ge 5^5$, the polynomial $\mathcal {C}(x,y)$ in (26) has to be reducible. We consider all possible non-trivial factorizations of $\mathcal {C}(x,y)$, noting the symmetry which keeps $\mathcal {C}(x,y)$ fixed when we interchange x and y. Without loss of generality, we fix a monomial ordering by taking $x>y$ and start with all factorizations of the leading monomials $x^4 y^4$ which are symmetric with respect to interchanging x and y. There are 22 possibilities listed in 1. Each factor has the form

$$\begin{aligned} p_m(x,y) = m(x,y) + \sum _{m'<m} c_i m'(x,y), \end{aligned}$$

where m(x, y) is the leading monomial from the factorization of $x^4y^4$. For each of the monomials $m'(x,y)$ with $m'<m$ and for each of the factors $p_m(x,y)$ we use a different variable $c_i$ as coefficient.

We use the notion of Gröbner bases (see for instance [12]) in order to solve for the coefficients with the help of the computer algebra program MAGMA [9]. Namely, we subtract the products of the generic factors $p_m(x,y)$ from $\mathcal {C}(x,y)$ in (26) and compute a Gröbner basis of the ideal generated by the coefficients of this difference. The elimination ideal with respect to $\lambda _1$ and $\lambda _2$ provides necessary conditions on $\lambda _1$ and $\lambda _2$ for the particular factorization to exist. More details can be found in 1. A similar approach has, for example, been used in [5]. We obtain the following necessary conditions:

• (a) $\lambda _1=0$, or

• (b) $\lambda _1=1$ and $\lambda _2=-1$, or

• (c) $\lambda _1^3 -\lambda _1^2\lambda _2 - \lambda _1\lambda _2^2 + \lambda _2^3 -\lambda _2=0$.

For each of these cases, we recompute the equation for the curve $\mathcal {C}(x,y)$ in (25).

First, assume that $\lambda _1=0$. In this case, (13) yields

$$\begin{aligned} 2\dfrac{\lambda _2+1}{\lambda _2-1} \left( \dfrac{x^2 y^2 + 2 z^2 (x+y)^2 + z^4}{x^2y^2+2z^2(x^2+y^2)-z^4}\right) , \end{aligned}$$

(30)

and from the numerator we get the equation

$$\begin{aligned} \mathcal {C}(x,y) = x^2 y^2 + 2 z^2 (x+y)^2 + z^4. \end{aligned}$$

(31)

The equation factors as

$$\begin{aligned} \mathcal {C}(x,y) = \left( x y + 2 \alpha z (x - y) - z^2\right) \left( x y - 2 \alpha z (x - y) - z^2\right) \end{aligned}$$

(32)

where $\alpha ^2=2$. For $q=5^k$ and k odd, $\alpha \in {\mathbb F}_{q^2}\setminus {\mathbb F}_q$ and $\alpha ^q=-\alpha$. Then $(\alpha z)^q = \alpha z$, i.e., $\mathcal {C}(x,y)$ factors over ${\mathbb F}_q$. For $y=-x$, equation (30) reduces to

$$\begin{aligned} 2\dfrac{\lambda _2+1}{\lambda _2-1} \left( \dfrac{x^2 - 2 z^2}{x^2 + 2 z^2}\right) . \end{aligned}$$

This implies that the curve has the ${\mathbb F}_q$-rational point $(\alpha z,-\alpha z)$ off the line $x=y$, and we do not get a permutation polynomial for k odd.

For k even, $\alpha \in {\mathbb F}_q$. Then the two factors in (32) are conjugates over ${\mathbb F}_{q^2}[x,y]$. Any ${\mathbb F}_q$-rational point is hence a root of both factors, and also of their difference which equals $\alpha z (x-y)$. Hence the curve has no ${\mathbb F}_q$-rational points off the line $x=y$, we get a permutation polynomial when k is even. This completes the proof of item (i) in Theorem 2.

Next, for case (b) assume that $\lambda _1=1$ and $\lambda _2=-1$. Then (13) yields

$$\begin{aligned} \dfrac{x^4y^4 + z^2(x^4y^2 + x^3y^3 + x^2y^4) - z^4(x^4 + x^3y + x^2y^2 + xy^3 + y^4)}{(x^2-2z^2)^2(y^2-2z^2)^2}, \end{aligned}$$

(33)

and from the numerator we get the equation

$$\begin{aligned} \mathcal {C}(x,y) = x^4y^4&+ z^2(x^4y^2 + x^3y^3 + x^2y^4)\nonumber \\&-z^4(x^4 + x^3y + x^2y^2 + xy^3 + y^4). \end{aligned}$$

(34)

The equation factors as

$$\begin{aligned} \mathcal {C}(x,y) =&\left( x^2y^2 + 2\alpha z( x^2y + xy^2) + z^2(2x^2 + xy + 2y^2)\right) \nonumber \\&\left( x^2y^2 - 2\alpha z( x^2y + xy^2) + z^2(2x^2 + xy + 2y^2)\right) , \end{aligned}$$

(35)

where $\alpha ^2=2$. Eq. (33) must not have a pole. Condition (23) requires that $q=5^k$ with k even, and hence $\alpha \in {\mathbb F}_q$. Then the two factors in (35) are conjugates over ${\mathbb F}_{q^2}[x,y]$. Any ${\mathbb F}_q$-rational point is hence a root of both factors. Computing the prime decomposition of the zero-dimensional ideal generated by the two factors we find that the only solutions are $(0,0)\in {\mathbb F}_q^2$ and $(\alpha z,-\alpha z),(-\alpha z,\alpha z)\in {\mathbb F}_{q^2}^2\setminus {\mathbb F}_q^2$. As the curve has no ${\mathbb F}_q$-rational points off the line $x=y$, we get a permutation polynomial when k is even. This completes the proof of item (ii) of Theorem 2.

For case (c), assume $s(\lambda _1,\lambda _2)=\lambda _1^3 -\lambda _1^2\lambda _2 - \lambda _1\lambda _2^2 + \lambda _2^3 -\lambda _2=0$. As the case $\lambda _1=0$ is covered in case (a), we can assume $\lambda _1\ne 0$. Then the equation for the curve is

$$\begin{aligned} \mathcal {C}(x,y)=&(\lambda _1 + \lambda _2 + 1) x^2 y^2- z^2 (\lambda _1^2 + 2 \lambda _1 - \lambda _2^2 + 2 \lambda _2 - 2) (x^2 + y^2)\nonumber \\&\quad + z^2 (\lambda _1 - \lambda _2 - 1) x y + z^4 (-\lambda _1^2 + 2 \lambda _1 + \lambda _2^2 + 2 \lambda _2 + 1). \end{aligned}$$

(36)

Using similar techniques as described in 1, we find that $\lambda _1=0$ for all possible non-trivial factorizations of this polynomial of degree 4. As this contradicts our assumption, there are no permutation polynomials in this case. Note, however, that case (c) is not excluded by Proposition 1. The condition $s(\lambda _1,\lambda _2)=0$ is only necessary for h(x) to have a root in $\mu _{q+1}\setminus \{1,-1\}$, i.e., that one does not obtain a permutation polynomial.

Going back to (11) and (12), we now consider the case when $\lambda _2=1$. Recall that

$$ (\Phi ^{-1}\circ g\circ \Phi )=\dfrac{\Delta (z,x)z^q-z\Delta (z^q,x)}{\Delta (z^q,x)-\Delta (z,x)}. $$

Again choosing $z\in {\mathbb F}_{q^2}\setminus {\mathbb F}_q$ with $z^q=-z$ we get that the denominator is

$$\Delta (z^q;x)-\Delta (z;x)=2\lambda _1z^5.$$

Similarly, computing the numerator we get

$$\Delta (z;x)z^q-z\Delta (z^q;x)=-2z(\lambda _1+2)x^5+2z^3x^3+2z^5x.$$

In this case

$$\begin{aligned} \dfrac{(\Phi ^{-1}\circ g\circ \Phi )(x)-(\Phi ^{-1}\circ g\circ \Phi )(y)}{x-y} \end{aligned}$$

is a polynomial in ${\mathbb F}_{q^2}[x,y]$, and hence has no poles. After simplifying we obtain the following curve

$$\begin{aligned} \mathcal {C}(x,y)=x^4+x^3y+xy^3+y^4+x^2y^2+A(x^2+xy+y^2)+B, \end{aligned}$$

(37)

where $A=\dfrac{-z^2}{\lambda _1+2}$, $B=\dfrac{-z^4}{\lambda _1+2}$. The degree of the curve in (37) is smaller than the degree of the curve in (26). Therefore the case of $\mathcal {C}(x,y)$ being absolutely irreducible has already been covered above.

Hence, assume that $\mathcal {C}(x,y)$ in (37) is not absolutely irreducible and it is decomposed as follows:

$$\begin{aligned} (x^2+\alpha _1xy+\alpha _2y^2+\alpha _3x+\alpha _4y+\alpha _5)(\beta _1x^2+\beta _2xy+\beta _3y^2+\beta _4x+\beta _5y+\beta _6). \end{aligned}$$

Comparing the coefficients of this decomposition and $\mathcal {C}(x,y)$ in (37) we first obtain that $\beta _1=1$, $\beta _2=3$, $\beta _3=1$, $\alpha _1=3$, $\alpha _2=1$, $\beta _4=-\alpha _3$, $\beta _5=-\alpha _4$, $\beta _6=\alpha _5$. Moreover, we get that $\beta _6^2=B$ and $\beta _6=2A$. Thus $B=(2A)^2$ which implies that

$$\begin{aligned} \dfrac{4z^4}{(\lambda _1+2)^2}=\dfrac{-z^4}{\lambda _1+2}, \end{aligned}$$

(38)

and so $\lambda _1=-1$.

Now assume that $\lambda _1=-1$ and $\lambda _2=1$. Then the curve has the equation

$$\begin{aligned} \mathcal {C}(x,y) = x^4 + x^3y + x^2y^2 - z^2(x^2 + xy + y^2) + xy^3 + y^4 - z^4. \end{aligned}$$

(39)

The equation factors as

$$\begin{aligned} \mathcal {C}(x,y) = \left( (x - y)^2 + \alpha z(x + y) - 2z^2\right) \\ \nonumber \left( (x - y)^2 - \alpha z(x + y) - 2z^2\right) , \end{aligned}$$

(40)

where $\alpha ^2=2$. As before, $\alpha z\in {\mathbb F}_q$ for $q=5^k$ and k odd. For $y=-x$, we get

$$\begin{aligned} \mathcal {C}(x,-x) = (x+2\alpha z)^2 (x-2\alpha z)^2. \end{aligned}$$

(41)

This implies that the curve has the ${\mathbb F}_q$-rational point $(2\alpha z,-2\alpha z)$ off the line $x=y$ and we do not get a permutation polynomial for k odd.

For k even, $\alpha \in {\mathbb F}_q$ and the two factors in (15) are conjugates over ${\mathbb F}_{q^2}[x,y]$. Any ${\mathbb F}_q$-rational point is hence a root of both factors. Computing the prime decomposition of the zero-dimensional ideal generated by the two factors we find that the only solutions are $(\alpha z,-\alpha z),(-\alpha z,\alpha z)\in {\mathbb F}_{q^2}^2\setminus {\mathbb F}_q^2$. As the curve has no ${\mathbb F}_q$-rational points, we get a permutation polynomial when k is even.

For all the other decompositions of $\mathcal {C}(x,y)$ in (37), we obtain a contradiction after computing its Gröbner basis by MAGMA. This completes the proof of item (iii) of Theorem 2.

In all items in the statement of Theorem 2, the values of $\lambda _1$ and $\lambda _2$ do not satisfy at least one of the conditions of Proposition 1 and thus h(x) does not have any roots in $\mu _{q+1}$. $\square$

Remark 1

Items (ii) and (iii) in Theorem 2 have already been obtained in [2] and [14], respectively.

5 Comparison with existing permutation trinomials

Definition 1

[36] Two permutation polynomials $f(x),g(x)\in {\mathbb F}_q[x]$ are said to be quasi-multiplicative (QM) equivalent, if there exists $d\in \mathbb {Z}$, $1\le d\le q-1$ with $\gcd (d,q-1)=1$ and $f(x)=ag(cx^d) \pmod {x^{q}-x}$ , where $a,c\in {\mathbb F}_q^*$. If $c=1$, then $f(x),g(x)\in {\mathbb F}_q[x]$ are called multiplicative equivalent.

In this section, we show that the permutation trinomial considered in this paper is not QM equivalent to some known classes. We first observe that two QM equivalent permutations must have exactly the same number of terms. Therefore, we only need to compare the permutation trinomials found in this paper with known permutation trinomials over ${\mathbb F}_{q^2}$ where $q=5^k$. We use the method in [36] for this purpose. In order to determine whether the permutation polynomial $f(x)=x^{4q+1}+\lambda _1x^{5q}+\lambda _2x^{q+4}\in {\mathbb F}_{q}[x]$ is QM equivalent to any permutation trinomial of the form $g(x)=a_1x^{s_1}+a_2x^{s_2}+a_3x^{s_3}\in {\mathbb F}_q[x]$, we will use the following strategy:Step 1: Determining whether there exists an integer k, $1\le k\le q^2-1$, such that $\gcd (k,q^2-1)=1$ and $\{ks_1,ks_2,ks_3\}\equiv \{4q+1, 5q, q+4\} \bmod (q^2-1)$.Step 2: Comparison of the coefficients of f(x) and $b_2g(b_1x^k)$. In the above strategy, if Step 1 is not satisfied, then f(x) and g(x) will not be QM equivalent, otherwise we will go on with Step 2 and compare the coefficients of f(x) and $b_2g(b_1x^k)$.

In [2], Bai and Xia characterized the multiplicative equivalence of f(x) when $(\lambda _1,\lambda _2)=(1,4)$ and their result can be modified to the more general setting that we consider in this paper. The proof of the following is very similar to Proposition 1 in [2], therefore it is omitted.

Proposition 3

In characteristic 5, the polynomial $f(x)=x^{4q+1}+\lambda _1x^{5q}+\lambda _2x^{q+4}\in {\mathbb F}_{q}[x]$ with $q=5^k$ is multiplicative equivalent to the following permutation trinomials of ${\mathbb F}_{q^2}$:

• $f_1(x)= \lambda _1 x+x^{(4\cdot 5^{k-1}+1)(q-1)+1}+\lambda _2 x^{(5^{k-1}+1)(q-1)+1}$,

• $f_2(x)= x+\lambda _1 x^{\frac{2q+1}{3}(q-1)+1}+\lambda _2 x^q$,

• $f_3(x)= \lambda _2 x+x^q+\lambda _1 x^{\frac{q+5}{3}(q-1)+1}$.

Bai and Xia presented a list of known polynomials in Table 3 in [2] to which f(x) is not multiplicative equivalent. Therefore we omit the polynomials listed in Table 3 in [2] and we consider the polynomials given in Table 1 below. We applied the method in [36] above using MAGMA and we have verified that f(x) is not QM equivalent to any of them. To the best of our knowledge, the list in Table 1 below is complete.

Table 1 The known permutation trinomials of ${\mathbb F}_{q^2}$

We now consider case (i) in Theorem 2, where $\lambda _1=0$ and we have the binomial $f(x)=x^{4q+1}+\lambda _2 x^{q+4}$. Observe that f(x) is QM equivalent to the linearized polynomial $g(x)=x^{q} + b x \in {\mathbb F}_{q^2}[x]$, where $f(x)=g(x^{q+4})\bmod (x^{q^2}-x)$ with $b=\lambda _2\in {\mathbb F}_q$. Since g(x) is linearized, Theorem 7.9 in [28] tells that $g(x)=x^{q} + b x$ permutes ${\mathbb F}_{q^2}$ if and only if g(x) only has the root 0 in ${\mathbb F}_{q^2}$. This happens if and only if $(-b)^{q+1}\ne 1$. Indeed, if $g(\omega )=0$, for some $\omega \in {\mathbb F}_{q^2}^*$, then $-b =\omega ^{q-1}$ and therefore $(-b)^{q+1} = 1$. Conversely, if $(-b)^{q+1} = 1$, then $-b = \gamma ^{k(q-1)}$, for some $k\in {\mathbb Z}$ and some primitive element $\gamma \in {\mathbb F}_{q^2}^*$. In that case, $g(\gamma ^k) = 0$. Hence, g(x) permutes ${\mathbb F}_{q^2}$ if and only if $(-b)^{q+1}\ne 1$. In our case where $b=\lambda _2\in {\mathbb F}_q$, this corresponds to $(-\lambda _2)^{q+1}=(-\lambda _2)^2=\lambda _2^2\ne 1$ (i.e. $\lambda _2\ne \pm 1$).

Remark 2

Note that this QM equivalence holds in any characteristic p since $f(x)=x^{(p-1)q+1}+\lambda _2 x^{q+p-1}= g(x^{q+p-1}) \bmod (x^{q^2}-x)$ with $g(x)=x^q+\lambda _2 x$.

Appendix A. Factorizations of \(\mathcal {C}(x,y)\)

1.1 Appendix A.1. Overview

We consider all factorizations of $\mathcal {C}(x,y)$ given in (26). Out of 108 non-trivial factorizations of the leading monomial $x^4 y^4$, it is sufficient to consider the 22 cases that are invariant with respect to interchanging x and y. We did not impose that symmetry on the factors themselves, but used different coefficients $c_i$ for all factors. For each of the 22 cases listed below, we consider the coefficients with respect to x and y of the difference of $\mathcal {C}(x,y)$ in (26) and the product of the factors. Those generate an ideal in the polynomial ring with variables $A_0,A_1,B_0,B_1$ and $c_i$. From the substitutions (27) we obtain additional polynomial relations between $A_0, A_1, B_0, B_1$ and $\lambda _1,\lambda _2$. We treat z as a variable, too. In the derivation of the equations, we made the following assumptions: $\lambda _2\ne 1$, $\lambda _1+\lambda _2+1\ne 0$, $\lambda _1+\lambda _2-1\ne 0$, and $z\ne 0$. Those can be accounted for by considering the saturation of the ideal by the corresponding polynomials, i.e., computing ideal quotients.

While computer algebra systems like MAGMA [9] provide implementations of all the required algorithms, the computations can be simplified a lot in our case. As we are only interested in the solutions of the system of polynomial equations, we can replace any non-square-free polynomial by its square-free part. Moreover, if a polynomial in the basis of an intermediate result splits, we can treat each factor separately. We first use so-called grevlex order, and in the final step an elimination order to obtain the conditions on $\lambda _1$ and $\lambda _2$. The whole computation took less than 3 hours, with cases 7 and 19 taking about $45\%$ and $25\%$ of the total time, respectively. The calculations did no use more than 1 GB of memory.

When the final Gröbner basis contains the constant 1, then we have no solution to the original equations or those equations imply that some of the expressions that are assumed to be zero vanish. We summarize those cases by just stating that we obtain a contradiction.

1.2 Appendix A.2. The 22 cases

• 1. $(x^2 + c_{10} x y^4 + c_9 x y^3 + c_8 x y^2 + c_7 x y + c_6 x + c_5 y^4 + c_4 y^3 + c_3 y^2 + c_2 y + c_1)(y + c_{11}) (x + c_{16} y^4 + c_{15} y^3 + c_{14} y^2 + c_{13} y + c_{12}) (y^2 + c_{18} y + c_{17}) (xy + c_{24} x + c_{23} y^4 + c_{22} y^3 + c_{21} y^2 + c_{20} y + c_{19})$ In this case, we obtain a contradiction.

• 2. $(y + c_1) (x + c_6 y^4 + c_5 y^3 + c_4 y^2 + c_3 y + c_2) (y^3 + c_9 y^2 + c_8 y + c_7) (x^3 + c_{24} x^2 y^4 + c_{23} x^2 y^3 + c_{22} x^2 y^2 + c_{21} x^2 y + c_{20} x^2 + c_{19} x y^4 + c_{18} x y^3 + c_{17} x y^2 + c_{16} x y + c_{15} x + c_{14} y^4 + c_{13} y^3 + c_{12} y^2 + c_{11} y + c_{10})$ Here, we again get a contradiction.

• 3. $(y + c_1) (x + c_6 y^4 + c_5 y^3 + c_4 y^2 + c_3 y + c_2) (x^2 y^2 + c_{18} x^2 y + c_{17} x^2 + c_{16} x y^4 + c_{15} x y^3 + c_{14} x y^2 + c_{13} x y + c_{12} x + c_{11} y^4 + c_{10} y^3 + c_9 y^2 + c_8 y + c_7) (x y + c_{24} x + c_{23} y^4 + c_{22} y^3 + c_{21} y^2 + c_{20} y + c_{19})$ In this case, we obtain two possibilities: either $\lambda _1=0$ or $\lambda _1^3 -\lambda _1^2\lambda _2 - \lambda _1\lambda _2^2 + \lambda _2^3 -\lambda _2=0$.

• 4. $(y + c_1) (x + c_6 y^4 + c_5 y^3 + c_4 y^2 + c_3 y + c_2) (x y + c_{12} x + c_{11} y^4 + c_{10} y^3 + c_9 y^2 + c_8 y + c_7) (x y + c_{18} x + c_{17} y^4 + c_{16} y^3 + c_{15} y^2 + c_{14} y + c_{13}) (x y + c_{24} x + c_{23} y^4 + c_{22} y^3 + c_{21} y^2 + c_{20} y + c_{19})$ Here we get $\lambda _1=0$.

• 5. $(y + c_1) (x + c_6 y^4 + c_5 y^3 + c_4 y^2 + c_3 y + c_2) (x y^2 + c_{13} x y + c_{12} x + c_{11} y^4 + c_{10} y^3 + c_9 y^2 + c_8 y + c_7) (x^2 y + c_{24} x^2 + c_{23} x y^4 + c_{22} x y^3 + c_{21} x y^2 + c_{20} x y + c_{19} x + c_{18} y^4 + c_{17} y^3 + c_{16} y^2 + c_{15} y + c_{14})$ We again have $\lambda _1=0$.

• 5. $(x^3 y^3 + c_{18} x^3 y^2 + c_{17} x^3 y + c_{16} x^3 + c_{15}x^2 y^4 + c_{14} x^2 y^3 + c_{13} x^2 y^2 + c_{12} x^2 y + c_{11} x^2 + c_{10} x y^4 + c_9 x y^3 + c_8 x y^2 + c_7 x y + c_6 x + c_5 y^4 + c_4 y^3 + c_3 y^2 + c_2 y + c_1) (y + c_{19}) (x + c_{24} y^4 + c_{23} y^3 + c_{22} y^2 + c_{21} y + c_{20})$ We have either $\lambda _1=0$ or $\lambda _1^3 -\lambda _1^2\lambda _2 - \lambda _1\lambda _2^2 + \lambda _2^3 -\lambda _2=0$.

• 6. $(x^2 + c_{10} x y^4 + c_9 x y^3 + c_8 x y^2 + c_7 x y + c_6 x + c_5 y^4 + c_4 y^3 + c_3 y^2 + c_2 y + c_1) (y + c_{11}) (y + c_{12}) (x + c_{17} y^4 + c_{16} y^3 + c_{15} y^2 + c_{14} y + c_{13}) (x + c_{22} y^4 + c_{21} y^3 + c_{20} y^2 + c_{19} y + c_{18}) (y^2 + c_{24} y + c_{23})$ In this case, we get a contradiction.

• 7. $(y + c_1) (y + c_2) (x + c_7 y^4 + c_6 y^3 + c_5 y^2 + c_4 y + c_3) (x + c_{12} y^4 + c_{11} y^3 + c_{10} y^2 + c_9 y + c_8) (x y + c_{18} x + c_{17} y^4 + c_{16} y^3 + c_{15} y^2 + c_{14} y+ c_{13}) (x y + c_{24} x + c_{23} y^4 + c_{22} y^3 + c_{21} y^2 + c_{20} y + c_{19})$ We have $\lambda _1=0$.

• 8. $(y + c_1) (y + c_2) (x + c_7 y^4 + c_6 y^3 + c_5 y^2 + c_4 y + c_3) (x + c_{12} y^4 + c_{11} y^3 + c_{10} y^2 + c_9 y + c_8) (x^2 y^2 + c_{24} x^2 y + c_{23} x^2 + c_{22} x y^4 + c_{21} x y^3 + c_{20} x y^2 + c_{19} x y + c_{18} x + c_{17} y^4 + c_{16} y^3 + c_{15} y^2 + c_{14} y + c_{13})$ Here, $\lambda _1=0$ or $\lambda _1^3 -\lambda _1^2\lambda _2 - \lambda _1\lambda _2^2 + \lambda _2^3 -\lambda _2=0$.

• 9. $(y + c_1) (y + c_2) (y + c_3) (x + c_8 y^4 + c_7 y^3 + c_6 y^2 + c_5 y + c_4) (x + c_{13} y^4 + c_{12} y^3 + c_{11} y^2 + c_{10} y + c_9) (x + c_{18} y^4 + c_{17} y^3 + c_{16} y^2 + c_{15} y + c_{14}) (x y + c_{24} x + c_{23} y^4 + c_{22} y^3 + c_{21} y^2 + c_{20} y + c_{19})$ Here, we get a contradiction.

• 10. $(y + c_1) (y + c_2) (y + c_3) (y + c_4) (x+ c_9 y^4 + c_8 y^3 + c_7 y^2 + c_6 y + c_5) (x + c_{14} y^4 + c_{13} y^3 + c_{12} y^2 + c_{11} y + c_{10}) (x + c_{19} y^4 + c_{18} y^3 + c_{17} y^2 + c_{16} y + c_{15}) (x + c_{24} y^4 + c_{23} y^3 + c_{22} y^2 + c_{21} y + c_{20})$ We again get a contradiction.

• 11. $(x^2 + c_{10}xy^4+c_9xy^3+c_8xy^2+c_7xy+c_6x+c_5y^4+ c_4y^3+ c_3y^2 + c_2y + c_1) (y^2+c_{12}y+c_{11})(xy+c_{18}x+c_{17}y^4+c_{16}y^3+c_{15}y^2+c_{14}y+c_{13}) (xy+c_{24}x+c_{23}y^4+c_{22}y^3+c_{21}y^2+c_{20}y+c_{19})$ In this case we obtain $\lambda _1=0$.

• 12. $(x^2 + c_{10}xy^4 + c_9xy^3 + c_8xy^2 + c_7xy + c_6x + c_5y^4 + c_4y^3 + c_3y^2 + c_2y + c_1)(x^2y^2 + c_{22}x^2y + c_{21}x^2 + c_{20}xy^4 + c_{19}xy^3 + c_{18}xy^2 +c_{17}xy + c_{16}x + c_{15}y^4 + c_{14}y^3 + c_{13}y^2 + c_{12}y + c_{11})(y^2 + c_{24}y + c_{23})$ In this case we obtain that either $\lambda _1=0$ or $\lambda _1^3-\lambda _1^2\lambda _2 - \lambda _1\lambda _2^2 + \lambda _2^3-\lambda _2=0$.

• 13. $(x^2+c_{10}xy^4+c_9xy^3+c_8xy^2+c_7xy+c_6x+c_5y^4+c_4y^3+c_3y^2+c_2y+c_1)(x_2+c_{20}xy^4+c_{19}xy^3+c_{18}xy^2+c_{17}xy+c_{16}x+c_{15}y^4+c_{14}y^3+c_{13}y^2+c_{12}y+c_{11})(y^2+c_{22}y+c_{21})(y^2+c_{24}y+c_{23})$ We obtain a contradiction in this case.

• 14. $(y^3+c_3y^2+c_2y+c_1)(x^3+c_{18}x^2y^4+c_{17}x^2y^3+c_{16}x^2y^2+c_{15}x^2y+c_{14}x^2+c_{13}xy^4+c_{12}xy^3+c_{11}xy^2+c_{10}xy+c_9x4c_8y^4+c_7y^3+c_6y^2+c_5y+c_4)(xy+c_{24}x+c_{23}y^4+c_{22}y^3+c_{21}y^2+c_{20}y+c_{19})$ We obtain a contradiction.

• 15. $(y^4+c_4y^3+c_3y^2+c_2y+c_1)(x^4+c_{24}x^3y^4+c_{23}x^3y^3+c_{22}x^3y^2+c_{21}x^3y+c_{20}x^3+c_{19}x^2y^4+c_{18}x^2y^3+c_{17}x^2y^2+c_{16}x^2y+c_{15}x^2+c_{14}xy^4+c_{13}xy^3+c_{12}xy^2+c_{11}xy+c_{10}x+c_9y^4+c_8y^3+c_7y^2+c_6y+c_5)$ We again get a contradiction.

• 16. $(xy^2+c_7xy+c_6x+c_5y^4+c_4y^3+c_3y^2+c_2y+c_1)(x^2y+c_{18}x^2+c_{17}xy^4+c_{16}xy^3+c_{15}xy^2+c_{14}xy+c_{13}x+c_{12}y^4+c_{11}y^3+c_{10}y^2+c_9y+c_8)(xy+c_{24}x+c_{23}y^4+c_{22}y^3+c_{21}y^2+c_{20}y+c_{19})$ In this case we obtain $\lambda _1=0$.

• 17. $(x^3y^3+c_{18}x^3y^2+c_{17}x^3y+c_{16}x^3+c_{15}x^2y^4+c_{14}x^2y^3+c_{13}x^2y^2+c_{12}x^2y+c_{11}x^2+c_{10}xy^4+c_9xy^3+c_8xy^2+c_7xy+c_6x+c_5y^4+c_4y^3+c_3y^2+c_2y+c_1)(xy+c_{24}y^4+c_{23}y^4+c_{22}y^3+c_{21}y^2+c_{20}y+c_{19})$ Here we have $\lambda _1=0$ or $\lambda _1^3 -\lambda _1^2\lambda _2 - \lambda _1\lambda _2^2 + \lambda _2^3 -\lambda _2=0$.

• 18. $(x^2y^2+c_{12}x^2y+c_{11}x^2+c_{10}xy^4+c_9xy^3+c_8xy^2+c_7xy+c_6x+c_5y^4+c_4y^3+c_3y^2+c_2y+c_1)(xy+c_{18}x+c_{17}y^4+c_{16}y^3+c_{15}y^2+c_{14}y+c_{13})(xy+c_{24}x+c_{23}y^4+c_{22}y^3+c_{21}y^2+c_{20}y+c_{19})$ We get $\lambda _1=0$ or $\lambda _1^3 -\lambda _1^2\lambda _2 - \lambda _1\lambda _2^2 + \lambda _2^3 -\lambda _2=0$.

• 19. $(xy+c_6x+c_5y^4+c_4y^3+c_3y^2+c_2y+c_1)(xy+c_{12}x+c_{11}y^4+c_{10}y^3+c_9y^2+c_8y+c_7)(xy+c_{18}x+c_{17}y^4+c_{16}y^3+c_{15}y^2+c_{14}y+c_{13})(xy+c_{24}x+c_{23}y^4+c_{22}y^3+c_{21}y^2+c_{20}y+c_{19})$ In this case we obtain $\lambda _1=0$.

• 20. $(xy^3+c_8xy^2+c_7xy+c_6x+c_5y^4+c_4y^3+c_3y^2+c_2y+c_1)(x^3y+c_{24}x^3+c_{23}x^2y^4+c_{22}x^2y^3+c_{21}x^2y^2+c_{20}x^2y+c_{19}x^2+c_{18}xy^4+c_{17}xy^3+c_{16}xy^2+c_{15}xy+c_{14}x+c_{13}y^4+c_{12}y^3+c_{11}y^2+c_{10}y+c_9)$ We again get $\lambda _1=0$.

• 21. $(x^2y^2+c_{12}x^2y+c_{11}x^2+c_{10}xy^4+c_9xy^3+c_8xy^2+c_7xy+c_6x+c_5y^4+c_4y^3+c_3y^2+c_2y+c_1)(x^2y^2+c_{24}x^2y+c_{23}x^2+c_{22}xy^4+c_{21}xy^3+c_{20}xy^2+c_{19}xy+c_{18}x+c_{17}y^4+c_{16}y^3+c_{15}y^2+c_{14}y+c_{13})$ In this case we obtain that either $\lambda _1=0$ or $\lambda _1^3 -\lambda _1^2\lambda _2 - \lambda _1\lambda _2^2 + \lambda _2^3 -\lambda _2=0$, or $\lambda _1=1, \lambda _2=-1$. Note that the last one is the same as the result of Bai and Xia [2].