Introduction

Integrodifference equations (IDEs) are a modelling framework that describes a population density in continuous space and discrete time by exploring the growth and dispersal processes separately (Kot and Schaffer 1986). They have been successfully used to study the spread dynamics of annual plants (Andersen 1991), populations in a river system (Lutscher et al. 2010), and populations with moving habitats (Zhou and Kot 2011). This approach has also been expanded to consider population interactions such as consumption (Neubert et al. 1995), parasitism (Cobbold et al. 2005), and competition (Li 2018).

In a variety of organisms such as perennial plants, echinoderms (Black and Moran 1991; Tyler and Young 1998), and colonial insects (Hakala et al. 2019), dispersal happens at some stages in their life history, with other stages being more sessile. The IDE framework can be expanded to consider these dynamics by explicitly adding a non-dispersing stage of a population. Such IDE models find that local interactions of these organisms may limit the number of dispersing recruits that are produced, which may lead to a slower spread rate. For example, Cobbold et al. (2005) and Marculis and Lui (2016) found that parasitism of more sessile stages destabilize the spatial distribution of the entire population and reduce the spread rate. In a model of competition of different green crab genotypes (Kanary et al. 2014), an increased sessile adult survival of the entire population leads to an increased spread rate of the top competitor and a decrease in the spread rate of the lower competitor. However, this dynamic has not been previously included in consumer-resource systems, which includes both herbivore–plant and predator–prey interactions.

When considering consumer-resource dynamics in organisms with limited movement, group defense mechanisms may allow resource to become more resistant to consumption. These group defense mechanisms reduce consumption intensity as resource density increases (Dubois et al. 2003). This behavior occurs in various taxa where adults have limited movement. For example, bees produce social waves that repel predators (Kastberger et al. 2008), and kelp provide habitat for predators of their grazers, which induces cryptic behavior in grazers with subsistence off of kelp detritus rather than active grazing (Karatayev et al. 2021). A previous model without stage-dependent dispersal considered the spatial dynamics of a resource using group defense (Venturino and Petrovskii (2013)), where they found oscillatory spatial distributions at high initial resource densities caused by group defense. The potential for group defense to qualitatively affect dynamical outcomes of interacting species raises the question of how group defense in a sessile stage might affect overall spread given dispersive juveniles.

In this paper, we present and analyze an IDE model of the spatiotemporal dynamics of a consumer-resource system where adults have limited movement and resource present group defense. In “Model”, we introduce the model, which is based on the ideas presented by Kanary et al. (2014), and provide a nondimensional version which we will analyze. In “Results”, we analyze two features of the spatiotemporal dynamics: the dispersal-induced instabilities of the resource-only system and the spread rate of resource. Finally, in “Discussion”, we discuss how these results lead to a further understanding of how local interactions affect the spread of organisms.

Model

In this section, we extend an integrodifference model to consider motile, dispersing juveniles and the local interactions between sessile adult stages. A similar extension was previously considered in Kanary et al. (2014), and a formal construction of this model is analogous to that in Arroyo-Esquivel et al. (2022). Consider a region in 1-dimensional space denoted by \(\Omega \subseteq \mathbb {R}\). At each time step m and point in space \(x\in \Omega\), our model follows population densities of consumer \(P_m(x)\) and resource \(N_m(x)\) populations at reproductive age (hereafter adults).

For each population \(i=P,N\), at each time step m, a fraction \(\delta _i\) of the adult population survives to the next time step in the absence of consumption. Consumers consume adult resource following a unimodal, Type IV Holling functional response (Andrews 1968). This functional form, denoted by G(P, N), has an attack intensity of the consumer \(\gamma _N\) and a group defense intensity parameter \(\sigma _N\). With these parameters, the Type IV Holling functional response takes the form:

$$\begin{aligned} G(P,N) =\frac{\gamma _NPN}{1+\sigma _NN}. \end{aligned}$$
(1)

A simple calculation shows that this functional form reaches its maximum consumption intensity at a resource density of \(1/\sqrt{\sigma _N}\). At higher resource densities, the consumption intensity decreases.

Juveniles of both populations disperse following a kernel \(k_i\), for \(i=P,N\), where \(k_i(x,y)\) represents the probability density function of a dispersing individual starting in point \(y\in \Omega\) to arrive at point x. Following dispersal, a fraction of those juveniles survive and become adults at the next time step. Consumers produce juveniles that survive to become adults proportional to their consumption intensity with a factor \(\gamma _P\). Resources produce juveniles by a constant per-capita factor R, where \(R>1-\delta _N\) (i.e., more juveniles are produced than adults die) for population persistence. The fraction of newly setting resource juveniles that survive to become adults depends on local consumer and resource densities. Consumers consume settling resources before they can provide with group defense mechanisms with a constant intensity \(\gamma _S\). Local resources further limit resource settlement through intraspecific competition with intensity \(\beta\). This makes the resource density have a carrying capacity proportional to \(1/\beta\).

These assumptions lead to the system of equations:

$$\begin{aligned} \begin{aligned} P_{m+1}(x)&=\delta _P P_m(x)+\gamma _P\int _\Omega k_P(x,y)\frac{P_{m}(y)N_m(y)}{1+\sigma _N N_{m}(y)^2}dy,\\ N_{m+1}(x)&=\delta _NN_m(x)\exp \left( -\frac{\gamma _N P_m(x)}{1+\sigma _N N_m^2(x)}\right) \\&+R\frac{\exp \left( -\gamma _S P_m(x)\right) }{1+\beta N_m(x)}\int _\Omega k_N(x,y)N_m(y)dy. \end{aligned} \end{aligned}$$
(2)
Table 1 Description of each of the parameters of the model
Full size table

A summary of the parameter’s meanings and dimensions is found in Table 1. To simplify our analysis, we first nondimensionalize the model. We use the same nondimensionalization as in Arroyo-Esquivel et al. (2022). For each m, let \(p_m=\gamma _SP_m,n_m=\beta N_m\). Then, if \(\gamma _p=\gamma _P/\beta ,\) and \(\gamma _n=\gamma _N/\gamma _S,\) and \(\sigma =\sigma _N/\beta ^2\), our nondimensional version of the model is

$$\begin{aligned} \begin{aligned} p_{m+1}(x)&=\delta _p p_m(x)+\gamma _p\int _\Omega k_p(x,y)\frac{p_{m}(y)n_m(y)}{1+\sigma n_{m}(y)^2}dy,\\ n_{m+1}(x)&=\delta _nn_m(x)\exp \left( -\frac{\gamma _n p_m(x)}{1+\sigma n_m^2(x)}\right) \\&+R\frac{\exp \left( - p_m(x)\right) }{1+n_m(x)}\int _\Omega k_n(x,y)n_m(y)dy. \end{aligned} \end{aligned}$$
(3)

Note that we have also changed the indices of \(\delta _i\) and \(k_i\) in order to preserve clarity.

In the case the dispersal dynamics in Eq. 3 are disregarded (by choosing \(k_i(x,y) = \delta (x-y)\) the Dirac delta), our system reduces to that studied in Arroyo-Esquivel et al. (2022):

$$\begin{aligned} \begin{aligned} p_{m+1}&=\delta _p p_m+\gamma _p\frac{p_{m}n_m}{1+\sigma n_{m}^2},\\ n_{m+1}&=\delta _nn_m\exp \left( -\frac{\gamma _n p_m}{1+\sigma n_m^2}\right) +R\frac{\exp \left( - p_m\right) }{1+n_m}n_m. \end{aligned} \end{aligned}$$
(4)
Table 2 Summary of the stability results of the fixed points of Model 4
Full size table

The fixed points of Model 4 and their stability are relevant for the analyses we will perform in “Results”. Here, we present those results, also summarized in Table 2. Model 4 has four fixed points: an unstable extinction fixed point (0, 0), a resource-only fixed point \((0,n^*)\) where \(n^*\) is

$$\begin{aligned} n^*=\frac{R}{1-\delta _n}-1, \end{aligned}$$
(5)

and, when \(\sigma \ne 0\), two coexistence fixed points \((p^\wedge ,n^\wedge )\) and \((p^\vee ,n^\vee )\). The lower coexistence fixed point \((p^\vee ,n^\vee )\) is always unstable, whereas the higher coexistence point \((p^\wedge ,n^\wedge )\) exchanges stability with the resource-only point \((0,n^*)\) via a transcritical bifurcation at the bifurcation value for \(\gamma _p\):

$$\begin{aligned} \gamma _p^*:=(1-\delta _p)\frac{1+\sigma n^{*2}}{n^{*}}. \end{aligned}$$
(6)

The resource-only fixed point is stable when consumer conversion intensity is under a given threshold \(\gamma ^*_p\) (i.e. \(\gamma _p<\gamma _p^*\)) and unstable otherwise. In addition, the positive coexistence fixed point becomes biologically infeasible as it becomes stable as \(p^\wedge\) becomes negative. We can thus say that the positive coexistence fixed point is unstable whenever it is biologically feasible.

In the case the resource-only equilibrium is stable (when \(\gamma _p<\gamma _p^*\)), this stability is global, i.e., all trajectories converge to the equilibrium. In the case there are no stable fixed points (when \(\gamma _p>\gamma _p^*\)), the system converges globally to a quasiperiodic consumer-resource cycle.

Results

Dispersal-induced instabilities

In this section, we explore how dispersal affects the stability of the consumer-resource dynamics by analyzing Model 3. Dispersal can induce instabilities in stable population densities, a mechanism first observed by Turing (1990) and further analyzed by Levin (1974). In the case of IDEs, this mechanism can be analyzed following the linearization process of Neubert et al. (1995). Throughout this section, we assume that the dispersal kernels only depend on the distance between the two points \(x,y\in \Omega\), i.e., \(k_i(x,y) = k_i(x-y)\). We can write Model 3 in the same form as the model presented in Kanary et al. (2014):

$$\begin{aligned} \begin{aligned} p_{m+1}(x)=&P_p(p_m(x),n_m(x))+S_p(p_m(x),n_m(x))\\&\int _\Omega k_p(x-y)R_p(p_m(y),n_m(y))dy,\\ n_{m+1}(x)=&P_n(p_m(x),n_m(x))+S_n(p_m(x),n_m(x))\\&\int _\Omega k_n(x-y)R_n(p_m(y),n_m(y))dy. \end{aligned} \end{aligned}$$
(7)

In addition, we will assume that dispersing juveniles do not die or escape the habitat during the dispersal process, i.e.,

$$\begin{aligned} \int _\Omega k_i(x-y)dx=1 \end{aligned}$$

for both \(i=p,n\). Using this assumption, we linearize the system near a stable equilibrium as follows. Let \((\overline{p},\overline{n})\) be a stable equilibrium of System 4, then if \(p_{m}=\overline{p}+\xi _m,n_m=\overline{n}+\eta _m\), where \((\xi _m,\eta _m)\) is a small perturbation around \((\overline{p},\overline{n})\), we linearize the first equation of System 7 as

$$\begin{aligned} \overline{p}+\xi _{m+1}=&\;P_p(\overline{p},\overline{n})+\left( \frac{\partial P_p}{\partial p_m}\xi _m+\frac{\partial P_p}{\partial n_m}\eta _m\right) \\&+\left( S_p(\overline{p},\overline{n})+\left( \frac{\partial S_p}{\partial p_m}\xi _m+\frac{\partial S_p}{\partial n_m}\eta _m\right) \right) \\&\int _\Omega k_p(x-y)\left( R_p(\overline{p},\overline{n})+\left( \frac{\partial R_p}{\partial p_m}\xi _m+\frac{\partial R_p}{\partial n_m}\eta _m\right) \right) dy. \end{aligned}$$

Multiplying the terms around the integral and disregarding higher-order terms yields

$$\begin{aligned} \begin{aligned}\ xi_{m+1}=&\left( \left( \frac{\partial P_p}{\partial p_m}+R_p(\overline{p},\overline{n})\frac{\partial S_p}{\partial p_m}\right) \xi _m+\left( \frac{\partial P_p}{\partial n_m}+R_p(\overline{p},\overline{n})\frac{\partial S_p}{\partial n_m}\right) \eta _m\right) \\&+\int _\Omega k(x,y) S_p(\overline{p},\overline{n})\left( \frac{\partial R_p}{\partial p_m}\xi _m+\frac{\partial R_p}{\partial n_m}\eta _m\right) dy \end{aligned} \end{aligned}$$

and a similar equation for \(\eta _{m+1}\). Then, given J(F) as the Jacobian matrix of a given function F evaluated at \((\overline{p},\overline{n})\), our linearized system, in matrix form, is

$$\begin{aligned} \begin{aligned} \left( \begin{array}{c} \xi _{m+1}(x) \\ \eta _{m+1}(x) \end{array}\right)&=J\left( \begin{array}{c} P_p+R_p(\overline{p},\overline{n})S_p \\ P_n+R_n(\overline{p},\overline{n})S_n \end{array}\right) \left( \begin{array}{c} \xi _{m}(x) \\ \eta _{m}(x) \end{array}\right) \\ {}&+\int _\Omega K(x,y)J\left( \begin{array}{c} S_p(\overline{p},\overline{n}) R_p \\ S_n(\overline{p},\overline{n}) R_n \end{array}\right) \left( \begin{array}{c} \xi _{m}(y) \\ \eta _{m}(y) \end{array}\right) dy \end{aligned} \end{aligned}$$
(8)

where \(K(x,y)=\hbox {diag}(k_p(x-y),k_n(x-y))\) and the integral represents rowwise integration. To study how dispersal leads to instabilities in the system, let \(\gamma _p<\gamma _p^*\), where \(\gamma _p^*\) is defined by Eq. 6. This makes the resource-only fixed point \((0,n^*)\) to be stable. Thus, let \((\overline{p},\overline{n})=(0,n^*)\). Then, the linearized system (Eq. 8) is

$$\begin{aligned} \begin{aligned} \xi _{m+1}(x)=&\delta _p \xi _m(x)+\int _\Omega k_p(x-y)\frac{\gamma _p n^*}{1+\sigma n^{*2}}\xi _m(y)dy,\\ \eta _{m+1}(x)=&-\left( \frac{\delta _n\gamma _n}{1+\sigma n^{*2}}+\frac{R}{1+n^*}\right) n^*\xi _m(x)+\left( \delta _n-\frac{Rn^*}{(1+n^*)^2}\right) \eta _m(x)\\ {}&+\int _\Omega k_n(x-y)\frac{R\eta _m(y)}{1+n^*}dy. \end{aligned} \end{aligned}$$
(9)

We then take the Fourier transform of Eq. 9. By doing this, our system simplifies to

$$\begin{aligned} \left( \begin{array}{c} \hat{\xi }_{m+1}(\omega ) \\ \hat{\eta }_{m+1}(\omega ) \end{array}\right) =\left( {\textbf {A+KJ}}\right) \left( \begin{array}{c} \hat{\xi }_{m}(\omega ) \\ \hat{\eta }_{m}(\omega ) \end{array}\right) \end{aligned}$$
(10)

where \(\hat{f}\) corresponds to the Fourier transform of a given function f, i.e.,

$$\begin{aligned} \hat{f}(\omega )=\int _{-\infty }^\infty \exp (i\omega x)f(x)dx. \end{aligned}$$
(11)

To properly apply the Fourier transform to the functions \(\xi (x)\) and \(\eta (x)\), we assume that \(\xi (x)=\eta (x)=0\) for \(x\notin \Omega\). The matrices \({\textbf {A,K,J}}\) in Eq. 10 satisfy

$$\begin{aligned} \begin{aligned}{} {\textbf {A}}=&\left( \begin{array}{cc} \delta _p &{} 0 \\ -\left( \frac{\delta _n\gamma _n}{1+\sigma n^{*2}}+\frac{R}{1+n^*}\right) n^* &{} \delta _n-\frac{Rn^*}{(1+n^*)^2} \end{array}\right) \\ {\textbf {K}}=&\left( \begin{array}{cc} \hat{k_p}(\omega ) &{} 0 \\ 0&{} \hat{k_n}(\omega ) \end{array}\right) \\ {\textbf {J}}=&\left( \begin{array}{cc} \frac{\gamma _p n^*}{1+\sigma n^{*2}} &{} 0 \\ 0&{} \frac{R}{1+n^*} \end{array}\right) . \end{aligned} \end{aligned}$$
(12)

Decay of \(\hat{\xi }_m(\omega )\) and \(\hat{\eta }_m(\omega )\) for all \(\omega\) guarantees the decay of \(\xi _m(x)\) and \(\eta _m(x)\), which would imply stability of the carrying capacity equilibrium. The matrix \({\textbf {A+KJ}}\) has a triangular form, and thus, the eigenvalues are

$$\begin{aligned} \begin{aligned} \lambda _1=&\delta _p+\hat{k_p}(\omega )\frac{\gamma _p n^*}{1+\sigma n^{*2}},\\ \lambda _2=&\delta _n-\frac{Rn^*}{(1+n^*)^2}+\hat{k_n}(\omega )\frac{R}{1+n^*}. \end{aligned} \end{aligned}$$
(13)

If both populations disperse following a Laplace kernel with mean dispersal distance \(1/a_i\) for \(i=p,n\),

$$\begin{aligned} k_i(x-y)=\frac{a_i}{2}\exp \left( -a_i|x-y|\right) , \end{aligned}$$
(14)

then the Fourier transform of these kernels is

$$\begin{aligned} \hat{k}_i(\omega )=\frac{a_i^2}{a_i^2+\omega ^2}. \end{aligned}$$
(15)

Note that \(0\le \hat{k}_i(\omega )\le 1\) for all \(\omega\), which implies that if \(\gamma _p<\gamma _p^*\), then \(0<\lambda _1<1\) and \(\lambda _2<1\) for all \(\omega\). For \(\lambda _2\), for any \(R,\delta _n>0\), the inequality \(\lambda _2<-1\) does not have a real solution. This implies that dispersal of a Laplace kernel will not induce instabilities in a resource-only state.

If we choose instead a double-gamma distribution,

$$\begin{aligned} k_i(x-y)=\frac{a_i^2}{2}|x-y|\exp \left( -a_i|x-y|\right) \end{aligned}$$
(16)

for \(i=p,n\), then their Fourier transform is

$$\begin{aligned} \hat{k}_i(\omega )=\frac{a_i^2(a_i^2-\omega ^2)}{(a_i^2+\omega ^2)^2}. \end{aligned}$$
(17)

Similar to in the case of Eqs. 15 and 17 satisfies \(\hat{k}_i(\omega )\le 1\), which implies \(\lambda _1<1\) and \(\lambda _2<1\) for all \(\omega\). Equation 17 has a global minimum of \(-\frac{1}{8}\). If \(\hat{k}_p(\omega )=\frac{-1}{8}\), then we find that \(\lambda _1<-1\) is satisfied when

$$\begin{aligned} \gamma _p>\frac{8(1+\delta _p)(1+\sigma n^{*2})}{n^*}>\gamma _p^* \end{aligned}$$

which implies that \(\lambda _1>-1\) for \(\gamma _p<\gamma _p^*\). If \(\hat{k}_n(\omega )=\frac{-1}{8}\), then the expression \(\lambda _2<-1\) has a solution whenever

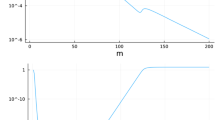
$$\begin{aligned} R>(1-\delta _n)\left( \frac{9}{8}-\frac{1+\delta _n}{1-\delta _n}\right) ^{-1} \end{aligned}$$

provided that \(\frac{9}{8}-\frac{1+\delta _n}{1-\delta _n}>0\) or \(\delta _n<\frac{1}{17}\), and thus, instabilities will only be caused by dispersal for high local resource mortalities. We can compare that, at low local mortalities of resource, the eigenvalue \(\lambda _2\) is almost unchanged as the frequency \(\omega\) changes (Fig. 1a), whereas at high local mortalities, the eigenvalue has a wider range of change and crosses the threshold of \(\lambda =-1\) (Fig. 1b). This suggests that dispersal of resource does not affect its stability when most of the reproductive adults can survive more than one time step.

Fig. 1
figure 1

Values of \(\lambda _2\) in Eq. 13 as the Fourier transform frequency \(\omega\) varies, when \(k_n\) follows the double-gamma distribution kernel (Eq. 16). In these figures, we use \(R=20\), and \(a_n=1\) with two values for resource adult survival: a \(\delta _n=0.9\) and b \(\delta _n=0.01\). Note that, for high resource mortalities (subfigure b), some frequencies of the Fourier transform \(\omega\) produce an eigenvalue \(\lambda _2<-1\), which induces instabilities caused by dispersal

Full size image

The spatial pattern formation presented by these dynamics is in Fig. 2. Even in the presence of instabilities caused by the dispersal of resources, consumers are not able to invade. This shows that although resource density is varying, a low consumer conversion rate (\(\gamma _p<\gamma _p^*\)) makes it impossible for consumers to invade and have any influence over the resource population, making this system essentially a resource-only system.

Fig. 2
figure 2

Distributions of consumers \(p_t(x)\) and resources \(n_t(x)\) after 1000 time steps with an initial distribution being a random perturbation of the uniform distributions \(p_0(x)=0\) and \(n_0(x)=n^*\). In these simulations, we use a double-gamma kernel (Eq. 16) with \(a_n=1\) and \(a_p=5\). The other parameters of the model are \(\delta _p=0.8,\gamma _N=0.1,\sigma =1,R=20,\gamma _p=0.7\), and \(\gamma _p^*\) with two values for consumer adult survival: a \(\delta _n=0.9\) and b \(\delta _n=0.01\). In the case of low consumer mortality (a), the system is unable to escape the fixed point and converges to the uniform distribution of the fixed point \((0,n^*)\). In the case of high consumer mortality (b), the dispersal-induced instabilities cause the resource to fluctuate through space. Even in this case, the low conversion efficiency of \(\gamma _p\) consumers makes the consumer population unable to invade

Full size image

Spread rate of resource

In a general integrodifference framework, the spread rate of a population is calculated by analyzing when the extinction equilibrium of the system (0, 0) becomes unstable (Zhou and Kot (2013)). This also works in the case of a single-population dynamics system with sessile stages (Cobbold and Stana (2020)). In the case of System 3, the extinction equilibrium of resource (0, 0) is always unstable, which implies that the resource is always able to invade when rare. Instead of explicitly calculating the spread rate, we numerically estimate the time it takes for the population to reach a specific population density at a given point in space.

To do this, let \(\Omega =[-L/2,L/2]\) for habitat length L. In addition, let the initial conditions be a constant consumer density \(p_0\) (i.e., \(p_0(x)=p_0\)) and the resource at carrying capacity at a single point at 20% of the length of the habitat (i.e., \(n_0(x)=n^*\delta (x-a)\), where \(\delta (x)\) is the Kronecker delta, and a is the point that represents 20% of the length of \(\Omega\)). We then calculate the time it takes for the resource to reach a population density of 80% its carrying capacity at 80% of the habitat length, i.e., we find the time M that satisfies

$$\begin{aligned} M=\min _m \{n_m(b)=0.8n^*\} \end{aligned}$$
(18)

where b is the point that represents the 80% of the length of the habitat. An example of this procedure is in Fig. 3. In this case, \(M=28\). We then explore how changing different parameters of the model makes these transient times vary.

Fig. 3
figure 3

Distributions of consumers \(p_t(x)\) and resources \(n_t(x)\) at a initial setup and b after 30 time steps. In these simulations, we use a Laplace kernel (Eq. 14) with \(a_n=1\) and \(a_p=5\). The other parameters of the model are \(L=10,\delta _p=0.8,\gamma _N=0.1,\sigma =1,R=20,\gamma _p=0.7\gamma _p^*\), and \(\delta _n=0.9\)

Full size image

The results of these numerical experiments are in Fig. 4. Intuitively, as more consumers are present in the environment (higher initial consumer density \(p_0\) and consumer survival \(\delta _p\)), the time to spread increases, and as more resource juveniles are produced (higher R (h)) and disperse further (higher \(a_n\) (i)), the time to spread decreases. Notice however that too high of a resource dispersal \(a_n\) leads to an increase in the time it takes for the population to reach a high density. This is caused due to a loss of dispersing individuals at the edges of the domain. More surprisingly, increasing adult resource survival (higher \(\delta _n\)) and increasing the attack intensity (\(\gamma _n\)) lead to an increase in this time, and consumer conversion intensity (\(\gamma _p\)) and group defense intensity (\(\sigma\)) have a minimal impact.

To explain these results, note that a higher adult resource survival \(\delta _n\) leads to a higher value of \(n^*\) in Eq. 5. This higher value of \(n^*\) takes longer to be reached, thus making the conditions of Eq. 18 take longer to be satisfied. Although group defense intensity itself did not have an impact over the time it takes for the population to reach carrying capacity on the other side of the domain, group defense explains why the consumption might not have a big impact over the time to spread, which is the case when there is no group defense at offspring production intensities orders of magnitude smaller than when there is group defense (Fig. 5). This is because group defense makes consumption less important at high resource densities, which means the source population at the left of the habitat is not impacted by consumption and allows to source new juveniles that will eventually overcome consumption at a similar density. A similar argument explains the low impact of consumer conversion intensity \(\gamma _p\) over the spread time.

Fig. 4
figure 4

Number of time steps M required for the population to reach 80% of its carrying capacity at 80% of the habitat \(\Omega\) (Eq. 18) when varying a single parameter in Model 3. Unless it’s the parameter being changed, in these simulations, we use a Laplace kernel (Eq. 14) with \(a_n=1\) and \(a_p=5\). The other parameters of the model are \(L=10,\delta _p=0.8,\gamma _N=0.1,\sigma =1,R=20,\gamma _p=0.1\), and \(\delta _n=0.9\)

Full size image
Fig. 5
figure 5

Number of time steps M required for the population to reach 80% of its carrying capacity at 80% of the habitat \(\Omega\) (Eq. 18) when varying the consumer offspring production in Model 3 in the case where there is no group defense. In these simulations, we use a Laplace kernel (Eq. 14) with \(a_n=1\) and \(a_p=5\). The other parameters of the model are \(L=10,\delta _p=0.8,\gamma _N=0.1,\sigma =0,R=20\), and \(\delta _n=0.9\)

Full size image

To make the value M independent of the parameters of the model, we repeat the analysis with an arbitrary threshold that does not depend on any parameters. By choosing such threshold to be equal to 1, in Fig. 6, we observe that resource survival (\(\delta _n\)) does not have a big impact on spread speed, while most of the other parameters have a similar behavior to the one observed in Fig. 4. The most likely unintuitive difference is that consumer survival (\(\delta _p\)) does not affect in any way the ability of the resource to spread to the other side of the domain. However, this makes sense as consumption at low densities is weak, and thus, the main factor affecting spread is how much of the resource is able to survive once settled. This also explains the small decrease in the time M as resource survivability becomes high enough.

Fig. 6
figure 6

Number of time steps M required for the population to reach a density of 1 at 80% of the habitat \(\Omega\) (Eq. 18) when varying a single parameter in Model 3. Unless it’s the parameter being changed, in these simulations, we use a Laplace kernel (Eq. 14) with \(a_n=1\) and \(a_p=5\). The other parameters of the model are \(L=10,\delta _p=0.8,\gamma _N=0.1,\sigma =1,R=20,\gamma _p=0.1\), and \(\delta _n=0.9\)

Full size image

Discussion

In this paper, we explored how local interactions of sessile organisms in a consumer-resource system affect the spread rate of resource. Two main results arise from this exploration: sessile resource adults stabilize the spatial distribution of resource, and group defense leads to a slower spread rate.

We find that, when the consumers cannot invade the resource, and when most adults survive to the next reproduction period (high \(\delta _n\)), these sessile adults stabilize the distribution of resource and prevent the resource carrying capacity to be destabilized by dispersal. This destabilization required a fat-tailed kernel, which leads to accelerated invasions (Kot et al. 1996). These stability results also provide more evidence to the argument that increased dispersal leads to a negative correlation between spatial stability and synchrony in population densities between patches (Abbott 2011).

In the case of resource spread when rare, we found no effect of increasing the group defense intensity (\(\sigma\)) in the spread rate of the resource. However, group defense allows. There is evidence that would suggest group defense should have a negative impact on the spread rate. For example, the decrease in consumption could lead to higher intraspecific competition, which affects juvenile survival (Morin 1986; Wilson 1989) and spread (Oricchio and Dias 2020). However, none of these studies looked at this question in the context of organisms presenting group defense. Another way that group defense might decrease spread rate, not modelled here but biologically feasible, is if resources’ energy investment in group defense reduces energy availability for reproduction (Sasmal and Takeuchi 2020). Our model suggests these impacts are compensated by the reduced effect of increased consumption, which does have an effect when group defense is not included in the model (\(\sigma = 0\)), which explains why \(\sigma\) has no effect on the spread of the population.

Another feature of our model is the implicit inclusion of stage structure in the spatial dynamics. The importance of stage structure in dispersal dynamics was first observed by Hastings (1992) using spatially explicit models with continuous space and continuous time and with discrete space and discrete time. In the case of continuous space and discrete time, previous analyses that expand the IDE framework to consider stages with limited movement also implicitly included stage structure (Kanary et al. 2014; Veit and Lewis 1996). We find a similar general result to those previous analyses, where local interactions in the stages with limited movement affect the spread rate of the population. In our model, intraspecific competition slows down spread, in contrast to competitive systems, where a high survival of adults promotes the spread of the top competitor (Kanary et al. 2014), and analogous to single population dynamics where high mortality of stages with limited movement can lead to an Allee effect which slows spread rates (Veit and Lewis 1996).

As with any model, we made a number of simplifying assumptions in our model. First, we only consider the case where consumers resource upon adult resource or settling juveniles. Growth of species with limited movement as adults such as urchins (Allen 2008) and tunicates (Olson and McPherson 1987) has been linked to the consumption of their dispersing larvae. We suspect dispersing larvae consumption will reduce the impact of local interactions and give more emphasis on the dispersal dynamics. Second, we assume that the dispersing individuals are the juveniles. This assumption does not capture populations where larvae have limited movement ability compared to their adult stages such as a consumer-resource interaction between dragonflies and frogs (Caldwell et al. 1980). We speculate the model that captures those dynamics would have a similar structure to this one, which would imply that juvenile interactions would be the main constraint on of spread dynamics.

Another limitation is that our environment is spatially homogeneous. In reality, spatial heterogeneity may lead to different dynamics than the ones observed in our model. In our model, the only factor that produces habitat heterogeneity for resource is the distribution of consumer population. However, other potential factors of heterogeneity not accounted by our analysis are substratum topography (Erlandsson et al. 2005; Köhler et al. 1999) and resource availability (Grabowska and Kukliński 2016). These factors can be included in our model with spatially variable survival or reproductive functions. This could render our problem intractable, which would require numerical analysis to be well explored.

Finally, we assumed both consumer and resource have limited movement as adults. However, by setting the proportion of sessile adults that survive (\(\delta _i\) for \(i=p,n\)) equal to 0, our model allows only one of the two species to have limited movement as adults. As seen in the dispersal-induced instabilities (“Spread rate of resource”), this is a sufficient condition for instabilities of resource at carrying capacity.

In conclusion, in a consumer-resource system, local interactions between sessile adults are key to determining the ability of resource to spread by limiting their production of offspring through consumption. Similar results were obtained when modelling invasive algae, where the consumption of the substrate in the soil slowed the spread rate of the algae (Britton-Simmons and Abbott 2008). These observations contrast with those seen in competitive models, where competition acts on a more regional scale by allowing the coexistence of competitors in space (Allen et al. 1996) or stopping the invasion front of the higher competitor (Kanary et al. 2014). These models exemplify the use of the IDE framework in a wider range of interactions between species such as perennial plants and animals with limited movement.