Abstract
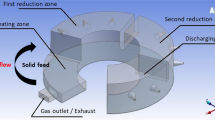
The effect of different lower air inlet tube inclinations on the gas dynamics, including concentration, fluid flow profile, temperature, and heat transfer potency, to the bottom part of a rotary hearth furnace (RHF), were investigated. The lower air-inlet tube inclination was varied from 5° to 25° upwards with the horizontal to maximize the burner efficiency. The inlet tube configuration with the lower two air-inlet tubes inclined at 10° upwards emerged as the most efficient tube orientation in the present burner system. This air inlet configuration of the burner produced the maximum heat transfer efficiency in transferring the combustion heat produced in the freeboard region to the bottom pellet layer region. Moreover, it was also able to produce better CO post-combustion efficiency.











Similar content being viewed by others
Abbreviations
- \(C_{1\varepsilon } ,C_{2\varepsilon } ,C_{3\varepsilon } ,C_{\mu }\) :
-
Constants of standard k-ε model
- C P :
-
Specific heat at constant pressure, J/kg K
- C pm :
-
Average specific heat at constant pressure, J/kg K
- C k :
-
Concentration of gas component k (CO and CO2), moles/m3
- D k :
-
Diffusion coefficient for gas species k (CO and CO2), m2/s
- E :
-
Total energy per unit mass, J/kg
- E a :
-
Activation energy, J/mol
- G b :
-
Production of turbulent kinetic energy by buoyancy, J/m3s
- G k :
-
Production of turbulent kinetic energy by velocity gradient, J/m3s
- g j :
-
Component of gravitational vector in the jth direction, m/s2
- I :
-
Radiation intensity, W/m2 sr
- I b :
-
Black body radiation intensity, W/m2
- I bw :
-
Black body radiation at furnace temperature, W/m2
- I in :
-
Intensity of incoming ray, W/m2 sr
- K :
-
Equilibrium constant
- K eff :
-
Effective thermal conductivity of the pellet, W/m K
- k :
-
Turbulent kinetic energy, m2/s2
- \(k_{{Fe_{x} O_{y} }} ,k_{C}\) :
-
Rate constant which follows the Arrhenius law
- k o :
-
Pre-exponential constant, m2/s
- M :
-
Molecular weight, kg/mol
- \(\overrightarrow {n}\) :
-
Outward normal vector
- P :
-
Total pressure inside the pellet, atm
- \(P_{{CO,CO_{2} }}\) :
-
Partial pressure of CO and CO2.
- p :
-
Pressure, Pa
- Q :
-
Total heat of the reaction \(Q = \sum\limits_{i} {R_{i} \left( { - \Delta H_{i} } \right)}\) Ri represents the reaction rate for the species ‘i’ in mol/m3, and ΔH represents the heat of the ith reaction in J/mole
- R :
-
Universal gas constant, J/mol K
- r :
-
Distance of a point from the centre of the pellet, m
- \(\overrightarrow {r}\) :
-
Position vector, m
- S chem :
-
Source term of heat of chemical reaction, J/m3 s
- S k :
-
Source term of gas species k (CO and CO2) in species transport equation, J/m3 s
- S rad :
-
Source term for heat of radiation, J/m3 s
- Sc t :
-
Turbulent Schmidt number
- \(\overrightarrow {s}\) :
-
Unit direction vector, m
- T :
-
Pellet temperature, K
- T 0 :
-
Initial temperature of pellet, K
- t :
-
Time, s
- u i :
-
Velocity component, m/s
- Y i :
-
Mass fraction of species i
- Y P :
-
Mass fraction of any product species
- Y R :
-
Mass fraction of any reactant species
- \(\beta\) :
-
Coefficient of thermal expansion
- \(\delta_{ij}\) :
-
Kronecker delta
- \(\varepsilon\) :
-
Dissipation rate of turbulent kinetic energy per unit mass, m2/s3
- \(\varepsilon_{w}\) :
-
Wall emissivity
- K:
-
Absorption coefficient, 1/m
- \(\mu\) :
-
Molecular viscosity, kg/m s
- \(\mu_{eff}\) :
-
Effective viscosity, kg/m s
- \(\mu_{t}\) :
-
Turbulent viscosity, kg/m s
- \(v_{i,r}\) :
-
Stoichiometric coefficient for reactant i in reaction r
- \(v_{i,r}^{\prime\prime}\) :
-
Stoichiometric coefficient for product i in reaction r
- ρ :
-
Density, kg/m3
- σ :
-
Stefan-Boltzmann constant, W/m2 K4
- \(\sigma_{k}\) :
-
Turbulent Prandtl number for k in standard k-ε model
- \(\sigma_{\varepsilon }\) :
-
Turbulent Prandtl number for ε in standard k-ε model
References
Chatterjee A 2010 Sponge Iron production by Direct Reduction of Iron Oxide. PHI Learning Private Limited, New Delhi, pp 1–252
Pargeter J K, Hanewald R H and Dombrowski D E 1985 Operating experience at INMETCO and application of the process to the production of DRI. Conservation and Recycling. 8: 363–375
Liu Y, Wen Z, Lou G, Li Z, Yong H Q and Feng X H 2014 Numerical investigation of the effect of C/O mole ratio on the performance of Rotary Hearth Furnace using a combined model. Metall. Mater. Trans. B. 45: 2370–2381
Ishikawa H, Kopfle J, McClelland J and Ripke J 2008 Rotary hearth furnace technologies for iron ore and recycling applications. Arch. Metall. Mater. 53: 541–545
Fruehan R J 2005 New steel making processes: drivers, requirements and potential impact. Ironmaking and Steelmaking. 32(1): 3–8
Halder S and Fruehan R J 2008 Reduction of iron-oxide-carbon composites: Part II. Rates of reduction of composite pellets in a rotary hearth furnace simulator. Metall. Mater. Trans. B. 39(6): 796–808
Otsuka K and Kunii D 1967 Reduction of powdery ferric oxide mixed with graphite particles. J. Chem. Eng. of Japan. 2(1): 46–50
Rao Y K 1971 The kinetics of reduction of hematite by carbon. Metall. Trans. B. 2: 1439–1447
Fruehan R J 1977 The rate of reduction of iron oxides by carbon. Metall. Trans. B. 8: 279–286
Srinivasan N S and Lahiri A K 1977 Studies on the reduction of hematite by carbon. Metall. Trans. B. 8(1): 175–178
Ajersch F 1987 Chemical and physical characteristics affecting the reduction kinetics of iron oxide pellets with solid carbon. Can. Metall. Quart. 26(2): 137–144
Sun S and Lu W K 1999 Building a mathematical model for the reduction of iron ore in ore/coal composites. ISIJ Int. 39(2): 130–138
Shi J and Donskoi E 2005 Modeling the reduction of an iron ore-coal composite pellet with conduction and convection in an axisymmetric temperature field. Math. Comput. Model. 42(1–2): 45–60
Donoskoi E and Mcelwain D L S 2001 Mathematical modeling of non-isothermal reduction in highly swelling iron ore-coal char composite pellet. Ironmak. Steelmak. 28(5): 384–389
Sun K and Lu W K 2009 Mathematical modeling of the kinetics of carbothermic reduction of iron oxides in ore-coal composite pellets. Metall. and Mat. Trans. B. 40(B): 91–104
Saleem S, Mishra S and Roy G G 2020 A simulation study of reduction kinetics for sponge iron production in a rotary hearth furnace. Can. Metall. Q. 59(2): 180–188
Wu Y L, Jiang Z Y, Zhang X X, Wang P and She X F 2013 Numerical simulation of the direct reduction of pellets in rotary hearth furnace for zinc containing metallurgical dust treatment. Int. J. Miner. Metall. Mater. 20(7): 636–644
Liu Y, Su F Y, Wen Z, Li Z, Yong H Q and Feng X H 2014 CFD Modelling of flow temperature and concentration field in a pilot scale Rotary Hearth Furnace. Metall. Mater. Trans. B. 45(B): 251–261
Saleem S and Roy G G 2021 Influence of burner nozzle configuration, and inlet gas composition on combustion, gas dynamics, temperature and concentration profile in a rotary hearth furnace. Ironmak. Steelmak. 48(3): 229–241
Saleem S and Roy G G 2020 Effect of oxygen enrichment on flow field, temperature, and gas concentration profile inside a pilot-scale rotary hearth furnace. Metall. Trans. B. 51(6): 2735–2755
http://hyperphysics.phy-astr.gsu.edu/hbase/Sound/souspe.html
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Sooraj, S., Mishra, S., Kumar, B. et al. Optimization of lower air inlet tube configuration for maximizing burner efficiency based on gas dynamics, and heat transfer potency in a Rotary Hearth Furnace. Sādhanā 48, 65 (2023). https://doi.org/10.1007/s12046-023-02095-2
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s12046-023-02095-2