Abstract
Printing inks typically consist of a functional component dispersed within a low-viscosity resin/solvent system where interparticle interactions would be expected to play a significant role in dispersion, especially for the high-aspect-ratio nanocarbons such as the graphite nanoplatelets (GNPs). Rheology has been suggested as a method for assessing the dispersion of carbon nanomaterials in a fluid. The effects of phase volume of ammonia plasma-functionalized GNPs on a near-Newtonian low-viscosity thermoplastic polyurethane (TPU) resin system have been studied using shear and quiescent oscillatory rheology. At low concentrations, the GNPs were well dispersed with a similar shear profile and viscoelastic behavior to the unfilled TPU resin, as viscous behavior prevailed indicating the absence of any long-range order within the fluid. Particle interactions increased rapidly as the phase volume tended toward maximum packing fraction, producing rapid increases in the relative viscosity, increased low shear rate shear thinning, and the elastic response becoming increasingly frequency independent. The nanoscale dimensions and high-aspect-ratio GNPs occupied a large volume within the flow, while small interparticle distances caused rapid increases in the particle–particle interactions to form flocculates that pack less effectively. Established rheological models were fitted to the experimental data to model the effect of high-aspect-ratio nanocarbon on the viscosity of a low-viscosity system. Using the intrinsic viscosity and the maximum packing fraction as fitting parameters, the Krieger–Dougherty (K–D) model provided the best fit with values. There was good agreement between the estimates of aspect ratio from the SEM images and the predictions of the aspect ratio from the rheological models. The fitting of the K–D model to measured viscosities at various phase volumes could be an effective method in characterizing the shape and dispersion of high-aspect-ratio nanocarbons.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Printed electronics offer the potential for thinner, flexible, and environmentally friendly devices produced by higher-throughput processes with reduced production costs.1 Conductive carbon paste stands out as a promising material due to its low production cost and controllable electronic properties.2 Advantages of carbon include low cost, disposability, chemical inertness, the ability to be modified or functionalized for electrochemical sensors, and the ability to be used as an intercalation material in energy storage.3 These can then be dispersed in a viscous carrier fluid to create inks and coatings for a wide range of applications, including printable electronics, sensors, smart packaging, and active coatings.
Graphite nanoplatelets (GNPs) are high-aspect-ratio graphitic nanocarbons, with a typical thickness of 0.05 μm and diameter of 2.6 μm.4 Good dispersion of high-aspect-ratio nanocarbons is essential for utilizing their enhancement properties.5 However, achieving good dispersion of nanocarbons within a fluid has proven to be difficult5 with the inert,5,6,–7 hydrophobic,5,7 ultra-high interfacial area per volume,8 and highly agglomerated nature of carbon nanomaterials5 leading to a tendency to agglomerate. When atomic motions in neighboring particles drive them together, the van der Waals forces, if not counteracted, will cause particles to adhere upon contact.9,10 Repulsive forces arising from like charges or a protecting moiety on the surface of particles can be large enough and of long enough range to counteract the van der Waals forces to give a colloidally stable suspension.9
Altering the surface chemistry of the carbon nanomaterials is an efficient method for helping to overcome these problems.6 Acid treatments have been used with the aim of adding carboxyl and hydroxyl groups to the surface of carbon nanotubes (CNTs) to improve solubility with common solvents and epoxy resins.5,11 Surfactants have been shown to improve the dispersion of CNTs in polymers and solvents5 and have been used to promote steric repulsion, which forces CNTs far enough apart to prevent agglomeration.11 However, the addition of any polymer to the surface of a particle must be accounted for by increasing the effective particle radius.9,12
Plasma functionalization offers a dry,5 scalable,5,6,13 nonpolluting,6,7,13 fast,7 one-step method of surface modification with the aim of making carbon nanomaterials more hydrophilic by adding polar groups to aid dispersion.5 A wide variety of plasma treatments have been used including O2, NH3, and CF46,13 with an aim to increase the polarity of the surface of CNTs and the overall adhesion of CNTs to the surrounding polymer matrix.6,7,13 Ammonia plasma treatment has been shown to increase the surface nitrogen content on CNTs,5,6,–7 in the form of amine, imine, nitrile, and imide groups.6,7 These plasma-treated CNTs showed higher free surface energy and smaller contact angles with water, attributed to the additional polar hydroxyl, carboxyl, and amide groups on the surface of CNTs5 this increased surface polarity increases chemical affinity to polar resins and solvents and, with it, dispersion. Amine groups attached to CNT walls have even been shown to lead to the formation of covalent bonds with an epoxy resin, improving the interface between the nanotubes and the epoxy.14
Rheology has been suggested as a method for assessing the dispersion of carbon nanomaterials in a fluid, and dispersed nanoparticles will show different rheological behaviors compared to their agglomerated counterparts.11 The viscosity of a particle suspension is largely a function of particle volume fraction, ϕ,8,9,10,–11 particle shape,8,10 interactions between particles,8 particle size distribution,8,9,10,–11,15 suspension structure, surface properties,10,11 adsorbed species,10 and the hydrophilic/hydrophobic nature of the particles/polymer.10 Nanoparticles in a suspension are subject to particle–particle forces, particle–fluid interactions, viscous forces under flow, and Brownian forces.16 For suspensions of colloidal particles, nonhydrodynamic forces such as Brownian, electrostatic, and London–van der Waals forces become significantly important.9,17
Much of the work on the effect of particles on suspension viscosity has focused on noninteracting particles in Newtonian fluids.9,15,17,18 The fundamental work into the effect of particle aspect ratio on suspension viscosity, such as the work by Mueller et al.15 focused on noninteracting, macrosized particles such as glass beads and glitter,15 with aspect ratios much lower than those typically found in carbon nanomaterials. Previous works on the dispersion of carbon nanomaterials using rheology have focused on carbon black (CB),19,20,–21 CNTs,11,16,19 carbon nanofibers (CNFs),19,22 GNPs,23,24 and graphene oxide (GO),16 typically at low volumes and in high-viscosity resin systems used in composite manufacture. The ability to characterize the microstructure and flow properties of dispersions is essential for understanding and controlling their rheological properties.25 The rheology of dispersions is an important processing parameter, and the ability to characterize and understand the effect of GNPs on the fluid viscosity of resin systems is essential in manipulating flow properties to create optimized ink formulations.25
Printing inks typically consist of a functional component dispersed within a resin/solvent system. The resin/solvent systems used in printing inks are typically of much lower viscosity than the resin systems used in melt processing; therefore, interparticle interactions would be expected to play a much more significant role in dispersion, especially for high-aspect-ratio nanocarbons such as the GNPs. Shear and oscillatory rheometry were used to characterize the effect high loadings of high-aspect-ratio nanocarbons have on the rheological properties of a low-viscosity, near-Newtonian resin system for use in inks and coatings. Many of the viscosity suspension models are based on spherical particles, frequently micro sized. This work looks at their applicability to nanodimension high-aspect-ratio platelets.
Method
Materials
Ammonia plasma-functionalized GNPs (Haydale GNP-NH3-STD) and a commercially available thermoplastic polyurethane (TPU) were used.
Ink synthesis
First, 12.5 wt% of TPU was dissolved into diacetone alcohol (Sigma-Aldrich) under mechanical stirring at 70°C to create the resin system. A density of 2.2 g/cm3 was used to calculate the volume of GNPs.4 Four phase volumes (ϕ), ϕ = 0.068, 0.090, 0.114, 0.136 of NH3 GNP were wet in the TPU resin for 24 h. These were then further dispersed using a paint shaker (Minimix MK 4, Merris Development Engineers Ltd.) to ensure good dispersion of the mill base, before being passed through a triple roll mill. Directly following milling, the suspensions were then mixed with the paint shaker to ensure good uniformity throughout the milled ink.
Rheometry
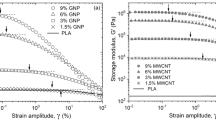
A stress-controlled rheometer (Malvern Kinexus Pro) was used to assess the rheological properties of the fluids. A 40-mm-diameter roughened parallel plate geometry was used to negate the risk of wall slip due to the heavily filled nature of the fluids. A gap of 0.5 mm was found experimentally to minimize wall slip and prevent particles jamming. The temperature was kept constant at 25°C using a Peltier cooling system. A solvent trap was used during rheological characterization to reduce solvent loss from the samples. Diacetone alcohol is often used in inks as it is slow evaporating.26 The materials were first subjected to an up-down shear ramp from 0.01 to 100 (Pa), ensuring consistent preshear of the material with the measurement of instantaneous viscosity taken from the down ramp. Equilibrium viscosity measurements were taken between 0.1 and 100 (s−1). Before quiescent viscoelastic measurements were made, the linear viscoelastic range (LVR) of the materials used was assessed. In the LVR, the viscoelastic parameters, such as G′, are independent of strain or strain amplitude,18 demonstrating that the microstructure of the fluid responds without changing.9 Outside of this region, the microstructure is broken down or built up by the flow. To identify the LVR, strain amplitude sweeps were taken at 0.25, 1, and 10 Hz for the highest and least filled systems, and a complex strain of 1% was selected. The LVR decreased with increasing ϕ as suggested by Barnes.10 A frequency sweep was taken between 0.25 and 10 Hz, allowing for determination of the viscoelastic parameters. The results displayed are a mean of three measurements for each ink.
Analysis
The Solver Add-in in Microsoft Excel was used to fit a curve to the experimental data for the instantaneous viscosity at 1.17 s−1. Generalized reduced gradient (GRG) nonlinear was selected as the solving method with 100,000 iterations using the intrinsic viscosity, [η], and maximum packing (ϕm) as the fitting parameters, as suggested by Mueller et al.15
Results and discussion
Particle characterization
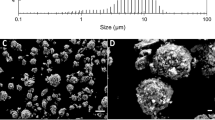
The particle size distribution was estimated by SEM imaging of a screen-printed coating (Fig. 1). There is a wide particle size distribution of the GNPs with platelet diameter ranging from ≈ 1 to 8 μm. The platelets have generally fallen flat to form a paved type structure; however, within this structure are large gaps where the high-aspect-ratio platelets are unable to pack efficiently, with GNPs at various angles relative to the substrate in good agreement to the work on GNP-based inks by Potts et al.27 and the work on graphite composites by Kasgoz et al.19 The thickness of these platelets can be estimated to be ≈ 0.75–100 nm from the platelets which have not fallen flat and whose edges are visible. Three roll milling appears to be an effective technique for initial dispersion of GNPs in a low-viscosity resin system, and as indicated by the absence of any large agglomerates, the dispersion is initially stable over the 24-h period between dispersion and coating.
Rheological characterization
Characterization of the microstructure and flow properties of dispersion is essential for understanding and controlling their rheological properties.25 Established rheological models were fitted to the experimental data to characterize the particles allowing for the prediction of the effect that increasing GNP concentration has upon the suspension viscosity.
The majority of the models for the viscosity of suspensions are derived from Einstein’s equation for the viscosity of dilute suspensions of hard spheres (equation 1). This equation is typically only valid for very dilute suspensions, φ > 0.01 of hard spheres, as it assumes the flow around a particle does not influence the velocity field of any other particle,9,25 and therefore, the flow around each particle can be described by the hydrodynamic equations of motion, with inertia neglected.17 The suspension viscosity is directly proportional to the viscosity of the continuous medium, η0, and is affected by the shape of the particles, represented by the intrinsic viscosity, [η], and the volume of the dispersion, ϕ;
Increases in viscosity with particle loading come from the hydrodynamic disturbance of the flow field as it is diverted around the particles.9,16 When a sphere is pulled out toward a rod or squashed down to a disk, giving higher-aspect-ratio particles, the diversion of the streamlines increases and, with it, the viscous energy dissipation and therefore the viscosity.9,10 In Einstein’s equation, this increase in aspect ratio is represented by an increase in [η].
At higher concentrations, hydrodynamic interactions between particles become increasingly important.25 Batchelor adapted Einstein’s equation to account for hydrodynamic interactions by adding a second-order correction22 (equation 2),
The Einstein–Batchelor equation has been validated for suspensions of hard sphere φ > 0.1.25 Above this point, multiparticle interactions become increasingly important with increasing concentration25 and the above equations tend to fit poorly for concentrated regimes as they assume a finite value for viscosity as ϕ → 1. However, this is unrealistic as the typical maximum packing for monodisperse hard spheres is ϕ = 0.74.15
The more successful models for predicting the viscosity of concentrated dispersions tend to include ϕm as a variable.15 For calculating the viscosity of medium to high concentrations of particles, the Krieger–Dougherty (K–D) equation has been found to be more useful9;
Maximum packing, ϕm, is the point where enough particles have been added for the viscosity to appear infinite.15,18 Maximum packing is a function of particle factors, such as particle shape and particle size distribution, with higher-aspect-ratio particles and narrow particle size distributions being related to lower maximum packing fractions.9,18,25 Maximum packing increases with particle polydispersity as the smaller particles can fit in the gaps between the bigger ones.17,18 This effect of particle size distribution is more pronounced in the concentrated regime, ϕ > 0.50 for spheres, where particle interactions become increasingly important.12,18
Particle asymmetry has a strong effect on [η] and ϕm and hence on the viscosity concentration relationship.18 The zero shear [η] increases with particle aspect ratio as the high-aspect-ratio particles occupy a greater volume in the flow.25 Higher-aspect-ratio particles lead to higher values of [η] and lower values of ϕm as the particles pack poorly and produce greater increases in viscosity for higher-aspect-ratio particles than spheres at the same phase volume.8,18
Flow also affects the maximum packing fraction, especially with high-aspect-ratio particles, with the flow aligning the particles into a more favorable arrangement. This allows them to pack more effectively, causing an increase in maximum packing with increasing shear rate.9,11,18
It was previously found experimentally that the product of ϕm[η] is often around 2,9 and the K–D model is often simplified to the Maron–Pierce model (equation 4). This model was found to be useful for predicting the viscosities of suspensions of fibrous or otherwise irregular particles,12 with Metzner10 describing it as “the best empirical expression for the effect of filler on viscosity.”
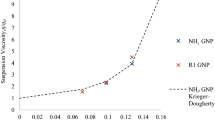
These models were fitted to the experimental data for the NH3 GNP suspensions (Fig. 2). A best fit (R2 = 0.999) was found by fitting the K–D model to the experimental data using an intrinsic viscosity [η] = 6.37 and maximum packing fraction ϕm = 0.151 (Fig. 2), with an especially good fit found at higher phase volumes in agreement with the work on CNFs of Xu et al.11,22 The K–D model slightly overpredicts the viscosity for the most dilute concentration, ϕ = 0.068, as previously seen by Mueller et al.,15 but overall a good fit is obtained.
The intrinsic viscosity [η] = 6.37 is significantly higher than that for submicron spheres [η] = 2.7,18 in agreement with the literature because [η] increases as a sphere is squashed to a disk or elongated to a rod to give higher-aspect-ratio particles.9 There is good agreement with the [η] = 5.40 and ϕm = 0.189 found for graphite by Kasgoz et al.19 with the slightly higher [η] and lower ϕm for the GNPs, likely a consequence of the GNPs nanoscale high-aspect-ratio particles occupying a greater volume in the flow and causing enhanced flow line distortion and particle–particle interaction.
Barnes9,18 proposes a simple model relating the intrinsic viscosity of very high-aspect-ratio disks to the particle aspect ratio (equation 5), where the aspect ratio is defined in such a way that it is always greater than unity.9
Using [η] = 6.37 for GNPs gives a particle aspect ratio of 21.23. This shows good agreement with the technical data sheet where the aspect ratio of the GNPs was in the range of 26–96 and the SEM images where aspect ratio was seen to be approximately 10–100.
The maximum packing fraction ϕm = 0.151 of the GNPs is like the ϕm = 0.189 found for graphite by Kasgoz et al.19; however, this figure is lower than the ϕm = 0.233 found for glass fibers with a similar intrinsic viscosity, [η] = 6.0,18 and the ϕm = 0.343 found for prolate Wollastonite particles, [η] = 6.07, by Mueller et al.15 This disagrees with the trend for lower ϕm with increasing particle aspect ratio [η, 12], as nonspherical particles typically occupy a greater volume in the flow at the same ϕ; therefore, the minimum separation at a given ϕ is lower, and hence, ϕm is also lower.15
Fitting of the Krieger–Dougherty model has been shown as an effective method for assessing the particle aspect ratio and dispersion quality of GNPs in a low-viscosity resin system. The polydisperse nature of the GNP suspensions must be considered as it would lead to lower measured relative viscosities than would be expected for a monodisperse suspension.18 Therefore, the values of [η] and ϕm must be considered as an average and not an exact value, as a monodisperse suspension would be expected to have higher viscosity leading to higher [η] and lower ϕm.
The Maron–Pierce equation also provides a good fit (R2 = 0.967) using a ϕm = 0.205 and is a simpler single variable fit. The ϕm calculated is far lower than the ϕm = 0.680 for smooth spheres, and ϕm = 0.44 for rough spheres,12 and closer to the value of ϕm = 0.18 found for carbon fibers (Ar = 7) by Kitano et al.12 Therefore, it can be concluded that the Krieger–Dougherty model offers the best evaluation of the effect of particles on the suspension viscosity. While the Maron–Pierce model provides an acceptable fit, the assumption that [η]ϕm = 2 does not accurately describe the effect for high-aspect-ratio nanoplatelets, as they show lower maximum packing fraction than would be expected for particles with their aspect ratio. The Einstein–Batchelor (E–B) model provides a poor fit, especially at higher concentrations, as it underestimates the exponential effect of particle additions as ϕ → ϕm predicted in the literature.15
Increasing the concentration of NH3 GNPs increased the viscosity and the amount of non-Newtonian, shear thinning behavior, producing an upwards shift in the viscosity–shear rate curves with the onset of shear thinning behavior moving to lower shear rates in good agreement with the works in the literature on macroscale particles10,12,15 and the work on exfoliated GNPs in high-viscosity melt polymers by King et al.24 (Fig. 3). Viscosity and shear thinning behavior increases with concentration as the volume of GNP in the flow increases, increasing particle–polymer interactions and increasing particle–particle interactions as interparticle distance decreases.
At ϕ = 0.068, 0.091, 0.114 the GNP suspensions show a similar shear profile to the unfilled TPU resin system (Fig. 3). A low-shear-rate Newtonian plateau is visible as Brownian forces overcome shear to maintain a random distribution and orientation of the GNPs despite the increasing shear. This indicates the absence of structure within the fluid with well dispersed GNPs and minimal particle interactions, allowing liquid-like behavior to dominate.
At ϕ = 0.136, there is a large increase in the low shear viscosity with increases in shear thinning behavior across the whole shear range measured, with shear thinning behavior seen even at low shear rates. As shear rates decrease, the fractal nature and high specific area of the GNPs cause them to flocculate to form a weak network of connected interacting particles, causing increases in viscosity as the flocculates trap the continuous phase preventing it from deforming at the same rate as the rest of the matrix. The introduction of structure to the fluid disrupts the random orientation and dispersion of the particles, with Brownian motion less significant for these larger flocculates; therefore, unable to restore the random distribution of the particles, the low-shear-rate Newtonian plateau is replaced by shear thinning behavior.
At higher shear rates, shear forces overcome the random spatial dispersion and orientation of particles to orient the particles and particle structure with the flow, reducing flow line distortion and allowing particles to move more freely over one another reducing the viscosity. Viscosity is higher and shear thinning behavior is greater and occurs at lower shear rates for higher concentrations, as there is a reduction in the typical minimum interparticle distance with increasing concentration, increasing the probability of particle–particle interactions that cause increased viscosity as particles must move out of one another’s way to align with the flow.
The dependence of the shear stress on shear rate can be seen in Fig. 4a. Below ϕ = 0.091, the suspensions show a similar response to the unfilled resin with a near-linear relationship between shear stress and shear rate, as the near-Newtonian properties of the resin dominate. Above φ = 0.114, the curve becomes increasingly convex with concentration as shear thinning behavior increases. Although conventionally plotted on a log–log scale to create a linear relationship, the shear rate/shear stress relationship is also plotted on a linear scale to enable the intercept on the shear stress axis to be clearly identified. All the suspensions show a zero intercept on the shear stress axis indicating the absence of a yield stress (Fig. 4b). Yield stress was previously attributed to the formation of a dense 3D network of particles capable of elastically storing energy.5 The ϕ = 0, 0.068, 0.091 also show a near straight line through the origin indicating near-Newtonian behavior. At higher concentrations, the curve becomes increasingly convex indicating an increase in shear thinning behavior.
Small amplitude oscillatory shear (SAOS) 18,25 is a quiescent measurement of the viscoelastic properties of a material. This viscoelastic response can be split into an in-phase elastic response, G′, and a 90° out of phase viscous response, G′′.9,28 Frequency sweeps are used to identify the time dependent response of a material.25 In a frequency sweep, short times correspond to high frequencies and behavior is dominated by the elastic response, and long times correspond to low frequencies and the viscous behavior dominates.9
Increasing concentration increases G′ at all measured frequencies, as the particles occupy a greater volume within the fluid, which increases particle–polymer interactions as the particle surface area in contact with the suspending fluid increases and increases particle–particle interactions capable of elastically storing energy as interparticle distance decreases. G′ becomes increasingly frequency independent with a low-frequency plateau developing. This is in good agreement with the works on carbon black20,21 (Fig. 4). This low-frequency plateau has previously been attributed to increased network type particle–particle interactions capable of elastically storing energy as interparticle distances decrease.21 This suggests the formation of increased network type interactions11 under periods of slower flow (Fig. 5). This shows good agreement with the shear data (Fig. 3) where shear thinning behavior was observed at low shear rates as a network began to form.
G′′ also increases with ϕ at all concentrations as seen in the literature20; however, the increases are more frequency dependent with linear increases in G′′ with frequency (Fig. 6a). For all phase volumes G′′ > G′, \(G^{\prime } \propto \omega^{2}\), and \(G^{\prime \prime } \propto \omega\), viscous liquid-like behavior dominates. The fluids are in the terminal/viscous zone and have not agglomerated to form a dense 3D network. For the lowest phase volumes G′′ ≫ G′, with a very low measured G′ with this behavior characteristic of a Newtonian fluid as would be expected for a dilute suspension.21
The low concentration ϕ = 0.068, 0.091 suspensions show a similar G′ and G′′ response with increasing frequency as the unfilled resin, further indicating that the particles are well dispersed, as the resin properties dominate.16
These results show good agreement with the proposed qualitative model by Trappe and Weitz21 for the effect of increasing ϕ on network development in carbon black suspensions. Increasing ϕ GNP increases the magnitude of G′ with G′ becoming increasingly frequency independent, while G′′ continues to increase linearly with frequency. They proposed that increasing phase volume increases the magnitude of a purely elastic network, with a frequency-independent G′, interspaced by a purely viscous suspending fluid, where G′′ is linearly dependent on frequency. This suggests an elastic network of GNP particles forming interspaced by the viscous TPU resin system.
A Han plot, a modified form of the Cole–Cole model, can provide insight into the homogeneity of a polymer matrix.29 At ϕ < 0.091, the GNP suspensions show a similar profile to the unfilled resin indicating they are homogenously dispersed, and the flow behavior of the resin dominates (Fig. 6b).29 At ϕ > 0.114, the curve begins to deviate from that of the unfilled and lower volume suspensions at low viscous shear moduli as elastic forces arising from interparticle interaction become increasingly important.
The phase angle, δ, represents the ratio of viscous to elastic forces within the fluid, with a theoretically pure Newtonian fluid having δ = 90 and a Hookean elastic solid having δ = 0. Increasing concentration decreases the phase angle at all measured frequencies as the number of particle–particle and particle–polymer particles capable of elastically storing energy increase (Fig. 7a).
All inks show phase angles > 76 over the measured frequency range, showing that in this range of viscous behavior dominates and liquid-like behavior prevails indicating the absence of structure within the fluid. At the lowest GNP concentrations, ϕ = 0.068, 0.091, the phase angle response to frequency is like the unfilled resin, with a phase angle > 88 at low frequencies showing near-Newtonian behavior with phase angle decreasing with increasing frequency as elastic forces become increasingly important at shorter time scales. The phase angle is higher than the unfilled resin at the highest frequency, probably due to the GNPs interrupting polymer–polymer interactions capable of elastically storing energy.
At ϕ = 0.114 and 0.136, there is a decrease in phase angle starting at approximately 1 Hz for the ϕ = 0.136 ink. G′ became increasingly frequency independent with increasing concentration with a low-frequency plateau developing. This can be attributed to network type particle interactions (Fig. 7a). This network formation causes the ink to show more solid like behavior at shorter times.
At higher frequencies, the phase angle and thus the proportion of elastic forces of all the inks ϕ < 0.136 begin to converge while the ϕ = 0.136 ink maintains a higher proportion of elastic behavior, even at the highest frequencies and therefore shortest times. The van Gurp–Palmen plot presents the phase angle as a function of the absolute complex modulus (Fig. 7b). All curves with phase volume ϕ < 0.091 show a similar shape profile to the unfilled TPU resin system, suggesting the particles are homogenously dispersed throughout the matrix.29 While at the higher phase volumes, especially ϕ = 0.136, the phase angle deviates from the matrix, again showing a reduction in phase angle at lower complex shear moduli, as a result of increased elastic energy storage due to particle–particle interactions.
The complex viscosity calculated from the SAOS measurements is displayed as a function of frequency in Fig. 8. Increasing the GNP concentration increased the complex viscosity at all measured frequencies as GNP–GNP and GNP–TPU interactions increase. Increasing GNP concentration increased the frequency dependency of the suspensions, with the complex viscosity decreasing with frequency. As seen in the elastic shear modulus, G′ (Fig. 5) and the phase angle, δ (Fig. 7a) at low frequencies, and therefore long times, the interparticle interactions increase and give increased viscosity.
The complex viscosity, η*, as a function of angular frequency, ω, can be related to the shear viscosity, η, as a function of shear rate, \(\dot{\gamma }\), using the Cox–Merz rule (equation 6)29
The Cox–Merz rule is used for the GNP suspensions in Fig. 9. At low phase volumes, ϕ < 0.091, the complex viscosity shows good correlation with the shear viscosity. However, with increasing GNP concentration, the shear viscosity curve increasingly deviates from that of the complex viscosity, which was previously suggested to be due to the formation of a solid-like structure within the suspension.29
The nanoscale dimensions of the GNPs lead to decreased interparticle distances than would be found for larger particles. The high particle aspect ratio, Ar = 21.23, indicated by the high intrinsic viscosity [η] = 6.37, mean that the GNPs occupy a large volume within the flow. These factors combine to indicate that particle interactions increase rapidly as ϕ → ϕm, causing rapid increases in viscosity. These increased particle interactions can be seen by the large increases in viscosity, the development of low shear rate shear thinning, and the development of the low-frequency plateau in G′ in the ϕ = 0.136 suspension, as the GNPs begin to interact to form a network of particles. These high levels of particle interactions lead to lower maximum packing fractions. In general, flocs are not tightly packed, giving a larger effective particle radius.11 These flocs pack less effectively leading to relatively low values of ϕm considering the particle aspect ratio. This poor packing ability can be seen in the SEM images where particles are lying at various angles relative to the substrate with GNP free gaps visible within the coating.
Conclusions
The effects of phase volume of ammonia plasma-functionalized GNPs, a high-aspect-ratio nanocarbon, on a near-Newtonian low-viscosity thermoplastic polyurethane resin system has been studied using shear and quiescent oscillatory rheology.
SEM imaging showed the polydisperse nature of the GNPs following dispersion with a typical size of 1–8 μm and thickness of 0.75–100 nm. This would give the particles a range of aspect ratios between 10 and 100 nm. The GNPs have dimensions within the nanoscale, which shows that they have been well dispersed following three roll milling.
Established rheological models were fitted to the experimental data to model the effect of high-aspect-ratio nanocarbon on the viscosity of a low-viscosity system. Using the intrinsic viscosity, [η], and the maximum packing fraction, ϕm, as fitting parameters, the Krieger–Dougherty (K–D) model provided the best fit (R2 = 0.999) with values of [η] = 6.37 and ϕm = 0.151. From these parameters, it was estimated that the GNPs had an aspect ratio of approximately 21.23, proving three roll milling is an efficient method for dispersing GNPs. There was good agreement between the estimates of aspect ratio from the SEM images, Ar = 13–106, and the predictions of the aspect ratio from the rheological models, Ar = 21.23. Therefore, the fitting of the K–D model to measured viscosities at various phase volumes could be an effective method in characterizing the shape and dispersion of high-aspect-ratio nanocarbons.
At low concentrations, ϕ = 0.068, 0.091, and 0.114, the GNPs were well dispersed with a similar shear profile and viscoelastic behavior to the unfilled TPU resin, as viscous behavior prevailed indicating the absence of any long-range order within the fluid. Particle interactions increased rapidly as ϕ → ϕm as indicated by rapid increases in the relative viscosity, increased low shear rate shear thinning, and G′ becoming increasingly frequency independent in the ϕ = 0.136 suspension. This is because the nanoscale dimensions and high-aspect-ratio GNPs occupy a large volume within the flow with small interparticle distances that cause rapid increases in the particle–particle interactions to form flocculates that pack less effectively to give a low value of ϕm.
References
Hatala, M, Gemeiner, P, Hvojnik, M, Mikula, M, “The Effect of Ink Composition on the Performance of Carbon-Based Conductive Screen Printing Inks.” Journal of Materials Science: Materials in Electronics, 30 1034–1044 (2019)
Hua, C, Li, X, Shen, L, Lei, H, Guo, X, Liu, Z, Kong, Q, Xie, L, Chen, C-M, “Influence of Co-Solvent Hydroxyl Group Number on Properties of Water-Based Conductive Carbon Paste.” Particuology, 33 35–41 (2017)
Phillips, C, Al-Ahmadi, A, Potts, S-J, Claypole, T, Deganello, D, “The Effect of Graphite and Carbon Black Ratios on Conductive Ink Performance.” Journal of Materials Science, 52 9520–9530 (2017)
Haydale Graphene Industries, “HDPlas Technical Data Sheet,” [Online]. Available: https://www.graphene-info.com/files/graphene/HDPlas-GNP-Technical-Sheet-2.03.pdf. [Accessed 14 2 2018].
Williams, J, Broughton, W, Koukoulas, T, Rahatekar, SS, “Plasma Treatment as a Method for Functionalising and Improving the Dispersion of Carbon Nanotubes in Epoxy Resins.” Journal of Materials Science, 48 1005–1013 (2013)
Felten, A, Bittencourt, C, Pireaux, J, Van Lier, G, Charlier, J, “Radio-Frequency Plasma Functionalisation of Carbon Nanotube Surface O2, NH3, and CF4 Treatments.” Journal of Applied Physics, 98 074308 (2005)
Saka, C, “Overview on the Surface Functionalization Mechanism and Determination of Surface Functional Groups of Plasma Treated Carbon Nanotubes.” Critical Reviews in Analytical Chemistry, 48 (1) 1–14 (2018)
Rueda, MR, Auscher, M-C, Fulchiron, R, Perie, T, Martin, G, Sonntag, P, Cassagnau, P, “Rheology and Applications of Highly Filled Polymers: A Review of Current Understanding.” Progress in Polymer Science, 66 22–53 (2017)
Barnes, HA, A Handbook of Elementary Rheology. University of Wales Institute of Non-Newtonian Fluid Mechanics, Aberystwyth (2000)
Barnes, HA, A Review of the Rheology of Filled Viscoelastic Systems. British Society of Rheology Review (pp. 1–36) (2003)
Litchfield, DW, Baird, DG, The Rheology of High Aspect Ratio Nano-particle Liquids. British Society of Rheology Review (pp. 1–60) (2006)
Metzner, A, “Rheology of Suspensions in Polymeric Liquids.” Journal of Rheology, 29 739–775 (1985)
Utegulov, Z, Mast, D, He, P, Donglu, S, Gilland, R, “Functionalization of Single-Walled Carbon Nanotubes Using Isotropic Plasma Treatment: Resonent Raman Spectroscopy Study.” Journal of Applied Physics, 97 104324 (2005)
Gojny, F, Nastalczyk, J, Roslaniec, Z, Schulte, K, “Carbon Nanotube-Reinforced Epoxy-Composites: Enhanced Stiffness and Fracture Toughness at Low Nanotube Loading.” Composites Science and Technology, 64 2363–2371 (2004)
Mueller, S, Llewellin, E, Mader, H, “The Rheology of Suspensions of Solid Particles.” Proceedings of the Royal Society A, 466 1201–1228 (2010)
Cassagnau, P, “Linear Viscoelasticity and Dynamics of Suspensions and Molten Polymers Filled with Nanoparticles of Different Aspect Ratios.” Polymer, 54 4762–4775 (2013)
Jeffrey, D, Acrivos, A, “The Rheological Properties of Suspensions of Rigid Particles.” AIChE Journal, 22 (3) 417–432 (1976)
Barnes, HA, Hutton, JF, Walters, K, An Introduction to Rheology. Elsevier Science Publishers, Amsterdam (1989)
Kasgoz, A, Akin, D, Ayten, AI, Durmus, A, “Effect of Different Types of Carbon Fillers on Mechanical and Rheological Properties of Cyclic Olefin Copolymer (COC) Composites.” Composites Part B: Engineering, 66 126–135 (2014)
Amari, T, Uesugi, K, Hiroaki, S, “Viscoelastic Properties of Carbon Black Suspension as a Flocculated Percolation System.” Progress in Organic Coatings, 31 171–178 (1997)
Trappe, V, Weitz, D, “Scaling of the Viscoelasticity of Weakly Attractive Particles.” Physical Review Letters, 85 (2) 449–452 (2000)
Xu, J, Chatterjee, S, Koelling, KW, Wang, Y, Bechtel, SE, “Shear and Extensional Rheology of Carbon Nanofibre Suspensions.” Rheological Acta, 44 537–562 (2005)
Oxfall, H, Ariu, G, Gkourmpis, T, Rychwalski, R, Rigdahl, M, “Effect of Carbon Black on the Electrical and Rheological Properties of Graphite Nanoplatelets/Poly(Ethyl-Butyl-Acrylate) Composites.” eXPRESS Polymer Letters, 9 (1) 66–76 (2015)
King, J, Via, M, Morrison, FA, Wiese, K, Beach, E, Cieslinski, M, Bogucki, G, “Characterization of Exfoliated Graphite Nanoplatelets/Polycarbonate Composites: Electrical and Thermal Conductivity, and Tensile, Flexural, and Rheological Properties.” Journal of Composite Materials, 46 (9) 1029–1039 (2011)
Willenbacher, N, Georgieva, K, “Rheology of Disperse Systems.” In: Product Design and Engineering, pp. 7–49 (2013)
Leach, R, Pierce, R, The Printing Ink Manual. Kluwer Academic Publishers, Dordrecht (1999)
Potts, S-J, Lau, YC, Dunlop, T, Claypole, T, Phillips, C, “Effect of Photonic Flash Annealing with Subsequent Compression Rolling on the Topography, Microstructure and Electrical Performance of Carbon-Based Inks.” Journal of Materials Science, 54 8163–8176 (2019)
Claypole, J, “Application of Advanced Rheometric Techniques to Printing Fluids.” Swansea University Thesis, 2015
Kim, YH, Kwon, SH, Choi, HJ, Choi, K, Kao, N, Bhattacharya, SN, Gupta, RK, “Thermal, Mechanical and Rheological Characterization of Polylactic Acid/Halloysite Nanotube Nanocomposites.” Journal of Macromolecular Science, Part B, 55 (7) 680–692 (2016)
Acknowledgments
Funding was provided by Engineering and Physical Sciences Research Council (Grant No. EP/l015099/1), the European Social Fund via the Welsh Government and Haydale Graphene Industries. The authors acknowledge the assistance of Sarah-Jane Potts for the SEM images.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Claypole, A., Claypole, J., Holder, A. et al. Rheology of high-aspect-ratio nanocarbons dispersed in a low-viscosity fluid. J Coat Technol Res 17, 1003–1012 (2020). https://doi.org/10.1007/s11998-020-00319-2
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11998-020-00319-2