1 Introduction

Today’s increasingly automated and interconnected world is characterized by continually emerging challenges, ever-changing professions, and the enduring quest for new solutions (Barak, 2009; OECD, 2014). Future citizens will be required to not only use their knowledge in standard problems but to look for creative solutions—creative mathematical solutions, in particular (Clements, 2013). Another feature of contemporary life is that knowledge tends to be more and more specialized. Correspondingly, it becomes increasingly important for people from different disciplines and with different backgrounds to bring their expertise together and to seek new, creative solutions collaboratively. In short, “collaboration, along with creativity, is considered an important skill for the twenty-first century” (Molad et al., 2020, p. 202).

Mathematics educators aim to foster students’ mathematical creativity. Students should not only be able to solve problems routinely or with a fixed set of heuristics, generic rules that help “in solving a range of non-routine problems” (Mousoulides & Sriraman, 2014, p. 253); students should also be able to work creatively with mathematics (Silver, 1997), to think outside the box, make new connections, and have so-called Aha! moments. Accordingly, mathematics education research has increasingly focused on mathematical creativity (e.g., Leikin & Pitta-Pantazi, 2013; Sheffield, 2013; Singer, 2018).

Most of the studies addressing students’ mathematical creativity focus on individual students. Often, multiple solution tasks (MSTs; Leikin, 2009) are used. Students are asked to solve the MSTs in as many ways as possible, based on the assumption that “solving mathematical problems in multiple ways is closely related to personal mathematical creativity” (Leikin & Lev, 2013, p. 185). Researchers investigate the outcomes of the individual creative process, the solutions of MSTs (product view), or, more recently, the creative process itself, for example, the phases of the creative process (process-view) (see Pitta-Pantazi et al. 2018).

Schindler and Lilienthal (2020) conducted an explorative case study with a single student working on an MST and—using eye-tracking together with eye-tracking stimulated recall interviews (SRIs)—identified phases of the creative process (see Fig. 1). Four main phases were found, as follows (1) Looking for a start: This phase is about trying to identify different approaches to the MST that afford novel solutions. It may be guided by heuristics such as looking for symmetries. (2) Idea/intuition: In this phase, students get an idea or intuition about how the problem can be solved. This can be connected to so-called Aha! moments accompanied by sudden certainty and affective responses, such as excitement. (3) Working further, step by step: After having an intuition about how to approach the problem, this phase includes the reasoning of working out a solution in problems that require certain reasoning steps. It also includes verification processes of the steps in reasoning. (4) Finding a solution/discarding the approach: Finally, the ‘working further, step-by-step’ phase may lead to finding a solution, confirmed by a final verification, or to discarding the approach, for example, when students consider their approach too similar to a previous one.

Fig. 1
figure 1

Phases of the creative process of a single student (see Schindler & Lilienthal, 2020)

Full size image

Yet, what does the creative process look like in collaborative work, and what are its phases? Despite the need in today’s world for collaboration and collaborative creative work (Levenson, 2011), students’ collaborative creative work in mathematics has rarely been studied. Yet, for educators to support students’ collaborative creative work and to foster their ability to work together creatively, it is important to know how ideas come up, how the students take turns, and what phases are involved in collaborative creative work in mathematics. Whether the creative process has similar phases in collaborative work and in solo work has not yet been investigated, nor has whether there are other phases and if the phases of the process are more volatile or similar. The aim of this paper is to explore the creative process of students as they work on an MST collaboratively. We asked the research question, what phases does the collaborative creative process of students working on an MST include?

To pursue this research question, we conducted an explorative case study, where two students jointly worked on an MST. Methodically, we drew on Schindler and Lilienthal’s (2020) work, using a similar design—eye-tracking together with eye-tracking SRI—and we extended it from solo to partner work, where two students worked on an MST together, both wearing eye-tracking glasses, and both were interviewed in a subsequent eye-tracking SRI. We traced the collaborative creative process of the dyad, worked out its phases inductively, and we here present a tentative model of their creative process, which we finally compare to the one developed for individual students (Schindler & Lilienthal, 2020).

2 Mathematical creativity

Although the significance of creativity is widely acknowledged and an increasing interest in mathematical creativity education is evident (Clements, 2013; Leikin & Pitta-Pantazi, 2013; Sheffield, 2013; Singer, 2018), there is no commonly accepted conceptualization nor a commonly accepted definition of mathematical creativity as of yet (Leikin, 2009). Correspondingly, creativity is conceptualized in diverse ways in mathematics education research. Similar to “big-C Creativity”, which models extraordinary or absolute creativity expressed in outstanding contributions by eminent figures (Wallas, 1926), the term “little-c creativity” is used in mathematics education (e.g., Sriraman et al., 2014) to denote relative or personal creativity of non-professional mathematicians, including school-age students (Schindler et al., 2018; Sheffield, 2018).

2.1 Multiple solution tasks

Creativity is considered to be key for the ability to discover unique and diverse ideas (Guilford, 1967), and it is understood as comprised of four aspects, namely fluency (the ability to generate many solutions), flexibility (the ability to find a wide variety of solutions), originality (the ability to come up with unique solutions), and elaboration (the level of detail with which the solutions are elaborated). Studies investigating students’ creativity in mathematics education often use MSTs. The concept of MST was introduced in mathematics education by Leikin (2009) based on Torrance Tests of Creative Thinking (Torrance, 1974). Students are asked to solve MSTs in multiple ways, using different properties, theorems, representations, or relationships (Leikin, 2009). Often, students’ written products are then evaluated (e.g., Levav-Waynberg & Leikin, 2012) since the ability to produce different solutions is considered to reflect personal mathematical creativity (Leikin & Lev, 2013).

While a focus on written solutions of MSTs has been useful, this focus on the product cannot, in principle, help researchers to discern the creative process in detail. However, better to understand how to support students in their creative work, it is important to look closely into the creative process (Leikin & Pitta-Pantazi, 2013). Accordingly, researchers have started to take a process-focused view on creativity and to investigate the creative process itself (see Pitta-Pantazi et al. 2018).

2.2 The creative process and its phases

In the few studies that address the creative process, stage models are prominent (see Pitta-Pantazi et al. 2018). Such models often build on Wallas’ (1926) four-stage model of creativity, which includes the stages preparation, incubation, illumination, and verification. However, this model was developed for eminent, professional mathematicians, and even though it has been applied to describe relative creativity processes of school-age students as well (e.g., Sitorus & Masrayati, 2016), it is arguable whether it is apt for this purpose (Haavold & Birkeland, 2017) since in students’ creative work on MSTs, for example, the working time is much shorter, which may well affect incubation and the nature of illumination.

Because of these issues and the lack of a model of students’ creative work on MSTs, Schindler and Lilienthal (2020) conducted a study with the aim of exploring the process of working on MSTs. Based on a case study of a student individually working on an MST, using eye-tracking and eye-tracking SRI, they inductively identified and found four main phases of the creative process (see description in Introduction, Fig. 1): (1) Looking for a start, (2) Idea/intuition, (3) Working further, step by step, and (4) Finding a solution/discarding the approach. Interestingly, they found signs of what they called ‘mini-incubation’: Moments when the student’s mind, while doing something else, reached some insight into other approaches for the problem. For example, the student realized a mistake in a previous approach while working on another one. That means that although he had already finalized the previous approach, something in his mind triggered him to go back to this approach. Also, the fact that the student found new approaches while he was working on other ones might be an indication of ‘mini-incubation’ (see Schindler & Lilienthal, 2020, for more detail).

In this study, in line with that of Schindler and Lilienthal (2020), we regarded students’ process of working on an MST as a creative process, where often “students have intuitions, or illuminations, a certain excitement about having figured something out, and sudden certainty and insight” (p. 1582). In MSTs, students are asked to solve a problem in as many ways as possible, which is based on the theoretical assumption that “solving mathematical problems in multiple ways is closely related to personal mathematical creativity” (Leikin & Lev, 2013, p. 185). We have detected a hesitancy among researchers in mathematics education research about whether solving a problem in multiple ways is a creative activity. However, previous research indicates that students working on MSTs develop different intuitions and have illuminations, together with excitement, sudden certainty and insight, elements that are at the heart of making the process creative (Schindler & Lilienthal, 2020). In our study, we did not intend to investigate or qualify whether the students’ process working on an MST is creative or not; rather, we regarded the work on an MST as a creative process and intended to explore its phases.

2.3 Creativity and collaboration

In our conceptualization of collaboration, we follow scholars such as Dillenbourg (1999), and Roschelle and Teasley (1995), and draw on Seidouvy’s (2019) definition of collaboration: “Collaboration is regarded as a dynamic process in which the group members work jointly on the same problem. It conveys the idea of a coordinated and mutual effort by the group members in order to solve a task together” (p. 44). We consider collaborative work to be student-centered in a way that the group members are principal architects of their joint efforts; they are not assigned different roles or tasks (Seidouvy, 2019). Accordingly, in this case study, we considered the students’ process of jointly working on the MST a collaborative creative process in mathematics.

Previous research has partially investigated group work with MSTs; however, the aim has not yet been to investigate the phases of the process. Rather, researchers investigated the effects of group work on the students’ creative work. Molad et al. (2020) investigated post-high school students working on geometry MSTs, individually and in small groups. They reported positive effects of group work on fluency and flexibility but no significant differences regarding originality. Among other findings, they saw that students who worked in a group also showed significantly greater fluency and flexibility when later working alone. Levenson (2011), who introduced the term collective mathematical creativity, investigated student interactions in three classes of elementary school students’ regular whole-class discussions when novel ideas were picked up, developed, and verified by the class (including the respective teachers). Levenson identified processes that can be involved when students work creatively together, such as “a certain adaptation of previous solutions” (p. 229) or that the presentation of an intuition, working on it further and expanding it, and verifying it, may be carried out by different students who each contribute. Levenson also found that presenting or working on one solution can create the foundation on which an intuition about another solution develops in another student. Levenson’s study offers promising insights into students’ collaborative work on MSTs, and it indicated that “a more comprehensive study, involving student […] interviews, would most likely lead to greater insights into the processes of collective mathematical creativity” (p. 233). In our work, we followed up on this conclusion.

2.4 Eye tracking and eye-tracking stimulated recall interviews in mathematics education

Eye tracking—the recording of eye movements—has gained increasing significance in mathematics education research in recent years (Andrá et al., 2015; Schindler & Lilienthal, 2019). Since around 2014, the number of studies using eye tracking in mathematics education has increased (Schindler, 2021) with the studies covering a variety of topics, including different mathematical content domains such as arithmetic, algebra, functions, geometry, statistics and probability, as well as different mathematical processes such as reasoning, problem solving, and modelling (see Lilienthal & Schindler, 2019; Schindler, 2021; Strohmaier et al., 2020). Eye tracking allows for a recording of spatio-temporal sequences of gaze points that indicate visual attention. The connection between gaze and visual attention exists due to the anatomy of the human eye, where sharp vision is possible only in a small area of the retina, called the fovea (Holmqvist et al., 2011). Only when the light entering through the pupil falls directly onto this area can objects be perceived sharply. Therefore, eye tracking captures foveal, overt attention (Carrasco, 2011; Posner, 1980).

Previous research on students’ work in the field of geometry investigated the potential that eye tracking may have for gaining insights into students’ thought processes and reasoning (Schindler & Lilienthal, 2019). The results indicated that eye tracking offers various opportunities, but also that students’ eye movements can be ambiguous (Schindler & Lilienthal, 2019). For example, looking back and forth between two corners of a diagram can indicate that the student is envisioning a line between the corners, comparing the angles at the corners, comparing the adjacent areas through peripheral vision, or something else. Schindler and Lilienthal (2019) concluded that eye-tracking SRI can be a useful addition to eye-tracking data if students’ thought processes or reasoning in the domain of geometry are studied. In eye-tracking SRI, the students are invited to recall their thoughts based on an eye-tracking video of their work on the task, where their gaze is visualized as a dot wandering around in the video of the scene. Schindler and Lilienthal (2020) used eye tracking and SRI in a case study to investigate the creative process of a student working on an MST. They concluded that “even though ET SRI has certain risks to be taken into account, our study illustrated that this method may help researchers to get closer insights into complex reasoning processes and thoughts. These thoughts can be quick, sophisticated, complex, affective, or intuitive, which may make them difficult to express by school students in thinking aloud protocols only” (p. 1583). Finally, using this design, they were able to trace the creative process and to work out its phases inductively. In this paper, we report on a study that builds on this work and uses DUET SRI for a pair of students working on an MST.

3 Method

3.1 Participants and task

To inquire into the collaborative creative process, we conducted an explorative, qualitative case study investigating the collaborative creative process of two graduate education students, Helen and Ilias (pseudonyms).

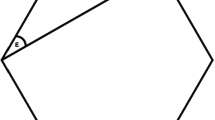
The students worked collaboratively on a geometry MST: They were asked to infer, in as many ways as possible, the angle size of ℇ (Fig. 2) in a regular hexagon (which is 30°). We used this particular MST since it had been proven to give rich results in previous studies and to be suitable for eye-tracking studies (Schindler & Lilienthal, 2020; Schindler et al., 2018).

Fig. 2
figure 2

Hexagon MST

Full size image

Both Helen (23 years old) and Ilias (29 years old) were in the teacher education program, with a focus on special education. They participated in this study voluntarily. Both were in the first year of the Master’s program, which is a required part of the teacher education program in Germany, and they had finalized their bachelor’s degree with good to average grades. Both students studied mathematics for primary school education as a school subject. In their previous university studies, they had participated in a mathematics course on Euclidean geometry and a didactics course on geometry, yet they had not learned about mathematical creativity or giftedness in their course work.

3.2 Eye tracking and stimulated recall interviews

3.2.1 Eye tracking

Our study was a dual eye-tracking study, which means “simultaneously tracking two people’s visual behaviors as they work on the same display (dual eye-tracking, DUET)” (Shvarts & Abrahamson, 2019, p. 1–2; see Lilienthal & Schindler, 2017, for portable, dual eye-tracking). In our study, both students wore eye-tracking glasses. This allowed us to observe the students working with pen and paper without strongly limiting head and body movement, while at the same time allowing us to track the gaze, even during moments when the students looked away from the task sheet, such as when they made eye contact. The eye-tracking glasses, Tobii Pro Glasses 2, were relatively unobtrusive for the participants, due to the low weight of the glasses (45 g) and the pocket-sized, rather lightweight recording unit (315 g). They are comparatively easy to operate and come with a high-resolution, wide-angle scene camera, four ‘eye cameras’ tracing eye movements, and a microphone for synchronized sound recording. The scene camera allows HD recordings of the participants’ visual fields with a resolution of 1920 × 1080 pixels and a field of view of 82° (horizontal) × 52° (vertical). The eye cameras, in combination with near-infrared illumination, track eye movements at a sampling rate of 50 Hz. Under good lighting conditions, the gaze estimation accuracy is reported to be below 1° for small gaze angles (less than 15°) but can be up to 3° for large gaze angles (more than 15°; Tobii, 2017). Prior to the students’ work on the MST, both glasses were calibrated through a one-point-calibration procedure detailed by Tobii. The glasses were each connected to a recording unit, which the students wore on their bodies (Fig. 3). The recording units were connected to one computer each, which was operated by one researcher each (the first and second authors of this article, Fig. 3). The students were not able to see the computers while working on the MST since the computers were placed behind them. The cables, which were at the students’ backs, were not disruptive.

Fig. 3
figure 3

Sketch of the experimental setup for eye-tracking data collection

Full size image

3.2.2 Stimulated recall interviews using eye-tracking video as stimulus

The key motivation behind carrying out SRIs is the promise that “cognitive processes can be investigated by inviting subjects to recall, when prompted by a video sequence, their concurrent thinking during that event” (Lyle, 2003, p. 861). As stimulus, we used the eye-tracking videos of the students’ collaborative work on the MST (e.g., Helen saw her own eye-tracking video). These videos show the scene view of the particular student (i.e., what the students looked at in the experiment, including their gestures, writing, drawing, and audio), overlaid with a gaze circle. By providing a rich, interwoven web of visual, audio, gestural, and motion context, together with an indication of the visual focus, such eye-tracking videos serve as particularly strong stimulus for SRI (Schindler & Lilienthal, 2020), and allow for a deep level of recall (Stickler & Shi, 2017). Recalling thoughts is also facilitated by a short duration between the event, the collaborative creative work on an MST, and the interview itself. We minimized the intermediary time and started with the SRIs a few minutes after the students had finalized their work on the MST. During the SRIs, the students and interviewers watched the eye-tracking video. At the beginning of the interviews, the interviewers briefly explained what eye-tracking videos are and how the students could identify their gaze. They were then told that they would watch the video together with the interviewer and were invited to comment on the video and recall their thoughts during the work on the MST. The interviewer explained that process, and how the video could be paused as well as wound back or forward as desired. When watching the eye-tracking video, the students commented on what happened (e.g., Helen: “Here, you see it again, I was searching further…”) and the interviewer gave prompts for the students to comment (e.g., interviewer: “Here you look at her quickly?”). The two SRIs were recorded with one external camera each (see Fig. 4).

Fig. 4
figure 4

Collected data and the preparation for analysis

Full size image

3.3 Data and data analysis

The data in our study were comprised of the eye-tracking videos from Helen and Ilias with the corresponding audios from their collaborative work (16 min.), the SRI video from Helen (38 min.), the SRI video from Ilias (55 min.), and their writing/drawing on paper. For the data analysis, we prepared the data as follows: We merged the eye-tracking videos of both students into one video (Fig. 4) in a time-synchronized manner. We transcribed this video in order to analyze it. We also transcribed the SRI videos of both students.

To explore the collaborative creative process in as much detail as possible, we used data from students’ writing and drawing, the synchronized eye-tracking video, the transcript of the eye-tracking video including all the utterances, as well as the transcripts from the SRI videos from Helen and Ilias. We analyzed the eye movements, gestures, and utterances in the synchronized eye-tracking videos, as well as their reflections in the SRI. We analyzed the data chronologically, in order of appearance in the students’ collaborative work on the MST, then matched the reflections in the SRIs to the respective place in the students’ collaborative work on the MST.

Because our research question is explorative, we chose to use an inductive data analysis method, following Mayring’s (2014) content analysis. To trace the collaborative creative process of the two students working on the MST in its phases, we intentionally decided not to use a deductive analysis building on the phases found earlier by Schindler and Lilienthal (2020) for solo work on MSTs. Instead, we intended to be open for other, new phases, and therefore started from scratch, from the data material at hand with an inductive approach. We first visualized the students’ eye movements in a diagram and paraphrased all content-bearing elements from the collaborative work and the SRIs in chronological order with respect to the research question (see Sect. 4.1 for an example). We then conducted a transposing/category development step, in which we worked out the phases of the creative process (e.g., “looking for a start”)—and also noted what they did in this case (e.g., “trying to find new relationships in the diagram”). This enabled us to find similarities among the ten approaches that the students worked on in total. We conducted a category revision step looking through all categories and data again, revising the category system. After this, we produced process charts of every approach that the students worked on (see Sect. 4), which included the phases of their creative collaborative process. We created charts that capture the phases of the students’ collaborative process on every approach, including the individual spaces of the particular students, which we derived from the eye movement videos together with the respective SRIs, as well as the collaborative space, where the students made their thinking and reasoning explicit to one another (see Fig. 6 for an example). Finally, based on the data and phases from all approaches, we looked for similarities and created a tentative model as an abstraction of the ten processes that displays the collaborative creative process schematically.

4 Results

In total, the students worked on ten approaches to the MST.Footnote 1 We cannot report the students’ whole collaborative creative work on all ten approaches in detail but instead report the collaborative creative process and its phases in one of these ten approaches—the first one, chronologically—as an example. We then present an overview of the ten approaches that the students worked on and, finally, present the tentative model that we have developed inductively.

4.1 Example of one approach on which the students worked

In this section, we detail the collaborative creative process of the two students for one approach, which we called the ‘red approach’, since the students used a red pen to note it. We follow this process chronologically and finally present the process chart (Fig. 6).

4.1.1 Looking for a start

In the beginning, after the students had read the text of the task, the instructor opened a paper with a diagram. For approximately six seconds, both students remained silent, until both said, “Okay”, and Ilias said, “I’d say we could start with…”, grabbing a pen. The eye-tracking data, together with the SRIs, shed light on what had happened in the initial six seconds where both students remained silent. Both students got an idea of how to solve the problem, both were certain about it—and their ideas appeared to be very similar. Figure 5 visualizes both students’ eye movements within these six seconds.

Fig. 5
figure 5

Ilias’s and Helen’s initial eye movements on the task

Full size image

Ilias’s eye movements indicate that he focused on the upper triangle, envisioning a perpendicular line (arrows 4 and 5), then paid attention to the right-angled triangle on the left part. Watching the video of his eye movements in the SRI, Ilias described that “it was my first thought directly, looking that direction, to draw the perpendicular line, from the angle center to the horizontal line. To create this right-angled triangle.” Asked by the interviewer about how he came up with the idea, he answered several times “cause I saw it” in the diagram. It appeared as if the impulse to go for the perpendicular line and the right triangle was originating from the diagram. Helen’s eye movements indicate that she first paid attention to the upper triangle, then envisioned the perpendicular line (to the middle of the hexagon), then paid attention to the left part (arrows 7 and 8) and the right part (arrows 9 and 10) of the upper triangle. In the SRI, she described that she “immediately scanned the first three corners” and then “I had this corner (upper left one) and immediately went to the middle, and mentally drew this line.” She reported, “then he [Ilias] started saying it. That was… that was literally simultaneous.” We called this initial phase of the students each looking for a way to solve the problem as “looking for a start,” which led to an intuition about how to solve the problem.

4.1.2 Presenting the approach, step by step

After these initial six seconds, the students started talking. Ilias presented an approach, step by step.

Ilias::

I’d say we could start with… (taking a red pen)

Helen::

A right angle.

Ilias::

A right angle (showing the angle bisector with the pen)

Helen::

Yes, exactly.

Ilias::

Angle bisector here (pointing to upper angle). Then we’ll have 60°, 90° (pointing to right angle), and can calculate this one (pointing to angle epsilon)

Helen::

(simultaneously) the rest.

Ilias::

Right? (looking at Helen, Helen looking back, mutual eye contact)

Helen::

Exactly.

In this phase, Ilias made eye contact with Helen, with Helen looking back, leading to mutual eye contact. In the SRI, Ilias commented on why he looked at Helen:

I didn’t want to leave her out, we were supposed to work together, and I somehow found it, I mean, it just started, and I had immediately taken the pen, like, let’s do it like this, and this, and this. I am sometimes a bit forceful when it comes to this. I don’t want to step on someone’s toes and then it’s better to look once more if she agrees with what I’m saying. Not that I am making a huge mistake and she’ll say, later on, come on, you did something wrong there. I kind-of want to confirm it a little bit.

Helen in turn agreed and the students took this as agreement to proceed. We called this phase, which also involved collaborative verification, “presenting the approach, step by step.”

4.1.3 Calculating

After the presentation of the approach, the students calculated the angle size of epsilon. We called this phase “calculating:”

Ilias::

Okay, so we have…

Helen::

Well, you know it actually, oh, no…

Ilias::

Yes, sure!

Helen::

Yes.

Ilias::

60°, 90°

Helen::

(chuckling softly) 60, 90°

Ilias::

So, 180 minus 150.

Helen::

Wait, 60 and 90.

Ilias::

Makes 150 (looking at Helen)

Helen::

(simultaneously) 150 (looking back at Ilias, mutual eye contact)

Ilias::

So, 180 minus 150

Helen::

30°.

In this phase, towards the end they again made eye contact and in turn proceeded to put their solution to paper.

4.1.4 Writing and drawing

After their calculation, the students started writing down the solution and drawing the lines and angles. During this phase, which we called “writing and drawing,” Ilias again took the lead and started writing 180° − (90° + 60°) = 30° on the paper, next to the diagram. When Ilias started writing, Helen advised, “Draw the auxiliary line directly as well.” Yet, he first finalized writing 180° − (90° + 60°) = 30°, while they talked about it (e.g., Ilias: “60?”, Helen: “Exactly. Half of 120, right?”). In the SRI, Helen explained that she disliked the order of first writing and then drawing:

That bothered me because I always draw a sketch first. And ‘cause I’d do the line first and ‘cause he was the one writing. I would have immediately drawn the line first. I think this is why I said that, regarding the sketch. (…) This is always my style, to first sketch and then calculate. (chuckling)

After Ilias had finished the writing, the researcher in the room said, “you can also draw in the diagram, okay?”, picking up Helen’s utterance from before. Helen, in turn, said, “Yes, I just wanted to say, maybe you can…”, and Ilias drew the perpendicular line. Instructed by Helen, Ilias then also labelled the angles of the right-angled triangle. He then put the cap on the pen and put it down.

After finalizing this approach, Helen’s gaze went back and forth between their calculation and their drawing in the diagram, indicating that she once more checked and verified the approach. However, the students did not discuss this anymore, and Ilias simultaneously started looking for another way to approach the problem. Figure 6 visualizes the students’ work on the red approach in a process chart.

Fig. 6
figure 6

Process chart for the students’ work during the red approach (best viewed in color)

Full size image

4.2 Overview of student approaches

Figure 7 gives a schematic overview of the eight approaches that the dyad put on paper, in the chronological order they emerged and in the colors the students used.

Fig. 7
figure 7

Approaches that Helen and Ilias put on paper (best viewed in color)

Full size image

The students also discussed a ninth and tenth approach: In the unfinished ninth approach, they discussed using trigonometry but let go of this idea. They then developed a tenth approach that drew on a trapezoid and its angle sum but did not put this down on paper either.

Of the eight approaches that were written down, not all were fully mathematically correct, since the students partially missed reasoning steps when they inferred facts from the appearance in the diagram. However, in line with previous research we consider these approaches to be appropriate (Leikin & Lev, 2013; Schindler et al., 2018): “The notion appropriateness has replaced the notion of correctness … to allow evaluation of reasonable ways of solving a problem that potentially lead to a correct solution outcome regardless of the minor mistakes made by the solver” (Leikin, & Lev, 2013, p. 391).

4.3 The collaborative creative process and its phases

Figure 8 presents process charts of the collaborative creative process the students went through in the ten approaches. For the red and blue as well as the green and orange approaches, the two approaches are presented in one chart since they were interwoven: In both cases, one student (Helen) had an intuition or even worked out an approach while the dyad was working on another approach. For example, Helen had the idea for the blue approach while brainstorming in the very beginning when working on the MST but only mentioned it after the students had finalized the red approach.

Fig. 8
figure 8

Process charts of the students’ ten approaches (best viewed in color)

Full size image

When comparing the creative process of the ten approaches and searching for similarities among them in order to develop a tentative model of the collaborative creative process, we found apparent similarities among the processes for each approach. For example, the students always individually looked for a start and they often had an idea or intuition that they then presented to the other student (note that in every instance only one student presented their idea, not both at the same time; see dotted lines in Fig. 9). However, the processes differed in a way that in some approaches, one student was presenting a whole approach (red, blue, green, orange, pink, light green, dark blue), while in the other cases, a student was bringing only an idea or intuition into play, and the two students then worked collaboratively to work out the approach (yellow, trigonometry, trapezoid). Accordingly, our analysis resulted in a tentative model with two branches (Fig. 9): Branch A, “presenting an approach,” differs from branch B, “developing an approach together,” in the way the students interacted in the discussion and how a new approach was developed. In the following, we elaborate on this aspect and on the phases in more detail.

Fig. 9
figure 9

Helen’s and Ilias’s collaborative creative processes

Full size image

4.3.1 Looking for a start and intuition/idea

Every approach began with the students looking for a start to solve the problem in a different way. For the first two approaches, certain features of the diagram caught their eye right away; they just “saw it” (Ilias) and went from there. In the looking-for-a-start-phase, the students hardly talked. Often there were only eye movements perceivable until the students brought forward an idea or intuition. For the first two approaches, this phase took only five or six seconds, whereas for the later approaches, the phase was extended. The students then applied heuristics to find new approaches. These heuristics involved looking around in the diagram, at something else, and parts that haven’t been used yet (green, orange, light green, yellow, dark blue approaches), looking at aspects in the diagram that have already been used (pink approach), in particular, scanning triangles from previous solutions and trying to find the same triangle elsewhere (trigonometry and trapezoid approaches), trying to find new relationships (yellow approach), scanning writings from previous solutions (trigonometry and trapezoid approach) and hoping for sudden insight (dark blue approach). Both students mentioned that they used heuristics (Ilias: “What other technique can we use?” Helen: “I was just thinking about the…”), yet did not discuss them explicitly in their group work.

Towards the end of the time of the task, the students ran out of ideas, which appeared to go along with emotional arousal in the phase of looking for a start. In the SRIs, the students commented that “it was just over” (Helen) and “I’m starting to despair” (Ilias).

During the looking-for-a-start phase, the students came up with ideas or intuitions on how to solve the problem. These ideas/intuitions often went along with certainty and sometimes also were described as Aha! moments by the students in the collaborative work on the MST and also in the SRI.

4.3.2 Branch A: presenting an approach, step by step, and finding a solution

In this phase, which is included in Branch A of our model, one of the students presented an idea while the other was listening, helping to calculate, and verifying. Even though the students both were involved, and we do not know if the student presenting would have succeeded in all cases without the mathematical and social-affective support by the other, we distinguish this process of one student predominantly presenting an approach in its steps from another working mode, where the students collaboratively developed an approach based on one student’s intuition as a start (Branch B, see next section). In Branch A, the presenting student had an idea in mind and explained and developed the steps.

In the first approach, their process stood out: The students put more emphasis on the calculation, which took longer than in the approaches that followed. The students appeared to first generally agree on the idea (using angle sum, right angle, and angle bisector of 120°) and then developed the calculation (180°–90°–60° = 30°) in a detailed discussion. The reason for the strong focus on the calculation in their first approach may be that this was not an easy task for them. In the first approach, they also needed to figure out the magnitude of the angle epsilon for the first time. For all further approaches, they knew that 30° would be epsilon’s magnitude (the solution to the geometry problem), so they knew easily when their solution was correct and did not need to be so attentive to the calculation.

In another instance, we found that while Ilias was presenting the green approach, step by step, Helen developed the orange approach, yet not explicitly. While responding to Ilias’s explanation and utterances, saying “yes”, nodding, and uttering “mhm” affirmatively, Helen was developing another approach, step by step, at the same time. This reminded us of what Schindler and Lilienthal (2020) described as “mini-incubation: a shortened incubation period that occurs while the student is working on another approach to the same MST” (p. 1583). In the case of ‘mini-incubation’ in our study, the new idea appeared from a different source than a direct ‘looking for a start’ (similar to Schindler and Lilienthal’s finding) and it was interesting to see that this process ran in parallel to the explicit activity in the collaborative space. That Helen was developing another approach was barely perceivable in the group work situation itself, as we captured it only through her eye movements and her according report in the SRI. Only the fact that she did not react to Ilias’s attempts to make eye contact with her while he explained the green approach, which they had always made in the approaches before, indicated that something else was going on.

In another instance, Ilias had the idea for an approach (dark blue) but then was hesitant to present it. The eye-tracking video showed that he first looked around at relevant triangles he intended to use, and then his gaze remained relatively still, approximately in the middle of the hexagon, on a place without any stimulus. Ilias’s comments in the SRI suggest that after developing his idea and thinking through his approach quietly, he was reluctant to mention it to Helen because it was similar to a previous one. He then intentionally decided to go further with it, to bring it into the shared collaborative space since he eventually decided it was a new version.

4.3.3 Branch B: presenting an intuition, working further, step by step, and finding solution

As mentioned before, in three cases, one student brought an intuition to the shared space, and they developed an approach together, based on the intuition. In one of the three cases, the students then worked out an approach that ended up on paper (yellow); in one case they did not want to pursue the idea further (trigonometry approach), and in one case they finally decided not to put it on paper because they felt it was too similar to other approaches they used before (trapezoid approach).

In this working mode, one student did not present their idea in all its steps, but, rather, they brainstormed together based on an initial intuition. In their interpretation of the situation, the students appreciated this kind of group work, as Ilias’s comment in the SRI illustrates: “I think it worked wonderfully together. Well, I see the same angle, she sees it as well. She mentions it. It was great. It works perfectly.”

4.3.4 Decision to proceed/abort

A moment or phase that appeared to be significant for students’ work on the MST was when they were making decisions on whether or not to proceed with their approach. Normally, this happened after the students had finalized a solution: They then considered whether they wanted to put their approach onto paper or discard it and come up with something else. In eight out of the nine approaches that they finalized, they agreed to continue and put the approach on paper. This agreement took place in different ways, as follows.

In three cases (red, blue, and dark blue approaches) the students made mutual eye contact, which served as a non-verbal agreement: They looked at each other, and then one of them took a pen and started drawing and writing.

In two cases (orange and green approach), only the person presenting looked at the other person to agree, while the other one did not look back, which the first person took as agreement and proceeded. In one such case (green approach), Helen did not look back because she was busy developing another approach at the same time. In the other case (orange approach), Ilias did not look back since he did not understand what she meant (“I didn’t understand it”) and was focusing on the angle that Helen talked about, trying to understand her way of thinking.

In another case (pink approach), agreement was confirmed by Helen taking the pen and starting to write, though Ilias had presented the approach. Taking the pen appeared to be an act of showing agreement.

Finally, in two cases (yellow and light green approaches), the students verbally agreed to proceed and put the approach on paper. While for the yellow approach, this was a quick decision (Ilias: “So, shall we do it?” Helen: “Yes.”), for the light green approach, they had a longer discussion: Ilias (who had presented the approach in the first place) repeatedly argued that this approach is “complete nonsense in the end” and “trash, practically,” since it “at the end of the day is exactly the same as that one (referring to the green approach), only much more complicated.” Ilias did not want to use the same approach twice. Helen, on the other hand, suggested not to disregard this approach, but to “write it down.” Her reason was that “we’re supposed to find as many ways as possible.” Her suggestion to proceed in turn made Ilias write it down.

In two cases (the trigonometry and trapezoid approaches), the students aborted their approach. In one case, they discarded the idea quickly after Ilias had brought forward his intuition. Helen mentioned twice that “That’ll probably work, but we’d need the length measurements, wouldn’t we?” After a short discussion about whether or not they could figure out the measurements, Ilias was convinced that this wouldn’t be productive to pursue. In the SRI, he commented, “we only have a diagram without indications of measurements. Which Helen then—thank God—says! Otherwise, I would have probably lost myself in these thoughts. (…) And then it becomes clear to me and the idea is discarded rapidly. Since you cannot calculate it.” In the other case, the students discarded an approach that they had finalized and could have drawn and written down: the trapezoid approach. They went through the whole reasoning, step by step, together and eventually realized that this approach was very similar to previous ones. Helen concluded, “That doesn’t offer much, right? Not really. Nothing new,” with Ilias replying “Nope. Then we’re here again”, referring to the dark blue approach.

4.3.5 Writing and drawing

The students started drawing and writing only after they had thought through all steps and had committed to their approach. They discussed the role of drawing and writing initially when they had finalized the first, red approach: Helen, who was “bothered” when Ilias did not draw in the diagram directly, suggested drawing right away, which was acknowledged by the researcher in the room. In the next approach (blue), they picked up on this: After having discussed their idea and having agreed on it, Ilias began drawing epsilon into the right angle, asking “Then this here is also epsilon, right?”, with Helen replying “Right. Or epsilon prime.” Ilias agreed (“Yes, epsilon prime, exactly.”) and accordingly marked \(\varepsilon ^{\prime}\). They then continued, writing 180°–120° = 60°, 60°: 2 = 30°, with Helen helping Ilias on what to write. In all further approaches, the students always drew first and wrote afterwards.

It was apparent in the eye-tracking videos that both students’ gazes were following the writing closely, indicating that the student who was not writing also paid attention to the details. In the SRI, Ilias commented on his gaze closely following Helen’s writing of the yellow approach: “I am checking up on her”, since “it needs to be correct.” In general, in the phase of writing and drawing, verification processes were often involved.

5 Discussion and conclusion

The aim of the research reported in this paper was to explore the collaborative creative process of students collaboratively working on an MST. We used a novel research design in mathematics education: DUET SRI. Our explorative case study offers tentative findings, and the results should not be generalized without caveats: We used only one dyad of students in one particular domain (geometry) with one task (hexagon MST). Yet, through the rich data we were able to trace the dyad’s collaborative process in detail, with high resolution and interesting insights.

Based on the students’ work on ten approaches for the hexagon MST, we inductively worked out phases of the dyad’s collaborative creative process and developed a tentative model of the collaborative creative process of the two students. Comparing the collaborative creative process found in this study to the creative process found by Schindler and Lilienthal (2020) in a case study with an individual student, we see similarities between the processes (see Fig. 10).

Fig. 10
figure 10

Tentative models of the individual and the collaborative creative process

Full size image

For example, for the dyad, we identified a looking for a start phase as did Schindler and Lilienthal (2020) for a single student. In the dyad’s work on the MST, the students thought about the problem individually for some seconds and often used heuristics to come up with an idea, which was similar to the process of the single student working alone. This often led to ideas or intuitions, similarly to the individual student in the previous study. Also, we found cases of “mini-incubation” (p. 1581), for example, when something in the green approach triggered Helen to develop an intuition for the orange idea and then to develop it while working on the other one. The mini-incubation in this case was similar to the one found in Schindler and Lilienthal’s study in a way that a new intuition appeared from some other source than a direct ‘looking for a start’. As for collaborative work, it connects to Levenson’s (2011) finding that “one student leads the group in one direction which then reminds another student about the possibility of another direction” (p. 230). It was interesting to observe how Helen succeeded in developing her approach while, at the same time, she reacted and responded to Ilias in their collaborative work. Here, individual work on one approach and collaborative work on another one appeared to happen at the same time, though with challenges. Accordingly, mini-incubation in this case was a process that ran in parallel with the explicit activity in the collaborative space.

On the other hand, the collaborative creative process differed from the one found for individual work. The fact that two students are involved adds complexity to the process in different ways. For example, for the dyad’s work on the MST we found two branches of their collaborative creative process, the first where one student presented an idea to the other student while the other one was listening, helping to calculate, and verifying (Sect. 4.3.2), and the second where one student brought forward an intuition to the shared collaborative space, and they brainstormed and developed an approach together (Sect. 4.3.3). This process connects to collective creativity (Levenson, 2011), which is “considered to occur when the social interactions between individuals yielded new interpretations that the individuals involved, thinking alone, could not have generated” (p. 216) and to Levenson’s finding that students may expand on other students’ ideas.

The moment where the dyad decided to proceed with an approach or discard it was particularly interesting. The students had slightly different motives: For example, while Helen was striving for fluency (many approaches) and wanted to write down an approach, Ilias was striving for flexibility (diversity in the approaches) and wanted to discard it because of its similarity to a previous one. Naturally the decision of whether to proceed or discard was more complex for the dyad than for a single student: They often agreed through eye contact but also verbally or, for example, using gestures (picking up the pen) as acknowledgment (Sect. 4.3.4).

For teaching and learning activities, our results indicate that collaborative partner work on an MST can be a rich activity and that the creative core of this process does not differ from solo work. The analysis indicates that especially in the later approaches, the students tried to develop approaches together, step by step, rather than showing and telling. In a sense, the students’ feeling of running out of ideas appeared to intensify their collaborative brainstorming. This indicates that even without clear individual ideas (or especially without them), the students tend to be creative together. For educators, it is important to know that situations where neither of the students has a ready-made plan already in their minds are particularly ripe for students to be creative together. Our study shows that the collaborative work on the MST was not like working on a routine problem several times, but that the process involved divergent thinking, illuminations and so-called Aha! moments, which confirms the finding of Schindler and Lilienthal (2020) about the creative aspects of working on MSTs.

All in all, the rich data in our study offered highly detailed insights into the creative collaborative process: We observed many subprocesses, some of which took only a few seconds and could trace back to both the students’ individual spaces as well as the collaborative shared space. We feel that creating and using process charts (see Fig. 8) is an enriching intermediate representation for analyzing the process. We also saw how the students perceived their collaborative creative process as useful and were glad about it. These insights were facilitated by a novel design; DUET SRI. In the SRIs, which took place directly after the students’ collaborative work, we observed that through the rich stimulus of the eye-tracking video along with the temporal proximity, the students were able to recall their thoughts very well. They did not forget their thoughts; quite the contrary, they were still very involved and sometimes even wanted to go on brainstorming about further ideas. Our study illustrated that DUET SRI has great potential for investigating mathematical learning activities.

In conclusion, our study, which explored the collaborative creative process of two students working together on an MST, revealed that the collaborative creative process involved phases similar to the creative process in solo work (e.g., looking for a start, idea/intuition). However, the collaborative creative process had more complexity and was more volatile, for example, in the ways the students worked on the approaches. Based on the exploration of the phases, we developed a tentative model of the students’ collaborative creative process, which has—unlike the solo creative process—two branches reflecting different ways that students develop approaches in collaborative creative work. Our findings can help educators support students’ collaborative creative work. Here, not only the phases and the different branches of the collaborative creative process are important, but also findings about how the students decide to discard approaches or proceed with them, and insights about how different student motives may contribute to these decisions. Educators can facilitate collaborative creative work, for instance, by encouraging the students to discuss explicitly these aspects, as well as the role of writing and drawing, to avoid potential inhibitions during the collaborative creative work. Finally, we hope that our case study, the findings, and insights can be a starting point for further discussion and empirical research on the collaborative creative process.