Abstract
Histories of mathematical practice account for mathematical knowledge and action by interpreting presently-available evidence as traces of the events, contexts, and relations that make up the past. Interpretations depend on the assumptions one makes about how mathematical knowledge works, insofar as it is knowledge and insofar as it is mathematical. Though the specific rules and their meanings can differ from context to context, mathematics is a kind of ruly knowledge, expected to follow orderly patterns and principles wherever it is found. The contexts and activities of mathematical practice—how that knowledge is made, shared, applied, and understood—are necessarily less ruly, and different practices leave or occlude different kinds of evidence for historical interpretation. The apparent ruliness of mathematics can be both a resource and an obstacle for understanding its unruly pasts. Historians’ interpretive assumptions and goals have been shaped by centuries of interaction between mathematics research, history, and education.
As a guide for mathematics educators and education researchers to historical perspectives on mathematical practice, this article briefly introduces four major interpretive traditions that inform the present discipline of mathematics history. It then illustrates some interpretive approaches and challenges through the history of blackboards in mathematical practice before explaining the two broad kinds of historical interpretation applied to mathematical practices. Reconstruction involves understanding the conditions and contexts of practices in a single historical moment. Genealogy, by contrast, connects elements of the past across time through transmission, interpretation, adaptation, and other kinds of preservation and change.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction: mathematics’ traces
History is a tracing discipline. As much as pedagogues and researchers alike prize the value of imagining, illuminating, or recovering past worlds, the practice of history often hinges on other verbs—following, speculating, interpolating—that focus on what can be known indirectly from a past that is fundamentally unrecoverable and, in many respects, unimaginable. Historians make mediated understandings, deriving interpretations from materials available in the present that can be connected, one way or another, to the past. Historical events, contexts, and contingencies are both the object of historical inquiry and that inquiry’s chief impediments, continually transforming what those in the past left behind. To learn and master history is to become a disciplined tracer, knowing how to reason from fleeting apparitions of past lives to coherent accounts of other times.Footnote 1
Mathematical practice leaves a variety of traces, some intentional, some accidental, some direct, and some incidental. Not every piece of mathematical writing intended to last in perpetuity survives for historical interpretation, and all are altered through transmission, conservation, and use. But the bulk of sources available for the history of mathematical practice were to some extent meant for future readers, from sun-hardened clay tablets to inked vellum manuscripts, to books and articles printed and bound on library shelves. Other durable artifacts were meant more for users in their moment, but endure in forms that remain at least somewhat legible to a trained interpreter: notes, copybooks, instruments. Non-mathematical sources—letters, ledgers, reports, buildings, writing implements, paintings, photographs—may still carry traces of mathematical practices, and (more often) furnish information about those practices’ conditions and contexts, as well as clues to how other sources of evidence may have survived or been transformed between moments of mathematical practice and historical interpretation.
Traces are made, not simply found. Past decisions about what to produce, conserve, preserve, restore, commemorate, discard, or demolish, together with uneven conditions for doing so, mean that historians’ sources come from a small and unrepresentative fraction of the events and contexts for which they stand. Historians use theories and inferences to render presently available materials into traces of bygone subjects. Accordingly, historians’ understandings of what it means to know and practice mathematics contribute to the meaning of their sources, not just the other way around. Both historians and past and present mathematicians develop accounts of mathematics as part of their scholarly practice, and those accounts can be in tension. Different kinds of evidence, different methods, and different assumptions support different ways of understanding how mathematical ideas and practices relate to each other and to their wider contexts, how they change, and how they become manifest in texts and other artifacts.
Historians’ and mathematicians’ assumptions about the nature of mathematics and its practices vary across historical contexts, change over time, and can be opaque or ambiguous even where authors attempt to spell them out. For some, mathematics is orderly and mechanical, for others it is capricious and inspired. Yet, even across this variation, certain experiences, values, and modes of thought seem to unite mathematics across contexts. Indeed, such apparent affinities (we might say, with Wittgenstein 1953, §67–68, such family resemblances) make it possible to recognize past knowledge and practice as mathematical at all. The empirical and philosophical certainty most people feel that two and two make four, while not a cultural universal (Barany 2014), can surely be taken for granted when interpreting most historical sources.
Mathematics is, in this sense, a ruly kind of knowledge. Presently recognizable orders and patterns, even if not understood in the same terms by those in the past, seem nonetheless to have necessarily governed past actions and conclusions. In past and present, numbers mostly add up, circumferences and diameters have about the same ratios, ruler and compass constructions will not ordinarily trisect an angle, no matter the surrounding culture or context. This ruliness makes it possible to infer quite a lot from limited, indirect evidence of past practices: if a practitioner records (or even merely implies) just the inputs and outputs of a calculation, then in many circumstances one can confidently guess at the calculation’s omitted parts. At the same time, practitioners’ presumptions of ruliness limited what they preserved: there is little reason to keep what is obvious, ubiquitous, or inevitable. Practitioners’ records show much more clearly what they did not take for granted than what they did, but what they did take for granted is often more important for understanding their practices.
Moreover, the less practitioners record, the less they leave indirect or circumstantial evidence of other aspects of their practice, the unruly, informal, provisional parts that would never be preserved directly. Indeed, in many times and places (including our own), a basic part of mathematical practice has involved learning to look past these unruly features and to regard them as irrelevant to the knowledge mathematicians produce (Barany & MacKenzie 2014). That is, misrepresenting the history of mathematical practice has frequently been part of mathematical practice itself. Such unwritten or written-out aspects are often precisely those of greatest historical interest, establishing the contextual specificity of past mathematics. Where ruly affinities tend to collapse distinctions among contexts, historians aim to understand the past in its contextual specificities. Putting the past in context means reconstructing relationships within a single moment and tracing genealogies of change over time. These two aims demand reckoning with the unruly pasts of ruly knowledge.
2 A disciplinary chimera
The history of mathematics is a disciplinary chimera. To understand the goals, methods, and premises that have shaped historical interpretations of mathematics, it is helpful to distinguish four major traditions of scholarship: as branches, respectively, of mathematics, education, philosophy, and history.Footnote 2 These disciplinary traditions have interacted, clashed, and transformed, with intellectual, methodological, and professional consequences whose effects resonate across many notable touchstones and conflicts in historical interpretation (e.g. Pyenson 1995, Schneider 2016). Each tradition has harbored different notions of what mathematical practice is, as well as how and why to study it, making mathematical practice itself a chimeric subject. Accordingly, the values and implications of studying “mathematical practice” or “mathematical practices” vary with (and within) disciplinary traditions. These affect what readers from fields including contemporary mathematics education can gain from histories of mathematical practice from these respective traditions, and how readers must make sense of such histories.
2.1 History as mathematics
Long before the history of mathematics had an established disciplinary identity as a branch of history, it was a branch of mathematics. To this day, in many parts of the world, mathematics historians are most likely to be trained or employed in departments of mathematics, even as their methodologies and perspectives have embraced other traditions. To be sure, many mathematicians have turned to history as amateurs—sometimes quite skillfully and knowledgeably—without imagining their research to contribute to mathematical knowledge. Others produce disciplinary histories that affirm values and construct a shared past to support current norms and identities (see Graham et al. 1983). These range widely in style and focus, encompassing alike E. T. Bell’s famous (notorious) biographies and Florian Cajori’s sprawling surveys of curricula or notations.
Practices figure throughout these histories, indexing the characters and conditions of individuals, institutions, and ideas. Here, practices are just what mathematicians do and how they do it, and are rarely interrogated as such, except perhaps for their variety or peculiarity. Such practices are the stuff of history in an older sense of the term, referring not to the science of explaining events and contexts over time but rather to that of assembling, systematizing, and interpreting masses of facts and artifacts, as in a natural history of botanical or geological specimens or a medical history taken by a physician. Histories of practices, which collect the many things mathematicians do, are in this sense distinct from the history of practice, which explains some aspect of the totality of what mathematicians do, but the former are essential resources for the latter.
Still within the mathematical tradition of history of mathematics, at least two kinds of historical inquiry have been seen as producing mathematical knowledge in themselves (see Grabiner 1975, Goldstein 2010). The first—associated with famous names like Montucla (Richards 2006), De Morgan (Richards 1987), Peacock (Lambert 2013), Cantor (Lützen & Purkert 1994), Dickson (Fenster 1999), Neugebauer (Jones et al. 2016), and Bourbaki (Aubin & Paumier 2016)—derives broadly from the premise that understanding the genealogical development of concepts can be a means of understanding the nature of mathematical reasoning. Informed by their authors’ retrospective conceptual frameworks, these histories show patterns, anticipations, and principles that connect past mathematics to the present. The second uses histories-as-collections to multiply perspectives and thereby suggest new ideas, which may be cast as old ideas that have been recovered. Both of these approaches tend to focus on ideas and their relationships, sometimes clarified by considering specific practices or general questions of practice without necessarily demanding such considerations.
2.2 History as pedagogy
The second major tradition in the history of mathematics emerged as a branch of mathematics education when the latter began to be considered a distinct field of scholarship from mathematics. History had long been a source of examples and exercises for students, as well as a means of structuring conceptual expositions. Several authors in the mathematical tradition, notably Montucla and De Morgan, saw their histories as tools for education, using the historical pattern of a concept’s development as a template for comprehending the concept in the present. Educators’ interests in how people learned and challenged concepts—in and beyond explicitly pedagogical settings—have supported generalizations about conceptual and cognitive aspects of mathematical practice. At the same time, concern for the conditions and tools of mathematical learning have made histories from this pedagogical tradition especially attentive to the historical and cultural varieties of specific practices. Studies of changing practices supported broader theories of the nature of mathematical learning and inquiry, which motivated further historical studies. This pattern is notable, for example, in the voluminous pedagogical and historical works of David Eugene Smith beginning in the 1890s.
2.3 History as philosophy
A third tradition, history of mathematics as a branch of philosophy, has used past expressions and debates about mathematical ideas to explore the nature of mathematics, often focusing on questions about rigor, foundations, and classifications of mathematical knowledge. Some practices with significant foundational implications, such as geometrical construction or symbolic manipulation, have been important for their implications about rational thought and logical certainty. Philosophical histories tend to decontextualize specific practices, representing them in idealized forms based on how past authors claimed their mathematics worked or how present philosophers imagine it could or would have worked. A compass construction, here, is not a set of actions performed by a person at a place and time in the past, but rather a set of principles about reasoning and its theoretical possibilities. In this way, philosophers turn specific historical practices into evidence of general philosophical practice.
2.4 History as history
In these first three traditions, the history of mathematics is primarily a resource for understanding something about mathematics in the present. While historians in the fourth tradition—as a branch of the scholarly discipline of history—are likewise informed by present-day concerns, their explicit aim is to understand the past. History has been a genre and a topic for as long as people have been chronicling their past, but it is a comparatively recent scholarly discipline, long postdating the academic organization of mathematics and philosophy. In this vein, histories explain relationships within historical contexts and account for change across time using theories, methods, and frameworks that can be as varied and contentious as those of other disciplines. Mathematics was a significant focus for figures like Paul Tannery or George Sarton (e.g. 1936) who articulated a place for science as a distinctive subject for professional historians.
Mathematical practice, in the historical tradition of the history of mathematics, has meant many things according to researchers’ frameworks and interests. Specific situated practices—writing, teaching, applying, measuring, conjecturing, calculating, designing, and so on—are vital components of analyses that place mathematical activity in its historical circumstances, explaining not just past mathematics but elements of the past societies of which it was a part (e.g. Robson & Stedall 2009). Here, broadly, practices are aspects of historical actions and conditions connected to artifacts like books and tools that serve as evidence for understanding the past under a variety of rubrics. However, practice has also referred to specific approaches to historical inquiry that focus on how mathematics came about—materially, conceptually, or otherwise—as opposed to histories centered on concepts, institutions, or other aspects of the past.
In each tradition, notwithstanding their many fruitful convergences and interactions, historical evidence and inquiry serve different ends. Analyses can be trained on explaining the past, informing the present, or characterizing something seen as timeless, and this distinction changes which historical contexts matter and how they guide interpretations. Translations, interpretations, depictions, and even calculations ostensibly derived from the same evidence can appear very differently depending on researchers’ goals and assumptions, and claims that may be elementary in one tradition are often nonsensical in another. While the many dimensions of these tensions and contrasts are beyond the scope of this article, the ensuing analysis hinges repeatedly on the central point that evidence and its interpretation depend integrally on both the researcher’s understandings of mathematics and the goals those understandings serve.
3 An erasing discipline
Mathematics is an erasing discipline. As much as pedagogues and researchers alike prize the value of showing, explaining, and displaying, the practice of mathematics often hinges on other verbs—replacing, eliminating, resolving—that focus on what can be legitimately ignored or discarded, precisely so that one’s focus can be safely trained on what matters more. In settings of drill or discovery, people wield tentative figurations to articulate, manipulate, explore, and understand. Their tentative quality makes these activities effective means of knowing, letting mathematicians rewrite the established properties and relations among the things they study as they go. To learn and master mathematics is to become a disciplined eraser, knowing what and how to blot out among the fleeting apparitions of mathematical practice to make way for mathematical knowledge. To do mathematics well is to embrace a certain kind of historical obfuscation.
Since the early nineteenth century, the iconic instrument of this play of figuration and obfuscation has been the blackboard. My sociological research has connected blackboards to a variety of contemporary mathematical media and methods, from scrap paper jotting to coffee room chatter to browsing online preprint repositories (Barany & MacKenzie 2014). Blackboards can help explain how mathematicians produce, conserve, manipulate, discard, and relate to material artifacts—both those that may survive for historical analysis and those that do not. Understanding mathematicians’ material practices is essential for understanding the wider gamut of mathematical practice, material and otherwise, because (absent the capacity to travel in time and read minds) historians depend on material traces for evidence. In particular, the sociology of blackboards in current mathematics underscores a distinction evident in many forms and settings both present and past, that those who do mathematics have different uses for materials they intend to keep and those they intend to discard or erase. Moreover, the deliberately kept materials most likely to be available to historians are highly unrepresentative of many of the activities of greatest interest in histories of mathematical practice, including those associated with learning, everyday reckoning, local collaboration, and creativity. Mathematical practitioners constantly navigate between persistent and fleeting media, and their historians must constantly infer from what persists to what does not.
As a medium of mathematical higher education, blackboards trace to new regimes of elite engineering training in Napoleonic France. Blackboards and mathematics were not an instant or obvious pairing, and both blackboards and mathematics changed in tandem over the first half of the nineteenth century. As physical objects, blackboards are designed to be durable while the practices they support are meant to be transient.
The earliest traces of blackboard mathematics, accordingly, are not to be found on classroom walls. Consider the records of the Administrative Council of the École Polytechnique in Paris. Minutes of the noon meeting on 10 Vendémiaire in year 14 of the French Republican calendar (2 October 1805 in its soon-to-be-restored Gregorian counterpart) report that efforts to varnish the elite military academy’s blackboards had yet to give a satisfactory result, and the chemists were invited to try again.Footnote 3 On 19 March 1806, the Council was advised of the need to repaint the boards in the amphitheaters and study rooms and asked permission to have two large new amphitheater boards made. On 21 April 1808, they recorded an allocation for the repair and painting of study room boards. Later that year, they note 49.38 Napoleonic francs paid for 4000 sticks of chalk—about US$500 in today’s dollars based on the value of the coins’ gold content, not far from currently prevailing rates per stick.
Such minutiae of educational administration give a glimpse of a world of practice. The school’s faculty struggled with temperamental writing surfaces, but believed it worth the effort of some of France’s finest chemists to improve them. They installed blackboards in both lecture theaters and study rooms, suggesting uses including presentation, drill, and examination. Students and faculty used the boards enough to wear them down, requiring regular upkeep including painting. Repair and painting expenses continue to be itemized in budgets from 1809 and 1810, but a decade later these fall in a category of furniture maintenance capacious enough for an “etc.” (1818, 1819). Batches of 4000 sticks of chalk recur in records of 1810 and 1811, the latter noting the school’s commissary as destination, and by 1817 one finds chalk grouped with pens and paper as “objects of daily consumption.” Blackboards and their associated apparatus thus faded into routine, unproblematic features of instructional settings.
Minutes and ledgers are technologies of political and fiscal accounting designed to last. Entered in formal cursive on lined paper bound in sturdy volumes committed to official archives, they memorialize what was notable to administrative authorities at precisely noted times and places. We can know with some confidence what blackboards and chalk cost to use because that was the measure of their value that mattered to these record-keepers. To find other measures of their value, other indications of their implications, one must turn to other kinds of records.
4 Tracing blackboard practice
Erasable and large-scale writing media have long histories, in mathematics and otherwise. Wax tablets and portable slates date to antiquity, and some of the earliest examples of writing of any kind are clay tablets that began as erasable media for numerical and other kinds of inscription and became fixed by baking in the sun (Robson 2008, 27–40). Wall writing, for instance as cave art, may well predate even wall building as a collective human practice.
The earliest evidence of systematic practices of erasable writing on large, shared surfaces—as a deliberate combination of two much older modes of writing—dates to fifteenth-century Europe, in the form of depictions of choral education in woodcuts and organ portals (Owens 1998, esp. 82). To the extent writing could facilitate musical instruction these surfaces offered an efficient way for a group of singers to regard the same writing together. An epoch-making transformation in the wider structures, contexts, and aims of European education between the eighteenth and nineteenth centuries vastly expanded blackboards’ settings and uses. These changes included broader systematic regimes of instruction, new genres of pedagogical writing, new systems of training and coordination for instructors, and new conceptions of the role of education in making citizens and supporting state enterprises. As pedagogues introduced blackboards into more and more settings for more and more purposes, they left a corresponding proliferation of traces.
Records of educational institutions offer some of the most direct information about blackboards’ uses. In addition to budgets and committee minutes, formal reports and reviews indicate how blackboards mattered for observers who mattered to school officials. These show, for example, how an engineer trained at the École Polytechnique subsequently crossed the Atlantic and introduced comprehensive blackboard-based mathematics instruction at the school’s American counterpart, the military academy at West Point (Phillips 2015). Here, blackboards were most important as a setting for drill and examination. As cadets marked their sections of a board under their instructor’s exacting eye, they were meant to learn character and discipline alongside mathematics.
More blackboards in more places created commercial opportunities and material commonplaces that manifest other kinds of evidence for historians. Authors of textbooks, guides, and institutional histories remarked on the technology, often on the basis of firsthand experiences (e.g. Pillans 1854, xlv–xlvii; Claris 1895, 110, 117). Blackboards appear incidentally in personal narratives, including emerging genres of fiction that prized verisimilar contextual detail. Each mention offers a peek at blackboards’ contexts, uses, values, and associations. By the mid-nineteenth century, there was a sufficient market to support published guides and manuals for blackboard instruction (e.g. Bumstead 1841, Alcott 1843). Their idealizations and prescriptions, as well as what they take for granted or presume to need explanation, can be read in historical context to infer about classroom activities (Wylie 2012). Turning blackboards from novelties into commodities, promoters and manufacturers for blackboards and associated paints and accessories left implicit information about imagined and actual practices in patents, advertisements, and trade journals (Ackerberg-Hastings et al. 2008, 21–34).
Other kinds of sources show blackboards’ changing mathematical contexts and uses. Warwick’s (2003) study of nineteenth-century Cambridge mathematical physics began with the realization that certain physicists used the backs of student examinations to draft their scientific papers, thereby preserving an ordinarily discarded category of pedagogical ephemera. These helped Warwick connect up a great mass of other pedagogical ephemera with contemporary and retrospective accounts into an explanation of the cultural, practical, technological, and intellectual emergence of a system of examination and training concentrated around a specific style of written problem-solving. This, in turn, allowed new inferences about practices linked to blackboards (dated in Cambridge mathematics to the mid-nineteenth century) and other apparatus by connecting these to the conditions and goals of training and scholarship. These sources indicate specific blackboard-based practices while at the same time supporting accounts of problem-solving, education, theory-formation, and other aspects of mathematical practice not confined to that specific medium.
Carrying the story of blackboard practice into the twentieth century opens further kinds of sources. Photographs—and later film recordings—become more widespread, each sometimes portraying blackboards directly (often as portrait backdrops or in other staged configurations) and sometimes depicting them incidentally in the background. Records of manufacture, architectural planning, and installation tend to be more extensive in more recent institutional archives, and interview collectionsFootnote 4 add technical, organizational, and anecdotal evidence for blackboard uses. While some nineteenth century classroom and laboratory spaces survive today with blackboards intact, many more of their twentieth century counterparts remain in use. More recent philosophical and sociological narratives (e.g. Barthes 1972, Barany & MacKenzie 2014, Greiffenhagen 2014) provide both contemporaneous accounts of blackboard culture, context, and practice, and frameworks for reinterpreting evidence from other settings. Marking what blackboard practice leaves behind in the present can suggest new means of tracing such practice from the past by showing connections to other more durable material practices (such as note-taking) and supporting generalizations about constraints and conditions of blackboard use.
Very few of these sources of evidence, from early modern woodcuts to academic reports to teaching manuals to commercial ephemera to plans to photographs, display blackboard mathematical practice directly. Each must be interpreted in view of specific contexts and actors to understand the conditions and assumptions behind past blackboard actions and the patterns of mathematical activity they supported. Marking out what was possible, imagined, and taken for granted, one can delimit and project concrete actions, what they meant, and how they amounted to mathematical practice.
5 Reconstruction
To understand mathematical practice in its specific time and place requires reconstructing actions and meanings from available traces. Historians make sense of these traces by identifying relevant contexts that delimit and explain how those traces came about, what they might have meant, and to whom. Traces gain meaning through a multiplication of contexts: the 1806 École Polytechnique note about repainting blackboards gives information about mathematical practice because, from other sources, we know something about the role of mathematics in the school’s curriculum, the conceptual elements of that curriculum that survive in other pedagogical media such as posters or textbooks, the relationship between administrative records and the actions they document and authorize, the material parameters of writing with chalk on painted surfaces (even as the exact chalk and surfaces in question do not survive), the living traditions of lecturing and examination in mathematics and other fields, and much else.
5.1 Putting sources together
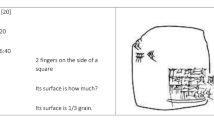
Mathematical practices themselves produce objects that, when assembled and interpreted, can establish meaningful contexts. Textual practices rendered on durable media survive from a wide range of times and places, and permit detailed inferences about both textual and para- or non-textual aspects of mathematical practice and knowledge (Herreman 2001).Footnote 5 Sometimes, textual traces form their own kinds of context, especially when assembled into coherent wholes whose ruly organization can be read back into individual inscriptions. Systematically examining a collection of more than 800 clay tablets excavated in the late nineteenth century, for instance, can give a picture of an entire Mesopotamian scribal curriculum that, when viewed as a whole, suggests how scribes learned to use and interpret specific kinds of writing related to numbers and magnitudes, which in turn implies specific computational practices (Proust 2008). Where individual tablets show the end product of a moment of scribal-mathematical practice, a sample across a curriculum (even if minuscule compared to all the tablets produced in that curriculum) can suggest underlying practices because curricula follow identifiable ruly patterns related to learning and applying skills and methods.
Surviving clay tablets are only a tiny fraction of the artifacts produced in ancient mathematics, and attributing their original contexts and functions can require extraordinarily resourceful and subtle interpolation (Ritter 1993; Robson 2008), but they were nonetheless produced directly in the course of the practices being reconstructed. For most histories of ancient Greek mathematics, by contrast, most available text survives only through long chains of copying, revising, and circulating writing on media less durable and less well-preserved than clay tablets. The oldest surviving fragments lack diagrams, arguments, and explanations found in later documents, but were likely produced in contexts where comparable apparatus existed in non-surviving media. Greek mathematical texts are thus reassembled and interpolated from fragmentary and sometimes contradictory traces, using contextual knowledge not just about ancient mathematics but about the long history of scribal and critical cultures through which ancient texts have been transmitted and interrogated (Chemla 2012, ch. 1–3). Where individual authoritative texts may be elusive, comparing features from the texts and subtexts of massed corpora—what collections of Greek-attributed text tend to include, presume, and imply—can still permit quite precise conclusions about how, for instance, ancient geometers approached problems of geometric construction and deduction (Netz 1999; Sidoli & Saito 2009).
Assumptions about how practice and writing relate to each other play a crucial role in filling in the vast gaps that surround the comparatively meager traces that survive from ancient practice. To reconstruct mathematical reasoning, one must develop an idea of what would not be recorded as well as what would be. This involves what Wagner (2009) calls a “critical economy of anachronisms,” a choice of what to presume about the relationship between past and present mathematics to allow meaningful inferences about the former, and what deliberately to unlearn so that one can grapple with what made the past different. In the 1970s, professional, methodological, and philosophical differences informed an impassioned debate over how to reconstruct the reasoning behind geometric relationships in ancient texts that appeared to modern eyes to correspond to algebraic deductions that were far easier to understand (Wagner 2009; Schneider 2012; Robson 2008, ch. 9). Some saw evidence of ancient algebraic or quasi-algebraic thought in the resonances between ancient geometry and modern algebra; others insisted on the radical difference between ancient geometric reasoning and its later known algebraic counterparts. These different perspectives gave starkly different accounts of the nature and significance of ancient mathematical practice from similar textual evidence.
Corpora of surviving texts constitute their own mathematical contexts, beyond the lost texts one might reconstruct on their basis. Curating and transmitting mathematical texts, for instance as pedagogical or philosophical canons, is in itself a kind of mathematical practice (Netz 1998). Collections of canonical texts can consequently be read as evidence of the mathematical values and practices of the scholars who assembled them and the conditions under which those scholars interpreted them (Ying 2014). Pedagogical contexts have, historically, been especially rich settings for producing and propagating texts that can support analyses of mathematical knowledge and practices that reach far beyond the classroom (Meskens 2013; Schubring 2019). Mathematical practices that assemble and preserve texts, by that virtue, promote the survival of sources that those who curated them considered especially important. These historical records are biased, but the bias is informative. The ruliness of mathematical corpora, including norms for structuring texts and collections and for relying on explicit and implicit relationships between texts, allow surviving sources to speak for those that do not survive.
5.2 Beyond the page
Every mathematical text is produced and used in its own social and institutional context, with its own interpretive traditions. Many of these contexts can be inferred from those texts and can in turn show how those texts were used and what they meant to their users (Høyrup 1994). Texts’ preoccupations and presumptions embed them in philosophical frameworks with practical implications for textual and para-textual mathematical reasoning (Mancosu 1996; Bos 2001). Often, genres and structures within texts—tables, examples, indices—imply rules for how they were constructed or how they should be read. Asking how to make sense of a text in the scientific and cultural contexts of its production and use can show what mathematical problems meant, what competences and cognitive facilities were required to understand and solve them, and how these competences and facilities might manifest in settings away from the text in question (Netz 2002; Brechenmacher 2007; Goldstein 1995, 2008; Chemla 2009, 2015; Barany 2012; Ferreirós 2016; Wagner 2017).
Mathematical texts often imply or refer explicitly to contexts and practices of mathematics beyond the page. To reconstruct the material contexts where such texts were read and applied, or from which such texts derived, historians connect these texts to sources in a wide range of other genres, and to a variety of kinds of more-or-less-ruly knowledge. Legal, commercial, and pedagogical texts, ruly in their own ways, join with maps, instruments, manufactures, and other products of mathematical practice to give shape to those practices and their meanings. These sources, while offering insight into mathematical concepts and applications alike, tend to hinge on uses and interpretations of mathematics in settings where mathematical knowledge is just one tool or concern among many.
Beyond its varied historiographical meanings, mathematical practice has also had specific historical meanings whose investigation has offered insights into their historiographical counterparts. Among the most significant is the model of mathematical practice associated with “practical” or “mixed” mathematics in early modern Europe, and the associated identity of “mathematical practitioner” that emerged in this period (Johnston 1991; Cormack et al. 2017; cf. Epple et al. 2013). The early historiography of early modern practical mathematics plied large collections and close readings of pedagogical and commercial texts to track how practitioners built on each other’s writing and connected mathematical learning to other kinds of activity, such as surveying, engineering, navigation, astronomy, or alchemy. Tracking descriptions and adaptations of specific methods across sources, one can infer what techniques a specific practitioner might have known; following those techniques in the present and marking errors and divergences can then give insight into how practitioners combined available techniques for specific applications, such as projecting a map (Leitão & Gaspar 2014). New, hybrid genres of mathematical texts showed new conceptions of what mathematics was and how it could be done (Taylor 2011). To reconstruct how those conceptions translated into practical mathematics, historians have looked to student notes, commercial patents, legal documents, and other sources to characterize how, where, and why mathematical practitioners plied their practices (e.g. Jardine 2018; Schotte 2019).
Reconstructions of mathematical practice, whether the conceptual reasoning of an ancient geometer or the navigational calculation of an early modern sailor, rely on the possibility of following along with past mathematical procedures and implications. One understands an ancient proof, in part, by learning to be convinced by it, adopting the contextually-informed perspectives that make it convincing. Because historical moments of conviction must inevitably depend to some extent on thoughts and actions that cannot be traced directly from materials available in the present, their historical reconstruction must inevitably depend on thoughts and actions rooted in the interpreter’s conception of mathematics. The ruliness of mathematics powerfully constrains how past practices might have added up. But the same rules can have multiple manifestations, and that same ruliness can muddy distinctions between the necessary and contingent, and leave room for misleading excesses of empathy casting modern understandings backward.
6 Genealogy
For some kinds of source material and some kinds of historical questions, it can be possible to trace relationships between mathematical practices changing over time even as major features of their contexts and meanings in a given moment remain obscure (Goldstein 2019). The mechanisms of cultural, social, political, and other forms of reproduction linking societies across time can be confoundingly obscure, and subject to fundamental theoretical disagreement. The mechanisms of mathematical reproduction, in comparison, are relatively straightforward, confined to a manageable mix of contexts of teaching and learning, of reading and writing, of making sense out of mathematical things alone and together with others—though not, to be sure, free from interpretive divergences and difficulties. These mechanisms can be traced through a variety of kinds of evidence, and as with reconstruction, some aspects are more susceptible to such tracing than others.
The basic method of the genealogy of mathematical practice is to identify something that changes over time, and then to interpret that change in its relevant contexts to understand some aspect of mathematical practice and its corresponding transformations. Particularly in the mathematical tradition of the history of mathematical practice, the changing entity could be a mathematical concept in itself, as inferred at specific times and places from written sources (e.g. Youschkevitch 1976; Lützen 1982). Comparing concepts logically or heuristically across time can indicate models of conceptual change, and these can, in turn, suggest ways of rationally reconstructing missing elements in a sequence of conceptual development (e.g., famously, Lakatos 1976). Or one can relate sequences of concepts to each other, establishing an interlocking chain of motivations and reasoning that can suggest practices of interpretation and inquiry through the relationship between different areas of knowledge and application (Kjeldsen & Lützen 2015).
Evidence from textual circulation, transmission, commentary, and adaptation that supports reconstructions of practices and contexts in a given time (e.g. Chemla 2012) can also, of course, be interpreted as evidence of changing ideas and practices over time (e.g. Rommevaux et al. 2001). For the latter, one marks errors, emendations, and divergences not to undo them to recover an original but rather to understand what scribal and interpretive practices made those changes likely, unremarkable, or meaningful. Combined with other sources of information about interpretive contexts, comparing successive readings and rewritings of a source allows nuanced accounts of changing practices and frameworks (e.g. Goldstein 1995, Guicciardini 1999, Ehrhardt 2011). Where relatively complete networks of textual circulation can be established, more likely (but still not common) for more recent mathematics, small variations in expression signal gradual appropriations and appreciations of new techniques (Roque 2015). Continuities and changes to elements of composition such as size, format, and layout can supply otherwise elusive contextual information, and can be especially informative for understanding the significance of major transitions such as from manuscript to print (De Young 2012). Philosophers have attempted to classify other aspects of variation over time under the rubric of style, marking points of variability and stabilization in relations between mathematical texts (Rabouin 2017).
Such changes suggest features of the broader contexts that constrain and enable different kinds of mathematical practice. What Epple (2011) calls the “epistemic configurations” of mathematical thought and practice set the terms for any mathematical activity, textual or otherwise, and can depend on social, technical, and other developments that reach far beyond the specific mathematical questions or circumstances surrounding a concept or activity of interest. Textual evidence must then be understood as a situated intervention within an epistemic configuration, symptomatic but not determinative of the technical matrix that gives it meaning. Many aspects of these configurations are simply irrecoverable. Epple compares their reconstruction to reproducing a musical performance from a piece of sheet music. Without the identical instruments, performance spaces, musical training, and cultural contexts of listening and appreciation, one can never have an authentic experience of a past performance in its integral entirety. But performing the music on our own terms nonetheless gives substantive information about the techniques, expectations, affects, and qualities of its past manifestations, and comparing music from different contexts can show, moreover, how these changed between those contexts even if the whole of what was changing remains inaccessible.
The concrete labor of mining and its associated mathematical practices exemplify this well. There is relatively little direct evidence of such labor and practice from the eighteenth century, and technical manuals and surveys are limited and distorted guides. However, read in the proper contexts, changes in successive editions of such documents can show the development of precise concerns, expectations, and technical responses in underground surveying and related practices (Morel 2018). In a more theoretical context, Friedman (2018) traced successive conceptualizations of the practice of paper folding, navigating between material and philosophical parameters to understand what folding meant to successive theorists in and about mathematics.
Stepping away from fine-grained chains of textual transformation, such text-and-context approaches to genealogy can be used to pick out larger-scale distinctions across longer times and wider geographies. Focusing on a single identifiable mathematical problem, such that a genealogical relationship can be inferred even from a vastly disconnected sequence of fragments, Netz (2004) identifies the emergence of different modes of formulation, methods of solution, and frameworks of technical practice and interpretation over centuries of mathematical culture around the Mediterranean. While precise mechanisms of these changes in mathematical practice remain obscure, their nature and implications stand out across the major shifts excerpted from a long historical sequence of adaptation and reinterpretation.
Notwithstanding genealogies focused on clay tablets, mathematical instruments, erasable writing surfaces, and other entities that are not, in themselves, mathematical texts, genealogies of mathematical practice predominantly center on conventional mathematical texts precisely because such texts are central to so much of mathematical practice, written and otherwise. Because mathematical training and practice involves producing, reproducing, interpreting, manipulating, and deploying texts, historians can identify features and distinctions among a great variety of mathematical practices by interrogating, in turn, the variegated texts they involved. The exegetical practice of historical interpretation, in this respect, has much in common with the exegetical practice of many kinds of text-oriented mathematics, reasoning from reading to doing and writing and back again to reading, and so on (see Barany & MacKenzie 2014). By the same token, other modes and media of mathematical transmission are all the more difficult to trace, and rely all the more on presumptions about the ruly qualities of mathematical writing to support inferences about what was not written.
7 Conclusion: history’s traces
Historians investigate the past, but the past in itself is not the point of the investigation. Different traditions of historical inquiry have been defined, in part, by how they mobilize perspectives on the past to investigate different kinds of relationships: conceptual, cognitive, contextual, material, pedagogical, philosophical, and many others. Such mobilizations involve yet more relationships, explicit and implicit, between texts and actions, production and reception, materials and affordances, preservation and corruption, contexts of use and of historical analysis. Historians mass these relationships by formulating traces of the past that tie what one can interrogate in the present to what one can stipulate about the past.
One aspect of mathematics that makes it identifiable as mathematics is the practice of supposing and imposing order. Historically, creators and interpreters of mathematics have sought and used such orderly perspectives on numbers, measures, shapes, and signs. Historians, in their own ways, seek interpretive order from the unruly patchwork of relations discernible through traces from various kinds of historical (often textual) evidence. These parallel projects of ordering offer both a resource for histories of mathematical practice and a challenge. The ruliness of mathematics constitutes a resource for ordering history’s traces, and this makes the resulting historical interpretations dependent on how one understands and mobilizes the ruliness of mathematics.
In history as in mathematics, tracing is also erasing. By picking out specific contexts and transformations, historians constitute historical relations by making limited traces stand for constellations of past knowledge and practice that remain in nearly every particular untraced and untraceable. Most of the past, like most of the present, does not exist in the form of legible relationships, prone to exegesis. Most of the past, like most of the present, does not stand ready as a source of historical, mathematical, or any other kind of systematic knowledge. If there is one lesson in the history of science writ large, it is that it takes a tremendous amount of collective work and imagination to make knowledge from the world. Making orderly relations by tracing and interpreting is also an act of banishing the unruly world that escapes, subverts, complicates, or defies those relations.
Histories of mathematical practice, in this regard, make order out of making order, establishing relations in time and space between past efforts to establish, record, and mobilize other kinds of relations. Where actors in the past ordered and erased, historians establish their own interpretive relations by tracing both the past’s ordering and erasing, inferring from surviving artifacts and regimes what actions and understandings had to be subordinated or exposed to loss in the process. Such interpretation is inevitably recursive, with historical (in the sense of made by historians) understandings projecting and informed by historical (in the sense of being made in the past) understandings. The promises and limits of histories of mathematical practice are, by this virtue, those of the wider collection of interpretive regimes for making sense of understanding.
Notes
This brief overview sets aside many other often-commingled traditions in the history of mathematics, as varied as biography, orientalism, philology, archaeology, biblical humanism and antiquarianism, universal history, Marxist theory, and speculative fiction. The history of the history of mathematics is, in its own way, a chimeric subject that has been addressed from multiple mixing disciplinary perspectives, including mathematical historiography, book history, disciplinary and institutional history, history of science, philosophy of science, literary studies, and mathematics. See Richards (1995), Dauben & Scriba (2002), Wardhaugh (2012), Remmert et al. (2016).
Archives of the École Polytechnique, Palaiseau, France, with thanks to Olivier Azzola.
Especially notable is the Princeton Mathematics Oral History Project, AC057, Princeton University Archives, Department of Rare Books and Special Collections, Princeton University Library.
Wardhaugh (2010) gives an accessible introduction to text-oriented historical methods.
References
Ackerberg-Hastings, A., Kidwell, P., & Roberts, D. (2008). Tools of American mathematics teaching, 1800–2000. Baltimore: Johns Hopkins University Press.
Alcott, W. A. (1843). Slate and black board exercises. New York: Newman.
Aubin, D., & Paumier, A.-S. (2016). Polycephalic Euclid? Collective practices in Bourbaki’s history of mathematics. In Remmert et al. (Eds.) Historiography of Mathematics in the 19th and 20th Centuries (pp. 185–218). Cham: Birkhäuser.
Barany, M. J. (2012). ‘That small and unsensible shape’: Visual representations of the Euclidean point in sixteenth-century print. Spontaneous Generations, 6, 148–159.
Barany, M. J. (2014). Savage numbers and the evolution of civilization in Victorian prehistory. British Journal for the History of Science, 47(2), 239–255.
Barany, M. J., & MacKenzie, D. (2014). Chalk: Materials and concepts in mathematics research. In C. Coopmans, et al. (Eds.), Representation in scientific practice revisited (pp. 107–129). Cambridge: MIT Press.
Barthes, R. (1972). The Brain of Einstein. In R. Barthes, Mythologies. Trans. A. Lavers (pp. 68–70). New York: Farrar, Straus and Giroux.
Bos, H. J. M. (2001). Redefining geometrical exactness: Descartes’ transformation of the early modern concept of construction. New York: Springer.
Brechenmacher, F. (2007). La controverse de 1874 entre Camille Jordan et Leopold Kronecker. Revue d’histoire des mathématiques, 13, 187–257.
Bumstead, J. (1841). The blackboard in the primary school. Boston: Perkins & Marvin.
Chemla, K. (2009). On mathematical problems as historically determined artifacts: Reflections inspired by sources from ancient China. Historia Mathematica, 36, 213–246.
Chemla, K. (Ed.). (2012). The history of mathematical proof in ancient traditions. Cambridge: Cambridge University Press.
Chemla, K. (2015). Proof, generality and the prescription of mathematical action: A nanohistorical approach to communication. Centaurus, 57, 278–300.
Claris, G. (1895). Notre École Polytechnique. Paris: Librairies-imprimeries réunies.
Cormack, L. B., Walton, S. A., & Schuster, J. A. (Eds.). (2017). Mathematical practitioners and the transformation of natural knowledge in early modern Europe. Cham: Springer.
Creager, A. (2013). Life atomic: A history of radioisotopes in science and medicine. Chicago: University of Chicago Press.
Dauben, J. W., & Scriba, C. J. (Eds.). (2002). Writing the history of mathematics: Its historical development. Basel: Birkhäuser.
De Young, G. (2012). Mathematical diagrams from manuscript to print: Examples from the Arabic Euclidean transmission. Synthese, 186(1), 21–54.
Ehrhardt, C. (2011). Évariste Galois: La fabrication d’une icône mathématique. Paris: Éditions de l’École des Hautes Études en Sciences Sociales.
Epple, M. (2011). Between timelessness and historiality: On the dynamics of the epistemic objects of mathematics. Isis, 102, 481–493.
Epple, M., Kjeldsen, T. H., & Siegmund-Schultze, R. (Eds.) (2013). From ‘mixed’ to ‘applied’ mathematics: Tracing an important dimension of mathematics and its history. Oberwolfach Reports, 10, 657–733.
Ferreirós, J. (2016). Mathematical knowledge and the interplay of practices. Princeton: Princeton University Press.
Fenster, D. D. (1999). Leonard Dickson’s history of the theory of numbers: An historical study with mathematical implications. Revue d’histoire des mathématiques, 5, 155–175.
Friedman, M. (2018). A history of folding in mathematics: Mathematizing at the margins. Cham: Springer.
Ginzburg, C. (2012). Threads and traces: True, false, fictive. Trans. A. C. Tedeschi & J. Tedeschi. Berkeley: University of California Press.
Grabiner, J. V. (1975). The mathematician, the historian, and the history of mathematics. Historia Mathematica, 2, 439–447.
Graham, L., Lepenies, W., & Weingart, P. (1983). Functions and uses of disciplinary histories. Dordrecht: Reidel.
Goldstein, C. (1995). Un théorème de Fermat et ses lecteurs. Saint-Denis: Presses Universitaires de Vincennes.
Goldstein, C. (2008). How to generate mathematical experimentation and does it provide mathematical knowledge? In U. Fest, et al. (Eds.), Generating experimental knowledge (pp. 61–85). Berlin: MPIWG.
Goldstein, C. (2010). Des passés utiles: mathématiques, mathématiciens et histoires des mathématiques. Noesis, 17, 135–152.
Goldstein, C. (2019). Long-term History and Ephemeral Configurations. In B. Sirakov, P. Ney de Souza & M. Viana (Eds.), Proceedings of the International Congress of Mathematicians—Rio de Janeiro, 2018 (Vol. 1, pp. 487–522). World Scientific.
Greiffenhagen, C. (2014). The materiality of mathematics: Presenting mathematics at the blackboard. British Journal of Sociology, 65(3), 502–528.
Guicciardini, N. (1999). Reading the Principia: The debate on Newton’s mathematical methods for natural philosophy from 1687 to 1736. Cambridge: Cambridge University Press.
Herreman, A. (2001). La mise en texte mathématique. Methodos. https://doi.org/10.4000/methodos.45.
Høyrup, J. (1994). In measure, number, and weight: Studies in mathematics and culture. Albany: State University of New York Press.
Jardine, B. (2018). Instruments of statecraft: Humphrey Cole, Elizabethan economic policy and the rise of practical mathematics. Annals of Science, 75(4), 304–329.
Johnston, S. (1991). Mathematical practitioners and instruments in Elizabethan England. Annals of Science, 48(4), 319–344.
Jones, A., Proust, C., & Steele, J. M. (Eds.). (2016). A mathematician’s journeys (pp. 61–106). Cham: Springer.
Kjeldsen, T. H., & Lützen, J. (2015). Interactions between mathematics and physics: The history of the concept of function—teaching with and about nature of mathematics. Science and Education, 24, 543–559.
Lakatos, I. (1976). Proofs and refutations: The logic of mathematical discovery. Ed. J. Worrall & E. Zahar. Cambridge: Cambridge University Press.
Lambert, K. (2013). A natural history of mathematics: George Peacock and the making of English algebra. Isis, 104(2), 278–302.
Leitão, H., & Gaspar, J. A. (2014). Globes, rhumb tables, and the pre-history of the Mercator projection. Imago Mundi, 66(2), 180–195.
Lützen, J. (1982). The prehistory of the theory of distributions. New York: Springer.
Lützen, J., & Purkert, W. (1994). Conflicting tendencies in the historiography of mathematics: M. Cantor and H.G. Zeuthen. In E. Knobloch, & D. E. Rowe (Eds.), The history of modern mathematics (Vol. III, pp. 1–42). San Diego: Academic Press.
Mancosu, P. (1996). Philosophy of mathematics and mathematical practice in the seventeenth century. Oxford: Oxford University Press.
Meskens, A. (2013). Practical mathematics in a commercial metropolis: Mathematical life in late 16th century Antwerp. Dordrecht: Springer.
Morel, T. (2018). Five lives of a Geometria subterranea (1708–1785): Authorship and knowledge circulation in practical mathematics. Revue d’histoire des mathématiques, 24, 207–258.
Netz, R. (1998). Deuteronomic texts: Late antiquity and the history of mathematics. Revue d’histoire des mathématiques, 4, 261–288.
Netz, R. (1999). The shaping of deduction in Greek mathematics. Cambridge: Cambridge University Press.
Netz, R. (2002). Counter culture: Towards a history of Greek numeracy. History of Science, 40, 321–352.
Netz, R. (2004). The transformation of mathematics in the early Mediterranean world: From problems to equations. Cambridge: Cambridge University Press.
Owens, J. (1998). Erasable tablets. In J. Owens, Composers at work: the craft of musical composition, 1450–1600 (pp. 74–107). New York: Oxford University Press.
Phillips, C. (2015). An officer and a scholar: Nineteenth-century West Point and the invention of the blackboard. History of Education Quarterly, 55(1), 82–108.
Pillans, J. (1854). Elements of physical and classical geography. Edinburgh: Blackwood.
Proust, C. (2008). Quantifier et calculer: usages des nombres à Nippur. Revue d’histoire des mathématiques, 14, 143–209.
Pyenson, L. (1995). Inventory as a route to understanding: Sarton, Neugebauer, and sources. History of Science, 33, 253–282.
Rabouin, D. (2017). Styles in mathematical practice. In K. Chemla & E. Fox-Keller (Eds.), Cultures without culturalism: The making of scientific knowledge (pp. 262–306). Durham: Duke University Press.
Remmert, V. R., Schneider, M. R., & Sørensen, H. K. (Eds.). (2016). Historiography of mathematics in the 19th and 20th centuries. Cham: Birkhäuser.
Richards, J. L. (1987). Augustus De Morgan, the history of mathematics, and the foundations of algebra. Isis, 78, 7–30.
Richards, J. L. (1995). The history of mathematics and l'esprit humain: A critical reappraisal. Osiris, 10, 122–135.
Richards, J. L. (2006). Historical mathematics in the French eighteenth century. Isis, 97, 700–713.
Ritter, J. (1993). Les Pratiques de la raison en Mésopotamie et en Egypte aux IIIe et IIe millénaires. Thesis, Université de Vincennes à Saint-Denis (Paris VIII).
Robson, E. (2008). Mathematics in Ancient Iraq: A social history. Princeton: Princeton University Press.
Robson, E., & Stedall, J. (Eds.). (2009). The Oxford handbook of the history of mathematics. Oxford: Oxford University Press.
Rommevaux, S., Djebbar, A., & Vitrac, B. (2001). Remarques sur l’histoire du texte des Éléments d’Euclide. Archive for History of Exact Sciences, 55(3), 221–295.
Roque, T. (2015). L'originalité de Poincaré en mécanique céleste: pratique des solutions périodiques dans un réseau de textes. Revue d’histoire des mathématiques, 21(1), 41–109.
Sarton, G. (1936). The study of the history of mathematics. Cambridge: Harvard University Press.
Schneider, M. R. (2012). Contextualizing Unguru’s 1975 attack on the historiography of ancient Greek mathematics. In Remmert et al. (Eds.) Historiography of Mathematics in the 19th and 20th Centuries (pp. 245–267). Cham: Birkhäuser.
Schotte, M. (2019). Sailing school: Navigating science and skill, 1550–1800. Baltimore: Johns Hopkins University Press.
Schubring, G. (Ed.). (2019). Interfaces between mathematical practices and mathematical education. Cham: Springer.
Sidoli, N., & Saito, K. (2009). The role of geometrical construction in Theodosius's spherics. Archive for History of Exact Sciences, 63(6), 581–609.
Taylor, K. (2011). Vernacular geometry: Between the senses and reason. BSHM Bulletin, 26(3), 147–159.
Wagner, R. (2009). For some histories of Greek mathematics. Science in Context, 22(4), 535–565.
Wagner, R. (2017). Making and breaking mathematical sense: Histories and philosophies of mathematical practice. Princeton: Princeton University Press.
Wardhaugh, B. (2010). How to read historical mathematics. Princeton: Princeton University Press.
Wardhaugh, B. (Ed.). (2012). The History of the history of mathematics: Case studies for the seventeenth, eighteenth and nineteenth centuries. Oxford: Peter Lang.
Warwick, A. (2003). Masters of theory: Cambridge and the rise of mathematical physics. Chicago: University of Chicago Press.
Wittgenstein, L. (1953). Philosophical investigations. Trans. G.E.M. Anscombe. Oxford: Basil Blackwell.
Wylie, C. (2012). Teaching manuals and the blackboard: Accessing historical classroom practices. History of Education, 41(2), 257–272.
Ying, J.-M. (2014). Mathematical canons in practice: The case of nineteenth-century Korean scholar Nam Pyŏng-Gil and his evaluation of two major algebraic methods used in East Asia. East Asian Science, Technology and Society, 8, 347–362.
Youschkevitch, A. P. (1976). The concept of function up to the middle of the 19th century. Archive for History of Exact Sciences, 16(1), 37–85.
Acknowledgements
I thank the special issue’s editors, the journal’s editor in chief, this article’s anonymous referees, and especially Catherine Goldstein for their engagement, encouragement, and suggestions. No funding bodies were harmed in the making of this article, at least not directly.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Barany, M.J. Histories of mathematical practice: reconstruction, genealogy, and the unruly pasts of ruly knowledge. ZDM Mathematics Education 52, 1075–1086 (2020). https://doi.org/10.1007/s11858-020-01175-5
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11858-020-01175-5