Abstract
Much remains under-researched in how learners make use of domain-specific feedback. In this paper, we report on how learners’ can be supported to overcome logical circularity during their proof construction processes, and how feedback supports the processes. We present an analysis of three selected episodes from five learners who were using a web-based proof learning support system. Through this analysis we illustrate the various errors they made, including using circular reasoning, which were related to their understanding of hypothetical syllogism as an element of the structure of mathematical proof. We found that, by using the computer-based feedback and, for some, teacher intervention, the learners started considering possible combinations of assumptions and conclusion, and began realising when their proof fell into logical circularity. Our findings raise important issues about the nature and role of computer-based feedback such as how feedback is used by learners, and the importance of teacher intervention in computer-based learning environments.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In research on the teaching and learning of proof and proving, an under-researched issue is the extent to which students are competent in identifying logical circularity in proofs and how such competency can be enhanced (Hanna and de Villiers 2008; Sinclair et al. 2016; Stylianides et al. 2016). Rips (2002) has argued that the psychological study of reasoning should include a natural interest in patterns of thought such as circular reasoning, since such reasoning may indicate fundamental difficulties that people may have in constructing, and in interpreting, even everyday discourse. However, Rips claims that up until his study in 2002 there appeared to be no prior empirical research on circular reasoning. While Rips reports on a study of young adults, Baum et al. (2008) report findings with younger students—indicating that by 5 or 6 years of age, children show a preference for non-circular explanations and that this appears to have become robust by the time youngsters are about 10 years of age.
While learners’ preference for non-circular explanations may be robust by the time they are 10 years old, within mathematics education Heinze and Reiss (2004) report that from grade 8 to 13 in Germany an unchanging two-thirds of pupils fail to recognise circular arguments in mathematical proofs. Such evidence illustrates that pupils are in need of considerable support in order to identify and overcome circular reasoning in mathematical proofs. As Freudenthal (1971) observed “you have to educate your mathematical sensitivity to feel, on any level, what is a circular argument” (p. 427). All these studies, and the statement by Freudenthal, suggest that there are still many aspects to be examined in order to have deeper understanding of students’ ways of thinking concerning deductive proofs, so that they can be provided with better learning support.
Considering the current situation and gaps described above, this paper explores issues of how learners’ can be supported to overcome logical circularity during their proof construction processes, and how feedback supports the processes. We particularly focus on learners’ use of feedback as the latter is a key aspect of assessment for learning and something which is recognised as “one of the most powerful influences on learning and teaching” (Hattie and Timperley 2007, p. 81). Despite considerable research related to assessment and feedback there remain many open questions. In particular, much remains under-researched about how domain-specific formative feedback can improve learners’ learning processes. For example, Stylianides et al. (2016) state that it is necessary to investigate “productive ways for assessing students’ capacities to engage not only in producing proof but also to engage in processes that are ‘on the road’ to proof” (p. 344).
The aim of this paper is to consider an overarching question of how feedback can support learners who accept or construct a proof with errors. In order to achieve this purpose, in this paper we work with the following specific research questions (RQs), which we consider as useful to explore and expand our thinking on how to support students’ proving processes;
RQ1: What patterns of proof construction processes can be identified as learners use the web-based learning support system?
RQ2: How is the feedback from the online system used by learners to overcome logical circularity during proof construction?
To address our research questions, we first clarify the nature of logical circularity in geometrical proofs and why students might accept or construct a proof that contains a logical circularity (Sect. 2). In particular we show that issues with propositions and hypothetical syllogism are the underpinning ideas that can inform feedback to support students’ proof learning. In Sects. 3 and 4, we review relevant literature on learners’ use of feedback, including computer-based feedback, and develop conceptual ideas for characterising the types of feedback provided by our web-based learning support system for learning deductive proofs (hereafter, the system). In Sect. 5, after describing our system, we provide our methodology for studying the use of computer-based feedback during the proof construction process. We present, in Sect. 6, an analysis of selected episodes collected as students worked on proof problems using the system. These episodes qualitatively illustrate how learners who have just started learning to construct mathematical proofs made various mistakes, including using circular reasoning, and how these relate to the use of their universal/singular propositions and hypothetical syllogisms in their proof construction processes. Finally, in Sects. 7 and 8, we discuss our findings and answer our research questions. Through answering our research questions and subjecting our findings to critical discussion, we aim to provide insights into productive ways of using assessment in proof learning, as well as into issues related to the teaching and learning of mathematics with computer-based learning environments, and methodological approaches to studying learning processes.
2 Logical circularity in geometrical proofs
We begin by clarifying logical circularity in deductive proving. In mathematics, Euclid’s Elements is one of the oldest texts that organised various mathematical statements logically. Each proposition is carefully ordered so that only already-proved propositions are used to prove new propositions. Thus, for example, the proposition ‘the base angles of an isosceles triangle are equal’ is not proved by using an angle bisector, as is common in current textbooks, because this can fall into logical circularity if a geometric construction of angle bisector is proved by using the proposition that the base angles of an isosceles triangle are equal. Such an approach entails assuming just what it is that one is trying to prove (Weston 2000, p. 75). In logic, reasoning using circular arguments is considered a fallacy as the proposition to be proved is assumed (either implicitly or explicitly) in one of the premises, and this results in logical circularity.
Such circular reasoning can happen within a proof. For example, Bardelle (2010) provides an example of some undergraduate mathematics students in Italy being presented with the diagram in Fig. 1 as a ‘visual proof’ of Pythagoras’ theorem. The students were asked to use the figure to help them develop a written proof of the theorem.
Bardelle relates how one student focused on the rectangles that surround the central square. By defining a as the short side and b the longer one (as in Fig. 2), the student used Pythagoras’ theorem to get \(c=\sqrt {{a^2}+{b^2}}\) and thence, by squaring both sides, the student obtained Pythagoras theorem c2 = a2 + b2. This is another, and rather local example, of a student using a circular argument or circulus probandi (arguing in a circle). While we acknowledge it is important to educate students to evaluate critically various processes of circular reasoning between theorems or within proofs, in this paper we focus on the latter because our focus is lower secondary school students who have just started learning deductive proofs.
A rectangle from Fig. 1
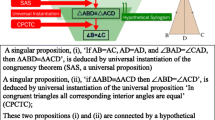
In the case of the teaching of proof in geometry, triangle congruency is commonly used (Jones and Fujita 2013). In this context at least two types of logical argument are employed to structure deductive reasoning. One is universal instantiation, which takes a universal proposition (such as, in congruent triangles all corresponding interior angles are equal) and deduces a singular proposition (for example, if ∆ABD ≡ ∆ACD, then angle ABD = angle ACD). The other type of logical argument is hypothetical syllogism, where the conclusion necessarily results from the premises (Miyazaki et al. 2017a).
Appreciation of proof structure is recognised as an important component of learner competence with proof (Heinze and Reiss 2004; McCrone and Martin 2009; Miyazaki et al. 2017a), and this inclusion might relate to why students accept or construct a proof with logical circularity. For example, Kunimune et al. (2010) report on data from grade 8 and 9 students, showing that as many as a half of grade 9 and two-thirds of grade 8 pupils were unable to determine why a particular geometric proof presented to them was invalid; that is, they could not see circular reasoning in the proof in which the conclusion (‘the base angles of an isosceles triangle are equal’) was used as one of the premises for deducing the two triangles are congruent. We consider this oversight as being due to a lack of understanding of the role of syllogism, which would lead to accepting or constructing a proof which includes a circular argument. A proof of the proposition ‘the base angles of an isosceles triangle are equal’, for example, can be done by connecting two deductions: (1) deducing two triangles are congruent; (2) deducing if two triangles are congruent then corresponding angles are equal. However, if a learner lacks an understanding of hypothetical syllogism, he or she may use ‘the base angles of an isosceles triangle are equal’ as one of the premises in order to deduce that the base angles of an isosceles triangle are equal. In so doing, he or she would be using a circular argument.
Our interest in this paper is in how students who accept or construct such proofs can be supported in their learning of proof structure, and we focus on the use of computer-based feedback in this paper as an example of a way of providing such support.
3 Feedback supporting learners’ proof construction processes
3.1 Feedback for learning
Feedback is one of the strategies for assessment of learning that is known to promote learning (Black and Wiliam 2009). Amongst many definitions of feedback, we take feedback as “information with which a learner can confirm, add to, and overwrite, tune, or restructure information in memory, whether that information is domain knowledge, meta-cognitive knowledge, beliefs about self and tasks, or cognitive tactics and strategies” (Winne and Butler 1994, p. 5740). Shute (2008) identified two main functions of formative feedback: verification (simple judgement of whether an answer is correct) and elaboration (providing relevant cues to guide the learner towards the correct answer). Clark (2012) states “The objective of formative feedback is the deep involvement of students in meta-cognitive strategies such as personal goal-planning, monitoring, and reflection” (p. 210), and, as such, it is related to self-regulated learning.
In the teaching and learning of mathematics, feedback can be used by students to choose appropriate procedures or improve problem-solving strategies. Rakoczy et al. (2013) found that written process-oriented feedback (i.e. “suggesting how and when a particular strategy is appropriate” p. 64) might foster grade 9 students’ mathematical learning. This implies that certain types of feedback might be more effective than others. Hattie and Timperley (2007) claim that “Effective feedback must answer three major questions asked by a teacher and/or by a student” (p. 86), namely, ‘Where am I going? (What are the goals?)’, ‘How am I going? (What progress is being made toward the goal?)’, and ‘Where to next? (What activities need to be undertaken to make better progress?)’. In order to realise ‘how learners are going’, they identify the following four elements (p. 90):
-
Task: “Feedback can be about a task or product, such as whether work is correct or incorrect.”
-
Process: “Feedback information about the processes underlying a task also can act as a cueing mechanism and lead to more effective information search and use of task strategies.”
-
Self-regulation: “Feedback to students can be focused at the self-regulation level, including greater skill in self-evaluation or confidence to engage further on a task.”
-
Self: “Feedback can be personal in the sense that it is directed to the “self,” which… is too often unrelated to performance on the task.”
They argue that while task-based feedback may be the least effective form, it can help when the task information is subsequently used for “improving strategy processing or enhancing self-regulation” (pp. 90–91).
From these existing studies, and given that what makes feedback most effective for learners is complex, it remains uncertain whether, or how, a combination of task- and process-based feedback might be effective when students are learning sophisticated mathematical topics such as deductive proving.
3.2 Learners’ use of computer-based feedback
The use that learners make of computer-based feedback, defined as “assessment feedback to students created and delivered using a computer” (Marriott and Teoh 2013, p. 5), continues to be a growing interest in educational research (Wang 2011; Bennett 2011; Attali and van der Kleij 2017). Based on their meta-analysis, Hattie and Timperley (2007) reported that computer-assisted instructional feedback is one of the effective forms of feedback in that it can provide cues or reinforcement for improving learning. Narciss and Huth (2006, p. 310) termed informative tutoring feedback as that providing “strategically useful information for task completion, but [which] does not immediately present the correct solution” and bug-related tutoring feedback as that “guiding students to detect and correct errors.” They found both to be particularly effective because such feedback can provide useful strategies to correct errors as well as requiring learners to apply corrective ways to further attempts to solve the problems. This is similar to process-based feedback described above.
Nevertheless, learning with computer-based feedback is not clear-cut. For example, Attali and van der Kleij (2017) report on their experimental research in which they examined the feedback effects of different question formats (multiple choice/constructed response), timing (immediate/delayed) and types (knowledge or results/correct responses/elaborated feedback). They found that the effects of different types of feedback and timing can vary and that this might be related to learners’ initial responses to the problems and their prior knowledge concerning the problem. As such, elaborated (or process-based) feedback is useful in general, but when the learners’ prior knowledge to the problem is low, it is not particularly effective. In contrast to this finding, Fyfe et al. (2012) found that feedback can be more beneficial for learners with little prior knowledge compared with those who have some knowledge. Perhaps, as Attali and van der Kleij (2017) wrote, it is important that “Prior knowledge is considered to be the most important factor to consider for adapting instruction to an individual learner” (p. 167), something that might indicate the importance of human interventions in the computer-learning environment. Panero and Aldon (2016) also reported that, with technology-based learning environments, both teachers and students might become more effective at using feedback by seeking efficient ways of using it.
Of these many complexities, one interesting area that needs further study is domain-specific computer-based feedback in advanced mathematical topics, such as proving, as the existing studies have rather focused on “lower-level learning outcomes such as rote memorisation” (Attali and van der Kleij 2017, p. 155).
4 A web-based system to support the learning of deductive proofs in geometry
4.1 Online feedback provided by the system
Given the various errors that learners can make in the process of learning to prove, they are likely to benefit from support and feedback not only in recognising errors but also in ways to refine their proof in accordance with the type of error they may be making. Our system is designed to support such learning (the current system is online at http://www.schoolmath.jp/flowchart_en/home.html). In particular, the system is designed to support overcoming of students’ difficulties in proofs that are particularly related to the use of universal/singular propositions and hypothetical syllogisms (see Sect. 2). As we showed in an earlier study, adopting a flow-chart format and closed/open problems can enrich the learning experience of the use of universal/singular propositions and hypothetical syllogism (see Miyazaki et al. 2017b).
In our system, flow-chart proofs (see Ness 1962) are used and various proof problems in geometry are available, including ones that involve the properties of parallel lines and congruent triangles. Learners tackle proof problems by dragging sides, angles and triangles to cells of the flow-chart proof and the system automatically transfers figural to symbolic elements so that learners can concentrate on logical and structural aspects of proofs. Feedback is shown when answers are checked. The geometry proof problems include both ordinary proof problems such as ‘prove the base angles of an isosceles triangles are equal’ (an example of a ‘closed’ problem) and problems by which learners construct different proofs by changing premises under the given limitation to draw a conclusion (these we categorise as ‘open’ problems). In the latter case, the correct answers can be reviewed so that students may be encouraged to find other proofs.
For example, the problem in Fig. 3 is intentionally designed so that learners can freely choose which premises they use to prove that AB = CD (note that information such as AB//CD is not stated explicitly at this level of problem because this problem is for practicing how to use singular and universal propositions with two-step reasoning in later stages the problems are stated with more mathematical rigor). A learner might decide, for instance, that a singular proposition that ∆ABO and ∆CDO are congruent may be used to show that AB = CD by using the universal proposition ‘If two figures are congruent, then corresponding sides are equal’. Based on OA = OC as an assumption, ∆ABO ≡ ∆CDO can be shown by assuming BO = DO and angle BOA = angle DOC using the SAS condition. However, other solutions are also possible. One approach might be to use the fact that ∆ABO ≡ ∆CDO can be shown by assuming OA = OC, angle BOA = angle DOC and angle OAB = angle OCD, using the ASA condition for congruency. Two stars show this problem has two solutions, and each of them changes to yellow when found. As learners can construct more than one suitable proof, we refer to this type of problem situation as ‘open’. This open situation can be used to scaffold students’ understanding of the structure of proofs, in particular the use of universal propositions and thinking forwards/backwards to seek premises and conclusions in proofs (see Miyazaki et al. 2015, for the case without technology).
4.2 Domain-specific computer-based feedback for supporting students’ learning of deductive proofs
In the main, our system gives bug-related tutoring feedback (Narciss and Huth 2006); that is, once a learner clicks ‘Check your answers’, something which can be done at any time, the system checks for any error via a database. These errors are recognised in terms of the use of singular/universal propositions and hypothetical syllogism. For example, Fig. 3 shows feedback for a proof of an ‘open’ problem where the proof falls into logical circularity. In this case, the conclusion AB = CD is used as the one of three conditions to deduce the congruence of triangle ∆ABO ≡ ∆CDO. As a result, the system shows a message ‘You cannot use the condition to prove your conclusion!’. This message does not provide a correct answer but is designed to prompt the learner to think why they received such a message and to re-examine their proof.
We take feedback from the system as ‘information given by the computer to learners, which they can use to check their answers, modify their answers and strategies for better proof constructions, and seek different proofs’. For describing such feedback in detail, we use Hattie and Timperley’s framework ‘Where am I going?’, ‘How am I going?’ and ‘Where to next?’.
Our system provides cues for ‘Where am I going?’ by clearly stating the goal of the problem, and for ‘Where to next?’ by giving a message such as ‘This is correct! But it is not the only answer. Find out more!’ or ‘You have found all answers’. The system also provides ‘How am I going?’ feedback through task-, process- and self-regulation feedback. ‘Self’ type feedback is outside the remit of our web-based system because it is more linked to the role of the teacher. Table 1 summarises the overall features of the system’s feedback for ‘How am I going?’.
Our research interest is in how the above computer-based feedback, in particular information for ‘How am I going?’ (task/process/self-regulation based), is used in the context of learners construction of deductive proofs in geometry.
5 Methodology
5.1 Study design, data collection and participants
We initially piloted the English-language version of the system in 2010–13 in the UK with a range of individual or grouped learners (with groups of up to 4). These learners had previously learned about congruent triangles, but none had much prior experience of deductive proof based on properties of lines and angles and congruent triangles. They used our web-based system to tackle one or more of the problems, either with or without explicit instructions from researchers. During this pilot study, it was gradually noticed that students often misused universal propositions in order to justify their reasoning, and produced proofs with logical circularity when they undertook open proof problems with two steps of reasoning.
As stated above, the web-based proof learning system was primarily developed to support learners’ learning of deductive proofs in geometry. During the pilot studies, it was evident that the system provided a research tool not only to reveal students’ lack of understanding of syllogism, but also to study the learning processes by examining how learners respond to feedback messages from the system when they make various errors. Therefore, we decided to collect data systematically from a total of 15 learners’ experiences using the system, focusing on their errors and how they used feedback during sessions that took 30–60 min. The typical session comprised the following structure:
-
First learners were introduced to the system by interviewers, during which it was explained how to use it with an introductory open problem. One computer was shared within small groups in order to encourage their collaborative learning and dialogue. If necessary, learners were reminded of the conditions for congruent triangles.
-
Following this introduction, they were asked to undertake one or two more relatively easy open problems. This was used for the interviewers to assess their initial understanding of the structure of proofs.
-
Finally, they were asked to solve problems that include two steps in the proof, and, if they were very successful, then more difficult problems.
Participants’ activities were observed and recorded by a video camera. As stated above, we particularly used the problems with one or two steps in the proof, as our participants had relatively little experience in constructing geometrical proofs. The interventions from the interviewers were kept to a minimum, because we wanted to see how the feedback from the system would be used by the learners. However, we sometimes had to give ad hoc interventions when they totally lost the notion of what they had to do, or needed clarification on what to do, etc. This is something we learnt from our early trialling; that learners can spend too long a time on just one proof problem and develop some frustrations towards learning proofs—which was not our primary research interest.
For this paper, we have selected three cases from our data; one case was a pair of high-attaining secondary school students aged 14 years (WS1 and WS2), a second case was an individual undergraduate primary trainee teacher (R), while the third case was a pair of undergraduate primary trainee teachers (J1 and J2). We chose these three cases because we found interesting reactions to the system, and the feedback received, during the proving processes as well as their experiencing of correct/incorrect reasoning. Table 2 summarises their activities and the durations of the video data.
5.2 Data analysis procedure
After initial examinations of the video data, we selected the following problem-solving episodes from each case, and then extracted in total 432 utterances, and then numbered them for data analysis.
-
WS1 and WS2: Lesson II-2 (64 utterances), III-1 (76 utterances), III-2 (63 utterances)
-
J1 and J2: II-1 (29 utterances), III-1 (36 utterances), III-2 (65 utterances), V-1 (37 utterances)
-
R: II-2 II-2 (16 utterances), III-2 (46 utterances)
We chose these cases because these episodes were particularly related to learners’ use of universal propositions and errors of logical circularity, as well as their reactions to feedback including overcoming difficulties in their proof construction processes. The methodological challenge was, as Stylianides et al. (2016) pointed out, how to assess and analyse students’ processes on the road to proof. To do so we first identified in total 36 proof construction ‘phases’. Each phase commenced with learners’ attempts to construct a proof and ended when they managed to complete a correct proof or they completely lost their directions despite receiving feedback of various kinds from the system. By identifying these phases we were able to examine the learners’ proof construction processes more closely. For identified phases, we undertook a detailed qualitative analysis to ascertain patterns of proof construction processes in terms of errors which learners made (informed by Sect. 2) and the types of feedback they received (informed by Sect. 3) and, where necessary, interventions by the interviewers. We use this analysis as evidence to answer our research questions.
For example, phase III-2/Ph2 in Table 3 is the second phase of proof construction lesson III-2. In this phase, WS1 and WS2 were undertaking a proof requiring two steps in an open problem context with the interviewer T.
In this example, pair WS1 and WS2 started their proof construction with errors. As they did not notice that they were using the conclusion to prove the conclusion (utterances 24–28), we categorised them as lacking an understanding of syllogism. Subsequently, following the process-based feedback related to logical circularity (e.g., utterance 28) and task-based feedback related to the use of a universal proposition (e.g., utterance 32), they noticed that they used the conclusion (as well as a wrong universal proposition) in their proof and corrected these by themselves (utterances 29–32). In utterance 33 they received feedback on a correct answer. The interviewer T encouraged them to find another proof. We summarise this proof construction process as a pattern ‘Proof construction with errors → Process/task based feedback → Proof construction without errors’. Our approach to the analysis of our qualitative data is to see what patterns can be identified in each case.
We are aware that the sample size is small and therefore we do not intend to propose generalised findings. Also, we do not claim effectiveness of the web-based system based on a few sessions; that is, we do not intend to claim that by using our system learners can completely overcome their difficulties in their learning of proof. Yet, as proving consists of rather complex mathematical processes, we consider qualitative analysis is necessary prior to undertaking a larger-scale study. As the students’ proof construction processes that we identified contain a rich source of information, we use these data as a step towards more in-depth research.
6 Findings
6.1 Patterns in the proof construction process
By following the above procedure of analysis, we identified a total of 36 proof construction phases. Based on an analysis of these 36 proof construction phases, we could identify 12 patterns of proof construction (see Table 4) grouped into four broad categories:
-
Proof construction without errors (PC without Es)
-
Starting proof construction with errors, reacting to feedback, finishing without errors (PC with Es → FB → PC without Es)
-
Starting proof construction with errors, reacting to feedback with interventions, finishing without errors (PC with Es → FB with interventions → PC without Es)
-
Starting proof construction with errors, reacting to feedback with interventions, finishing with errors (PC with Es → FB → PC with Es).
Necessary interventions were forms of ad hoc support by the interviewers, which were given when the participants were completely lost after they received feedback from the system. The 12 patterns of proof construction, grouped into the four broad categories, are summarised in Table 4.
Figure 4 shows the process of proof construction by each of the three sets of learners, WS1 and WS2, J1 and J2, and R (with the shaded boxes being identified patterns in each phase of the proof construction).
Table 4 and Fig. 4 capture several points related to learners’ proof construction processes, and feedback use (this is, of course, still limited to the context of proof construction with the system). First, it seems J1 and J2 have sound understanding as they have successfully completed proof constructions, often without any formative feedback from the system. R often started proof constructions with errors, but after receiving feedback from the system and ad hoc interventions by the interviewer, could complete two-step proofs. Meanwhile, on one occasion, R did attempt to construct a proof that included a circular argument (III-1/Ph3). WS1 and WS2 received much feedback from the system, plus ad hoc interventions by the interviewer, e.g., explaining the goals of tasks, two-step proofs, etc. Sometimes they lost their directions (e.g., II-2/Ph1 and 3 or III-1/Ph2 and 4). Towards the end of the session, they started completing proofs with feedback only from the system without ad hoc support by the interviewer, and in fact received less feedback. However, they still constructed a proof with a circular argument.
6.2 Students’ use of feedback
While J1 and J2 could use both process- and task-based feedback well to improve their proofs, both R, and WS1 and WS2, in contrast, needed interventions by the interviewer (as captured in Fig. 4) in addition to feedback from the system. For example, the interviewer had to clarify the goal of a two-step proof for R. In a first attempt, R needed a further clarification of how to complete a proof in a flow-chart form (III-1/Ph2). While R could use task-based feedback well to correct the proof format in general, further clarification from the interviewer was needed when R received the first process-based feedback in III-1/Ph3. This further clarification related to why a circular argument is not allowed in a proof, as well as how to use singular propositions properly.
For the case of WS1 and WS2 in their II-2 and III-1 phase, their proof construction started from ‘PC with Es → Process FB → PC with Es’ or ‘PC with Es → Process/task FB → PC with Es’, meaning they could not use feedback from the system by themselves and their learning was a rather ineffective trial–error approach. Ad hoc interventions by the interviewer were necessary. In particular, they really struggled to construct a correct proof with two steps (III-1/Ph2 and III-1/Ph4), showing confusion about using singular propositions.
36 | WSs | [trying several proofs and then received feedback as they used BO = CO twice] |
37 | WS2 | Let’s use these ones, because they are bigger (AB = CD again) |
38 | WS1 | We just used this one! |
39 | WS2 | Hang on. [feedback, you cannot use the conclusion …] |
40 | WS1 | We just used them, just used them |
41 | WS2 | That is wrong! |
42 | WS1 | Leave that one. Maybe that one and that one… how about that one (AB) and that one (BO), the line that one (AB) and that one (BO) [WS1 is highly confused now] |
43 | WS2 | You cannot re-use it |
44 | WS1 | Why not? |
45 | WS2 | No [feedback for using the same sides of the triangle twice] BO and BO, you cannot use the same one twice |
After this failure, the interviewer suggested that they start again, and not use the SSS condition. With these ad hoc interventions they finally managed to complete correct proofs with process-based feedback from the system as well as a clarification by the interviewer (III-1/Ph5 and Ph6). These cases indicate that the feedback from the system might not be enough and it might be necessary to intervene in students’ early proving processes, if they repeatedly make mistakes in both singular and universal propositions (e.g., the pattern ‘PC with Es → Process/task FB → PC with Es’).
6.3 Learners’ experience with circular reasoning with the system
In the lesson III-1, J1 and J2 completed the two proofs with little difficulty. On being prompted by the interviewer, they then tried to find a different proof, and, in the phase III-1/Ph3 (categorised as ‘PC without Es’), they not only refuted using the SSS condition for the problem (utterances 27–28), but also eliminated other possibilities for answers (utterances 31–36). This illustrates their capacity to identify logical circularity, grasping the relationship between premises and conclusion; that is, as a combination of universal instantiations and syllogism.
27 | J2 | You could do all the … |
28 | J1 | All the sides? |
29 | J2 | Yes… actually no, because… |
30 | J1 and J2 | You are trying to prove [AB = CD] … |
31 | J1 | And if you can’t use this line [AB] then we can’t use the other angle… because it is not included… |
32 | J2 | You mean those [ABO and CDO]? |
33 | J1 | Yes, it is not included [as AB cannot be used]… and we’ve already got others… |
34 | J1 | How about AO-OAB-AB? |
35 | J2 | You cannot use these, because… |
36 | J1 | Because these ones [AB and CD] which we are trying to prove… |
In particular, they exchanged their thoughts about a possible proof before they actually constructed a proof with SSS, and without support from the system during their attempts. They also explored very similar reasoning during Lesson III-2 on why angles ABO = ACO (the conclusion) cannot be used as one of premises.
In the case of J1 and J2, they could argue why a proof cannot contain a circular argument without any feedback from the system. However, the other two cases are quite different from J1 and J2 in terms of dealing with a circular argument. For example, R firstly constructed correct answers by using SAS and ASA individually during phase III-1/Ph2 and 3, recognised as ‘PC with Es → Process/task based FB → PC without Es’. This suggests that R could understand universal instantiation. However, R considered that it would be possible to use the SSS condition as one of the answers of the open problem to prove AB = CD, which indicated that R was lacking understanding of hypothetical syllogism. R then tried to change the condition (ASA) and then complete a proof (Fig. 5, left). This failed because R used angles ABO = CDO instead of angles OAB = OCD.
The system gave the message “Let’s find two angles at the end of this side” (Fig. 5, right), encouraging R to find a different angle or side of the triangle (utterance 27), as well as prompting R to explain why the proof was wrong. As shown below, R still had difficulty identifying the error (utterance 33), but managed to correct the mistake (utterance 35).
33 | R: | Am I not using the same lines? |
34 | T: | You are using the same lines |
35 | R: | … but angles are not on the same lines… |
36 | T: | That is right |
This was a short but important moment for R, and finally, after some thought in silence (2 s), R noticed the correct proof was the one already completed. R reasoned that it was not possible (utterances 37–44 below) to create different proofs using SSS because in this case R realised that AB = CD had to be used as one of premises, which had already been rejected by the system. This shows that R might have started developing an understanding of this aspect of syllogism.
37 | R: | [2 s silence] I don’t think there is any more answer |
38 | T: | No. So you are confident, just two [answers]? |
39 | R: | Yes |
40 | T: | Yes that is right. Because in this problem these two (AO = CO) are assumed already. So you need to use, like you did, if you choose angles AOB and COD, and angles ABO and CDO, then |
41 | R: | … they are not on that line |
42 | T: | That is right. That is right. And we have discussed, we cannot use that one |
43 | R: | Because |
44 | T: | Yes, because this is… |
45 | R: | What you are trying to find! [laugh] |
46 | T: | That is right! [laugh] |
In the case of R, the process-based feedback worked well, but for WS1 and WS2 it was a lot more difficult than expected for them to understand why the conclusion cannot be used as one of the premises in deductive proofs. For example, in the proof construction process of WS1 and WS2 (III-1/Ph2), without any hesitation, their first attempt involved using the SSS condition (Fig. 6).
They could identify pairs of sides and angles in their proof (Fig. 6), but they made a mistake as they put ‘angles AOB = COD are congruent’, rather than ‘triangles OAB and OCD’; regardless, they chose SSS as a condition of triangle congruence. This suggests that they also did not have a good understanding of universal instantiation. More importantly, they failed to notice that they should not use the conclusion AB = CD in their proof. The system first highlighted the mistake of logical circularity. After receiving the message that “You cannot use the conclusion to prove your conclusion!”, and with additional ad hoc interventions from the interviewer, they started considering that AB = CD should not be used in their proof in III-2/Ph5. With this consideration they began to understand why AB = CD should not be used.
However, when they started a new problem in III-2, they still used the conclusion as one of the premises in their proof. Thus, the cases from WS1 and W2 illustrate that the understanding of the meanings and roles of premises and conclusions might be very difficult for learners who have just started learning mathematical proof. Moreover, from the point of view of structure of proof, their experience shows that they did not see the whole structural relationship between premises and conclusion. In order to identify the circular argument as a serious error, learners need to understand at least the role of syllogism which connects premises with conclusions.
On the positive side, WS1 and WS2 gradually received less and less feedback from the system, and towards the end of the activity (Lesson III-2), at least WS1 started grasping why the conclusion cannot be used in their proofs (III-2/Ph4, ‘Self-regulation FB-PC without Es’).
46 | WS1 | [Reviewing the already answered proofs] Three angles we can use, we have used two, so it must be the other one |
47 | WS2 | [Suggesting ABO again] |
48 | WS1 | No, which could be. Go back |
49 | WS2 | So we use these ones [BAO and CAO] |
50 | WS1 | Yes |
51 | WS2 | So then that one [ABO] |
52 | WS1 | No, middle one [AOB] |
53 | WS2 | But that one was used? |
54 | WS1 | No wasn’t |
55 | WS2 | No wasn’t [laugh]. So if we use that one [AOB] [completing a proof] |
As can be seen from the dialogue above, reviewing already-answered proofs (self-regulation) was useful in guiding WS1 and WS2 to construct a different proof by themselves (utterance 46). While WS2 still suggested using angle ABO, which is the conclusion, WS2 was very confident that they should not use it. This resulted in their constructing a correct proof without formative feedback from the system. At this point they had received both process- and task-based feedback from the system, and the ways they performed with the system indicate they had started internalising feedback from the system and could correct errors by themselves.
7 Discussion
In this paper our focus is the use of domain-specific computer-based feedback by students who are learning the structure of proof but accept or construct a proof with logical circularity. In order to study this issue, we conceptualised students’ difficulties in terms of the use of universal/singular propositions and hypothetical syllogism (Sect. 2). The ways that feedback provided by the system is related to students’ difficulties is shown in Sect. 4. In Sects. 6.1–6.3 we provide our analysis of learners’ proof processes using feedback from the system and, in some cases, ad hoc interventions. Now we discuss our findings in relation to our research questions, although, as we have already noted, these are necessarily tentative because of the sample size.
In terms of the patterns of proof construction processes (RQ1), as we demonstrated in Table 4 and Fig. 4, we identified various patterns of use of the feedback by learners during their proof construction processes. These patterns include proof constructions started without errors (‘PC without Es’), ones that started with errors but by using feedback from the system, learners could manage to correct their errors and construct proofs without errors (‘PC with Es → FB → PC without Es’), ones that started with errors but, following interventions, finished without errors (‘PC with Es → FB with Interventions → PC without Es’), and ones that started with errors and then finished with errors (‘PC with Es → FB → PC with Es’). For example, in the case of J1 and J2 their patterns were mostly ‘PC without Es’ or ‘PC with Es → FB → PC without Es’. Other learners (e.g., WS1 and WS2) appeared to have difficulties with why a circular argument cannot be used in a proof (e.g., ‘PC with Es → FB → PC with Es’).
We found, as did Panero and Aldon (2016) and Attali and van der Kleij (2017), that in computer-based learning environments the teacher’s role continues to be important. Here we found that feedback from the system was useful for the interviewers to give specific ad hoc interventions for some learners who were relying on trial–error based learning or ‘PC with Es → FB → PC with Es’ loops (e.g., WS1 and WS2, II-2/Ph3–4 or III-1/Ph4–5). Thus, while we found that computer-based feedback can be effective to improve learning (as did Narciss and Huth 2006 and; Wang 2011), human intervention cannot be under-estimated. This conclusion applies, in particular, for those who have limited understanding. In our study context, if patterns of attempted proof construction such as ‘PC with Es → feedback → PC with Es’ are repeatedly observed, then the feedback from the system might not be enough and interventions might be necessary.
In terms of how feedback was used to overcome logical circularity in proofs (RQ2), both task- and process-based feedback (Hattie and Timperley 2007) supplied by the system provided guidance on what might help learners construct correct proofs. Our cases showed that learners started bridging the gap in their logic in syllogism (e.g., R, and WS1 and WS2 towards the end of their proving) after receiving both task- and process-based feedback. Self-regulated feedback rarely occurred in our cases, although learners were directed to what different proofs could be produced (e.g., WS1 and WS2, III-2/Ph4).
Overall, in order to support students’ learning, this conclusion suggests, for all cases, that considering possible combinations of premises and conclusion, and checking whether or not a proof falls into logical circularity, sometimes prompted by the system’s feedback in the open problem contexts, are useful to overcome logical circularity. This result echoes what Freudenthal (1973) suggested, that in order to make learning mathematics meaningful “the first step is to doubt the rigour one believes in at this moment” (p. 151).
8 Conclusion
With feedback recognised as one of the effective ways to improve learning, our aim was to explore how domain-specific, computer-based, ‘bug-related’ tutoring feedback (Narciss and Huth 2006) is used by learners in order to overcome their difficulties in their proof construction processes, especially when there was logical circularity in their deductive proving. We took three cases with five learners and examined their proof construction processes. It was still challenging for us to assess how the students were ‘on the road’ to proofs (Stylianides et al. 2016). Our methodological approach was to segment the proof construction processes into ‘phases’, and record what errors the learners made and their reactions to the feedback given by the system. We found that through learners receiving both task- and process-based feedback supplied by our online learning system, this helped them overcome logical circularity in their proving and to construct correct proofs.
Our findings raise important issues about the nature and role of computer-based feedback. For example, while both Rakoczy et al. (2013) and Hattie and Timperley (2007) state that feedback for effective strategies (process-based) is more effective than just stating right or wrong answers (task-based), it may be that for advanced topics, such as proofs, the combinations of both types might be necessary including human interventions. Also, the use of feedback might be related to learners’ understanding of proofs, and this suggestion again echoes the claims of other studies on learners’ prior knowledge and understanding and feedback use (e.g., Fyfe et al. 2012; Attali and van der Kleij 2017). In order to investigate these points in more depth, a larger data set is needed set in order to evaluate if the learning with open proof problems and the system, including the feedback format and timing, can effectively improve students’ understanding of deductive proof with computer-based learning.
Our study is limited to congruency-based geometrical proof using the flow-chart format and, in particular, ‘open’ proof tasks. Even so, we obtained rich data from our sample and found that our methodological approach worked well. Nevertheless, the challenge still exists to examine, for example, how to assess proof construction processes in wider contexts such as progressing from ‘open’ to ‘closed’ (i.e., single solution) problem formats with more mathematically-rigorous conditions. In addition to this, insights are needed into how computer-based feedback can be used to support proving processes in other proof formats (such as two column proofs), or in topics such as algebra. On top of this, insights are needed into what pedagogical approaches would be necessary in the classroom. A related issue that Sinclair et al. (2016, p. 706) identify in relation to overcoming logical circularity in deductive proving is learners “understanding the need for accepting some statements as definitions to avoid circularity”. Further research into all these matters should enrich understanding of the teaching and learning of mathematical proofs and proving, not only logical circularity within proofs but also logical relationships between theorems, which we did not explore much in this paper.
References
Attali, Y., & van der Kleij, F. (2017). Effects of feedback elaboration and feedback timing during computer-based practice in mathematics problem solving. Computers and Education, 110, 154–169.
Bardelle, C. (2010). Visual proofs: An experiment. In V. Durand-Guerrier, S. Soury-Lavergne, & F. Arzarello (Eds.), Proceedings of CERME 6 (pp. 251–260). Lyon: INRP.
Baum, L. A., Danovitch, J. H., & Keil, F. C. (2008). Children’s sensitivity to circular explanations. Journal of Experimental Child Psychology, 100(2), 146–155.
Bennett, R. E. (2011). Formative assessment: A critical review. Assessment in Education: Principles, Policy and Practice, 18(1), 5–25.
Black, P., & Wiliam, D. (2009). Developing the theory of formative assessment. Educational Assessment, Evaluation and Accountability, 21(1), 5–31.
Clark, I. (2012). Formative assessment: Assessment is for self-regulated learning. Educational Psychology Review, 24(2), 205–249.
Freudenthal, H. (1971). Geometry between the devil and the deep sea. Educational Studies in Mathematics, 3, 413–435.
Freudenthal, H. (1973). Mathematics as an educational task. Dordrecht: D. Reidel.
Fyfe, E. R., Rittle-Johnson, B., & DeCaro, M. S. (2012). The effects of feedback during exploratory mathematics problem solving: Prior knowledge matters. Journal of Educational Psychology, 104(4), 1094–1108.
Hanna, G., & de Villiers, M. (2008). ICMI study 19: Proof and proving in mathematics education. ZDM - The International Journal of Mathematics Education, 40(2), 329–336.
Hattie, J., & Timperley, H. (2007). The power of feedback. Review of Educational Research, 77(1), 81–112.
Heinze, A., & Reiss, K. (2004). Reasoning and proof: Methodological knowledge as a component of proof competence. In M. A. Mariotti (Ed.), Proceedings of CERME 3. Bellaria, Italy: ERME. Retrieved from http://www.dm.unipi.it/~didattica/CERME3/proceedings/Groups/TG4/TG4_Heinze_cerme3.pdf.
Jones, K., & Fujita, T. (2013). Interpretations of National Curricula: The case of geometry in textbooks from England and Japan. ZDM - The International Journal on Mathematics Education, 45(5), 671–683.
Kunimune, S., Fujita, T., & Jones, K. (2010). Strengthening students’ understanding of ‘proof’ in geometry in lower secondary school. In V. Durand-Guerrier et al (Ed.), Proceedings of CERME6 (pp. 756–765). Lyon: INRP.
Marriott, P., & Teoh, L. (2013). Computer based assessment and feedback: Best practice guidelines. York: Higher Education Academy.
McCrone, S. M. S., & Martin, T. S. (2009). Formal proof in high school geometry: Student perceptions of structure, validity and purpose. In M. Blanton, D. Stylianou & E. Knuth (Eds.), Teaching and learning proof across the grades (pp. 204–221). London: Routledge.
Miyazaki, M., Fujita, T., & Jones, K. (2015). Flow-chart proofs with open problems as scaffolds for learning about geometrical proofs. ZDM Mathematics Education, 47(7), 1211–1224.
Miyazaki, M., Fujita, T., & Jones, K. (2017a). Students’ understanding of the structure of deductive proof. Educational Studies in Mathematics, 94(2), 223–229.
Miyazaki, M., Fujita, T., & Jones, K., & Iwanaga, Y. (2017b). Designing a web-based learning support system for flow-chart proving in school geometry. Digital Experience in Mathematics Education, 3(3), 233–256.
Narciss, S., & Huth, K. (2006). Fostering achievement and motivation with bug-related tutoring feedback in a computer-based training for written subtraction. Learning and Instruction, 16(4), 310–322.
Ness, H. (1962). A method of proof for high school geometry. Mathematics Teacher, 55, 567–569.
Panero, M., & Aldon, G. (2016). How teachers evolve their formative assessment practices when digital tools are involved in the classroom. Digital Experiences in Mathematics Education, 2(1), 70–86.
Rakoczy, K., Harks, B., Klieme, E., Blum, W., & Hochweber, J. (2013). Written feedback in mathematics: Mediated by students’ perception, moderated by goal orientation. Learning and Instruction, 27, 63–73.
Rips, L. J. (2002). Circular reasoning. Cognitive Science, 26, 767–795.
Shute, V. J. (2008). Focus on formative feedback. Review of Educational Research, 78, 153–189.
Sinclair, N., Bussi, B., de Villiers, M., Jones, K., Kortenkamp, U., Leung, A., & Owens, K. (2016). Recent research on geometry education: An ICME-13 survey team report. ZDM Mathematics Education, 48(5), 691–719.
Stylianides, A. J., Bieda, K. N., & Morselli, F. (2016). Proof and argumentation in mathematics education research. In A. Gutiérrez et al (Eds.), The second handbook of research on the psychology of mathematics education (pp. 315–351). Dordrecht: Sense Publishers.
Wang, T. H. (2011). Implementation of web-based dynamic assessment in facilitating junior high school students to learn mathematics. Computers & Education, 56(4), 1062–1071.
Weston, A. (2000). A rulebook for arguments. Indianapolis: Hackett.
Winne, P. H., & Butler, D. L. (1994). Student cognition in learning from teaching. In T. Husen & T. Postlethwaite (Eds.), International encyclopedia of education (2nd edn., pp. 5738–5745). Oxford: Pergamon.
Acknowledgements
This research is supported by the Daiwa Anglo-Japanese foundation (No. 7599/8141) and the Grant-in-Aid for Scientific Research (Nos. 15K12375, 16H03057), Ministry of Education, Culture, Sports, Science, and Technology, Japan. We thank the three anonymous reviewers and the editor for their valuable suggestions.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Fujita, T., Jones, K. & Miyazaki, M. Learners’ use of domain-specific computer-based feedback to overcome logical circularity in deductive proving in geometry. ZDM Mathematics Education 50, 699–713 (2018). https://doi.org/10.1007/s11858-018-0950-4
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11858-018-0950-4