Abstract
The notion of mathematical modelling has multiple interpretations in research literature and has been included in curriculum documents in various ways. This study presents a thematic analysis of nine professional modellers’ conceptions of the notion of mathematical modelling, representing scholarly knowledge. The result is organised according to four main aspects of modelling, that is description, understanding, abstraction and negotiation, representing key features of mathematical models and how people are affected by, or engage in, modelling work. The paper concludes with a discussion of some potential benefits for mathematics education that might be drawn from the study from the perspective of the ‘gap’ between mathematical modelling in educational and non-educational contexts, in terms of curriculum design and teaching practice
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Written curricular documents often include information about key learning outcomes for students to achieve. How these are presented draws on the different political, social, cultural and historical contexts within which they have been developed. However, these documents commonly include words that may be described as signals, triggering some type of reaction of the reader (Nöth 1990) for what to teach and learn. How teachers, textbook authors and others interpret these words and their importance will therefore have an impact on how and what will be taught and learnt in the classroom. In mathematics education, one such word or notion is mathematical modelling.
There is no consensus among researchers in mathematics education about what constitutes mathematical modelling (Sriraman and Kaiser 2006) and the notion has been addressed differently within national curriculum documents around the globe (Borromeo Ferri 2013). This paper draws on interview data collected for an earlier study, which analysed professional modellers’ work with, and opinions on, teaching mathematical modelling (Frejd 2015, 2017; Frejd and Bergsten 2016). Here, the interviewees’ answers to the question “What does mathematical modelling mean to you?” will be analysed and discussed with respect to its educational relevance. As mathematical modellers often engage in discussing their models and communicating them to others, there is a rationale for investigating their conceptions of mathematical modelling in an interview format. Assuming that their professional education and working experience constitute scholarly knowledge of developing, using and evaluating mathematical models, an analysis focusing on their conceptions could be informative for mathematics education.
Thus our research question is as follows: What conceptions do professional modellers express about the notion of mathematical modelling? Based on our answer to this question, we also consider some potential benefits for mathematics education that might be drawn from the study. More specifically, we discuss possibilities for reducing the gap between modelling in school and modelling as a professional activity, provide suggestions concerning how to embed and define the notion in curriculum design, and we identify didactic principles viable for the design of modelling activities in the classroom.
After outlining a background to the study concerning how the notion of mathematical modelling has been addressed in research literature (Sect. 2), examples of research on how the notion has been conceptualized in workplace studies are discussed (Sect. 3). Section 4 includes some remarks on mathematical modelling in curriculum documents. Sections 5 and 6 present the methodology and results of the empirical study, followed by a critical discussion (Sect. 7) and remarks on the educational relevance of the study (Sect. 8).
2 The notion of mathematical modelling in educational research literature
There is a diversity of theoretical approaches used in educational research on mathematical modelling, some of which also draw on different conceptions about the notion of mathematical modelling (Geiger and Frejd 2015; Kaiser and Sriraman 2006). While space does not allow a review of all these approaches and conceptions, we make some comments relevant to the purpose of our discussion. The modelling cycle approach, sometimes described as “traditional” in mathematics education (Williams and Goos 2013) and often linked to the modelling competencies approach, has also been called “ideal”, not aiming to match empirical findings on students’ modelling work (Borromeo Ferri 2006). Given the historical roots of modelling cycles, i.e., as models of what occurs in modelling, it is of relevance here to make a distinction between components of modelling and how they connect, and the processes occurring in modelling activities (Borromeo Ferri 2006). Regarding the former, the conceptualisation of modelling in the modelling cycle approach draws on a separation of two distinct “worlds”, the real world and the mathematical world, and some kind of “translation” between these (e.g., Kaiser et al. 2006), including the “step” from the real world to the mathematical world (i.e., mathematisation). In the emergent modelling approach (e.g., Treffers 1987) the notion of mathematisation has a central role and has been further differentiated into horizontal mathematisation (from the real world to mathematics) and vertical mathematisation (within mathematics), while in the critical mathematics education approach its character along with its social implications are being analysed (e.g., Jablonka and Gellert 2007; Keitel et al. 1993).
The purpose of a modelling (or mathematisation) process is not always to describe and understand the real world through the use of mathematics but also to change the world (Niss 2015). In this context a distinction between the goals of modelling in terms of descriptive and prescriptive modelling has been made (e.g., Meyer 1984, p. 61). Regarding the latter, Niss (2015) wrote that its “ultimate aim is to pave the way for taking actions based on decisions resulting from a certain kind of mathematical considerations” (p. 69). Prescriptive modelling is found, for example, in politics and finance as well as in educational assessment. Such models can often not be validated empirically and a decision to use them needs to be based on a discussion of critical questions (Niss 2015; cf.; Jablonka 1997).
In the Anthropological Theory of the Didactic approach, mathematical activity is being recognised as “a modelling activity in itself” (Garcia et al. 2006, p. 232), with direct implications for the organization of teaching with a focus on problem solving. In this context one would need to make a distinction between the activity of developing mathematical models, the product of the activity (i.e., the model itself, and its use), and the goal of the activity, aspects not always clearly differentiated in discussions on the notion of modelling. Indeed, the expression “mathematical modelling” may refer to both, the concept (notion) of modelling and the activity of doing modelling (cf. the reification process in language from verbs to nouns).
In their presentation of “current perspectives” on mathematical modelling in education, Kaiser and Sriraman (2006) relate the perspectives identified to their respective “central aims”, background, and to different theoretical approaches to modelling (see Table 1). These perspectives point to a range of different realisations of teaching practice related to mathematical modelling.
Considering this wide spectrum of conceptions of, and approaches to, the teaching of mathematical modelling, it seems viable to explore conceptualisations of mathematical modelling with reference to its scholarly knowledge.
3 Descriptions of mathematical modelling by professional modellers
In research on workplace mathematics it has often been pointed out how mathematics remains ‘hidden’ or ‘frozen’, often in technology (e.g., Keitel et al. 1993; Williams and Wake 2007). However, in workplaces where mathematics has a central position, such as in professional modelling, it is not always hidden in ‘black boxes’ (e.g., Drakes 2012; Frejd and Bergsten 2016). Mathematical modellers gain experience in talking about their modelling work, as a central task for them is to discuss their models with clients and other experts (Frejd and Bergsten 2016). However, only a few research studies seem to explicitly explore professional modellers’ conceptions of mathematical modelling (e.g., Drakes 2012; Gainsburg 2013). Some studies have addressed the issue implicitly in terms of how the modellers work (e.g., Frejd and Bergsten 2016; Gainsburg 2006).
Drakes (2012) interviewed 14 professors, all working with modelling at different universities, about the notion of mathematical modelling. Of the three main themes she identified, the first referred to modelling as the activity of setting up a model to be used as a “description of a real life situation using a mathematical framework” (p. 39), while in the second mathematical modelling was seen as an entire process. In addition to setting up the model, it also included “solving, analysing and verifying the model [as well as] refining the model for more accurate results or using the model for prediction” (p. 40). According to the third theme, mathematical modelling “does not need a definition” (p. 40), as it is just the same as problem solving.
In the context of engineering and engineering education, Gainsburg (2006, 2013) studied modellers’ conceptions of mathematical modelling explicitly as well as implicitly through their workplace practice. In her workplace study involving structural engineers she concluded that “modelling–transforming hypothetical structures into mathematical or symbolic language for the purpose of applying engineering theory—is the heart of their profession” (Gainsburg 2006, p. 27). She described the engineers as being engaged in a modelling process that included understanding the phenomenon, mathematizing, and keeping track of what has been modelled. In Gainsburg’s later work (2013), four veteran engineers and four instructors in engineering education were interviewed. While they “confirmed the importance of mathematical models in engineering”, they did not attach much value to highlighting them explicitly in coursework (p. 272). The veterans described the purpose of models as “solving for or predicting behavior…[or] stood in for phenomena” (p. 275), whereas the instructors used terms such as “understand phenomena, see trends and relationships, and manipulate the represented system” (p. 276). None of the instructors mentioned computer models when describing mathematical models, in sharp contrast to the veterans for whom these were essentially synonymous. The instructors also emphasized several central “subconcepts” connected to modelling, including “uncertainty, subjectivity, idealization, assumption, and the importance of practical implications” (p. 278).
Based on her own experience of working in a real world modelling team, Spooner (2017) characterised key components of an authentic modelling process as “forming a group, establishing a shared understanding, defining a task, recognising and identifying the essential aspects of the situation, forming the model, testing the model and improving the model and overall process” (p. 630). These components concern the activity of model development, which may not always be a focus in workplaces where mathematical models are central. In a study by van der Wal et al. (2017), focusing on techno-mathematical literacy, 14 technical engineers were interviewed about their working experiences. It was concluded that in this context “model making is hardly used by engineers with a background in higher professional education, but is used at the academic level” (p. 100), indicating that the engineers did not explicate the use of mathematical modelling in their workplace practice.
In contrast, the professional modellers in the study by Frejd and Bergsten (2016) recognised mathematical modelling as a central part of their work. Their modelling activities were characterised as data-generated, model-generated or theory-generated modelling, all including computer support and communication with clients and colleagues/experts about the usefulness and effectiveness of a model (Frejd and Bergsten 2016, p. 29). This paper enlarges upon those characteristics by exploring the professional modellers’ descriptions of the notion of mathematical modelling.
Højgaard (2010) sees communication as essential to modelling and it has had prominence in discussions of modelling activities in mathematics teaching. For example, textbooks about modelling for university students (e.g., Dym 2004; Velten 2009) as well as research literature (e.g., Jablonka 1997; Perrenet et al. 2017) include criteria for developing and assessing the quality of mathematical models. In this context one aspect emphasised is communication. Also Drakes (2012) and Frejd and Bergsten (2016) found that professional modellers are engaged in communication practices to exchange information with clients, overcome barriers and discuss results. Communication could thus be seen as highly relevant also in a discussion about the very notion of mathematical modelling.
4 Mathematical modelling in curriculum documents
The notion of mathematical modelling has been incorporated in various ways in different national curricula: in Germany, The Netherlands, the Scandinavian countries and the United Kingdom, the ‘contextual’ approach—realistic modelling—is applied, while in France, Italy, Portugal and Spain the more ‘theoretical’ approach—epistemological modelling—is “strongly” represented (Borromeo Ferri 2013, p. 20). It could here be added that when comparing the Scandinavian curricula, mathematical modelling looks different in the different countries. Approaches range from explicit descriptions of mathematical modelling as ability or competence (Sweden and Denmark) with more or less detailed definitions in terms of atomistic or holistic views of the modelling process, to implicit descriptions of mathematical modelling where the terms are used but not explained or not used at all (Norway and Finland) (Finnish National Board of Education 2003; Niss and Højgaard Jensen 2002; Skolverket 2012; Utdanningsdirektoratet 2013). Borromeo Ferri (2013) also remarks, with reference to historical roots, that “teaching and learning of mathematical modelling has a different emphasis in Europe than in the United States, South America, or Asian countries” (p. 22).
Blum and Niss (1991) identified six types of approaches for embedding mathematical modelling within curricula. The spectrum of approaches ranges from embedding mathematical modelling within other subjects than mathematics, to not teaching mathematics as a stand-alone subject but integrating it within other subjects/courses to facilitate mathematical modelling. In the other approaches the organisation and goals of the mathematics courses vary in terms of their focus on pure mathematics, applied mathematics and problem solving. To some extent, these categorisations relate to the idea of holistic and atomistic approaches to mathematical modelling (Blomhøj and Højgaard Jensen 2003). Of these “extreme positions” (p. 128) along a continuum, the holistic approach emphasises mathematical modelling as an entire process including a set of sub-processes (for example, validation) that all need to be considered in modelling work. The atomistic approach has its focus mainly on “the processes of mathematising and of analysing models mathematically” (p. 128). A rationale suggested by the authors for using the latter approach (with the cited focus) in mathematics education is that it supports the learning of mathematics. However, for developing students’ modelling competence a balance between the two approaches is recommended (p. 137).
When mathematical modelling is not clearly defined and explained in curriculum documents it may cause different types of interpretations entailing different implications for teaching. The variety of descriptions of mathematical modelling in curricula could indicate a weak influence from its scholarly knowledge. To what extent mathematicians and modellers have been involved in curriculum development may differ between countries. However, when a curriculum is shaped mainly by educational stakeholders rather than professional practices it might lose parts of its raison d’être, that is “what its reasons are to be here, in front of us, waiting to be studied, mastered, and rightly utilised for the purpose it was created to serve” (Chevallard 2006, p. 26). This paper investigates professional modellers’ conceptions of mathematical modelling, representing scholarly knowledge, as a means to contribute to a curriculum design that does not lose too much of the raison d’être of mathematical modelling.
5 Methodology
In the studies by Frejd and Bergsten (2016), nine professional modellers were interviewed. Before they elaborated on how they work with mathematical modelling, they were asked: What does mathematical modelling mean to you? Their answers to this question were not analysed in our previous studies but will provide the empirical base for exploring modellers’ conceptions about the notion of modelling in this paper.
The notion conceptions has been used with different connotations in mathematics education research literature (Furinghetti and Pehkonen 2002). According to Thompson (1992), the usefulness of distinguishing between teachers’ knowledge and beliefs in research can be questioned, and she defines teachers’ conceptions as:
Mental structures, encompassing beliefs and any aspect of teachers’ knowledge that bears on their experience, such as meanings, concepts, propositions, rules mental images, and the like. (p. 141)
Also Phillip (2007, p. 259) uses a similar definition. The notion of conceptions is here seen as an umbrella term (Furinghetti and Pehkonen 2002) in the sense that the researcher does not distinguish between beliefs and preferences or beliefs and mental images. Some researchers also include knowledge in conceptions (e.g., Lloyd and Wilson 1998, p. 249), while others clearly separate knowledge and conceptions (e.g., Ponte 1994, quoted in Furinghetti and Pehkonen 2002). A balanced view is found in the writings of Pratt (1992), who sees conceptions as general key constructs when interacting with the world: “Conceptions are specific meanings attached to phenomena which then mediate our response to situations involving those phenomena” (p. 204).
For the purpose of this paper we use conceptions as an umbrella term in line with the definition by Thompson (1992), drawing on her arguments about the usefulness of exploring conceptions rather than beliefs to gather information about research participants’ mental structures for the object of the study.
True to the background of the non-conformity of descriptions of mathematical modelling (as outlined in the previous sections), we did not assume any specific view or theoretical approach regarding how professional modellers would describe the notion. We therefore found a thematic analysis adequate for our explorative investigation. Braun and Clarke (2006) state that a thematic analysis is primarily “a method for identifying, analysing and reporting patterns (themes) within data” (p. 78), giving it both theoretical freedom and flexibility by not assuming an essentialist or constructionist approach. Not taking into account contexts and social relationships as possible explanations of the participants’ opinions (latent themes), we aimed to identify semantic themes reflecting main patterns we could identify in our data (Braun and Clarke 2006, p. 86). This means we performed an inductive analysis, which Braun and Clarke (2006, p. 83; emphasis in original) define as “a process of coding the data without trying to fit it into a pre-existing coding frame, or the researcher’s analytic preconceptions”. While acknowledging that our formulations of the key notions and follow up questions, as well as the interview setting itself, are constituent elements of the discourse that developed, and that “researchers cannot free themselves of their theoretical and epistemological commitments” (Braun and Clarke 2006, p. 84), we hoped that this type of analysis would capture the conceptions held by the interviewees.
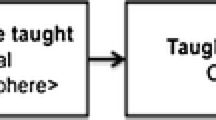
A first analysis led to a characterization of the view of each interviewee on the notion of mathematical modelling by our coding of chunks of the interview data (see Table 2). As some codes recurred across interviewees we conducted a second analysis of the codes (and their interrelations) from the perspective of the research question. This second analysis, and an overall review of the data, led to the identification of four final main themes and linked subthemes, drawing on the principle that data within the themes should “cohere together meaningfully, while there should be clear and identifiable distinctions between themes” (Braun and Clarke 2006, p. 91). We could then construct our final thematic map (Braun and Clarke 2006, pp. 89–91) which is presented in Fig. 1 in Sect. 6.
In the next section we analyse excerpts from the interview data underlying the codes in Table 2 and the final thematic map in Fig. 1.
6 Results
During our analysis we could identify four codes of a more general character as main themes for categorising the informants’ conceptions about the notion of mathematical modelling: description, understanding, abstraction, and negotiation.
6.1 Analysis of the empirical data
6.1.1 Description
Four of the interviewees related mathematical modelling to a description of a “reality”, “system”, or “problem”.
For the Banking modeller, modelling is “to mathematically describe reality”, drawing on assumptions and simplifications that could contribute to weaknesses of the model:
From a real situation try to develop a kind of theory dressed up in mathematical language, often drawing on assumptions and simplifications. One tries to find a way to mathematically describe this situation. […] It’s only models it’s not reality […] one must also be aware of the weaknesses of a model, models develop all the time. (Banking)
In addition, the Banking modeller expresses that modelling always has a specific purpose, in this case to “produce a prognosis”. The use of the expressions “weaknesses” and “models develop” also suggests that assumptions made are open for critique and that a model always remains imperfect.
Also the Traffic modeller uses the term description but refers to “process” and “system” as the domain of the modelling work: “Some kind of process or system that we try to describe using mathematical formulas”. He also emphasises the constraints, that a model is not “capturing the whole reality” and sees the validation process as problematic when encountering “new things”.
The Aircraft industry modeller terms the description of reality as a re-creation of reality—through mathematics. To make design work and validation possible in complex contexts, the modelling needs to take place at different levels (“partial systems”), an issue also raised by the Traffic modeller:
Constructing a pretty good description of reality so that you re-create reality mathematically, modelling realities. This can then be used for making predictions, extrapolations and analyses of the present state of things. [In complex contexts such as air industry] there is modelling of different partial systems, all needed for the design work and validation and verification. (Aircraft industry)
Instead of a “re-creation of reality” the modeller in Climate explicitly talks about a translation into mathematics, while at the same time seeing mathematical language as necessary for the construction of a “conceptual world”. In this case it is a description of a “problem”, and the “reality” is mainly physics, which already is a theorization. Modelling is also involved when the computer is used for solving the mathematized problem.
6.1.2 Understanding
There were two modellers who emphasised understanding, when talking about mathematical modelling, and one modeller who made an explicit distinction between description and understanding in modelling.
In the case of Insurance, one needs to understand a “reality” of complex human behaviour by trying to identify a few “characteristic elements”:
There may be a million factors behind human behaviour but perhaps three or four of them are central actually explaining 90% of what happens. We construct the models to understand reality, the complexity of which needs to be simplified in a model trying to approximate and capture the main elements. (Insurance)
Here, the identification of the main factors that explain how humans behave in different situations contributes to an understanding of “the dynamics of reality”.
Also the modeller in Physics talks about “how reality works” but uses words such as “knowledge” and “understanding” rather than “description”. For him, similarly to the Climate modeller, one purpose of “breaking down” some reality into discrete parts (“primarily in mathematical terms and concepts”) is to make them available for computer codes. Another purpose is to get “knowledge and understanding”.
The Biology modeller made a distinction between mathematical modelling aiming at description or understanding: “A tool either for describing something (such as a process) or for understanding which process that has some impact”. Here the term “description” refers to “getting an overview of large data sets” to make them comprehensible, whereas “understanding” involves a theoretical stance aiming at providing new knowledge. His addition of the remark “[modelling] could be seen as a language or an art” might indicate that he conceptualises description as rule based work (“language”) while understanding also involves creativity (“art”).
6.1.3 Abstraction
One of the interviewees framed modelling as a more general abstraction in terms of “representational forms” and “data structures”, reflecting the dominating role of computers in his work:
We don’t work with explicit mathematical models any more […] it is more about representational forms and data structures, that is, direct computer representations of the problem, which also count as models. (Scheduling)
For the Scheduling modeller, “traditional” mathematical (optimization) models are no longer seen as adequate and his modelling work consists of “almost any type of abstraction” directly from the problem into computer language, “drawing on mathematical symbolism”.
6.1.4 Negotiation
One of the modellers (Various areas) emphasised the social context in which models are developed and used. More than the specific role of mathematics the consideration of the “whole problem” was emphasised, also involving “a lot of communication”:
One always needs to consider the whole problem and not only keep focus on the mathematical parts; to identify the problem is a long and slow process, finding the key processes, variables and quantities, and the necessary data […], it requires quite a lot of communication. (Various areas)
As model validation is “extremely difficult”, it requires human negotiation:
To validate the model is extremely difficult […] Without a human negotiation, trusting too much on mathematical models as a ground, things can go completely wrong. (Various areas)
6.2 Thematic map
From the analysis above we can characterise the four main themes as follows:
-
Description: modelling as description, translation, or re-creation of some kind of reality or system in mathematical terms
-
Understanding: modelling as use of mathematics to understand how reality works, what factors impact
-
Abstraction: modelling as direct abstraction of a problem using mathematical and computer representations
-
Negotiation: modelling as human activity involving negotiations about the problem, variables, data, how the model works and its risks
For the construction of a thematic map we drew on Table 2 and the analysis in Sect. 6.1 to include some subthemes for the purpose of providing more structure to our relatively comprehensive themes, and for “demonstrating the hierarchy of meaning within the data” (Braun and Clarke 2006, p. 92). The thematic map resulting from our analysis is shown in Fig. 1. The left-hand main themes, description and abstraction, represent key features of a mathematical model, while the right-hand themes, understanding and negotiation, relate to individuals, that is how people are affected by or engage in the modelling work.
7 Discussion
The diversity of approaches to modelling discussed in Sect. 2 may be viewed as an indicator of a research field that is both complex and comprehensive. It may also, however, signal confusion related to educational practice when multiple descriptions of modelling are being used in research literature. In addition, the word modelling is associated with both the process of doing modelling and the concept of modelling. Also in this study the left- and right-hand sides of the thematic map mirror a ‘floating’ interpretation of the term mathematical modelling among professional modellers.
7.1 Findings
When looking at the outcomes of our analysis of the empirical data from the aspects of the activity of developing mathematical models, the product of the activity, and the goal of the activity (see Sect. 2), it is clear that they reflect a floating interpretation of the expression mathematical modelling. There is often no clear distinction between conceptualising modelling as a concept/notion or as a process/activity. Most of the modellers, however, responded mainly in terms of the goal of the activity, as partly implied in the themes description, understanding, and abstraction of reality. These results are aligned with the modellers’ descriptions described by Gainsburg (2013) of predicting behaviour, understanding phenomena, and identifying trends and relationships (cf. Sect. 3). Regarding the theme of abstraction, it is interesting that also some of Gainsburg’s (2013) participants “conflated mathematical and computer models during their interviews” (p. 275).
One modeller in our study (Various areas) had a focus on the development and product of modelling, emphasising the role of human negotiation with respect to the usefulness and effectiveness of the model (cf. Jablonka 1997; see also Frejd and Bergsten 2016). Some of the other modellers’ comments can also be sorted within the activity of developing mathematical models, connected to two of the themes identified by Drakes (2012), i.e., an atomistic or holistic view of the modelling process. As one example of the former in our data, one finds “some kind of process or system that we try to describe using mathematical formulas” (Traffic). The holistic view is represented, for example, by the Air industry modeller but most clearly expressed in the statement “One always needs to consider the whole problem and not only keep focus on the mathematical parts” (Various areas), including aspects related to validation. The product of the activity was an important aspect here but could also be identified in our analysis as modelling in terms of the construction of a tool, as expressed by the Biology modeller.
7.2 Methodology
It is not possible to generalise the results beyond this particular sample; rather, the study presents a case of how a set of professional mathematical modellers with different types of expertise conceptualise mathematical modelling. The outcomes need to be seen in relation to our aim of identifying aspects of the notion of mathematical modelling based on scholarly knowledge that may contribute to mathematical modelling in education.
The analysis was based on one interview question and follow-up questions, not considering further relevant information provided during the rest of the interview. This was deliberate as we presented this question in the beginning of the interview, in order to get a spontaneous response. While we consider this procedure as having set a strong focus on how modelling was conceptualised by the participants, it could also be seen as a constraint in terms of levels of depth and width of possible outcomes from the analysis. For the purpose of this paper, however, we found the information provided through this procedure and our thematic analysis valuable, as further elaborated in the next section.
The term conceptions was used as an umbrella term for the participants’ beliefs and knowledge; the extent to which the modellers’ answers were based on beliefs or on knowledge therefore remains an open question. In the paper by Frejd and Bergsten (2016) the analysis of these modellers’ “modelling activity schemes” showed that the issue of communication, for example, was essential for all participants. This does not imply, however, that all participants would include communication as an important part of their conceptions of mathematical modelling.
We are aware that auxiliary questions such as ‘What do you refer to as reality?’ or ‘What is mathematics to you?’ could have produced more information about these central notions in their descriptions. Indeed, almost all modellers used the word “reality” explicitly, as for example “understand the dynamics of reality” (Insurance). Even though reality is a common theme in their descriptions, the modellers are dealing with different kinds of reality connected to their areas of expertise, as some of them made clear. While the Scheduling modeller expressed some reflectiveness about the notion of reality, generally the term was not much problematized. The word “mathematics” (or “mathematically”) often occurred side by side with “reality”, as in “recreate reality mathematically” (Aircraft industry). What is referred to by “mathematics” is not discussed but seems taken as given, although in some cases more specific terminology was used, such as “mathematical symbolism” (Scheduling). It is therefore not possible to make any claims from these interview data on how the participants’ conceptions of the nature of mathematics might have influenced their conceptions of modelling.
8 Educational relevance
In this section we discuss our results in relation to a potential reconciliation of differences between professional modelling and modelling in school, regarding goals, knowledge base, and experience, with implications for curriculum design and teaching practice.
8.1 Bridging the ‘gap’
The literature reports significant differences between modelling work in educational and non-educational contexts regarding knowledge and experience, objectives and consequences of the modelling activity (for references, see Frejd and Bergsten 2016, p. 31). This study also highlighted such ‘gaps’, for example that the modellers’ descriptions of mathematical modelling most strongly related to its goals which do not directly translate to educational goals of school mathematics (cf. Frejd and Bergsten 2016; Gainsburg 2006). Further, in conceptions of mathematical modelling in education drawing on the modelling cycle (e.g., Kaiser et al. 2006; Lesh and Doerr 2003), reality and mathematics define the two main domains involved. What is expressed by the modellers in this study resembles the type of dichotomy between reality and mathematics that is underlying the conception of the modelling cycle. While a comparison of the descriptions of modelling by our participants with Blomhøj and Højgaard Jensen’s (2003) framework indicates some similarities as well as some discrepancies, our participants did not talk about modelling in terms of a cyclic process. Modelling cycles have been characterised as “normative” and seen as “an ideal way of modelling” (Borromeo Ferri 2006, p. 89), and are sometimes referred to in teaching “realistic or applied modelling” (Kaiser and Sriraman 2006). However, that this modelling perspective in education to some extent mirrors how professional modellers work, has been questioned (Gainsburg 2006, p. 29).
Results from this study could help to bridge the gap between modelling work in educational and non-educational contexts. For example, Gainsburg (2006) argued that the teaching of modelling in school in the US at that time tended to focus on developing descriptive models based on pre-defined data sets, in contrast to structural engineering where lack of accessible data and physical referents is common. Our results show (the theme description) that professional modellers also refer to descriptive models. The issue concerning lack of data might be resolved with reference to the sub themes computer representation of problem and data structures related to abstraction, in terms of developing accessible data through computer simulations. By reference to the theme negotiation it could be suggested that students not only communicate with peers but sometimes also get opportunities to discuss with experts during modelling activities (cf. Frejd 2017) as a constituent part of modelling in school. Interdisciplinary teaching may facilitate this type of communication (Frejd and Bergsten 2016).
8.2 Mathematical modelling in curriculum design and teaching practice
The themes and subthemes in Fig. 1 may offer some suggestions for curriculum design regarding mathematical modelling. For example, the themes description and understanding of (the dynamics of) reality or some system could be used in a curriculum as goals, calling for students to develop abilities to construct descriptions/overviews of some realistic situations, aiming at an understanding of how reality works, with the use of mathematical language. Subthemes related to description and understanding could be an explicit part of the curriculum. The theme abstraction indicates that the key role of using technology in mathematical modelling work would need to be highlighted in the curriculum. Finally, the theme negotiation would need to be made explicit, in particular in the context of prescriptive models. Indeed, the subtheme communication is a central component in modelling (see Sect. 3) and would also, from a professional perspective, need to be emphasised in teaching, for example in group activities and projects (Frejd and Bergsten 2016).
While there generally are no direct implications for teaching practice from empirical research, it is still possible to use categories derived from research to formulate didactic principlesFootnote 1 that can serve as guidelines for designing teaching practice. The four main themes emerging from this study, framed in a thematic map, are examples of such research based categories, which may be used to formulate specific didactic principles guiding the design of modelling activities in the mathematics classroom, potentially linking the design to professional modelling. Drawing on the data and analysis presented here, we see the following didactic principles as viable for the planning of teaching activities involving mathematical modelling.
-
Explicitness of the goal of the activity: Making explicit the goal of the modelling work (describe–understand–predict–engage in critical discussion); how a mathematical description/re-creation of the problem can contribute to the goal
-
Focus on the problem: Setting up/defining the problem, and considering the whole problem during the entire modelling work
-
System level: Seeing the problem as framed through a system, considering partial systems to be modelled separately
-
Assumptions and simplifications: Questioning why the variables/parameters chosen are important, and what has been neglected (and how that might contribute to the ‘error’)
-
Relevance and accuracy of data: Considering the quality of the data/quantities used for estimating the influence of the selected variables within the model
-
Role of technology: Realising that the use of computers (and other types of technology) is crucial for modelling work but also in itself involves a modelling activity
-
How the model works: Considering how the model works when being tried out (validation); whether it is possible to try it out or not, and how useful and effective it is for its purpose
-
Communication: Discussion/negotiations between the participants throughout the modelling activity about the above issues
The eight didactic principles may be used as a ‘checklist’ in the design of modelling activities within mathematics teaching, from the perspective of professional modelling. The first principle, fundamental for all teaching activities, is about clarifying the goal of the activity and establishing what type of knowledge the activity aims to develop. The problem is central in the whole modelling activity, involving the principles about how it may be framed through a system and what assumptions and simplifications students would need to consider. Indeed, the problem might also slightly change during the process: “The evolution of the problem has to be studied together with the evolution of its solution” (Jablonka 1997, p. 40). The principles about data relevance and accuracy and the effectiveness of the model are important parts for making the activity realistic for the students. The remaining principles refer to how the role of technology and communication can be emphasised in the design of the activity (cf. Williams and Goos 2013), and the crucial issue of a critical reflection on how the model works and its implications. Here the selection of problem is critical as students need to have the possibility of making judgements about how the model works (cf. Gainsburg 2006, p. 33).
This ‘guideline’ for teaching mathematical modelling is aligned to several of the perspectives on modelling in Table 1, in particular Realistic or applied modelling, Socio-critical and sociocultural modelling, and to some extent Epistemological or theoretical modelling. Guidelines similar to those in the list above are certainly also found in the literature, suggesting what aspects teachers would need to consider when designing mathematical modelling activities (e.g., Dym 2004; Jablonka 1997; Lesh and Doerr 2003; Velten 2009). By basing suggestions for the education of mathematical modelling on empirical data reflecting professional modellers’ descriptions of the notion of mathematical modelling, our aim has been to strengthen the input from scholarly knowledge on curriculum development.
Notes
Didactic principles can be defined as “norms or general theses orienting and instilling the process of education a functional sense thus granting the premises of efficient fulfillment of the objectives in view” (Roman and Faragau-Dragos 2008, p. 666).
References
Blomhøj, M., & Højgaard Jensen, T. (2003). Developing mathematical modelling competence: Conceptual clarification and educational planning. Teaching Mathematics and its Applications, 22(3), 123–139.
Blum, W., & Niss, M. (1991). Applied mathematical problem solving, modelling, applications, and links to other subjects: State, trends and issues in mathematics instruction. Educational Studies in Mathematics, 22(1), 37–68.
Borromeo Ferri, R. (2006). Theoretical and empirical differentiations of phases in the modelling process. ZDM Mathematics Education, 38(2), 86–95.
Borromeo Ferri, R. (2013). Mathematical modelling in European education. Journal of Mathematics Education at Teachers College, 4(2), 18–24.
Braun, V., & Clarke, V. (2006). Using thematic analysis in psychology. Qualitative Research in Psychology, 3, 77–101.
Chevallard, Y. (2006). Steps towards a new epistemology in mathematics education. In M. Bosch (Ed.), Proceedings of CERME4 (pp. 21–30). Barcelona, Spain; FUNDEMI IQS–Universitat Ramon Llull.
Drakes, C. I. (2012). Mathematical modelling: From novice to expert. (Dissertation). Simon Fraser University, Burnaby, Canada.
Dym, C. L. (2004). Principles of mathematical modelling. New York: Elsevier Academic Press.
Finnish National Board of Education. (2003). National core curriculum for upper secondary schools. http://www.oph.fi/download/47678_core_curricula_upper_secondary_education.pdf. Accessed 4 Apr 2018.
Frejd, P. (2015). Mathematical modellers’ opinions on mathematical modelling in upper secondary education. In G. A. Stillman, W. Blum & M. S. Biembengut (Eds.), Mathematical modelling in education research and practice: Cultural, social and cognitive influences (pp. 327–337). Cham: Springer.
Frejd, P. (2017). Mathematical modelling as a professional activity—lessons for the classroom. In G. A. Stillman, W. Blum & G. Kaiser (Eds.), Mathematical modelling and applications: Crossing and researching boundaries in mathematical modelling education (pp. 371–388). Cham: Springer.
Frejd, P., & Bergsten, C. (2016). Mathematical modelling as a professional task. Educational Studies in Mathematics, 91(1), 11–35.
Furinghetti, F., & Pehkonen, E. (2002). Rethinking characterizations of beliefs. In G. C. Leder, E. Pehkonen & G. Törner (Eds.), Beliefs: A hidden variable in mathematics education? (pp. 39–57). Dordrecht: Kluwer Academic.
Gainsburg, J. (2006). The mathematical modeling of structural engineers. Mathematical Thinking and Learning, 8(1), 3–36.
Gainsburg, J. (2013). Learning to model in engineering. Mathematical Thinking and Learning, 15(4), 259–290.
Garcia, F., Gascón, J., Higueras, L., & Bosch, M. (2006). Mathematical modelling as a tool for the connection of school mathematics. ZDM Mathematics Education, 38(3), 226–246.
Geiger, V., & Frejd, P. (2015). A reflection on mathematical modelling and applications as a field of research: Theoretical orientation and diversity. In G. A. Stillman, W. Blum & M. S. Biembengut (Eds.), Mathematical modelling in education research and practice: Cultural, social and cognitive influences (pp. 161–171). Cham: Springer.
Højgaard, T. (2010). Communication: The essential difference between mathematical modeling and problem solving. In R. A. Lesh, P. L. Galbraith, C. R. Haines & A. Harford (Eds.), Modeling students’ mathematical modelling competencies (ICTMA13) (pp. 255–264). New York: Springer..
Jablonka, E. (1997). What makes a model effective and useful (or not)? In S. K. Houston, W. Blum, I. D. Huntley & N. T. Neill (Eds.), Teaching and learning mathematical modelling (pp. 39–50). Chichester: Albion Publishing.
Jablonka, E., & Gellert, U. (2007). Mathematisation—demathematisation. In U. Gellert & E. Jablonka (Eds.), Mathematisation and demathematisation: Social, philosophical and educational ramifications (pp. 1–18). Rotterdam: Sense Publishers.
Kaiser, G., Blomhøj, M., & Sriraman, B. (2006). Towards a didactical theory for mathematical modelling. ZDM Mathematics Education, 38(2), 82–85.
Kaiser, G., & Sriraman, B. (2006). A global survey of international perspectives on modelling in mathematics education. ZDM Mathematics Education, 38(3), 303–310.
Keitel, C., Kotzmann, E., & Skovsmose, O. (1993). Beyond the tunnel vision: Analysing the relationship between mathematics, society and technology. In C. Keitel & K. Ruthven (Eds.), Learning from computers: Mathematics education and technology (pp. 243–279). Berlin: Springer.
Lesh, R., & Doerr, H. M. (2003). Foundations of models and a modeling perspective on mathematics teaching, learning, and problem solving. In R. Lesh & H. M. Doerr (Eds.), Beyond constructivism: Models and modeling perspectives on mathematics problem solving, learning, and teaching (pp. 3–33). Mahwah: Erlbaum).
Lloyd, G. M., & Wilson, M. (1998). Supporting innovation: The impact of a teacher’s conception on functions on his implementation of a reform curriculum. Journal for Research in Mathematics Education, 29, 248–274.
Meyer, W. J. (1984). Concepts of mathematical modeling. Mineola: Dover.
Niss, M. (2015). Prescriptive modelling—challenges and opportunities. In G. A. Stillman, W. Blum & M. S. Biembengut (Eds.), Mathematical modelling in education research and practice: Cultural, Social and Cognitive Influences (pp. 67–79). Cham: Springer.
Niss, M., & Højgaard Jensen, T. (Eds.). (2002). Kompetencer og matematiklæring—Ideer og inspiration til udvikling af matematikundervisning i Danmark [Competencies and mathematical learning—ideas and inspiration for the development of mathematics teaching and learning in Denmark]. Copenhagen: UVM.
Nöth, W. (1990). A handbook of semiotics. Bloomington: Indiana University Press.
Perrenet, J., Zwaneveld, B., van Overveld, K., & Borghuis, T. (2017). Quality criteria for mathematical models in relation to models’ purposes: Their usefulness in engineering education. In G. A. Stillman, W. Blum & G. Kaiser (Eds.), Mathematical modelling and applications: Crossing and researching boundaries in mathematical modelling education (pp. 141–152). Cham: Springer.
Phillip, R. A. (2007). Mathematics teachers’ beliefs and affect. In F. Lester (Ed.), Second handbook of research on mathematics teaching and learning, Vol. 1 (pp. 257–315). Charlotte: Information Age.
Ponte, J. P. (1994). Knowledge, beliefs, and conceptions in mathematics teaching and learning. In L. Bazzini (Ed.), Proceedings of the fifth international conference on systematic cooperation between theory and practice in mathematics Education (pp. 169–177). Pavia: ISDAF.
Pratt, D. D. (1992). Conceptions of teaching. Adult Education Quarterly, 42(4), 203–220.
Roman, I., & Faragau-Dragos, M. (2008). Applying didactic principles to teaching agronomic disciplines. Bulletin UASVM Horticulture, 65(2), 666.
Skolverket. (2012). The subject syllabus for mathematics. http://www.skolverket.se/polopoly_fs/1.174554!/Menu/article/attachment/Mathematics.pdf. Accessed 4 Apr 2018.
Spooner, K. (2017). Authentic mathematical modelling experiences of Upper Secondary School: A case study. In G. A. Stillman, W. Blum & G. Kaiser (Eds.), Mathematical modelling and applications: Crossing and researching boundaries in mathematical modelling education (pp. 627–637). Cham: Springer.
Sriraman, B., & Kaiser, G. (2006). Theory usage and theoretical trends in Europe: A survey and preliminary analysis of CERME4 research reports. ZDM Mathematics Education, 38(1), 22–51.
Thompson, A. G. (1992). Teachers’ beliefs and conceptions: A synthesis of the research. In D. Grouws (Ed.), Handbook for research on mathematics teaching and learning (pp. 127–146). New York: Macmillan.
Treffers, A. (1987). Three dimensions. A model of goal and theory description in mathematics instruction—the Wiskobas project. Dordrecht: D. Reidel.
Utdanningsdirektoratet. (2013). Upper secondary education. https://www.udir.no/laring-og-trivsel/lareplanverket/finn-lareplan/. Accessed 4 Apr 2018.
Van der Wal, N. J., Bakker, A., & Drijvers, P. (2017). Which techno-mathematical literacies are essential STEM skills for engineers of the future? International Journal of Science and Mathematics Education, 15(Supplement 1), 87–104.
Velten, K. (2009). Mathematical modeling and simulation. Introduction for scientists and engineers. Weinheim: Wiley.
Williams, J., & Goos, M. (2013). Modelling with mathematics and technologies. In M. A. Clements, A. J. Bishop, C. Keitel, J. Kilpatrick & F. K. S. Leung (Eds.), Third international handbook of mathematics education (pp. 549–569). Berlin: Springer.
Williams, J., & Wake, G. (2007). Black boxes in workplace mathematics. Educational Studies in Mathematics, 64(3), 317–343.
Acknowledgements
The authors wish to thank the reviewers and the editor for the valuable comments and suggestions on earlier versions of this paper.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Frejd, P., Bergsten, C. Professional modellers’ conceptions of the notion of mathematical modelling: ideas for education. ZDM Mathematics Education 50, 117–127 (2018). https://doi.org/10.1007/s11858-018-0928-2
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11858-018-0928-2