Optimization of Water Distribution Systems Using Genetic Algorithms: A Review

Abstract

Water distribution networks are crucial for supplying consumers with quality and adequate water. A water distribution system comprises connected hydraulic components which ensure water supply and distribution to meet demand. Optimization of water distribution networks is carried out to minimize resource utilization and expenditure or maximize the system’s efficiency and higher benefits. Genetic algorithms signify an effective search technique for non-linear optimization problems and have gained acceptance among water resources planners and managers. This paper reviews various developments in the optimization of water distribution systems using the technique of genetic algorithms. These developments are pertinent to creating novel systems for distributing water and the expansion, reinforcement, and rehabilitation process for prevailing water supply mechanisms.

Graphical Abstract

1 Introduction

Water is the unique feature of Earth that distinguishes it from other known planets. The global water availability is ample to meet all present and future demands. However, water distribution in time and space is a major constraint in water utilization [1, 2]. The availability of fresh water in some areas is minimalistic. It is not even adequate to meet the population’s basic consumption and sanitation needs [3]. Water has become a limiting factor for human health, productivity, and, thus far, economic development [4]. This also affects maintaining and conserving a clean environment and healthy ecosystem.

Further, the present world’s demographic, commercial and technological trends have also sped up the modification of the environment that sustains life. Human activities are the principal drivers of detrimental changes in the environment. Environmental changes directly impact the quantity and timing of precipitation in a watershed [5,6,7]. With the increase in variability in precipitation and landscape modification due to excessive growth of food and energy sectors and migration of people to urban areas, the quality and quantity of freshwater resources have been severely threatened. All these factors have immensely pressured the utilization and distribution of water [8]. There is also a global acknowledgment that the Water Distribution Systems (WDSs) are severely underfunded and thus need to be designed efficiently and economically [9].

One of the most important pieces of societal infrastructure is the water distribution systems (WDSs), which are constantly improving and expanding because of rising water needs and population expansion. Designing cost-effective WDSs is a challenging undertaking that requires solving many nonlinear network equations simultaneously while optimizing network elements’ dimensions, locations, and operating states like pipes, pumps, tanks, and valves [10]. This work gets considerably more difficult when the optimization problem contains more real-world elements, more objectives other than the least-cost economic measure (such as probable fire damage), and more requirements for the developed system to meet (such as water quality) [11]. Traditional approaches had problems such as dependence on the starting point and entanglement in local minima. As a result, they could not find solutions that were close to optimal for complex, multi-objective pipe network issues [12]. In order to avoid local minima, researchers started to use soft computing techniques which employ meta-heuristic algorithms (such as genetic algorithms, simulated annealing, etc.) for water distribution system design issues [13,14,15,16]. The subjective nature of data cannot be classified or quantified using traditional approaches. However, they are often useful in other ways. They also fail to formally establish any approach for handling missing data. Soft-computing techniques are used in various fields where decision-making is vital [17, 18]. In decision analysis, these help decision-makers make wise conclusions that have been well considered.

Evolutionary algorithms (EAs) have gained popularity as a method for tackling water resource optimization issues over the past three decades [19]. Engineering design, creation of management strategies, and model calibration are just a few of the domains where evolutionary algorithms (EAs) have been successfully and extensively employed to solve water resources optimization problems. One of the most widely utilized EA approaches to handle optimization issues is the employment of genetic algorithms [20, 21]. The inspiration for GAs was from population genetics and the evolution at the scale of population. Additionally, Mendelian knowledge of genetic structure (like chromosomes, genes, and alleles) and mechanisms like mutation and gene recombination were also included while developing GAs. Based on the binary encoding of the solution parameters, Holland [22] developed the fundamental GA. It uses multi-point crossover and bit-flip mutation to evolve the solutions [23, 24]. Later, several GA (binary/real coding) variations with various genetic operators were developed and deployed in various water resource applications [25].

Genetic algorithms are based on Charles Darwin’s theory of natural selection, which holds that species change and adapt to their environments to survive (Darwin) [26, 27]. Over time, many GA variations have been created. Although most of these variations utilize the same fundamental ideas of natural selection and the survival of the fittest, they employ various strategies and upgraded processes to increase search direction and support the method’s enhanced convergence. Using the natural selection and genetics concepts, Goldberg and Kuo presented stochastic approaches to optimize water distribution networks. Simpson et al. [28] used simple genetic algorithms (GA) and came up with a solution that was close to the ideal [29].

The current paper aims to provide an in-depth and organized assessment of numerous works in WDS design and optimization utilizing genetic algorithms. Many types of research are pertinent to the strengthening, expansion, and rehabilitation of WDS’s design. The paper aims to facilitate quick familiarization with various genetic algorithm applications for developing new WDSs and reinforcing and restoring those that already exist. This study could be seen as an effort to update the review of earlier research papers on applying GAs to WDS optimization. This paper also adds to the existing literature review by providing a thorough and systematic assessment of publications for operational optimization of WDSs from the 1990s to the present. Furthermore, it highlights significant historical developments, the current research and application status of WDS optimization, and some future concerns. In order to serve as a single point of reference for quickly locating papers of interest, a table has been provided containing an extensive list of publications on the subject that contain detailed and thorough material.

Not all the studies that have been evaluated in this paper offer mathematical definitions of the optimization model that was employed. Because clear formulation was partially or not offered in the articles, the analysis presented in this paper is therefore restricted to our interpretation of the information provided.

2 Literature Analysis and Limitations of the Study

A thorough analysis of all pertinent studies on the optimization of water distribution systems using genetic algorithms from the 1990s to 2021 was carried out to identify the relevant existing literature following the goal of this study. Records retrieval began with a subject search for “water distribution,” “water distribution systems,” “water distribution network,” “water distribution pipe,” “water supply system,” “water supply network,” and “water supply pipe,” “optimization” and “genetic algorithms” [30]. The search was restricted to publications that used genetic algorithms to optimize water distribution systems [31]. The libraries searched for this study included Science Direct, Springer, American Society of Civil Engineering (ASCE), Google Scholar, Wiley Online Library, MDPI, IEEE, IWA Publishing, and other relevant libraries. The number of documents/research papers published in the most reputed journal related to Optimization of Water Distribution Systems using Genetic Algorithms and other techniques shows in Fig. 1 and 2. Figure 3 shows the collaboration map among countries with regard to optimization of water distribution systems using genetic algorithms and other similar techniques. The co-authorship links between countries have been represented in a two-dimensional space in order to illustrate this. As a result of this collaboration, high-impact studies can be generated primarily through complementary practices, experiences, and skills, which are all of benefit to the research community. The most relevant word as a keyword used in Optimization of Water Distribution Systems is shown in Fig. 4.

Fig. 1

Annual and the cumulative number of publications related to optimization of water distribution systems using genetic algorithms and other similar techniques

Fig. 2

Number of documents/research papers published in the most reputed journal and conferences related to optimizing water distribution systems using genetic algorithms and other similar techniques

Fig. 3

Spatial distribution of publications and collaboration network among countries related to optimization of water distribution systems using genetic algorithms and other similar techniques

Fig. 4

Most relevant and frequent keywords used in optimizing water distribution systems

This paper is organized following broad categorization and design problems addressed in different publications (Figs. 1 and 2). The design problems include new system design, optimization, pressure management, pipe size selection according to slope and pressure head, strengthening of existing systems, expansion, and considerations for performance, time, uncertainty, and recuperation (Fig. 5). The table, which lists many publications in chronological sequence, comprises a considerable proportion of this review work. Figure 6 illustrates relationships between the five most relevant author keywords (left field) and the five main keywords inferred from optimization (right field). Each study is categorized based on the optimization model it uses (objective functions and decision variables), the water quality parameter(s), the network analysis, the optimization method, and the test network(s) it employs. The table also includes the result of each study. The paper aims to give readers a complete list of representative publications on the subject so they can use it as their key source of information when looking up relevant articles on the optimization of water distribution systems using genetic algorithms.

Fig. 5

Thematic evaluation map regarding optimization of water distribution systems

Fig. 6

Sankey diagram showing the methods (right) employed in the water distribution network and pump selection strategies (left) adopted in optimization evaluations

Not all the studies that have been evaluated in this paper offer mathematical definitions of the optimization model that was employed. Because clear formulation was partially or not offered in the articles, the analysis presented in this paper is therefore restricted to our interpretation of the information provided.

3 Optimal Design of Water Distribution Systems

The mechanism that feeds or distributes water from the water source to suit the needs of the consumers is known as a water distribution system (WDS). This process is accomplished via the pressure-driven operation of pumps, main and service pipes, storage tanks or reservoirs, and accompanying machinery in a closed system. Water distribution systems are described by Ostfeld [32] as the interconnected connection of water sources, pipes, and hydraulic control modules, such as valves, pumps, regulators, and reservoirs, to supply water to the end users with standard pressure (Fig. 7).

Fig. 7

TreeMap of keywords used in optimization technique for water distribution systems

Water distribution systems are one of civilized society’s most important organizational assets. A system of nonlinear equations is used to mimic the hydraulic dynamics inside a pressured, looping pipe network. The energy and continuity equations are considered simultaneously for obtaining the solution to these equations, along with a head loss function [33]. The cluster analysis provided by CiteSpace detected the cluster labels. The five labels were water distribution system, genetic algorithms, optimization, water supply, and optimization networks (Fig. 7). Clusters of optimization techniques based on the co-occurrence of the keywords show that the genetic algorithm was utilized most. The mathematical description of the optimum design for a generic water distribution mechanism is described in Eqs. (1–5).

3.1 Objective Functions

The design of an economical and profitable WDS is a discrete challenge in optimization as each pipe size must be chosen from a range of commercial size diameters. The number of diameters available commercially, raised to the power of the number of pipes in the network, is used to calculate the search space [34]. For instance, if a WDS has 12 pipelines and six different commercial pipe sizes are available, the search space size would be 6 12, or 2, 17, 67, 82, 336 different pipe combinations. Consequently, the search space is vast, even for a modest pipe network. A complex problem in water distribution network design is the simultaneous optimization of pipe sizes and other network elements while solving many complicated, nonlinear, and discontinuous hydraulic equations [35, 36].

Figure 8 depicts the objectives of a generic optimization model of WDS design. The objectives can be classified into four separate groups [37]. The first set of objectives, categorized under economic objectives, comprises construction and rehabilitation expenses and estimated operations and maintenance costs for the system. The second set of objectives, the community objectives, consists of various services provided to WDS customers. These include the benefit function’s lack of water quality, deficit pressure at demand nodes, possible fire damage, and the system’s hydraulic failure. The third set of objectives representing the WDS robustness, dependability, and resilience are grouped under performance objectives. These objectives represent the service level of the WDS to the customer and the overall efficiency of the WDS. The final set of objectives is the environmental objectives. These relate to the greenhouse gas emissions and emissions during the installation and operation of WDS. Under the following restrictions, the objective functions must be reduced or maximized.

Fig. 8

Classification of WDS’s generalized optimization model’s aims

In order to identify the best pipe sizes for a specified network layout and demand, a water distribution system must be optimized. The ideal pipe dimensions that satisfy all implicit (conservation of energy and mass) and explicit (hydraulic and design constraints) constraints are chosen in the final network [38].

The entire aim of solving conditions in water distribution systems is to determine how much water flows through the pipes along with any pumps and valves if any are present) and how much water heads at the nodes. The pressures at nodes and the velocities in each pipe are typically calculated. In 1988, Todini and Pilati [39] delivered a ground-breaking study that revolutionized how water distribution systems would be solved [40]. Many formulations based on various arrangements of the network’s unknowns had previously been proposed. Four popular formulations are as follows:

• 1. Formulation of flow equations or Q-equations using the unknown flows (Qs) in each pipe;

• 2. Formulation of head equations or H-equations using unknown heads or HGLs (Hs) at each node;

• 3. The formulation of loop flow correction equations, also known as LFC-equations, in terms of unknown loop flow corrections (LFCs), which is a technique close to the manual Hardy Cross approach for solving networks;

• 4. Formulation of the Q-H equations in terms of unknowable flows and unknowable heads [39].

The flow rate,${q}_{i}$ (flow into and out of the node) and the number of pipes n linked at the node, ${q}_{i}$ and n, are inputted into the continuity equation and applied to each node. It is written as:

$$\sum_{i=1}^{n}{q}_{i}=0$$

(1)

With ${h}_{i}$ representing the head loss in each pipe and m representing the number of pipes in the loop, the energy equation is applied to each loop in the distribution network. The energy equation is given as:

$$\sum_{i=1}^{m}{h}_{i}=0$$

(2)

The local head losses and friction head losses add to the head loss. The Hazen-Williams equation is employed to determine head loss. This equation, which links frictional energy loss and the physical characteristics of the pipe to the flow of water in a pipe, is empirical. The Hazen-Williams coefficient, known by its initials C and employed in the Hazen-Williams equation [41], is a dimensionless quantity. The equation has the following form:

$${h}_{f}=4.72{C}^{-1.85}\times {Q}^{1.85}\times {D}^{-4.87}\times L$$

(3)

where, ${h}_{f}$ is the head loss, $Q$ is the flow rate, $C$ is the Hazen–Williams coefficient,$D$ is the pipe inside diameter, and $L$ is the pipe length.

The network’s overall cost is the objective function in a single-objective optimization paradigm [42]. Network growth, strengthening, and rehabilitation are mostly merged into a single least-cost objective in single-objective models. The assumption is that the pipe’s capital cost per unit length is non-linearly linked to its diameter and that a single equation may be applied for all sizes. Thus, the capital cost of pipes (including laying and jointing) may be stated as follows:

$$f\left({D}_{1},\dots {D}_{n}\right)=\sum_{j=1}^{N}c({D}_{j}, {L}_{j})$$

(4)

where c (D_j, L_j) is the cost of the jth pipe having diameter D_j and the length L_j, and N is the total number of pipes in the system. While as in multi-objective models, the net benefit or system running expenses are added as extra objectives. A generic multi-objective optimization model for the optimum design of the WDS can be written as:

$$Minimize/maximize \left({f}_{1}\left(x\right), {f}_{2}\left(x\right), . . . , {f}_{n}\left(x\right)\right)$$

(5)

Equation (5) illustrates the choice variables and objective functions to be reduced (e.g., system capital expenses) or maximized (e.g., system resilience). Most studies have explored the best design, operation, and rehabilitation of WDS at a specific period, regardless of how they are related to one another (separately). Optimal WDS design is the emphasis of some studies [43, 44], whereas optimal WDS operation scheduling [45, 46] is the focus of others. Additionally, some studies have concentrated on the rehabilitation of WDNs [47, 48]. Most multi-objective problems (MOPs) used for WDS optimization are described by pairing two or more objectives.

The first WDS design challenge to be solved using multi-objective evolutionary optimization was by Walski et al. [49]. They worked on reducing network pressure and costs. Todini [40], Costa et al. [50], Prasad and Park [51], Zheng et al. [52], Wang et al. [53], Beygi et al. [54], Johns [55], and Jafari [56] are just a few of the multi-objective optimizations for least-cost design (LCD), better water quality and maximum resilience of WDSs that have been explored in the literature. The advantage of multi-objective optimization methods is that they can produce a set of optimal solutions known as a Pareto front [57], illustrating the trade-offs between various objectives, particularly those in conflict. After these solutions have been analyzed, one or a limited number are chosen based on a specific criterion.

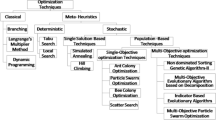
The optimal design of WDNs is complicated; hence many researchers have used various efficient mathematical techniques to address the issue [58]. The methods and techniques for optimization can be divided into two main groups: (1) deterministic methods, which primarily rely on calculating the objective function gradient and/or function evaluations, and (2) heuristic techniques, which primarily rely on an exploratory approach, natural phenomena, or even artificial intelligence.

In WDN optimization, linear programming (LP) [59,60,61], non-linear programming (NLP) [38, 62,63,64], integer linear programming (ILP) [65], non-linear programming (NLP) [66, 67], integer non-linear programming (INLP) [68], and (DP) [69] are the most commonly used deterministic techniques. Mixed-integer programming refers to optimization issues that involve both continuous and integer data (MIP). These algorithms make it possible to pinpoint the precise location of an ideal solution [48]. However, they frequently reach optimal local outcomes that might not be the global best ones. Additionally, the necessity of derivative evaluations may, in some circumstances, make the optimization process more difficult.

In the 1990s, WDS optimization changed partly due to the emergence of metaheuristics and the advancement of personal computers. A metaheuristic in operations research is a method created to create a partial search algorithm (heuristic) that may provide the best answer to an optimization issue, typically with incomplete or defective data. Because they do not try to escape from the local optimum. Meta-heuristics have been introduced as a result of these shortcomings. Meta-heuristic algorithms can be thought of as “higher level” heuristics since the word “meta” denotes “upper-level methodology.”

A metaheuristic is a sophisticated algorithm created to address many difficult optimization problems. The following traits are common to metaheuristics [70]. They are derived from nature, i.e., they use physics and biology principles. They are stochastic, i.e., incorporate random components, and do not require linearizing assumptions. Most metaheuristics are population-based, flexible, and capable of providing a nearly optimal priority set in a single algorithm run when used to address multi-objective optimization problems. The primary advantage of metaheuristics over deterministic optimization is their ability to resolve complicated optimization issues that no deterministic algorithm can.

Genetic algorithms, harmony search, evolutionary algorithms, differential evolution, cross-entropy, simulated annealing, cuckoo-search algorithm, honey bee mating optimization, tabu search, particle swarm optimization, ant-colony optimization, harmony search, shuffled complex evolution, mine blast algorithm, and shuffled frog leaping algorithm, among others. Some meta-heuristic algorithms have been developed and widely used for WDS optimization.

These methods have the benefits of not requiring derivative calculations and not relying on the original selection of decision variable values. The chance of discovering optimal global solutions utilizing these cutting-edge techniques is higher than in the case of deterministic methods due to the exploratory character of heuristic algorithms. The biggest drawback of these methods is the increased computing effort.

Initially, different methods were primarily connected to the EPANET network simulator to solve network equations; for pressurized water distribution networks, EPANET is a hydraulic simulator that can do extensive hydraulic and water quality simulations [71]. The typical components of a water distribution network include pipes (links), pipe junctions (nodes), pumps, control valves, and tanks/reservoirs [72]. EPANET solves the water distribution network for water flow in each pipe, pressure at each junction, water level in each tank, and chemical species concentration, among others. While performing the hydraulic analysis, EPANET resolves the conservation of mass and energy equations of the water distribution network. These EPANET simulations, particularly water quality studies, require a lot of computer work, so ANNs were used in their place because they require less computation [73]. In Fig. 6, the Sankey diagram shows the methods (right) employed in evaluation strategies (left) adopted in optimization evaluations.

3.2 General Constraints

The constraints of a WDS design general optimization model can be categorized into four groups shown in Fig. 9.

Fig. 9

A generic optimization model’s constraints

Hydraulic constraints are stated in terms of physical principles that regulate fluid flow inside a pipe network. The laws are the conservation of mass (the continuity equation) and energy conservation [74].

Except for the source, each junction node must meet the following continuity constraint:

$$\sum {Q}_{in}-\sum {Q}_{out}={Q}_{e}$$

(6)

where Q_in is the flow into the junction, Q_out is the flow out of the junction, and Q_e is the external inflow or demand at the junction node. The demands, Q_e, are considered positive under this convention.

For each basic loop in the network, the energy conservation constraint is as follows:

$$\sum {h}_{f}-\sum {E}_{p}=0$$

(7)

where E_p is the energy delivered into the liquid by a pump, and the head loss term, h_f, is expressed in formulas of Hazen-Williams or Darcy-Weisbach. Additional energy conservation requirements are provided for pathways between any two of the nodes when there are numerous source nodes. Thus P-1 independent equations are required for a network with P source nodes. For each node, the least head constraint in the network is given as:

$${H}_{k}\ge {H}_{k}^{min};\, k=1,\dots ,M$$

(8)

where, ${H}_{k}$ is the head at node k; ${H}_{k}^{min}$ is the minimum required head at the same node, and $M$ is the total number of nodes in the system.

The energy constraints of Eq. (7) result in the formulation of a non-linear optimization problem. Also, the water supply pipes are made in various sizes, further complicating the optimization process.

System constraints are a result of the WDS operational requirements and limitations. These include pressure at demand nodes, water quality at demand nodes, tank water level bounds, flow velocity in pipes, and water extraction limits, for example. Pipe diameter limitations are one example of a constraint on choice variables, limits on pipe lengths, and pump station capacity constraints.

3.3 Decision Variables

A decision variable is also known as a control variable. An optimization model can have one to thirteen different decision variables. A pipe’s diameter or size or a pipe segment’s length with a fixed (known) diameter is the decision variable used in most optimization models. Using two, three, or more types of a choice variable is significantly less common than using only one type. The decision variables describe the properties of each hydraulic component in the design, including the pipes [75,76,77,78], nodes [79], pumps [80,81,82], tanks [75, 83], and valves [80]. WDS decision variables are categorized in a broad optimization model based on the elements or aspects of WDS which drive the optimization process. The decision variables grouped according to different elements of WDS are given in Fig. 10.

Fig. 10

Decision variables of a general optimization model

3.3.1 Pipes

The primary goal of the basic optimization model is to identify the pipe sizes (or diameters) that have the lowest design costs for the network while still meeting nodal pressure requirements. Thus, unlike other network components (such as pumps, tanks, and valves), pipes are always considered when optimizing WDS design. For a specific pipe network structure, two different forms of choice variables exist, including pipe sizes/diameters and pipe segment lengths with a constant (known) diameter. Single-pipe designs are WDS design optimization problems where pipe sizes/diameters are used as decision variables. In contrast, split-pipe designs are problems where pipe segment lengths have a constant diameter. The design of WDS is a difficult problem that necessitates a thorough selection of decision factors in order to reduce the search space, even if only pipe diameters are optimized. To choose or decide on pipe routes when there is no predetermined network topology, for example, when developing a new or expanded WDS, additional decision variables are needed. Pipe closures and openings to modify a pressure zone boundary within a WDS are other forms of pipe decision variables that may be used.

3.3.2 Pumps

Incorporating pumps into the WDS design optimization has two key objectives. The first is the design of the pump or the capital cost, and the second is the cost of running the pump because of electricity use. The cost of administering WDSs is typically dominated by electricity, one of the highest marginal costs for water utilities because of the rising price of electricity. As a result, pumps necessitate the network’s design and operation to be included in the optimization [84]. As a result, an optimization model should incorporate the minimization of the pump design or capital cost and the pump operating cost to obtain the minimum amount of electricity consumed by pumps.

Three different decision variables in the model are used to control pumps. A pump position is the first thing considered when designing a new or strengthening and updating an existing WDS. The second factor is pump size, which can be expressed as a pump capacity, pump type, pumping power, pump head/height, pump operating curve/head-flow, or pump size combined with the number of pumps. The third factor is a pumping schedule, which specifies when the pump is turned on and off during a scheduling window (e.g., 24 h). Each choice affects the size of the search space and, ultimately, the computing effectiveness of the optimization algorithm.

3.3.3 Tanks

Storage tanks, also known as tanks, play an important function in WDSs and contribute to their efficiency and dependability. However, they are not frequently considered in WDS design optimization problems [10]. The literature has employed a variety of decision variable types to manage the model’s tanks, and a few objectives (or objective functions) have been devised to assess tank performance primarily. However, there is no established generic framework for modeling tanks. Therefore the usage of those variables and aims appears to vary among studies. Decision variables concerning tanks in WDS optimization include the location of the tank [83, 85], storage volume of tanks [85], levels of operation [86], tank heads [87], tank elevations [60], the ratio between width and height [88], the ratio between emergency volume and total volume [88]. A WDS’s hydraulic behavior can change depending on whether or not there are pumps and tanks. This is a significant challenge for any optimization technique since it generates a discontinuity (i.e., a significant difference in behavior with or without a tank at a certain place), which the algorithm must correctly control. The setup of the tank inside a simulation model, including its connection to the system, how the overflow valve operates, and how upper and lower level limits are taken into account, can also greatly impact how effectively the optimization run works.

3.3.4 Valves

The inclusion of valves in WDS design optimization problems is quite random, and explanations of their implementation are frequently very brief and lacking in specificity. The valve numbers and locations play a role in the overall system design, especially when the system’s reliability or resilience is considered. This is because the shutdown of valves used to isolate a portion of the WDS during an emergency (e.g., a pipe break or a water quality incident) creates a change in hydraulic behavior. Utilizing the settings of valves to manage the network’s pressure distribution (using pressure-reducing valves, or PRVs) [51] or to control the timing of flows and flow rate values (using either FCVs or PRVs, respectively) [89] is another application.

The combined design of the pipe network and isolating valve system poses a significant challenge to optimization techniques. In addition to the number of decisions growing exponentially as more valves are added, evaluating the effects of different valve system designs requires looking at a huge number of (probabilistic) scenarios, which makes the entire procedure computationally inefficient. Furthermore, when a WDS is broken down into manageable subsystems, the placement and status of isolating valves can also constitute decision variables.

3.3.5 Nodes

Node grouping is one of the key elements influencing the WDS demand estimation’s accuracy. However, in many studies, node groups have either been predetermined or presumed to exist based on engineering intuition or knowledge (e.g., grouping nodes with similar demand patterns or close together). Given the intricate hydraulic relationship between the pipe flows/nodal pressure at sensor locations and the requirement for node groups, especially in large networks, identifying appropriate node groups using such methodologies is challenging (mostly loop-dominated). The decision variables associated with nodes in the optimization of water distribution systems include flow rates from sources, future nodal demands, threshold demands, and hydraulic heads at junctions.

3.3.6 Water Quality

When designing WDSs, water quality characteristics should not be overlooked, as they might cause several issues with how well the systems work. Providing a suitable operating strategy to satisfy water quality-based requirements in other situations would be challenging or impossible. It is also noteworthy that, in most research, the only aspect of water quality taken into account during the WDS optimization process is chlorine residual, and water age is rarely examined [90].

3.4 Solution Techniques Used for WDS Optimization

Water resources planners and researchers have used several analytical methods to design and operate WDSs. The first study on the design and optimization of WDSs can be dated back to 1895 [91] and is based on the notion of economic velocity. Economic velocity was in use until the 1950s [92, 93]. The design was eventually replaced by the concept of the system’s lowest (annual) costs, also referred to as the least-cost design [94,95,96]. The earlier studies involved time-intensive and complex manual calculations, and thus the field garnered the attention of very few researchers and designers.

Rapid progress was witnessed in WDSs optimization during the 1960s to 1990s, which began with the introduction of computers in network analysis in 1957 [97]. Many iterative methods [98, 99] and simulation packages [71, 100] were developed after the introduction of computers. The methods were used to obtain deterministic solutions to non-linear network equations associated with network design and operations. Some of the most common methods using this approach include linear programming (LP) [60, 101], and non-linear programming (NLP) [64, 102], among others.

Another noteworthy improvement in optimizing WDSs was the inclusion of stochastic approaches employing laws of biological evolution [103] and genetics [104]. These methods gained popularity during the 1990s because these methods were capable of overcoming the limitations of deterministic methods for solving real-world problems [28]. Since the 1990s, various evolutionary algorithms (EAs) have been employed for the design optimization of WDSs. These include genetic algorithms [28, 105], shuffled leaping frog algorithm [106, 107], ant-colony optimization [108, 109], particle swarm optimization [110,111,112,113], harmony search [114, 115], genetic heritage evolution by stochastic transmission [116] and differential evolution [117,118,119]. Genetic algorithms (GAs) have been the most commonly applied evolutionary algorithms for water resources [70].

Genetic algorithms are automatic, domain-independent approaches for developing solutions to existing models or creating new models capable of emulating actual systems [120]. A collection of pipe network designs is considered in the GA-based approaches. A string of binary bits represents each design. On the other hand, substrings indicate the diameter of a specific pipe segment. An artificial genetic code is connected with the pipe network design based on a mapping between the coded substrings and the design variables. GAs have been created for low-cost, new, and augmentation of existing WDSs. Compared with non-linear programming methods, the results have proven to be more cost-effective and resulted in lower-cost solutions [121].

The type of problem under consideration for WDS optimization determines the solution technique. It also depends on the expertise of the specialist and his familiarity with software or tool [122]. However, the choices have seldom been dependent upon the performance of a model. Rather these are based on the expert’s preference, familiarity level, and availability of the software [37].

4 Genetic Algorithms

Genetic Algorithms (GAs) are randomized search methods to identify the optimal values of decision variables or parameters in pre-existing models. GAs are based on replicating evolutionary and natural selection processes [22]. Evolution is a process by which a species adapts generation by generation to fit in its natural habitat. Figure 11 shows the flow diagram of a basic Genetic Algorithm process. A simple evolutionary process model contains the following features:

• a. Population: the individuals within a population die and are replaced by “offspring.”

• b. Breeding: the offspring are formed by a combination of genes from parents through the process of breeding.

• c. Selection: By selection, fitter individuals of a population have a greater chance of breeding and raising their offspring than less-fit individuals.

Fig. 11

Flowchart of a basic GA Process

These features are retained in the GA optimization process. For instance, there is a requirement for the optimal design of a scheme. For this, first, a population of various designs is considered. Numerical values are then used to designate different design parameters [123]. The numerical values can be integers, real numbers, or Boolean values, and the design is encoded into a binary string. This form is analogous to a “chromosome.” The population is initially selected randomly within the search space described by the limiting values of the variables.

In order to select parents for breeding, a comparative fitness assessment of each individual is performed. Fitness here refers to how efficiently the proposed design will meet its objective. The parents can then be selected by Roulette-Wheel selection or Tournament selection. The former consists of selecting parents from a population with a probability of selection proportional to each individual’s fitness. The latter chooses two individuals randomly, and the fitter individual becomes a parent [27]. The design parameters obtained from the two parents are then combined to form a better-performing offspring. In a conventional Genetic Algorithm, the binary strings of the two parents (the chromosomes) are split at any arbitrary location. The second part of the strings is switched over to form offspring. The process is known as “crossover.” Therefore, this offspring will include some design attributes from each parent. However, in a more general design, the genetic information of the two parents is pooled together, and a feasible offspring is then grown from the pool of genetic possibilities [124]. One-point, two-point, or k-point crossover, uniform crossover, shuffle crossover, and three-parent crossover is typical crossover approaches used in the WDS optimization problems. In a one-point crossover, a crossover point is chosen randomly along the chromosome’s length. The new child is created by adding the genes of the first parent before the crossover point and the second parent after the crossover point. Genetic material is switched between two or more randomly chosen sites along the length of a chromosome during two-point or k-point crossover.

Because GAs is problem-specific, the crossover is used while treating the chromosomes like a collection of distribution pipelines. Here, altering even a single gene on a chromosome entail removing the existing pipe and installing a new one with a different diameter. In order to find the best solution, it is preferable to experiment with and test numerous pipe configurations. After experimenting with several crossover operators, the k-point crossover was chosen as the preferred crossover method. With N_p being the total number of pipelines in the distribution system, the number of crossover sites is calculated as (0.8 Np) rounded to the nearest integer. Crossover points’ positions are chosen at random. Figure 12 shows single and multiple numbers of crossover points for a 6-pipe distribution network.

Fig. 12

An example of a single and k-point crossover

Some random changes can also be introduced in the breeding process by a mechanism called “mutation.” A mutation probability of (1/l) is considered standard in the literature. ‘l’ here represents the length of the chromosome. In a simple GA, mutation can be induced by replacing a binary digit 0 with 1 or vice-versa. A simple example of this type of mutation is illustrated in Fig. 13. Some extra possibilities are introduced into the genetic material pool from which the offspring is grown [125]. Thus, selection and breeding procedures are employed to generate a new population of solutions. The new solutions replace the original ones and contain better individuals than those in the original population. Therefore, the process can be applied iteratively to produce successive populations, each better than the preceding one and terminating when no significant improvement is spotted over many generations. This simple and non-sophisticated mathematical technique works well for large and complex systems. However, the method it is based on is an efficient and robust natural process of producing designs for complex living creatures.

Fig. 13

Mutation in Genetic Algorithms

Some implementations of GAs use the concept of elitism. Here, the fittest chromosomes from one generation are selected in limited numbers and then copied into the next generation. Elitism is employed to shield the fittest chromosomes to prevent crossover and mutation. The elite chromosomes follow the least expensive distribution networks while abiding by every generation’s pressure and velocity constraints. Before crossover and mutation for the following generation, the two top performers from each generation are saved.

5 Applications to Water Distribution Systems

GAs have been used widely and successfully to handle water resource optimization challenges in various fields. These include problems with model calibration, engineering designs, and developing new strategies for management [70, 126]. One of the widespread applications of genetic algorithms has been in the design of water distribution systems (WDSs). A water distribution system connects various hydraulic components like pipes, tanks, valves, pumps, and reservoirs, conveying water from the source to the consumer. WDSs is one of the most vital and cost-intensive municipal infrastructure assets crucial to public health [127]. For designing an economically efficient WDS, various complex mathematical procedures are required. The task involves solving many non-linear network equations and optimizing network components’ size, location, and operational statuses, such as pumps, pipes, tanks, and valves [128]. The complexity of the task further increases when the system design is expected to comply with many requirements (for instance, water quality), contains additional purposes besides a low-cost economic metric (for example, probable fire damage), and incorporates additional real-world elements (e.g., uncertainty, staging of construction).

In a pipe network optimization problem, the key concept of GA is to choose a population of initial solution points dispersed randomly in the optimization space, then converge them iteratively to better solutions until the requirements are fulfilled. A brief description of the steps involved in utilizing GA for pipe network optimization is given below:

6 Population Initialization

In the process of a genetic algorithm, population initialization is the first step. An initial population of coded strings (binary) representing pipe network solutions with a population size of N is generated at random by the GA. In the current generation, the population is a subset of all possible combinations of pipe sizes.

7 Calculating the Network Costs

The GA decodes every substring into its associated pipe size for each of the N strings in the population before calculating the total network cost, including the cost of materials and construction.

7.1 Hydraulic Analysis of Pipe Networks

For every network design in the population, a steady-state hydraulic network solver calculates the heads and discharges under the given demand patterns. Any pressure shortfalls are noted after comparing the actual nodal pressures to the lowest permitted pressure heads. Similar to this, any deviations in velocity are recorded when comparing the actual water velocities at the pipes with the anticipated water distribution network velocities.

7.2 Calculating the Penalty Cost

If a pipe network does not adhere to the pressure and velocity limits, the GA assesses a penalty cost for each network design in the population; for instance, a pressure violation at a specific node if the node’s pressure is less than or more than the desired pressure.

7.3 Calculating the Overall Network Cost

The sum of the network cost (Step 2) and the penalty cost (Step 4) is then used to determine the cost of each network in the present population.

7.4 Calculating the Fitness

It is assumed that the fitness of the coded text is a function of the overall network cost. Fitness can be calculated as the inverse of the total network cost for each specified pipe network in the current population (Step 5).

7.5 Generation of a New Population

By using a selection process based on the fitness of initial members, the GA produces new members for the upcoming generation.

7.6 Crossover Operator

For each pair of parent strings chosen in Step 7, crossover happens with a certain probability. A uniform crossover operator is frequently employed for pipe network optimization with a relatively high string size.

7.7 The Mutation Operator

For each bit in the crossover-effected strings, there is a certain likelihood of mutation. Maintaining genetic diversity from one generation of a population to the next is the aim of the mutation operator.

7.8 Creation of Subsequent Generations

Using Steps 2 through 9, the three operators mentioned above create a new generation of pipe network designs. To create the next generations, the GA repeats the process. The final costs and pipe network designs are saved, and the less expensive cost options that adhere to the necessary limits are updated.

GAs are the most frequently applied evolutionary algorithm for designing and optimizing WDSs [129]. An immense effort has been devoted to developing and applying optimization methods to solve problems associated with the design optimization of WDS in the last three decades. Since the first application of GA in the mid-1990s [28, 85], much advancement towards this approach has been made. These methods utilize the GA approach in combination with some other methods to optimize WDS designs [130, 131] like fmGA [132], non-crossover dither creeping mutation-based GA (CMBGA) [133], adaptive locally constrained GA (ALCO-GA) [55], evolutionary algorithm (EA) [134]. Some methods use a combination of stochastic and deterministic approaches for developing more efficient solutions. These include a combined Genetic Algorithm and Linear Programming method (GA-LP/GALP) [135, 136] and a combined GA and ILP [137] method. Most of these studies exclusively solve a basic single-objective, i.e., minimizing the cost of pipe inhibited by the nodal pressure requirement. Thus, the number of variants of GAs or a combination of GAs with other methods has been routinely utilized to discover optimal WDS solutions. Some important publications employing genetic algorithms and their variants for the optimal solution of WDSs are given in Table 1.

Table 1 Papers on water distribution networks optimization by using genetic algorithms

Initially, GAs were applied to simple benchmark problems. However, recently GA applications have progressed towards more complex and realistic water distribution systems. The larger size and complex nature of networks demand better quality, near-optimal solutions for these systems, which should be available in practice. Thus, computational effectiveness is a crucial concern for the extensive acceptance of GAs to optimize large, real-world WDSs. This issue has been addressed by many researchers using two key approaches. The first approach comprises finding the best possible solution inside a genuine computational budget rather than finding the universal optimal solution [138]. The second approach involves increasing the computational efficiency of the optimizing process [139]. The design problems can be broadly classified into two (i) design of new systems; and (ii) augmentation of existing systems.

8 Design of New Systems

The design optimization of WDSs consists of determining each network component’s size, location, and operational statuses, such as pipes, pumps, tanks, and valves, while maintaining the lowest possible cost of design and operation at their minimum. The design will be based on the type of network under consideration, i.e., a branched or looped and gravity or pumped system. In a branched or looped network, there is an essential distinction in the problem’s complexity at the network analysis stage for defining flows in pipes. Nodal demands are used to calculate flow distribution in a branched network. On the other hand, in a looped network, the flows can assume alternative and multiple paths from source to consumer. For a gravity-based system, the design cost of a network concerning specified nodal pressure is minimized, and the only decision variable involved is the size or diameter of the pipes. These include widely known networks like the two-loop network [60], the Hanoi network [99], and the Balerma irrigation network [130]. The optimization problem for the pumped WDSs is more complicated than the gravity WDSs. This is because the pumps required in this system must be selected based on parameters like location, operational status, and operation for extended period simulation (EPS) and their size [80, 140].

Goldberg and Kuo [104] pioneered using GAs for pipe network optimization. This probabilistic method was used to improve a pipeline for steady-state flow. The size of pipes supplying a specific amount of water at an acceptable pressure level at the nodes was one of the selection criteria. Murphy and Simpson [141] employed GAs to solve the Gessler issue, which consists of two reservoirs connected by 14 pipelines. Davidson and Goulter [142] used GAs to construct a branched pipe network to identify the best configuration for a network with a single source and several nodes. Walters and Lohbeck [143] used GAs to identify the best pipe diameters in a branching pipe network. Simpson et al. [28] applied a GA search to identify the pipe network optimization problem alternatives. Earlier, single-objective models were used to optimize WDS design problems. Different objectives were grouped into one, i.e., the most economical design [144]. A multi-objective optimization approach using genetic algorithms was first used in the late 1990s [145], which considered electricity cost and a pump as objectives. In recent times, multiple objectives are considered in addition to the cost reduction, including pressure deficit [146, 147] or excess pressure [148] at network nodes, the penalty cost for violating the pressure constraint [147], greenhouse gas (GHG) emissions [83, 149] and water quality [150].

9 Augmentation of Existing Systems

The increase in water demands due to rapid population growth coupled with the development and expansion of urban areas stresses that the WDSs be upgraded continuously. The upgradation involves strengthening (pipe paralleling), rehabilitation (pipe cleaning and relining), and expansion.

9.1 Strengthening

System strengthening refers to enhancing an existing WDS to meet future needs. This is accomplished by laying duplicated pipes parallel to the existing water mains. As a result, it is often referred to as parallel network growth or pipe paralleling [74]. The strengthening of existing WDs has been achieved using GA [105, 151], or GA in combination with Artificial Neural Networks (ANNs) [152], fast messy genetic algorithms (fmGA) [153], and non-dominated sorting genetic algorithm II [78]. The complexity of network strengthening problems can increase by including water quality considerations. These applications include decision variables of water quality in addition to pipe size optimization [154].

9.2 Rehabilitation

An existing network that is not working satisfactorily can also be rehabilitated using the basic algorithm of pipe sizing. There are many options for network rehabilitation, including pipe removal, replacing old pipes with pipes of any set of existing diameters, inserting pipes with the same size or smaller inserts, duplication of pipes of any diameter, pipelining, pipe cleaning, or taking no action. Simpson et al. [28] studied a water distribution system consisting of two reservoirs and 14 pipes. Five new pipes were added to the system, and three pipes were rehabilitated using GAs. Suppose adequate money is available to upgrade the entire network to a reasonable standard. In that case, the optimization can be specified as minimizing the expenditure of upgrading subject to satisfactory network performance [155]. This approach works well for a small to medium-sized network. However, numerous problems arise for larger networks when the approach is applied to these. The first problem is that less finance would be available than required for rehabilitation. Secondly, the number of variables becomes extremely large, posing difficulties in implementing numerical techniques. In practice, with limited capital, it is expected that only a minor subset of the network pipes will be selected for rehabilitation [156].

On the one hand, using a variable for expressing each pipe in the network is inefficient. Conversely, selecting a set of candidate pipes in advance for improvement is unreasonably restrictive. These problems can be overcome using a multi-objective approach [157]. The multi-objective approach finds all-possible solutions for a range of costs up to the maximum amount of money available. It also involves developing a set of non-inferior solutions, i.e., solutions that any other solution cannot improve on both conditions [158]. For the generation of multi-objective optimal solutions, applied GAs include structured messy genetic algorithms (SMGA) [157] and non-dominated sorting genetic algorithm-II (NSGA-II) [156].

9.3 Expansion

The expansion of a WDS involves developing or extending an existing system beyond its original boundaries. The primary objective of expansion is to reduce the cost of design and operation. The expansion comprises two interdependent design problems: first, the newly constructed network is linked to the current one; and secondly, the existing system’s strengthening, rehabilitation, and up-gradation to convey increased water demands. Thus, expanding a WDS is a complicated process involving designing new and existing systems. An example of expanding an existing water distribution network is the Anytown network problem. The Anytown water distribution system, set up by Walski et al. [49], has characteristics and complications typical of those realized in most real systems. The network is considered a realistic benchmark for comparison and testing optimization software. Several solutions involving genetic algorithms for design optimization were applied to the network from time to time. Murphy et al. [159] obtained a standard genetic algorithm (SGA) to control the tanks and pumps as added design variables. The design of the “Anytown” water distribution network was significantly improved using structured messy genetic algorithms (SMGA) [85]. The proposed design had improved capabilities and was more cost-effective than the earlier attempts. In the succeeding years, some more aspects were added to the original design, including water quality [160], the expense of building and operating treatment facilities [32], and new tank size [81, 88].

Despite the developments in network optimization, developing new designs for the system or rehabilitation of an existing one using a fully automatic optimization technique remains challenging. This is especially true for large and complex systems where numerous elements are involved in the design. In order to overcome the limitations faced during the design of large systems, many designers divide the problems associated with complex designs into multiple phases [161]. These are then solved individually to reduce the search space and speed the simulation process [162].

10 Problem Elements in Design

10.1 Pipe Sizing

The simplest application of GA is the determination of pipe diameters of a WDS. A set of pipes is selected from commercially available sizes, which minimizes the construction cost for a given layout plan network and maintains sufficient pressure at all network nodes. Using the GA approach, an integer value is assigned to different pipe sizes, 1,2,3 [130]. The network design is thus defined by a “chromosome,” which can be a binary or integer string of these numbers. A network solver (simulation routine) analyses each candidate design for node pressure, and another routine determines the construction cost. Many solutions which do not have satisfactory nodal pressures are generated during evolution. These solutions are not discarded for being infeasible. However, they are designated feasible and add a penalty function to the cost, penalizing insufficient pressures. Judicious selection of penalty function will enable the GA to converge on an optimum solution in which all pressures are adequate [163]. Besides aiding new network designs, GA can also be employed to design extensions of existing networks.

The GA approach has been utilized to design several water distribution systems, enabling considerable cost savings compared to conventional schemes. The importance of GAs in designing pipeline distribution systems is reflected by the extensive use by various researchers and engineers for decades. Goldberg and Kuo [164] used GA for the steady-state optimization of the liquid pipeline. Savic and Walters [74] developed a computer model known as GANET that involved applying GA to optimize the least-cost design of water distribution networks. Vairavamoorthy and Ali [165] used GA, including a variable penalty coefficient depending on the degree of violation of the pressure constraints, to optimize pipeline designs. Keedwell and Khu [166] combined the GA approach with a local representative cellular automata approach to improve water distribution networks’ economics. Many researchers and planners reflect on other significant GA applications for pipeline system designs [129, 156] [156, 167, 168].

10.2 Layout

The simple method described above necessitates that all pipelines have at least the least diameter in any solution. A problem in which at least one pipe has zero diameters (i.e., be omitted from the design) cannot be managed without substantial modifications to the algorithm, as the elementary topology of the network is changed by excluding links [75]. This needs reorganization of the input data to the solver for network analysis. More primarily, it will lead to the creation of disconnected networks (networks in which one or more nodes are isolated from the source). With the increase in the network size, there is a rapid decrease in the chance of forming a connected network using a random set of diameters. The chance becomes zero or negligible for a network involving hundreds of pipes [169]. In such a case, the simple GA approach becomes obsolete, and other methods must be adopted. The method used should be capable of simultaneously identifying the optimal layout and size of non-zero pipes. Cembrowicz [170] discusses many approaches using different GA coding and applying them to real problems. Walters and Smith [124] explained that a very effective genetic design algorithm that generates the least cost tree-like networks could be the foundation for a looped distribution network.

A single-pipe design refers to challenges connected with WDS designs that use pipe widths or diameters as decision variables. In contrast, a split-pipe design refers to problems associated with pipe segment lengths of a specified diameter [136, 171]. Single-pipe designs provide better quality results than the split-pipe design as no redundant restrictions are imposed by split-pipe designs [146]. Extra decision variables are required to construct or pick pipe routes in the case of an undetermined network configuration (for example, while establishing a new or extending an existing WDS). These variables can be expressed as a binary selection of a link that should be incorporated into the pipe route [65].

10.3 Pressure Regulation

One of the significant worries that water distribution organizations face is leakage from water distribution systems. A decrease in pressure affects leakage substantially. One economical method for executing pressure decrease is changing the system design by resetting stop valves, along with most system links [172]. This can partly separate higher-level zones from low-lying ones, diminishing the latter’s pressures. A stop valve in the on/off setting is signified by a binary digit, giving a direct GA coding. Nonetheless, the standard GA administrators are ineffective because crossover and mutation frequently lead to disconnected and infeasible systems [173]. The problem was overcome by a more efficient evolution package in which connected and feasible networks are produced from the pooled designs of parents.

10.4 Calibration

A primary tool for the efficient design and operation of water distribution systems is the mathematical simulation of the system [32, 153]. In any case, models constantly require the integration of numerical parameters whose exact values are unknown. For example, pipe roughness can only be assessed. There may be a lack of precision or certainty in recording pipe diameters [78]. Network calibration is a technique for selecting the values of unknown parameters. It is also an optimization process where the difference between the set of observed and modeled values is minimized. GAs improves network calibration accuracy significantly compared to the traditional trial-and-error method [174].

10.5 Pump Scheduling

The cost of pumping water is one of the most important operational aspects of water supply distribution systems that requires optimization. Ordinarily, a water supply system is fed by several electric pumps, most likely from a few independent sources, which feed water to various reservoirs dispersed throughout the system. The optimization issue is determining which pumps to operate at what times of day to fulfill the anticipated demand for water at the least electricity expense [85].

The solution to the problem is worked out using GAs. The decision on which pump to operate and when to operate is coded as a binary signal corresponding to off and on. The comprehensive schedule for 24 h is specified by a string with 24 bits for every pump in the network. Software is required to simulate the pipework, pump, and reservoir system for 24 h for each schedule created [175]. Suppose variable speed pumps are used in place of fixed speed pumps. In that case, several bits are required for defining operating speed, and thus longer strings are also needed [80, 176].

The limitations on the schedule should be consciously dealt with. The volume in any reservoir cannot be negative. It cannot be allowed to drop below the minimum safe level at any point in time. Also, a reservoir cannot store more than the full volume and overspill because over-pumping is undesirable [148]. Further, the total volume delivered to each reservoir should be equivalent to the amount of water withdrawn from each reservoir over 24 h. For the above limitations, penalty functions must be developed to ensure the practicability of the final optimum schedule.

10.6 Test Networks

Several test networks have been used in the optimization of WDS. These networks have different sizes, complexity, and components. Small gravity-based WDSs with a single source and a limited number of nodes and pipelines [50] or those networks comprising a single source, single pump, single pipe, and single tank [132] are the simplest of WDS networks. An example of a large network is EXNET [177], which consists of two sources, nearly 2500 pipes and control valves. The real-world optimization problems of WDS design include complex, large networks with several elements. The most commonly used test networks for WDS optimization are given in Table 2.

Table 2 Commonly used test networks for WDS optimization

The type of problem under consideration, the analyst’s level of knowledge, and familiarity with the particular method/tool all influence the solution technique chosen. However, frequently there is no explicit explanation given as to why one methodology was chosen over another or why a different methodology was not used. The analyst’s preference, level of familiarity, and software accessibility are frequently taken into consideration while making this decision rather than a comparison of the tests run utilizing two or more different solution techniques.

11 Present Status and Challenges

Since the 1970s, much effort has been put into applying and developing optimization techniques to address WDS design optimization problems. The first techniques utilized were deterministic and included LP, NLP, and MINLP. After the first widely used GA applications in the mid-1990s, there was a shift towards stochastic approaches, which subsequently came to dominate the area. To date, a wide variety of those techniques have been used to optimize the design of WDSs. Most of those studies examine the suggested optimization approach using a limited set of benchmark networks, such as the Hanoi network, New York City tunnels, and the two-loop network, and only address a simple single-objective of least-cost design issue (i.e., pipe cost minimization constrained by the nodal pressure requirement). Without elaborating on why the chosen method worked better for a given test network, the typical result was an improved or equivalent optimal solution that was attained more quickly than by techniques previously employed in the literature. As a result, research has been somewhat constrained by the need to apply novel metaheuristic optimization techniques to relatively straightforward design issues without knowing the fundamentals of how algorithms work.

Despite the many benefits, a few issues must be handled before genetic algorithms may grow and evolve to help solve WDS optimization problems. Genetic algorithms are always assumed to work best with a certain initial population. The population size has an impact on the solution’s quality as well. The algorithm requires more processing time when a huge population is considered. The smaller population, though, could result in inadequate solutions. Finding the right population size is, therefore, a constant challenge. For GA, premature convergence is a frequent problem. It may result in allele deletion, making it challenging to identify a gene. Premature convergence states that the solution will be suboptimal if the optimization problem coincides too early. Convergence property must be addressed effectively to obtain a globally optimal solution rather than a locally optimal one (Shirajuddin et al. 2022).

The driving force, or fitness function, determines the fittest individual in each algorithm iteration. A costlier fitness function can be altered if there are not many iterations. The cost of computation may rise as the number of iterations rises. The fitness function choice is based on its applicability and computing cost. GAs must include both crossover and mutation operators. The presence of these operators has a significant impact on how GAs performs. The right balance between these operators is necessary to guarantee global optima. The probabilistic nature cannot determine the precise degree required for an efficient and ideal solution. For a particular issue, GAs need a certain encoding technique. There is no overarching process for determining if a specific encoding system is appropriate for any real-world issue. Two different encoding systems are needed if there are two distinct challenges. Furthermore, little attention has been paid to understanding why some algorithm variations perform better than others for particular case studies [162]. With more effective optimization techniques, WDS simulations might still be computationally prohibitive, especially as the model’s accuracy and the number of its decision variables increases.

However, despite numerous attempts, there is not yet a technique that has been widely accepted for comparing or evaluating algorithm performance for both single- and multi-objective WDS design challenges. A method for evaluating the best solution obtained, the speed of convergence, and the spread and consistency of the solutions are used to compare the performance of various single-objective algorithms [161]. A method has also been devised to assess an algorithm’s success by determining the efficacy of its parameters (like crossover and mutation) using their various values. Performance measures were proposed and are frequently used in multi-objective optimization to compare the effectiveness of different algorithms in terms of the quality of the Pareto fronts produced). As no single performance metric is compatible and comprehensive, comparing solutions is far more difficult than in single-objective optimization. This may be why several WDS design studies have restricted their analysis to a two-objective Pareto front.

12 Future Research Directions

Future research challenges for optimization of WDS design are linked to model inputs, algorithm and solution techniques, search space and computing efficiency, and solution post-processing. The optimum approach to represent different forms of uncertainties in the optimization process must be investigated concerning model inputs. The planning for ideal WDSs may be impacted by future uncertainties, such as climate change, population shifts, and economic development, making flexible design one of the interesting research fields over the coming decades.

In terms of algorithm and solution approach, a significant study area shows development in understanding algorithm performance and search behavior. Changing the fundamental structure of GAs has been used extensively to optimize water distribution systems. The optimality of a GA-derived solution can be improved by resolving the present difficulties. The proper number of crossover and mutation operators should be selectable. Self-Organizing GA, for instance, modifies the crossover and mutation operators following the given issue. It can speed up computation by saving time. Additional research may be considered to minimize premature convergence in GAs. Genetic algorithms imitate the course of natural evolution. There may be room to simulate aspects of natural evolution, like how the human immune system reacts and how viruses mutate.

The search space and computing efficiency have recently been noted to be important. Dynamic (i.e., staged and flexible) design and real-world WDS optimization problems are predicted to remain essential and promising study areas in the future because both the decrease in the search space and a gain in computational efficiency are relevant. How responsive the generated solution(s) are to the optimization model used is an unresolved question concerning solution post-processing. The selection of a practical and representative subset of the non-dominated solutions that could be helpful to the decision-makers when using a multi-objective optimization approach is still a challenge. As a result, techniques need to find a few practical solutions, such as when a slight improvement in one target results in a significant deterioration in at least one other objective. The research community would be benefited from a comprehensive comparison of the various available approaches for optimization of water distribution systems concerning decision variables, search space reduction, and enhancement of computing efficiency, which may use a variety of benchmark instances of different sizes and complexity. Future studies must incorporate the comparison because it can help to enhance choice variable coding further.

13 Summary and Conclusions

This paper deals with optimizing WDS genetic algorithms using Gas from the 1990s to the present. The review features articles covering various topics, including the design of new systems, improvement and enhancement of existing systems, time, parameter uncertainty, water quality, and operational considerations. The importance of this paper comes from the fact that it compiles a significant number of research papers on the application of GAs for WDS design optimization over the recent past. As a result, it might make it possible for researchers to locate their articles of interest quickly. The review evaluates the present status, field-specific limitations, future trends, and requirements of WDS optimization models using genetic algorithms.

The study highlights that GAs have been utilized to solve many water engineering optimization challenges. GAs displays their accurate worth when applied to very large search spaces. They normally need hundreds or thousands of generations to be formed before converging on the best solution. The enumeration of all solutions will be more efficient for smaller problems. One of the major advantages of the GA technique over other optimization methods is that it tends to converge onto the global optimum, other than a local optimum. Another advantage stemming from using a population of solutions is that a variety of near-optimal solutions can be obtained and saved. GAs was found to work better for variables with discrete values rather than continuous variables. However, continuous variables can be discretized before applying GAs to obtain solutions. GAs have been considered a valuable tool for optimizing engineering designs of water distribution systems. A substantial increase in efficiency can be achieved by coupling GAs with other techniques, especially for large and complex engineering systems. The role of genetic operators, such as crossover, mutation, and selection in optimal design, is also detailed in the paper. It has been highlighted how GA and its variations can be used to optimize WDS and its components. The difficulties and problems highlighted in this study will aid practitioners in conducting their studies. The goal of this study is to not only present the source of current research on the GAs application in WDS optimization but also to highlight the limitations and future scope of the research. It will encourage scholars to comprehend GA’s fundamentals and apply that understanding to their research challenges.

It was shown in this study that there is still a lack of consensus among researchers and practitioners regarding the best way to construct a WDS design optimization model, how to include all pertinent objectives and constraints, and whether and how to take into account different sources of uncertainty, while still enabling an effective search for the best solution to be achieved. There is no agreement on which optimization technique is best for a specific design problem, whether a single or multiple-phase optimization concept is to be used, or how engineering judgment can be best incorporated into the process. However, various generic and problem-specific optimization methods have been developed and applied over the years.

In order to create techniques for objectively comparing and validating various optimization algorithms and concepts on substantial, real-world issues, the research community must work together. Using WDS design problems of various sizes and complexity, it is also necessary to analyze the currently available methods for narrowing the search space, improving computational efficiency, and choosing efficient Pareto non-dominated solutions that represent a useful subset for decision-makers. Despite the vast quantity of material written about the design optimization of WDSs over the past three decades, there will be many research challenges in the years to come.