1 Introduction

Contemporary world stumble upon countless multifarious real-time predicaments in which the underlying computation quandary are incredibly intricate to resolve generally because of its unusually towering dimensionally allied search space that are non-linear, non-continuous, non-differentiable, non-convex in nature. It is not an overstatement if said that need of optimization is all over the place ranging from scheduling [1, 2] to deployment of wireless sensor networks [3, 4] to engineering design [5, 6] to robotic navigation [7] to image processing [8,9,10]. In more or less all these activities, one intends to accomplish certain goals by optimizing quality, profit or time as these resources are valuable and inadequately available in the real world. In such state of affairs, usage of traditional or classical optimization algorithms fall short and doubtlessly have an inadequate scope in endowing inclusive elucidations thereby becoming computationally demanding. This quest unquestionably show the ways en route for the inevitability of expansion and add-ons to the existing classical optimization techniques to evolve into progressive modern technological optimization processes dexterous enough to attain affluent way out appropriate for modern day’s practical problems. Thus, Evolutionary Computation (EC) focuses on the study of the class of global optimization algorithm principally dealing with figurative practice of perceptions, principles, and procedures mined from the elementary understanding of how natural systems advances to support and solve composite computational problems to further arrive towards most suitable solution. Nonetheless, some prime challenges that tend to swivel around EC which demands to be addressed are: Lack of accepted benchmark problems; Lack of standard algorithms and implementations, Lack of mechanism for fine parameter control and tuning, Lack of methods to measure performance etc., Presently substantial amount of work has been carried forward concentrating typically on the procedures of natural selection thus developing new algorithms inspired by human. However, human behavior and evolution give power to human to familiarize with their atmospheres at rates that surpass that of other nature based evolution namely swarm, bio-inspired, plant-based or physics-chemistry based thus instigation yet other compartment of Nature-Inspired Optimization Algorithm (NIOA) [11,12,13,14] i.e. Human-Inspired Optimization Algorithms (HIOAs).

Due to the thought supremacy and intelligence seized by human, human do hold an exceptional position amongst the entire living creatures thus anticipating that the algorithm inspired from or based on human behavior can undoubtedly surpass other algorithms. Numerous human-inspired optimization algorithms have been proposed and the same has been applied to solve hefty set of problems as highlighted in Table 1. Given the significance of HIOAs in the variety of domains, there is a strapping requirement of a study that should provide a comprehensive overview of HIOAs highlighting and covering the entire major elements related to the algorithm. Besides, huge number of human inspired optimization algorithms is presented in the literature and every algorithm is different from another in some or the other way. Therefore, examining, reviewing and deeply learning every algorithm is not just intricate but at times not feasible so researcher who is not very familiar with HIOAs shall be constantly in a dilemma about the choice of the algorithm under variety of circumstances. This work shall try filling up the research gap thus acting as a bridge by endowing a brief yet inclusive overview of the different algorithms induced by the human experiences by analyzing, assessing, documenting and intensely testing the same over color satellite imagery. This paper classically gives attention to not just comparing of several human based meta-heuristics however, also tries to accumulate obligatory information such as fundamental building blocks, common structure opted by HIOAs, elements of HIOAs (namely nature of algorithm, number of solution, fundamental methodology followed and source of inspiration by each algorithm) and advancements in the direction of accomplishing the connotation of HIOA for MLT color satellite image segmentation and further classification of HIOA based on few criteria such as Socio-Political Philosophy, Socio-Competitive Behavior, Socio-Cultural/Socio-Interaction, Socio-Musical Ideologies and Socio-Emigration/Socio-Colonization making it easier for the new researcher to garner idea about which HIOA would be suitable for the problem they intend to resolve. A number of research challenges with HIOA are discussed. Further, open future research directions are also recommended for researchers to pursue. Total 51 well-accepted and renowned stochastic HIOAs are taken into account in the present work. Consequently, this paper provides an acquainted detail of the different HIOAs developed so far over last two decades. Further, incredibly inadequate amount of work has been carried out using HIOA in the field of image segmentation thereby this paper explores and comprehends HIOA based multilevel thresholding image segmentation carried so far and further implements and compare few popular HIOAs (six HIOAs namely Corona virus Herd Immunity Optimization (CHIO), Forensic-Based Investigation Optimization (FBIO), Battle Royale Optimization (BRO), Political Optimizer (PO), Heap-Based Optimizer (HBO) and Human Urbanization Algorithm (HUA)) for color satellite image segmentation. Further, six HIOAs are compared with a popular Swarm based optimization algorithm namely Particle Swarm Optimization (PSO) [15]. For the same, Tsallis entropy and newly developed t-entropy have been exploited as objective functions in this paper. The t-entropy has not been employed for MLT predominantly with HIOA and this paper tends to draw attention to this as a major contribution. Lastly, comparative study using the mentioned objective functions over the color satellite images in MLT domain has been carried out meticulously to investigate the effectiveness of the mentioned HIOA. Some of the Human-Inspired Optimization Algorithms (HIOA) introduced over the years has been tabulated in Table 1 along with its year of introduction, author, application areas and additionally citation has been emphasized as per Google Scholar (Dated: 21.01.2022). Further, line charts shown in Figs. 1 and 2 is employed to depict the citations of different HIOAs (Harmony Search algorithm being the highly cited) and year-wise development of HIOAs respectively. The commonly used abbreviation is tabulated in Table 2.

Table 1 Human-Inspired Optimization Algorithms (HIOAs) and their applications
Full size table
Fig. 1
figure 1

The citation as per Google Scholar for various HIOAs available in literature

Full size image
Fig. 2
figure 2

Various HIOAs developed and proposed over years since 1994 till date (As per surveyed)

Full size image
Table 2 Abbreviation used for Human-Inspired Optimization Algorithms (HIOAs) surveyed in this paper
Full size table

The remaining sections of the paper are organized as follows: The elements of HIOAs and its common structure literature are put forward in Sect. 2. Section 3 draws attention towards the Classification of HIOAs. Additionally, challenges and open research issues have been evidently brought to light in Sect. 4. Application in MLT domain is emphasized in Sect. 5 that elaborates upon the problem formulation, objective functions utilized, literature review on HIOA in MLT domain over recent years and to end with experimental results along with the discussions on the same. Last but not the least, conclusion alongside few future research directions is offered in subsequent section i.e. Sect. 6.

2 Elements of Human-Inspired Optimization Algorithms (HIOAs) and Its Common Structure

Humans have been extensively recognized as the most ingenious species across the globe acquiring abundant cognitive capabilities and processing power because of which they are referred as 'developed cultural species'. These cultural species so called human have inimitable dependence on culturally or ethnically disseminated knowledge all through the human race (across generations, across society) basically because of the socio-atmosphere around. In society (human society) every individual is speeding towards their objectives delivering the best version of own self and disseminating knowledge in one way or the other may it be in the field of sports, politics, music, stock market or searching a suitable place for oneself. Thereby such rapid movement of human to attain their goals leads to one important concept known as competition in the society. Considering all these, the plentiful available variants of Human inspired Optimization Algorithms, are solely inspired by the different factors associated with human and the supporting environment. This section basically draws attention towards the same i.e. the different resource of inspiration as one of the component. Apart from that, Table 3 summarizes the list of HIOAs emphasizing on the methodologies opt by each, nature of each of the HIOAs, source of inspiration for each HIOAs and number of solutions that each HIOAs generate. Beside, this section also highlights the fact that though different HIOAs tag along expansive set of perceptions however, fundamental methodologies remain the same for all. Despite the fact that HIOA has progressed significantly over the years, it is being widely applied in several research domain and application areas are thereby growing with each passing years. This calls for the necessity of a universal framework / structure making it simpler for the researcher in terms of realization. With this perception in mind, and scrounging the aid from Table 3, a common framework for HIOAs has been planned and the same is projected via a flowchart in Fig. 3. The majority of HIOA tag along the common structure that basically consist of five imperative steps namely Initialization process, Evaluation process, Construction process, Update process and Decision process.

Table 3 Summary of the different components related to Human-Inspired Optimization Algorithms (HIOA)
Full size table
Fig. 3
figure 3

Flowchart depicting common structure of HIOAs

Full size image

3 Classification of Human-Inspired Optimization Algorithms (HIOAs)

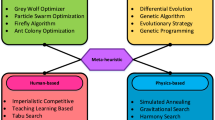
There are 51 Human Inspired Optimization Algorithms have been surveyed as listed in Table 3. In this section, a variety of categorization criterion is taken into account to classify HIOAs and the same has been recorded in Table 4 and diagrammatically depicted in Fig. 4. Further out of the total HIOAs surveyed, number of HIOAs falling under the designated category has been highlighted in Fig. 5. Classifying any algorithms based on source of inspiration is quite common yet effectual. Thereby, in this paper as well the categorization is carried out with in the similar way i.e. using source of inspiration(a scrupulous realm HIOA emulates) and based on the same, categories such as Socio-Political Philosophy (Political HIOA), Socio-Competitive Behavior (Competitive HIOA), Socio-Cultural / Socio-Interaction (Interactive HIOA), Socio-Musical Ideologies (Musical HIOA) and Socio-Emigration / Socio-Colonization (Emigrational HIOA) has been formulated.

Table 4 Classification of Human-Inspired Optimization Algorithms (HIOA) as per
Full size table
Fig. 4
figure 4

Classification hierarchy of Human-Inspired Optimization Algorithms (HIOA) as per Table 4

Full size image
Fig. 5
figure 5

Number of Human-Inspired Optimization Algorithms (HIOA) under different categories

Full size image

4 Major Challenges and Open Research Issues

Although HIOAs have proved its efficacy and recognition in numerous application domains, nevertheless quite a few challenging issues predominantly from theoretical viewpoint related to such algorithms does prevail [16]. The basic methodology of all HIOAs is even though revealed evidently for the researcher however, under what exact circumstance these algorithms needs to be employed remain a foremost challenge. Further, the entire HIOAs comprises of parameters that are essentially reliant on algorithm. The lack of general mechanism to finely tune the parameter scrupulously to enhance the performance of the underlying algorithm is yet an added challenge for the researcher to look upon. Additionally, various HIOAs need to be compared and the conclusion is driven totally based on the performance parameters employed to do the same. With this comes a new challenge that researcher requires to glance ahead i.e. the choice of suitable performance parameters. Furthermore, it is quite evident that HIOAs is associated with diverse applications [Table 3 clearly highlights the same] involving diminutive or restrained problem size, nonetheless, if these algorithm can be scaled up by means of approaches like of parallel computing is still a core inquest yet to be responded.

Few open research issues have been highlighted below:

  1. (a)

    Constructing a unified mathematical framework for HIOAs. To facilitate such integrated structure, multi-disciplinary approach to learn algorithm from diverse viewpoint is the requirement.

  2. (b)

    Self-tuning framework for HIOAs is another challenging research issue. To achieve the same, bi-objective process for parameter tuning needs to be considered wherein algorithm to be tuned can be used to tune itself.

  3. (c)

    Significance of benchmarks and identifying useful benchmarking to test different HIOAs.

  4. (d)

    Deciding on appropriate performance measures for fairly comparing different HOAs. To achieve the same, unified framework for comparison of algorithm is the necessity.

  5. (e)

    Introduction of mechanism to scale up HIOAs to handle broad range of predicaments. In order to achieve the same, generalized method need to be established that would cater to the need of variants of problems ranging from small-scale to large scale to real life problems.

  6. (f)

    Establishing ways and measures to accomplish most favorable balance of Intensification and Diversification in HIOAs.

  7. (g)

    Launching of techniques to successfully cope up with nonlinear restraints.

  8. (h)

    Coming up with approaches to utilize HIOAs in the realm of Machine Learning and Deep Learning.

5 Application of HIOAs in Multi-Level Thresholding Domain

Image segmentation [17, 18] is essentially the foremost and elementary procedure to examine and construe the acquired image in innumerable computer vision applications [19] wherein thresholding is considered enormously imperative in this domain. Considering the two categories of thresholding namely bi-level and multilevel, Multilevel Thresholding (MLT) segmentation methods has certain limitation while making a search for the best thresholding values comprehensively to optimize the objective function in which thresholding values increases thus swelling the computational cost. In simpler words, MLT methods turn out to be computationally complex as the number of thresholds grows. In order to address such imperfection and resolve other issues related to MLT, researchers are captivated towards quite a few methodologies inspired either by nature or from human behavior that can be extensively employed.

5.1 Problem Formulation

The fundamental notion of multi-level thresholding is to discover more than one threshold for a given image that further permits the images that has been segmented to accomplish the required criterion by optimizing specific objective function/s, with the threshold values as input parameters [20]. Assume that the image f comprising of L gray levels needs to be segmented into p partitions \(\left( {{\text{C}}_{1} ,{\text{ C}}_{2} ,{ } \ldots ,{\text{C}}_{{\text{i}}} ,{ } \ldots {\text{C}}_{{\text{p}}} } \right)\) using set of (p-1) threshold values \({\text{TH}} = \left( {{\text{t}}_{1} ,{\text{t}}_{2} , \ldots ,{\text{t}}_{{\text{i}}} ,...,{\text{ t}}_{{{\text{p}} - 1}} } \right)\), where \({\text{t}}_{1} < {\text{t}}_{2} < , \ldots .,{ } < {\text{t}}_{{{\text{p}} - 1}}\). For example, L = 256 for an 8-bit image and the grey levels are between 0 and 255 [20]. Hence, a pixel containing certain gray level \({\text{g }}\) belongs to class \({\text{C}}_{{\text{i}}}\) if \({\text{t}}_{{{\text{i}} - 1}} < {\text{g}} < {\text{t}}_{{\text{i}}}\) for \({\text{i}} = 1,{ }2, \ldots ,{\text{p}}\).The technique of determining the set of optimal thresholds \(TH^{opt}\) that optimizes the objective function \({\text{F}}\left( {{\text{TH}}} \right)\) is referred to as single objective thresholding. The mathematical expression is as follows:

$$ TH^{opt} = \mathop {\arg \max /\min }\limits_{0 \le TH \le L - 1} \left\{ {F(TH)} \right\} $$
(1)

For multi objective MLT,

\(F\left( {TH} \right) = \left( {F_{1} \left( {TH} \right), F_{2} \left( {TH} \right), \ldots ,F_{j} \left( {TH} \right), \ldots ,F_{n} \left( {TH} \right)} \right)\) , where \({\text{n}} > 1\).

5.2 Objective Functions

Selection of objective functions plays a crucial role in Multi-Level Thresholding-based image segmentation. Though numerous objective functions are proposed and available widely in the literature however, that makes it even more difficult in terms of selection when an image type varies making objective functions critically dependent on the algorithm as well as image type. This section elaborates on the two objective functions namely Tsallis and t-entropy that have been considered alongside six HIOAs in MLT domain for the color satellite image segmentation.

5.2.1 Tsallis Entropy

Multi-level thresholding [21] seeks to find the best threshold values for segmenting an image into different groups while maintaining a desired property (objective function). The threshold values are used as decision variables in the optimization process, which includes maximization or minimization of an objective function.

Suppose, an image I with L gray levels are classified into K classes \(\left( {C_{1} , C_{2} , \ldots ,C_{i} , \ldots C_{K} } \right)\) using a set of \({\text{nt}}\) threshold point \(T = \left( {th_{1} ,th_{2} , \ldots ,th_{i} ,..., th_{K - 1} } \right)\), where \(th_{1} < th_{2} < , \ldots ., < th_{K - 1}\). Here for 8 bit image \({\text{L}} = 256\) and gray level lie within the range \(\left[ {0,{ }255} \right]\). Therefore, a pixel with gray level g is belongs to class \(C_{i}\) if \(t_{i - 1} < g < t_{i}\) for \(i = 1, 2, \ldots ,K\). Thus single objective thresholding problem is the process of selecting the set of thresholds T′ which optimizes the objective function F(T) such that

$$ T^{\prime } = \arg \max /\min_{0 \le T \le L - 1} \left\{ {F\left( T \right)} \right\} $$
(2)

where, the objective function F(T) represents the desired property to be satisfied in order to obtain the segmented image I. In this paper, Tsallis entropy has been taken as objective function and the brief mathematical implementation of that is presented as follows.

Tsallis entropy is the generalization of Boltzmann–Gibbs entropy measure which is introduced by Constant in Tsallis [14, 22]. Based on the concept of multi-fractal theory, Tsallis entropy measure can be generalized to a non-extensive system using an entropy formula given in Eq. (3).

$$ S_{q} = \frac{{1 - \mathop \sum \nolimits_{i = 1}^{k} \left( {p_{i} } \right)^{q} }}{q - 1} $$
(3)

where, \(0 \le {\text{p}}_{{\text{i}}} \le 1\) denotes the probability of the state i. In the case of gray level image, it represents the occurrence of the ith gray level in the image. Tsallis parameter q signifies the measure of non-extensivity of the system under consideration. By applying pseudo additivity entropy rule it can be written as:

$$ S_{q} \left( {f + b} \right) = S_{q} \left( f \right) + S_{q} \left( b \right) + \left( {1 - q} \right).S_{q} \left( f \right).S_{q} \left( b \right) $$
(4)

Here, f and b represent the foreground and background classes of the image which is separated by threshold value \( {\text{t}}\). Suppose,

\(\left\{ \begin{gathered} \left( {{\text{p}}_{1} ,{\text{p}}_{2} , \ldots \ldots \ldots \ldots ,{\text{p}}_{{\text{L}}} } \right)|{\text{p}}_{{\text{i}}} \ge 0,{\text{i}} = 1,{ }2, \ldots ...,{\text{L}}.; \hfill \\ {\text{L}} = {\text{number of discrete gray levels}};{ }\mathop \sum \limits_{{{\text{i}} = 1}}^{{\text{n}}} {\text{p}}_{{\text{i}}} = 1 \hfill \\ \end{gathered} \right\}\) is the probability distribution of the gray level intensities of the image. Then the probability distribution of the f and b classes are given by the following expression:

$$ P_{f} = \frac{{p_{1} }}{{P^{f} }}, \frac{{p_{2} }}{{P^{f} }}, \ldots ., \frac{{p_{t} }}{{P^{f} }}{\text{ and }}P_{b} = \frac{{p_{t + 1} }}{{P^{b} }}, \frac{{p_{t + 2} }}{{P^{b} }}, \ldots ., \frac{{p_{L} }}{{P^{b} }} $$
(5)

where,

$$ P^{f} = \mathop \sum \limits_{i = 1}^{{t_{1} }} p_{i} {\text{ and }}P^{b} = \mathop \sum \limits_{i = t + 1}^{L} p_{i} $$
(6)

Consequently for each class, Tsallis entropy can be formulated as:

$$ S_{q}^{f} \left( t \right) = \frac{{1 - \mathop \sum \nolimits_{i = 1}^{t} \left( {{\raise0.7ex\hbox{${p_{i} }$} \!\mathord{\left/ {\vphantom {{p_{i} } {P^{f} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${P^{f} }$}}} \right)^{q} }}{q - 1}{,}\quad \, S_{q}^{b} \left( t \right) = \frac{{1 - \mathop \sum \nolimits_{i = t + 1}^{L} \left( {{\raise0.7ex\hbox{${p_{i} }$} \!\mathord{\left/ {\vphantom {{p_{i} } {P^{b} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${P^{b} }$}}} \right)^{q} }}{q - 1} $$
(7)

For bi-thresholding, sum of the both information measure for foreground and background is maximized. Therefore, the finding of optimal threshold can be formulated as follows:

$$ t_{opt} = {\text{Arg max}}\left[ {S_{q}^{f} \left( t \right) + S_{q}^{b} \left( t \right) + \left( {1 - q} \right) \cdot S_{q}^{f} \left( t \right) \cdot S_{q}^{b} \left( t \right)} \right] $$
(8)

Subject to the following constraints:

\(\left| {P^{f} + P^{b} } \right| - 1 < S < 1 - \left| {P^{f} + P^{b} } \right|\) where,

\(S\left( t \right) = S = S_{q}^{f} \left( t \right) + S_{q}^{b} \left( t \right) + \left( {1 - q} \right) \cdot S_{q}^{f} \left( t \right) \cdot S_{q}^{b} \left( t \right)\)(45).

This formulation can be easily extended to multi-level by the following expression:

$$ \left( {t_{1} ,t_{2} , \ldots \ldots ,t_{m} } \right) = {\text{Arg max}}\left[ {S_{q}^{1} \left( t \right) + S_{q}^{2} \left( t \right) + \ldots + S_{q}^{M} \left( t \right) + \left( {1 - q} \right) \cdot S_{q}^{1} \left( t \right) \cdot S_{q}^{2} \left( t \right) \ldots ..S_{q}^{M} \left( t \right)} \right] $$
(9)

where,

$$ S_{q}^{1} \left( t \right) = \frac{{1 - \mathop \sum \nolimits_{i = 1}^{{t_{1} }} \left( {{\raise0.7ex\hbox{${p_{i} }$} \!\mathord{\left/ {\vphantom {{p_{i} } {P^{1} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${P^{1} }$}}} \right)^{q} }}{q - 1}{ },{\text{ and }}S_{q}^{M} \left( t \right) = \frac{{1 - \mathop \sum \nolimits_{{i = t_{m} + 1}}^{L} \left( {{\raise0.7ex\hbox{${p_{i} }$} \!\mathord{\left/ {\vphantom {{p_{i} } {P^{M} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${P^{M} }$}}} \right)^{q} }}{q - 1},{\text{ and }}M = m + 1 $$
(10)

Subject to the following constraints:

$$ \begin{gathered} \left| {P^{1} + P^{2} } \right| - 1 < S^{1} < 1 - \left| {P^{1} + P^{2} } \right|, \left| {P^{2} + P^{3} } \right| - 1 < S^{2} \hfill \\ < 1 - \left| {P^{2} + P^{3} } \right|\& \left| {P^{m} + P^{m + 1} } \right| - 1 < S^{M} < 1 - \left| {P^{m} + P^{m + 1} } \right| \hfill \\ \end{gathered} $$
(11)

where, \(P^{1} , P^{2}\) and \(P^{m + 1}\) corresponding to \(S^{1} , S^{2}\) and \(S^{M}\) have been computed using \(t_{1} , t_{2} , \ldots \ldots ,t_{m}\) respectively.

5.2.2 t-entropy

A new measure of entropy called t-entropy has been proposed by Chakraborty et al. in the year 2021 [23]. Suppose, an image I associate with normalized histogram \({\varvec{p}} = \left( {p_{0} ,p_{2} ,p_{3} , \ldots \ldots \ldots \ldots ,p_{L - 1} } \right)|p_{i} \ge 0, i = 0,1,2, \ldots .L - 1; \) where L is the number of gray levels in the image I and \(\mathop \sum \limits_{i = 0}^{L - 1} p_{i} = 1\). Then the t-entropy \(\left( {H_{c} } \right)\) of the image is computed as the following expression:

$$ H_{c} \left( {\varvec{p}} \right) = \mathop \sum \limits_{i = 0}^{L - 1} p_{i} \tan^{ - 1} \left( {\frac{1}{{p_{i}^{c} }}} \right) - \frac{\pi }{4} $$
(12)

where, \(c\) is a positive constant.

Now, if there are \(nt = K - 1\) thresholds \(\left( t \right)\), partitioning the normalized histogram into \( K\) classes, then the entropy for each class may be computed as,

$$ H_{c}^{1} \left( {th_{1} } \right) = \mathop \sum \limits_{i = 0}^{{th_{1} - 1}} \frac{{p_{i} }}{{w_{1} }}\tan^{ - 1} \left( {\frac{1}{{\left( {{\raise0.7ex\hbox{${p_{i} }$} \!\mathord{\left/ {\vphantom {{p_{i} } {w_{1} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${w_{1} }$}}} \right)^{c} }}} \right) - \frac{\pi }{4} $$
$$ H_{c}^{2} \left( {th_{2} } \right) = \mathop \sum \limits_{{i = th_{1} }}^{{th_{2} - 1}} \frac{{p_{i} }}{{w_{2} }}\tan^{ - 1} \left( {\frac{1}{{\left( {{\raise0.7ex\hbox{${p_{i} }$} \!\mathord{\left/ {\vphantom {{p_{i} } {w_{2} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${w_{2} }$}}} \right)^{c} }}} \right) - \frac{\pi }{4} $$
$$ \begin{array}{*{20}c} \vdots \\ \vdots \\ \end{array} $$
$$ H_{c}^{K} \left( {th_{nt} } \right) = \mathop \sum \limits_{{i = th_{nt} }}^{L - 1} \frac{{p_{i} }}{{w_{nt} }}\tan^{ - 1} \left( {\frac{1}{{\left( {{\raise0.7ex\hbox{${p_{i} }$} \!\mathord{\left/ {\vphantom {{p_{i} } {w_{nt} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${w_{nt} }$}}} \right)^{c} }}} \right) - \frac{\pi }{4} $$
(13)

where,

$$ w_{1} \left( {th_{1} } \right) = \mathop \sum \limits_{i = 0}^{{th_{1} - 1}} p_{i} , \, w_{2} \left( {th_{2} } \right) = \mathop \sum \limits_{{i = th_{1} }}^{{th_{2} - 1}} p_{i } , \ldots \ldots \ldots \ldots , \, w_{K} \left( {th_{nt} } \right) = \mathop \sum \limits_{{i = th_{nt} }}^{L - 1} p_{i} $$
(14)

where, for ease of computation, two dummy thresholds \(th_{0} = 0, th_{nt} = L - 1\) are introduced with \(th_{0} < th_{1} < \ldots < th_{n - 1} < th_{nt}\). Then the optimum threshold value can be found by

$$ \varphi \left( {th_{1} ,th_{2} , \ldots \ldots ,th_{nt} } \right) = Arg\max \left( {\left[ {H_{c}^{1} \left( {th_{1} } \right) + H_{c}^{2} \left( {th_{2} } \right) + \ldots + H_{c}^{K} \left( {th_{nt} } \right)} \right]} \right) $$
(15)

During the experiment, the positive constant \(c\) had been tested over \(\left[ {0.01, 20} \right]\) and found that \(c = 0.1\) is best for multi-level thresholding based image segmentation over the tested datasets.

5.3 Literature Survey on HIOAs Based MLT

Optimization is a methodology of making a design or the system as fully functional as possible that is finely accomplished by a well-tuned algorithm. Nature instead of being fully deterministic is evolutionary, vibrant and resourceful. The nature-inspired algorithms use the best combination and evolution strategy in a given situation However, a new meta-heuristic Human-Inspired Optimization Algorithms (HIOA) is introduced that uses social behavior in human dynasties. Numerous researchers have advocated quite a lot of optimization approaches wherein a variety of entropy has been exploited as an objective functions. The recent literature of HIOA based MLT has been presented in Table 5. Different parameter’s and algorithms abbreviation used in the papers surveyed in Table 3 with its full form is tabularized respectively in Table 6 and Table 7. Total 21 HIOA-MLT papers have been discussed in Table 3 where different papers collected over the years is presented in Fig. 6. Whereas, Fig. 7 indicates the percentage of papers which are surveyed in Table 5 utilizing different types of images.

Table 5 Literature reports on HIOA based multi-level thresholding
Full size table
Table 6 Different qualitative parameters mentioned in the paper surveyed in Table 5 and its full form
Full size table
Table 7 Different algorithms mentioned in the paper surveyed in Table 5 and its full form
Full size table
Fig. 6
figure 6

Number of HIOA-MLT based paper published over years

Full size image
Fig. 7
figure 7

Number of surveyed HIOA-MLT paper as per types of images

Full size image

5.4 Experimental Results and Discussion

This section presents the experimental results that has been computed with the help of six HIOA namely Corona virus Herd Immunity Optimization (CHIO), Forensic-Based Investigation Optimization (FBIO), Battle Royale Optimization (BRO), Political Optimizer (PO), Heap-Based Optimizer (HBO) and Human Urbanization Algorithm (HUA). The result of the six HIOAs considered is further compared with very established Particle Swarm Optimization (PSO) algorithm. Further, Tsallis entropy on one hand and t entropy on the other over color satellite images has been considered as an objective functions. The parameters setting of the corresponding methods have been prearranged in Table 8. All seven HIOA have been used in their original versions. Nevertheless, the parameters of each algorithm have been fine-tuned to determine the best values subsequently to produce a good segmentation result within a rational amount of time. In order to do so, a series of experiments has been performed where segmentation is conducted for different threshold numbers and the test images. The value of each parameter has been selected practically (experimentally) with the objective of coming within the reach of the best segmentation. The experimental study includes the evaluation of Tsallis’ and t entropy, as objective functions. For the reasonable comparison amongst HIOA methodologies, each execution of the tested objective functions considers the Number of Function Evaluations, NFE = 1,000 * d, as stopping criterion of the optimization process. This criterion has been designated to encourage compatibility with previously published works in the literature. The experiments are evaluated considering the number of threshold values (TH) set to 6 and 8 which correspond to the d-dimensional search space in an optimization problem formulation. Furthermore, FE is also a crucial performance index used to measure the efficiency of HIOA. In comparison to computational complexity, FE permits some technical aspects such as the computer system where the experiments run and is implemented, that has direct impact on the running CPU time thereby concentrating only on the capacity of the algorithm to search within the solution space. Each execution of the tested objective functions considers the Number of Function Evaluations, NFE = 1,000*d, as stopping criterion of the optimization process. For measuring the optimization ability of the HIOAs, mean fitness \(\left( {\overline{f}} \right)\) and standard deviation \(\left( \sigma \right)\) have been calculated. On the other hand, segmentation efficiency of the HIOA based models is measured by computing three well known parameters in image segmentation domain i.e. Peak Signal-to-Noise Ratio (PSNR), Feature Similarity Index (FSIM) and Structural Similarity Index (SSIM). MatlabR2018b and Windows-10 OS, × 64-based PC, Intel core i5 CPU with 8 GB RAM are the hardware and software requirements incorporated during the experiment. With the intention to verify the efficiency of different NIOA, experiment is conducted using 20 color satellite images. The mentioned algorithms are tried and explored on images extracted from the site of Indian Space Research Organization (ISRO) [24] [https://bhuvan-app1.nrsc.gov.in/imagegallery/bhuvan.html#]. The original color satellite image is shown in Fig. 8.

Table 8 Parameter setting of HIOAs
Full size table
Fig. 8
figure 8

Original color satellite image (Input Image)

Full size image

5.4.1 Results Over Tsallis Entropy for Color Satellite Image

Figure 9 highlights the visual segmented results of the original image of Fig. 8 using six different HIOA (PO, CHIO, HBO, FBIO, BRO and HUA) which is further compared with one of the popular algorithm i.e. PSO with Tsallis entropy as objective function over 6 and 8 thresholds for a color satellite image. Table 9 projects numerical comparison of various aforesaid HIOA with Tsallis entropy as objective function over 6 and 8 thresholds for the satellite image considering numerous parameters such as fitness function \(\left( {\overline{f}} \right)\), standard deviation (σf), Computational time (Time (sec)), FSIM, PSNR and SSIM. Additionally, the entries that are highlighted in boldface indicate the best performance results. Table 9 clearly bring to light that PO accomplishes the best result over the threshold value (nt = 6) for every parameters taken into account while PSO bestows the worst end result when compared amongst all the six tested HIOAs. Further, for thresholds value (nt = 8) for parameters namely \(\left( {\overline{f}} \right)\), Time (sec), FSIM, PSNR and SSIM, PO exhibits the best result whereas HUA attains the best value in terms of (σf). On the other hand for the same threshold value, yet again PSO bestows the worst end result when compared amongst all the six tested HIOAs. The fitness value of PO is judged against other six HIOAs and PSO considered. A non-parametric significance proof known as Wilcoxon’s rank test has been performed wherein such proof authorizes to estimate differences in the result amid two associated methods. A p-value of less than 0.05 (5% significance level) sturdily supports the condemnation of the null hypothesis, thereby signifying that the best algorithm's results vary statistically noteworthy from those of the other peer algorithms and that the discrepancy is not due to chance. Table 10 tabulates the pair-wise comparison among HIOA (PO vs. CHIO; PO vs. HBO; PO vs. FBIO; PO vs. BRO; and PO vs. PSO) depending on Wilcoxon p-values over Satellite image for Tsallis entropy for 6 and 8 number of thresholds. All the Wilcoxon p-values obtained and thereby projected in Table 10 are less than 0.05 (5% significance level) with h = 1 is an apparent proof not in favor of the null hypothesis, inferring that the PO fitness values for the performance are statistically superior. This further indicates that PO in amalgamation with Tsallis entropy as objective function is proficient enough to bring into being consistent solution irrespective of the threshold values as in all the cases of comparison for both nt = 6 and 8 value of \(p < 0.05\) and \( h = 1\).

Fig. 9
figure 9

Segmented results of different HIOAs using Tsallis entropy over nt = 6 and 8

Full size image
Table 9 Numerical comparison of HIOA for Tsallis entropy as objective function over satellite image
Full size table
Table 10 Comparison among HIOA depending on Wilcoxon p-values over satellite image for Tsallis entropy
Full size table

5.4.2 Results Over t- Entropy for Color Satellite Image

Figure 10 highlights the visual segmented results of the original image of Fig. 8 using six different HIOA (PO, CHIO, HBO, FBIO, BRO and HUA) which is further compared with one of the popular algorithm i.e. PSO with t-entropy as objective function over 6 and 8 thresholds for a satellite image. Table 11 projects numerical comparison of various aforesaid HIOA with t-entropy as objective function over 6 and 8 thresholds for the satellite image considering numerous parameters such as fitness function \(\left( {\overline{f}} \right)\), standard deviation (σf), Computational time (Time (sec)), FSIM, PSNR and SSIM. Additionally, the entries that are highlighted in boldface indicate the best performance results. Table 11 clearly bring to light that PO accomplishes the best result over the threshold value (nt = 6) for every parameters taken into account except for (σf) wherein CHIO attains the best (σf) value. PSO bestows the worst end result when compared amongst all the six tested HIOAs. It is to be noted that for the same threshold value i.e. nt = 6, HUA in regard to fitness function \(\left( {\overline{f}} \right)\) attains the same value as that of PSO. Further, for thresholds value (nt = 8) for the entire parameters, PO exhibits the best result. On the other hand for the same threshold value, yet again PSO bestows the worst end result when compared amongst all the six tested HIOAs for parameters fitness function \(\left( {\overline{f}} \right)\), Computational time (Time (sec)), FSIM, PSNR and SSIM whereas BRO attains the worst value for standard deviation (σf). The fitness value of PO is judged against other six HIOAs and PSO considered. A non-parametric significance proof known as Wilcoxon’s rank test has been performed wherein such proof authorizes to estimate differences in the result amid two associated methods. A p-value of less than 0.05 (5% significance level) sturdily supports the condemnation of the null hypothesis, thereby signifying that the best algorithm's results vary statistically noteworthy from those of the other peer algorithms and that the discrepancy is not due to chance. Table 12 tabulates the pair-wise comparison among HIOA (PO vs. CHIO; PO vs. HBO; PO vs. FBIO; PO vs. BRO; and PO vs. PSO) depending on Wilcoxon p-values over Satellite image for t-entropy for 6 and 8 number of thresholds. All the Wilcoxon p-values obtained and thereby projected in Table 11 are less than 0.05 (5% significance level) with h = 1 is an apparent proof not in favor of the null hypothesis, inferring that the PO fitness values for the performance are statistically superior. However, Table 11 additionally indicates that PO in amalgamation with t-entropy as objective function is proficient enough to bring into being consistent solution when the threshold value (nt = 8) however, as its clear from the table that when the threshold value (nt = 6), there is no significant difference (as \(p > 0.05\) and \(h = 0\)) between PO and few HIOAs namely CHIO. HBO, FBIO and BRO but PO outperforms HUA and PSO as depicted by the value of p and h (as \(p < 0.05\) and \(h = 1\)).

Fig. 10
figure 10

Segmented results of different HIOAs using t- entropy over nt = 6 and 8

Full size image
Table 11 Numerical comparison of HIOA for t-entropy as objective function over satellite image
Full size table
Table 12 Comparison among HIOA depending on Wilcoxon p-values over satellite image for t-entropy
Full size table

5.4.3 Discussion on the Performance Comparison Among Different Objective Functions Employed

From the values obtained for different parameters in the tables highlighted above (Tables 9 and 11), it is evident that on comparing different HIOA’s for the satellite images using two prominent objective functions namely Tsallis and t-entropy for different threshold values (nt = 6 and 8), Tsallis entropy outperforms for every HIOA’s as well as PSO over parameters such as fitness function \(\left( {\overline{f}} \right)\), standard deviation (σf), Computational time (Time (sec)), FSIM, PSNR as well as SSIM. It is noteworthy to highlight that different HIOA’s generates high fitness values for all threshold values considering Tsallis entropy to segment the standard color images as compared to segmentation using t-entropy as an objective function. Further, it can be deduced and inferred from the experimental outcome that every HIOAs in combination with Tsallis entropy outperforms the HIOA combination with t-entropy in almost all cases and almost all parameters taken into consideration. On the other hand, considering Tables 10 and 12, it is apparent that for every parameter considered in the scenario, every HIOA’s in combination with Tsallis entropy generates better result and proves superior to that of HIOA combined with t-entropy as an objective function for every threshold values. This surely indicates that though t-entropy is the newly introduced concept rarely employed in image segmentation, Tsallis entropy as an objective function presents an interesting and unconventional choice for satellite image segmentation task and further, same has been clearly highlighted in Fig. 11a, b, c and d. In addition, the another analysis made from the above mentioned tables is that as the number of threshold enhances computational time increases no doubt but values for FSIM, PSNR and SSIM also amplify for the objective function considered under this scenario.

Fig. 11
figure 11

Comparison among Tsallis and t-entropy over Color Satellite Images

Full size image

6 Conclusion and Future Research Directions

Amongst the list of algorithms instigated and existing in literature, deciding upon an algorithm entails not just a meticulous understanding of its theoretical fundamentals but also require systematically comprehending upon the different components of algorithm along with its different parameters and application areas. This work attempted and strived towards concentrating on these issues and talks about pertinent conceptions related to HIOAs such as components, classification, common structure, application areas, work carried out till date and many more. A number of optimization technique inspired from human behavior and intelligence for MLT color satellite image segmentation problem considering two significant objective functions i.e. Tsallis’ and t-entropy has been discussed in this paper. To reveal the connotation of HIOAs in the field of MLT image segmentation six different algorithms namely Corona virus Herd Immunity Optimization (CHIO), Forensic-Based Investigation Optimization (FBIO), Battle Royale Optimization (BRO), Political Optimizer (PO), Heap-Based Optimizer (HBO) and Human Urbanization Algorithm (HUA) has been implemented and further compared among themselves and with one of the popular Swarm based optimization algorithm i.e. Particle Swarm Optimization (PSO). The comparison is made taking into account numerous parameters such as fitness function \(\left( {\overline{f}} \right)\), standard deviation \(\left( {\sigma_{f} } \right)\), Computational time (Time (sec)), FSIM, PSNR and SSIM based on the evaluation of two predominant objective function as revealed earlier (Tsallis’ and t-entropy). The results and contribution of this paper have been summarized as follows:

  1. (a)

    The numerical outcome demonstrates that Political Optimizer (PO) confirmed and exhibited its competence and accuracy over other HIOA’s (as depicted in Sect. 5.4) and PSO signifying that PO is most suitable HIOA for MLT image segmentation process of color satellite image with Tsallis’ entropy as objective function.

  2. (b)

    Though t-entropy as the objective function is the recently introduced and rarely employed in image segmentation, Tsallis entropy as an objective function under different circumstances provides an attention-grabbing result and thus can be an eccentric preference for satellite image segmentation task.

  3. (c)

    Both objective functions considered in this paper in connection with different HIOA are though suitable for color satellite image segmentation however, result of t-entropy as the objective function is dependent on the threshold value.

  4. (d)

    Lastly as mentioned earlier, it is to be noted that as the number of threshold increases, values for FSIM, PSNR and SSIM also intensifies for both of the objective function considered under this scenario. Also, with tsallis entropy as objective function, different HIOAs as well as PSO considered for the experimental purpose generated high fitness values irrespective of threshold values considered.

No doubt, HIOAs have evidently proved itself as an effective mechanism to unravel intricate real-world optimization problems; it can still be further explored. With this, few research directions has been projected below that shall hopefully turn out to be useful for the researcher to excavate and discover HIOAs further.

  1. (a)

    Proficient but less obscure HIOA (lesser number of operators, tuning parameters etc.) is the need of an hour. Parameterless HIOAs can be good work in future [25, 26].

  2. (b)

    Development of HIOAs based image clustering especially histogram based image clustering should an emergent research topic [27,28,29,30]

  3. (c)

    Exploring and analyzing each HIOAs that fits the best for the problem one intend to resolve at times is not just tiresome but also not realistic so more parameters need to be identified to classify HIOAs making it easier for the researcher to select the suitable one.

  4. (d)

    From the above table i.e. Table 5 that highlights the literature review of HIOA on MLT domain undoubtedly point out that maximum HIOAs has been employed for MLT image segmentation for standard gray scale images (Fig. 7) however, very less work has been performed for satellite images, medical images and even standard color images. Exploring and applying HIOAs over these variant of images could be a good work.

  5. (e)

    Also, Table 5 brings to lights the usage of different objective functions, wherein maximum work has been done with Otsu and Kapur as objective functions. Exploring more of the existing objective function and applying the same or applying Two-Dimensional (2D) objective functions like 2D Otsu, 2D Tsallis, 2D-Renyi, 2D Cross etc., over diverse HIOAs in MLT domain could be interesting as well as challenging.

  6. (f)

    Hybridization and parallel models has always proved efficient and could be a great future research. In this regard, hybridization [31] of for instance Social Learning Optimization inspired Archimedes Optimization Algorithm or a novel PSO model based on Simulating Cohort Intelligence. Recently human intelligences or human social communication based PSO models are developed and provided outstanding results [15, 32, 33].

  7. (g)

    Though t-entropy generated acceptable result, however, it could not be proved commendable when compared with the other objective functions under similar circumstances. Consequently, improvised variant of t-entropy could be a good work.

  8. (h)

    Initial parameters are heuristically assumed so there is always a scope to find a specific / standard method to fix, control and tune the initial parameters. This could be looked upon. Introducing novel performance measures to evaluate the success of an algorithm is also a necessity.

  9. (i)

    Lastly, inspiration taken from behavior of quantum particles to develop metaheuristic optimization algorithms [34] is as well gaining popularity and applied in numerous application domain. In this perspective, introducing a quantum inspired HIOA could be a great research work that can be conducted in future.