1 Introduction

High-speed marine craft can benefit from application or aerodynamically supported wings or platforms. Examples include racing boats of hydroplane and tunnel-hull types, wing-in-ground vehicles, and fast amphibious platforms (Matveev and Kornev 2013). Their air-supported lifting elements often operate in strong ground effect, which usually enhances lift and reduces drag, whereas the upper surfaces of these wings either are weakly affected by the proximity to water or may not even contribute to the lift, e.g., if they used as cargo platforms. The wings of this sort are usually referred to as ram wings (Gallington and Miller 1970).

The most remarkable of aerodynamically assisted marine craft are wing-in-ground (WIG) vehicles. Large, up to 500 tons in displacement, WIG craft were developed in Russia in the last century for military purposes, but they were later abandoned due to high cost and unclear fit into the naval strategy. Smaller, more economical WIG crafts were intermittently produced in several countries, and projects for large WIG transports are still actively considered. One of the most important concerns with these vehicles is their stability and dynamics in open sea conditions due to potentially dangerous high-speed flight close to water.

An extensive list of references on WIG craft is given in a review by Rozhdestvensky (2006). As concerns ram wings operating at low clearances to the ground (less than 0.1 of the wing chord), an important work of Windall and Barrows (1970) can be noted where it was first shown that the airflow under ram wings becomes primarily two-dimensional in a horizontal plane. Gallington and Miller (1970) developed a simplified theory, carried out validating experiments, and constructed experimental model prototypes of ram wings. Staunfenbiel (1987) analyzed the stability of WIG craft, emphasizing dependency of their aerodynamic coefficients on height. One of the first attempts to use viscous solvers of computational fluid dynamics to model three-dimensional WIG was described by Hirata and Kodama (1995). A number of extensions of the extreme-ground-effect (EGE) potential-flow theory for ram wings, including lift-augmenting mechanisms, compressibility effects, and stability, are detailed in the book by Rozhdestvensky (2000). Benedict et al. (2002) analyzed the WIG take-off regimes when the wing is in close proximity to water. Tuck (1984), Barber (2007), and Zong et al. (2012) calculated water surface deformations caused by wings steadily flying in ground effect. Matveev and Chaney (2013), and Liang et al. (2014) modeled airfoils heaving above water surfaces.

Steady and unsteady aerodynamics of ram wings can be effectively modeled with help of EGE theory which assumes potential flow with dominant horizontal air velocities in the channel formed between the wing and the underlying surface (Windall and Barrows 1970; Rozhdestvensky 2000). The EGE theory has been previously validated against experimental data for ram wings with and without side plates (Rozhdestvensky 2000; Matveev 2013) and for power-augmented ram wings where air-based front propulsors produce high-speed airflow incident on the wing even in static conditions (Matveev 2008; Matveev and Soderlund 2008). Simplified modeling for heave-and-pitch motions of ram wings was developed by Matveev (2013). However, from the seaworthiness perspective, the roll dynamics is also of major importance in disturbed environments, such as water surface waves. The present study addresses modeling of small-amplitude 3-DOF motions of a ram wing with aerodynamic coupling between roll, heave, and pitch.

2 Mathematical Model

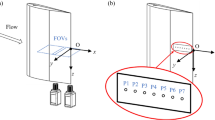
A ram wing flying close to the water surface is considered as shown in Fig. 1. The viscous effects are neglected. The distance from the wing’s lower surface to the water is assumed to be much smaller than the wing chord. With additional assumptions of small slopes of the water waves and small attack angle of the wing, the horizontal (x and z) components of the airflow velocity under the wing become much greater than the vertical (y) component. This allows us to apply the two-dimensional extreme-ground-effect theory developed by Rozhdestvensky (2000). If compressibility effects are also neglected, then the mass conservation principle results in the following equation for the perturbed velocity potential φ in the channel under the wing,

$$ \frac{\partial }{\partial x}\left(h\frac{\partial \varphi }{\partial x}\right)+\frac{\partial }{\partial z}\left(h\frac{\partial \varphi }{\partial z}\right)=U\frac{\partial h}{\partial x}-\frac{\partial h}{\partial t} $$
(1)

where h = yp − yw is the local height of the channel between the wing and water, yp and yw are the vertical coordinates of the wing lower side and the water surface, respectively, and U is the constant forward speed of the vehicle. In the applied here, reference frame translating with the vehicle along axis x, the velocity of the incident airflow is −U. Rozhdestvensky (2000) showed that the appropriate boundary conditions in the limit of small ground clearances are φ = 0 at the wing leading edge and the zero gage pressure on the other edges, which imposes the following requirement for the velocity potential at those boundaries,

$$ 2U\frac{\partial \varphi }{\partial x}-2\frac{\partial \varphi }{\partial t}-{\left(\frac{\partial \varphi }{\partial x}\right)}^2-{\left(\frac{\partial \varphi }{\partial z}\right)}^2=0 $$
(2)
Fig. 1
figure 1

Schematic of ram wing moving over waves. Dashed lines in (b) represent wave crests

Full size image

After determining a solution for φ, the pressure distribution on the wing lower surface can be calculated from the unsteady Bernoulli equation,

$$ p\left(x,z,t\right)=\rho \left[U\frac{\partial \varphi }{\partial x}-\frac{\partial \varphi }{\partial t}-\frac{1}{2}{\left(\frac{\partial \varphi }{\partial x}\right)}^2-\frac{1}{2}{\left(\frac{\partial \varphi }{\partial z}\right)}^2\right] $$
(3)

where ρ is the air density. After that, the instantaneous lift force and coordinates of the center of pressure are found by integrations as follows,

$$ L(t)={\int}_0^c\ {\int}_{-s/2}^{s/2}\ p\left(x,z,t\right)\kern0.1em \mathrm{d}z\mathrm{d}x $$
(4)
$$ {x}_p(t)=\frac{1}{L}{\int}_0^c\ {\int}_{-s/2}^{s/2}\ x\ p\left(x,z,t\right)\kern0.1em \mathrm{d}z\mathrm{d}x $$
(5)
$$ {z}_p(t)=\frac{1}{L}{\int}_0^c\ {\int}_{-s/2}^{s/2}\ z\ p\kern0.1em \left(x,z,t\right)\kern0.1em \mathrm{d}z\mathrm{d}x $$
(6)

where c and s are the wing chord and span, respectively (Fig. 1b).

In this study, only heave, pitch, and roll motions are considered. Since the vehicle is assumed to translate at a constant forward speed and the underwing lift force dominates in the EGE theory, the other forces (drag, thrust, lift on upper wing side, etc.) are much smaller and only weakly affected by ground effect. Hence, these forces and their moments are neglected in the present analysis of heave-pitch-roll motions. However, if one intends to do detailed modeling of a practical vehicle, these forces can be directly added to the present model.

Under the assumptions of low-amplitude motions and zero non-diagonal products of inertia, the governing dynamics equations can be written in simplified forms as follows,

$$ M{\ddot{z}}_{\mathrm{cg}}=L- Mg $$
(7)
$$ {I}_{zz}\ddot{\alpha}=L\left({x}_p-{x}_{\mathrm{cg}}\right) $$
(8)
$$ {I}_{xx}\ddot{\psi}=L\left({z}_p-{z}_{\mathrm{cg}}\right) $$
(9)

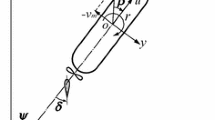
where xcg, ycg, and zcg are the coordinates of the vehicle’s center of gravity, α and ψ are the trim and roll angles, respectively, M is the vehicle’s mass, Ixx and Izz are the moments of inertia with respect to x and z axes, respectively, and g is the gravitational constant.

The numerical implementation of the model described above is accomplished using a finite-difference method. The second-order spatial discretization and the first-order time stepping are applied for finding the velocity potential, pressure distribution, and simulating vehicle’s dynamics. The wing planform is divided into cells with dimensions ∆x and ∆z along x and z axes, respectively. At a node (xi,  zj) away from the wing edges, the discretized form of Eq. (1) for the unknown perturbation velocity potential φ can be written as follows,

$$ \frac{h_{i+1,j}-{h}_{i-1,j}}{2\Delta x}\frac{\varphi_{i+1,j}-{\varphi}_{i-1,j}}{2\Delta x}+{h}_{i,j}\frac{\varphi_{i+1,j}-2{\varphi}_{i,j}+{\varphi}_{i-1,j}}{{\Delta x}^2}+\frac{h_{i,j+1}-{h}_{i,j-1}}{2\Delta z}\frac{\varphi_{i,j+1}-{\varphi}_{i,j-1}}{2\Delta z}+{h}_{i,j}\frac{\varphi_{i,j+1}-2{\varphi}_{i,j}+{\varphi}_{i-1,j+1}}{{\Delta z}^2}=U\frac{h_{i+1,j}-{h}_{i-1,j}}{2\Delta x}-{\left(\frac{\partial h}{\partial t}\right)}_{i,j} $$
(10)

where the local channel height and its time derivative (vertical velocity) are treated as known parameters from the previous time step. The boundary conditions (Eq. (2)) at the trailing and side edges are nonlinear with respect to φ. They are discretized with one-sided spatial derivatives and solved iteratively together with Eq. (1). For example, at the trailing edge (x1 = 0) the following numerical scheme is used,

$$ 2U\frac{-3{\varphi}_{1,j}+4{\varphi}_{2,j}-{\varphi}_{3,j}}{2\Delta x}-2\frac{\varphi_{1,j}-{\hat{\varphi}}_{1,j}}{\Delta t}-{\left(\frac{\partial \varphi }{\partial x}\right)}_{1,j}\frac{-3{\varphi}_{1,j}+4{\varphi}_{2,j}-{\varphi}_{3,j}}{2\Delta x}-{\left(\frac{\partial \varphi }{\partial z}\right)}_{1,j}\frac{\varphi_{1,j+1}-{\varphi}_{1,j-1}}{2\Delta z}=0 $$
(11)

where \( {\hat{\varphi}}_{i,j} \) is the velocity potential value from the previous time step. The coefficients (∂φ/∂x)1, j and (∂φ/∂z)1, j are initially taken as known parameters from the previous step. Then, a linear system of equations (Eqs. (10), (11)) is solved for φi, j. The derivatives (∂φ/∂x)1, j and (∂φ/∂z)1, j are evaluated with this new solution and substituted back into Eq. (11). This process is repeated until a converged solution is obtained for the velocity potential at each time step.

The input parameters in the present model include the wing geometry, initial conditions, and the water surface elevations. Mesh-independence studies have been conducted to establish the adequate spatial step. The sensitivities of the lift coefficient, CL = 2L/(ρU2S), and the longitudinal center of pressure, xp, to the cell size, ∆x, for a selected ram wing (described in section 3) in the equilibrium flight are shown in Fig. 2. As one can see, having 20 spatial intervals along the chord (and the same number along the span for a ram wing with aspect ratio of one) is sufficient to obtain mesh-independent results; this mesh was employed for all parametric calculations presented below. In time-dependent simulations with varying time step ∆t, it was found that the condition ∆t = ∆x/(2U) is adequate; selecting shorter time steps does not produce a noticeable effect.

Fig. 2
figure 2

Dependence of lift coefficient and center of pressure on the cell size

Full size image

Most simulations in this study are conducted in the presence of low-amplitude water waves. The water surface elevations are described using the standard regular wave theory (Lewandowski 2004) in the reference frame translating along axis x with the vehicle speed U,

$$ {y}_w=A\ \sin \left[\omega t-k\left(x+ Ut\right)\ \cos \chi - kz\ \sin \chi \right] $$
(12)

where A is the wave amplitude, ω = 2π/T is the angular frequency, T is the period, k = 2π/λ = ω2/g is the wave number, λ is the wavelength, and χ is the direction of wave propagation in the Earth-fixed frame of reference (Fig. 1b), so that χ = 0° and χ = 180° correspond to the following and head waves, respectively. The wave amplitude is selected as A = λ/60, according to one of the common relationships for low-amplitude regular waves. Since the vehicle translation occurs at high Froude numbers, defined as \( Fr=U/\sqrt{gc} \), an assumption commonly used for ground-effect vehicles is invoked that wave systems are not affected by the flying craft. It was shown by Barber (2007) that effects of the water surface deformations on the vehicle’s steady and unsteady aerodynamic coefficients are very small for typical non-augmented ram wings such as considered in this paper. However, these effects may need to be accounted for in case of power-augmented ram wings, especially at low Froude numbers.

The current mathematical model was previously validated for cases of steady flow around several configurations of ram wings in the extreme ground effect (Rozhdestvensky 2000; Matveev 2013), as well as for power augmented ram platforms hovering over solid ground and water (Matveev 2008; Matveev and Soderlund 2008). One validation example is given in the next section. No accurate measurements for unsteady motions of ram wings in the extreme ground effect are available in the technical literature, so conducting such experiments would represent a promising topic for future research.

3 Validation and Simulation Results

One validation example is shown here for the flat ram wing with side plates tested by Gallington and Miller (1970). The configuration with the main geometric parameters is shown in Fig. 3(a). The test data for the pressure coefficient on the wing lower surface and numerical predictions obtained with the present model are given in Fig. 3(b) for α = 5.7°, hp/c = 0.033, ht/c = 0.017, and the wing aspect ratio of 2/3. An agreement can be considered satisfactory keeping in mind unknown experimental uncertainties.

Fig. 3
figure 3

Tested ram wing setup and comparison of pressure coefficient along the wing centerline: squares, test data; line, numerical results

Full size image

One representative configuration has been chosen in this study to illustrate dynamics of ram wings. The main specifications are listed in Table 1. The wing has an S-shaped lower surface (Fig. 1(a)) to ensure its stability without employing a tail wing (Matveev and Kornev 2013). The distance between the wing lower surface and the chord line is described by an equation yL(x) =  − d sin (2πx/c). In the EGE theory, only lift on the lower side is accounted for so the upper side is not specified. In the equilibrium’s steady motion over a flat surface, the wing trailing edge gap is selected as yp(0)/c = 0.04, trim angle (between the chord line and horizontal plane) is α = 4°, and the lift coefficient is CL = 0.209. The center of gravity lies in the wing center plane, so the equilibrium roll angle is ψ = 0°.

Table 1 Main parameters of ram wing
Full size table

To demonstrate stability of the selected setup, time histories of the vehicle’s vertical position of the center of gravity and pitch and roll angles upon initial deviations from the equilibrium (∆ycg/c = 0.01, ∆α = 1°, ∆ψ = 1°) are shown in Fig. 4. The kinematic parameters approach the equilibrium values after a transient process. Initially, the altitude further increases since the pitch angle is greater than the equilibrium value. The pitch angle monotonically decreases to equilibrium (Fig. 4b), while the altitude initially increases due to a high pitch angle and then decreases (Fig. 4a). The roll motions show heavily damped oscillations.

Fig. 4
figure 4

Heave, pitch, and roll motions (solid curves) after initial deviations from equilibrium values (dashed horizontal lines)

Full size image

A series of simulations has been carried out to model ram wing motions over regular water waves. Five different wave headings were explored ranging from the following waves (χ = 0°) to head waves (χ = 180°) with increments of 45°. The wavelength was set to three wing chords, λ/c = 3. At the start of simulations, the wing was assigned the equilibrium state. The wave amplitude was slowly increased from zero to the final value, A/λ = 1/60, to avoid any abrupt transient events. Eventually, the wing motions reached steady-state limit-cycle oscillations. Time variations of kinematic variables over three cycles in such regimes are illustrated in Fig. 5.

Fig. 5
figure 5

Variation of the vehicle kinematic variables in motion over waves. (a–c) Solid curves, in head waves; dotted curves, in following waves. d–f Solid curves, in bow waves; dotted curves, in quartering waves. (g–i) Solid curves, in beam waves. Horizontal dashed lines in all sub-figures represent values in equilibrium steady flight over flat surface

Full size image

In case of the head and following wave headings (Fig. 5a–c), the frequency of vehicle’s encounter with waves is high (the highest is for head waves), since the effective wavelength with respect to the moving wing is short (Fig. 1a). The heave and pitch amplitudes are greater for the following waves than for the head waves, as in the former case the wing has longer time to react to variations of the underlying surface. The heave motions only slightly deviate from sinusoidal functions, while non-linear distortions are more pronounced in the pitch response. The roll motions are absent, since there is no disturbing moment with respect to the x-axis at parallel courses of waves and the vehicle. The time-averaged position of the vehicle is greater than that in flight over the flat surface (dashed lines in Fig. 5), implying that the time-averaged lift is higher. This nonlinear effect has been known to happen for wing-in-ground craft moving over wavy surfaces (Rozhdestvensky 2006).

Simulation results for situations with bow (χ = 145°) and quartering waves (χ = 45°) are shown in Fig. 4(d–f). The frequencies of encounter are smaller than in previous cases due to oblique wave headings with respect to the wing direction. The heave amplitudes are greater for the quartering seas, as well as the time-averaged heave and pitch. With the appearance of the heeling moment, the roll motions are also present (Fig. 5f).

Simulated motions for the case with beam waves (χ = 90°) are depicted in Fig. 5(g–i). The roll amplitudes are the highest at this wave heading (Fig. 5i). The heave and pitch motions are also present (Fig. 5(g–h)), since variations in the under-platform channel in the transverse z-direction also lead to variation of the total lift force and longitudinal center of pressure. The heave and pitch amplitudes are even greater than for other wave headings. However, the period of these oscillations is several times higher, as the vehicle speed is perpendicular to the wave heading, and the period is defined only by the wave speed. In the limit of long waves (low-frequency forcing), the vehicle would essentially follow the wave contour.

Besides the wave headings, the lengths and amplitudes of waves also affect the vehicle motions. Another set of simulations was conducted in this study for a range of wavelengths, while the amplitude was kept as the same fraction of wavelength, A = λ/60. With increasing the absolute wave height, it is possible to encounter situations when the vehicle will collide with the water surface, which in practice often leads to catastrophic consequences. Hence, it is important to know the maximum wavelength that will allow a wing to fly without contact the water. Results of simulations are presented in Fig. 6 in form of vehicle’s heave, pitch, and roll amplitudes normalized by the wave amplitude (for heave) and by the maximum wave slope kA (for pitch and roll), Since oscillations are not sinusoidal in large-amplitude waves, the effective amplitude of heave motion is defined as follows,

$$ {y}_1=\left[\max \left({y}_{\mathrm{cg}}(t)\right)-\min \left({y}_{\mathrm{cg}}(t)\right)\right]/2 $$
(13)

where ycg(t) is the vertical position of the center of gravity over at least one period of oscillations in the limit-cycle regime. The amplitudes of pitch and roll motions are defined similar to Eq. (13).

Fig. 6
figure 6

Normalized amplitudes of heave, pitch, and roll in motion over waves with variable wavelength and wave headings: Δ, head; ∇, bow; ◊, beam; □, quartering; o, following. Bold symbols correspond to longest waves with no contact between vehicle and water

Full size image

For the chosen ram wing configuration, it was found that almost all wave headings (with the exception of beam waves) had maximum limiting wavelengths that allowed the wing not to touch water (Fig. 6). The smallest range of permissible wavelengths appears to be in head waves, as the wing does not have enough time to respond to the variation of the clearance and fly over the wave crests. The wave headings in order of increasing maximum permissible wavelength correspond to the bow, following, and quartering waves, respectively (Fig. 6). In case of the beam waves, the frequency of encounter is sufficiently small, so even in long and high waves, the vehicle has ample time to follow the wave contour without touching the surface, and its normalized heave and roll amplitudes approach one in the limit of very long waves.

Besides flying over surface waves, ram wings are likely to encounter other obstacles on the underlying surface, such as low-height islands and floating ice in water or ice ridges on ice sheets. The unsteady response of the wing to such non-uniformities can be also modeled with the current method. As an example, a triangular bump is considered here that may have variable orientation with respect to the vehicle heading (Fig. 7). The bump length and height are selected as L/c = 2 and H/c = 0.04, respectively, with two orientations, β = 0° and 60°.

Fig. 7
figure 7

Top view of ram wing moving toward a bump. Dashed-dotted line indicates bump peak and side view of a triangular bump

Full size image

The variations of the vehicle’s kinematic parameters are shown in Fig. 8. The non-dimensional time intervals tU/c with at least some portion of the wing being above the bump are 2–5 at orientation 0° and 0.13–6.87 at 60°. In both cases, the center of gravity moves up and then relaxes back to the equilibrium value with a small overshoot, and the heave motion is more pronounced for the longer-influencing oblique bump. The pitch response is similar but somewhat delayed in the beginning for β = 60°, and it is more oscillatory for β = 0° due to more abrupt disturbance. Also, oscillatory roll motions are present only for the oblique incidence, since one side the vehicle feels the bump presence earlier. Even though the bump height equals to the equilibrium flying height of the platform trailing edge (over the flat horizontal surface), no contact with ground occurs due to sufficient increase of the lift force resulting in the effective rise of the flying height.

Fig. 8
figure 8

Heave, pitch, and roll motions of ram wing passing over the bump with orientations: β = 0°, solid curves; β = 60°, dotted curves. Dashed lines indicate equilibrium values

Full size image

4 Conclusions

A dynamic model for roll-heave-pitch motions of a ram wing has been developed using the extreme-ground-effect theory. It allows us to simulate motions of a vehicle flying over non-uniform surface. The model is computationally economical, since viscous effects are neglected and flow under the wing is considered to be two-dimensional.

The main conclusions of this paper include the following. The model is found to reasonably agree with test data for a ram wing in a steady condition. It is numerically confirmed that an S-shape of the wing lower surface can provide stability of tailless WIG craft. Nonlinear effects are more pronounced for pitch angles than other kinematic variables. The time-averaged vertical positions of the vehicle increase in the presence of waves in comparison with a flight above a flat surface. All motions (heave, pitch, and roll) have the greatest amplitudes in beam waves, although the oscillation periods are also longest in such conditions. The head waves are most dangerous from a collision standpoint, since a ram wing may not have enough time to respond to the water surface variation. Oblique course headings toward transverse obstacles on the ground can be recommended to reduce effective slopes of these obstacles along the vehicle direction.

The present model can be also used to evaluate motion amplitudes and occurrence of regimes when the wing touches water/ground. It can be extended by including other forces (e.g., thrust, drag), adding other degrees of freedom, introducing control surfaces (flaps), and simulating random waves and wind gusts. With incorporation of elements of the planing hull theory, one can possibly simulate takeoff and landing phases, as well as brief contacts between water and the wing flying in rough sea conditions.