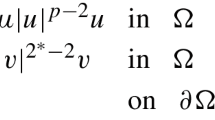Abstract
In this paper, we consider the coupled elliptic system with critical exponent and logarithmic terms:
where \(\Omega \subset {\mathbb R}^N\) is a bounded smooth domain, \(2p=2^*=\frac{2N}{N-2}\) is the Sobolev critical exponent. When \(N \ge 5\), for different ranges of \(\beta ,\lambda _{i},\mu _i,\theta _{i}\), \(i=1,2\), we obtain existence and nonexistence results of positive solutions via variational methods. The special case \(N=4 \) was studied by Hajaiej et al. (Positive solution for an elliptic system with critical exponent and logarithmic terms, arXiv:2304.13822, 2023). Note that for \(N\ge 5\), the critical exponent is given by \(2p\in \left( 2,4\right) \); whereas for \(N=4\), it is \(2p=4\). In the higher-dimensional cases \(N\ge 5\) brings new difficulties, and requires new ideas. Besides, we also study the Brézis–Nirenberg problem with logarithmic perturbation
where \(\mu >0, \theta <0\), \(\lambda \in {\mathbb R}\), and obtain the existence of positive local minimum and least energy solution under some certain assumptions.
Similar content being viewed by others
Data availability
No data was used for the research described in the article.
References
Alfaro, M., Carles, R.: Superexponential growth or decay in the heat equation with a logarithmic nonlinearity. Dyn. Partial Differ. Equ. 14, 343–358 (2017)
Ambrosetti, A., Rabinowitz, P.H.: Dual variational methods in critical point theory and applications. J. Funct. Anal. 14, 349–381 (1973)
Bialynicki-Birula, I., Mycielski, J.: Wave equations with logarithmic nonlinearities. Bull. Acad. Polon. Sci. 23, 461–466 (1975)
Bialynicki-Birula, I., Mycielski, J.: Nonlinear wave mechanics. Ann. Phys. 100, 62–93 (1976)
Brézis, H., Nirenberg, L.: Positive solutions of nonlinear elliptic equations involving critical Sobolev exponents. Commun. Pure Appl. Math. 36, 437–477 (1983)
Brézis, H., Lieb, E.H.: A relation between pointwise convergence of functions and convergence of functionals. Proc. Am. Math. Soc. 88, 486–490 (1983)
Carles, R., Gallagher, I.: Universal dynamics for the defocusing logarithmic Schrodinger equation. Duke Math. J. 167, 1761–1801 (2018)
Carles, R., Pelinovsky, D.: On the orbital stability of Gaussian solitary waves in the log-KdV equation. Nonlinearity 27, 3185–3202 (2014)
Chen, Z.J., Zou, W.M.: Positive least energy solutions and phase separation for coupled Schrödinger equations with critical exponent. Arch. Ration. Mech. Anal. 205, 515–551 (2012)
Chen, Z.J., Zou, W.M.: Positive least energy solutions and phase separation for coupled Schrödinger equations with critical exponent: higher dimensional case. Calc. Var. Partial Differ. Equ. 52, 423–467 (2015)
Colin, M., Jeanjean, L.: Solutions for a quasilinear Schrodinger equation: a dual approach. Nonlinear Anal. 56, 213–226 (2004)
Deng, Y.B., He, Q.H., Pan, Y.Q., Zhong, X.X.: The existence of positive solution for an elliptic problem with critical growth and logarithmic perturbation. Adv. Nonlinear Stud. 23, 20220049 (2023)
Hajaiej, H., Liu, T.H., Song, L.J., Zou, W.M.: Positive solution for an elliptic system with critical exponent and logarithmic terms. arXiv:2304.13822 (2023)
Lieb, E., Loss, M.: Analysis. Graduate Studies in Mathematics, vol. 14. American Mathematical Society, Providence (2001)
Lin, T.C., Wei, J.C.: Ground state of \(N\) coupled nonlinear Schrödinger equations in \(\mathbb{R} ^n, n\le 3\). Commun. Math. Phys. 255, 629–653 (2005)
Liu, T.H., You, S., Zou, W.M.: Least energy positive solutions for \(d\)-coupled Schrödinger systems with critical exponent in dimension three. J. Differ. Equ. 367, 40–78 (2023)
Poppenberg, M., Schmitt, K., Wang, Z.-Q.: On the existence of soliton solutions to quasilinear Schrodinger equations. Calc. Var. Partial Differ. Equ. 14, 329–344 (2002)
Wang, Z.-Q., Zhang, C.: Convergence from power-law to logarithm-law in nonlinear scalar field equations. Arch. Rational Mech. Anal. 231, 45–61 (2019)
Wei, S.: Multiple solutions for logarithmic Schrödinger equations. Nonlinearity 32, 2201–2225 (2019)
Vazquez, J.: A strong maximum principle for some quasilinear elliptic equations. Appl. Math. Optim. 12, 191–202 (1984)
Willem, M.: Minimax Theorems. Birkhäuser, Boston (1996)
Ye, H.Y., Peng, Y.F.: Positive least energy solutions for a coupled Schrödinger system with critical exponent. J. Math. Anal. Appl. 417, 308–326 (2014)
Acknowledgements
This work is partially supported by NSFC (No.12171265). The authors wish to thank the anonymous referee so very much for his/her valuable suggestions and comments.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supported NSFC (No.12171265).
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Hajaiej, H., Liu, T. & Zou, W. Positive solution for an elliptic system with critical exponent and logarithmic terms: the higher-dimensional cases. J. Fixed Point Theory Appl. 26, 11 (2024). https://doi.org/10.1007/s11784-024-01099-7
Accepted:
Published:
DOI: https://doi.org/10.1007/s11784-024-01099-7
Keywords
- Schrödinger system
- Brézis–Nirenberg problem
- critical exponent
- logarithmic perturbation
- positive solution