A stochastic model of ant trail formation and maintenance in static and dynamic environments

Abstract

Colonies of ants can complete complex tasks without the need for centralised control as a result of interactions between individuals and their environment. Particularly remarkable is the process of path selection between the nest and food sources that is essential for successful foraging. We have designed a stochastic model of ant foraging in the absence of direct communication. The motion of ants is governed by two components - a random change in direction of motion that improves ability to explore the environment, and a non-random global indirect interaction component based on pheromone signalling. Our model couples individual-based off-lattice ant simulations with an on-lattice characterisation of the pheromone diffusion. Using numerical simulations we have tested three pheromone-based model alternatives: (1) a single pheromone laid on the way toward the food source and on the way back to the nest; (2) single pheromone laid on the way toward the food source and an internal imperfect compass to navigate toward the nest; (3) two different pheromones, each used for one direction. We have studied the model behaviour in different parameter regimes and tested the ability of our simulated ants to form trails and adapt to environmental changes. The simulated ants behaviour reproduced the behaviours observed experimentally. Furthermore we tested two biological hypotheses on the impact of the quality of the food source on the dynamics. We found that increasing pheromone deposition for the richer food sources has a larger impact on the dynamics than elevation of the ant recruitment level for the richer food sources.

1 Introduction

Ant colonies, functioning as highly organized living systems, are able to solve complex tasks at the group level without centralised control (Gordon, 2019). In this study, we focus on exploring foraging behavior, particularly the formation of well-defined pheromone trails between the nest and a food source (Czaczkes et al., 2015). Our primary objective is to investigate the pheromone-based mechanisms driving successful foraging and understand how food quality feedback influences this process.

Collective animal behaviour, in particular the behaviour of ants, can be understood using diverse approaches. One approach is to study generic multi-agent complex systems, where interactions among numerous agents, combined with noise, give rise to emergent global patterns (Detrain & Deneubourg, 2006). Specifically a direct description of ant systems can be employed to characterize patterns within ant colonies (Sumpter, 2006). Studies in the field of collective behaviour often find applications across various domains, offering solutions to seemingly unrelated problems through the principles of biomimicry (Ratnieks, 2008). A well known use of ant models, for example, is in solving optimization problems using so called ‘ant colony optimization algorithms’ (ACO) (Dorigo & Birattari, 2010; Doerr et al., 2012).

The anatomy and the abilities of individual ants differ between (and even within) species. For example, some ants rely on sight or direct interactions between individuals for navigation Hölldobler (1976); Wehner (2003); Steck et al. (2009); Barrie et al. (2023); Evison et al. (2008); Czaczkes et al. (2013), but for many species communication is primarily based on deposition and detection of pheromones (Jackson & Ratnieks, 2006; Steck, 2012; Czaczkes et al., 2015). These pheromones can differ in their purpose and in their physical properties (Dussutour et al., 2009; Evershed et al., 1982), which are the subject of ongoing studies (Vander & Alonso, 2019). Nevertheless, most ant behavior models postulate that individual ant movement decisions are primarily influenced by pheromone-based mechanisms (Amorim et al., 2019; Boissard et al., 2013; Lecheval et al., 2021). Our work is inspired by Argentine ants (L. humile), known for relying extensively on collective information encoded in pheromone signals rather than private information acquired through visual memory, as demonstrated by Thienen et al. (2016). While visual memory can contribute to reducing uncertainty when combined with a pheromone trail, its standalone efficacy for Argentine ants is limited Clifton et al. (2020). Previous research on Argentine ants by Aron et al. (1989) indicates that paths are marked and favored even in the absence of specific recruiting incentives. The nature of this marking, whether it involves a distinct recruitment pheromone or is simply a less concentrated form of the same pheromone, remains uncertain. One of our main goals here is to compare different pheromone-based mechanisms in combination with (or in the absence of) navigation and to investigate the efficiency of foraging based on these alternative mechanisms. Additionally, our study aims to contribute insights into the question of how many pheromones are essential for successful foraging.

In the presence of multiple path options, Argentine ants show the capability to choose the shortest path, as demonstrated by Goss et al. (1989). Additionally, when presented with two food sources, they can distinguish and select the richer one, as illustrated by Csata et al. (2020). Furthermore, in dynamic environments, Argentine ants demonstrate the ability to quickly adapt to changes in food concentration, reallocating the majority of foragers to the richest food source. This adaptive behavior was observed in a study by Latty et al. (2017), where a colony was provided with a choice between three food sources, periodically varying in concentration. The research conducted by Reid et al. (2012) indicates that Argentine ants exploiting foods of different qualities exhibit distinct trail behaviors, particularly in the frequency of U-turns, resulting in different amounts of trail marking. The dynamic phenomena observed in Argentine ants provide a foundation for the selection and validation of our approach.

Behavioural rules used by ants to communicate are becoming increasingly well understood but vary between different species. Mathematical modelling can aid in distinguishing between different biological hypotheses relating to ant behaviour (Bicak, 2011; Edelstein-Keshet, 1994; Ermentrout & Edelstein-Keshet, 1993; Watmough & Edelstein-Keshet, 1995; Amorim, 2015). Colony behavior, driven by both local and global interactions, can demonstrate a rich variety of emergent behaviours including synchronization, oscillation, milling and switching to name but a few. These patterns, not exclusive to ants, emerge as consequences of interactions in complex multi-agent systems, often in the presence of noise (Detrain & Deneubourg, 2006; Deneubourg & Goss, 1989; Solé et al., 1993; Boi et al., 1999; Bonabeau et al., 1998; Yates et al., 2009).

Various modeling approaches have been employed to investigate foraging behaviors in ants, and a comprehensive review of both experimental and modeling literature is available in works such as Detrain and Deneubourg (2006); Boissard et al. (2013). Within this broad spectrum of models, there exists a class focused on understanding decision-making of ants when presented with pre-established routes incorporating decision nodes (Reid et al., 2011). This approach is adaptable to a variety of dynamic scenarios and offers easier experimental control than experiments in the unconstrained space. The geometry of the space is essentially one-dimensional, and its graph-like structure allows the formulation of various theoretical optimization problems. This enables the testing of ants’ problem-solving capabilities in these scenarios.

Our goal is to construct and investigate a two-dimensional model that captures decision-making of ants in an environment not constrained by corridors or grids, which limit the state space of the Markov models (Deneubourg et al., 1990) or models based on cellular automata (Ermentrout & Edelstein-Keshet, 1993; Watmough & Edelstein-Keshet, 1995) that have been used to represent other ant experiments. In line with the work of Calenbuhr and Deneubourg (1992) we introduce a stochastic model of ant foraging which incorporates a minimal number of biological assumptions. Ants move by a correlated random walk (Kareiva & Shigesada, 1983) in an off-lattice environment (as opposed to being constrained to the lattice points) within a continuous two-dimensional space, similarly to Amorim (2015); Ryan (2016); Caillerie (2018). The off-lattice nature of the agents guarantees the absence of any artifacts attributed to lattice-induced influences in the resulting ant behavior. Communication between ants is based on up to two distinct pheromones (depending on the model alternative), resolved and dynamically updated on a fine lattice, that diffuse and evaporate in the environment, enabling both information spread and dissipation. The lattice nature of the pheromone dynamics is combined with the off-lattice nature of the correlated random walk to ensure biological realism of the model. As in nature, the motion of our simulated ants is not deterministic. Indeed, we deliberately incorporate an element of randomness in the ants’ movement rules which we will demonstrate to be an adaptive advantage in the dynamical environment (Deneubourg et al., 1983; Dussutour et al., 2009).

Previous advancements in fully spatial models of ant behaviour, as demonstrated in works like Perna (2012); Boissard et al. (2013); Vela-Pérez et al. (2015); Amorim and Goudon (2021), involve exploring motion and trail formation in a free two-dimensional space without specifying the locations of the nest and food source. A different approach to the understanding of the dynamic response of ants to the chemical stimulus has been explored by Calenbuhr and Deneubourg (1992) where the trail is explicitly modeled by the stationary solution to an emission-diffusion problem and ants are characterized by the stimulus–response relationship. The works of Couzin and Franks (2003); Amorim et al. (2019) provide a more detailed understanding of ant motion along pre-existing trails by observing that ants perform sinusoidal trajectories along the trail rather than moving in a straight line. Couzin and Franks (2003) and Ryan (2016) explore in more detail lane formation, which emerges from ant avoidance mechanisms, which are not included in our work. The fully two-dimensional models proposed by Amorim (2015); Ryan (2016); Caillerie (2018) provide complex insights into the foraging process, including spontaneous trail formation, foraging behavior, and dynamic adaptation to alternative food sources when the current one is depleted. These models, while offering valuable perspectives, are constructed based on diverse assumptions regarding the number and characteristics of pheromones and the homing mechanism. Throughout this paper, we will draw connections between the various assumptions made in these models and the modeling choices we adopt.

The paper is organized as follows. In Sect. 2 we formulate the model and give details about its implementation. In Sect. 3 we investigate the ability of our model ants to solve basic tasks essential for colony survival. We explore three pheromone-based mechanisms, aiming to quantify the minimal number of pheromones required for a successful foraging mechanism, contributing new perspectives to the findings of Saund and Friedman (2023). The challenges posed to our colony of ants involve tasks such as food source discovery and establishment of reliable trails between the nest and the food source even in a dynamically changing environment and in the presence of multiple food sources. We test two biological hypotheses that reflect different forms of dynamical feedback due to food sources of different quality: either through the pheromone deposition, or through the number of recruited ants, both potentially depending on the food quality. We use optimized numerical simulations (specific description of program optimization tools, which we used can be found in Sect. 2.12) to show that our proposed model can mimic realistic ant behaviour.

2 Methods

We propose a mathematical model of a single colony of ants and study the formation of a trail to food located in a close vicinity of their nest. Our model is inspired by Argentine ants which are able to optimize foraging between multiple food sources of different quality, but is versatile enough to be applied to different ant species (Latty et al., 2017; Deneubourg et al., 1990). The model is based on the following assumptions (hereafter the word “ants” refers to “virtual ants”):

• 1. Ants do not interact directly, only through pheromones.

• 2. Ants move at a constant speed, the same for all ants (Perna, 2012; Vittori, 2006).

• 3. The motion of each ant is governed by a correlated random walk.

• 4. Ants use attractive pheromones for communication (Czaczkes et al., 2015).

• 5. Pheromones diffuse and decay (Robinson et al., 2008).

• 6. The amount of pheromone that an ant may carry is limited.

• 7. The proportion of ants, which deposit pheromone while traveling towards food or nest is approximately constant for L. humile (Aron et al., 1993).

• 8. Ants alter their motion in response to the pheromone concentration which they sense using their antennae and process using a Weber’s law (Calenbuhr & Deneubourg, 1992; Perna, 2012).

• 9. The pheromones are attractive and depending on the model a single type or two types of pheromones are used (Dussutour et al., 2009; Saund & Friedman, 2023).

• 10. The pheromones diffuse at the same rate but have different decay and role: (1) long and short lasting (Jackson et al., 2007; Robinson et al., 2008; Hölldobler, 1971; Hölldobler et al., 1994; 2) one for nest-orientation (Steck, 2012) and one for food discovery (Dussutour et al., 2009; Morgan, 2009; 3) one for orientation, one for recruitment (Hölldobler, 1971; Breed & Bennett, 1985; Maschwitz & Schönegge, 1977; Attygalle et al., 1988; Hölldobler et al., 1994).

• 11. Ants switch between two phases: food-searching and nest-searching.

• 12. Ants recruit other foragers using stereotypical behavioral patterns in the nest (Suckling et al., 2011; Aron et al., 1993; Van Vorhis Key & Baker, 1986; Reid et al., 2012).

• 13. Once the food is found the assessment of its quality takes a fixed amount of time (Vittori, 2006, 2004).

• 14. There are no births or deaths on the time-scale of interest (i.e. the total number of ants is constant).

• 15. Ants move on an infinite two dimensional plane.

The model can be characterised by four distinct phenomena: the random motion of ants, the deposition of pheromones, the physical process of pheromone diffusion and decay in the environment and the response of ants to the perceived pheromone signal.

2.1 Motion of ants

We model the motion of the ants using a correlated random walk (Codling & Hill, 2005; Codling et al., 2008, 2010) in discrete time. The discrete-time nature of this model reflects the movement characteristics of real ants, which navigate through discrete steps. Specifically; the change in orientation is given by the update rule

$$\begin{aligned} \omega _{n+1}^i&= \omega _n^i + f(c) + \sigma \kappa _1(c) \xi _n^i\,, \end{aligned}$$

(1)

where $\omega _n^i$ represents the direction of motion in the n-th step of the i-th ant (see Fig. 1a). Consequently, the angular deviation between steps for ant i is given by $\varphi _n^i = \omega ^i_{n+1}-\omega ^i_n = f(c) + \sigma \kappa _1(c) \xi _n^i$. The first term, f(c), represents the deterministic response of an ant to the perceived pheromone concentration, c, in its direction of motion and the second term, $\sigma \kappa _1(c) \xi _n^i$, is an angular noise, which accounts for imprecision of motion, whose magnitude depends on its perceived pheromone concentration with $\kappa _1(0)=1$ in the absence of pheromones in the environment.

Fig. 1

Main components of the model. a The motion of a single ant consists of a series of discrete steps in a continuous space with a fixed step size L (constant speed assumed). The direction of motion at a given step is denoted by $\omega _n$. The difference between two consecutive steps ($\varphi _n = \omega _{n+1}-\omega _n$), i.e., the angular deviation, follows stochastic dynamics given by Eq. (1). b Model alternatives 1–3 capture different use of pheromones and visual navigation cues. In Model 1 a single pheromone (red) is used to mark the path from the nest as well as from the food source. This pheromone is attractive to the ants searching for food (or nest). In Model 2 a single pheromone (blue), attractive to the food-searching ants, is used to mark the path from the food. Ants use a stochastic compass to find the nest, explained in panel (c). Model 3 uses two attractive pheromones - red and blue to mark the nest and food location, respectively. The ants in a food/nest searching phase are attracted to the blue/red pheromone. c The stochastic compass has a deterministic component (yellow direction), which informs the ant about the true direction of the nest and adjusts the ant’s direction $\omega _n$ to be aligned with it. The added stochastic component given in Eq. (4) models the imprecise nature of the information about the nest location resulting in the direction of walk along the green arrow. The magnitude of the noise decreases for smaller distances capturing the smaller uncertainty in the nest direction when the nest is nearby (Color figure online)

In the absence of pheromones the directional change for the i-th ant in the n-th step is $\varphi _n^i=\sigma \xi _n^i$ (i.e., $f(0)=0$). This represents a normally distributed random variable with a zero mean and constant variance, $\sigma ^2$, when $\xi _n^i$ is drawn from the standard normal distribution.

The randomness in the movement of individual ants is important for the behaviour of the whole colony (Dussutour et al., 2009; Rausch et al., 2019; Wu et al., 2020). We will demonstrate that this noise at the individual-level plays a significant role in each of the phases of colony behaviour - foraging, trail formation and adaptation to changes in the environment.

The position of an ant i in Cartesian coordinates is calculated according to the following update rules

$$\begin{aligned} x_{n+1}^i= & {} x_n^i+ L\cos \left( \omega _{n+1}^i\right) , \end{aligned}$$

(2)

$$\begin{aligned} y_{n+1}^i= & {} y_n^i+ L\sin \left( \omega _{n+1}^i\right) , \end{aligned}$$

(3)

where L is the constant spatial step size (Perna, 2012; Vittori, 2006). Experiments of Bicak (2011) indicate that ants traverse a distance equivalent to two body lengths in 0.5 s (on average). Therefore, we choose a step size L and time step in agreement with this result. Bicak also demonstrated experimentally for Pharaoh’s ants that the angular deviations between discrete, fixed time steps can be well approximated by a normally distributed random variable. Motion of ants is simulated using an individual-based stochastic method.

2.2 Pheromone deposition

The ants can deploy multiple pheromones that differ in their purpose and in their physical properties. Although our model is aimed at capturing behavior of Argentine ants, we study more general navigational strategies so that the model is applicable to a range of different species. We assume that all ants in the system are in one of the two states - either they are foraging (i.e. searching for food) or they are searching for the nest. Each ant deposits and follows a pheromone according to its state. Deposition of pheromones serves to provide information about the environment to other ants. To test the efficiency of different use of pheromones we study three models (Models 1–3), shown in Fig. 1b:

M1::

A single pheromone (shown in red in Fig. 1b) signals both the food and the nest location. An ant deposits a unit of the red pheromone at each step (whilst its pheromone is not depleted) when it is in the food-searching or nest-searching state and at the same time follows the profile of the same pheromone. Ants orient themselves solely based on the pheromone concentration, modified by the uninformed random deviations.

M2::

A single pheromone (shown in blue in Fig. 1b) is used to signal the position of the food by the ants in the nest-searching state, once they have discovered the food. Orientation is governed by following the deposited pheromone while foraging and using stochastic (visual) navigation (Fig. 1c) while searching for the nest.

M3::

One pheromone (red) is employed for nest location, whilst another pheromone (blue) signals the location of a food source. An ant deposits a unit of the red pheromone at each step (whilst its pheromone is not depleted) when it is in the food-searching state, and a unit of the blue pheromone when it is in the nest-searching state. An ant follows the blue pheromone when in the food-searching state and the red pheromone when in the nest-searching state as shown schematically in Fig. 1b. Ants are able to distinguish between the two pheromones and to determine their intensity.

Ants deposit pheromones only for a fixed number of steps, starting when entering the respective state (e.g. food-searching or nest-searching). This represents a limited supply of the pheromone for each ant in one excursion, replenished when an ant returns to the nest. For reference, all of the parameters of the model are given in Table 1.

Table 1 Parameters of the model with references and their settings for the basic simulation

2.3 Stochastic visual navigation in Model 2

Model 2 incorporates the ability of ants to use visual cues to find their way back to the nest. Indeed, using both social cues, like pheromone trails, and individual cues, such as visual signals, is common in ants (Barrie et al., 2023). These visual cues may be based on the ant’s memory and may include the location of the sun, local cues such as trees, rocks, etc., or other sources of environmental information, as studied in Hölldobler (1976); Wehner (2003); Evison et al. (2008); Steck et al. (2009); Baddeley et al. (2012); Czaczkes et al. (2013); Graham and Philippides (2017); Zeil and Fleischmann (2019); Barrie et al. (2023).

If the center of a circular-shaped nest has coordinates $(x_N,y_N)$ and the position of the focal nest-searching ant (indexed by i) in the n-th step is $(x^i_n,y^i_n)$, then the direction of motion in the $(n+1)$-th step is defined as

$$\begin{aligned} \omega ^i_{n+1} = {\bar{\omega }}^i_n + \min \{ 1, \kappa _2 d^i_{N}\} \xi _n^i \end{aligned}$$

(4)

where ${\bar{\omega }}_n^i$ is the angle pointing towards the center of the nest from the perspective of the focal ant at its n-th step and $\xi _n^i$ are standard normal variables, uncorrelated through the ants and steps. Denoting $A = \arctan \left( \frac{y_N-y^i_n}{x_N-x^i_n}\right)$ this equals

$$\begin{aligned} {\bar{\omega }}_N^i = {\left\{ \begin{array}{ll} \pi + A &{} \text {when}\quad x_N< x_n^i, \\ A &{} \text {when}\quad x_N> x_n^i, \\ \frac{\pi }{2} &{} \text {when}\quad x_N = x_n^i \quad \& \quad y_N > y_n^i, \\ -\frac{\pi }{2} &{} \text {when}\quad x_N = x_n^i \quad \& \quad y_N < y_n^i. \end{array}\right. } \end{aligned}$$

(5)

The Euclidian distance $d^i_{N} = \Vert (x_N,y_N)-(x_n^i,y_n^i) \Vert$ between the ant and the nest center affects the precision of the navigation. The extent of navigational guidance provided by visual cues relies on factors such as the distribution of visual objects in the environment, their apparent size, and their relative contribution to the overall panoramic scene, see (Zeil & Fleischmann, 2019). This is attributed to the fact that, with increasing distance, visual cues may become less visible and be obstructed, potentially reducing the duration for which landmarks remain observable. For example, within a field of grass, a distant tree might be infrequently visible, while a closer tree could be seen more consistently. Similarly, beyond the crest of a hill, a distant visual marker may be entirely out of sight. Consequently, reliance on memory may become more important as the ant moves farther away from the nest.

Moreover, the immediate surroundings of the nest offer a more familiar landscape to the ants, characterized by reliable landmarks but also other familiar cues such as tactile and olfactory cues (Zeil & Fleischmann, 2019). This observation aligns with the documented behavior of new foragers, who undergo a pre-foraging phase (Freas & Spetch, 2023). During this phase, filled by trips concentrated around the nest, ants familiarize themselves with the panorama surrounding the nest entrance before they start foraging.

To reflect this we implemented large uncertainty when the ant is far from the nest and small uncertainty when close to the nest into our model in Eq. (4), see Fig. 1c. This is modulated by the parameter $\kappa _2$, see Table 1. The magnitude of uncertainty for distances that are too large (i.e., $d_N^i>1/\kappa _2$), is bounded from above, as captured by the second term on the right-hand side of Eq. (4).

2.4 Diffusion and decay of pheromones

Pheromones deposited in the environment diffuse and decay/evaporate over time. Although not much is known about the precise magnitude of pheromone diffusion coefficients, the decay properties in terms of the half-life of the pheromones used by some ant types are known at least approximately. In particular, it is known that some pheromones persist in the environment for hours while others are only detectable for minutes (Hölldobler, 1971; Hölldobler et al., 1994; Jeanson et al., 2003; Jackson et al., 2007; Robinson et al., 2008). We first outline a continuous diffusion model for the concentration c(x, y, t) of a given pheromone at location $(x,y) \in {\mathbb {R}}^2$ at time t.

When no pheromone is added to the environment c(x, y, t) would evolve according to the two dimensional diffusion-degradation equation:

$$\begin{aligned} \frac{\partial c}{\partial t}= D \left( \frac{\partial ^2 c}{\partial x^2} + \frac{\partial ^2 c}{\partial y^2} \right) - \lambda c , \end{aligned}$$

(6)

where D is a diffusion and $\lambda$ is a rate of degradation for the given pheromone, which can be linked to its half-life. Depending on the model type, we consider one (Model 1, 2) or two (Model 3) types of pheromones. Therefore, the description of the system requires a single or two independent diffusion equations for $c_R(x,y,t)$ and $c_B(x,y,t)$ (subscripts R/B denote the red/blue pheromone) with respective diffusion coefficients $D_R$ and $D_B$ and degradation coefficients $\lambda _R$ and $\lambda _B$ (with values given in Table 1).

The pheromone concentration provides valuable information for the ants, who further enhance it by depositing additional pheromones. We assume that all ants update their positions and headings simultaneously, depositing a fixed amount of pheromone at their current locations in every time step of their discrete (in time) random motion with a fixed time step. While this simplification may deviate from the reality where ants might deposit pheromones irregularly or even continuously with a variable length of the continuous depositions (see for instance Aron et al. (1989) for details on trail-laying behavior for the Argentine ant (L. humile), which includes the empirical distributions of these continuous deposition events and the gaps between them) it remains effective as long as the average amount of deposited pheromone per unit of time (during deposition periods) is relatively consistent. This approach allows our model to capture the essential features of pheromone-based trail formation and maintenance. Although our primary emphasis is on discrete deposition events, our model is adaptable and, in principle, can accommodate various deposition patterns.

Since the positions and headings of all ants are updated synchronously, these pheromone depositions can be modeled by the addition of point-source terms in the continuous-time and continuous-space model in Eq. (6), making the problem time inhomogeneous. Due to the linearity of the diffusion equation, we can decouple the problem into many independent subproblems corresponding to each deposition event and solve the full problem using a superposition of the individual solutions. However, working with such a solution is numerically expensive, particularly later in the simulation after many deposition events and in the presence of many ants. Thus we instead use a discretized (in both time and space) version of the diffusion-degradation Eq. (6) on a fine lattice and couple the (discrete-space and discrete-time) numerical solution of the pheromone dynamics to the stochastic motion of the ants, which itself works in the continuous space and discrete time.

For simplicity, we consider a bounded square domain of dimension 30$\times$30 cm as our state space, supplemented by zero Dirichlet boundary conditions at all boundaries. We use an explicit finite difference method for the numerical solution of our equations. Specifically, we use a forward difference approximation for the discretisation of the time derivative and central difference approximation for the spatial derivatives with a spatial lattice size $h = \Delta x = \Delta y$ and a time step $\Delta t$ (see Table 1 for the default choice of the parameters). Our problem is encoded in matrix form to optimize numerical efficiency. The time step between each position updates (and the duration between two pheromone deposition events) is defined to be 0.5 s but to obtain a stable scheme (and to satisfy a von Neumann stability condition $D \frac{\Delta t}{h^2} \le \frac{1}{2}$), depending on the value of D one may need to run multiple diffusion steps p in a single step of the full simulation. We used $D=0.05$ mm$^2$/s (see Fig. 5), which allowed us to take $p=1$ diffusion steps per simulation step, as summarized in Table 1. The effect of the parameter h is demonstrated in Fig. 2e, where we ran the stochastic simulation for $h=1$ mm and $h=0.5$ mm while keeping the randomly generated numbers the same.

2.5 Response to pheromone concentration

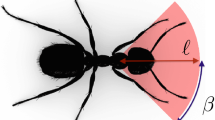
The pheromone concentration affects both the deterministic component, f(c), and the amplitude of the stochastic component, $\sigma (c)$, in the angular update Eq. (1). We assume that the deterministic response function depends solely on concentrations at the tips of the antennae i.e. $f(c) = f\left(c_{-\frac{\pi }{6}},c_\frac{\pi }{6}\right)$. Here $c_\frac{\pi }{6}=c(x_i+l\cos (\omega _n^i+\pi /6),y_i+l\sin (\omega _n^i+\pi /6))$ is the pheromone concentration at the left antenna of ant i and $c_\frac{-\pi }{6}$ is defined analogously for the right antenna, where l is the antenna length, uniform across all ants. There is evidence that organisms, including ants, are able to evaluate environmental signals and modify the direction of motion in response to them. In animals (Calenbuhr & Deneubourg, 1992) a common form of the response function is known as Weber’s law (Weber, 1834), which been confirmed experimentally for ants (Perna, 2012). Generally ants follow the direction of higher pheromone concentration (Suckling et al., 2011). The function f(c) encodes the Weber’s law describing the response of the i-th ant to pheromone concentration, c:

$$\begin{aligned} f\left(c_{-\frac{\pi }{6}},c_\frac{\pi }{6}\right)={\left\{ \begin{array}{ll} -\frac{\pi }{6} &{} \text {if } \Gamma>\alpha , \text { and }\, c_{-\frac{\pi }{6}}>c_{\frac{\pi }{6}}, \\ \frac{\pi }{6}&{} \text {if } \Gamma>\alpha , \text { and }\, c_{\frac{\pi }{6}}>c_{-\frac{\pi }{6}},\\ 0 &{} \text {otherwise,} \end{array}\right. }\, \end{aligned}$$

(7)

where

$$\begin{aligned} \Gamma =\left| \frac{c_\frac{\pi }{6}-c_{-\frac{\pi }{6}}}{c_\frac{\pi }{6}+c_{-\frac{\pi }{6}}}\right| , \end{aligned}$$

(8)

is the relative difference in concentration of pheromone at the end of each antennae and $\alpha$ is a given detection threshold, commonly called the just-noticeable difference (JND). Weber’s law allows ants (and analogously other animals) to efficiently process information from the environment that may span many orders of magnitude. Note that there are more complex models of the ant’s response to the pheromone signal in the literature, for instance the full sector model (Amorim et al., 2019), where the sensing area consists of a sector-shaped region instead of just two points, considered here.

Ability to detect pheromone is also limited by absolute concentration, thus the input into the Eqs. (7) and (8) in terms of the pheromone concentrations c(x, y) is modified to $c^*(x,y)$ where

$$\begin{aligned} c^*(x,y) = {\left\{ \begin{array}{ll} c(x,y) &{} \text {when} \quad c(x,y) > c_\text {det} \\ 0 &{} \text {otherwise} \end{array}\right. } \end{aligned}$$

(9)

The constant $c_\text {det}$ (in Table 1) represents the minimal detectable pheromone concentration. Note that the above equation differs from the work of Amorim and Goudon (2021) (their Eq. (2.5)), in which subthreshold pheromone concentrations are truncated to the value of the threshold. Their choice results in small sensitivity to errors when close to the threshold due to the continuity of the truncated response to the pheromone signal. The rationale behind our choice is that a detectable signal on one antenna should result in a strong preference to turn toward this side when the signal on the other antenna is not detectable. We compared the impact of the rule on the simulated ant behaviour in Appendix C.

The magnitude of the stochastic component of the angular update Eq. (1), $\sigma \kappa _1(c)$, is also affected by the detected pheromone concentration. When the pheromone density is high (above the given threshold $c_{\min }$, see Table 1) the amplitude of the noise term decreases but never disappears completely. The function that we propose in our model is

$$\begin{aligned} \kappa _1(c)= \min \left \{ 1, \frac{c_{\min }}{\max \left\{c_{\frac{\pi }{6}}, c_{-\frac{\pi }{6}}\right\}} \right \}. \end{aligned}$$

(10)

Note that the turning angle dynamics involve a stochastic perturbation by a Gaussian random term. This perturbation persists even when there is no pheromone present. When the magnitude of the added Gaussian noise is small, the turning angle distribution tends to be bimodal. Conversely, with larger noise magnitudes, the distribution becomes broad and unimodal, as observed by Bicak (2011). The parameter $\sigma$ denotes the variance of the additive noise influencing directional changes.

2.6 Pheromone detection – transformation from the lattice to the continuous space

The motion of ants in our model depends on the pheromone concentration sampled by the ants’ antennae. Having a discrete pheromone signal we need to approximate the concentration at an arbitrary point in the continuous state space. We interpolate this value from the four closest lattice points, based on their distances. If (x, y) is the location at which we are computing the pheromone concentration and $(x^G,y^G)$ for $G\in \{1,2,3,4\}$ are the positions of the four closest lattice points at distances $d^G$ then the concentration c(x, y) is computed as a weighted average

$$\begin{aligned} c(x,y) = \frac{\sum _{G=1}^4 w^G c(x^G,y^G)}{\sum _{G=1}^4 w^G} \end{aligned}$$

(11)

with weights $w^G = 1-d^G/d_\text {max}$. The scaling factor $d_\text {max}$ is set to be the maximal possible distance, i.e., $d_\text {max} = \sqrt{2}h$. Alternatively, one could use a bilinear approximation, leading to similar results when h is small.

2.7 Pheromone deposition – transformation from the continuous space to the lattice

Ants in our simulation move in a continuous space and deposit a fixed amount of pheromone m per step (see Table 1). The recently deposited pheromone forms localized peaks, which are noticeable at a small spatial scale in our simulation. The peaks, which are close to each other, are smoothed out due to the presence of diffusion, resulting in the accumulation of diffused pheromone droplets into a coarse-grained pheromone profile, potentially leading to path formation. However, when the peaks are too isolated (rare depositions) or too strong (large deposited amounts, small diffusion), the overall pheromone field will be composed of individual isolated peaks even at later times. This scenario can lead to failures in trail establishment and subsequent trail following. Vela-Pérez et al. (2015) avoid this phenomenon (they refer to it as overcrowding) by incorporating an explicit mechanism to prevent it, which forces the ants to move away from the regions with pheromone concentrations larger than certain threshold.

Alternatively, one may consider that ants deposit pheromone in a continuous trace. Although such a continuous deposition may smooth out the pheromone distribution, and therefore smooth out the scattered pheromone, it may lack complete realism. Specifically, Aron et al. (1989) showed that the length of deposition events for Argentine ants can be accurately approximated by an exponential distribution with mean length being smaller than the ant’s size, considered in our work. Thus, while the pheromone depositions are discrete events, each of them can be characterized by a short continuous path. In light of this we introduce two modular mechanisms to preserve the realism of the process and at the same time regulate the roughness of the pheromone field while keeping the deposition process discrete: (1) repeated deposition of the amount m/k of the pheromone at k equal distances along the step, as demonstrated in Fig. 2 a, which produces a more continuous pheromone trail (see Fig. 2a for the schematic visualization and Table 1 for the value of the parameter k); and (2) use of a Gaussian-based deposition kernel with a given width, $\rho$ (see Fig. 2b and Table 1), measured by its standard deviation. We present a comparison of the simulation with and without the mechanisms to regulate the ruggedness of the deposited pheromone field in Appendix D. Figure 2b shows the pheromone distribution along the direction of motion of the ant and an initial part of the simulation for different values of coefficients k and $\rho$.

Moreover, the ants deposit pheromones at their location in a continuous space. To update the discrete pheromone field, the step (1) is followed by a redistribution of the deposited pheromone to the four closest lattice points, depending on their distance to the deposited location. Only then we perform step (2), in which each of the four components are further distributed according to the chosen deposition kernel. The advantage of such an approach is the possibility to use a discretized kernel, which is precomputed at the start of the simulation and therefore makes the deposition computationally effective. We truncate the deposition kernel, only depositing to the lattice points within a radius $4\rho$. The deposition kernel is normalized, thus only transferring the pheromone. It is worth noting that Vela-Pérez et al. (2015) employs a Gaussian deposition kernel, in an approach similar to ours. However, in contrast to our methodology, the pheromone in their model does not undergo further diffusion.

The discretization of the m/k units of the pheromone deposited at a location (x, y) to the closest four lattice points $(x^G,y^G)$ for $G\in \{1,2,3,4\}$ is computed by the following formula

$$\begin{aligned} m^G = \frac{m w^G}{k \sum _{G=1}^4 w^G} \end{aligned}$$

(12)

where the weights $w^G$ are the same as above.

2.8 Pheromone visualization

Figure 2c shows an example of a simulation with a nest (yellow) and two food sources (blue) of different quality (we assume that the food quality results affects the amount of deposited pheromone – below we explain in detail how the quality of the food may impact the stochastic process). Each pheromone type is visualized in a different color channel (red, blue) and normalized (maximum concentration equals 1 for each pheromone) so that also small concentrations are visible. Figure 2d shows how the different combinations of the two pheromone concentrations mix together to give the resulting color.

Fig. 2

Implementation of the stochastic motion and pheromone deposition dynamics of ants. a Diagram of the simplest case when within each step the ant deposits the same amount of pheromone in k equidistant locations, which lie in a continuous phase space. To transform the added pheromones from the continuous space to the discrete fixed regular lattice used for the pheromone distribution the pheromone amounts from each location are distributed to the closest lattice points depending on their distances. b After decomposing the pheromone to the closest lattice points we then apply a precomputed discrete Gaussian kernel of a width $\rho$ (truncated beyond the distances $4\rho$) to each of the lattice points with a new deposition to obtain a wider and smoother pheromone trace. Different values of the number of depositions within a single step (k) and the kernel widths ($\rho$) lead to different smoothness and width of the pheromone trace. In Fig. 5 we show the effect of the choice of the diffusion parameter D and the parameter $\rho$ on stochastic foraging. c Simulation of a scenario with a nest (yellow) and two food sources of different quality (affecting the amount of pheromone ants deposit once the food is found). The recent portion of the trajectory (last 10 steps) is shown for each ant. The background color shows the scaled combined amount of both pheromones in the environment, according to the color scale in (d). d The pheromone intensities of the red/blue pheromones are scaled to their maximum value and then combined according to the shown color palette. e Short term dynamics for two different values of the step size h. Both simulations used an identical set of randomly generated numbers to obtain comparable results (Color figure online)

2.9 Simulation overview

We consider N ants in each simulation with a fixed nest and food source(s) placed away from the nest. All active ants are initially evenly spaced around the perimeter of the nest, with each ant oriented in the direction of the outward normal to the circular edge. At each step, we update the position of each ant using difference Eqs. (2)-(3), where the motion of the i-th ant is described by a correlated random walk given by Eq. (1). Each time-step in the simulation corresponds to 0.5 s.

At the beginning of the simulation ants leave the nest in the food-searching state. They randomly explore the environment and forage for food. When an ant discovers a food source it changes its state to a nest-searching state. At each step each ant deposits a fixed amount of pheromone with a type (red or blue) consistent with its state. However, the amount of pheromone that an ant can deposit in a given state is limited and after it runs out the ant no longer deposits a pheromone. We assume that the red/blue pheromone can be deposited for at most $t_R$ or $t_B$ time steps, respectively (values in Table 1).

2.10 Recruitment

We implemented a simple recruitment model. At the beginning of the simulation some of the N total ants remain in the nest and do not participate in foraging (there are $N_r$ such waiting ants and $N_a = N-N_r$ active ants). When a recruiter ant finds a food source and returns to the nest, it recruits $n_r$ ants from the waiting pool (if available). The newly recruited ants are initialized with the location of the recruiter and initial direction opposite to the recruiter. Not all of the initially foraging ants have to be recruiters (one can set the proportion of recruiters, which will be randomly selected from the foragers at the beginning of the simulation), although all our simulations presented within this work start with all initially foraging ants acting as recruiters. The recruited ants are not considered recruiters for further ants waiting in the nest. All ants (recruiters or non-recruiters) deposit pheromone to mark the trail in the nest-searching phase, which starts once they have found the food source. However, only recruiters assess the quality of the food. They do this at every encounter with the food (we formally include this duration as part of the following nest-searching state).

2.11 Sources of food

The simulation allows for several food sources in the environment. These can be either fixed in time and contain unlimited amount of food, or change dynamically over time. Each food source has a circular shape, specified by the position of its center $(x_F, y_F)$ and the radius $r_F$. We also define the total amount of food $m_F \in {\mathbb {N}}$ (each ant takes one unit) and its quality $q_F$, the latter within the interval (0, 1] where 1 corresponds to the richest food source. Note that we set the $m_F$ large enough so that the food source does not run out in our simulation.

Recruiter ants spend a fixed amount of time, $t_E$, evaluating the food quality when they find the source first and repeat this reevaluation at every encounter with a food source. We consider two possible mechanisms for how the quality of the food source affects the simulation: (1) The amount of deposited pheromone in the nest-searching phase depends linearly on the quality of the food (equal to $m q_F$, where m is the default amount of pheromone deposited in one step); or, the number of ants initiated by a single recruiter depends linearly on the quality of the food (equal to $n_r q_F$, up to rounding).

2.12 Implementation details

We implemented the stochastic discrete-continuous hybrid model in the programming language Python using open-source libraries. At the start of each simulation, we generate all necessary random variables and precompute all values and matrices that will not be updated during the simulation. We create a single nest, all the necessary food sources, a lattice with initially zero pheromone concentration and initialize the ants. In each step, we calculate all new ant positions, deposit pheromones into the environment, update the pheromones according to the diffusion-degradation dynamics, assess food, and recruit the ants, when appropriate. The simulation ends after a fixed number of steps.

We have optimized the program using the library line-profiler. In most cases this was done by finding the most efficient library for the task, selecting the most efficient numerical method coded in the most efficient way (e.g. explicit scheme and matrix form for the pheromone dynamics), or by transferring all calculations, which did not need dynamic updating to the initialization. We used threads to write results to the files and multiprocessing to run multiple simulations at once.

3 Results

We tested our mathematical models of ant foraging in several different scenarios using the numerical simulation method described above.

3.1 Comparison of models and mechanisms in the presence of a single static food source

First, we considered three different types of the model (in Fig. 1b) to establish the mechanisms which lead to successful foraging. Both nest and food were circular in shape with radii $r_N=20$ mm and $r_F=15$ mm, respectively, and a separation distance $d_{NF}= 140$ mm between the centres. We chose the ant-specific parameters of the model to represent a common type of ant - an Argentine ant (L. humile), with a body length of approximately 2 mm. Initially the environment was pheromone-free. The simulation parameters are summarised in a Table 1.

Each simulation with this set-up included $N=300$ ants, $N_a = 200$ of which were active foragers and recruiters at the start of the simulation, while the remaining $N_r = 100$ were passively waiting in the recruitment pool in the nest. Initially, all active ants started at the nest and explored the environment for food sources. At the same time in Models 1, 3 they deposited the long-lasting nest marking pheromone for a limited time. In Model 2 (where the ants have ability of stochastic navigation back to the nest) no pheromone was deposited to mark the location of the nest. When an ant discovered the food source it changed its state and started following the nest-marking pheromone (or used stochastic navigation in Model 2) and depositing the food-marking pheromone. While in Model 1 the nest- and the food-marking pheromones had identical properties (although could be distinguished by their type), in Model 3, consistently with the biological insight, the food-marking pheromone was short-lived (Jackson et al., 2007; Robinson et al., 2008). The recruiters spent time $t_E = 15$ s after each finding of the food source to evaluate its quality. When comparing the times in each phase (nest-searching, food-searching we included this exploration time in the nest-searching phase of the simulation). Once a recruiter ant returned back to the nest it activated $n_r$ new foragers from the recruitment pool, if available. These ants were not recruiters themselves, i.e., although they followed and deposited the pheromones in the same way as the recruiters, thus reinforcing the established trails, they neither evaluated the quality of the food, nor recruited new ants. All ants that found the food source took one unit of the food and count the food towards a total upon their return. This provided us a metric by which to measure the efficiency of the trail formation and maintenance.

Snapshots from an example simulation are presented in Fig. 3a-c for the scenario with a single food source. Initially, ants dispersed randomly, following the default correlated random walk. While in Model 1, even after 20 min of the simulation, the ants were unable to locate the food source, in Models 2 and 3 the path started forming quickly, after 1 min of the simulated time, and was further reinforced. The inability of the ants in Model 1 to find the food source was a result of the pheromone they released, which attracted the ants back to the surroundings of the nest.

Fig. 3

Formation and refinement of the trail in the Models 1–3. a The pheromone distributions at times $t\in \{1,5,10,20\}$ min for Models 1–3 are plotted on the same scale. b The raster plots show the events of finding the food (blue) or the nest (red) in time for each simulated ant (vertical axis). The simulation was initiated with 200 ants. Additional 100 ants were introduced in the simulation through recruitment. We do not provide the raster plots for Model 1 since this simulation showed no events of finding the food throughout the simulated time period. c The total amount of accumulated food in the nest. After an initial transient the quantity grows approximately linearly, showing a persistent path (Color figure online)

Figure 3b shows the raster plot of all events of finding the food/nest in blue/red, respectively, for each ant in the simulation. Model 2 showed the fastest trail establishment, the straightest path and the fastest accumulation of the collected food in the nest. The total amount of accumulated food, shown in Fig. 3c, is linear, which means a steady rate of food accumulation. The fast speed of food collection is caused by the stochastic (visual) nest-finding navigation, which leads to the food finding pheromone being released very close to the shortest path from the food to the nest. In Fig. 6 we show the proportion of the ants in different states throughout the simulation, leading to a steady pattern, consistent with the constant rate of food accumulation (where the rate of food accumulation equals the numerical derivative of the total collected food function in Fig. 3c).

The research conducted by Thienen et al. (2016) emphasized the significance of collective information (pheromones) over private information (visual memory). Although previous studies on Argentine ants (Aron et al., 1989) suggested the use of a single pheromone for path marking and reinforcement, it remains unknown whether this pheromone differs from a recruitment pheromone in composition or concentration. Consequently, it is important to investigate the dynamics in the presence of two pheromones. This is reflected in our Model 3, where we deviate from the assumption of compass navigation and introduce a second, long-lived nest-marking pheromone.

The elimination of compass navigation and the introduction of the second pheromone lead to a diminished food accumulation rate and a less straight trail, particularly in the short term after its establishment. While further simulations are required for a systematic assessment of path optimality, similar to previous findings demonstrating Argentine ants’ ability to select the shortest path (Goss et al., 1989), our Model 3 observations indicate that ants consistently form and maintain relatively straight trails to the food source. This occurs despite the model avoiding the strong and potentially unrealistic assumption of compass navigation, particularly for certain ant species. Consequently, our primary focus is directed towards the two-pheromone model.

3.2 Dynamical patterns and limitations of the models

Occasionally, we observed an unexpected yet biologically realistic emergent phenomenon in Model 3 when a mix of ants in both (food- and nest-searching) phases concentrate in a certain region of the space, following each others deposited pheromones. This type of spontaneously “milling behavior” has been observed in the real ant colonies (Couzin & Franks, 2003; Deneubourg & Goss, 1989). In our model these mills are a result of ants who are searching for food following the pheromone depositions of the ants searching for the nest (and vice versa) in a particular spatial configuration. This may have disastrous consequences for ant colonies, in particular in the case of strongly following ants, (e.g. army ants) which sometimes get trapped in a so called “death spiral” in which the majority of the colony forms a positively reinforcing mill (Delsuc, 2003). We note, however, that this behavior observed in our simulations was rare and temporary (simulations containing this behaviour were included in our results). Similar model behavior was mentioned in the work of Vela-Pérez et al. (2015), in which the authors incorporated a mechanism to avoid clustering in a small spatial region.

The environment at the start of the simulation is initialised without pheromone, hence some ants may wander far from the nest and temporarily become lost. Such “losses” also occur in real colonies (Wystrach et al., 2013). Although there were some ants that failed to find the trail quickly and thus explored a wider region of space before discovering the trail, this inhomogeneity in ant behaviour may be advantageous to the colony as a whole, since these “far-ranging” ants may be able to discover other sources of food or adapt to a changing environment (Deneubourg et al., 1986; Calenbuhr & Deneubourg, 1990). In reality, food sources may become depleted and ants need to be able to respond efficiently to such situations.

Since the process of trail formation is stochastic, the time to establish the trail between food and nest is a random variable. With small probability all ants may get lost and the trail will never be established, however, the probability of such failure is very small, particularly when the number of the ants is large. With $N=300$ ants we observed effective trail formation in every simulation we ran.

The pheromone profile along the trail may exhibit a non-monotonic pattern. While we consistently observed substantial differences in the concentration of nest-marking pheromone between the nest and the food, with the highest concentration close to the nest, the same is not true for the food-marking pheromone. The food-marking pheromone maintains an approximately constant level (although slightly higher at the food source than the nest), dispersed with local peaks and valleys, as illustrated in Appendix E. We observed some instances where ants in the nest-searching phase (following the yellow pheromone profile in Fig. 12) reorient themselves and follow the path in the opposite direction, with the potential for multiple reorientations before reaching the target. These reorientation events are even more prevalent among ants searching for food than those searching for the nest, which agrees with the flatter and less distinctive signal provided by the pheromone profile (blue profile in Fig. 12).

3.3 Multiple food sources

We next explored whether our model ants are able to take advantage of multiple food sources and maintain multiple trails. We placed two food sources at the same distance away from the nest but at different subtending angles, see Fig. 4a. We measured the ability to maintain two trails (to food sources F1 and F2) using a non-dimensional measure of the absolute difference between the total accumulated food from the food sources F1 and F2, scaled by their sum. Denoting the total accumulated food in the nest from source F by $M_F$ the measure is defined as $|M_{F2}-M_{F1}|{\big/}(M_{F2}+M_{F1})$. This measure is equal to zero when the ants accumulate the food from the two sources at exactly the same rate, i.e., maintain both trails and use them equally. On the other hand, if only one of the food sources is used for foraging the measure equals 1.

Figure 4a reports the mean ± SEM of the time traces of the measure $|M_{F2}-M_{F1}|{\big/}(M_{F2}+M_{F1})$ (averaged through the repeats). It shows that ability to maintain two paths simultaneously grows with the subtending angle between the food sources. This is likely caused by the diminished interference between the established trails. If the angle between the food sources is sufficiently small then the two food sources are effectively in competition with each other for trail formation (Beckers et al., 1992).

Figure 4a shows another interesting pattern. The longer the simulation, the more preference towards a single food source is observed. This may be caused by the instability of the system, i.e., once there is a preference towards a one of the food sources this preference is reinforced in time. Symmetry breaking occurs because stochastically more ants find one of the food sources earlier than the other. The increased pheromone deposition on this trail leads to increased recruitment to the food source. This stochastic positive reinforcement of the trails leads to the choice of one of the food sources over the other with equal probability as often observed in experiments (Deneubourg & Goss, 1989; Beckers et al., 1990; Jeanson et al., 2012). However if the subtending angle between the two food sources is too large the two trails are essentially independent and can both establish and coexist.

Fig. 4

Three biological scenarios. a Two food sources are located at an equal distance $d_{N,F} = 140$ mm from the nest at different angles. This angle impacts the absolute difference between the accumulated food from sources F1 and F2 scaled by their sum, defined as $|M_{F2}-M_{F1}|{\big/}(M_{F2}+M_{F1})$ (± SEM, $n=10$ replicate simulations), which we refer to as the amount bias. As the angle grows the ants are able to maintain two independent trails at a higher rate. The asymmetry is more pronounced when the dynamics is run for longer times. b Two food sources are located at different distances from the nest with the food source F2 being twice as valuable as the food source F1 (the ratio of $d_{N,F2}/d_{N,F1}$ distances is 0.75, 1, 1.25, and 1.5). The simulations show the preference for the path to a richer food source in terms of the amount/utility bias of the food collected from F2 as compared to F1 (± SEM, $n=10$). The amount bias is as defined as in panel (a) (although without the absolute value), while the utility bias is defined as $(U_{F2}-U_{F1}){\big/}(U_{F2}+U_{F1})$ where the utility associated with the food from F2 is twice as large as that associated with F1. The outcome of the simulations is shown at times $t\in \{5, 10, 20\}$ min. c Adaptation to alternating food sources is possible in our model. Two food sources F1 and F2 are located at equal distance from the nest but on opposite sides. Initially, only the food source F1 is present (0–20 min). Then the food source F1 disappears while the food source F2 is introduced (20–60 min). There are two further changes in the food source location at times 60 min and 100 min. The figure shows how the ants adapt and form the trail towards the newly introduced food source by showing the rate of accumulation of each food to the nest (±SD, $n=10$ – SD is shown to magnify the error bar width) (Color figure online)

3.4 Food sources of a differing quality

One of the key biological puzzles in ant foraging is how the quality of the food affects the foraging process (Detrain & Deneubourg, 2008; Price et al., 2016; Jeanson et al., 2012). For instance, Reid et al. (2012) show that Argentine ants exploiting different quality foods show different trail behaviour in terms of U-turns and deposited amounts of pheromone. The question of dependence of foraging behavior on the food quality is important to allow ant communities to effectively allocate their own resources (workforce, etc.) in order to exploit the best food sources present in their environment.

We tested two hypotheses of how the quality of the food feeds back into the ant behavior within the framework of our model. We assumed that the quality of the food source, assessed by the recruiter ants: (1) Affects the amount of food-signalling pheromone deposited in each step (P-model); or (2) Affects the number of ants recruited for foraging (R-model). While the first mechanism leads to a stronger pheromone signal in the trail during the whole simulation the second mechanism leads to a larger number of ants early in the simulation before the recruitment pool runs out. We tested all possible combinations of the feedback effect: P, R, RP, and X where the X corresponds to no feedback on the food quality.

Specifically, all models contained $N_a=200$ initially active ants and $N_r=200$ ants in the recruitment pool. Both mechanisms of pheromone deposition and recruitment were present in the simulation but the dependence on the food source quality was only included in the appropriate model. In the null model (X) each of the $N_a$ ants were able to recruit 4 new ants and each ant currently in the nest-searching state deposited one unit of pheromone per step. In the P model we used food-dependent feedback in the pheromone deposition, i.e., the deposited pheromone on the way from the richer food source was 1, while from the less rich food source it was 0.5 (while the recruitment model was identical to the X model). In model R we used food-dependent feedback in the recruitment model, i.e., an ant returning from the richer food source recruited twice as many ants (4) than for the less rich food source (2) (while the pheromone model was identical to the X model). Finally, in the RP model we combined the food-dependent pheromone model (as in the P model) and the food-dependent recruitment model (as in the R model).

The main biological question we addressed in our simulations was when (and by which mechanism) ants form trails to the food sources that are more distant but at the same time more rich. We used a set of four comparisons, schematically depicted in Fig. 4b. The food source F1 was positioned at a distance 140 mm from the nest while the doubly valuable (rich) food F2 was positioned at four alternative distances on the opposite side of the nest to the food source F1. The ratio of $d_{N,F2}/d_{N,F1}$ distances were chosen as 0.75 (the richer food is closer), 1 (equal distance), 1.25, and 1.5 (the richer food is further away).

The results of our simulations for different relative distances of the food sources F1 and F2 and for the different models (P, R, RP, X) are shown in Fig. 4b. We used a larger state space of dimensions 500 $\times$ 500 mm. The two panels correspond to the two measures of food source preference, similar to the one used in panel A of the figure: (Left) Bias towards the total amount of food accumulated in the nest from the richer food source F2, $(M_{F2}-M_{F1})\big/(M_{F2}+M_{F1})$ (the same measure as in the panel A except lacking the absolute value); and (Right) Bias towards the total utility of food accumulated in the nest from the richer food source F2 (utility may correspond to the nutrient amount, etc.). The quality of a single unit of the food F1, $q_{F1}=0.5$, is half the quality of the single unit of the food F2, $q_{F2}=1$. Denoting the utility of the total accumulated food in the nest from source F by $U_F = q_FM_F$ the measure is defined as $(U_{F2}-U_{F1})\big/(U_{F2}+U_{F1}) = (2M_{F2}-M_{F1})\big/(2M_{F2}+M_{F1})$. The utility of a food source (F) at a specified time is a combination of its food quality ($q_F$) and the accumulated amount of this food in the nest ($M_F$) up to this time. A simple back-of-the-envelope argument indicates that, in a system with an established trail and a fixed number of ants moving at a constant speed, the rate of food accumulation is inversely proportional to the distance between the nest and the food source. This arises from a straightforward consideration that, neglecting noise, it takes more time to transport a unit of food along the trail when the food source is farther away, thereby increasing the marginal time cost of the food. Note that the food source bias lies within the interval $[-1,1]$ independent of whether we are using the amount- or utility-based measure.

It has been previously observed that Argentine ants are capable of selecting the richer food source when offered two foods at the same distance from the nest (Csata et al., 2020). Moreover, they are able to rapidly track changes when a colony is offered a choice between three feeders containing a sucrose solution that periodically change in concentration (Latty et al., 2017) – the majority of foragers re-allocate to the richest food source at each change. The question is whether the colony would prefer a richer food source, which is further away.

Our simulations in Fig. 4b, based on 10 replicates in each scenario, show a few interesting related biological predictions. First, the ants in our simulations show preference for richer food sources even when they lie further from the nest. This is observed for the relative distance of the food $d_{N,F2}/d_{N,F1} = 1.25$. Preference towards one of the food sources can be seen from two properties of the data visualizations: (1) From the sign of the utility-based measure of the bias towards the richer food source; and (2) from the dynamics of the bias either amount- or utility-based. We observe that for the models involving pheromone feedback the preference of the food source F2 grows in time (supported by the simulations in both panels). In addition, the utility-based preference towards the richer food source is positive for exactly the same model alternatives. Note that when the richer food source is too far from the nest (as it is for the ratio of distances $d_{N,F2}/d_{N,F1} = 1.5$) the relative richness of the food source F2 to F1 can no longer offset its relative distance.

The delayed preference for the richer but more distant food source arises because ants first encounter and establish a trail towards the closer food source. Upon discovering the more distant food source, they have a chance to establish a second trail, but the initial trail is already reinforced, causing a time delay in the transition. When the distances are roughly equal, average discovery times are comparable, while significantly different distances require the farther source to have substantially higher quality to compensate for the extended waiting time until exploring ants, deviating from the established trail, discover it.

A further observation is that in the models involving pheromone feedback the dynamics were much more sensitive to the quality of the food sources compared to the models involving recruitment feedback. The models on the horizontal axis in Fig. 4b were ordered by the magnitude of this effect, showing that modulating the amount of deposited pheromone had a strong effect on the dynamics while modulating the recruitment had almost no effect. This may be due to the fact that the recruitment pool ran out in our simulations very fast and after 5 min of the simulation there were no more ants to be recruited. Additionally, the pheromone presents a stronger feedback loop compared to recruitment partly because recruitment is not specific to the food source. The response to the pheromone can be further enhanced by starvation (since the detection thresholds are significantly lower after a long starvation period) as was previously shown for the Argentine ants by Thienen et al. (2016).

3.5 Adaptability to changing environment

In our model the adaptability of ants is facilitated by the limited persistence of pheromone gradients due to decay or diffusion. By choosing the lifetime of the food-marking pheromone to be shorter than that of the nest-marking pheromone (Jackson et al., 2007; Robinson et al., 2008) we allow the model ants to respond to the relative transience of the food source and the relative permanence of the nesting site. The diffusion coefficients of the food-marking and nest-marking pheromones are chosen to be the same.

In order to investigate the adaptability of ant behaviour (similar to questions studied by Dussutour et al. (2009)) we dynamically altered the environment. In particular, we changed the location of the food source (to the same distance but opposite direction from the nest) once the trail to the original food source F1 had been established (after 20 min). The adaptation to the new food source F2 involved the decay of the original pheromone trail, random exploration of the space for other food sources and the formation of a new pheromone trail to the relocated food source. After letting the dynamics settle into a new regime (40 min) we switched the new food source F2 back to the original location F1 and repeated the change once more (see the schematic description in Fig. 4c). We repeated the whole dynamical protocol for 10 independent replicates, each starting in an environment without pheromone.

Finding a new food source and establishing a new trail in our simulations was always successful but the timescale at which it happened varied. We observed that the first trail to a food source F1 was established in approximately 5 min and persisted for the remaining 15 min at a steady efficiency in terms of the food accumulation rate (see Fig. 4c). After relocation of the food source (from F1 to F2) the adaptation to a new food source took about 20 min, after which the trail was formed and the new food was again transferred at a roughly steady rate to the nest.

Interestingly, after the next relocation of the food source from F2 to its original location F1 the adaptation of a fraction of approximately 20% ants was almost immediate, while the rest of the ants were delayed in their response (although the response was faster than 20 min). The fast adaptation was caused by the ants that did not have time to adjust to the previous food source relocation (from F1 to F2) and were thus still located close to F1. These ants were able to find the newly added food source in their vicinity quickly. The same early onset pattern is visible after the last change of the food source F2, showing that the memory from the previous dynamical regime was not completely erased.

4 Discussion

We proposed three mathematical models of ant foraging based on a combination of pheromones and/or visual navigation. The aim of the models was to capture the most important aspects of ant foraging behaviour inspired by the Argentine ants whilst making the models simple enough to understand and test biological hypotheses.

We studied how many pheromones are needed to successfully forage for food. Earlier work on Argentine ants (Aron et al., 1989) suggests that exploratory trails and food recruitment trails may be marked by the same pheromone. Authors of a recent study Saund and Friedman (2023) showed that the exploration and food-gathering of big headed ants (P. megacephala) in the Y-maze laboratory setup can be also explained by a single-pheromone model, in contrast with the previous results in Dussutour et al. (2009) where a two-pheromone model was proposed. Our models offer new perspectives on this question. We compared three models that differ in the number and use of pheromones, namely, models with a single pheromone, a single pheromone combined with orientation, and two pheromones. We found that the single-pheromone model is unable to explain ant foraging in unconstrained space, in contrast to recent results in the Y-maze. Namely, if ants are programmed to follow a single pheromone, positive feedback by ants simultaneously following and depositing this pheromone could create an artificial high pheromone gradient and cause the ants to mill futilely until all the pheromone deposited had diffused/decayed. Although the parameters of our model are aimed at capturing ant of the species L. humile, as it is a well studied ant this behaviour likely persists for a wide range of parameter values for the single-pheromone model. The confusion emergent in our model of the single-pheromone signal in free-space may not be exhibited in the Y-maze due to its constrained one-dimensional character.

Our single-pheromone model with visual navigation demonstrated that for ants able to navigate back to the nest using vision, one pheromone may suffice, as shown also in Amorim (2015); Clifton et al. (2020); Wagner et al. (2022). However, the ability to use visual orientation to find the nest is not inherent to every species of ants and even in those for which it is, practical consideration mean it is not always possible. For instance, Argentine ants are known to utilize pheromone information more than visual memory (Thienen et al., 2016). Two pheromones, considered also in Caillerie (2018), may be therefore necessary for successful foraging. We have shown that two pheromones with different physical properties are sufficient to achieve a variety of realistic biological behaviours. This is in agreement with Dussutour et al. (2009); Jackson and Ratnieks (2006) arguing that more pheromones provide information on different timescales and allow better adaptation to variable environments. We note that the pheromones in our model do not contain information about orientation and direction, as is considered for instance by Boissard et al. (2013); Caillerie (2018).

The model we study for the majority of the paper is a correlated random walk with a deterministic contribution that allows ants to follow the pheromone signal through processing of sensory inputs at the antennae (corresponding to the resource they are currently seeking) and a Gaussian stochastic contribution that diminishes in strength when the pheromone signal is very strong. Although existing models are typically based on correlated random walk with Gaussian angle deviations, Vela-Pérez et al. (2015) use a heavy tail distribution, a distinctive feature compared to the rest of the literature. In contrast, Amorim (2015) simplifies the typically considered correlated random walk to pure diffusion, which makes the model similar to bacterial chemotaxis models.

Both pheromones in our model diffuse and decay, marking the location of a food source or a nest. By prohibiting direct interaction between ants, including also crowding effects, which are not taken into account here, but were considered for instance in Couzin and Franks (2003); Amorim et al. (2019), we ask whether interactions through a global but dynamic pheromone field are sufficient to allow realistic foraging strategies. It is also possible that we could extend the model by allowing ants to employ more that two pheromones potentially allowing the ants to achieve more complex tasks. However, we have shown that ants can perform basic foraging behaviour using only two.

We systematically investigated our mathematical model through numerical simulations, exploring a range of parameter combinations and environmental scenarios. Our model successfully replicates the formation, tracking, and maintenance of a distinct trail between the nest and a discovered food source, aligning with observations from other spatial models (Amorim, 2015; Ryan, 2016; Caillerie, 2018). Our primary contribution, distinguishing it from existing work, lies in the minimal assumptions regarding the homing process. Specifically, in our model, ants follow a nest-marking pheromone deposited during the foraging state, serving as a guide for homing. The simulated ants’ ability to return to the nest depends on the establishment of a pheromone field, which may encounter disruptions due to decay and variability, posing challenges for homing. Despite these challenges, our results demonstrate a monotonous profile of the nest-marking pheromone along the established trail, gradually increasing as the nest is approached. This contrasts with the food-marking pheromone, which exhibits small variation with local peaks and valleys. This is related to our observation that ants can follow the path also in the “wrong” direction (e.g. the food-searching ants in direction towards the nest) but it is more prevalent for the ants looking for food, which do not have a monotone signal to follow.

In contrast to our model assumptions, Ryan (2016) assumes ants take a direct path back to the nest, while Amorim (2015) incorporates a stable nest-informing potential, making the second pheromone unnecessary. On the other hand, the model proposed by Caillerie (2018) shares key similarities with our model, albeit with differences in component details. It includes two states- foraging and nest returning- and employs two pheromones. Ants deposit one pheromone and follow the other in each state, collectively solving tasks such as finding food, returning to the nest, and adapting to obstacles on the established trail, all without knowledge of the locations of the source or nest. The primary distinction lies in the information carried by the pheromones; while the model by Caillerie (2018) incorporates orientation and direction information, our model only considers the amount of pheromone at a given location.

A particularly important part of the model is the randomness in the motion of each ant. Stochastic behaviour allows ants to explore the environment for food and, once found, to refine the trail between the nest and the food source. It also provides adaptability to the colony since ants can deviate from established trails and discover new food sources (Deneubourg et al., 1983).

Foraging efficiency depends on the ants’ ability to exploit multiple food sources. There is clearly a trade-off between having a strong pheromone profile that is easy to follow but restricts ants’ abilities to explore their surroundings and a weaker trail which allows for a more thorough exploration of the environment at the cost of a loss of reliability in exploiting discovered food sources and a risk to be exposed to predation. In our model, we have found that the number of food sources that a colony can exploit simultaneously depends on the locations of such food sources. Maintaining two trails with a given limited number of ants is less likely if the food sources are close to each other (while at the same distance from the nest), probably because the pheromone trails interfere with each other; therefore, ants face a choice between the two food sources. As soon as the symmetry between the pheromone intensities of the two trails is broken, positive feedback reinforces the stronger of the two trails. Random exploration may lead ants to reinvent the forgotten trail later; however, we found that the probability of maintaining a single trail increases with time. This is consistent with the experimental observations by Beckers et al. (1992) but also with theoretical work of Ryan (2016), who finds that despite initial discovery of both food sources only one is preferred thanks to pheromone reinforcement and the food source choice is symmetric. The extension of the question to more than two food sources was studied by Nicolis and Deneubourg (1999). They presented an analytical argument demonstrating an interesting outcome – in the presence of multiple equidistant food sources, exploitation may be asymmetric, with one food source being exploited more while the others are exploited less, but equally to each other. Foraging decisions in the presence of multiple food sources in spatial models were studied also in other works (Caillerie, 2018; Amorim, 2015). However, these works did not explicitly show the case of two identical and equidistant food sources. This would be particularly interesting in the latter model since the approach is not agent-based and does not contain inherent randomness.

The efficiency of foraging depends on the proximity and quality of the food sources. We explored how the food source quality influences the foraging process. We tested two quality-dependent feedback strategies, one for which the amount of pheromone used to signal food depends on food quality, the other for which the number of ants recruited for foraging depends on food quality. We have found that the ants in our model prefer a richer food source even if it is further away. Models incorporating pheromone feedback influence the dynamics much more than models incorporating recruitment feedback. Moreover, we found that the sign of the relative utility of the food source (based on the total amount and quality of food collected by all ants in the nest from this food source) is indicative of which food source will be preferred. The utility reflects both differing quality and proximity of the food source as it depends on the amount as well as time to carry the food to the nest. The food source with a higher utility (positive relative utility) will dominate over time. This is an emergent property of the model, which provides a time-dependent strategy for the allocation of the resources in the presence of multiple food sources.

In contrast to our numerical simulations, Beckers et al. (1990), who studied L. niger ants, observed that when ants establish a path to a sub-optimal food source before a better food source is available, switching to the higher-quality source can be challenging due to the strong reinforcement of the existing trail. This behavior has been replicated in the theoretical model by Nicolis and Deneubourg (1999). On the other hand, Beckers et al. (1990) also observed T. caespitum ants, which can switch to the optimal food source even when a suboptimal trail is established first. In their review, Czaczkes et al. (2015) suggested that L. niger ant’s inability to switch may be due to relying solely on trail pheromones, in contrast to T. caespitum, which directly guide recruits toward food. This differs from our model, which is designed to resemble Argentine ants, and which shows that under dynamics governed exclusively by pheromones, a gradual preference for the higher-quality food source emerges. This occurs irrespective of whether the food sources are equally distant or if the higher quality option is slightly farther from the nest than the suboptimal one. Notably, this preference is observed only when the deposition of the food-signaling pheromone is proportional to the food quality. However, since the closer food source is more likely to be discovered and established first, it takes time until the ants gradually transfer from exploiting the suboptimal to the optimal food source.

While we did not specifically investigate the scenario of two equally rich food sources at different distances, our results offer robust support, allowing us to predict how the system will behave in such a situation. Our findings suggest that the closer food source is likely to be preferred for two primary reasons. Firstly, the proximity of the food source increases the likelihood of its being discovered first, leading to an earlier construction of a trail. Secondly, the closer food source, keeping all other properties the same, allows the ants to dynamically accumulate more food due to the smaller time cost per unit of food under the assumption of constant speed of the ants, i.e., positive relative utility for the closer food. Consequently, the closer food source is dynamically favored. This result is a special case of our more general finding that the positive relative utility of one food source to the other causes dynamical preference of ants towards this food source. In line with our predictions, both Amorim (2015) and Caillerie (2018) observed a preference for the path towards the closer food source. Notably, Caillerie (2018) reported a simulation where two sources were simultaneously exploited, with the closer one attracting more ants. However, it remains uncertain whether this was just a temporary phenomenon (which would align with our findings) or a more robust scenario.

Additionally, our model ant colony is able to adapt to dynamic changes in the environment, such as changes in the placement of food sources. Our simulations contain a food source, which is switching its location in the plane, in analogy to the experimental investigation by Dussutour et al. (2009), where the food relocates from one branch in the Y-maze to another. Similarly to these empirical findings, ants in our model are able to adapt to the relocated food. In addition, when we relocate food to its previous position we observe that less time is needed for adaptation and the colony partially remembers its previous foraging activity. This partial memory in our simulations is caused by the fraction of ants that remain in proximity to the initial location of the food source even after it has been relocated to a different position. It is important to note that the relocation of the food source, which is the focus of our study, is fundamentally similar to scenarios involving depleting food sources, as explored in works such as Caillerie (2018); Ryan (2016). Our simulations reveal that ants typically exploit only one food source at a time before environmental changes, triggered by factors like food depletion or food relocation, require their search for an alternative food source, which is yet unexplored.

In this article, we used simple but realistic models which capture the pertinent features of ants’ foraging behaviour. We have shown that model ants are capable of a variety of complex tasks, such as foraging for stationary and moving food sources. We explored the choices made when food sources are located at different distances from the nest and adaptively repositioned. We have shown that our model ants are capable of discerning different quality food sources and that pheromone feedback is much more sensitive to food quality feedback than recruitment feedback. This provides a testable hypothesis on the biological behaviour of real ant communities. There are many tasks that real ants have been shown to be capable of, which we have yet to test for in our model ant colony (Reid et al., 2011; Robinson et al., 2009; Nicolis & Deneubourg, 1999), e.g. navigating U-shaped traps. These are problems of substantial biological interest which we hope to address in future publications.

Appendices

Appendix A: the effect of diffusion D

The effect of the choice of the diffusion parameter D and the parameter $\rho$ on stochastic foraging is shown in Fig. 5.

Fig. 5

a The total amount of accumulated food in the nest in time in Model 2. The figure shows results for the mean ± standard error of the mean for 10 simulations for different choices of the diffusion constant D. In the absence of diffusion ($D = 0$) the food search is slow. For the value $D = 0.05$ the food search is effective and the food accumulates at a constant rate (linear total accumulation). For the value $D = 1$, ants are able to find the food quickly, but their effectiveness decreases over time, because the pheromone profile scatters rapidly in the environment. b The total amount of accumulated food in the nest for different values of the deposition width kernel $\rho$. Food searching is most efficient with the largest value $\rho = 2$. c The pheromone distributions at times $t \in \{5,10,15,20\}$ min. The figure displays the results of the selected simulations from the set analyzed in graph (a). The three simulations use the same seed for the random variables and the same value of $\rho =1$. The values of the diffusion constant $D \in \{0, 0.05, 1\}$ are used. d Analogous to c with a fixed $D=0.05$ and varying $\rho \in \{ 0.5, 1, 2\}$. The three simulations use the same seed for generating the random variables (Color figure online)

Appendix B: proportion of ants in different states

Proportion of the ants in different states throughout the simulation is shown in Fig. 6.

Fig. 6

Dynamics of the ant activity for the Models 2 and 3. a The gray shading shows the total number of foraging ants in the simulation of the Model 2. The number of foraging ants increases due to recruitment by the ants that brought food back to the nest. Top: The number of ants searching for food (blue shaded region) shown along with the number of ants, which found the food source within 30 s windows (blue curve, markers located in the centers of each bin). Bottom: The number of ants searching for the nest (red shaded region) shown along with the number of ants finding the nest within 30 s windows. b Analogous results to a for Model 3 (Color figure online)

Appendix C: truncation of the pheromone field

Fig. 7a shows the proportion of ants, which perceived detectable pheromone amounts on both/one/none antennae at each iteration in the reference simulation (same parameters as in Fig. 3) using our truncation rule (Eq. (9)). These results show that it is extremely rare for an ant to perceive a detectable signal on one antenna and non-detectable signal on the other (the red region between the blue and the yellow regions is not visible by eye). The total 2, 1 and 0 event proportions (taking all times together) were approximately 0.32, 0.00041 and 0.68 respectively.

Fig. 7

Effect of truncation of the pheromone sensing on the perceived signal for small pheromone concentrations in the reference simulation with a single food source. Each antenna of the ant at a given time can perceive a significantly high pheromone signal with concentration larger than the detection threshold $c_\text {det}$, or a signal below the detection threshold. The recorded proportions of ants in each iteration, which detected two/one/zero significantly large signals using their two antennae, are displayed in the panels in the same vertical order as the legend (the narrow red sector lies between the blue and the yellow). a The thresholding rule means that ants perceive concentrations lower than the detection threshold as 0. b The thresholding rule means that ants perceive concentrations lower than the detecting threshold as $c_\text {det}$ (Color figure online)

We have also performed a simulation (shown in Fig. 7b), in which we changed the truncation rule from Eq. (9) to the one implemented by Amorim et al. (2019) and keeping other components of the model the same we computed the analogous event counts. We obtained proportions 0.21, 0.00019 and 0.79 respectively. Note that the truncation rule of Amorim et al. (2019) perceives pheromone concentrations smaller than the detection threshold $c_\text {det}$ as the threshold value.

Figure 7 suggests that although the events where the ant only senses one superthreshold concentration are extremely rare the modeling detail leads to a noticeable difference in the proportions of the events where the ant senses none or two superthreshold concentrations. The Amorim et al. (2019) rule results in an earlier trail formation, as shown in Fig. 8.

Fig. 8

Effect of truncation of the pheromone sensing on the ant dynamics for small pheromone concentrations in the reference simulation with a single food source. Raster plots showing switching between the food-searching and nest-searching state. Events at which an ant found the food are shown as blue dots, whereas events at which an ant found their nest are shown as red dots. a The thresholding rule means that ants perceive concentrations lower than the detection threshold as 0. b The thresholding rule means that ants perceive concentrations lower than the detecting threshold as $c_\text {det}$ (Color figure online)

Figure 9 suggests that this difference can be attributed to more ants being idle in terms of the foraging process (no state changes during the whole simulation) under our rule, perhaps because they lost the pheromone trace. Figure 9 shows the distribution of the number of state changes (food searching, nest searching) per ant in the 20 min long simulation.

Fig. 9

Effect of truncation of the pheromone sensing on the number of changes between the ant states for small pheromone concentrations in the reference simulation with a single food source. The results in this figure are based on three replicate simulations. Each ant is followed for the whole duration of the simulation and all its state changes are recorded (from the food-searching to the nest-searching state or back, each change counts equally) leading to the displayed histogram of state changes. The leftmost bar of the histograms contains all ants, which did not find food even once throughout the 20 min long simulation. a The thresholding rule means that ants perceive concentrations lower than the detection threshold as 0. b The thresholding rule means that ants perceive concentrations lower than the detecting threshold as $c_\text {det}$ (Color figure online)

Appendix D: comparison of deposition mechanisms

Figure 10 compares two simulations with the same parameters (as in Fig. 3) but with different deposition mechanism used. The panel Fig. 10a shows our reference simulation with four depositions per step, decomposition of the deposited pheromone signal into four closest lattice points, and a Gaussian smoothing of each of these four pheromone concentrations. In contrast, panel Fig. 10b uses one deposition per step at the closest lattice point.

Fig. 10

Effect of Gaussian deposition and multiple pheromone depositions per step on the number of changes between the ant states in the reference simulation with a single food source. Each ant is followed for the whole duration of the simulation and all its state changes are recorded (from the food-searching to the nest-searching state or back, each change counts equally) leading to the displayed histogram of state changes. a Each ant deposits the same amount of pheromone (m/4) 4 times per step. Each pheromone deposition in continuous space is first decomposed to the four closest lattice points. Each amount is further smoothed by a Gaussian discrete kernel with a SD = 1.5 mm, truncated at four times SD. b Each ant deposits m units of pheromone once per step size and deposits it at the location of the closest lattice point. No further decomposition of the signal or diffusion is used

Figure 10 shows a shift of the bulk distribution towards left when pheromone deposition is less smooth, leading to a less efficient foraging. This observation is supported by Fig. 11, which indicates denser foraging behavior in the first half of the simulation for the model with a smoother pheromone deposition process.

Fig. 11

Effect of Gaussian deposition and multiple pheromone depositions per step on the ant dynamics in the reference simulation with a single food source. Raster plots showing switching between the food-searching and nest-searching state. Events at which an ant found the food are shown as blue dots, whereas events at which an ant found their nest are shown as red dots. a Each ant deposits the same amount of pheromone (m/4) 4 times per step. Each pheromone deposition in continuous space is first decomposed to the four closest lattice points. Each amount is further smoothed by a Gaussian discrete kernel with a $SD = 1.5$ mm, truncated at four times SD. b Each ant deposits m units of pheromone once per step size and deposits it at the location of the closest lattice point. No further decomposition of the signal or diffusion is used (Color figure online)

Appendix E: pheromone profile along the path

Figure 12 shows the pheromone profile along the path in a reference simulation with a single food source (parameters as in Fig. 3) with one distinction – the food and the nest were located on the same y-level of the space. For simplicity, we averaged the pheromone along the vertical direction considering only values within the red rectangle, as shown in Fig. 12. This rectangle contains the trail and most of its surroundings.

Our results suggest that while the nest-marking pheromone has an overall increasing pattern as one gets closer to the nest, the food-marking pheromone does not have a monotone behavior (unless early in the simulation).

Fig. 12

Pheromone concentration along the trail. The figure shows an average concentration of the pheromone marking the food location (blue) and nest location (yellow) as a function of the horizontal position between the food and the nest. The average was computed using information within the narrow rectangle between the nest (yellow circle) and the food source (blue circle) (Color figure online)