Liquid Immiscibility and Thermodynamic Assessment of the Al₂O₃–TiO₂–SiO₂ System

Abstract

Phase equilibria in the TiO₂–SiO₂ system have been studied experimentally using DTA and SEM/EDX. The thermodynamic parameters for the TiO₂–SiO₂ system have been assessed considering new experimental data of the present work and from the literature. Moreover, the miscibility of the liquid in the Al₂O₃–TiO₂–SiO₂ system has been studied at 2013 K in air and shrinkage of the miscibility gap at 3.8 mol% Al₂O₃ has been demonstrated. The experimental data obtained in the present work and literature as well as the thermodynamic databases for the binary Al₂O₃–TiO₂, TiO₂–SiO₂, and Al₂O₃–SiO₂ systems have been used to derive the thermodynamic description of the Al₂O₃–TiO₂–SiO₂ system using the CALPHAD approach. Solid phases have been modeled using the compound energy formalism. The liquid phase has been described by the two-sublattice partially ionic liquid model. A set of self-consistent parameters have been proposed, which resulted in a reasonably good agreement between the calculated and experimental data on the phase equilibria, liquid immiscibility, and thermodynamic properties in the Al₂O₃–TiO₂–SiO₂ system.

1 Introduction

Alumina-based materials are widely used as refractory and filter materials in metal production. Research and development of ceramic filter materials for metal melt filtration need availability of thermodynamic databases to model the interactions of a liquid metal alloy containing oxide inclusions with a filter that can be coated with various ceramic coatings. Moreover, possible interactions of ceramic filters with coatings can be modeled to improve efficiency of the complex ceramic filter system. In practice, Al₂O₃-based filter systems are currently being developed for aluminum-based melt filtration.^[1,2] Oxide films and Al₂O₃ particles formed during melting and alloying can be present as a suspension on the surface of the melt or inside the melt because of flow turbulence. Spinel inclusions appear due to the presence of magnesium ions in the aluminum melt, mainly coming from the refractories of the furnace. Magnesium entering the molten aluminum also leads to the formation of non-metallic inclusions other than spinel. TiO₂ coating deposited on corundum is supposed to filter actively spinel MgAl₂O₄ from Al-based molten alloy. The reduction of TiO₂ can then lead to the formation of Al₃Ti or (Al,Si)₃Ti.^[3] Therefore, to model Al melt filtration process, one should consider the Al–Mg–Ti–Si–O system. As a part of the mentioned complex system, the Al₂O₃–TiO₂–SiO₂ sub-system was recently investigated experimentally.^[4] Being a continuation of the study of the oxide system, the aim of the present work is a critical evaluation of available data on phase relations as well as thermodynamic modeling of the ternary system and assessment of thermodynamic parameters in the Al₂O₃–TiO₂–SiO₂ system to derive a self-consistent thermodynamic database using the CALPHAD approach by applying the Thermo-Calc software.^[5]

2 Literature Review

2.1 Binary Al₂O₃–TiO₂ System

The Al₂O₃–TiO₂ system is characterized by the formation of an intermediate compound Al₂TiO₅, also known as tialite, which has a pseudobrookite-type Fe₂TiO₅ structure with the lattice parameters of a = 0.3605, b = 0.9445, and c = 0.9653 nm.^[6] According to the authors own experimental data,^[7] the Al₂TiO₅ phase forms by the peritectic reaction L + Al₂O₃ ↔ Al₂TiO₅ at 2112 K and decomposes into Al₂O₃ and TiO₂ at temperature of 1552 K, and also participates in a eutectic reaction L ↔ TiO₂ + Al₂TiO₅ at 1999 K and 14.9 mol% of alumina. Al₂TiO₅ is nearly stoichiometric compound with a negligible homogeneity range. The mutual solubility of Al₂O₃ and TiO₂ is negligible too. A recent thermodynamic assessment of the Al₂O₃–TiO₂ system^[8] was accepted in the present work. The calculated phase diagram agrees well with the experimental data.^[7] Considering the disordering of Al⁺³ and Ti⁺⁴ cations between the octahedral sites M1 and M2, the Al₂TiO₅ phase was modeled using the model (Al⁺³,Ti⁺⁴)₁^M1(Al⁺³,Ti⁺⁴)₂^M2(O⁻²)₅.

2.2 Binary Al₂O₃–SiO₂ System

Mullite Al₆Si₂O₁₃ is the only stable crystalline phase in the Al₂O₃–SiO₂ system at atmospheric pressure. The character of mullite melting as congruent or peritectic is under discussion in the literature. However, the data from Fabrichnaya et al.^[9] showing the peritectic reaction L + Al₂O₃ ↔ Al₆Si₂O₁₃ at 2166 K and a eutectic reaction L + SiO₂ ↔ Al₆Si₂O₁₃ at 1855 K and 97.64 mol% of SiO₂ were accepted in this work. The compound Al₆Si₂O₁₃ has a mullite-type structure with a = 0.7452, b = 0.7581, and c = 0.2851 nm.^[10] The solid solution homogeneity range of mullite bends towards higher Al₂O₃ contents with temperature increase. The mutual solubility of Al₂O₃ and SiO₂ is negligible. The thermodynamic assessment of the Al₂O₃–SiO₂ system presented by Dumitrescu and Sundman^[11] was accepted in the present work after verification by Fabrichnaya et al.^[9]

2.3 Binary TiO₂–SiO₂ System

First studies^[12,13,14] were carried out in a reducing atmosphere, which caused the formation of Ti₂O₃ and Ti₃O₅ in addition to TiO₂. Nevertheless, Umezu and Kakiuchi^[12] detected the formation of immiscible liquids in melts (35.7–75.1 mol% TiO₂ at 1853 K) and determined a eutectic reaction at 15.0 mol% TiO₂ and 1773 K. In air, Bunting^[15] observed the eutectic at 8.0 mol% TiO₂ and 1813 K and did not report liquid immiscibility since the study was limited to 15.8 mol% TiO₂. Rickers and Hummel^[16] reported a solid solution of (SiO₂ + TiO₂) and relocated the eutectic to 17.0 mol% TiO₂ and 1813 K. Agamawi and White^[17] confirmed the eutectic at 8.0 mol% TiO₂^[15] but at 1843 K. Later, DeVries et al.^[18] specified the eutectic point (8.1 mol% TiO₂ and 1823 ± 4 K) previously determined by Bunting,^[15] and also confirmed the presence of stable immiscibility in the liquid phase extending from 15.0 to 90.8 mol% TiO₂ at 2053 K. McTaggart and Andrews^[19] reported the presence of two liquids existing between 15.9 and 92.2 mol% TiO₂ above 2038 K. The presence of the two-liquid region was subsequently confirmed,^[20,21] but without experimental details. Kirschen et al.^[22] and Kirillova et al.^[23] carried out the high temperature investigations (up to 2533 K), however contradictory data on the boundaries of the miscibility gap were reported. Despite a number of studies of the phase equilibria in the TiO₂–SiO₂ system, it was concluded that there are still several inconsistencies in the description of this system, and a new experimental study is necessary.

Taking into account the miscibility gap data, the TiO₂–SiO₂ system was first assessed by Kaufman^[24] using the CALPHAD method. Next thermodynamic assessments were performed by DeCapitani and Kirschen^[25] and Kirschen et al.^[22] using the Margules-type excess polynomial model and assuming the interaction parameters to be either temperature independent or dependent. An optimized phase diagram using a sub-regular solution model was recently proposed.^[23] Based on their own experimental data, the critical point of the miscibility gap (2416 K at 58.9 mol% TiO₂) was calculated as the lowest in comparison with other calculations.^[22,24,25] Since these assessments are incompatible with the ionic two-sublattice liquid model, a new thermodynamic description of the system needs to be developed. Using all up-to-date experimental data, the TiO₂–SiO₂ system was newly assessed by Boulay et al.^[26] using the partially ionic model to describe the liquid phase. However, the Ti⁺⁴ cations introduced on the first sublattice were only considered in^[26] rather than the mixing of Ti⁺² and Ti⁺³ on the cationic sublattice and Ti⁺⁴ as a neutral TiO₂ species on the anionic sublattice as accepted in the present work regarding the Ti–O system.^[7,27] Therefore, their assessment^[26] is not accepted in the present work.

2.4 Ternary Al₂O₃–TiO₂–SiO₂ System

A literature review and an extensive experimental study of solid–liquid phase equilibria in the Al₂O₃–TiO₂–SiO₂ system in air were carried out by the present authors.^[4] The phase equilibria in the Al₂O₃–TiO₂–SiO₂ system were investigated in the temperature range from 1486 K to melting by energy-dispersive X-ray spectroscopy (EDX) and X-ray diffraction (XRD) to confirm phase assemblages in the annealed samples. The solid-state invariant reaction SiO₂ + Al₂TiO₅ ↔ Al₆Si₂O₁₃ + TiO₂ was found at 1743 K. On the liquidus projection, three invariant reactions were observed: eutectic L ↔ TiO₂ + SiO₂ + Al₂TiO₅ at 1750 K and transitional type reactions L + Al₆Si₂O₁₃ ↔ SiO₂ + Al₂TiO₅ at 1779 K and L + Al₂O₃ ↔ Al₆Si₂O₁₃ + Al₂TiO₅ at 2007 K. No ternary phases were observed in the system.^[4] Data on the crystal structures of all solid phases in the Al₂O₃–TiO₂–SiO₂ system are given in Table 1. Experimental investigation of the miscibility gap extending into the ternary system from the TiO₂–SiO₂ side was carried out by Kirschen et al.^[22] A substantial contraction of the miscibility gap was found at an Al₂O₃ content of 4.0 mol% at 2073 K and a single-phase liquid at 10 mol% above 1970 K.

Table 1 Data on the crystal structures of the solid phases of the Al₂O₃–TiO₂–SiO₂ system

The thermodynamic description of the Al₂O₃–TiO₂–SiO₂ system was first undertaken by Kaufman^[24] using the CALPHAD approach. The calculated isothermal sections in the temperature range of 1000–2800 K indicated extended miscibility gap in the liquid (up to about 25% Al₂O₃). Kaufman also indicated the tie-lines change at low temperatures resulting in a reaction at 1707 K: Al₆Si₂O₁₃ + TiO₂ ↔ SiO₂ + Al₂TiO₅. Wherein, three-phase equilibria (SiO₂ + TiO₂ + Al₆Si₂O₁₃) and (Al₆Si₂O₁₃ + TiO₂ + Al₂TiO₅) are stable above 1707 K, and (SiO₂ + Al₆Si₂O₁₃ + Al₂TiO₅) and (SiO₂ + Al₂TiO₅ + TiO₂) are stable below this temperature. However, these data contradict the experimental ones^[4,33] at which the opposite stable equilibria were found above and below the reaction temperature. The liquidus projection of the Al₂O₃–TiO₂–SiO₂ system was also calculated^[22] with emphasis on the immiscibility in the liquid using the thermodynamic description derived on the basis of their own experimental data.

3 Experimental Part

Two samples of the TiO₂–SiO₂ system were prepared by solid-state reaction from high-purity oxide powders (TiO₂ 99.990% and SiO₂ 99.995%, ~ 40 mesh, Alfa Aesar, Germany). Three samples of the Al₂O₃–TiO₂–SiO₂ system were prepared by co-hydrolysis followed by thermal decomposition of aqueous solutions.^[33] The initial solutions were aluminium tri-sec-butoxide C₁₂H₂₇AlO₃ (M = 246.32 g mol^–1, ρ = 0.967 g cm^–3, 97%), titanium(IV) isopropoxide C₁₂H₂₈TiO₄ (M = 284.23 g mol^–1, ρ = 0.955 g cm^–3, 97%), and tetraethoxysilane C₈H₂₀SiO₄ (M = 208.33 g mol^–1, ρ = 0.934 g cm^–3, 98%) produced by Alfa Aesar, Germany. Details of the sample preparation routine can be found elsewhere^[4,33] The samples were heat treated at targeted temperatures in a muffle furnace (NABERTHERM, Germany) in order to achieve a pseudo-equilibrium state of the samples followed by furnace-cooling, and then examined.

X-ray diffraction study was carried out using an URD63 X-ray diffractometer (Seifert, FPM, Freiberg, Germany) with CuKα radiation (λ = 1.5418 Å). ICSD (Inorganic Crystal Structure Database, 2017, Karlsruhe, Germany)^[34] was used for interpretation of the powder diffraction patterns. Qualitative and quantitative analyses of the XRD patterns were performed by Rietveld analysis using MAUD software.^[35,36] Microstructure examination was done using LEO 1530 Gemini (Zeiss, Germany) equipped with an EDX detector (Bruker AXS Mikroanalysis GmbH, Germany). DTA measurements were performed on (i) TG-DTA SETSYS Evolution-1750 (SETARAM Instrumentation, France) in air using B-type tri-couple DTA rod (Pt/PtRh10% thermocouple) and open Pt crucibles and (ii) TG-DTA SETSYS Evolution-2400 (SETARAM Instrumentation, France) using tungsten DTA rod and open W crucibles and employing a permanent inert He flow. The heating and cooling curves were recorded at the rates of 10 and 30 K min^-1, respectively. Temperature calibration of SETSYS Evolution-2400 was done using melting points of Al, Al₂O₃, and temperature of solid-state transformation in LaYO₃^[37]

4 Thermodynamic Models

4.1 Liquid

The ionic two-sublattice model^[38,39] is applied to the Al₂O₃–TiO₂–SiO₂ system, using the formula (Al⁺³,Ti⁺²,Ti⁺³)_P(O^–2,Va,AlO_3/2,O,SiO₄^–4,SiO₂,TiO₂)_Q. P and Q are the number of sites on each sublattice that vary depending on the composition to keep electroneutrality. The same model can be used for both metallic and oxide melts. At a low oxygen content, the model becomes equivalent to the substitutional solution model considering interactions between metallic atoms. The liquid phase in the Al₂O₃–TiO₂ system was reassessed in the previous work^[7] using the formula (Al⁺³,Ti⁺²,Ti⁺³)_P(O^–2,Va,AlO_3/2,O,TiO₂)_Q. Even as phase interactions with the metal were not considered in that study, the species Ti⁺², Ti⁺³, Va, and O originated from the description of the Ti–O system. Since there is a continuous liquid solution in the Ti–O system from Ti to TiO₂, vacancies are necessary to have consistent description of this binary system. The description of the liquid phase in the Al₂O₃–SiO₂ system is accepted from the works of Dumitrescu and Sundman^[11] and Fabrichnaya et al.^[9] They both used a simple associated solution model considering interactions only between neutral species: (AlO_3/2,SiO₂). For the TiO₂–SiO₂ system, the ionic two-sublattice model is applied using the formula (Ti⁺²,Ti⁺³)_P(O^–2,Va,SiO₄^–4,SiO₂,TiO₂)_Q. However, the species SiO₄^–4 cannot be formed in the TiO₂–SiO₂ system due to a wide liquid immiscibility, i.e. TiO₂ does not participate in either destroying or sharing network of SiO₂. In this case, the liquid TiO₂ is described by the neutral species TiO₂ and the liquid SiO₂ by neutral SiO₂. Thus, this model can be reduced to the (SiO₂,TiO₂) substitutional model and the corresponding interactions parameters were only assessed in this work.

The ionic two-sublattice model was developed within the framework of the compound energy formalism (CEF)^[40] widely used in CALPHAD assessments. CEF is proposed to describe thermodynamic models of phases with two or more sublattices that exhibit a variation in composition. For a two-sublattice model, the Gibbs energy is defined as

$$\Delta {G}^{\varphi }=\sum_{i}\sum_{j}{y}_{i}^{s}\cdot {y}_{j}^{t}\cdot {G}_{i,j}^{S}+\mathrm{R}\cdot T\cdot \sum_{s}{\alpha }_{s}\sum_{i}{y}_{i}^{s}\cdot \mathrm{ln}\left({y}_{i}^{s}\right)+\Delta {G}^{ex},$$

(1)

where ${y}_{i}^{s}$ and ${y}_{j}^{t}$ are the mole fractions of constituents i and j on the sublattices s and t, respectively; ${\alpha }_{s}$ is the number of sites on sublattice s per mole of formula unit of a phase. The excess Gibbs energy term associated with the different sublattices is described with Redlich–Kister equation as

$$\Delta {G}^{ex}=\sum_{s}{y}_{i}^{s}\sum_{t}{y}_{j}^{t}{y}_{m}^{t}{L}_{j,m}^{t}+\sum_{t}{y}_{j}^{t}\sum_{s}{y}_{i}^{s}{y}_{k}^{s}{L}_{i,k}^{s}.$$

(2)

The binary interaction parameters ${L}_{i,k}^{s}$ between i and k species on the sublattice s are signified as

$${L}_{i,k}^{s}=\sum_{n}{}^{n}{L}_{i,k}{({y}_{i}^{s}-{y}_{k}^{s})}^{n}.$$

(3)

Hereinafter, a colon is used to separate species on different sublattices, and a comma is used to separate the species on the same sublattice.

4.2 Mullite

Mullite is a part of the orthorhombic aluminosilicates system of general composition Al₂(Al_2+2xSi_2−2x)O_10−x. The structure of mullite (space group: Pbam) can be derived from the closely related but structurally simpler sillimanite (Al₂SiO₅, with x = 0; space group: Pbnm). In sillimanite, edge-connected AlO₆ octahedra form chains running parallel to the crystallographic c-axis and are cross-linked by double chains with alternating AlO₄ and SiO₄ tetrahedra. In mullite, part of Si⁺⁴ is replaced by Al⁺³, which also leads to the formation of oxygen vacancies. The formation of O vacancies is accompanied by a displacement of the tetrahedral positions next to the bridging O atoms to new distorted tetrahedral positions that form triclusters. Thus, three different Al sites were described in mullite: one octahedral (O), one tetrahedral (T) as in sillimanite, and a distorted tetrahedral (T*) site assigned to Al in the tetrahedral triclusters.^[41,42] Considering this, mullite phase was modeled on the basis of a sublattice description within CEF using the formula ${({\mathrm{Al}}^{+3})}_{1}^{O}{({\mathrm{Al}}^{+3})}_{1}^{{T}^{*}}{({\mathrm{Al}}^{+3},{\mathrm{Si}}^{+4})}_{1}^{T}{({\mathrm{O}}^{-2},\mathrm{Va})}_{5}$.^[9,11] The description is accepted in this work.

According to Schneider,^[43,44,45] Ti⁺⁴ is incorporated into the mullite structure at the Al⁺³ positions in the AlO₆ octahedra. The resulting model for mullite in the Al₂O₃–TiO₂–SiO₂ system is then ${({\mathrm{Al}}^{+3},{\mathrm{Ti}}^{+4})}_{1}^{O}{({\mathrm{Al}}^{+3})}_{1}^{{T}^{*}}{({\mathrm{Al}}^{+3},{\mathrm{Si}}^{+4})}_{1}^{T}{({\mathrm{O}}^{-2},\mathrm{Va})}_{5}.$

This model gives a new neutral end-member ${({\mathrm{Ti}}^{+4})}_{1}^{O}{({\mathrm{Al}}^{+3})}_{1}^{{T}^{*}}{({\mathrm{Al}}^{+3})}_{1}^{T}{({\mathrm{O}}^{-2})}_{5}$, a hypothetical Al₂TiO₅ with the mullite-type structure. The Gibs energy of this end-member is adjusted as

$${^\circ G}_{{\mathrm{Ti}}^{+4}:{\mathrm{Al}}^{+3}:{\mathrm{Al}}^{+3}:{\mathrm{O}}^{-2}}={^\circ G}_{\mathrm{CORUND}}+{^\circ G}_{{\mathrm{TiO}}_{2}}+{a}_{1}$$

(4)

where ${^\circ G}_{\mathrm{CORUND}}$ is the Gibbs energy of corundum Al₂O₃,^[46] ${^\circ G}_{{\mathrm{TiO}}_{2}}$ is the Gibbs energy of rutile TiO₂,^[27] and ${a}_{1}$ is the optimized parameter.

The remaining three parameters in the mullite system (in bold) are evaluated using the reciprocal reactions (Eqs. (5) to (7)):

$${^\circ G}_{{\mathrm{Al}}^{+3}:{\mathrm{Al}}^{+3}:{\mathrm{Al}}^{+3}:\mathrm{Va}}+{^\circ G}_{{\mathrm{Ti}}^{+4}:{\mathrm{Al}}^{+3}:{\mathrm{Al}}^{+3}:{\mathrm{O}}^{-2}}={^\circ {\varvec{G}}}_{{\mathbf{T}\mathbf{i}}^{+4}:{\mathbf{A}\mathbf{l}}^{+3}:{\mathbf{A}\mathbf{l}}^{+3}:\mathbf{V}\mathbf{a}}+{^\circ G}_{{\mathrm{Al}}^{+3}:{\mathrm{Al}}^{+3}:{\mathrm{Al}}^{+3}:{\mathrm{O}}^{-2}}$$

(5)

$${^\circ G}_{{\mathrm{Al}}^{+3}:{\mathrm{Al}}^{+3}:{\mathrm{Si}}^{+4}:{\mathrm{O}}^{-2}}+{^\circ G}_{{\mathrm{Ti}}^{+4}:{\mathrm{Al}}^{+3}:{\mathrm{Al}}^{+3}:{\mathrm{O}}^{-2}}={^\circ{\varvec{G}}}_{{\mathbf{T}\mathbf{i}}^{+4}:{\mathbf{A}\mathbf{l}}^{+3}:{\mathbf{S}\mathbf{i}}^{+4}:{\mathbf{O}}^{-2}}+{^\circ G}_{{\mathrm{Al}}^{+3}:{\mathrm{Al}}^{+3}:{\mathrm{Al}}^{+3}:{\mathrm{O}}^{-2}}$$

(6)

$${^\circ G}_{{\mathrm{Ti}}^{+4}:{\mathrm{Al}}^{+3}:{\mathrm{Si}}^{+4}:{\mathrm{O}}^{-2}}+{^\circ G}_{{\mathrm{Al}}^{+3}:{\mathrm{Al}}^{+3}:{\mathrm{Si}}^{+4}:\mathrm{Va}}={^\circ {\varvec{G}}}_{{\mathbf{T}\mathbf{i}}^{+4}:{\mathbf{A}\mathbf{l}}^{+3}:{\mathbf{S}\mathbf{i}}^{+4}:\mathbf{V}\mathbf{a}}+{^\circ G}_{{\mathrm{Al}}^{+3}:{\mathrm{Al}}^{+3}:{\mathrm{Si}}^{+4}:{\mathrm{O}}^{-2}}$$

(7)

All these reactions are assumed to have $\Delta G=0$.

4.3 Pseudobrookite

Aluminum titanate Al₂TiO₅ (tialite) has a pseudobrookite structure (space group: Cmcm). For the Al₂O₃–TiO₂ system, the three-sublattice model for pseudobrookite Al₂TiO₅ was applied^[8] and the description is accepted in this work. In brief, the cation disordering in Al₂TiO₅ was described with the formula ${({\mathrm{Ti}}^{+4},{\mathrm{Al}}^{+3})}_{1}^{\mathrm{M}1}{({\mathrm{Ti}}^{+4},{\mathrm{Al}}^{+3})}_{2}^{\mathrm{M}2}{\mathrm{O}}_{5}.$ In normal pseudobrookite structure, the M1 sites are fully occupied by the Ti⁺⁴ cations and the M2 sites by Al⁺³. The degree of inversion is then determined as occupancy of M1 by Al⁺³. According to experimental data,^[6,47,48] the degree of cation disorder is close to 0.667, which corresponds to complete disorder. In the presence of SiO₂, the substitution of the Al⁺³ cations by Si⁺⁴ in Al₂TiO₄ is expected,^[49,50] although no experimental details on the crystal structure were found. Also considering the ionic radii concept (Al⁺³ = 0.054 nm, Si⁺⁴ = 0.041 nm, and Ti⁺⁴ = 0.061 nm), the structural incorporation of Si⁺⁴ into both the M1 and M2 sublattices is proposed in this work. Thus, the formula for the pseudobrookite phase is extended accordingly ${({\mathrm{Ti}}^{+4},{\mathrm{Al}}^{+3},{\mathrm{Si}}^{+4})}_{1}^{\mathrm{M}1}{({\mathrm{Ti}}^{+4},{\mathrm{Al}}^{+3},{\mathrm{Si}}^{+4})}_{2}^{\mathrm{M}2}{\mathrm{O}}_{5}.$

The Gibbs energy of normal pseudobrookite Al₂TiO₅ is described by the end-member ${({\mathrm{Ti}}^{+4})}_{1}^{\mathrm{M}1}{({\mathrm{Al}}^{+3})}_{2}^{\mathrm{M}2}{\mathrm{O}}_{5}$ (or ${^\circ G}_{{\mathrm{Ti}}^{+4}:{\mathrm{Al}}^{+3}};$ here and further in the discussion of pseudobrookite, the oxygen index is omitted). To model the degree of inversion in Al₂TiO₅, the end-member ${({\mathrm{Al}}^{+3})}_{1}^{\mathrm{M}1}{({\mathrm{Ti}}^{+4})}_{2}^{\mathrm{M}2}{\mathrm{O}}_{5}$ (or ${^\circ G}_{{\mathrm{Al}}^{+3}:{\mathrm{Ti}}^{+4}}$) is used. The values for the ${^\circ G}_{{\mathrm{Ti}}^{+4}:{\mathrm{Al}}^{+3}},$ ${^\circ G}_{{\mathrm{Al}}^{+3}:{\mathrm{Ti}}^{+4}},$ ${^\circ G}_{{\mathrm{Al}}^{+3}:{\mathrm{Al}}^{+3}}$ (or ${^\circ G}_{{\mathrm{Al}}_{3}{\mathrm{O}}_{5}}^{\mathrm{tialite}}$), and ${^\circ G}_{{\mathrm{Ti}}^{+4}:{\mathrm{Ti}}^{+4}}$ (or ${^\circ G}_{{\mathrm{Ti}}_{3}{\mathrm{O}}_{5}}^{\mathrm{tialite}}$) were taken from the previous assessment.^[8]

A new neutral end-member ${({\mathrm{Si}}^{+4})}_{1}^{\mathrm{M}1}{({\mathrm{Al}}^{+3})}_{2}^{\mathrm{M}2}{({\mathrm{O}}^{-2})}_{5},$ a hypothetical Al₂SiO₅ with the pseudobrookite structure, is found in the pseudobrookite system. To define corresponding parameters, a simplified model ${({\mathrm{Al}}^{+3},{\mathrm{Si}}^{+4})}_{1}^{\mathrm{M}1}{({\mathrm{Al}}^{+3},{\mathrm{Si}}^{+4})}_{2}^{\mathrm{M}2}{\mathrm{O}}_{5}$ can be considered in this case. Similarly to the description of Al₂TiO₅, the four thermodynamic parameters for new end-members can be expressed only by two independent parameters related to normal and inverse structures, respectively, ${^\circ G}_{{\mathrm{Si}}^{+4}:{\mathrm{Al}}^{+3}}$ and ${^\circ G}_{{\mathrm{Al}}^{+3}:{\mathrm{Si}}^{+4}}:$

$${^\circ G}_{{\mathrm{Si}}^{+4}:{\mathrm{Al}}^{+3}}={^\circ G}_{\mathrm{ANDAL}}+{a}_{2},$$

(8)

$${^\circ G}_{{\mathrm{Al}}^{+3}:{\mathrm{Si}}^{+4}}=2\left({^\circ G}_{\mathrm{ANDAL}}+{a}_{2}\right)+{a}_{3}-{^\circ G}_{{\mathrm{Al}}_{3}{\mathrm{O}}_{5}}^{\mathrm{tialite}}-4\mathrm{R}T\mathrm{ln}0.5,$$

(9)

where ${^\circ G}_{\mathrm{ANDAL}}$ is the Gibbs energy of andalusite,^[51] ${^\circ G}_{{\mathrm{Al}}_{3}{\mathrm{O}}_{5}}^{\mathrm{tialite}}$ (or ${^\circ G}_{{\mathrm{Al}}^{+3}:{\mathrm{Al}}^{+3}}$) is the Gibbs energy of a fictive compound Al₃O₅ with the pseudobrookite structure,^[8] and ${a}_{2}$ and ${a}_{3}$ are the optimized parameters.

The fourth parameter ${^\circ G}_{{\mathrm{Si}}^{+4}:{\mathrm{Si}}^{+4}}$ (or ${^\circ G}_{{\mathrm{Si}}_{3}{\mathrm{O}}_{5}}$) is determined by the reciprocal reaction

$${^\circ G}_{{\mathrm{Si}}^{+4}:{\mathrm{Al}}^{+3}}+{^\circ G}_{{\mathrm{Al}}^{+3}:{\mathrm{Si}}^{+4}}-{^\circ G}_{{\mathrm{Al}}^{+3}:{\mathrm{Al}}^{+3}}-{^\circ G}_{{\mathrm{Si}}^{+4}:{\mathrm{Si}}^{+4}}=\Delta {G}_{1},$$

(10)

where $\Delta {G}_{1}=0$.

The remining two parameters in pseudobrookite model, ${^\circ G}_{{\mathrm{Ti}}^{+4}:{\mathrm{Si}}^{+4}}$ and ${^\circ G}_{{\mathrm{Si}}^{+4}:{\mathrm{Ti}}^{+4}},$ are related to the mentioned parameters by the following reciprocal reaction

$${^\circ G}_{{\mathrm{Si}}^{+4}:{\mathrm{Si}}^{+4}}+{^\circ G}_{{\mathrm{Ti}}^{+4}:{\mathrm{Ti}}^{+4}}-{^\circ G}_{{\mathrm{Ti}}^{+4}:{\mathrm{Si}}^{+4}}-{^\circ G}_{{\mathrm{Si}}^{+4}:{\mathrm{Ti}}^{+4}}=\Delta {G}_{2},$$

(11)

where $\Delta {G}_{2}$ is the non-zero value optimized in this work ($\Delta {G}_{2}=\Delta {G}_{3}+\Delta {G}_{4}$), which could be defined by Eqs. (12) and (13):

$${^\circ G}_{{\mathrm{Ti}}^{+4}:{\mathrm{Si}}^{+4}}=1/3{^\circ G}_{{\mathrm{Ti}}_{3}{\mathrm{O}}_{5}}^{\mathrm{tialite}}+2/3{^\circ G}_{{\mathrm{Si}}_{3}{\mathrm{O}}_{5}}+\Delta {G}_{3},$$

(12)

$${^\circ G}_{{\mathrm{Si}}^{+4}:{\mathrm{Ti}}^{+4}}=2/3{^\circ G}_{{\mathrm{Ti}}_{3}{\mathrm{O}}_{5}}^{\mathrm{tialite}}+1/3{^\circ G}_{{\mathrm{Si}}_{3}{\mathrm{O}}_{5}}+\Delta {G}_{4}.$$

(13)

4.4 Rutile, Corundum and SiO₂-Based Phases

The corundum phase is the Al₂O₃-rich solid solution, which crystallizes with trigonal symmetry in the space group $R\overline{3 }c.$ Since no reliable information on any solubility in rutile, corundum, and SiO₂-based phases is reported, these phases are described as stoichiometric. The description of corundum is taken from Hallstedt,^[46] the description of rutile is from Hampl and Schmid–Fetzer,^[27] and the descriptions of Q-SiO₂, C-SiO₂, and T-SiO₂ are all from Hillert et al.^[51]

5 Results and Discussion

5.1 The Binary TiO₂–SiO₂ System

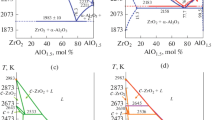
According to DTA measurements up to 1923 K in air, the eutectic temperature in the SiO₂-rich side of the TiO₂–SiO₂ system was determined to be 1818 K (Fig. 1a). The non-intensive and long-drawn-out thermal effect observed for the sample TS-2 can probably be explained by the viscosity of the sample. The temperature obtained in air is in a good agreement with most published data, however this value is more than 60 K higher than that reported by Kirillova et al.^[23] although the experimental conditions were similar. DTA measurement of the sample TS-1 in He indicated a decrease in the temperature of eutectic (1798 K; Fig. 1a). In Fig. 2a, SEM/EDX revealed the eutectic composition measured for the sample TS-2 after melting in DTA, which was equal to 8.7 mol% TiO₂. The microstructure examination of the sample TS-1 after DTA melting (up to 1923 K) in air did not reveal the eutectic formation, probably due to the glass formation. However, a SiO₂ enriched matrix containing 7.0 mol% of TiO₂ and practically pure TiO₂ grains were observed, which indicates the presence of a two-phase field (L1-SiO₂ + TiO₂) discussed below. The temperature and composition of the eutectic reaction are summarized along with the literature data in Table 2.

Fig. 1

DTA heating curves of the samples (a) TS-1 and TS-2 related to eutectic (in air and in He), and (b) TS-1 related to monotectic reaction (in He). No undercooling effects were observed

Fig. 2

Microstructures of the samples (a) TS-2 after DTA heating up to 1973 K in air; (b) TS-1 after DTA heating up to 2273 K in He, fine TiO₂ solids are distributed in SiO₂-rich L1; (c) TS-1 after heat treatment at 2013 K in air; (d) ATS-3 after heat treatment at 2013 in air; (e) ATS-7 after heat treatment at 2013 in air; and (f) ATS-8 after heat treatment at 2013 in air

Table 2 Invariant equilibria in the TiO₂–SiO₂ system

To study liquid immiscibility in the TiO₂–SiO₂ system, the sample TS-1 was heated up both in air and in an He atmosphere. The sample exhibiting the miscibility gap resulted in the separation of the melt into two liquids: one rich in SiO₂ called L1 and the other rich in TiO₂ called L2 (including the TiO₂ grains and the surrounding matrix). Merely on visual examination, the sample TS-1 heat treated at 2013 K in air followed by furnace-cooling was partially melted, however the temperature of the monotectic reaction L1 ↔ L2 + TiO₂ was not reached, revealing the presence of the two-phase field (L1-SiO₂ + TiO₂). As supporting evidence, no certain L2 spherulites were observed for the sample TS-1 melted in air (Fig. 2c), while the grains of practically pure TiO₂ and SiO₂-rich L1 were only detected (Table 3). The experiments in air above 2023 K are not possible in the current work. Therefore, the sample TS-1 was also heated up to 2273 K in a He atmosphere using DTA. In this case, the solidified microstructure of the sample is characterized by the appearance of TiO₂-rich spheres (L2) embedded in the SiO₂-rich matrix (L1) as illustrated in Fig. 2b, which indicates that the monotectic temperature was reached. Considering these data and literature data, this indicates a decrease in temperature of equilibria in the He atmosphere as compared to air. A similar behavior was observed for the MnO-containing system.^[52] When compared with the literature data, a decrease in the temperature of a monotectic reaction to 1962 K was found (Fig. 1b; Table 2). DeVries et al.^[18] discussed the effect of the atmosphere on the results of phase equilibria in the TiO₂–SiO₂ system: Umezu and Kakiuchi^[12] got substantially lower temperatures of eutectic and monotectic reactions in a strongly reducing atmosphere than DeVries et al. in air. However, the temperature of the monotectic reaction obtained by Kirillova et al.^[23] in a protective gas atmosphere (He) was not substantially different from the results^[18,19] obtained in air. Possible reasons for the fact that the equilibria temperatures in this work were lower than those reported in the literature could be both the effect of the oxygen partial pressure and the accuracy of the temperature measurement. Since faster diffusion occurs in the liquid state than in solid, it can be assumed that the compositions L1 and L2 correspond to the temperature of the monotectic equilibrium. However, the samples were heated to higher temperatures, and therefore the compositions of the two liquids could correspond to the temperatures higher than the monotectic temperature. Thus, there is uncertainty in indicated liquid compositions, since the temperature corresponding to the measured compositions L1 and L2 is not exactly known. On the other hand, the compositions L1 and L2 observed for the samples melted in a He atmosphere may differ from those obtained under air conditions. Since the experimental study of the sample in air at a higher temperature (above 2023 K) was not possible in the current work, the temperature of the monotectic reaction of 2053 K available from the literature^[18,23] is accepted. The compositions of the coexisting liquids L1 and L2 measured by EDX are given in Table 3.

Table 3 Sample compositions in the TiO₂–SiO₂ and Al₂O₃–TiO₂–SiO₂ systems along with SEM/EDX and XRD results

5.2 Liquid Immiscibility in the Al₂O₃–TiO₂–SiO₂ System

The microstructures of the samples ATS-3, -7, and -8 heat treated at 2013 K in air are shown in Fig. 2. One should keep in mind that the bulk sample compositions differ slightly from the nominal ones, therefore, only the sample compositions measured using EDX are considered (see Table 3). As discussed above, the temperature of the monotectic reaction in the TiO₂–SiO₂ boundary is about 2053 K. However, a tendency to the separation of the melt into two liquids was observed at 2013 K for the samples ATS-7 and -7a (Fig. 2e): the globular particles enriched in TiO₂ for the liquid rich in TiO₂ (L2) and the liquid rich in SiO₂ (L1) with TiO₂-rich inclusions. The samples ATS-7 and -7a contain 2.1-2.2 mol% Al₂O₃. In contrast, typical dendritic microstructures without separation were observed for the samples ATS-3 and -8 (Fig. 2d, f), which contain a slightly higher amount of Al₂O₃, 3.8 and 4.9 mol% Al₂O₃, respectively. This suggests that the miscibility gap extends into the ternary system by no more than 3.8 mol% Al₂O₃. It can be assumed that a clearer separation of two liquids would be observed at high temperatures (above 2053), but this cannot be done in the present work. The compositions of the coexisting liquids L1 and L2 measured by EDX are given in Table 3. The results obtained are in a good agreement with those proposed by Kirschen et al.,^[22] Fig. 3.

Fig. 3

Experimental miscibility gap with data by Kirschen et al.^[22] Solid triangles and spheres point to the compositions of the quenched coexisting liquids, open symbols denote the quench of a homogeneous liquid

5.3 Thermodynamic Optimization and Calculations

The Thermo-Calc software^[5] was applied to optimize thermodynamic parameters using the PARROT module within the CALPHAD approach,^[53] and the further calculations of the phase diagram were carried out in the POLY-3 module. During optimization, individual weights were assigned to every type of experimental data considering uncertainties of each experimental method. Thermodynamic descriptions of the binary subsystems Al₂O₃–TiO₂ and Al₂O₃–SiO₂ were accepted from the works of Ilatovskaia et al.^[7,8] and Dumitrescu and Sundman,^[11] respectively. Thermodynamic data for the solid phases in the TiO₂–SiO₂ system originated from Hampl and Schmid–Fetzer^[27] and Hillert et al.^[51] were accepted, and the liquid phase of the system was only re-assessed in this work. The thermodynamic parameters for the Al₂O₃–TiO₂–SiO₂ system were assessed in this work based on the phase equilibria data obtained by XRD, SEM/EDX, and DTA in the previous work^[4] and available in the literature.^{[17,22,54,55]}

5.3.1 The Binary TiO₂–SiO₂ System

The calculated phase diagram of the TiO₂–SiO₂ system is shown in Fig. 4a. Due to the large uncertainties in the reported liquid immiscibility data, different weights were assigned to the corresponding data points during optimization. Since a critical assessment of the available data was provided and the modeling was amended by their own experimental measurements at high temperatures, larger weight was given to the data of Kirillova et al.^[23] The critical point of the miscibility gap calculated by Kirillova et al.^[23] is at 2416 K and 58.9 mol% TiO₂. In this work, it is calculated to be at 2325 K and 46.25 mol% TiO₂. The eutectic point calculated in this work is at 1833 K and 4.0 mol% TiO₂. These results are compared with the experimental data in Table 2, showing reasonable agreement.

Fig. 4

Calculated (a) phase diagram of the TiO₂–SiO₂ system at p(O₂) = 0.21 bar (black) and p(O₂) = 1·10^–2.5 bar (red), and (b) activity of SiO₂ (in relation to the liquid state) in the TiO₂–SiO₂ system at 1800 and 1900 K and p(O₂) = 0.21 bar. Red marks are for He, see text for details

It should be noted that the data of Kirschen et al.^[22] are shown in Fig. 4a for comparison, but they were not accounted quantitatively in this work. Although Kirschen et al. performed very good levitation-quenching experiments for the TiO₂–SiO₂ binary system, the experimental temperatures were probably chosen too high (one should keep in mind that the uncertainty of the temperature measurement by optical pyrometer used in^[22] is about ± 50 K) as evidenced by the microstructure provided in their work. When the molten sample is quenched from above the critical temperature of miscibility gap, the homogeneous melt could decompose into two separated liquid phases, resulting in an interconnected structure but not well-dispersed droplets. That, in turn, makes it more difficult to interpret the results obtained. Such a behavior was observed by Kirillova et al.^[23] for the sample containing 50 mol% TiO₂ quenched from 2458 to 2533 K.

As discussed above, the experiments in an He atmosphere revealed a decrease in temperatures. Thus, the calculations performed at p(O₂) = 1·10^–2.5 bar are compared with the obtained experimental results in Fig. 4a. The selection of oxygen partial pressure for calculations is based on the results of Dilner et al.,^[52] where consistency between calculations and DTA measurements performed in the same device was found. According to the calculations, a decrease in the temperature of a monotectic reaction to 2025 K at p(O₂) = 1·10^–2.5 bar was found. The eutectic temperature calculated at p(O₂) = 1·10^–2.5 bar is also 23 K lower than that calculated in air. A similar temperature shift (20 K) for heating in air and in He was observed experimentally (see Fig. 1a). The agreement between calculations and the DTA results in this case is good.

Stolyarova and Lopatin^[56] measured the activity of SiO₂ in the BaO–TiO₂–SiO₂ system at 1900 K using high-temperature differential mass spectrometry. The activity of SiO₂ in the TiO₂–SiO₂ system at 1900 K for TiO₂–SiO₂ 1:1 is only available. The calculated activity of SiO₂ (in relation to the liquid state) in the TiO₂–SiO₂ system at 1800 and 1900 K at p(O₂) = 0.21 bar is compared with the experimental data in Fig. 4b. The experimental activity at 1900 K is well reproduced in this work.

5.3.2 The Ternary Al₂O₃–TiO₂–SiO₂ System

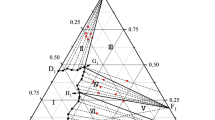
Using the assessed thermodynamic parameters from the binary systems, an interpolation was first performed. However, the interaction parameters were introduced into the mullite, pseudobrookite, and liquid descriptions to fit experimental data.^{[4,17,22,54,55]} The derived database is presented in Table 4. Using the derived Al₂O₃–TiO₂–SiO₂ thermodynamic description, the calculated isothermal sections of the Al₂O₃–TiO₂–SiO₂ system at 1486, 1722, 1747, and 1792 K are shown in Fig. 5 along with the experimental results^[4] indicating a good consistency despite the below-mentioned shortcomings.

Table 4 Thermodynamic description for the Al₂O₃–TiO₂–SiO₂ system.

Fig. 5

Isothermal section of the Al₂O₃–TiO₂–SiO₂ system determined experimentally^[4](left) and calculated (right) at p(O₂) = 0.21 bar and a 1722 K, b 1747 K, and c 1792 K

Data on the solid-state transformation and invariant equilibria on the liquidus of the Al₂O₃–TiO₂–SiO₂ system measured by DTA and SEM/EDX^[4] were accounted. Assuming that there is no solubility of other components in corundum Al₂O₃, the phase was modeled as stoichiometric. Limited solubilities in rutile TiO₂ and cristobalite SiO₂ were observed in the experimental work,^[4] however they were not modeled in this work due to the lack of reliable data. The evident solubility in C-SiO₂ may be explained by the experimental difficulty of reaching equilibrium in the SiO₂-rich region of the ternary system caused by the high viscosity. Parameters describing ternary extension of mullite and pseudobrookite were optimized based on the composition measurements^[4,55] However, an attempt to get a wider ternary extension of the homogeneity range of mullite leads to the solid-state reaction C-SiO₂ + Al₂TiO₅ ↔ Al₆Si₂O₁₃ + TiO₂ becoming inconsistent with the experimental results.^[4] It should also be noted that even if the ternary extensions of mullite and pseudobrookite are not considered in the calculations, the solid-state reaction does not occur, and the low-temperature assemblages are stable up to the solidus temperatures that leads to invariant reactions on liquidus inconsistent with the experimental data. Therefore, the Gibbs energy of the pseudobrookite phase was adjusted to be more stable than mullite to keep the solid-state reaction. This was the reason for the widespread extension of pseudobrookite into the ternary system and the negligible or even absent extension of mullite when pseudobrookite Al₂TiO₅ is thermally stable (above 1552 K^[7]). It should be noted that such discrepancy with the experimental data could be explained by the fact that the used thermodynamic descriptions of the binary Al₂O₃–SiO₂ and Al₂O₃–TiO₂ systems are not mutually consistent. Since some thermodynamic parameters describing the Al₂O₃–SiO₂ and Al₂O₃–TiO₂ systems were accepted unchanged, the conditions for optimization of newly obtained parameters were limited. In this case, a possible way to improve the reproduction of experimental data is to re-assess the parameters for the Al₂O₃–SiO₂ and/or Al₂O₃–TiO₂ systems. However, changing of these binary systems will most likely lead to inconsistencies in previous descriptions in which these systems have already been used. Therefore, the current thermodynamic description is used, however further re-optimization is considered to be necessary.

The complex description of the liquid phase was necessary to fit the parameters of melting relations determined recently.^[4] The results on the liquid immiscibility obtained in this work were also considered. Given the experimental data on liquidus, the ternary mixing parameters were optimized for the liquid phase (see Table 4). The calculated liquidus surface is presented in Fig. 6, whereas the calculated temperatures and compositions of invariant reactions are presented in Table 5 along with the experimental data. The agreement with the experimental data^[4] is relatively good and the calculations indicate the same character of the invariant reactions. The calculated critical point of the miscibility gap is at the composition 5.2Al₂O₃–62.1TiO₂–32.7SiO₂ (in mol%), which reproduces well the experimentally observed value of 3.8 mol% Al₂O₃ discussed above.

Fig. 6

Calculated liquidus projection of the Al₂O₃–TiO₂–SiO₂ system at p(O₂) = 0.21 bar. The enlarged area schematically shows the position of the monovariant lines, since they are in fact very close to each other

Table 5 Invariant reactions in the Al₂O₃–TiO₂–SiO₂ system

6 Conclusion

Phase equilibria in the TiO₂–SiO₂ system were studied using DTA and SEM/EDX, and the miscibility gap in liquid was observed. Moreover, the miscibility of the liquid in the Al₂O₃–TiO₂–SiO₂ system was studied at 2013 K in air, which demonstrated shrinkage of the miscibility gap at 3.8 mol% Al₂O₃.

The CALPHAD approach was applied to derive the thermodynamic descriptions of the TiO₂–SiO₂ and Al₂O₃–TiO₂–SiO₂ systems which are suitable for calculation of the phase diagrams in air conditions. However, including Ti⁺³ in the description of solid phases requires further experimental studies at low oxygen partial pressures, whereas Ti⁺³ was only considered in the liquid phase. The mullite and pseudobrookite phases were modeled within the compound energy formalism. For the liquid phase, the two-sublattice partially ionic model was applied. The present description reproduces the recent experimental data for the solid-state reaction C-SiO₂ + Al₂TiO₅ ↔ Al₆Si₂O₁₃ + TiO₂ and liquid immiscibility, although reproducing of the solid-state reaction required the introduction of a rather extended ternary solubility in the Al₂TiO₅ phase which was not observed experimentally. The calculated isothermal sections and liquidus projection are reasonably consistent with the experimental data.