Interdiffusion in L1₂-Ni₃Al Alloyed with Re

Abstract

Ternary interdiffusion in L1₂-Ni₃Al with ternary alloying addition of Re was investigated at 1473 K using solid-to-solid diffusion couples. Interdiffusion flux of Ni, Al, and Re were directly calculated from experimental concentration profiles and integrated for the determination of average ternary interdiffusion coefficients. The magnitude of main interdiffusion coefficients $\bar{\tilde{D}}_{\text{NiNi}}^{\text{Al}}$ and $\bar{\tilde{D}}_{\text{AlAl}}^{\text{Ni}}$ was determined to be much larger than that of the main interdiffusion coefficient $\bar{\tilde{D}}_{\text{ReRe}}^{\text{Al (or Ni)}}.$ A moderate tendency for Re to substitute for Al sites was reflected by its influence on interdiffusion of Al, quantified by large and positive $\bar{\tilde{D}}_{\text{AlRe}}^{\text{Ni}}$ coefficients. Similar trends were observed from ternary interdiffusion coefficients determined by Boltzmann-Matano analysis. Profiles of concentrations and interdiffusion fluxes were also examined to estimate binary interdiffusion coefficients in Ni₃Al, and tracer diffusion coefficients of Re (5.4 × 10⁻¹⁶ ± 2.3 × 10⁻¹⁶ m²/s) in Ni₃Al.

Introduction

Ni₃Al precipitation and the associated coherency through tetragonal distortion with the γ matrix is the key point behind the extensive use of Ni-base superalloys for high-temperature applications.[1] Multicomponent diffusion plays an important role in processing and degradation of these alloys that must possess exceptional high-temperature strength, microstructural stability, and oxidation resistance. Multicomponent diffusion mobility database[2] for γ phase, together with the alloying studies[3-10] to modify coherent precipitate (γ′) have yielded excellent design criteria to develop advanced superalloys. Recent development of refractory-based superalloys with L1₂ precipitates, and refractory-modified aluminide coatings[11-16] warrant a better understanding of interdiffusion in Ni₃Al with alloying additions.

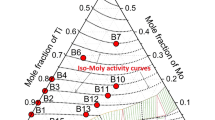
The ordered crystal structure of Ni₃Al consists of face centers (α sites) occupied by Ni atoms and corners (β sites) of the unit cell occupied by Al atoms. Highly electronegative substitutional elements (e.g., Pt, Cu, and Co) occupy the α sites, whereas highly electropositive elements (e.g., Ti, Ta, and Nb) occupy the β sites in Ni₃Al.[1] The relative site preference for a ternary alloying element can be best illustrated from the direction of the solubility lobes for the γ′ phase on the ternary isotherm of Ni-Al-X (X = alloying addition) system at 1273 K as shown by Fig. 1.[17] Site preference of ternary alloying additions to Ni₃Al has attracted significant interest as this true solid solution accepts a considerable amount of third elements into solution.[18-22]

Fig. 1

Solubility ranges of selected ternary alloying additions in Ni₃Al at 1273 K[11]

The alloying phenomenon ultimately plays an important role in enhancing the thermomechanical properties and high-temperature oxidation resistance of this intermetallic phase.[19-26] The substitutional ternary alloying additions to Ni₃Al was first classified by Guard and Westbrook[18] as Ni occupiers or Al occupiers or those with no preference. Several studies[27-29] have examined the change in site preference of alloying elements as a function of temperature and chemical composition of Ni₃Al.

The diffusion mechanism in ordered alloys is more complex than disordered solid solutions.[30] Diffusion can occur preferentially through α or β sites that Ni or Al atoms mainly occupy, respectively, and the diffusion coefficient largely depends on the alloy composition related to the degree of order.[31-33] While tracer diffusion studies in γ′ Ni₃Al are difficult since ²⁶Al is not readily available, self-diffusion of Ni and chemical/impurity diffusion in Ni₃Al binary and Ni₃Al-X ternary alloys (X = Ir, Ta, Pt, Nb, Mo, Cr, Fe, Ti) have been studied.[3-6] The temperature dependency of the diffusion for a ternary alloying addition is evident from Arrhenius rate law.[34-36] The β site occupiers have been observed to diffuse more slowly than the α-site occupiers.[30,37] In L1₂-ordered structure, each Ni atom is surrounded by 4 Al and 8 Ni atoms as nearest neighbors, where as an Al atom is surrounded by 12 Ni atoms as nearest neighbors. Consequently, the activation enthalpy of alloying elements can change because of the antisite-defect formation.[37]

To further understand the diffusion process in the L1₂ structure, to help improve the microstructural stability of Ni-base superalloys, and to help develop refractory-modified aluminide oxidation-resistant coatings, the authors examined the ternary diffusional interaction of Re additions to the L1₂ Ni₃Al phase. Solid-to-solid diffusion couples were assembled with various Ni₃Al-Re alloys and annealed at 1473 K for 5 h. Average ternary interdiffusion coefficients from an integration of interdiffusion fluxes and ternary interdiffusion coefficients via Boltzmann-Matano analysis were determined from concentration profiles obtained by electron probe microanalysis (EPMA). In addition, binary interdiffusion coefficients in Ni₃Al and tracer diffusion coefficients of Re in Ni₃Al were estimated.

Determination of Ternary Interdiffusion Coefficients

Based on Onsager’s formalism[38,39] and Fick’s law,[40] the interdiffusion flux $\tilde{J}_{i}$ of component i in a ternary system can be expressed in terms of two independent concentration gradients, ∂C _j /∂x by:

$$ \tilde{J}_{i} = - \tilde{D}_{i1}^{3} \frac{{\partial C_{1} }}{\partial x} - \tilde{D}_{i2}^{3} \frac{{\partial C_{2} }}{\partial x}\quad (i = 1,2) $$

(1)

where $\tilde{D}_{ij}^{3}$ refers to the ternary interdiffusion coefficients. An experimental determination of the four concentration-dependent interdiffusion coefficients can be carried out by the use of Boltzmann-Matano analysis with two independent diffusion couples that develop a common composition in the diffusion zone where the interdiffusion coefficients can be evaluated.[41,42]

Instead, the interdiffusion flux at any section x can be calculated directly from the concentration profile from the relation[43,44]:

$$ \tilde{J}_{i} = \frac{1}{2t}\int\limits_{{C_{i}^{ - } \,{\text{or}}\,C_{i}^{ + } }}^{{C_{i} (x)}} {(x - x_{\text{o}} )} dC_{i} \quad (i = 1,2,\, \ldots ,n) $$

(2)

where t is the time, $C_{i}^{ - }$ and $C_{i}^{ + }$ are the terminal concentrations, and x _o refers to the location of the Matano plane. Use of Eq 2 allows quantitative assessment of diffusional behavior for any components including zero-flux-planes (ZFPs) and flux-reversals that can develop during multicomponent interdiffusion.[43-46] In addition, the calculated interdiffusion fluxes can be related to interdiffusion parameters that can be employed to model and characterize concentration profiles.[47-50]

The interdiffusion flux $\tilde{J}_{i}$ determined from Eq 2 can be integrated over a selected region, x ₁ to x ₂, to yield an expression based on Eq 1[50]:

$$ \begin{aligned} \int\limits_{{x_{1} }}^{{x_{2} }} {\tilde{J}_{i} dx} & = - \int\limits_{{C_{1} (x_{1} )}}^{{C_{1} (x_{2} )}} {\tilde{D}_{i1}^{3} dC_{1} } - \int\limits_{{C_{2} (x_{1} )}}^{{C_{2} (x_{2} )}} {\tilde{D}_{i2}^{3} dC_{2} } \quad (i = 1,2) \\ & = \bar{\tilde{D}}_{i1}^{3} \left[ {C_{1} (x_{1} ) - C_{1} (x_{2} )} \right] + \bar{\tilde{D}}_{i2}^{3} \left[ {C_{2} (x_{1} ) - C_{2} (x_{2} )} \right]\quad (i = 1,2) \\ \end{aligned} $$

(3)

where $\bar{\tilde{D}}_{ij}^{3}$ corresponds to the average values of main and cross interdiffusion coefficients.

With $\bar{\tilde{D}}_{ij}^{3}$ taken as constants, Eq 1 is re-written as:

$$ \tilde{J}_{i} = - \bar{\tilde{D}}_{i1}^{3} \frac{{\partial C_{1} }}{\partial x} - \bar{\tilde{D}}_{i2}^{3} \frac{{\partial C_{2} }}{\partial x}\quad (i = 1,2 ) $$

(4)

If both sides of Eq 4 are multiplied by (x − x _o)^m and integrated over the diffusion zone between x ₁ and x ₂, one obtains in general[50]:

$$ \int\limits_{{x_{1} }}^{{x_{2} }} {\tilde{J}_{i} (x - x_{\text{o}} )^{m} dx} = - \bar{\tilde{D}}_{i1}^{3} \int\limits_{{C_{1} (x_{1} )}}^{{C_{1} (x_{2} )}} {(x - x_{\text{o}} )^{m} dC_{1} } - \bar{\tilde{D}}_{i2}^{3} \int\limits_{{C_{2} (x_{1} )}}^{{C_{2} (x_{2} )}} {(x - x_{\text{o}} )^{m} dC_{2} } \quad (i = 1,2) $$

(5)

If the exponent m is chosen to be zero, Eq 5 becomes identical to Eq 3. For m = 1, Eq 5 becomes[50]:

$$ \begin{aligned} \int\limits_{{x_{1} }}^{{x_{2} }} {\tilde{J}_{i} (x - x_{\rm o} )dx} & = - \bar{\tilde{D}}_{i1}^{3} \int\limits_{{C_{1} (x_{1} )}}^{{C_{1} (x_{2} )}} {(x - x_{\text{o}} )dC_{1} } - \bar{\tilde{D}}_{i2}^{3} \int\limits_{{C_{2} (x_{1} )}}^{{C_{2} (x_{2} )}} {(x - x_{\text{o}} )dC_{2} } \\ & = 2t\left\{ {\bar{\tilde{D}}_{i1}^{3} \left[ {\tilde{J}_{1} (x_{1} ) - \tilde{J}_{1} (x_{2} )} \right] + \bar{\tilde{D}}_{i2}^{3} \left[ {\tilde{J}_{2} (x_{1} ) - \tilde{J}_{2} (x_{2} )} \right]} \right\}\quad (i = 1,2) \\ \end{aligned} $$

(6)

Equations 3 and 6 provide four equations to solve for $\bar{\tilde{D}}_{11}^{3},$ $\bar{\tilde{D}}_{12}^{3} ,$ $\bar{\tilde{D}}_{21}^{3},$ and $\bar{\tilde{D}}_{22}^{3}$ and interdiffusion coefficients and can be easily set up from experimental concentrations and the corresponding interdiffusion fluxes. Thus, from the concentration profiles of a single diffusion couple, $\bar{\tilde{D}}_{ij}^{3} \;\;(i,j = 1, 2)$ coefficients, characteristic of the diffusion path, can be determined over selected composition ranges in the diffusion zone.[50] This analysis method has been directly employed in various studies[51-59] to determine average ternary interdiffusion coefficients. In this paper, this analysis is applied to the experimental concentration profiles for two segments, one on either side of the Matano plane; the two chosen composition ranges are $(C_{i}^{ - } - C_{i}^{\text{o}} )$ and $(C_{i}^{\text{o}} - C_{i}^{ + } )$ where $C_{i}^{\text{o}}$ refers to the concentration at the Matano plane. The average ternary interdiffusion coefficients, $\bar{\tilde{D}}_{ij}^{3},$ determined on either side of the Matano plane, are employed to model experimental concentration profiles using error-function solution for infinite ternary system given by Fujita and Gosting.[60]

The uncertainty in the $\tilde{D}_{ij}^{3}$ values evaluated by the Boltzmann-Matano analysis arise mainly from the errors in the experimental determination of the concentration gradients of two of the components (i = 1, 2) at the common composition of a pair of couples with intersecting diffusion paths. These errors can be appreciable (>100%), if the paths intersect at narrow angles and the concentration gradients of the components at the common compositions are comparable for the couple pair. On the other hand, the errors involved in the calculation of the integrals in Eq 3 and 6 of the present analysis are minimal and the errors in the determination of the $\bar{\tilde{D}}_{ij}^{3}$ values reported in this paper are estimated for $\bar{\tilde{D}}_{ij}^{3}$ to be less than 20% based on assumed uncertainties in concentrations of 3 at.%.[50]

Experimental Details

Ni-Al and Ni-Al-Re alloys were prepared by the vacuum arc melting of 99.97 wt.% Ni, 99.9 wt.% Al, and 99.2 wt.% Re, according to the compositions presented in Table 1. The alloys were cast into a semicylindrical mold with the diameter of 8 mm. The alloy rods were homogenized at 1473 K for 137 h in the vacuum furnace that was evacuated to a pressure lower than 10⁻² Pa. A thorough metallographic characterization with x-ray diffusion was carried out to confirm that all alloys reported in Table 1 were free of any second phase. The homogenized alloys were then sectioned into disks with an approximate height of 1.5 mm. The surfaces of alloy disks were ground metallographically down to 1200 grit and cleaned thoroughly prior to diffusion couple assembly.

Table 1 Nominal composition of alloys employed for diffusion couple studies

Table 2 presents diffusion couples that were assembled and analyzed in this study. To promote initial bonding, coupled alloys were placed in a Si₃N₄ jig and annealed at 1473 K for 0.5 h in a vacuum furnace. The metal disks have larger thermal expansion coefficients than the Si₃N₄ jig, and the discs can adhere to each other because of the compression during the annealing treatment. Each diffusion couple fabricated in this manner was then sealed in an evacuated transparent quartz capsule and annealed at 1473 K for 4.5 h in an atmosphere furnace. All diffusion couples were water quenched after the high-temperature anneal to preserve high-temperature microstructure and concentrations. In this study, the time required for the diffusion bonding treatment (0.5 h) was added to the total annealing time. Thus, concentration profiles from all diffusion couples were analyzed with diffusion anneal time of 5 h.

Table 2 Diffusion couples assembled and analyzed after an anneal at 1473 K for 5 h

Microstructural analysis by optical microscopy confirmed excellent bonding in all diffusion couples without any precipitation of other phases. Concentration profiles of the annealed diffusion couples were analyzed by JEOL-JXA-8900 EPMA. An accelerating voltage of 20 keV, a beam current of 50 nA, and a probe diameter of 1 μm were used for data acquisition of Ni Kα x-radiation peak using lithium fluoride (LiF) crystal, Al Kα x-radiation peak using thallium acid phthalate (TAP) crystal, and Re Lα x-radiation using LiFH crystal. Elemental standards of Ni, Al, and Re along with ZAF[61] correction were used for quantification of concentrations via point-to-point count technique. JEOL-JXA-8900 EPMA has a secondary electron resolution of 3 nm, and its uncertainty in concentration measurement is within ±0.1 at.%.

Results and Analysis

Profiles of Concentrations and Interdiffusion Fluxes

Figure 2 presents typical concentration profiles obtained by EPMA from the diffusion couple, Ni-25Al versus Ni-23.5Al-0.5Re annealed at 1473 K for 5 h. The x-axis is the distance from the Matano plane, and the open circles represent EPMA measurement. Scatter in the concentration profiles for all diffusion couples were minimum and within the experimental uncertainty associated with EPMA. The interdiffusion fluxes of individual components were then determined using Eq 2 from experimental concentration profiles that were smoothened with a series of weighted splines. Although no zero-flux plane was observed, a significant diffusional interaction between Al and Re was observed when Ni₃Al was diffusion annealed against Ni₃Al alloyed with Re. As shown in Fig. 2, interdiffusion of Al was reduced by the interdiffusion of Re against the gradient of Al. However, the diffusional influence of Re on Ni is difficult to ascertain from the profiles presented in Fig. 2. Determination of ternary interdiffusion coefficients can quantify the extent of these diffusional interactions and provide competent approaches to compositional design and modification of alloys and protective coatings.

Fig. 2

Concentration profiles of (a) Ni, (b) Al, and (c) Re obtained from diffusion couple Ni-25Al vs. Ni-23.5Al-0.5Re annealed at 1473 K for 5 h. Open circles and solid lines represent EPMA measurement and calculated concentration profiles, respectively

Average Ternary Interdiffusion Coefficients

From profiles of concentration and interdiffusion fluxes in Ni-Al versus Ni-Al-Re diffusion couples, average ternary interdiffusion coefficients, $\bar{\tilde{D}}_{ij}^{\text{Ni}} \;\,(i,j = {\text{Al}},{\text{Re}})$ and $\bar{\tilde{D}}_{ij}^{\text{Al}} \;\,(i,j = {\text{Ni}},{\text{Re}})$ were determined on either side of the Matano plane using Eq 3 and 6. They are reported in Table 3. The magnitudes of main diffusion coefficients, $\bar{\tilde{D}}_{\text{AlAl}}^{\text{Ni}}$ and $\bar{\tilde{D}}_{\text{NiNi}}^{\text{Al}}$ are similar to the interdiffusion coefficients of Al and Ni reported in literature for binary Ni₃Al at 1473 K.[3-10] Estimation of binary interdiffusion coefficients from the ternary diffusion couples and the comparison to the interdiffusion coefficients of Al and Ni reported in literature for binary Ni₃Al are presented in detail in section 4.4. The main interdiffusion coefficient, $\bar{\tilde{D}}_{\text{ReRe}}^{{}}$ is approximately 100 times smaller in magnitude than $\bar{\tilde{D}}_{\text{AlAl}}^{\text{Ni}}$ and $\bar{\tilde{D}}_{\text{NiNi}}^{\text{Al}} .$ Table 3 reports that $\bar{\tilde{D}}_{\text{AlRe}}^{\text{Ni}}$ coefficients are positive and comparable to the magnitude of $\bar{\tilde{D}}_{\text{AlAl}}^{\text{Ni}},$ while $\bar{\tilde{D}}_{\text{ReAl}}^{\text{Ni}}$ coefficients are negligibly small (<0.1 × 10⁻¹⁶ m²/s). Thus, the interdiffusion of Al can be strongly influenced by the interdiffusion of Re. The $\bar{\tilde{D}}_{\text{NiRe}}^{\text{Al}}$ coefficients are also positive, but 2 to 13 times smaller in magnitude than the $\bar{\tilde{D}}_{\text{NiNi}}^{\text{Al}} .$

Table 3 Average ternary interdiffusion coefficients determined from Ni-Al vs. Ni-Al-Re diffusion couples annealed at 1473 K for 5 h

The average ternary interdiffusion coefficients reported in Table 3 were used to generate concentration profiles using the error-function solution provided by Fujita and Gosting.[60] Excellent agreement between EPMA measurement and calculated concentration profiles were found for all couples. Typical examples are presented in Fig. 2 where open circles are the EPMA data, and solid lines are the calculated concentration profiles.

Ternary Interdiffusion Coefficients Determined by Boltzmann-Matano Analysis

From the diffusion couples Ni-Al versus Ni-Al-Re listed in Table 2, several intersecting compositions were found within the diffusion paths. Intersecting diffusion paths in Fig. 3 represent typical diffusion paths with one of the paths intersecting with its terminal end. In other words, Re concentration of that end remained constant with no concentration gradient. These intersection composition points may be used for the determination of interdiffusion coefficients using Boltzmann-Matano analysis. Uncertainty in ternary interdiffusion coefficients determined by Boltzmann-Matano analysis is higher than aforementioned in section 2 because of the low angle of intersecting paths combined with uncertainty in the measurement of concentration gradients. Nevertheless, the values of ternary interdiffusion coefficients determined in this study are reported in Table 4 and have the same order of magnitude when compared to average ternary interdiffusion coefficients presented in Table 3. The slight deviation in values and change in signs of the $\bar{\tilde{D}}_{\text{NiRe}}^{\text{Al}}$ coefficients are attributed to the uncertainty in concentration gradient of Re.

Fig. 3

Typical intersecting diffusion paths of Ni-Al vs. Ni-Al-Re diffusion couples annealed at 1473 K for 5 h. Compositions at these intersections were used for the determination of ternary interdiffusion coefficients based on Boltzmann-Matano analysis

Table 4 Ternary interdiffusion coefficients determined by Boltzmann-Matano analysis from Ni-Al vs. Ni-Al-Re diffusion couples annealed at 1473 K for 5 h

Estimation of Binary Interdiffusion Coefficients in Ni₃Al

The ternary interdiffusion coefficients $\tilde{D}_{\text{AlAl}}^{\text{Ni}}$ and $\tilde{D}_{\text{NiNi}}^{\text{Al}}$ approach the binary $\tilde{D}_{i}$ for Ni₃Al as the concentration of Re decreases to zero. Hence, values of $\tilde{D}_{i} \;\,(i = {\text{Ni or Al}})$ were estimated from ternary diffusion couples where Re concentration was negligibly small in segments of the diffusion zone (e.g., Fick’s law for substitutional binary alloys). Such regions were found in all couples since $\bar{\tilde{D}}_{\text{ReRe}}$ coefficients are much smaller than $\bar{\tilde{D}}_{\text{AlAl}}^{\text{Ni}}$ and $\bar{\tilde{D}}_{\text{NiNi}}^{\text{Al}}.$ The $\tilde{D}_{i}$ coefficients extrapolated from the ternary couples with large enough concentration difference (e.g., ΔC _Al or ΔC _Ni > 2 at.%) in terminal alloys is presented in Fig. 4. These values appear consistent with the available binary interdiffusion data[3-10] for Ni₃Al.

Fig. 4

Interdiffusion coefficients in Ni₃Al at 1473 K compiled from this investigation and literature review

Estimation of Tracer Diffusion Coefficient of Re in Ni₃Al

For a ternary component i diffusing into a binary alloy j-k, the cross interdiffusion coefficient $\tilde{D}_{ij}^{k} \;\,(i \ne j)$ becomes negligible at infinite dilution of component i in a j-k alloy.[62] Then the value of the main coefficient $\tilde{D}_{ii}$ approaches that of the tracer diffusion coefficient $D_{i}^{*}$ for component i:

$$ C_{i} \to 0\quad \tilde{J}_{i} = - \tilde{D}_{ii}^{k} \frac{{\partial C_{i} }}{\partial x} \cong - D_{i(jk)}^{ * } \frac{{\partial C_{i} }}{\partial x} $$

(7)

Thus, the tracer diffusion coefficients of Re in Ni₃Al alloy can be estimated from the main interdiffusion coefficient of Re, $\tilde{D}_{\text{ReRe}}^{\text{Ni (or) Al}},$ using Eq 7, provided the concentration of Re approaches zero within the diffusion zone so that the cross-interdiffusion coefficients, $\tilde{D}_{\text{ReAl}}^{\text{Ni}}$ or $\tilde{D}_{\text{ReNi}}^{\text{Al}},$ become negligible. Such regions were found in all couples since $\bar{\tilde{D}}_{\text{ReRe}}$ coefficients are much smaller than $\bar{\tilde{D}}_{\text{AlAl}}^{\text{Ni}}$ and $\bar{\tilde{D}}_{\text{NiNi}}^{\text{Al}}.$ Values of tracer diffusion coefficients of Re, $D_{\text{Re}}^{ * }$ were extrapolated from the main interdiffusion coefficients, $\tilde{D}_{\text{ReRe}}^{\text{Ni}}$ or $\tilde{D}_{\text{ReRe}}^{\text{Al}}$ as the concentration of Re, becomes zero. The extrapolations for $D_{\text{Re}}^{ * }$ from the ternary interdiffusion coefficients on the basis of Eq 7 are presented in Fig. 5 for Ni-24.4Al to Ni-24.8Al (at.%). The estimated values of $D_{\text{Re}}^{ * }$ are reported in Table 5.

Fig. 5

Extrapolation of $\tilde{D}_{\text{ReRe}}$ coefficient for the estimation of tracer diffusion coefficient of Re in Ni₃Al at 1473 K

Table 5 Tracer diffusion coefficients of Re in Ni₃Al extrapolated from ternary interdiffusion coefficients of diffusion couples annealed at 1473 K

Concluding Remarks

Ternary interdiffusion interactions of Re addition on the L1₂ Ni₃Al phase were examined using solid-to-solid diffusion couples annealed at 1473 K for 5 h. Average ternary interdiffusion coefficients were determined from an integration of interdiffusion fluxes for individual components. The magnitude of $\bar{\tilde{D}}_{\text{NiNi}}^{\text{Al}}$ and $\bar{\tilde{D}}_{\text{AlAl}}^{\text{Ni}}$ coefficients was determined to be much larger than that of $\bar{\tilde{D}}_{\text{ReRe}}$ coefficients. The $\bar{\tilde{D}}_{\text{AlRe}}^{\text{Ni}}$ coefficient was determined to be positive and large in magnitude; Re substitutes in Al site and influences the interdiffusion of Al significantly. The $\bar{\tilde{D}}_{\text{NiRe}}^{\text{Al}}$ coefficient was also positive but relatively low in magnitude; Re shows a lower tendency to occupy Ni sites. Consistency among ternary interdiffusion coefficients was observed from ternary interdiffusion coefficients determined by Boltzmann-Matano analysis. Profiles of concentrations were also examined to estimate binary interdiffusion coefficients in Ni₃Al. Tracer diffusion coefficient of Re at 1473 K was also estimated as $D_{\text{Re}}^{ * } = 5. 4\times 10^{ - 1 6} \pm 2. 3\times 10^{ - 1 6} \,{\text{m}}^{ 2} /{\text{s}}$ for Ni₃Al phase with Al concentration range of 24.4 to 24.8 at.%.