Abstract
The effect of austempering parameters on impact energy of non-alloyed cast iron with nodular graphite was examined. The analysis involved the austenitizing temperature in the range of 830-950 °C for the time of 60 min and the austempering temperature in the range of 300-400 °C for the time of 8, 16, 32 and 64 min. The value of the impact energy KV was determined. It has been found that the austenitizing temperature and austempering conditions affect the impact energy of ADI. The conducted analytical studies helped to develop a method for the selection of heat treatment parameters to obtain the ausferritic ductile iron with appropriate impact energy KV. The applied machine learning methods included support vector machine, decision trees, artificial neural networks and the method of variational component analysis.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Experimental data concern of us ausferritic ductile iron, used for testing, with the using methods of machine learning. Characteristics of this material indicate that final properties of products are affected not only by the chemical composition but also by the processing mode, including heat treatment parameters. The state of knowledge in this field is rapidly corrected, considering the fact that this material is very popular in the world of science, and heavily popularized in the industry (Ref 1,2,3).
Experimental studies aim to determine how different parameters of the manufacturing process affect the final results in both qualitative and quantitative manners (Ref 4,5,6). Analytical modeling tools, in particular the methods of machine learning, are expected to allow users to create models of approximation of properties on the example of KV. The analysis of experimental data should lead to determination of relationships in the form of mathematical formulas, rules, regulations and finally semi-symbolic models (Ref 7). The range of possible tools to use in the field of statistics and data mining or machine learning is enormous, but the choice of specific methods is dictated by the nature and type of data being processed.
During the hardening of cast iron, the austenitizing treatment, consisting of heating at a temperature higher than Ac1, should enrich the austenite with carbon to the boundary defined by the E’S line and homogenize the metal matrix. During the heating of cast iron with a ferritic microstructure, only carbon atoms derived from graphite separations diffuse into the austenite.
The process of austenitizing the metal matrix and the role of graphite in its carburizing is described in (Ref 8).
The effect of austenitizing depends on the chemical composition, input structure, nodular graphite dispersion, temperature and time of annealing, as well as on the homogeneity of the distribution of elements in eutectic grains and grain size. A single-stage austenitizing is the classical way of austenitizing cast iron before isothermal transformation (Ref 8, 9).
The analysis of the influence of austenite fraction on the impact strength or impact energy of ADI, taking into account the austenitizing temperature, temperature and time of austempering process in the range of upper and lower ausferrite, was investigated in (Ref 8, 10).
The chemical composition of non-alloyed nodular cast iron is limited primarily to the content of C, Si, Mn, S and P. From the standpoint of austenitizing, carbon, silicon and manganese are of particular importance.
In order to extend the processing window and therefore increase the austenite fraction, the following elements were added to ADI: Mn, Mo and Cu (Ref 10) as well as Cu and Ni (Ref 8).
The article presents studies for data from experiments on cast iron ADI, which analyzed the impact of the parameters of hardening with the isothermal transformation on the impact energy. The analysis involved the austenitizing temperature in the range of 830-950 °C for 60 min and the austempering temperature in the range of 300-400 °C for 8, 16, 32 and 64 min. For the approximation of ADI properties in the form of fracture energy, an overview of machine learning algorithms applicable to this problem was made (the dependent variable of a continuous type determines the selection of models that meet the assumptions of regression analysis). The innovation and scientific novelty of the work relative to the prior studies was to develop a method for the estimation of heat treatment parameters to obtain the ausferritic ductile iron with appropriate impact energy KV with the use of machine learning methods. The acquired knowledge about the process in the form of rules can be successfully used in the construction of knowledge bases for intelligent systems in foundry applications.
The Material Experiments and Methodology
Three different melts (W1, W2, W3) of ductile iron were used in the studies. Cast iron was melted in a medium frequency induction furnace of 3.5 tonne capacity. Nodularization was performed with VL53 M magnesium master alloy by a bell method in a slender ladle, while inoculation was carried out with FeSi75 ferrosilicon. The cast iron was poured in green molds to obtain YII ingots according to standard BS-EN 1563: 2012. The chemical composition of the three cast iron melts was determined by spark spectrometry. The percent content of the examined elements is shown in Table 1.
The values of cast iron critical temperatures determined by dilatometry during continuous heating and cooling at a constant speed of 0.019 K/s are presented in Table 2.
The choice of such chemical composition of the beam-type tests pieces resulted from the verification whether non-alloyed ductile iron (W1 melt) and low-alloy cast iron (W2, W3 melts) could meet specific requirements for high-quality ADI. In order to increase processing window and hence the austenite fraction in the matrix, Cu and Ni were added into two melts (W2 and W1). A selection of the chemical composition and its impact on the breaking energy is directly related to the quality of the casting material in the manufacturing process. Adding a small amount of Ni and Cu, the mechanical properties of ADI were improved.
To obtain a fully ferritic matrix, lower part of the YII ingot was subjected to two-step ferritizing annealing. Then, the ingot was cut as shown in Fig. 1 to prepare V-notched samples of 10 × 10 × 55 mm size. The method of sampling and cutting the notch was deliberately selected to eliminate the metallurgical variations in ingots. The samples were made from a standard ingot, but their sampling is unconventional. Impact test pieces were cut vertically in relation to the test part of the ingot. The idea was for the notch to be cut at the same height. In this way, the microsegregation resulting from different heights of sampling was eliminated.
Samples tested for the impact strength were austempered according to the schemes given in Fig. 2 and 3. Choice of two different thermal variants (austenitizing from top and bottom) is explained in (Ref 8), as well as clarification of heating to nominal temperature and cooling to intermediate temperatures. For each case of the heat treatment, toughness measurements were performed on three samples taken from a single YII ingot. Austenitizing was carried out in a chamber sillite furnace and ausferritizing in an SO140 furnace with salt bath.
The impact test was carried out on Charpy testing machine, type PSW 300, with a maximum impact energy of 300 J. The approach toughness versus temperature violations were reported in (Ref 9). In paper (Ref 9), there are two cast iron melts, but the heat treatment parameters are different. The temperature of the isothermal transformation is 300 and 400 degrees, and in the above-mentioned paper the isothermal quenching took place at 375 °C. The times of isothermal quenching in salt bath are also different: in the case of the reviewed paper it was: 8, 16, 32 and 64 min, while at paper (Ref 9)—15, 30, 45, 60 and 90 min. The experimental data were related to the ADI production in two variants of the heat treatment and three melts with different chemical compositions. For each variant of heat treatment, three attempts to break in accordance with BS-EN ISO 148-1: 2010 were made.
Experiments Results
The mechanical properties are presented in Table 3. Three different melts (W1, W2, W3) were made that differed in their chemical composition. Specimens for mechanical properties tests were taken from test ingots in order to determine the grade of the cast iron. They were also subjected to the metallographic research. The mechanical properties were determined using the INSTRON 8501 testing machine; hardness measurements were made on metallographic specimens using a Struers Duramin 500 hardness tester machine. Metallographic evaluation was performed on the etched specimens; the microstructure was observed using Nikon MA100 reversed metallographic microscope.
According to PN-EN 1563: 2012, there are seven cast iron grades. Three of them have a ferritic microstructure (EN-GJS 350-22, EN-GJS 400-18, EN-GJS 450-15), two of them have a ferritic–pearlitic microstructure (EN-GJS 500-7, EN-GJS 600-3), and one them pearlitic (EN-GJS 700-2). In the case of smelting number 1 (W1), the test specimens were subjected to a two-stage ferritizing annealing. Heat treatment was deliberately made to verify impact strength values depending on the type of cast iron microstructure after austempering. On the basis of present knowledge, it can be assumed that the ferritic matrix has a lower microsegregation than the ferritic–pearlitic or pearlitic matrix. Hence, it can be assumed that the microstructural differences of the matrix should influence the carburizing process. This approach to the scientific problem makes it possible to determine the suitability of a material with a ferritic matrix in the aspect of austempering when manufacturing ADI castings.
Microstructure Studies
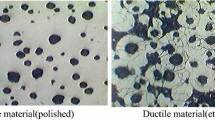
Inspections of the microstructure of cast iron test pieces following heat treatment using variant I demonstrate that austenitization for tγ = 830 °C occurred within a subcritical range, while for tγ = 860 °C within an intercritical range of Eutectoid Transformation. Therefore, as a result of isothermal transformation, both at a temperature 300 °C and 400 °C, a ferritic (tγ = 830 °C) or ferritic–ausferritic (tγ = 860 °C) matrix was obtained. Sample microstructure of cast iron subjected to heat treatment using variant I is presented in Fig. 4.
In variant II of heat treatment, austenite was transformed into lower austenite at a temperature tpi = 300 °C. On the other hand, at a temperature tpi = 400 °C austenite changed into upper austenite. This statement is based on hardness test results and microscopic tests. Sample microstructures are presented in Fig. 5 and 6.
Cast iron quenching using variant I and ausferritization at a temperature tpi = 400 °C allowed parameters corresponding to ADI to be obtained only for the highest temperature tγ = 900 °C. Cast iron austenitized at a temperature tγ = 860 °C due to the obtained values Rm, Rp0.2 and A5 met requirements for grade EN-GJS-800-8 (except for τpi = 8 min). The microstructure of this cast iron not only consisted of ausferrite, as required by the definition of ADI, but it also included free ferrite. Ductile iron quenched isothermally within an intercritical range having the structure of free ferrite and ausferrite is marked in literature as FADI (Ref 11). The resulting microstructure corresponding to FADI cast iron is presented in Fig. 7.
Two-phase austenitization using variant II and ausferritization at tpi = 300 °C resulted in ductile iron having mechanical properties (Rm, Rp0.2, A5) corresponding to standardized grades of ADI. Based on the mechanical properties, cast iron treated using variant II and ausferritized at tpi = 400 °C was classified as belonging to EN-GJS-800-8 grade. Regardless of the second-phase austenitization temperature, its effect on Rm and A5 was negligible. On the other hand, proof stress changed depending on the cooling temperature tγ′ = 830 °C, 860 °C and 900 °C: the lower the temperature interval between austenitization and ausferritization, the higher proof stress. As isothermal holding time increases, so does the values Rp0.2.
Data for Analysis
Analyzing the test data, it can be concluded that the problem of impact energy approximation uses a regression model based on discrete signals.
The data included a spreadsheet of 146 lines and 15 columns, which compiled the results of measurements and average values calculated on three samples from each austempering treatment. The data processing and initial analysis enabled identification of the variables to be considered in further studies. The mean values and standard deviations were skipped as the data re-processed, leaving only the original raw data. By splitting the system of columnar preliminary data, 432 records were obtained and formed a set of unique samples from different melts and treatment variants. It was assumed that the following variables would be taken into account:
Qualitative Variables
-
Variant Variant number collectively defining the heat treatment parameters, the domain of a variable (possible values): {V1; V2}. The qualitative variable.
-
Melt Melt number determining the chemical composition, the domain of a variable (possible values): {C1; C2; C3}. The qualitative variable.
-
Sample Sample number which, if samples are properly prepared, should have no effect; the domain of a variable: {S1; S2; S3}. The qualitative variable.
Quantitative Variables
-
TA(tγ) Nominal austenitizing temperature. The domain of a variable: < 830, 950 > [°C].
-
TA2 (tγ′) Austenitizing temperature after cooling to intermediate temperatures. The domain of a variable: {830; 860; 900; null} (°C) (lack of values for processes without cooling to intermediate temperatures—variant V1); the variable can also be treated as a qualitative variable depending on the adopted method of calculation,
-
TAF (tpi) Ausferritizing temperature; the domain of a variable: {300; 400} (°C)—this variable takes only two possible values; the variable can also be treated as a qualitative variable depending on the adopted method of calculation.
-
tAF(τpi) Ausferritizing time. The domain of a variable {8; 16; 32; 64} (min).
-
KV The value of impact energy KV, J; the domain of a variable: < 5.4, 19.9 > (J).
It is known (or assumed) that the KV variable is a function of melt variant, heat treatment variant, ausferritizing temperature and ausferritizing time, and details of its form remain unknown. The aim of the study is therefore to determine the form of this function.
where yn—corresponds to the fracture energy KV, J; X1n—three different melts designated as W1, W2, W3, respectively, X2n—corresponds to the heat treatment variants WI and WII (schemes of variants given in Fig. 3), X3n—corresponds to the ausferritizing temperature TAF1 = 300 °C or TAF2 = 400 °C; X4n—corresponds to the ausferritizing time TAF = 8; 16; 32; 64; min.
This means that, in a model of approximation, the KV variable becomes the dependent variable. The impact energy is thus a property whose value should be determined based on the course of production parameters (Ref 12).
Modeling the Effect of ADI Manufacturing Conditions on Impact Energy by the Methods of Machine Learning
Testing the Correlation
In the first step, we want to know the strength and direction of a linear relationship between the dependent variable (KV) and other quantitative (explanatory) variables. For this purpose, we use a Pearson linear correlation coefficient (Ref 13).
The correlation coefficients in Table 4 clearly show a strong dependence of impact energy on the ausferritizing temperature. The austenitizing temperature and the austenitizing temperature after cooling to intermediate temperatures have much weaker influence on impact energy. The time of ausferritizing has no effect on KV in the analyzed time.
In searches for a relationship, Fisher test (F test) is also applicable. It is used, among others, in the discussed further induction algorithms of CART decision trees. This test allows determining whether the explanatory variable (predictor) has a statistically significant effect on the dependent variable, even in situations when the predictor is of a qualitative character (Ref 14).
Like the melt (chemical composition), also variant has an effect on the impact energy. In this way, the assumption has been confirmed that sample composition has no effect on impact energy. Table 4 also shows that the effect of the chemical composition is less pronounced than that of the heat treatment parameters. Studies of the relationships allow capturing the bilateral systems of relationships in pairs. They allow noting that the effect of the most important predictor (TAF) can be modified by the effect of TA or TA2.
Regression Analysis. MARS
The next step in the research is an attempt to build a regression model. Having identified the significant explanatory variables, a model of multiple linear regression can be constructed. The equation derived for the regression model of impact strength takes the following form:
The coefficient of determination R2 indicates an 82% fit to empirical data (Fig. 8), while the standard error of estimation shows that on an average the impact energy calculated from the regression equation differs from the empirical value by 1.6472 J.
These results are not bad, but the linear regression does not allow for consideration of the impact of predictor variables, and also assumes a linear form of the model, what in the case under discussion has no justification (Table 5).
The question remains how qualitative variables affect KV and whether this effect can be quantified. Figure 9 presents a graph of the average KV groups designated by the variables called melt and variant (chemical composition and treatment option). It is clear that variant II of the heat treatment (with cooling to intermediate temperatures) raises the average values of impact energy. It can also be noted that melts 2 and 3 have higher average values of KV, which means that, like cooling to intermediate temperatures, also the addition of Cu and Ni improves the impact energy.
The example in Fig. 9 highlights the need for the application of approximation models allowing the use of both quantitative and qualitative variables. The tool used for modeling is the MARS method, which forms a component part of the STATISTICA™ package.
Multivariate adaptive regression splines (MARS) is the implementation of a generalization of the technique, the aim of which is to find the values of the output (dependent) variables based on the input variables (predictors). MARS is a nonparametric procedure that does not require any assumptions about the functional relationship between the dependent and independent variables. The dependence is constructed of the coefficients and so-called basis functions, fully determined by the data. The general mechanism of MARS functioning can be imagined as a multiple, segmented linear regression. The borders of segments (determined on the basis of data) define the “range of applicability” of each of the linear equations. MARS is adapted to the tasks in which there are both quantitative and qualitative predictor variables (Ref 15,16,17). The input space is divided into areas, which are referred to separate regression or classification functions. This approach makes MARS particularly useful when there are more dimensions in the entry (more than two variables), and when in the case of other techniques the dimensionality starts being a problem. The MARS technique is known especially in the field of data mining (Ref 18,19,20), since in this technique there is no need to make any assumptions about the type of relationship between the dependent and independent variables. Very good models (giving accurate predictions) are obtained in situations where the relationships are very complicated, non-monotonic and difficult for any parametric modeling (Ref 21, 22). MARS is used successfully also in the metal processing industry (Ref 23, 24).
For MARS model, the coefficient of determination R2 is 0.9 (90% fit of the model to the actual data, Fig. 10), which gives a better result than the multiple regression. However, an improvement of the model quality means the increased level of complexity. The model below should be used directly with qualitative variables coded 0, 1. As we can see, the model allows for both quantitative (TAF, TA2, TA) and qualitative (melt, variant) variables, which improves the quality of the prediction. The equation of MARS model of the impact energy takes the following form:
The Variational Components of VEPAC Module
As has already been stated, qualitative variables (heat treatment variant, melt) have a significant effect on impact energy. The impact strength (or rather the energy of fracture) is a continuous, quantitative variable. Other variables, although expressed in numbers of double precision, can be considered as classes of values (can take a finite number of states), and thus can be treated as categorical or qualitative variables. This enables the use of such tools as analysis of variance. In the case under discussion, the classification factors will be more numerous, and their number will correspond to the number of the important explanatory variables. The variables under control (heat treatment variant, melt, temperatures: TA, TAF, TA2) are called factors. ANOVA confirms the significance of variables, such as TAF, heat treatment variant, melt, as well as their interactions. ANOVA allows calculation of the average in each of the groups designated by relevant factors. The usefulness of factors is determined by statistical tests (Ref 22). As in the regression analysis, the fit of the prediction to the raw data is R2 = 0.9 (90%) (Fig. 11).
Observed vs. predicted values—ANOVA; R2 = 0.90 Fig. 12. The dependent variable vs. output of the neural network. R2 = 0.93
VEPAC—Variance Estimation and Precision, is intended for the analysis of variance in research and production. It is a set of techniques used to analyze the data obtained as a result of the experiments, which are controlled by both the fixed and random effects. In the VEPAC module, analysis alternative to the ANOVA is conducted on the basis of assessments by the method of restricted maximum likelihood estimation (REML). REML, in turn, uses quadratic forms to iteratively obtain estimates of the variance components. This method gives an even better fit of the model to real data than ANOVA (R2 = 0.91) and is able to incorporate more complex systems (Ref 25, 26).
The variability presents various systems of factors in a manner legible to the user. It also allows drawing additional conclusions, for example:
-
Cooling to intermediate temperatures after austenitizing raises the average impact strength.
-
The average impact strength increases in the melts with the addition of Cu and Cu + Ni.
-
The average impact strength is higher for the heat treatment variants where the ausferritizing temperature is 400 °C.
-
The austenitizing temperature after cooling to intermediate temperatures is of utmost importance for the melts without the addition of Ni, particularly in the case when the ausferritizing temperature is 300 °C—the lowest impact strength is attributed to the samples for which the austenitizing temperature after cooling to intermediate temperatures is 900 °C.
-
The austenitizing temperature strongly influences the impact strength only in special systems of parameters, e.g., for the heat treatment variant without cooling to intermediate temperatures (V1), in melts without Cu and Ni (C1), the austenitizing temperature does not affect KV, but in melts with the addition of copper and nickel (C2; C3), when the ausferritizing temperature is 400 °C, a clear influence of the austenitizing temperature is observed, and the lower is this temperature. The higher is the impact strength.
Forecasting KV is possible using the table of mean values in variation groups (Tables 6 and 7).
Artificial Neural Networks
Neural networks can perform several types of tasks in the modeling of technological (production) processes, including metallurgical and casting operations, using the following tools: regression, prediction, detection of patterns. The elementary operations performed by single artificial neural networks are of no particular interest, since actual neural computing power is the effect of a combination of many neurons in a network forming different structures (Ref 27,28,29). Neural networks are used in processing metals for many years, enjoying high popularity (Ref 30, 31).
The dependent variable was the impact energy (KV). The inputs to the network were: TA, TAF, TA2, variant, melt (the variables with fixed significance). Among the tested architectures, the best results were achieved by MLP (multilayer perceptron) networks, better than the RBF (radial networks).
For analysis, the MLP 15-4-1 network was chosen. This notation defines the network architecture, i.e., 15 input neurons (for each class of each variable—binarization—one signal); four neurons in the hidden layer and one neuron in the output specifying the KV output.
As a function of activation, the network of a given architecture uses a logistic function in the hidden and output layers, as a method for calculation of the error—the sum of squares, and as a training algorithm—the Broyden–Fletcher–Goldfarb–Shanno (BFGS) method of optimization.
Thus, designed network reflects the input data with the correlation of 0.97, which gives R2 = 0.93. This is a better result than the methods used previously (Fig. 12.).
The trained network allows making predictions for the indicated values of the input signals. The disadvantage of neural networks is, however, that they do not provide support for the understanding of dependencies operating under a given phenomenon. The notation in a semi-symbolic form is difficult to understand for the user and cannot be used outside the network model. The weights of neurons allowing approximation do not constitute a knowledge base in the traditional sense.
SVM—The Method of Support Vectors
In nonlinear models (linearly non-separable), the traditional method of analysis become less accurate. In recent years, some popularity has been gaining the SVM, a method of support vectors. This method determines to which of the two classes a given set of input data should belong by determining from training data the widest possible boundary between classes. It is a linear, binary and non-probabilistic classifier, which does not mean, however, that it is not suitable for the prediction of a dependent variable which may take more than two values, or for finding solutions to the nonlinear problems. The method of support vectors, although relatively young, has already found a number of practical applications (Ref 32, 33).
A solution to the problem of nonlinearity (when the vectors in the training set are not linearly separable) is the, so-called, kernel trick—mapping of training vectors to an area of greater dimension, where one can expect them to have the linear separability. The calculations are carried out using kernel functions (Ref 34, 35).
The method of support vectors uses 91 support vectors to build a hyperplane. The weakness of this method is the inability to visualize the multidimensional problems and the lack of a model in the form of equations or rules that could be presented to the user. The vectors are presented in tabulated form, difficult to interpretation. The prediction model, however, allows forecasting the indicated values of input signals (Fig. 13).
A summary of the method of support vectors: Regression type 1 (C = 10.000, epsilon = 0.100), Kernel: radial basis functions (RBF) (gamma = 0.167), Number of support vectors = 91 (37 connected).
CART
Classification and regression trees (CART) are one of a number of different embodiments of the induction algorithms of decision trees. Decision trees are an advanced form of knowledge representation, which creates rich possibilities of interpretation, both at the stage of knowledge acquisition (data mining), and in the phase of its use in decision-making process (Ref 36,37,38). Trees induction algorithm iteratively divides the learner data set into partitions, repeating this operation until each partition contains objects belonging to one class only (Ref 39, 40).
The tree containing 24 leaves was generated. This means that the algorithm has divided the range of KV variability into 24 classes with different averages and variances depending on the system of input variables.
Since the CART algorithm requires no initial assumptions about the significance of explanatory variables, the tAF variable (time of ausferritizing treatment) was also introduced into the model. The visualization of trees within a small space becomes impossible and unreadable. Decision trees are a graphical representation of the rules. Hence, using a tree, one can generate decision rules allowing approximation of the value of the KV variable. Also, other mechanisms of rule induction confirm the efficacy of the steel industry (Ref 41, 42). By application of a tree or a rule, the user can estimate the value of the fracture energy for various combinations of the heat treatment parameters.
The decision algorithm of CART tree allows post hoc investigation of validity of the variables used to build the tree. The tAF variable has been taken into account, although other algorithms demonstrated its marginal utility.
Among the models discussed, CART model has the best fit to the actual data. The coefficient of determination R2 = 0.967, or nearly 97% of the model fit (Fig. 10). In other words, the variability of impact energy is explained in 97% by the CART model, which is a very good result, bordering overfitting the model.
Like all models, CART model also allows for the analysis of residues (deviations from the model). It can be observed that in this case the residues are, on an average, not greater than 1 J, which means that the difference between the result yielded by the model and actual KV value obtained under the preset heat treatment parameters does not exceed 1 J in the vast majority of cases. The largest deviations in predicting KV occur with the values approaching 12 and 16 (Fig. 14). This will be explained by indicating the strength of rules for the KV classes with these average values.
Each rule in a CART model defines the class of KV values with the specified mean and variance. The variance for each class defines the quality (strength) of the rule that leads to the specified mean—in other words—a measure of confidence of the rule is usually the variance in the leaf determining the degree of deviation of individual values from the mean. The higher is the variance, the more differentiated cases hit the same class; the smaller is the variance, the more similar are the cases in a given class, or the cases with a common configuration of the heat treatment parameters.
Different classes have their mean value and variance. The higher is the peak of the class, the smaller is the variance. Some classes have been signed to make it easier to explain certain phenomena. For example, rules 36 and 37 exhibit the highest variance (greater than 1). Rule 36 reads.

This means that the samples from melt C1 (without Cu and Ni), subjected to austenitizing at a temperature of 830 or 950 °C, with the temperature and time of the ausferritizing treatment equal to 400 °C and 64 min, respectively, have the average impact energy of 11.542 J. The variance of 4.664, i.e., the standard deviation in this class, is 2.16 J, which makes this rule the “worst” one in the model. It means that this class covers all those cases (samples) which somehow have failed to find a better qualification. In a simplification, it can be said that the cases for which significant correlations could not be found were “inserted” to classes 36 and 37, thus giving the values most averaged and varied. The question is whether it would not be better to remove these rules from the model, assuming that the user would not wish to use them in the design of the heat treatment process as “unstable” configurations of parameters.
As a contrasting example, rule 44 can be given.

This means that the samples from melt C2 (containing Cu but without Ni), subjected to austenitizing at a temperature of 830 or 950 °C, subjected or not subjected to cooling to intermediate temperatures during austenitizing at a temperature of 860 or 900 °C, with the temperature of the ausferritizing treatment equal to 400 °C and the time of this treatment shorter than or equal to 32 min, have the average impact energy of 17.122 J. The variance of 0.103, i.e., the standard deviation in this class, is 0.321 J. The standard deviation so low ensures that the determination of heat treatment parameters will provide a result very close to the average obtained for this class.
A comparison of these two classes can be made by the comparison of histograms. The histogram presents a number of cases in each range of values. For class 36, the range of KV values extends from 8 to 15 J; for class 44, this range is 16.4-17.8 J.
To verify the CART model, especially in the area of concern (rules 36 and 37), it was decided to use a tool that is cluster analysis. For this purpose, the k-means clustering algorithm was applied. Clusters obtained by this method own many similarities to the classes from CART. In the range of KV values from 5 to 10 J, very distinct and strong clusters are present. The same is true for a high range of KV values, i.e., 15-20 J. Medium KV values (11-14 J) do not have their strong representatives in the form of clusters or classes. Hence, the conclusion follows that it will be much more difficult to “target” this area of KV variability through parameter settings, while it will be relatively easy to determine how to manage the process to obtain low or high impact energy.
Conclusions and Final Remarks
The analytical studies helped to develop a method for the estimation of heat treatment parameters to obtain the ausferritic ductile iron with appropriate impact energy KV. The following methods were considered:
-
Model of multiple regression,
-
Model of piecewise (segmented) regression by MARS algorithm,
-
ANOVA analysis,
-
Analysis using the VEPAC package,
-
Model of artificial neural networks,
-
Model based on the method of SVM support vectors,
-
Model based on the induction of CART,
-
Cluster analysis by k-means clustering algorithm.
All developed models are applicable in the approximation of fracture energy, yielding fairly good results. Forecasting based on each of these models will have a high reliability, and it is the user who will decide on the choice of the final tool. As part of the studies, validation and testing were performed on the developed models, and the results are shown in Tables 8 and 9.
These models, however, differ from each other and not only in the quality of approximation, which can be summarized in a comparison table. Each of these models offers a different way of achieving forecasts, which gives different functionalities and ease of interpretation. Table 9 presents different error measures for individual models, as well as their correlation and coefficient of determination in relation to the measurements we have. Regardless of the adopted measure, models with the use of decision trees proved to be the most precise and accurate. When evaluating analytical tools, we rely on experimental data. Measuring data is not always enough, we could always wish it was more, it was more repetitive, according to the rule: “The more can we do the better, the smaller the error will be.” According to the authors, the studies presented here show that in this specific case the best results are provided by the method of induction of CART decision trees, and this is due not only to the high quality of the obtained approximation, but also and especially to the easy use of the rule base, easy interpretation by human and potential possibility of using this method in other information technology tools. Ability to interpret the model provides the functionality in the eyes of technologists. Further studies should broaden the scope of approximation to other mechanical properties and can even take into account other parameters, e.g., the measurement data from foundry equipment (Ref 43). On the other hand, the acquired knowledge in the form of rules can be successfully used in the construction of knowledge bases for intelligent systems in foundry applications (Ref 44,45,46,47,48,49,50).
Material experiments conducted in the conditions presented in the article (with a specific chemical composition, with specific heat treatment parameters) constitute new knowledge that may be interesting for material researchers. The microstructure research allows for a qualitative assessment of the results achieved. Creating predictive models allow the extraction of knowledge about the studied process and the impact of its individual characteristics on the properties of the material. This knowledge in the form of rules, tables and equations can be used by the material engineer in the design of new materials with the desired properties.
References
D. Wilk-Kołodziejczyk, K. Regulski, and G. Gumienny, Comparative Analysis of the Properties of the Nodular Cast Iron with Carbides and the Austempered Ductile Iron with Use of the Machine Learning and the Support Vector Machine, Int. J. Adv. Manuf. Technol., 2016, 87(1), p 1077–1093
S. Daber, K.S. Ravishankar, and R. Prasad, Influence of Austenitising Temperature on the Formation of Strain Induced Martensite in Austempered Ductile Iron, J. Mater. Sci., 2008, 43, p 4929–4937
P. Skoczylas, A. Krzyńska, and M. Kaczorowski, The Comparative Studies of ADI, Versus Hadfield Cast Steel Wear Resistance, Arch. Foundry Eng., 2011, 11(2), p 123–126
G. Gumienny, Carbidic Bainitic and Ausferritic Ductile Cast Iron, Arch. Metall. Mater., 2013, 58(4), p 1053–1058
B. Mrzygłód, A. Kowalski, I. Olejarczyk-Wożeńska, H. Adrian, M. Głowacki, and A. Opaliński, Effect of Heat Treatment Parameters on the Formation of ADI, Microstructure with Additions of Ni, Cu, Mo, Arch. Metall. Mater., 2015, 60(3A), p 1941–1948
Z. Gorny, S. Kluska-Nawarecka, and D. Wilk-Kolodziejczyk, Heuristic Models of the Toughening Process to Improve the Properties of Non-Ferrous Metal Alloys, Arch. Metall. Mater., 2013, 58(3), p 849–852
I. Witten and E. Frank, Data Mining: Practical Machine Learning Tools and Techniques, Morgan Kaufmann, New York, 2000
T. Giętka and T. Szykowny, Microstructure and Mechanical Properties of ADI, Depending on Austenitization Methods and Parameters, Arch. Foundry Eng., 2012, 12(2), p 19–24
T. Giętka, K. Ciechacki, and T. Szykowny, The Influence of Temperature of Breaking on Impact Strength of ADI, Arch. Foundry Eng., 2015, 15(2), p 87–92
S. Dymski, Z. Ławrynowicz, and T. Giętka, Impact Strength of ADI, Arch. Foundry Eng., 2006, 6(21), p 369–376
V. Kilicli and M. Erdogan, The Strain-Hardening Behavior of Partially Austenitized and the Austempered Ductile Irons with Dual Matrix Structures, J. Mater. Eng. Perform., 2008, 17(2), p 240–249
G. Gumienny and T. Giętka, Continuous Cooling Transformation (CCT) Diagrams Of Carbidic Nodular Cast Iron, Arch. Metall. Mater., 2015, 60(2), p 705–710
K. Regulski, D. Szeliga, and J. Kusiak, Data Exploration Approach Versus Sensitivity Analysis for Optimization of Metal Forming Processes, Key Eng. Mater., 2014, 611–612, p 1390–1395
D. Wilk-Kołodziejczyk, G. Rojek, K. Regulski, S. Kluska-Nawarecka, and M. Adrian, Mathematical Formalisms to Represent Knowledge Concerning the Production Process of Austempered Ductile Iron, Metalurgija, 2016, 55(1), p 3–6
StatSoft, Inc. (2013). Electronic Statistics Textbook. Tulsa, OK: StatSoft. WEB: http://www.statsoft.com/textbook/. Accessed 21 Dec 2016
T. Ząbkowski and K. Gajowniczek, Forecasting of Individual Electricity Usage Using Smart Meter Data, Quant. Methods Econ., 2013, 14(2), p 289–297
J.H. Friedman, Multivariate Adaptive Regression Splines, Ann. Stat., 1991, 19(1), p 1–67
S.A. Balasubramanian, J. Manickavasagam, T. Natarajan, and J. Balakrishnan, An Experimental Analysis of Forecasting the High Frequency Data of Matured and Emerging Economies Stock Index Using Data Mining Techniques, Int. J. Oper. Res., 2015, 23(4), p 406–426
A. Abraham, D. Steinberg, and N.S. Philip, Rainfall Forecasting Using Soft Computing Models and Multivariate Adaptive Regression Splines, in Proceedings of the IEEE SMC Transactions: Special issue on Fusion of Soft Computing and Hard Computing in Industrial Applications (2001).
N.F. Butte, W.W. Wong, A.L. Adolph, M.R. Puyau, F.A. Vohra, and I.F. Zakeri, Validation of Cross-Sectional Time Series and Multivariate Adaptive Regression Splines Models for the Prediction of Energy Expenditure in Children and Adolescents Using Doubly Labeled Water, J. Nutr., 2010, 140(8), p 1516–1523
J. De Andrés, P. Lorca, Juez F. de Cos, and F. Sánchez-Lasheras, Bankruptcy Forecasting: A Hybrid Approach Using Fuzzy c-Means Clustering and Multivariate Adaptive Regression Splines (MARS), Expert Syst. Appl., 2011, 38(3), p 1866–1875
L. Plonsky, F.L. Oswald, Multiple Regression as a flexible alternative to ANOVA in L2 Research. Stud. Second Lang. Acquis. (2016). https://doi.org/10.1017/s0272263116000231.
A.K. Behera, J. Verbert, B. Lauwers, and J.R. Duflou, Tool Path Compensation Strategies for Single Point Incremental Sheet Forming Using Multivariate Adaptive Regression Splines, Comput. Aided Des., 2013, 45(3), p 575–590
A. Mukhopadhyay and A. Iqbal, Prediction of Mechanical Property of Steel Strips Using Multivariate Adaptive Regression Splines, J. Appl. Stat., 2009, 36(1), p 1–9
A.K. Imsland, P. Reynolds, G. Eliassen, A. Mortensen, Ø.J. Hansen, V. Puvanendran, T.A. Hangstad, O.D.B. Jónsdóttir, P.A. Emaus, T.A. Elvegård, S.C.A. Lemmens, R. Rydland, A.V. Nytrø, and T.M. Jonassen, Is Cleaning Behaviour in Lumpfish (Cyclopterus lumpus) Parentally Controlled?, Aquaculture, 2016, 459, p 156–165
P. Selemela, D.J. du Plessis, A Comparative Analysis of Urban Growth and Development in Traditional Authority and Non-traditional Areas: the Case of Rustenburg and Mahikeng Municipalities in the North West Province, South Africa. Urban Forum, Springer. https://doi.org/10.1007/s12132-016-9288-6
M. Beccali, M. Cellura, V.L. Brano, and A. Marvuglia, Forecasting Daily Urban Electric Load Profiles Using Artificial Neural Networks, Energy Convers. Manag., 2004, 45(18), p 2879–2900
H.S. Hippert, C.E. Pedreira, and R.C. Souza, Neural Networks for Short Term Load Forecasting: A Review and Evaluation, IEEE Trans. Power Syst., 2001, 16(1), p 44–55
J. Jakubski, P. Malinowski, M. St, and K.Major-Gabryś Dobosz, ANN Modelling for the Analysis of the Green Moulding Sands Properties, Arch. Metall. Mater., 2013, 58(3), p 961–964
L. Sztangret, D. Szeliga, J. Kusiak, and M. Pietrzyk, Application of Inverse Analysis with Metamodelling for Identification of Metal Flow Stress, Can. Metall. Q., 2012, 51(4), p 440–446
L. Rauch, L. Sztangret, and M. Pietrzyk, Computer System for Identification of Material Models on the Basis of Plastometric Tests, Arch. Metall. Mater., 2013, 58(3), p 737–743
D. Tomar and S. Agarwal, A Comparison on Multi-class Classification Methods Based on Least Squares Twin Support Vector Machine, Knowl. Based Syst., 2015, 81(C), p 131–147
V. Laurain, An Instrumental Least Squares Support Vector Machine for Nonlinear System Identification, Automatica, 2015, 54(C), p 340–347
A. Glowacz, Fault Diagnostics of DC Motor Using Acoustic Signals and MSAF-RATIO30-EXPANDED, Arch. Electr. Eng., 2016, 65(4), p 733–744
C.M. Santos, J.F. Escobedo, É.T. Teramoto, and S.H. Silva, Assessment of ANN and SVM Models for Estimating Normal Direct Irradiation (Hb), Energy Convers. Manag., 2016, 126, p 826–836
L. Breinman, J.H. Friedman, R.A. Olshen, and C.J. Stone, Classification and Regression Trees, Chapman and Hall, London, 1993
J.R. Quinlan, Induction on Decision Trees, Machine Learning, Kluwer Academic Publishers, Boston, 1986
G.V. Kass, An Exploratory Technique for Investigating Large Quantities of Categorical Data, Appl. Stat., 1980, 29(2), p 119–127
M. Łapczyński, A Regression Approach in Constructing CART Classification Trees, Sci. Papers Cracow Univ. Econ., 2005, 680, p 135–151 ((in Polish))
K. Regulski, J. Jakubski, A. Opaliński, M. Brzeziński, and M. Głowacki, The Prediction of Moulding Sand Moisture Content Based on the Knowledge Acquired by Data Mining Techniques, Arch. Metall. Mater., 2016, 61(3), p 1363–1368
Z. Górny, S. Kluska-Nawarecka, D. Wilk-Kołodziejczyk, and K. Regulski, Methodology for the Construction of a Rule-Based Knowledge Base Enabling the Selection of Appropriate Bronze Heat Treatment Parameters Using Rough Sets, Arch. Metall. Mater., 2015, 60(1), p 309–315
S. Kluska-Nawarecka, B. Śnieżyński, W. Parada, M. Lustofin, and D. Wilk-Kołodziejczyk, The Use of LPR (Logic of Plausible Reasoning) to Obtain Information on Innovative Casting Technologies, Arch. Civil Mech. Eng., 2014, 14(1), p 25–31
K. Smyksy, E. Ziółkowski, R. Wrona, and M. Brzeziński, Performance Evaluation of Rotary Mixers Through Monitoring of Power Energy Parameters, Arch. Metall. Mater., 2013, 58(3), p 911–914
P. Macioł and K. Regulski, Development of Semantic Description for Multiscale Models of Thermo-Mechanical Treatment of Metal Alloys, JOM, 2016, 68(8), p 2082–2088
A. Maciol, R. Wrona, A. Stawowy, and P. Maciol, An Attempt at Formulation of Ontology for Technological Knowledge Comprised in Technical Standards, Arch. Metall. Mater., 2007, 52(3), p 381–388
S. Kluska-Nawarecka, K. Regulski, M. Krzyżak, G. Leśniak, and M. Gurda, System of Semantic Integration of Non-Structuralized Documents in Natural Language in the Domain of Metallurgy, Arch. Metall. Mater., 2013, 58(3), p 927–930
S. Kluska-Nawarecka, D. Wilk-Kołodziejczyk, J. Dajda, M. Macura, and K. Regulski, Computer-Assisted Integration of Knowledge in the Context of Identification of the Causes of Defects in Castings, Arch. Metall. Mater., 2014, 59(2), p 743–746
G. Rojek and J. Kusiak, Industrial Control System Based on Data Processing, Artificial Intelligence and Soft Computing, Vol 7268, Lecture Notes in Computer Science , L. Rutkowski, M. Korytkowski, R. Scherer, R. Tadeusiewicz, L. Zadeh, and J. Zurada, Ed., SpringerVerlag, Berlin, 2012, p 502–510
S. Kluska-Nawarecka, Z. Gorny, D. Wilk-Kolodziejczyk, and A. Smolarek-Grzyb, The Logic of Plausible Reasoning in the Diagnosis of Castings Defects, Arch. Metall. Mater., 2007, 52(3), p 375–380
S. Kluska-Nawarecka, D. Wilk-Kolodziejczyk, K. Regulski, G. Dobrowolski, Rough Sets Applied to the RoughCast System for Steel Castings, Intelligent Information and Database Systems, in Proceedings of the Third International Conference, ACIIDS, 2011, Daegu, Korea, Vol. 6592 of Lecture Notes in Artificial Intelligence, pp. 52–61.
Acknowledgments
Financial support of The National Centre for Research and Development LIDER/028/593/L-4/12/NCBR/2013 is gratefully acknowledged.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Wilk-Kołodziejczyk, D., Regulski, K., Giętka, T. et al. The Selection of Heat Treatment Parameters to Obtain Austempered Ductile Iron with the Required Impact Strength. J. of Materi Eng and Perform 27, 5865–5878 (2018). https://doi.org/10.1007/s11665-018-3714-y
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11665-018-3714-y