Simulations of Texture Evolution in the Near-Surface Region During Aluminum Rolling

Abstract

Prediction of texture changes during cold rolling is important because they affect the recrystallization and anisotropy of an aluminum sheet during successive forming steps. During cold rolling of aluminum alloys, the through-thickness textural change in the subsurface layer depends heavily on the shear stresses exerted on the material. The intensity of this shear stress is determined by the value of and change in the coefficient of friction as the contact length between the rolls and metallic sheet changes. The quality of the texture prediction under constant and variable coefficients of friction are assessed for three established texture models: the grain interaction (GIA) model, the viscoplastic self-consistent (VPSC) approach, and the full-field crystal plasticity Düsseldorf Advanced Material Simulation Kit (DAMASK) code. The simulation results are compared with subsurface layer textures obtained from conducting experimental cold-rolling trials on an aluminum alloy, which are designed to maximize shear in a single rolling pass. The formulation of a variable coefficient of friction is crucial for ensuring both the reasonable prediction of rolling forces and changes in texture. GIA and DAMASK yield the best texture prediction results for a variable coefficient of friction model.

1 Introduction

Understanding textural changes during rolling is fundamental for controlling anisotropy and optimizing the formability of aluminum sheets. During industrial cold rolling of aluminum sheets, the final texture is influenced by the full history of the deformation gradient and by the microstructure and texture initially present in a hot band.^[1] In symmetric rolling, the material at the center of the strip experiences plane strain deformation and is not affected by shear. Nevertheless, the off-diagonal components of the deformation gradient (F_RD–ND and F_ND–RD) may intensify and dominate moving towards the strip surface. The intensity of F_RD–ND is largely determined by the friction characteristics between the rolls and metal strip surfaces, while the amount of F_ND–RD is established by the roll gap geometry (i.e. draughts). The influences of these two off-diagonal components have been analyzed experimentally during hot and cold rolling. Mishin et al.^[2] showed that strong friction at the contact surfaces between rolls and strips can form a heterogeneous texture throughout the thickness of a plate. The addition of shear forces to plane strain compression affects the activation of slip systems and, in turn, the changes in crystallographic textures. In hot rolling, where non-octahedral slip systems may be activated, Falkinger et al.^[3] reported that the presence of a high shear strain due to increased friction between the roll and metal surface (i.e., a high F_RD–ND) strengthens rotated cube and reduces the fraction of rolling texture components (Brass, S, and Copper), which dominate at the sheet center where the loading is in the form of plane strain compression. The texture at the center of the metal strip is characterized by rolling components pertaining to the β fiber. In addition, the cube texture at the center can be preserved even at thickness reductions greater than 75 pct.^[4]

Experimental results in literature involve analyses of the influence of F_ND–RD on texture. This off-diagonal component is established by the roll gap geometry and is easier to control than F_RD–ND, in which the value is controlled by surface friction. The roll gap is defined as the ratio l_c/h, where l_c is the length of contact between the rolls and the metal surface and h is the sample thickness. According to experiments, small draughts (i.e., l_c/h lower than 0.5) create shear texture in quarter thickness layers, while rolling with draughts with l_c/h values greater than five causes shear texture to appear at the strip surface.^[5] However, the modeling results of Mao^[6] suggest that a homogeneous texture can still be obtained for draughts greater than 5 if the thickness reduction per pass is less than 40 pct. Thus, a homogeneous texture can develop throughout the strip thickness for draughts with l_c/h values between 0.5 and 5. However, this range further depends on the amount of friction present between the rolls and the metal strip. Moreover, it has been proven that surface lubrication affects the through-thickness texture and the resulting r values during hot rolling of an ultralow carbon steel sheet.^[7] Mishin et al.^[5] concluded that the shear intensities at the surfaces between rolls and metal strips determine the penetration depth of the shear texture throughout the strip thickness; when shear increases, the shear texture can be observed in a deeper through-thickness layer than before. In contrast, Truszkowski et al.^[8] mentioned that the non-uniformity of the through-thickness penetration of shear deformation depends more on the l_c/h value because the shear due to friction between rolls and strips is restricted to a thin layer of 0.01 to 0.05 mm at the surface. The scholars provided a detailed comparison of through-thickness textural changes in aluminum for low and high draughts, determining that for l_c/h values lower than 0.5, the maximum velocity of metal flow occurs at the intermediate layers of strip thickness; thus, the shear texture appears at the same position. For l_c/h values higher than 5, a shear texture develops at the surface because the maximum velocity of metal flow is at the surface. In a later study, the researchers reported that low yield stress and strain hardening favor shear deformation and through-thickness inhomogeneity of the texture.^[9]

The influence of the roll gap geometry on textural change was assessed by extracting the deformation state inside the roll gap via finite element calculations; this state was used for texture prediction in simulations.^[10] The results confirmed that the penetration of the shear deformation into the strip thickness depends on the roll gap geometry, which influences the position of the neutral point. Moreover, the scholars showed that as the contact length increases, the normal stresses between the roll and strip can reach four to five times the material yield stress. In addition, a standard assumption of a constant Coulomb coefficient of friction results in overestimation of frictional forces. Nah et al.^[11] and Jiang et al.^[12] (aluminum) and Wauthier et al.^[13] and Pyon et al.^[14] (steel strips) considered asymmetric rolling to increase the influence of shear strain during cold rolling to obtain a random and uniform texture throughout the thickness and to control the grain size after the deformation process and during subsequent recrystallization annealing. The textural changes during symmetric and asymmetric cold rolling of the aluminum alloy AA 6111 were compared, revealing that conventional symmetric rolling cannot transmit shear deformation throughout the strip thickness.^[15] Moreover, the scholars showed that differences in texture between symmetric and asymmetric rolling start to appear if the thickness reduction is equal to or greater than 30 pct, and as the rolling reduction increases, the shear can penetrate the strip thickness for asymmetric rolling.

Symmetric and asymmetric cold rolling create differences in the through-thickness distribution of shear texture during cold rolling. In particular, Lee et al.^[16] reported that for unlubricated symmetrically rolled aluminum samples, the strip center exhibits a texture without shear components, which purely corresponds to a plane strain compression texture, while shear components are located close to the strip surface. In contrast, asymmetric rolling results in the formation of a uniform shear texture throughout the thickness. This difference is due to the net shear strain ε_RD–ND, which is positive after a pass for asymmetric rolling because the shear strain rate ${\dot{\varepsilon }}_{\text{RD}-\text{ND}}$ stays positive. In contrast, symmetric rolling has a zero net shear strain after the rolling pass because the shear strain rate ${\dot{\varepsilon }}_{\text{RD}-\text{ND}}$ reverses its sign from the entrance to the exit of the roll gap. Many experimental results concerning the influence of shear on textural changes are available, while simulation investigations remain limited. The first approach to predict textural changes involves the full constraints Taylor (FCT) model, where all grains of a polycrystalline aggregate deform together as a macroscopic body. Given that FCT yields satisfactory results for texture prediction under plane strain loading, Engler et al.^[17] and Pérocheau and Driver^[18] used this approach and imposed idealized strain states with variable nonzero shear strains; additionally, the scholars addressed through-thickness texture gradients and, especially, predicted the shear texture $\left\{ {00{1}} \right\}\langle 110\rangle$ near the strip surface. Similarly, Wagner et al.^[19] derived the strain distributions for various rolling sequences based on fluid dynamics to model through-thickness texture gradients with the FCT model. Later, Oscarsson et al.^[20] and Aukrust et al.^[21] coupled finite element simulations with the full constraint Taylor model to predict textural changes during hot rolling and extrusion, respectively.

However, as described in the texture review of Sidor et al.,^[22] the strain velocity field of each crystal (i.e., grain) is equal to the macroscopic strain velocity field in the FCT model; thus, each grain undergoes the same deformation as the whole sample. The main drawback of the FCT model is the violation of stress equilibrium at grain interfaces, which overestimates copper and S texture components and underestimates brass texture during cold rolling of aluminum. As described by Kocks and Chandra,^[23] other models consider the relaxation of some constraints present in the FCT. These approaches are named relaxed constraints Taylor (RCT) models, where some shear stress components are deliberately set to zero to leave the corresponding strain free. The relaxed components are chosen based on the simulated deformation process considering the expected shape change experienced by the grains in the microstructure. However, according to a comparison of different models used to simulate textural changes for AA 1200 in plane strain compression, RCT performs the poorest in terms of texture prediction under all thickness reduction conditions.^[24] Furthermore, for deformation modes that involve shear strain or highly complex deformation paths, establishing the components for relaxation becomes difficult. Thus, RCT models are not suitable for simulating textural changes in asymmetric or symmetric rolling with high shear stresses because they neglect grain interactions and thus predict textural changes deviating both qualitatively and quantitatively from experimental results. Approaches including grain interactions have been developed considering either two grains (LAMEL and ALAMEL models) or clusters of eight grains (GIA) as described by Van Houtte et al.,^[24] Delannay,^[25] and Crumbach et al.^[26] For these models, the strain rate tensor of the group of grains is equal to the prescribed strain rate for the polycrystal. However, for each grain inside the cluster, the strain rate can deviate locally from the mean strain rate of the polycrystal. Other approaches to simulate textural changes include viscoplastic self-consistent (VPSC) methods, the crystal plasticity finite element method (CP-FEM), and crystal plasticity fast Fourier transform (CP-FFT) simulations.^[27,28] However, different texture modeling approaches are not compared when a strong shear load is added to the compression load through the thickness.

Shore et al.^[29] used finite element simulations and the ALAMEL crystal plasticity approach to predict the influences of the process parameters of a single asymmetric rolling pass on the textural changes of the aluminum alloy AA 6016; however, only constant friction coefficients were considered. Crumbach et al.^[30] highlighted the importance of reliably predicting the texture resulting from cold rolling as an input for recrystallization models. Choi and Barlat,^[31] Choi et al.,^[32] and Tomé et al.^[33] applied the VPSC simulation approach to predict the anisotropy of material properties in various aluminum alloys. Engler et al.^[17] used VPSC to predict textural changes during cold rolling of aluminum alloys. Conversely, Falkinger and Mitsche^[34] and Choi et al.^[35] employed VPSC to simulate textural changes during hot rolling.

Experimentally, the presence of F_RD–ND or F_ND–RD alone is considered, and their evolution as a function of time is often simplified in simulations. The purpose of this work is to develop and present a full procedure for predicting the development of shear textures starting from the initial hot band texture before cold rolling because there is a clear lack of systematic simulations of shear textures in the literature. The scope of this study is restricted to the position at the subsurface layer through the thickness where shear is known to produce the most pronounced effect. However, the sheet center experiences simple plane strain compression loading. Several studies on plane strain compression loading have been published.^{[17,36,37,38]} The purpose of this work is first to show that with a variable friction model, textural changes can be predicted at the subsurface layer. Moreover, the texture prediction abilities of different crystal plasticity approaches are compared when shear loading becomes non-negligible. These loadings are more challenging for different crystal plasticity formulations, and comparisons among the different simulation approaches are absent in the literature for these loadings.

A constant and a variable friction model are implemented in commercial finite element software (ABAQUS) to model a cold-rolling pass and extract the deformation gradient path (F_RD–ND, F_ND–RD, and F_ND–ND) to model the shear textural changes close to the strip surface. Textural change is simulated using three different crystal plasticity approaches—GIA, VPSC, and DAMASK—and the results are compared and discussed. Details of these models are included in the Materials and Methods section.

2 Materials and Methods

2.1 Cold-Rolling Experiments and Texture Analyses of Aluminum Specimens

The shear textural changes of aluminum strip material close to the surface cannot be extracted directly from industrial production lines. During hot rolling, the material usually undergoes several cycles of recrystallization, which yield samples with complex textures. During cold rolling, a clear deformation texture can be obtained, but passes are usually performed with low friction in the mixed lubrication regime using low-roughness work rolls. Considerable shear components develop only from an accumulation of several rolling passes. Thus, tracing the shear texture components in the following study requires plastomechanical and textural simulations of several passes. Apart from long calculation times, the shear components reverse several times, and computational errors might accumulate. For this reason, laboratory trials are designed in this study to produce strips with the highest possible shear in the surface region after one rolling pass to yield samples with well-defined initial states and clear shear textures. The initial strip material (hot band) of alloy AA 5754 (ISO AlMg3) is obtained from an industrial hot mill at Speira with a thickness of 9 mm. The composition of the material is given in Table I.

Table I Chemical Composition of AA 5754 (in Wt Pct, Balance: Al)

The microstructure is analyzed by optical microscopy and electron backscatter diffraction (EBSD). A micrograph of the microstructure close to the surface of the strip is shown in Figure 1. A variation in grain size is noticeable moving from the center of the sample, where the grain size is 42 µm, to the surface, where the grain size is 16 µm, even if the material is fully recrystallized across the whole thickness in this initial state. The local through-thickness coordinate s (ND) is defined as s zero at the sheet center and one at the sheet surface. Figure 2 shows the orientation distribution functions (ODFs) derived from the EBSD maps of the sheet center (i.e., s of 0) and at the subsurface layer 3.83 mm from the sheet center (i.e., s of 0.85) in the normal direction. The ODFs are calculated from the EBSD single-grain orientations using a Gaussian approach with a half-scatter width of ψ₀ = 5 deg.^[39] Evidently, the hot strip reveals a through-thickness texture gradient, with a mild cube recrystallization texture in the strip center and a very weak and practically random texture in the surface layer.

Fig. 1

Optical micrograph of the initial material (longitudinal section RD–ND at the surface)

Fig. 2

Symmetric ODF sections from EBSD measurements for the center (a) and near-surface layer (b). The first section is at φ₂ = 0 deg, and the last section is at 90 deg, with a plot section every 5 deg

Samples 100 mm in width are cold rolled in a Laboratory Mill at the Institute of Metal Forming (IBF) of RWTH Aachen University. The width of the aluminum sheet is more than ten times the thickness of the sheet. This width ensures that the strain in the width direction is negligible compared to the plastic strains in other directions. The initial sheet dimensions are designed to obey the criterion of having strains along the width that are negligible or absent.^[40] From a large series of trials, a sample with a thickness reduction of 50 pct is chosen for further study. In this case, a work roll diameter of 410 mm is used at a mill speed of 40 mm/s. No lubricant is applied. The required specific roll force (1121.5 kN) is measured on a hydraulic screw-down system in the steady-state rolling regime. Subsequently, the samples are characterized via optical microscopy and EBSD. Figure 3 shows the microstructure of a longitudinal section (RD–ND) at the surface. The deformation and elongation of the grains along the RD are clearly visible. Several EBSD measurements are carried out at different heights through the thickness from the center to 85 pct of the half-sample thickness, which is close to the surface. Figure 4 shows the section plots of the ODF calculated based on an EBSD measurement at this position. The ODF is calculated from the orientations using the de la Vallee Poussin kernel in MTEX with a half-width of 5 deg. A distinctive shear texture comprising a 45 deg ND-rotated cube can be observed. In addition, a weak incomplete γ fiber is present, which is observed along angle φ₁ at Φ = 60 to 70 deg in the ODF section corresponding to φ₂ = 45 deg.

Fig. 3

Optical micrograph of the cold-rolled material (longitudinal section RD–ND at the surface)

Fig. 4

After cold rolling, ODF sections at 0, 10, 20, 30, 40, 45, 50, 60, 65, 70, and 80 deg are obtained at 85 pct of the sample half-thickness (s equal to 0.85). The round markers in the 0 deg section indicate the position of the exact cube orientation, while the square markers indicate the position of the 45 deg ND-rotated cube

2.2 Models Used to Simulate Textural Changes

2.2.1 Finite element model (FEM) of the cold-rolling process and friction models

The presence of friction is crucial in metal rolling processes to develop the horizontal force component necessary to drive a sheet through a roll gap. As defined by Deters et al.^[41] and Klocke,^[42] a friction model describes the mechanical interaction of surfaces acting on each other. Theoretical descriptions of friction often involve many parameters with complexities that depend on the forming process.^[43] Nevertheless, a key factor contributing to all friction models is the calculation of the critical frictional shear stress (${\tau }_{\text{crit},\text{R}}$).

This value can be used to calculate the point of relative motion and the maximum possible frictional shear stress $({\tau }_{\text{R}}$) between the friction surfaces. Coulomb^[44] established that motion occurs as soon as the frictional shear stress ${\tau }_{\text{R}}$ exceeds the critical frictional shear stress ${\tau }_{\text{crit},\text{R}}$, which is calculated as follows:

$${\tau }_{crit,R}=\mu {\sigma }_{N},$$

(1)

where $\mu$ is the constant coefficient of friction and ${\sigma }_{N}$ is the stress normal to the contact surface. Although the Coulomb friction model is widely used in many applications, it can be unsuitable for the combination of high coefficient of friction $\mu$ and normal stress ${\sigma }_{N}$ values prevailing in bulk forming. Figure 5 presents a schematic illustration of the validity range of the model.

Fig. 5

Schematic representation of the validity range of the Coulomb friction model determined with the simplified assumption of a negligible hydrostatic stress component ${\sigma }_{m}$ (adapted from Ref. [45])

The Tresca friction model given in Eq. [2] defines the critical frictional shear stress ${\tau }_{\text{crit},\text{R}}$ as a function of the shear flow stress $k$ of the weak friction partner:

$${\uptau }_{\text{crit},\text{R}}=mk,$$

(2)

where $m \in [\text{0,1}]$ is the friction factor that is used as a scaling factor and $k$ is the shear flow stress, which is half the yield strength of the material in the Tresca approach. In some processes, such as rolling, toggling between the validity areas shown in Figure 5 is possible. Orowan^[46] proposed a combination of the Coulomb and Tresca friction models to cover all conditions:

$${\tau }_{crit,R}=\left\{\begin{array}{c} \mu {\sigma }_{N} \,if\, {\sigma }_{N}<\frac{m k}{\mu }\, \left(Coulomb \,friction \,model\right),\\ m k \,if\, {\sigma }_{N}\ge \frac{m k}{\mu } \,\left(Tresca\, friction\, model\right).\end{array}\right.$$

(3)

In the rolling process, the contact conditions between the rolls and strip vary considerably from the entry to the exit of the roll gap. During cold rolling, the most important factors are the deformation of the topography of the soft strip material against the hard surface of the roll and the plastification of the strip, which causes the effective contact area to change. The pressure simultaneously increases towards the neutral point and decreases again towards the exit. Furthermore, the relative velocity between the surfaces varies from backwards to forwards slip. Thus, the assumption of a constant Coulomb friction factor along the roll gap length is not realistic. An overview of the advances in describing the surface contact interfaces in friction models for metal forming was given by Nielsen and Bay.^[47] In addition, Pawelski^[48] provided a thorough analysis of the tribological system in rolling. Pawelski^[48] showed that generally, the coefficient of friction increases in the roll gap to the neutral point due to the increasing fractional area of contact, while after the neutral point, it remains largely constant. Nevertheless, to date, only a partial theoretical understanding of all contact reactions has been reached. In the present paper, an empirical model of this type is implemented, which allows the study of the effect of different friction conditions on texture development.

In this work, the shear texture is investigated through a 2D temperature displacement coupled rolling model in ABAQUS Standard. Hojda^[49] provided a detailed description of the parametric setup of this model. The model has a symmetry plane in the transverse direction ${z}_{\text{TD}}$ and rolling direction ${x}_{\text{RD}}$, which serve as the symmetry boundary conditions. As a result, only the region above the symmetry plane of the ABAQUS Standard model, which is schematically shown in Figure 6, is simulated to reduce the calculation time. The model contains three parts: the work roll, the rolling stock, and the pusher. A detailed description of the model was published by Rabindran et al.^[50]

Fig. 6

Schematic illustration of the ABAQUS Standard rolling model with the material and mesh properties highlighted for the parts: pusher, rolling stock, and work roll. The following values are used: the roll bite angle between the roll gap entry and exit ${\alpha }_{b}$; the intermediate roll bite angle between the rolling position $x$ and the rolling direction ${x}_{RD}$ and the roll gap exit ${\alpha }_{b,x}$; the coefficients of heat transfer ${\alpha }_{c}$ and the emissivity $\varepsilon$; the total height reduction ${\varepsilon }_{h}$; the initial ${h}_{0}$ and final ${h}_{1}$ rolling stock height; the element edge length of the rolling stock ${l}_{EL}$; the projected arc length of contact ${l}_{c}$; the normal stress ${\sigma }_{N}$; the positive ${\tau }_{R,+}$ and negative ${\tau }_{R,-}$ frictional shear stress; the temperatures of the work roll ${T}_{roll}$ and the rolling stock ${T}_{stock}$; the velocities of the pusher ${v}_{pusher}$ and of the work roll ${v}_{roll}$; the outer ${r}_{roll}$; and the inner work roll radius ${r}_{i}$. $s$ describes the rolling stock position from the center ($s=0$) to the surface ($s=1)$. The reference region defines the evaluation section (Reprinted from Ref. [50], under the terms of the Creative Commons CC BY 4.0 licence, https://creativecommons.org/licences/by/4.0/)

The rolling stock is modeled as a deformable 2D planar part. Due to symmetry, only half the rolling stock height is simulated. The total height reduction ${\varepsilon }_{\text{h}}$ of the rolling stock induced by the work roll, neglecting elastic deformation effects, is calculated according to the following equation:

$${\varepsilon }_{h}=\left(\frac{{h}_{0}-{h}_{1}}{{h}_{0}}\right)\cdot 100,$$

(4)

where h₀ and h₁ are the strip thicknesses at the entrance and exit of the rolls, respectively. The projected arc length of contact ${l}_{c}$ between the work roll and the rolling stock can be determined based on geometrical considerations and neglecting work roll flattening, as suggested by Hitchcock^[51]:

$${l}_{c}=\sqrt{{r}_{roll} \Delta h-{\left(\frac{\Delta h}{2}\right)}^{2}},$$

(5)

where r_roll is the outer work roll radius and Δh is the difference between h₀ and h₁.

The linear notation describes the rolling stock position $s$ in the normal direction ${y}_{ND}$. The rolling process is in a steady state at the time the reference region enters the roll gap. The element mesh type is a 2D quadrilateral solid continuum model coupled with temperature and displacement (CPE4T). The edge length ${l}_{EL}$ of the quadratic mesh element of the rolling stock is calculated according to the following equation:

$${l}_{\text{EL}}=\frac{\left({h}_{0}/2\right)}{\text{EoH}},$$

(6)

where EoH is the number of elements over the height.

The Young modulus, Poisson ratio, and dissipation factor are set to 71 GPa, 0.33, and 0.9, respectively. The conductivity, density, and heat capacity of the material are measured for a typical aluminum alloy at a temperature of 20 °C. The user subroutine UHARD controls the hardening behavior of the rolling stock. This subroutine incorporates a modified version of the generalized Voce law introduced by Tomé et al.^[52]

The work roll is modeled as a deformable 2D planar circular ring to enable heat transfer, and it is constrained with a rigid-body constraint. A rigid-body part in the ABAQUS Standard is otherwise unable to simulate heat transfer. Modeling of the work roll as a ring reduces the number of elements and, thus, the simulation time. The inner radius ${r}_{\text{i}}$ is set to 80 pct of the outer radius ${r}_{\text{roll}}$ to keep the number of elements low. This phenomenon enables proper heat transfer at the same time. To further reduce the number of elements, a work roll mesh with an equidistant element edge length along the arc is prescribed with a single-biased seed method in the radial direction. Therefore, the finer and more quadratic elements appear closer to the outer surface of the work roll for good contact behavior, which can be observed schematically in Figure 6.

Equation [7] can be used to calculate the values required by the seed method. The projected arc length of contact ${l}_{\text{c}}$ ensures that the outer surface of the work roll is in contact with at least 10 elements of the rolling stock to guarantee a good result quality. Equation [7] gives the minimum ${l}_{\text{minEL}}$ and maximum ${l}_{\text{maxEL}}$ element lengths required to apply the single-biased seed method in the radial direction to the work roll to obtain a mesh gradient, as shown in Figure 6.

$$\begin{array}{c}{l}_{minEL}=min\left(2{l}_{EL}, \frac{{l}_{c}}{10}\right),\\ {l}_{maxEL}=2{l}_{minEL}.\end{array}$$

(7)

The work roll has the material properties of conductivity, density, and heat capacity of stainless steel grade X5CrNi18-10 (1.4301) for a temperature range of 20 °C to 200 °C. The pusher is modeled as rigid 2D planar, and its height ${h}_{\text{pusher}}$ is based on the rolling stock height. The element mesh type is 2D rigid (R2D2), and the element edge length is equal to the rolling stock ${l}_{\text{EL}}$.

$${h}_{pusher}=\left(\frac{{h}_{0}}{2}\right)+{l}_{EL}.$$

(8)

For the interactions between the parts, the work roll and pusher surfaces are defined as the master, and the rolling stock surface is defined as the slave. This approach avoids the penetration of the rolling stock surface into the work roll and pusher. The user subroutine FRIC (description of the friction behavior) describes the isotropic tangential contact behavior between the work roll and rolling stock. Within this subroutine, the combined friction model developed by Orowan^[46] was implemented and coupled with the ABAQUS Standard with the penalty friction formulation provided by Dassault Systèmes Simulia Corp.^[53]

The critical frictional shear stress ${\tau }_{\text{crit},\text{R}}(x)$ between the contacting work roll and the rolling stock surface is calculated according to Eq. [3] for each position along the arc of contact. The ABAQUS Standard applies the critical frictional shear stress as a boundary condition to determine the frictional shear stresses ${\tau }_{\text{R},+}$ and ${\tau }_{\text{R},-}$. The penalty friction formulation by Pawelski^[54] allows for a smooth transition between sticking and slipping. This formulation improves the numerical convergence. Additionally, a hard contact normal behavior with the penalty constraint is chosen. The heat transfer coefficient ${\alpha }_{\text{c}}$ between the work roll and rolling stock is set to 13 × ·10⁻³ W/(mm² K) in direct contact and decreases linearly to zero with a clearance of 0.25 mm to facilitate numerical contact establishment. Between the rolling stock and the pusher, a hard contact normal behavior with the penalty constraint and a frictionless tangential contact behavior is chosen.

At the beginning of the simulation, the pusher moves the rolling stock into contact with the work roll. After contact is established, the movement of the pusher slows and eventually stops. The velocity of the pusher ${v}_{\text{pusher}}$ is lower than that of the work roll ${v}_{\text{roll}}$ to ensure that the rolling stock is only brought in contact. This procedure simplifies the establishment of numerical contacts. Only the pass condition is relevant due to the steady-state (reference region) evaluation; therefore, the grip condition is neglected.

2.2.2 Grain interaction (GIA) model

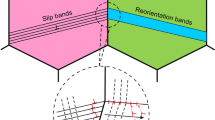
At the Institute of Physical Metallurgy and Metal Physics (IMM) of RWTH Aachen, Wagner^[55] and Crumbach et al.^[56] developed the principles of the GIA model, which is based on the classical full constraints theory of Taylor^[57] and is extended to account for grain interactions. For this purpose, a three-dimensional aggregate of eight brick-shaped grains is considered (Figure 7).

Fig. 7

Schematic representation of an undeformed GIA aggregate consisting of eight grains. Ai and Bi with $i\in \{1,\ldots,4\}$ are used to represent the grains

When applying a deformation, this grain aggregate deforms to a variant, as shown in Figure 8. The grain boundaries within the aggregate are labeled GB1 perpendicular to the RD, GB2 perpendicular to the TD, and GB3 perpendicular to the ND, while the interfaces with the surrounding material are denoted as interfaces IF1, IF2, and IF3, respectively.

Fig. 8

Schematic representation of a deformed GIA grain aggregate. $GBj$ and $IFj$ with $j\in \{1,\ldots,3\}$ are used to represent the grain boundaries within the grain aggregate and the grain interfaces to the surrounding material, respectively. The incompatibilities between the grains are emphasized by the displacement ${\varvec{u}}$. For easier identification, the nonvisible areas of grains $B1,\ldots,B4$ and $A1,\ldots,A4$ are shown with different line types

During deformation, different slip activities cause incompatibilities, such as grain overlap and gap formation at grain boundaries and interfaces. In each part of the eight grains, all shears ${\varepsilon }_{ij} (i\ne j)$ and principal strains ${\varepsilon }_{ij} (i=j)$ are relaxed, and the amount of relaxation of a given orientation is determined from a balance between the resultant gain in Taylor deformation energy E_Taylor and a penalty term E_relax. In combination with the Taylor energy, the deformation energy of the full aggregate E_def is determined and minimized over the eight grains according to Eq. [9]. This energy results in orientation changes in the grains and consequently determines the deformation texture. τ_n denotes the critical shear stress of grain n, ${\gamma }_{n}^{s}$ indicates the amount of shear of grain n on the slip system s, and E_GB and E_IF represent the relaxation energies between the grain boundaries and the environment, respectively.

(9)

At the beginning of deformation, the critical resolved shear stress ${\tau }_{n}$ is assumed to be the same for all slip systems in each grain of the eight grain aggregates, which determines ${E}_{\text{Taylor}}$. A detailed description of the GIA model is given by Crumbach^[58] and Engler et al.^[59] The GIA uses the deformation gradient tensor obtained from the ABAQUS finite element simulations after transformation into the local material coordinate system as input. ABAQUS finite element simulations provide the nodal coordinate (x_i) at each time step i for the target element along the strip thickness. The nodal coordinates X of the initial configuration are given as outputs. The point locations in the initial configuration (0), current configuration (i), and configuration (i + 1) are given by x₀ = X, x_i = X + u_i, and x_i+1 = X + u_i+1, respectively. From the nodal coordinates, the displacement increment between the configuration at time step (i + 1) and time step (i) can be calculated as follows:

$$\Delta \mathbf{u}={\mathbf{x}}_{i+1}-{\mathbf{x}}_{i}={\mathbf{u}}_{i+1}-{\mathbf{u}}_{i}.$$

(10)

The deformation gradients in the previous configuration (i.e., at instant time i) and in the current configuration [i.e., at instant time (i + 1)] are calculated as follows:

$${{\varvec{F}}}_{i}=\frac{\partial {{\varvec{x}}}_{i}}{\partial {\varvec{X}}}={\delta }_{ij}+\frac{\partial {{\varvec{u}}}_{i}}{\partial {\varvec{X}}}\quad \text{and} \quad{{\varvec{F}}}_{i+1}=\frac{\partial {{\varvec{x}}}_{i+1}}{\partial {\varvec{X}}}={\delta }_{ij}+\frac{\partial {{\varvec{u}}}_{i+1}}{\partial {\varvec{X}}}.$$

(11)

The incremental deformation gradient is obtained as follows:

$${\Delta {\varvec{F}}}_{i+1}={{\varvec{F}}}_{i+1}{{\varvec{F}}}_{i}^{-1}=\frac{\partial {{\varvec{x}}}_{i+1}}{\partial {{\varvec{x}}}_{i}}=\frac{\partial \left({{\varvec{x}}}_{i}+\Delta {\varvec{u}}\right)}{\partial {{\varvec{x}}}_{i}}={\delta }_{ij}+\frac{\partial \left(\Delta {\varvec{u}}\right)}{\partial {{\varvec{x}}}_{i}}.$$

(12)

From the incremental deformation gradient (∆F_i+1), the incremental displacement gradient (∆h_i+1) can be calculated as follows:

$${\Delta {\varvec{h}}}_{i+1}=\frac{\partial \left(\Delta {\varvec{u}}\right)}{\partial {{\varvec{x}}}_{i+1}}={\delta }_{ij}-{\Delta {\varvec{F}}}_{i+1}^{-1}.$$

(13)

The hydrostatic part needs to be removed; thus, the deviatoric incremental displacement gradient is given as follows:

$$\text{dev}\left(\Delta {\varvec{h}}\right)=\Delta {\varvec{h}}-\frac{1}{3}\cdot {\delta }_{ij}\cdot \text{trace}\left(\Delta {\varvec{h}}\right).$$

(14)

The deviatoric incremental displacement gradient [dev(∆h)] needs to be rotated to the local material frame coordinate system using the rotation matrix R as follows:

$${\Delta {\varvec{h}}}{\prime}={{\varvec{R}}}^{{\varvec{T}}}\cdot \text{dev}\left(\Delta {\varvec{h}}\right)\cdot {\varvec{R}}.$$

(15)

The rotation matrix (R) is calculated from the polar decomposition of the deformation gradient (F) as follows:

$${\varvec{F}}={\varvec{R}}\cdot {\varvec{U}}.$$

(16)

The final tensor component of ∆h′ in the frame of the local material coordinate system is then used in GIA. After the GIA simulation of the rolling process, the Euler angles need to be rotated because of the slight difference between the global rolling frame and the local material coordinate system of the material frame.

2.2.3 Viscoplastic self-consistent (VPSC) method

VPSC is a polycrystal plasticity algorithm developed by Lebensohn and Tomé.^[60] This algorithm is a mean-field model based on the behavior of an individual ellipsoidal grain embedded in a homogeneous matrix. Neglecting elastic strains, the viscoplastic deformation of the ellipsoidal grain is described with Eshelby tensors, and the deformation of an ensemble of grains is solved in a self-consistent manner. To this end, VPSC offers several options for coupling stress deviations with the associated strain rate deviations. In this study, an intermediate scheme with an effective inverse strain rate sensitivity n^eff of 10, which was introduced by Tomé,^[61] is used. In these simulations, the same generalized Voce hardening trends and hardening parameters as in GIA are used. In contrast to GIA and DAMASK, where the deformation gradient tensor is used, VPSC requires the plastic velocity gradient tensor as an input to simulate complex deformation histories.

The input for VPSC, L^vpsc is calculated as:

$${{\varvec{L}}}^{{\varvec{v}}{\varvec{p}}{\varvec{s}}{\varvec{c}}}={{\varvec{D}}}^{{\varvec{M}}{\varvec{i}}{\varvec{s}}{\varvec{e}}{\varvec{s}}-{\varvec{p}}}+\dot{{\varvec{R}}}{{\varvec{R}}}^{{\varvec{T}}}.$$

(17)

D^Mises-p is the plastic part of the rate of deformation, which is calculated from the deformation gradient with a standard plasticity algorithm based on the Von Mises yield model.^[53] Equation [17] represents an isotropic approximation of the ‘real’ plastic velocity gradient, which would result from a full elasto-viscoplastic implementation of VPSC. R is the rigid-body rotation, obtained from the polar decomposition of the deformation gradient in Eq. [16]. The second term in the sum of Eq. [17] represents the rigid-body spin.

All VPSC calculations are carried out in the co-rotational material frame defined by the polar composition in Eq. [16], and the input L^vpsc is rotated accordingly as follows:

$${{\mathbf{L}}^{{\varvec{v}}{\varvec{p}}{\varvec{s}}{\varvec{c}}}}^{\boldsymbol{^{\prime}}}={{\varvec{R}}}^{{\varvec{T}}}{{\varvec{D}}}^{\mathbf{M}\mathbf{i}\mathbf{s}\mathbf{e}\mathbf{s}-\mathbf{p}}{\mathbf{R}}+{\dot{\mathbf{R}}} .$$

(18)

This preprocessing procedure for the deformation gradient is successfully applied to simulate textural changes during hot rolling of thick plates^[3] neglecting, however, the contribution of the rotation rate $\dot{{\varvec{R}}}$. After the VPSC simulation, the final grain orientations are defined with respect to the co-rotating material frame; hence, they must be rotated back to the global rolling frame where all texture components are evaluated.

For VPSC, the velocity gradient obtained in the global reference system could be used as input for the crystal plasticity simulations, without need of expressing it in the co-rotational material frame. However, this cannot be done for GIA, whose formulation requires the displacement gradient tensor to be described in a co-rotational orthotropic sample coordinate system.^[58] For this reason, to be consistent in the comparison of VPSC and GIA, the input for both models was described in the co-rotational material frame.

In both GIA and VPSC, the constitutive law is described through the Voce hardening equation. According to Tomé et al.,^[52] the change in the threshold stress with respect to the shear strain in each grain is calculated as follows:

$${\widehat{\tau }}^{S}={\tau }_{0}^{S}+\left({\tau }_{1}^{S}+{\theta }_{1}^{S}\Gamma \right)\left(1-exp\left(-\Gamma \left|\frac{{\theta }_{0}^{S}}{{\tau }_{1}^{S}}\right|\right)\right),$$

(19)

where $\Gamma =\sum_{S}{\Delta \gamma }^{S}$ is the accumulated shear in the grain and τ₀, θ₀, θ₁, and (τ₀ + τ₁) are the initial critical resolved shear stress, the initial hardening rate, the asymptotic hardening rate, and the back-extrapolated critical resolved shear stress, respectively. The values used in both GIA and VPSC are listed in Table II.

Table II Voce Hardening Parameters Used for Cold-Rolling Simulations of Aluminum with GIA and VPSC

2.2.4 Düsseldorf advanced material simulation kit (DAMASK)

For modeling microstructural evolution during forming, full-field crystal plasticity simulations are considered the most accurate approach for simulating both in-grain microtextural changes and texture development in polycrystals. Compared to the GIA and VPSC models, full-field crystal plasticity allows the 3D geometry extracted from a microstructure to be input, thus yielding real grain shape and grain boundary distributions. Moreover, these simulations explicitly consider the crystallographic orientations for each grain. In detail, representative volume elements (RVEs) with real grain shapes and grain boundary distributions can be used, and the RVE can be subdivided into a regular grid of material points, with each grain described by several material points (Figure 9(a)). These RVEs are necessary for in-grain microtextural changes.

Fig. 9

Examples of representative volume elements (RVEs) used in crystal plasticity simulations: (a) microstructure formed by grains and (b) one orientation for one material point

Other simpler and more computationally efficient RVEs with single material points corresponding to grains and to crystallographic orientations (Figure 9(b)) can be used, as in this study. Herein, many orientations need to be input to obtain representative textural changes through calculation of the orientation distribution function (ODF). This simple RVE was successfully used by Han et al.^[62] to predict the changes in texture and yield surface during large strain forming operations.

DAMASK uses a large strain formulation in which the deformation gradient maps the material points of the reference configuration into the deformed configuration. For DAMASK, the deformation gradient used as input can be taken from the global reference system or from the co-rotational material frame of an FEM simulation as rigid rotations do not affect texture prediction because of the large strain formulation.

A detailed description of the software used was provided by Roters et al.^[63] In DAMASK, the mechanical equilibrium equation can be solved using a finite element (FEM) solver if the boundary conditions are nonhomogeneous; however, for periodic and homogeneous boundary conditions, a fast Fourier transform (FFT) spectral method is implemented.^[64,65] The spectral solver finds the equilibrium stress and the corresponding strain fulfilling the constitutive law at each material point. The constitutive laws implemented in DAMASK include the elastic behavior described by Hooke’s law, while the plastic behavior can be described through phenomenological crystal plasticity laws or through dislocation density-based models.

During cold-rolling simulations of aluminum, only one single phase is present, where the elastoplastic constitutive behavior is described by elastic constants describing the anisotropy of the crystals. The plastic part is predicted with a phenomenological power law. The elastic part is described with Hooke’s law through the anisotropic elastic stiffness tensor. Due to the cubic symmetry of the crystal, the only constants considered in the elastic stiffness tensor are C₁₁, C₁₂ and C₄₄. The plastic shear rate for each slip system α is described as follows:

$${\dot{\gamma }}^{\alpha }={\dot{\gamma }}_{0}^{\alpha }{\left|\frac{{\tau }^{\alpha }}{{\xi }_{c}^{\alpha }}\right|}^{1/m}sign\left({\tau }^{\alpha }\right),$$

(20)

where ${\dot{\gamma }}_{0}^{\alpha }$ is the reference shear strain rate, ${\tau }^{\alpha }$ is the resolved shear stress for slip system α, ${\xi }_{c}^{\alpha }$ is the slip system strength or shear resistance and m is the strain rate sensitivity exponent. The evolution of the critical shear strength of each slip system is described as follows:

$${\dot{\xi }}_{c}^{\alpha }=\sum_{\beta =1}^{{N}_{s}}{h}_{\alpha \beta }\left|{\dot{\gamma }}^{\beta }\right|,$$

(21)

where h_αβ is the hardening or interaction matrix describing the influence of slip system β on the hardening behavior of slip system Α and N_s is the total number of slip systems. The hardening matrix representing the interaction among different slip systems is calculated as follows:

$${h}_{\alpha \beta }={q}_{\alpha \beta }\left[{h}_{0}{\left(1-\frac{{\xi }^{\beta }}{{\xi }_{\infty }^{\beta }}\right)}^{a}\right].$$

(22)

With respect to the saturation of the slip system strength (${\xi }_{\infty }^{\beta }$), the strength hardening rate coefficient (h₀) and the hardening exponent (a) are obtained. The parameter q_αβ is given by the following equation:

$${q}_{\alpha \beta }=\left({q}_{\text{lat}}+\left({q}_{\text{self}}-{q}_{\text{lat}}\right){\delta }_{\alpha \beta }\right),$$

(23)

where δ_αβ is the Kronecker delta and q_self and q_lat are the self and latent hardening parameters, respectively. q_self is the diagonal term, while q_lat is the off-diagonal term of the hardening matrix. In this study, the latent hardening coefficient is set to 1.0 for coplanar slip systems and 1.4 for noncoplanar slip systems to make the hardening model anisotropic. Table III shows the values of each parameter used in the cold-rolling simulations for aluminum. The values are obtained by fitting the hardening curves used in GIA and VPSC with the phenomenological power law used in DAMASK (Figure 10). In these simulations, only the activation of octahedral slip systems $\left\{111\right\}\langle 01\overline{1 }\rangle$ is considered. The FFT spectral solver is used for cold-rolling simulations because boundary conditions are considered symmetric and periodic during rolling.

Table III Parameters of the Phenomenological Power Law Used for Cold-Rolling Simulations of Aluminum with DAMASK

Fig. 10

Plastic shear stress and strain for the Voce constitutive law used in GIA and VPSC and the refitted phenomenological power law used in DAMASK (all models use a self-hardening value of 1.0 and latent hardening value of 1.4)

3 Results and Discussion

3.1 Constant Friction Model

The first set of simulations is performed using the deformation gradient histories from finite element simulations obtained with constant coefficients of friction (μ). Three values are considered: μ = 0.2, 0.25, and 0.3. The FEM results are used as inputs for GIA, VPSC, and DAMASK. Figure 11(a) shows the deformation gradient histories of the material frame (i.e., F_ND–RD shows no variation as a function of time) inside the roll gap for these three constant friction values. In general, the deformation gradient components are not the ideal choice for describing strain variation during rolling because they may contain information on both rigid-body rotation and deformation. Thus, these components are plotted here only for convenience to highlight the differences in the deformation gradients for the various friction values. Conversely, Figure 11(b) shows the plastic strains from ABAQUS simulations for the different friction coefficients. Evidently, an increase in the coefficient of friction μ causes an increase in F_RD–ND and a shift in the neutral point inside the roll gap. For a coefficient of friction of 0.2, F_RD–ND remains lower than F_ND–ND in the whole rolling gap, while for a friction of 0.3, F_RD–ND reaches values higher than F_ND–ND. When the coefficient of friction is 0.25, the two components of the deformation gradient have the same value. The computed roll forces increase with increasing coefficient of friction and generally appear to be greater than the experimentally measured values under constant friction conditions.

Fig. 11

(a) Deformation gradient components (F_RD–ND, F_ND–RD, and F_ND–ND) inside the roll gap (for a through-thickness position of s equal to 0.85) for several values of the constant coefficient of friction (μ) given by the FE simulation. The circles indicate the position of the neutral point. (b) Plastic strain extracted from ABAQUS simulations

All rolling texture simulations begin with the texture obtained in the near-surface layer of the hot strip (Figure 2(b)). To limit the computation time, 4000 orientations are randomly sampled from the EBSD dataset. For the GIA simulations, the required eight grain aggregates are originally composed randomly; during the simulations, the eight grain aggregates are maintained. The same 4000 orientations are used in DAMASK using an RVE with one material point for each orientation.

The evolution of the relevant texture components as a function of time is extracted for the simulations with GIA, VPSC, and DAMASK. Table IV presents the texture components for which the change in volume fraction is evaluated during the simulations in terms of the Miller indices $\left\{ {hkl} \right\}\langle uvw\rangle$ and the Euler angles (φ₁, Φ, φ₂) according to Bunge’s notation.^[39] The brass, Goss, P, and invGoss orientations describe the α-fibers, while brass, copper, and S pertain to the rolling texture of the β-fibers. The 45 deg ND-rotated cube orientation $\left\{ {00{1}} \right\}\langle 110\rangle$ prevails with pronounced shear. The Q orientation is often observed in the recrystallization textures of aluminum alloys, but it is situated rather close to the 45 deg ND-rotated cube orientation. Therefore, in this study, the Q orientation is regarded as a shear texture component. The orientations labeled E and F constituting the γ fiber are typically observed in the shear textures of FCC materials. To calculate the volume fraction of each texture component, a misorientation of 15 deg around the ideal orientation is considered. If an orientation falls in an overlapping zone between two components, it is assigned to the texture component corresponding to the lowest misorientation. This procedure avoids the risk of counting the same orientation for several texture components.

Table IV Crystallographic Orientations Considered to Compare the Changes in the Aluminum Texture for Different Friction Conditions

Figure 12 shows the texture development characteristics of DAMASK, GIA, and VPSC for a constant coefficient of friction of 0.25. Changes in the volume fraction of texture components evidently occur inside the roll gap, but the final volume fraction of each texture component depends on the approach used in the simulation. The fractions of the exact cube, Goss, P and invGoss orientations are not shown because their volume fractions remain below 3 pct for all the simulations. All three simulation approaches predict the same textural changes in that the amounts of S, copper, and brass first increase inside the roll gap and then decrease towards the exit, with their final amounts being smaller than their initial amounts in the microstructure. However, for both DAMASK and VPSC, when the brass, copper, and S contents decrease, a high volume fraction of rotated 45 deg ND cube develops. Interestingly, in DAMASK and VPSC, the development of a rotated 45 deg ND cube is somewhat delayed compared to that in GIA. In GIA, the 45 deg ND-rotated cube fraction starts to develop before the β-fiber components (i.e., brass, copper, and S) are completely diminished. The final textures predicted by DAMASK and GIA preserve a non-negligible fraction of the Q orientation that is close to the corresponding experimental values. However, the VPSC model describes a reduction in the Q orientation. The amounts of the two γ fiber orientations E and F are approximately 5 pct for both DAMASK and GIA, while there is a strong increase in their volume fractions for VPSC (the evolution of E and F at a constant coefficient of friction is shown in Figures 21(a) through (c) in “Appendix”).

Fig. 12

Textural changes inside the rolling gap (for s equal to 0.85) extracted from DAMASK simulations (a), GIA (b), and VPSC (c) for a constant coefficient of friction of 0.25. The black arrows pointing to single points on the right indicate the position of the volume fraction of texture components obtained from experiments

The changes in the 22 deg RD-rotated cube, 22 deg TD-rotated cube, and 22 deg ND-rotated cube for the three texture models are shown in “Appendix.” Evidently, the changes in the 22 deg ND-rotated cube are similar for GIA and DAMASK, while VPSC overestimate the fraction of this texture orientation (Figure 19(a)). The fraction of 22 deg RD-rotated Cube is accurately predicted only by DAMASK (Figure 19(b)). The predicted fraction of 22 deg TD-rotated Cube is the same for GIA, DAMASK, and VPSC and lower than the fraction found in experimental sample (Figure 19(c)).

In Figure 13, the final textures from DAMASK, GIA, and VPSC simulations are compared with the texture obtained experimentally by plotting the amount of each texture component. The predicted values of the shear texture components—45 deg ND-rotated cube and Q orientation—are overestimated by GIA and DAMASK. DAMASK and GIA predict the development of β-fiber components (brass, S, and copper) reasonably well, while their fractions are negligible in VPSC. Moreover, DAMASK better predicts the development of a 22 deg RD-rotated cube, while GIA better predicts the development of a 22 deg TD-rotated cube. The fractions of the E and F orientations predicted by DAMASK and GIA are in good agreement with the experimental values, while VPSC overestimates them.

Fig. 13

Volume fractions of the final texture components obtained through simulations with a constant coefficient of friction of 0.25 and from experiments when s is 0.85

Similar simulations are performed for the other coefficients of friction, i.e., 0.2 and 0.3. For a value of 0.2, all the simulation models show no development of the shear components at 45 deg ND-rotated cube, Q, E, and F, while there is a continuous increase in all the β-fiber components with fractions that remain high in the final texture. Conversely, at a coefficient of friction of 0.3, all three simulation approaches yield higher fractions for the components 45 deg ND-rotated cube, Q, E, and F than at a coefficient of friction of 0.25. However, the amounts of the β-fiber components S, copper, and brass are either lower than 5 pct (DAMASK and VPSC) or equal to the amount in the initial microstructure (GIA). Thus, a variation in the coefficient of friction seems to have a strong influence on both the β-fiber components and the shear texture components, while the cube, Goss, invGoss, and P orientations are not significantly affected by the coefficient of friction.

In addition to comparing the volume fractions of the various texture components, for all the simulations, the final texture is compared with the experimental deformation texture by an assessment of the resulting orientation distribution functions (ODFs). Specifically, the texture indices of the differences between the simulated and the experimental ODFs are used to estimate the abilities of different simulation approaches to predict the final texture, as suggested by Van Houtte et al.^[24] Table V shows the differences in texture indices and the deviations in the roll forces determined by the finite element simulations against the experimental roll forces ∆F_Roll. The experimentally measured roll force is 1121.5 kN. A friction value of 0.2 yields an unsatisfactory texture prediction for DAMASK and VPSC, as indicated by the relatively large texture index. However, a constant friction value of 0.3 produces a texture that deviates from the experimental results for GIA and VPSC and considerably overestimates the roll forces. The results shown in Table V suggest that at high values of friction, full-field crystal plasticity predicts textural changes better than the other approaches. However, for low friction values, the prediction of texture with DAMASK is poorer than that with GIA. This worsening of texture prediction at a low friction can be attributed to the choice of the representative volume element (RVE), which has one material point assigned to each orientation. This RVE does not contain the real grain shape; thus, high deformation gradients are necessary to provoke a change in orientation. RVEs containing grains with many material points assigned to each orientation benefit from the grain boundaries promoting texture development. However, RVEs with full grain shapes are much more computationally expensive. Moreover, some authors^[36] have recently assessed that the value chosen for latent hardening in the phenomenological power law influences the amount of total cube texture predicted by the simulations. Another reason why the texture prediction of DAMASK improves with increasing coefficient of friction while that of the GIA and VPSC declines may be ascribed to the strain formulation used in the different simulation approaches. DAMASK is based on a large strain formulation, while GIA and VPSC can operate on small strain increments.

Table V Texture Index Differences Between the Experimental and Simulation Results and Roll Force Variations for Different Friction Conditions for Texture Simulations Performed with DAMASK, GIA, and VPSC

Figure 14 shows sections of the orientation distribution functions for both the experimental and final textures from the DAMASK, GIA, and VPSC simulations. The ODF intensity is generally higher for all the simulations than for the experiment, which is expected because in the simulations, only a few discrete orientations are considered compared to the experimental EBSD scans. For both the simulations and experiments, the highest intensity in the 0 deg section corresponds to the 45 deg ND-rotated cubes and Q orientations. In the 45 and 65 deg ODF sections for the experiment, DAMASK and GIA, the highest intensity corresponds to the 45 deg ND-rotated cube (marked by squares). The experimental ODF sections confirm that a certain amount of exact cube orientation is present in the microstructure, and only ODF sections from VPSC simulations show the remaining exact cube orientation. The GIA and especially the VPSC predict a strong intensity for the γ fiber in the ODF section corresponding to a φ₂ of 45 deg.

Fig. 14

Orientation distribution function sections for φ₂ equal to 0, 45, and 65 deg for the experiments and DAMASK, GIA, and VPSC simulations. The maximum intensity for the experiment is 6.46, while the maximum intensities are 12.90, 27.20, and 10.77 for DAMASK, GIA, and VPSC simulations, respectively. The round markers in the experimental ODF indicate the position of the exact cube orientation, while the square markers indicate the position of the 45 deg ND rotated cube

These findings agree with previous results presented in the literature,^[66,67] where for a high coefficient of friction at the roll and strip contact surface, the stable end texture moves from the copper orientation towards the ND-rotated cube orientation. In contrast, when the friction of the contact area between the roll and strip is small, e.g., because of good lubrication, the texture is composed of β-fibers (i.e., copper, brass, and S). In the present simulations, deformation gradients associated with friction coefficients less than or equal to 0.2 do not produce a relevant amount of shear texture but only a β-fiber orientation. Chen et al.^[66] observed homogeneous β-fibers throughout the thickness of an aluminum strip for a constant friction value of 0.1, while Kim and Lee^[67] showed that the shear texture dominates for friction values reaching 0.4. Thus, the present results obtained for variations in constant friction confirm previously published texture results, but in addition, they emphasize that a constant friction does not reflect the true contact changes between rolls and strips since it overestimates the roll forces of the cold-rolling process.

3.2 Variable Friction Model

Although the use of an appropriate constant coefficient of friction in finite element simulations can allow for the acceptable prediction of textural changes, a serious overestimation of the roll forces is observed. Moreover, as addressed above, it is unrealistic that the coefficient of friction will remain constant during a rolling pass. Friction is expected to change as a function of the contact length and contact pressure between the rollers and the sheet. Under dry rolling conditions, the progressive increase in the contact area causes a gradual increase in the coefficient of friction.^{[68,69,70,71]} As an alternative, the variable coefficient of friction model presented here considers a gradually increasing coefficient of friction from the entrance to a final value of 0.28 at the exit of the roll gap. The change in the coefficient of friction as a function of the position through the roll gap is described as follows:

$$\mu =2{\mu }_{1}\left(\frac{\varepsilon }{{\varepsilon }_{tot}}\right)+2\left({\mu }_{1}-{\mu }_{2}\right)\left(0.5-\frac{\varepsilon }{{\varepsilon }_{tot}}\right),$$

(24)

where the coefficients μ₁ equal to 0.18 and μ₂ equal to 0.1 are empirically chosen, while the ratio of the current strain to the total strain $\left({\varvec{\varepsilon}}/{{\varvec{\varepsilon}}}_{\mathbf{t}\mathbf{o}\mathbf{t}}\right)$ describes the relative coordinate in the roll gap. Figure 15(a) shows the changes in the coefficient of friction according to Eq. [24], scaled to the contact time from the entrance to the exit of the roll gap. Figure 15(b) shows the deformation gradient extracted from finite element simulations considering the variable friction model, while Figure 15(c) represents the plastic strain from the ABAQUS simulation. The deformation gradient is subsequently applied in DAMASK, GIA, and VPSC to predict the corresponding textural changes.

Fig. 15

Changes in the coefficient of friction as a function of time as the sheet passes through the roll gap (a) and deformation gradient components (F_RD–ND, F_ND–RD, and F_ND–ND) inside the roll gap for the variable friction model used in the DAMASK, GIA, and VPSC simulations (b). The circle in (b) indicates the position of the neutral point. (c) Changes in plastic strain from ABAQUS for the variable friction model

Figure 16 shows the textural changes inside the roll gap from the DAMASK, GIA, and VPSC simulations, while Figure 17 shows a comparison between the final volume fractions obtained from simulations and experiments for the variable coefficient of friction. In Figures 16(a) and (b), both DAMASK and GIA show the development of 45 deg ND-rotated cube, but this amount is lower than the fraction obtained with a constant friction coefficient. The volume fractions of brass, copper, and S increase inside the roll gap and decrease at the exit, as observed for constant friction. However, for variable friction, the final amounts of brass, copper, and S are greater, causing an overestimation of copper and S in GIA (Figure 16(b)). The variable coefficient of friction model improves the prediction of brass, S, and copper for DAMASK (Figure 16(a)), but it causes an underestimation of these components in VPSC (Figure 16(c)). The fraction of the Q orientation is overestimated in DAMASK and GIA, while its prediction is improved in VPSC for a variable friction coefficient. The variable coefficient of friction model decreases the fraction of the 22 deg ND-rotated cube for all models, improves the prediction of the 22 deg RD-rotated cube for VPSC, and negligibly influences the 22 deg TD-rotated cube (Figures 20(a) through (c) in “Appendix”). For the variable coefficient of friction model, the changes in E and F are effectively predicted by DAMASK and GIA, while they are still overestimated in VPSC. Nevertheless, the final volume fraction is lower than that of the constant friction approach (Figures 21(d) through (f) in “Appendix”).

Fig. 16

Textural changes inside the roll gap (for s equal to 0.85) extracted from DAMASK (a), GIA (b), and VPSC (c) for a variable coefficient of friction. The black arrows pointing to single points on the right indicate the position of the volume fraction of texture components obtained from experiments

Fig. 17

Volume fractions of the final texture components obtained through simulations with a variable coefficient of friction and from experiments when s is 0.85

By comparing the volume fractions shown in Figure 17 with the results obtained for constant friction (Figure 13), the predicted amount of the 45 deg ND-rotated cube decreases for all the simulation approaches, which leads to an improvement in DAMASK and GIA but a degradation in VPSC. The prediction of the Q orientation, which is overestimated in the constant friction model, improves for all the simulation approaches with variable coefficients of friction. The prediction qualities of the γ fiber components E and, particularly, F with the variable friction model slightly deteriorate for DAMASK and GIA. Conversely, for the VPSC approach, the fractions are comparable to those obtained than those obtained with constant friction and still much larger than those in the experiment. The estimation of the 22 deg ND cube degrades for DAMASK and VPSC because a lower fraction is predicted with a variable friction coefficient. However, the prediction of 22 deg RD cube is improved for VPSC and GIA. Interestingly, the rotated 22 deg TD cube component is not affected by friction variations. The variable coefficient of friction model improves the prediction of the volume fractions of β fiber components (brass, copper, and S) for VPSC and DAMASK but causes a great overestimation of both S and copper in GIA.

Figure 18 shows the corresponding ODF sections for simulations performed using the deformation gradient from the variable friction model. With a variable coefficient of friction, the difference in the texture indices for the DAMASK simulations is 1.92, while it is 1.70 for GIA and 2.1 for VPSC (Table V). Thus, there is an improvement in texture prediction with GIA when using the variable coefficient of friction model, while the DAMASK results are less accurate than those obtained using a constant coefficient of friction (especially when examining the ODF section corresponding to a φ₂ of 45 deg). The rapid decrease in the texture components at the roll gap exit in VPSC (Figure 16(c)) is a consequence of the shift in the texture peaks from their ideal positions, as is visible in the ODF sections for the rotated Cube 45 deg ND (Figure 18). This shift in the rotation peaks reflects the rotation of the material frame from the sample frame, which is strongest for VPSC and weakest for GIA (Figure 18). DAMASK also predicts a shift in the peak positions for the maxima of the texture components, but this shift is not as strong as that of VPSC. This difference can be a consequence of the different treatments of the continuum mechanics in all three simulation approaches.

Fig. 18

Orientation distribution function sections for φ₂ values of 0, 45, and 65 deg for the experiments and for the DAMASK, GIA, and VPSC simulations for the variable friction model. The maximum intensity for the experiment is 6.46, while the maximum intensities are 10.59, 16.52, and 11.33 for DAMASK, GIA, and VPSC, respectively. The round markers in the experimental ODFs indicate the position of the exact cube orientation, while the square markers indicate the position of the 45 deg ND-rotated cube

In the overall evaluation of texture models, the computational effort to obtain a result is important, especially if the models are to be used in optimization processes that require numerous runs for a specific configuration. DAMASK is the only model for computing an RVE at spatial resolution, whereas GIA and VPSC are based on statistical approaches. Although DAMASK has a high predictive capability, it consumes the most CPU time—approximately 1 hour on eight processors or 6.5 hours on a single processor per streamline—for the cases discussed above. The computation of a streamline in a GIA requires approximately 4 minutes on a single processor. The net computing time of VPSC is one minute on a single processor, but additional 4 minutes are required for preprocessing to extract the velocity gradient from the finite element calculation.

4 Summary and Conclusions

The textural changes during cold rolling of aluminum alloys were affected by the deformation history during the rolling pass. Especially in the near-surface layers of a rolled strip, high friction could prevail, resulting in the formation of a strong shear texture as opposed to the conventional β fiber plane strain texture typically observed in the center of the cold-rolled strip. In this study, we employed finite element simulations to determine the strain history of an aluminum alloy AA 5754 hot strip subjected to one cycle of cold rolling without lubrication to maximize the amount of shear in the surface region. The strain path was used as an input to three different texture models to assess their ability to predict shear textures, viz. the grain interaction (GIA) model, the viscoplastic self-consistent (VPSC) approach, and the full-field crystal plasticity DAMASK code. Texture simulations were performed under constant and variable friction conditions. The predicted textures were expressed as orientation distribution functions and compared to the experimental textures in terms of the volume fractions and the differences in texture indices of the main texture components. Furthermore, the simulated roll forces were considered to evaluate the quality of the underlying friction model.

While GIA and VPSC are fast codes, based on statistical approaches, DAMASK computes on a spatially resolved RVE. Accordingly, DAMASK showed best predictive quality but at the expense of significantly greater computational effort. Among the faster statistical approaches, the GIA model, which was based on grain-to-grain interactions within eight grain aggregates, was superior to the VPSC code, where grain interactions were approached in a statistical manner.

The assumption of a constant Coulomb coefficient of friction along the whole length of the roll gap required the use of a value of 0.25 to obtain acceptable agreement with the texture in cold-rolling experiments. The best texture agreement between the simulation and experimental results was obtained for DAMASK, followed by GIA and VPSC. However, a coefficient of friction of 0.25 was rather high, which in turn caused a 44 pct overestimation of the roll forces.

In addition to overestimating the roll forces, the assumption of a constant friction factor was physically not realistic. Therefore, a variable coefficient of friction model was implemented, which assumed a gradually increasing value to reflect the progressive increase in the contact ratios of the rolls and strip surfaces. The variable friction model improved the texture prediction for the GIA model and, to some extent, for VPSC and DAMASK. Simultaneously, reasonable roll forces were computed. In the variable coefficient of friction model, GIA showed lowest differences in texture indices, but DAMASK provided a better qualitative prediction of the volume fractions of the main texture components.

Appendix

See Figures 19, 20, and 21.

Fig. 19

Changes in the 22 deg ND-rotated cube (a), 22 deg RD-rotated cube (b), and 22 deg TD-rotated cube (c) for texture simulations with DAMASK, GIA, and VPSC for a constant coefficient of friction of 0.25. The black arrows in the graphs indicate the values obtained from the experiments

Fig. 20

Changes in the 22 deg ND-rotated cube (a), 22 deg RD-rotated cube (b), and 22 deg TD-rotated cube (c) for texture simulations with DAMASK, GIA, and VPSC considering a variable coefficient of friction. The black arrows in the graphs indicate the values obtained from the experiments

Fig. 21

Changes in E and F orientations at a constant coefficient of friction of 0.25 for DAMASK, GIA, and VPSC (a) through (c) and at variable coefficient of friction for DAMASK, GIA, and VPSC (d) through (f)