Incorporating Dislocation Mechanisms into a Phenomenological Cyclic Plasticity Model for Structural Alloys

Abstract

This article presents an approach to incorporating dislocation mechanisms into a phenomenological cyclic plasticity model that describes the cyclic hardening and softening response of structural alloys in the low cumulative plastic strain (microplastic) and high cumulative plastic strain (macroplastic) regimes. The cyclic constitutive model extends an existing microstructure-based Ramberg–Osgood type model, called MicroROM, for representing the stress-strain curves of Ni-based superalloys subjected to monotonic loading to cyclic loading by considerations of pertinent dislocation mechanisms in face-centered cubic (fcc) alloys and metals. The dislocation mechanisms considered include multipole trapping of dislocation pileups on parallel slip planes and its breakdown by cross slip, leading to the formation of low-energy dislocation structures by multiple slip. These considerations of the various dislocation mechanisms lead to a Ramberg–Osgood type constitutive model that describes the strain hardening response associated with single slip in the low cumulative plastic strain regime (before macroscopic yielding at 0.2 pct plastic strain offset), the strain hardening response during multiple slip in the high cumulative plastic strain regime (beyond macroscopic yielding at greater than 0.2 pct plastic strain offset), and the evolution of cyclic hardening to cyclic softening induced by the onset of shear localization. Applications of the extended cyclic plasticity model to several fcc metals and Ni-based superalloys are presented.

1 Introduction

The safe and efficient utilization of metallic materials in engineering structures subjected to cyclic loading requires an accurate cyclic plasticity model for representing the fatigue response including strain localization, crack initiation resistance and damage tolerance. One of the constitutive models that is commonly used in structural analyses and life-prediction assessment is the Ramberg–Osgood (RO) constitutive model,^[1] which is given by

$$\frac{{\Delta \varepsilon_{\text{t}} }}{2} = \frac{{\Delta \varepsilon_{\text{e}} }}{2} + \frac{{\Delta \varepsilon_{\text{p}} }}{2}$$

(1)

where the total strain amplitude is taken to be comprised of the sum of the elastic strain amplitude, as given by

$$\Delta \varepsilon_{\text{e}} = \frac{\Delta \sigma }{E}$$

(2)

and a plastic strain amplitude, ∆ε_p/2. The plastic strain amplitude is related to the stress amplitude, ∆σ/2, according to a power-law, which can be expressed as

$$\frac{\Delta \sigma }{2} = k\left( {\frac{{\Delta \varepsilon_{\text{p}} }}{2}} \right)^{n}$$

(3)

where n is the strain hardening exponent and k is the strength coefficient. Both k and n are empirical constants. For monotonic loading, k and n are evaluated by plotting stress, σ, and plastic strain, ε_p, in a double logarithmic plot. For cyclic loading, the empirical constants are evaluated by plotting the stress amplitude and the plastic strain amplitude of the stable hysteresis loops at cyclic saturation in a double logarithmic plot to obtain the slope, n, and the stress intercept, k. In case of cyclic softening, the stress amplitude and the plastic strain amplitude at the half fatigue life are used instead of the hysteresis loops. The RO model does not contain any internal variable so that integration of evolution equations of the internal variables is not necessary. As such, the RO model can be applied easily and efficiently. The Ramberg–Osgood model is implemented in a probabilistic life-prediction software, DARWIN^®,^[2] for performing structural analyses and life-prediction assessments of aero-engine components.

Recently, there has been a lot of interest in developing physics-based yield stress and constitutive models^[3,4,5,6,7] for predicting the onset of yielding as well as predicting the stress-strain response of Ni-based superalloys as functions of grain size as well as microstructural variables such as the volume and size of primary, secondary, and tertiary γ´ precipitates. One particular physics-based constitutive model is the microstructure-based Ramberg–Osgood Model, MicroROM,^[7] which describes the stress-strain response of Ni-based superalloys under monotonic loading conditions. One of the significant features of MicroROM is the use of two strain hardening regimes^[7,8]: (1) self-hardening (n₁) of the operative slip plane in the low plastic strain regime (before macroscopic yielding at less than 0.2 pct plastic strain offset under monotonic loading), and (2) latent hardening of multiple slip systems (n₂) in the high plastic strain regime (beyond macroscopic yielding at greater than 0.2 pct plastic strain offset under monotonic loading) for describing the hardening response of Ni-based superalloys. In MicroROM,^[7,8] the strain hardening exponents, which are n₁ and n₂, are correlated with microstructural variables such as the volume fractions and sizes of primary, secondary, and tertiary γ′ precipitates. The observation of two hardening regimes was also made in Ni-based superalloys subjected to cyclic loading.^[9,10] Furthermore, cyclic softening has also been treated and incorporated into a RO-type constitutive model.^[9] According to this RO-type power-law, the stress amplitude, σ_a, is governed by a power-law of the cumulative plastic strain according to

$$\sigma_{\text{a}} = k\left( {N\varepsilon_{\text{pa}} } \right)^{n}$$

(4)

where N is the number of fatigue cycles and ε_pa is the plastic strain amplitude. Since Nε_pa represents the cumulative plastic strain, the low and high plastic strain regimes correspond to low and high cumulative plastic strain regimes, respectively. The strain hardening exponent, n, is given by the slope of a double plot of log σ_a vs log ε_pa, resulting in

$$n = \frac{{d\log \left( {\sigma_{\text{a}} } \right)}}{{d\log \left( {N\varepsilon_{\text{pa}} } \right)}} = \frac{{d\log \left( {\sigma_{\text{a}} } \right)}}{d\log \left( N \right)}$$

(5)

since the imposed plastic strain amplitude is typically a constant for cyclic loading under an applied strain amplitude. The power-law approach is different from the relation of linear strain hardening, dσ/dε_p, vs stress that is often used for analyzing the strain hardening behaviors of fcc metals and alloys.^[11] It is important to note that Eqs. [3] and [4] are different and can lead to different n values after the onset of cyclic softening. In a previous study,^[9] Chan showed that for Ni-based superalloys, Eqs. [3] and [4] provided similar n values prior to cyclic softening but led to different n values after the onset of cyclic softening and shear localization due to shearing of γ′ precipitates by dislocations. Therefore, Eqs. [3] and [4] can be expected to result in different n values for fcc alloys after the onset of cyclic softening and shear localization.

The onset of cyclic softening in Ni-based superalloys has been shown to arise from two different dislocation mechanisms: (1) shearing of the ordered γ′ phases (L1₂ structure) by {111} slip into two halves, and (2) interaction of {111} slip with forest dislocations at the γ/γ′ interface.^[9,10] Despite these advances, the origin of the variability of strain hardening response in the low and high cumulative plastic strain regimes remains unclear. The dislocation mechanisms that control the transition of strain hardening in the low plastic strain regime (before macroscopic yielding) to those in the high plastic strain regime (beyond macroscopic yielding) remains elusive. To address these unresolved questions, an investigation has been undertaken to elucidate the cyclic hardening and softening mechanisms in face-centered cubic (fcc) metals and alloys for the purposes of identifying the dislocation processes operative in the low and high cumulative plastic strain regimes, with particular attention focused on the transition of self-hardening of single slip to latent hardening of multiple slip systems. Single-phase fcc metals and alloys have been selected for detailed examination and mechanistic modeling because considerable information on the dislocation mechanisms are available in the literature. In addition, the dislocation mechanisms in the single-phase fcc metals and alloys are not as complicated as those found in two-phase Ni-based superalloys, which contain shearable γ′ precipitates (L1₂ structure) dispersed in the fcc γ matrix. Slip processes in the two-phase Ni-based superalloys are also complicated by cross slip from the {111} planes to {010} planes to form incomplete and complete Kear–Wilsdorf (K-W) locks.^[12]

The objective of this article is to present the results of an investigation focused on the formulation of a cyclic plasticity model that is capable of treating the strain hardening and softening response of structural alloys on the basis of the dislocation mechanisms and structures associated with the underlying slip processes so that the sources of possible variability of cyclic strain hardening behavior can be identified and quantified. The framework of the cyclic plasticity model is motivated by cycle hardening and softening response and dislocation mechanisms reported for single-phase fcc metals and alloys in the literature.^{[13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29]} These experimental observations are highlighted in Section II. Formulation of the Ramberg–Osgood (RO) type cyclic plasticity model is presented in Section III. The proposed Ramberg–Osgood type model treats cyclic hardening in the low and high cumulative plastic strain regimes, as well as the onset of cyclic saturation followed by cyclic softening. Experimental evidence for the support of the proposed cyclic plasticity model is presented in Section IV. Model applications for several fcc metals and a Ni-based superalloy are presented in Section V, followed by Discussion and Conclusions

2 Cyclic Hardening and Softening in FCC Metals and Alloys

An extensive collection of cyclic hardening and softening curves have been reported by Li et al.^[13] for [−1 4 14]-oriented Ag single crystals tested at ambient temperature under fully reversed plastic strain-controlled conditions at a strain ratio, R_ε, of − 1. Figure 1 presents a double logarithmic plot of shear stress amplitude vs fatigue cycles for two shear strain amplitudes, which can be individually analyzed on the basis of Eqs. [4] and [5]. Three cyclic hardening/softening regimes can be discerned in Figure 1: (1) a small strain hardening exponent (n₁) in the low cumulative plastic strain regime, (2) a larger strain hardening exponent (n₂) in the high cumulative plastic strain regime, and (3) a negative strain hardening exponent (n₃) in the cyclic softening regime. The changes from n₁ to n₂ and from n₂ to n₃ are rather large, signifying substantial changes in the underlying dislocation structures during strain cycling. It should also be worthwhile to point out that the extent of the low cumulative plastic strain regime may be reduced by strain cycling at a higher strain amplitudes, as shown in Figure 1. As reported previously by Li et al.,^[13] the low cumulative plastic strain regime was dominated by single slip on a primary {111} slip plane. The high cumulative plastic strain regime was the results of the activation and interaction of intense primary and secondary slip. The cyclic softening regime corresponded to the onset of the formation of persistent slip bands (PSBs)^{[14,15,16,17]} and the dislocation ladder structure. Similar behaviors have been observed in Cu^{[14,15,16,17]} and Au^[18] single crystals.

Fig. 1

A double logarithmic plot of shear stress amplitude vs fatigue cycles for [−1 4 14]-oriented Ag single crystal^[13] tested under fully reversed plastic strain-controlled conditions (R_ε = − 1) showing: (1) a low cumulative plastic strain regime with a small strain hardening exponent (n₁), (2) a high cumulative plastic strain regime with a larger strain hardening exponent (n₂), and (3) a cyclic softening regime with a negative strain hardening exponent (n₃)

The cyclic hardening behaviors of Cu-30 pct Zn (α-brass) single crystals, a planar slip materials, tested under fully reversed strain-controlled conditions (R_ε = − 1) are presented in Figures 2(a) and (b) for low and high plastic strain amplitudes, respectively. At high plastic strain amplitudes of ∆γ/2 > 1.5 × 10⁻⁴, the relation between shear stress amplitude, τ_a, and fatigue cycle, N, in a double logarithmic plot is typically linear, as shown in Figure 2(a). At a lower plastic strain amplitude (∆γ/2 = 3.8 × 10⁻⁵), however, the relation between log τ_a vs N is bilinear and shows an apparent cyclic saturation in the second stage. The n₁ value is high initially with n₁ = 0.1099, but decreases to almost to zero (n₁ = 3.67 × 10⁻⁴) with increasing fatigue cycles, as shown in Figure 2(a). Both slopes are labelled as n₁ because the cumulative plastic strain is well below that for macroscopic yielding (N∆γ/2 < 3.8 × 10⁻³). The dislocation structure in this regime has been characterized as dislocation patches with segments of multipoles.^[19,20,21] The change of the n₁ value observed at this plastic strain amplitude is not well understood but the apparent cyclic saturation suggests a possible breakdown of multipoles and PSB formation. At high plastic strain amplitudes (above ∆γ/2 = 6 × 10⁻⁴), bilinear cyclic hardening curves are observed with a low n₁ value (n₁ < 0.0461) that transitions to a higher n₂ value (n₂ > 0.3578) during strain cycling, as shown in Figure 2(b). The transition was caused by a massive multiplication of dislocations as the results of primary and secondary slip.^[19,20,21]

Fig. 2

Cyclic hardening curves of Cu–30 pct Zn^[19,20] tested under fully reversed strain-controlled conditions (R_ε = − 1): (a) low plastic strain amplitudes (below ∆γ_p/2 = 3 × 10⁻⁴), and (b) high plastic strain amplitudes (above ∆γ_p/2 = 6 × 10⁻⁴)

The cyclic hardening/softening curves of [−5 7 9]-oriented Al single crystal,^[22] a wavy slip material, and those of polycrystalline 3003 Al^[23] are also available in the literature. Both alloys show a plateau region in the cyclic hardening curve similar to that observed in Cu-30 pct Zn^[19,20] and Cu single crystals.^[14,15] The plateau region has been attributed to the formation of a two-phase dislocation structure^[14,15] consisted of a ladder structure amid a structure of dislocation patches, loops, and veins.

Figures 3(a) and (b) show the cyclic hardening and softening curves of [−1 2 3]-oriented (single slip-oriented) Ni crystals^[24] and polycrystalline Ni,^[25] respectively. Both were tested under fully reversed strain-controlled conditions (R_ε = − 1). Figure 3(a) shows that the Ni single crystals exhibit a low strain hardening exponent (n₁ = 0.0157) in the low cumulative plastic strain regime but transition to higher strain hardening exponents as the fatigue cycles and the corresponding accumulated plastic strains are increased at both 292 K and 433 K. Cyclic softening is seen to commence as fatigue cycling exceeds 2 K to 3 K cycles. According to Bretschneider et al.,^[24] the dislocation structure associated with the cyclic softening regime was the ladder structure of persistent slip bands. In Figure 3(b), the cyclic hardening and softening curve of polycrystalline Ni shows a high cumulative plastic regime with a strain hardening exponent of n₂ = 0.3176 without a low n₁ and the absence of a low cumulative plastic strain regime. The cyclic softening region commences at about 1 K cycles with an n₃ value of about − 0.00794. The onset of the cyclic softening regime started with the formation of the ladder structure and persistent slip bands.^[25] The slip band spacing in polycrystalline Ni200 has also been shown to decrease with increasing cyclic straining.^[26]

Fig. 3

Cyclic hardening and softening curves of single crystal Ni^[24] and polycrystalline Ni^[25]: (a) [−1 2 3]-oriented Ni crystals, and (b) polycrystalline Ni

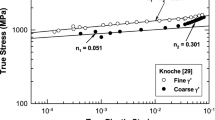
The cyclic hardening and softening curves of several single-phase structural alloys, which include Hastelloy C-22HS,^[27] 316L stainless steel (SS),^[28] and Alloy 617^[29] tested under fully reversed strain-controlled conditions (R_ε = − 1), are presented in Figure 4. For all three alloys, the strain hardening exponents are relatively low, typically of those encountered in the low cumulative plastic strain regime. A higher strain exponent (n₂) typically that of the high cumulative plastic strain regime is absent in these alloys. Instead, all three alloys exhibit cyclic softening with a negative n₃ value ranging from almost zero (n₃ = − 8.37510⁻³) to n₃ < − 0.021. The cyclic softening regimes in the three alloys have been identified to arise from the formation of the ladder structure and persistent slip bands, as well as the presence of intrusions and extrusions on the fatigued surfaces.^[27,28,29]

Fig. 4

Cyclic hardening and softening curves of Hastelloy C-22HS,^[27] 316L SS,^[28] and Alloy 617^[29] tested under fully reversed strain-controlled conditions (R_ε = − 1): (a) Hastelloy C-22HS and 316L SS, and (b) Alloy 617

A summary of the strain hardening exponents in the low cumulative plastic strain regime and in the high cumulative plastic strain regime for single-phase fcc single crystals and polycrystalline alloys is presented in Figure 5, which plots the n₁ and n₂ values as a function of the plastic strain amplitudes. The mean value of n₁ is 0.049 ± 0.087, while the mean value of n₂ is about 0.322 ± 0.250. The ± values that follow the mean values are the standard deviations. These mean values and the standard deviations can be utilized to derive the distributions of the n₁ and n₂ values. The ranges of n₁ and n₂ are also indicated in Figure 5 to show the large variability of the n₁ and n₂ values. There is a small overlap between the low and the high plastic strain regimes at n₁ = n₂ = 0.18-0.20. These n₁ and n₂ values are similar to those previously reported for Ni-based superalloys with the γ + γ′ microstructure.^[7,8,9,10]

Fig. 5

Plot of n₁ and n₂ vs plastic strain amplitude for single-phase fcc single crystals and polycrystalline alloys. The n₁ and n₂ values were determined from experimental data reported in the literature.^{[13,19,20,22,23,24,25,26,27,28,29]}

3 Proposed RO-Type Cyclic Constitutive Model

The proposed cyclic plasticity model is an extension of MicroROM^[7] to treating cyclic loading conditions. The approach is to replace stress and plastic strain in the power-law relation in MicroROM with the corresponding stress amplitude (∆σ/2) and the cumulative plastic strain, N∆ε_p/2, leading to a RO-type constitutive model given by^[9]

$$\frac{\Delta \sigma }{2} = k\left( {N\Delta \varepsilon_{\text{p}} /2} \right)\left[ {\frac{{N\Delta \varepsilon_{\text{p}} }}{2}} \right]^{{n\left( {N\Delta \varepsilon_{\text{p}} /2} \right)}}$$

(6)

where k is the strength coefficient, n is the strain hardening exponent, and N is the number of fatigue cycle. The cumulative strain is given by N∆ε_p/2. As evidenced by the experimental data presented in Figures 1, 2, 3 and 4, the presence of multi-linear relations between stress and fatigue cycles in the double logarithmic plot results in the variation of the stress intercepts, which represent the strength coefficients at various plastic strain regimes. Thus, k(N∆ε_p/2) can be taken to evolve with plastic deformation according to^[9]

$$k\left( {N\Delta \varepsilon_{\text{p}} /2} \right) = k_{1} + \left( {k_{2} - k_{1} } \right)\left[ {1 - \exp \left( { - \beta_{1} N\frac{{\Delta \varepsilon_{\text{p}} }}{2}} \right)} \right]$$

(7)

where k₁ is the strength coefficient in the low cumulative plastic strain regime and k₂ is the strength coefficient in the high cumulative plastic strain regime. In addition, a k₃ term, which is the strength coefficient of the cyclic softening regime, is also necessary for treating cyclic saturation and cycling softening. In Eq. [7], β₁ is an empirical constant that controls the rate of change of k from k₁ to k₂ with increasing cumulative plastic strains. The value of k₃ is not described by Eq. [7] but is determined by the stress at the onset of cyclic saturation or softening.

The experimental data shown in Figures 1, 2, 3, and 4 suggest that the strain-hardening exponent (n) can be taken to be^[8,9]

$$n\left( {N\Delta \varepsilon_{\text{p}} /2} \right) = n_{1} + \left( {n_{2} - n_{1} } \right)\left[ {1 - \exp \left( { - \beta_{2} N\frac{{\Delta \varepsilon_{\text{p}} }}{2}} \right)} \right]$$

(8)

where n₁ is the strain-hardening exponent in the low cumulative plastic strain regime, and n₂ is the strain hardening exponent for the high cumulative plastic strain regime. Like the k₃ term, an n₃ term, which is the cyclic strain softening exponent, is not described by Eq. [8], but is dependent on the cyclic saturation or softening mechanism. Both Eqs. [7] and [8] are of the Voce-type,^[30] which describe the evolutions of n and k from initial values of n₁ and k₁ to asymptotic values of n₂ and k₂ with increasing cumulative plastic strains, respectively. These parameters of k_i and n_i (i = 1, 2, and 3) are illustrated in Figure 6. Based on the experimental evidence highlighted in Figures 1 through 4, the low cumulative plastic strain regime is dominated by the single slip or mostly single slip, while the high cumulative plastic strain regime is dominated by slip on multiple slip systems. In contrast, cyclic softening represents the onset of the formation of the ladder structure and persistent slip bands with the occurrence of intrusions and extrusions on surface grains. Formulations of the mechanistic models for strain hardening and softening in the low and high cumulative plastic strain regimes are presented in the sections below.

Fig. 6

Plot of cyclic stress amplitude vs cumulative plastic strain depicts: (1) n₁ and k₁ in the low cumulative plastic strain regime, (2) n₂ and k₂ in the high cumulative plastic regime, and (3) n₃ and k₃ in the cyclic softening regime

3.1 Strain Hardening in the Low Cumulative Plastic Strain Regime

The small n₁ value in in the low cumulative plastic strain regime has been observed in single crystals oriented for single slip, e.g., in the [−1 2 3] orientation located at the center of the standard stereographic triangle. The dislocation structure is generally described as patches or veins. There is only one operative slip plane with dislocations with one Burgers vector.^[31] The dislocation patches and veins are comprised mostly of multipoles on parallel slip planes.^[31] Theoretical calculations by Neumann^[32] on the interactions of a free dislocation with dipoles and subsequent computations by Hazzledine^[33] on interactions of multipoles on parallel slip planes have shown that there are four types of dislocation interactions, including: (1) interchange, (2) destruction, (3) equilibrium, and (4) passing, depending on the relative positions of free dislocation with respect to the dipoles or multipoles. Under certain circumstances, the dipoles and multipoles can be unstable and be destroyed by the interacting dislocations. In contrast, multipoles on parallel slip planes can cause dislocation trapping^[34] that results in work hardening under monotonic loading. The analysis by Hazzledine^[34] showed that coplanar trapping of multipoles on parallel slip planes resulted in a power-law with a strain hardening exponent of 1/3, as given by^[34]

$$\tau = \tau_{k} + \frac{Gb}{{8\pi \left( {1 - \nu } \right)}}\left( {\frac{18}{{7bL_{as} }}} \right)^{1/3} \gamma_{\text{p}}^{1/3}$$

(9)

where τ_k is the friction stress of the slip system, G is shear modulus, ν is Poison’s ratio, b is magnitude of Burgers vector, L_as is the mean distance between active dislocation sources, and γ_p is the plastic shear strain. The 1/3 exponent in Eq. [9] is the result of a random distribution of active dislocation sources that leads to a quadrupling of the number of dislocations from these sources per stress increment.^[34] The mean distance, L_as, is related to the density of active dislocation sources.^[34]

The multipole trapping model of Hazzledine^[34] is extended to treat cyclic hardening in the low cumulative plastic strain regime where single slip is operative. A multipole of dissociated dislocations formed on two parallel slip planes under cyclic loading is shown schematically in Figure 7(a). At a distance less than that for passing, the dislocation loops on the two parallel slip planes are trapped and resist further slip unless the applied stress range is increased, thereby providing self-hardening for single slip. For cyclic loading, Eq. [9] can be modified to obtain

$$\frac{\Delta \sigma }{2} = M^{2/3} \left( {\frac{{\Delta \tau_{k} }}{2}} \right)\left[ {1 + \frac{Gb}{{4\pi \left( {1 - \nu } \right)\Delta \tau_{k} }}\left( {\frac{18}{{7bL_{as} }}} \right)^{1/3} } \right]\left( {\frac{{\Delta \varepsilon_{\text{p}} }}{2}} \right)^{1/3}$$

(10)

when ∆σ is stress range, ∆ε_p is the plastic strain range, and M is the Taylor factor. It is noted that the relations of ∆σ = M∆τ_k and ∆ε_p = ∆γ_p/M^[35] are invoked and substituted into Eq. [9] to obtain Eq. [10]. According to this model, the strain hardening exponent is 1/3, which is higher than those observed experimentally in the low cumulative plastic strain regime. The reason for the overprediction is due to the fact that the separation distance between the multipoles may not always be favorable for trapping, as trapping is only one of the four possible types of dislocation interactions. Beside trapping and interchange, other interactions include destruction, equilibrium, and passing. Destruction can lead to softening, while equilibrium and passing lead to a strain hardening of zero. Thus, only trapping can lead to a positive strain hardening exponent. The overall level of strain hardening depends on the probability of occurrence for these four types of interactions. These interaction probabilities were computed previously by Hazzledine^[33] as a functions of friction stress, and the relative distance y, defined in Figure 7(a), of a dislocation pile-up normalized by the critical distance, y_c, for multipole breakdown due to cross slip. A slip line is created when a dislocation passes through the slip plane at distance y, thus the distance y can be referred as the slip line spacing, as commonly done in the literature. Table I summaries the interaction probability, I_p, for multipole trapping as a function of the ratio of y/y_c for both low and high friction stresses. The product of I_p and the strain hardening exponent for trapping n_t = 1/3 gives the overall value for the strain hardening exponent n_1, which is dependent on the ratio of y/y_c. These results of computed n₁ values are tabulated in Table I and presented in Figure 7(b), which shows n₁ and I_p as a function of y/y_c in a double logarithmic plot. The results show clearly that the n₁ and I_p values are essentially independent of the value of the friction stress, τ_k, and depend mainly on the y/y_c ratio, which represents the relative distance of a multipole compared to the critical distance for maximum trapping prior to multipole breakdown due to cross slip.

Fig. 7

Self-hardening of dislocation multipoles on parallel slip planes in the low cumulative plastic strain regime: (a) schematics of dislocation multipoles on parallel planes, (b) strain hardening exponent (n₁) and interaction probability (I_p) as a function of normalized distance y/y_c

Table I A Summary of Interaction Probability (I_p) and Computed n₁ Value for Multipole Trapping. Values of I_p and n_t (= 1/3) are Taken from Hazzledine^[33]

The multipole configuration is not always stable.^[31,32,33] The stability of a multipole configuration depends on the spacing of the multipoles, l_s. According to Saada,^[36] the dislocations of the multipoles experience an attractive stress, which is given by^[36]

$$\sigma_{at} = - \frac{Gb}{{l_{s} }}$$

(11)

where σ_ar is the attractive interaction stress. The attractive stress is, however, resisted by the stress from the forest dislocations, given by^[36]

$$\sigma_{\text{f}} = \alpha_{\text{f}} \frac{Gb}{{l_{\text{f}} }}$$

(12)

where α_f is a constant and l_f is the spacing associated with the forest dislocation. Equilibrium of the dislocations in the multipoles requires that

$$\frac{{l_{s} }}{{l_{\text{f}} }} = \alpha_{\text{f}}^{ - 1}$$

(13)

The value of α_f ranges from 0.3 to 0.5.^[36] Thus, the l_s/l_f ratio is between 2 and 3, as shown in Figure 7(b). The result indicates that the multipoles may become unstable when y/y_c is less than 3. At y/y_c < 3, the attractive stress on the dislocations in the multipoles can cause one or more dislocations to cross slip, which in turn lead to the collapse of the multipoles. Based on these considerations, the range of n₁ values that can be achieved by single slip via the multipole trapping mechanism in the low plastic strain regime is from 0 to 0.165. This range of n₁ values is in agreement with the experimental data shown in Figure 5. Thus, the variability of the n₁ value in the low cumulative plastic strain regime originates from a variation in the slip line spacing (y) from the critical distance for maximum trapping (y_c).

Previously, Chan has shown the strain hardening exponent of Ni-based superalloys is given by^[7]

$$n_{1} = \frac{{\rho_{sk} }}{{\rho_{\text{f}} }}$$

(14)

where $\rho_{sk}$ is the density of superkinks in a dislocation forest of density, ρ_f. For single-phase fcc alloys, the counterpart of the superkink density is the sum of the mobile kink density, $\rho_{mk}$, and cross-slip dislocation density, ρ_xs. Thus,

$$n_{1} = \frac{{\rho_{mk} \left( {1 + \chi_{s} } \right)}}{{\rho_{\text{f}} }}$$

(15)

with

$$\chi_{s} = \frac{{\rho_{xs} }}{{\rho_{mk} }}$$

(16)

where the ratio of $\rho_{mk} /\rho_{\text{f}}$ in Eq. [15], which can be taken to be the strain hardening contributed by dislocation trapping, is given by

$$\frac{{\rho_{mk} }}{{\rho_{\text{f}} }} = 0.3\left( {\frac{y}{{y_{c} }}} \right)^{ - 0.908}$$

(17)

based on the results presented in Figure 7(b). Eq. [16] is the ratio of cross-slip dislocation density to the mobile kink density. In the absence of cross slip and near the point of instability, the strain hardening exponent decreases from 0.111 to 0.090 for y/y_c ratios increasing from 3 to 4, as shown in Figure 7(b). In addition, Figure 7(b) also shows that the strain hardening exponent further decreases from 0.09 to 0 when the y/y_c ratio increases from 4 to ∞. Within the single-slip region, the $\rho_{mk} /\rho_{\text{f}}$ ratio shows an average value of n₁ = 0.051 at y/y_c = 7.0, while the onset of cross-slip may be set at y/y_c = 4 so that n₁ = 0.09, leading to $\rho_{xs} /\rho_{\text{f}}$ = 0.039 and $\chi_{s}$ = 0.765. The critical value y_c is defined by the breakdown of the multipoles that occurs when cross slip allows dislocations to escape from the pile-up of multipoles. According to Wang,^[20] the expression for y_c is given by^[20]

$$y_{c} = \frac{{Gb\sin \zeta \left( {1 - \cos \zeta } \right)}}{{2\pi \tau_{k} \left( {\phi_{\text{p}} - \phi_{c} } \right)}}$$

(18)

where τ_k is the yield or friction stress in shear, $\zeta$ is the angle between the primary slip plane and the cross-slip plane, and ϕ_p and ϕ_c are the Schmid factors of the primary slip and the cross-slip systems, respectively. On the other hand, the propensity of a material to cross-slip depends on the stacking fault energy,^[20] dislocation core effects leading to splitting and the formation of partial dislocations,^[37] and the ability of a screw segment to constrict and cross-glide onto a cross-slip plane.^[38] The critical distance, y_c, is therefore expected to vary with the stacking fault energy and types of partial dislocations as both affect the ease of cross slip.

The strength coefficient, k₁, for the low cumulative plastic strain regime can be obtained from Eq. [10] by accounting for an n₁ value that can range from 0 to 0.33, leading to

$$k_{1} = M^{2/3} \tau_{k} \left[ {1 + \frac{{3n_{1} Gb}}{{8\pi \left( {1 - \nu } \right)\tau_{k} }}\left( {\frac{18}{{7bL_{as} }}} \right)^{1/3} } \right]$$

(19)

where the material parameters include the friction stress (τ_k), the shear modulus (G), the magnitude of the Burgers vector (b), and the mean distance between active dislocation sources (L_as).

3.2 Strain Hardening in the High Cumulative Plastic Strain Regime

Single slip in the low cumulative plastic strain regime can transition to multiple slip in the high cumulative plastic strain regime when the flow stress is increased. Multiple slip can arise from activation of secondary slip and/or cross slip. While cross slip can maintain the same Burgers vector as that involved in the primary slip, secondary slip would require the activation of a second Burgers vector. When a dislocation line on the primary slip plane comes into contact with a dislocation from an intersection secondary slip or cross slip, the two intersection dislocations would react to form three possible characteristic segments^[37,39,40]: (1) a mobile dislocation segment (kink), (2) a sessile segment (an immobile dislocation lock), and (3) a cross-glide segment. The cross-glide segment may not occur if a cross slip plane does not intersect with the primary slip plane. The three dislocation segments or junctions are illustrated schematically in Figure 8(a). Most of the dislocations in the dislocation forest in fcc materials are split into partials on the {111} planes.^[37,40] Since dislocation dissociation on either of the two possible {111} close-packed planes is equally probable for a given Burgers vector, formations of mobile, sessile, and cross-glide junctions are equally probable, leading to a maximum of one-third each for these three types of attractive intersections.^[40] The densities of mobile, sessile, and cross-glide dislocations are expected to evolve due to dislocation interactions during plastic deformation. Furthermore, the mobility of these intersection junctions are distinctly different. The mobile dislocation segment can expand, multiply, and propagate on the primary slip plane via the Frank-Reed mechanism.^[41] The sessile segment is immobile and resist further dislocation motion, but it contributes to the forest dislocation density. These sessile segments can be the Hirth locks,^[42] the Lomer-Cottrell locks,^[43,44,45] multi-junctions,^[46] and collinear dislocation configurations,^[47,48] in the order of increasing junction strengths.^[48] The Hirth lock is formed as the result of the interaction of two Shockley 1/6 < 1 2 1 > partial dislocations to form a 1/3 < 0 1 0 > sessile dislocation.^[42] The Lomer-Cottrell lock is formed as the reaction of two 1/6 < 1 2 1 > partial dislocations to form a 1/2 < 1 0 1 > sessile dislocation on a {0 0 1} plane, which is not a slip plane. In contrast, the cross-glide segment is of the screw dislocation type that can cross slip onto a cross-slip plane when it becomes constricted, depending on the stacking fault energy, and the presence of any dissociations into partials at the dislocation core. The cross-glide segment can cause significant strain hardening by rapid multiplication of dislocation via the double cross-slip mechanism.^[49,50] Dynamic high-voltage transmission electron microscopy (TEM) observations by Fujita and Yamada^[51] have confirmed that work hardening in Al occurs by dislocation multiplications via the Frank-Reed mechanism^[41] in the micro-plastic strain regime but proceeds via the double cross-slip mechanism^[49,50] near the onset of macro-plastic deformation (yielding). In fcc metals such as Cu and Al, a cell structure is formed when the three Burgers vectors on a {111} slip plane are all activated so that formation and rotation of the cell structure is feasible.^[16,17] For multiple slip in the high plastic strain regime, the strain hardening exponent, n₂, that results from latent hardening of multiple activated slip systems can be expressed as

$$n_{2} = N_{s} n_{1} = \frac{{N_{s} \rho_{mk} \left( {1 + \chi_{s} } \right)}}{{\rho_{\text{f}} }}$$

(20)

where N_s is the number of slip systems activated. For polycrystalline materials, five independent slip systems is required for plastic compatibility among grains. Thus, N_s = 5; as a result, n₂ has an average value of 0.255 and an upper bound (UB) value of 0.45, based on the corresponding values of 0.051 and 0.09 for n₁. The predicted n₂ values are presented in Figure 8(b), which are generally in agreement with the experimental data. The variability of the n₂ value originates from the inherent variability of n₁ as well as variations in the number of slip systems activated.

Fig. 8

(a) Schematics of dislocation intersections forming mobile junction, sessile junction, and cross-glide junction, and (b) strain hardening exponents n₁ and n₂ in the low and high cumulative plastic strain regimes, respectively. The n₁ and n₂ values were evaluated based on experimental data reported in the literature.^{[13,19,20,22,23,24,25]}

The strength coefficient, k₂, for the high plastic strain regime is likely determined by one or more of several low energy dislocation structures that are formed during cyclic loading of fcc metals and alloys. In particular, it is well-documented that the dislocation patches and the vein structure formed in the low cumulative plastic strain regime are replaced by a two-phase structure^[14] containing dislocation veins and the ladder structure. Depending on the crystal or grain orientation and strain amplitude, other low-energy dislocation structures that include the walled structure, the labyrinth or maze structure, and the cell structure are possible.^[13,16,31] A generic expression for the strength coefficient, k₂, for the high cumulative plastic strain regime is^[37,51]

$$k_{2} = \overline{\alpha }Gb\sqrt {\rho_{2} }$$

(21)

where $\overline{\alpha }$ is a function of the volume fraction of the ladder structure and the ratio of the flow stress of the ladder structure to that of the dislocation patches, and ρ₂ is the forest dislocation density associated with the high cumulative plastic regime, which may be correlated with the density of an equilibrium two-phase dislocation structures containing PSBs in a matrix of dislocation patches or veins.^[14] The expression for $\overline{\alpha }$, which is available in the article by Saada and Veyssiere,^[37] is functions of material parameters related to the dislocation structure and mobility. Similarly, k₁ can also be expressed in terms of Eq. [21] by replacing ρ₂ with ρ₁ where ρ₁ is the forest dislocation density associated with the low cumulative plastic regime.

The forest dislocation density, ρ_f, can be considered to evolve during plastic cycling from an initial value, ρ₁, to the saturated value, ρ₂, by the expression given by^[7]

$$\rho_{\text{f}} = \rho_{1} + \left( {\rho_{2} - \rho_{1} } \right)\left[ {1 - \exp \left( { - \beta_{3} N\frac{{\Delta \varepsilon_{\text{p}} }}{2}} \right)} \right]$$

(22)

where β₃ is an empirical constant. Besides the forest dislocation density, the strength coefficient can also be related to the slip line spacing, λ, or the dislocation cell size, l_f. Previously, Chan has shown that the slip line spacing is given by^[8]

$$\lambda = D_{g} \left( {\frac{{k_{o} }}{{k_{2} }}} \right)^{2} \left[ {\frac{{\Delta \varepsilon_{\text{p}} }}{2}} \right]_{{}}^{{ - 2n_{2} }} .$$

(23)

where k_o is an empirical constant related to the Hall–Petch constant and D_g is the grain size. As reported earlier, the slip line spacing may exhibit a critical lower limit, λ^*, given by^[8]

$$\lambda * = \frac{\alpha \mu b}{{k_{2} }} = 0.286\;\mu {\text{m}}$$

(24)

based on α = 0.3, μ = 8.156 × 10⁺⁴ MPa, and b = 2.8 × 10⁻¹⁰ m. The critical lower bound limit is likely determined by the relevant dislocation structure and represents the mean dislocation cell size.

3.3 Cyclic Softening

Experimental evidence indicates that the onset of cyclic softening in fcc metals and alloys commences with the formation of the ladder structure from dislocation patches in the vein structure to form a two-phase dislocation structure.^[14] The volume fraction of the ladder structure increases with increasing plastic straining and eventually results in a predominantly ladder structure when all of the dislocation patches are transformed to the ladder structure.^[24] The cyclic softening regime can be described in terms of the expression given by

$$\frac{\Delta \sigma }{2} = k_{3} \left( {\frac{{N\Delta \varepsilon_{\text{p}} }}{2}} \right)^{{n_{3} }}$$

(25)

where k₃ is the strength coefficient and n₃ is the cyclic softening exponent. The value of n₃ can be determined using Eq. [5] and the k₃ value can be obtained as the stress intercept. These model parameters (k₃ and n₃) are defined in Figure 6. The n₃ value is typically negative for cyclic softening, but can also be zero when cyclic saturation occurs. A negative n₃ value can generally be attributed the onset of the formation of the ladder structure for both single crystal^{[13,14,15,16,17,18,24]} and polycrystalline materials^{[25,27,28,29]} and a zero value of n₃ can be attributed to the formation of cyclic saturation in the form of a stable cell size such as those found in single crystal Al^[22] and in a polycrystalline Al alloy.^[23] The strength coefficient k₃ can be related to the critical stress for the onset of the ladder structure, which is also the critical stress for the instability of the dislocation patch structure. The transition from strain hardening due to multiple slip in the high cumulative plastic strain regime to the cyclic softening regime has yet to be formulated since numerous dislocation mechanisms are involved and the effort is reserved for future work.

4 Experimental Evidence and Supports for the Proposed Model

Experimental data from the literature are utilized to support the cyclic plasticity model. Figure 9 shows a verification of the evolution of the strain hardening exponent n, Eq. [8], as a function of cumulative plastic strain for Cu-30 pct Zn (α-brass).^[19,20] The n₁ values were determined from the low cumulative plastic strain regimes, while the n₂ values were evaluated from the high cumulative plastic strain regimes for various plastic strain amplitudes in the plots shown in Figures 2(a) and (b), which show the determination of the n₁ and n₂ values according to Eq. [5] over the range of relevant fatigue cycles. The specific n values are plotted in Figure 9 as a function of the cumulative plastic strains which were obtained as the product of the number of fatigue cycles and the plastic strain amplitudes. In Figure 9, the various symbols depict the cumulative plastic strain values over which the n values are obtained. The results show that the n₁ values occur at low cumulative plastic strains, while the n₂ values occur at high cumulative plastic strains. Based on these results, Eq. [8] was fitted to the experimental data in Figure 9 using n₁ = 0.03 (dashed curve) or n₁ = 0.04 (solid curve), n₂ = 0.36, and β₂ = 0.05. The general trend of the experimental data is well described by Eq. [8], but there is considerable scatter in the n₁ values compared to the n₂ values.

Fig. 9

The evolution of the strain hardening exponent, n, as a function of cumulative plastic strain showing its increase from n₁ to n₂. The n values were determined on the basis of experimental data from the literature.^[19,20]

The evolution of dislocation density in Hastelloy C-22HS, a single phase Ni-based alloy, subjected to monotonic and cyclic loading at room temperature was measured by in-situ neutron diffraction measurements by Huang et al..^[27] For monotonic loading, the specimen was tested under a controlled strain rate and was periodically held under prescribed strain levels where in-situ neutron diffraction measurements were performed for the entire stress-strain curve. Figure 10(a) presents the dislocation density as a function of plastic strain reported by Huang et al.^[27] for monotonic loading (filled circles). For cyclic loading, the fatigue specimen was tested under fully reverse condition under ± 1.0 pct strains and 0.5 Hz. The in-situ neutron diffraction measurements were performed at 7 intervals within a fatigue cycle at periodic cycles up to 1500 cycles. The dislocation density data for the cyclic case are plotted vs cumulative plastic strain and are shown in Figure 10(a) as filled diamonds. The dislocation density for the cyclic case is in agreement with the monotonic case initially at low cumulative plastic strains, but diverge at higher cumulative plastic strains. The cyclic dislocation density appears to saturate at 2.5 × 10⁺⁸ #/cm², while the dislocation density for the monotonic case is considerably higher without exhibiting a distinct saturation limit. Eq. [22] was fitted to the dislocation density data with an initial density ρ₁ = 1 × 10⁶ #/cm² and a saturation limit of ρ₂ = 3.5 × 10⁺⁹ #/cm². It is noted that dislocation density expressed in terms of number per unit area is equivalently to that expressed in terms of line per unit volume. Both units are commonly in the literature to describe dislocation density. The dislocation density results of Huang et al.^[27] were presented in #/cm², which is adapted in this paper. The general trend of the dislocation density measurements is captured by Eq. [22]. It should also be noted that the low plastic strain regime exhibiting the n₁ value lies well below the yield region (< 0.002 plastic strain). The yield stress of Hastelloy C-22HS is 370 MPa.^[27]

Fig. 10

Dislocation density (a) and dislocation cell size (b) as a function of plastic strain (montonic loading) or cumulative plastic strain (cyclic loading) for Hastelloy C-22HS. The experimental data are from Huang et al.^[27]

The dislocation spacing measurements reported by Huang et al.^[27] for Hastelloy C-22HS for monotonic and cyclic loading are presented in Figure 10(b), which shows the dislocation spacing as a function of plastic strain. For monotonic loading, the initial dislocation spacing (i.e., cell size) is essentially constant prior to the onset of macroscopic yielding. In this case, the dislocation spacing is about 20 μm, which is smaller than the average grain size of 90 μm. Beyond macroscopic yielding (0.2 pct plastic strain offset), the dislocation cell size decreases with increasing plastic strains with a slope of − 0.9089, which is in agreement with Eq. [23] and the previous result observed in a Ni-based superalloy.^[8] For cyclic loading, the dislocation spacing is in agreement with that of the monotonic case prior to yielding, but appears to show a saturation level that is different from that of the monotonic case. It is possible that the cyclic loading case is different because the applied plastic strain range was limited to ± 1 pct and the number of fatigue cycles was limited to 1500 cycles only so that the limiting cell size could not be reached within the applied fatigue cycles.

One of the potential applications of the cyclic plasticity model is in the prediction of fatigue crack nucleation, which is signified by the onset of softening followed the formation of fatigue crack formation. The number of fatigue cycles, N*, at which the onset of cyclic softening occurs has been identified for various fcc alloys.^{[13,18,24,25,27]} The plastic strain range in shear is shown as a function of N* in a double logarithmic plot in Figure 11. A regression fit for Ag single crystals results in a slope of − 0.6, which defines the onset cyclic softening. TEM evidence indicates that the onset of cyclic softening corresponds to the onset of persistent slip band (PSB) formation.^[14] The plot in Figure 11, which is reminiscent of that of plastic strain amplitude vs fatigue life cycle, shows that N* corresponds to the formation of PSBs and the event can be viewed as the precursor for the onset of fatigue crack formation. Also shown in Figure 11 are the data points for Au SC, Ni SC, polycrystalline Ni, and polycrystalline Hastelloy C-22HS.^[27] The results of these metals and alloys are generally in agreement with the Ag data and the regression line.

Fig. 11

Plot of shear strain amplitude vs the number of fatigue cycles for R_ε = − 1 at the onset of cyclic softening and PSB formation. Experimental data are from the literature.^{[13,18,24,25,27]}

5 Model Applications

5.1 Single-Phase Metals and Alloys

The key equations of the proposed constitutive model include Eqs. [6] through [8]. The key variables are the strain hardening exponent, n, and the strength coefficient, k, which have been described in terms of mobile dislocation density and forest dislocation density through Eqs. [14], [20], and [21]. Since the appropriate dislocation densities were not available, applications of the proposed model therefore were focused on Eqs. [6] through [8] using experimental data of n₁, n₂, k₁, and k₂ that were available from this study, as presented in Figures 1 through 4. The metals selected for model applications included Ag, Cu-30wt pct Zn, and Ni single crystals, as well as polycrystalline Ni. The inputs to the model were the n₁, n₂, k₁, and k₂ values determined from the experimental data.^{[13,19,20,24,25]} These parameters were used in conjunction with Eq. [6] to compute the cyclic stress vs cumulative plastic strain response for various metals and alloys. The empirical constants β₁ and β₂ in Eqs. [7] and [8] were obtained by fitting the calculated stress amplitude to cumulative plastic strain curves to the experimental data. The calculations encompassed the low cumulative plastic strain regime and the transition regime until the calculated curves merged with the high cumulative plastic strain regime. Thus, the calculated stress amplitude vs cumulative plastic strain curves are not independent model predictions, but merely fitted to the experimental data. For the onset of cyclic softening, Eq. [25] was utilized and fitted to the experimental data to determine the k₃ and n₃ values. The values of k_i, n_i, β₁, and β₂ for these model calculates are listed in Table II.

Table II Summary of the Model Constants Utilized in the Calculations of Cyclic Stress Amplitude—Cumulative Plastic Strain Curves for Selected fcc Metals and a Ni-Based Superalloy

Figure 12(a) presents the calculated cyclic shear stress amplitude vs cumulative plastic shear strain curve compared to the experimental data for Ag single crystals.^[13] The good agreement indicates that Eqs. [7] and [8] provide adequate representations of the evolution of n and k values with increasing cumulative shear strains when β₁ and β₂ are properly chosen. In addition, the cyclic softening curve is adequately represented by Eq. [25]. Similarly, the results for Cu-30wt pct Zn single crystals^[19,20] and Ni single crystals^[24] are presented in Figures 12(b) and (c), respectively. In the transition from the low to the high cumulative plastic regime, the flow stress increases with increasing cumulative plastic shear strains due to increases in the n and k values. For both metals, the evolution of n and k with cumulative plastic strains are well represented by Eqs. [7] and [8], respectively. The cyclic softening regime is absent for Cu-30wt pct Zn because such data had not been reported by the original authors^[19,20]. Figure 12(d) presents the calculated results for polycrystalline Ni.^[25] There is a good fit of the hardening response for the high cumulative plastic strain regime and the cyclic softening regime. The low cumulative plastic strain is absent for this alloy because the original authors^[25] did not report the stress-plastic strain response in this regime. For Ag single crystals, Ni single crystals, and polycrystalline Ni, the transition from cyclic hardening to cyclic softening occurs rather abruptly at the peak stress.

Fig. 12

Comparisons of the calculated and experimental data of stress amplitude vs cumulative plastic strain: (a) Ag single crystals, (b) Cu-30wt pct Zn single crystals, (c) Ni single crystals, and (d) polycrystalline Ni. The calculated curves are fitted to experimental data from the literature.^{[13,19,20,24,25]}

5.2 Ni-Based Superalloys

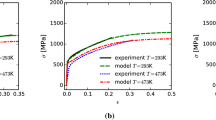
The applicability of the proposed RO-type model to treat the cyclic stress-strain behaviors of single-phase fcc alloys and Ni-based superalloys with the γ/γ′ microstructure can be elucidated by considering the characteristics of the various model parameters for the two groups of structural alloys, which are summarized in Table III. For both types of alloys, the low cumulative plastic strain regime is dominated by single slip with self-hardening being controlled by multipole trapping.^[34] The transition from the low to the high cumulative plastic strain regime is influenced by cross slip either by mobile ordinary dislocation kinks or superkinks.^[7,8,9,10] The high cumulative plastic strain regimes in single-phase fcc alloys and two-phase superalloys are both dominated by multiple slip with latent hardening and the n₂ values being controlled by dislocation intersections to form mobile kinks and sessile dislocation locks. The strength coefficient is related to the strength of the Lomer-Cottrell locks^[43,44] in fcc alloys, but is controlled by the strengths of incomplete and complete K-W locks^[12] in Ni-based superalloys. For cyclic softening due to localized slip, the softening mechanism is related to the formation of the ladder structure^[14,15] and/or the cell structure,^[16,17,31] while it is shearing of the γ′ precipitates in Ni-based superalloys. By virtues of these similarities, Eqs. [6] through [8] and multipole hardening are likely applicable to treat the deformation behavior of the Ni solid solution matrix (γ phase) in γ/γ′ Ni-based superalloys mechanisms. The k and n parameters in the proposed model, Eq. [6], are formulated to evolve with the cumulative plastic strain from initial values of k₁ and n₁ to asymptotic values of k₂ and n₂ according to Eqs. [7] and [8], respectively. In contrast, the k and n parameters in the traditional RO model are based on the stable hysteresis loops at cyclic saturation. Thus, the k and n parameters in the RO model correspond to k₂ and n₂ in the current model, Eq. [6], with N = 1 for the cyclic strain-strain curves at saturation. In addition, the current study has also identified conditions where the low plastic strain regime and the high plastic regime can overlap such that k₁ = k₂ and n₁ = n₂. The overlapped region of n₁ and n₂ is shown in Figure 8(b), which also depicts the corresponding variabilities. For illustration purposes, the cyclic plasticity model has been incorporated with MicroROM for predicting the cyclic stress-strain response of Ni-based superalloys. The resulting model, dubbed Cyclic MicroROM, has been applied to predicting the cyclic stress-strain response of a powder-metallurgy (PM) Ni-based superalloy called ME3 with the supersolvus microstructure subjected to fatigue cyclic under strain-condition at a strain ratio of R_ε = 0. The grain size is 24 to 34 μm. The volume fractions and γ′ sizes are 0.56 and 0.294 μm for secondary γ′ precipitates and they are 9.65 × 10⁻⁵ and 4.2 × 10⁻³ μm for tertiary γ′ precipitates, respectively. The values of n₁ and n₂ were calibrated to be 0.15 and the values of k₁ and k₂ were calibrated to be 2914 MPa by fitting model calculations to experimental data. Other pertinent material constants for ME3 can be found in earlier publications.^[7,8] The calculated stress range and mean stress for ME3 at 977 K are presented in Figure 13(a), while the corresponding plastic strain range are presented as a function of total strain in Figure 13(b), respectively. The calculated stress range, mean strain, and plastic strain range are compared against experimental data of ME3 from NASA.^[53,54] Figures 13 (a) and (b) show that the agreement between model calculations and experimental data are good for the stress ranges in Figure 13(a) and for the plastic strain ranges in Figure 13(b). The computed mean stress values agree with experimental data at low total strain ranges, but are too high at larger total strain range (> 0.5 pct). The higher mean stresses were reduced by a shakedown scheme that lowered the mean stress value, σ_m, with increasing plastic strain ranges according to an exponential decay law, as given by

$$\sigma_{\text{m}} = \sigma_{mo} \exp \left( { - c_{1} \Delta \varepsilon_{\text{p}} } \right)$$

(26)

where σ_mo is the initial elastic mean stress and c₁ is an empirical constant. The rate of decay is controlled by the empirical constant, c₁. The shakedown scheme reduced the mean stress values to match the experimental data, as shown in Figure 13(a). The shakedown scheme requires an accurate prediction of the plastic strain ranges in the micro-plastic regime, as shown in Figure 13(b). An inspection of the results indicates that an n₁ value of 0.15 is located at the boundaries between single slip in the low cumulative plastic strain regime and multiple slip in the high cumulative plastic strain regime, despite the applied total strain range is less than 0.8 pct. This finding indicates that the low and high plastic strain regimes might be overlapped and justifies the conditions of setting n₁ = n₂ = 0.15 and using k₁ = k₂ = 2914 MPa. The shakedown of mean stresses occur at stress amplitudes of 500-750 MPa. These stresses compare favorably with the critical stress for cross slip in Ni-based superalloys, which is about 542 MPa.^[8] Thus, the shakedown of mean stresses appears to correspond to the activation of cross slip and lies beyond the stability limit of multipole trapping associated with self-hardening of single slip plane by multipole hardening.

Table III A Comparison of the Underlying Dislocation Mechanisms Contributing to the Model Parameters in the Cyclic Plasticity Model

Fig. 13

Comparison of calculated and measured stress-strain response of ME3 subjected to strain-controlled cycling at R_ε = 0 at 977 K: (a) stress range and mean stress vs total strain range, and (b) plastic strain range vs total strain range. Experimental data are from NASA.^[53,54]

6 Discussion

One of the significant results of this investigation is the demonstration of the applicability of the power-law hardening formulation in the RO-type model for representing the cyclic hardening behavior of fcc metals and alloys. To the author’s knowledge, this is the first time that the different strain hardening values (n) in the low and high cumulative plastic strain regimes have been identified, evaluated, correlated, and linked to the underlying operative dislocation mechanisms in single-phase fcc metals and alloys. It is noted that none of the original authors in the literature had analyzed their experimental data in this manner^{[13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29]} nor in the review of this subject manner.^[31] In particular, this investigation shows that the strain hardening exponent (n) can be related to the ratio of the mobile dislocation density to the total forest dislocation density and the strength coefficient (k) is directly linked to the total forest dislocation density raised to the 1/2 power. The relationship between strength coefficient and dislocation density is supported by the well-known relationship between flow stress and dislocation density reported in the literature.^[37,52] In contrast, the treatment of strain hardening response under either monotonic or cyclic loading is fundamentally different from the approach that relates the strain hardening rate, dσ/dε_p, to decreasing stress that is frequently applied to fcc metals and alloys.^[11] Thus, the proposed approach offers a new perspective and understanding of the cyclic strain hardening behavior of fcc metals and alloys. When two intersection dislocations react during plastic straining, the mobile segment forms in conjunction with a sessile segment and a potential cross-slip segment.^[37,39,40] Each of these segments is at most one third of the total intersection dislocation line.^[40] Thus, the value of the mobile dislocation density is expected to be a fraction of the total forest dislocation density. As shown previously by Chan,^[7] the strain hardening exponent can be derived by considering the dislocation multiplication process and is given by the ratio of the mobile dislocation density to the total forest dislocation density.^[7] Instead of performing dislocation density measurements, the strain hardening exponent can be measured from a double logarithmic plot of stress vs plastic strain curve for monotonic loading^[7] and from a double logarithmic plot stress amplitude vs cumulative plastic strain curve for cyclic loading.^[8,9]

By analyzing the cyclic stress—cumulative plastic strain data in the literature,^{[13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29]} this investigation has revealed that a low n₁ value in the low cumulative plastic strain regime (i.e., the micro-plastic region) originates from slip on a single slip system in a single crystal or grains in polycrystalline alloy that are oriented for single slip with one activated Burgers vector.^[31] Self-hardening of the slip plane is caused by trapping of multipoles located on parallel slip planes.^[34] The level of self-hardening increases with decreasing distances between the slip planes.^[33,34] The strain hardening exponent (n₁) in the low cumulative plastic strain regime has a small value when the slip line spacing is large such that multipoles trapping is weak or non-existent. As microplastic straining continues, the slip bands harden and force activation of slip on parallel slip planes with decreasing spacing, thereby promoting higher levels of multipole trapping and increasing strain hardening. Single slip continues until the activation of slip on the cross slip and/or secondary slip plane,^{[13,16,17,18,19,20,21,22,23,24,25,26]} which leads to multiple slip with two or more activated Burgers vectors in the transition to the high cumulative plastic strain regime. A dislocation cell structure is formed in fcc metals and alloys when the three Burgers vectors on a {111} slip plane are all activated to enable rotation of the cell structure around the < 111 > axis.^[16,17] The high cumulative plastic strain regime, therefore, involves multiple slip on five independent slip systems. This sequence of cyclic hardening processes has been modeled in Eqs. [7] and [8] using the strain hardening (n) and the strength coefficient (k) as internal variables, which variations during the plastic strain process are described in appropriate evolution equations, without the need to identify or specify the exact dislocation variables or structures.

Using experimental values of n_i and k_i (i = 1, 2 and 3) evaluated for several fcc metals, the proposed RO-type model, Eq. [6] and the evolution equations for n, Eq. [7], and k, Eq. [8], were utilized to compute the cyclic stress amplitude vs cumulative plastic strain curves for Ag, Cu-30 pct Zn, and Ni single crystals, as well as that for polycrystalline Ni by calibrating the empirical constants, β₁ and β₂, in Eqs. [7] and [8] to fit the model to the experimental data. The calculated curves, presented in Figure 12, indicate that the increase in the calculated cyclic stress amplitude in the low and high cumulative plastic regimes including the transition region are in good agreement with the experimental data. Thus, the calculated curves are consistent with the experimental observations that single slip is dominant in the low cumulative plastic strain regime, multiple slip is dominant in the high cumulative plastic regime, and a transition from single slip to multiple slip occurs with increasing cumulative plastic strains. This finding is also consistent with Eqs. [15] and [20] which correlate the values of n₁ and n₂ with the number of slip systems activated. It is also important to point out that in Figure 5, the range of n₁ in low cumulative plastic strain regime overlaps with the range of n₂ in the high plastic strain regime. Within the overlapped region, n₁ = n₂ and k₁ = k₂ so that Eq. [5] can be reduced to the traditional RO model with both n and k being constant and independent of plastic strains or fatigue cycles because of cyclic saturation.

By virtues of Eqs. [15], [20], and [21], the cyclic plasticity model depicted in Eq. [6] can be expressed in an alternative form as given by,

$$\frac{\Delta \sigma }{2} = \overline{\alpha }Gb\left[ {\rho_{\text{f}} } \right]^{1/2} \left[ {\frac{{N\Delta \varepsilon_{\text{p}} }}{2}} \right]^{{\rho_{\text{m}}/ \rho_{\text{f}} }}$$

(27)

which indicates that the proposed RO-type cyclic plasticity model is fully described by the evolutions of forest dislocation density and the ratio of mobile density to the forest dislocation density. The first term on the right-hand side (RHS) of Eq. [27] is well established in the literature,^[37,52] while the second term on the RHS of Eq. [27] is a finding that is deduced from Eqs. [15], [20] and the model calculations shown in Figure 12. Eq. [27] is also consistent with the experimental data shown in Figure 12, which show different cyclic hardening behaviors in the low and high cumulative plastic regimes. The functional forms of n and k in the evolution equations, Eqs. [7] and [8], are also consistent with the experimental data presented in Figures 9 and 10, respectively. In particular, Figure 9 shows that the Voce equation^[30] with two asymptotic values of n₁ and n₂ represents a good description of the strain hardening response of Cu–30 pct Zn. The higher n₂ value supports that notion that the higher cumulative plastic regime involves dislocation intersections on multiple slip systems as postulated in Eq. [20], and the n₁ values is consistent with single slip in the lower cumulative plastic regime as given in Eq. [15]. Thus, Eq. [9] is fully supported by the experimental data presented in Figure 8(b). Furthermore, Figure 10 shows that the measured dislocation density in cyclically deformed Hastelloy is adequately represented by the Voce equation^[30] with two asymptotic values of ρ₁ and ρ₂ for the low and high plastic regimes, respectively. This finding is consistent with the notion that ρ₁ may be associated with forest dislocation density formed by multipole hardening by single slip,^[34] while the larger ρ₂ is consistent with the formation of low-energy dislocation structures by slip on multiple slip systems.^{[14,31,36,37]}

Another finding of this investigation is that the dislocation spacing is essentially constant in the low cumulative plastic strain regime (plastic strain < 0.04 – 0.05), as shown in Figure 10(b) for Hastelloy. In contrast, the dislocation spacing (i.e., cell size) decreases with increasing plastic strains in the high cumulative plastic strain regime (plastic strain > 0.04 – 0.05) due to the activation of multiple slip. In the low cumulative plastic strain regime, the dislocation spacing is determined by the spacing of the active dislocation sources^[55,56] and single slip occurs via the Frank-Reed mechanism.^[41] On the other hand, the dislocation spacing in the high cumulative plastic strain regime is determined by multiple slip via the double cross-slip mechanism,^[49,50] depending on the propensity to cross-slip based on stacking fault energy and dislocation core effects. Furthermore, the mean distance or spacing, L_as, between active dislocation sources can be related to the anelastic modulus and the density of active dislocation sources.^[55,56]

The current cyclic plasticity model is formulated on the basis of dislocation mechanisms pertinent in single-phase fcc metals and alloys. As such, the cyclic plasticity model has the same framework and share many characteristic as the previous model for two-phase Ni- based superalloys.^[7,8,9,10] For both single-phase Ni-alloys and two-phase Ni-based superalloys with the γ/γ′ microstructure, the strain hardening exponent is determined by the ratio of the mobile dislocation density to the forest dislocation density. Mobile kinks are relevant in the fcc γ-alloys, while superkinks are pertinent in the Ni-based superalloys with the γ/γ′ microstructure.^[7,8,9,10] Self-hardening of (111) slip in single-phase Ni-alloys is facilitated by multipole trapping. In Ni-based superalloys, (111) slip first occurs in the γ phase and then (111) slip penetrates the γ′ phase via a pair of superdislocations separated by an antiphase stacking fault. Based on this consideration, it appears that multipole trapping that occurs in the γ phase should also contribute to self-hardening of (111) slip in the γ′ phase in Ni-based superalloys as (111) shearing of the γ′ phase also occurs on parallel planes and it should induce dislocation trapping in γ′ since cross slip is more difficult in the γ′ precipitates than in the γ phase. The identification of dislocation trapping during planar slip in Ni-based superalloys is another important finding since this particular hardening mechanism has not been considered or appreciated in earlier studies.^{[3,4,5,6,7,8,9,10]} In a previous study,^[8] it has been shown that the strain hardening exponent, n₁, in the low plastic strain regime of Ni-based superalloys is given by

$$n_{1} = \frac{6\omega }{\pi }\left[ {f_{1}^{2} + f_{2}^{2} } \right]$$

(28)

where f₁ and f₂ are the volume fractions of primary and secondary γ′ precipitates in the Ni-based superalloys, respectively; ω is the average number of superkinks per unit number of forest dislocation per γ′ precipitate. Previously, the ω parameter has been evaluated by using experimental values of n₁, f₁, and f₂, and ω was determined to be about 0.1168 by fitting to experimental data.^[8] By recognizing that the n₁ value in the γ phase and the γ′ phase is essentially the same when multipole trapping occurs, the n₁ value may be computed via Eqs. [15] through [17] in the absence of cross slip. The resulting n₁ value may then be used in conjunction with Eq. [28] to evaluate the value of ω based on experimental values of f₁ and f₂. On this basis, the ω parameter can be considered as a measure of strain hardening value arising from multipole trapping of super-dislocation pairs in the ordered γ′ phase. The value of ω = 0.1168 is consistent with the upper bound value for n₁ for fcc metals and alloys shown in Figure 5, providing potential support that multipole hardening may be similar in both the γ and the γ′ phases.

7 Conclusions

Dislocation mechanisms have been incorporated into a phenomenological cyclic plasticity model based on the Ramberg–Osgood type formulation to describe the evolution of the strength coefficients and strain hardening exponents in the low and high cumulative plastic regimes of fcc metals and alloys. The evolution laws provide new perspective and understanding for analyzing the cyclic stress-strain response of this class of alloys. The conclusions reached as the results of this investigation are as follows:

• 1. The strain hardening behavior of single-phase fcc metals and alloys has been shown to exhibit a bilinear strain hardening behavior manifesting a small strain hardening exponent (n₁) in the low cumulative plastic strain (microplastic) regime and a higher strain hardening exponent (n₂) in the high cumulative plastic strain (macroplastic) regime. The value of n₂ is typically about 5x of the n₁.

• 2. The small n₁ value in the low plastic strain regime can be attributed to arise from single slip in grains or crystals that are oriented for easy slip. The variations in the n₁ value can be attributed to variations in the slip line spacing and cyclic hardening due to multipole trapping of dislocation arrays on parallel slip planes with the same Burgers vector. The upper limit of the n₁ values in the low plastic strain regime is affected by the breakdown of multipole trapping resulting from cross slip and/or secondary slip.

• 3. The high n₂ value in the high cumulative plastic strain regime in single-phase fcc metals and alloys has been shown to correlate with multiple slip that are known to increase with increasing the number of slip systems activated and the formation of mobile, sessile, and/or cross-glide junctions.

• 4. An extended cyclic plasticity model of the Ramberg–Osgood type is formulated to incorporate dislocation mechanisms that exert an influence on material parameters such strain hardening exponent (n) and strength coefficient (k). The model is capable of representing the cyclic hardening (n₁ and n₂) and softening (n₃) behaviors exhibited by single-phase fcc metals and alloys. Model calculations for Ag, Cu–30 pct Zn and Ni single crystals revealed that the evolutions of the n and k values with plastic straining are consistent with experimental observations of single slip in the low cumulative strain regime, multiples slip in the high cumulative plastic strain regime, and a transition from low n₁ to high n₂ values with increasing number of activated slip systems with increasing cumulative plastic strains.