1 Introduction

During recrystallization, new, deformation-free grains appear in a deformed microstructure, and grow to fully replace it. When the new grains both appear and grow after the end of deformation, the process is referred to as static recrystallization (SRX).[1] In the processing of steel, SRX takes place when annealing after cold rolling. SRX occurs also in the hot-rolling mill, when the material travels between stands. As a softening mechanism, the extent of SRX determines the force acting upon the next rolling stand. Moreover, steels are hot-rolled in the austenite phase, transforming into other phases in the subsequent cooling. The microstructure after this phase transformation depends also on the extent of SRX after hot rolling, in that the internal deformation of parent grains has a strong effect on properties such as grain size.[2] In accordance with this, SRX of austenite has been the subject of a wealth of experimental studies. These have mainly focused on the effect of deformation parameters on SRX kinetics and final grain size,[3,4,5,6] the evolution of crystallographic texture,[7,8,9,10,11] and that of substructure.[7]

In the same way as phase transformations, recrystallization has often been understood as a combination of nucleation and growth.[1] Hence, physics-based models for SRX have often included nucleation submodels.[12,13,14,15] However, nucleation has received little attention in experimental studies on SRX in austenite. For instance, an assessment of the evolution of nucleation rate for SRX after hot deformation is not available, which can be employed to validate the accuracy of nucleation models. In fact, conflicting predictions have been made in that sense by the proposed models for SRX in austenite: while some have predicted a continuous evolution of nucleation rate throughout the whole process of SRX,[12] others have assumed its early site saturation.[13,14,15] As a result, doubt persists on the character of nucleation rate evolution during SRX of austenite. On the other hand, experimental data on nucleation rate exist for both phase transformations (e.g., austenite-to-ferrite[16]) and SRX after cold deformation.[17]

Previous studies on SRX in austenite have made it clear that nuclei mainly form at the boundaries between deformed grains. However, systematic information on the contribution of the specific types of nucleation sites within boundaries has not been generated. This information becomes more relevant with the current advent of topology-based models for microstructural evolution, e.g., cellular automata.[12,18] Specifically, some studies have suggested a prominent role for the junctions of grain boundaries.[7,19] However, SRX in austenite has been successfully modeled considering all nucleation sites along boundaries to be equivalent, i.e., without assigning any special role to boundary junctions.[15] Clarification of the role of boundary junctions in the nucleation of SRX in austenite would benefit from its systematic experimental quantification. Similarly, inconsistent views have been reported on the role of annealing twin boundaries: a negligible role was implied in Reference 7, but they were proposed to be important in References 8 and 19. Also this inconsistency suffers from a lack of systematic experimental quantification. Additionally, the assessment of the nucleation potency per boundary, not performed to date, is required for the development of topology-based models.

Finally, nuclei in the SRX of austenite are generally assumed to form by strain-induced boundary migration (SIBM).[15] In this mechanism, one of the deformed grains at the boundary bulges into its neighbor.[1] While significant evidence for SIBM in the SRX of austenite has been provided, it referred to nucleation at grain-boundary sites.[7,19] By contrast, the nucleation mechanism at triple junctions has received limited attention, and is yet to be clarified.

Within this context, the aim of the present study is to provide further insight into the nucleation of SRX in hot-deformed austenite. Emphasis is placed on nucleation rate and the contribution of the different types of nucleation sites. Attention is also paid to the nucleation potency per boundary. In order to fulfill these goals, a Ni-30 pct Fe alloy was investigated. This alloy has often been employed as a model for the hot working of Fe–C–Mn steels,[7,20,21,22,23] owing to similar stacking fault energy (SFE) to the austenite in such steels.[24] However, unlike Fe–C–Mn steels, Ni-30 pct Fe remains in austenite phase when cooled to room temperature, which facilitates its microstructural characterization. In particular, samples of this alloy were deformed under conditions similar to those employed in an industrial hot-rolling mill, and then annealed to different stages within SRX. Information on nucleation was then extracted from these samples with electron backscatter diffraction (EBSD) analysis.

2 Experimental Methods

2.1 Model Alloy

Experiments were conducted with an alloy having the chemical composition indicated in Table I. The Ni-30 pct Fe composition was chosen in the light of similar SFE compared to the austenite in low-carbon steel.[24] The rest of the elements are present only at an impurity level, and are not expected to play a relevant role in the nucleation of recrystallization. The alloy was prepared by Goodfellow Ltd. UK from iron and nickel ingots with purity higher than 99.9 wt pct. The material was supplied in the form of a cold-drawn cylindrical bar with a diameter of 8 mm. From this bar, cylindrical specimens were prepared having a diameter of 5 mm and a length of 10 mm.

Table I Chemical Composition of the Alloy
Full size table

2.2 Thermo-mechanical Processing

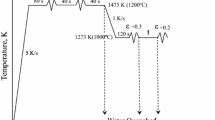
The specimens were subjected to the thermomechanical route shown in Figure 1 in a Bähr DIL 805A/D dilatometer. Temperature was controlled via an S-type thermocouple welded to the cylindrical surface of the specimen. Molybdenum disks were welded on both sides of the specimen to provide lubrication in the deformation step. Initially, the specimens were heated up to 1100 °C, with a holding time of 80 seconds to obtain a fully recrystallized microstructure with relatively large grain size (~ 90 µm). Such grain size was imparted to facilitate the association of the relatively small recrystallized nuclei to their nucleation sites. Afterward, the specimen was cooled down to 900 °C at a rate of 30 °C/s. This temperature was maintained for 15 seconds before deformation to obtain a homogeneous temperature in the sample. Deformation via uniaxial compression was then applied at a strain rate of 1 s−1 and up to a strain of 0.20, with the compression direction parallel to the cylindrical axis of the specimen. The temperature of 900 °C was maintained after deformation for different times up to 500 seconds to produce annealed conditions with different degrees of recrystallization. This was followed by quenching to room temperature with helium gas for subsequent microstructural characterization. This led to cooling times of 0.2–1 seconds before a temperature of 600 °C was reached, below which recovery and recrystallization are not expected in the material.[25] One sample was quenched immediately before deformation in order to analyze the initial microstructure.

Fig. 1
figure 1

Schematic of the thermo-mechanical processing route followed in this study. \(t\) accounts for the annealing time applied after deformation, and ranges between 1 and 500 s

Full size image

2.3 Microstructural Characterization via EBSD

Microstructural characterization was carried out on a cross-section as close as possible to the specimen’s cylindrical axis. The samples were cut with a Struers Minitom machine, and then ground following conventional steps. Mechanical polishing was performed with diamond paste of 3 and 1 µm and alcohol-based lubricant. For optical microscopy, samples were then etched with a solution containing 100 mL water, 25 mL hydrochloric acid, and 12 g FeCl3. For EBSD, samples were finished with OP-S colloidal silica mixed with ethanol. The EBSD maps corresponding to the various annealing times were collected in a Zeiss Ultra55 FEG-SEM equipped with an EDAX Hikari camera and OIM Data Collection v8 as pattern acquisition software. An aperture size of 120 µm and a working distance of 15 mm were employed. Maps were collected for an area of roughly 0.7 × 1.4 mm2, step size of 0.5 µm, and accelerating voltage of 15 kV. The EBSD map corresponding to the microstructure before deformation was obtained with a JEOL JSM 6500F FEG-SEM using an acceleration voltage of 20 kV, beam current of 1.2 nA, and working distance of 23.5 mm. The Kikuchi patterns were recorded with an Oxford-HKL Nordlys II camera and HKL Flamenco 5.11 as acquisition software, scanning an area of 0.7 × 0.7 mm2. The average confidence index (CI) ranged between 0.7 and 0.9 depending on the map. For all the analyzed conditions, the center of the scanned area was approximately coincident with the center of the specimen cross-section.

Post-processing of the EBSD maps was performed with the OIM Analysis v8 software. Cleaning was carried out using a neighbor orientation correlation algorithm to eliminate wild spikes. A noise-reduction bilateral filter was applied to achieve greater accuracy in the measurement of grain internal misorientations. Grains were constructed considering a misorientation threshold of 5 deg and at least 5 pixels, giving rise to a minimum detected grain size of 1.25 µm. The SRX fraction was calculated separating recrystallized and deformed grains based on the lower internal misorientations of the former.[26] Particularly, grains with an average grain orientation spread (GOS) smaller than 1.2 deg were considered recrystallized, and grains with a larger average GOS were considered as deformed. Kernel average orientation (KAM) values were calculated on 2nd-nearest neighbors. The density of geometrically necessary dislocations (GND) was extracted with the method proposed in Reference 27. For this aim, {111} < 110 > slip systems with Burgers vector length of 0.2518 nm[28] were taken into account.

For the identification of SRX grains, coincident site lattice (CSL) boundaries (i.e., annealing twin boundaries) were excluded. Hence, only boundaries with higher misorientation than the specified 5 deg threshold and not identified as CSL boundaries were considered as grain boundaries. CSL boundaries present in the investigated samples are mainly ∑3 boundaries (characterized by a 60 deg < 111 > misorientation) and ∑9 boundaries (characterized by a 38.9 deg < 110 > misorientation).[7,20] A tolerance of 3 deg with respect to the theoretical misorientation was allowed in the identification of CSL boundaries. Moreover, only boundaries for which the boundary traces in the scan matched the boundary plane as per the CSL misorientation were considered CSL boundaries. A deviation of 8 deg between boundary traces and plane was considered acceptable. Considering this, at least 215 SRX grains were analyzed for each annealing time. The error bars in the plots showing nucleation rate, fraction of nuclei, and nucleation efficiency account for the random error as determined via Poisson counting statistics.[29]

For the identification of nucleation sites, a nucleus was ascribed to a triple-junction site in case the junction had been consumed by the new grain. Otherwise, the nucleus was ascribed to a grain-boundary site. The analysis was restricted to short annealing times (up to 5 seconds), before SRX grains had undergone significant growth. The number of potential triple-junction sites and available length of grain-boundary sites was quantified in the deformed microstructure for an annealing time of 1 seconds. In the deformed microstructure, twin boundaries had partially lost their CSL character due to deformation.[20] However, a portion of the twin boundary was often still identified as CSL boundary. Identification of former twin boundaries (FTBs) in the deformed microstructure was thus based on straight shape, tendency to form bands inside parent grains, and a portion of the boundary being classified as CSL boundary. Application of this method resulted in a FTB fraction within the experimental uncertainty of the twin boundary fraction measured in the sample before deformation, where twin boundaries entirely possessed a CSL character. Boundaries with misorientations between 15 and 65 deg and not identified as FTBs were considered as (general) high-angle boundaries (HABs). Boundaries with misorientations between 5 and 15 deg were considered low-angle boundaries (LABs). In the deformed microstructure, relatively short LABs formed as a result of deformation and intersecting one of the boundaries of the deformed microstructure (but not extending across the whole deformed grain, i.e., not intersecting any other boundary) were often detected. However, they were not considered for the identification of nucleation sites. Therefore, nuclei formed at the intersection between those LABs and one deformed boundary (typically, a HAB) were considered as grain-boundary nucleation events (and not HAB–LAB events).

For the analysis of nucleation potency per boundary, each portion of boundary between deformed grains as delimited by two consecutive triple junctions (including those comprising FTBs) was assumed to be an individual boundary. Only boundaries that had been fully consumed by SRX grains (i.e., saturated boundaries) and having a minimum length of 30 µm were included in the analysis. Among those, boundaries for which the triple junctions were still distinguishable were found for annealing times up to 10 seconds. For longer times, identification was prevented by significant growth of the SRX grains into the deformed grains. As a result, 68 boundaries were considered for the calculations. The length of each individual boundary was calculated by drawing a straight line between the approximate positions of the triple junctions. In the boxplots presented, the upper whisker extends up to the last value lower than Q3 + 1.5(Q3-Q1), with Q3 and Q1 being the third and first quartiles, respectively. Conversely, the lower whisker extends up to the last value higher than Q3—1.5(Q3–Q1). The Kruskal–Wallis hypothesis contrast[30] was carried out with the corresponding function of the SciPy library of Python.

For the measurement of grain size, separate EBSD maps were obtained with step size of 5 µm, accelerating voltage of 20 kV and a scanned area of approximately 3 × 4 mm2. The average confidence index in these maps ranged between 0.6 and 0.7. Measurements were conducted in the center of the cross section, within the region of the specimen where deformation had been homogeneous. Grains were constructed using the same parameters described above. Grain size is given in terms of equivalent diameter.

3 Results

3.1 Microstructure Before and After Deformation

The microstructure of the material before deformation was fully recrystallized and had an average grain size of 88 µm (Figure 2(a)). The length fractions of the different types of boundaries are shown in Figure 2(c). CSL boundaries and general HABs accounted for the vast majority of boundary length, representing a fraction of almost 50 pct each. By contrast, only a small fraction corresponded to LABs (~ 3 pct of boundary length fraction). Among CSL boundaries, the density of ∑9 boundaries was negligible (less than 1 pct boundary length fraction), with the rest being ∑3 boundaries. Similar boundary fractions have been reported by other studies describing recrystallized microstructures in nickel alloys.[7,23,31,32] Annealing twins normally crossed the whole parent grain, intersecting its outer boundary at both ends. However, on some occasions, one of the twin ends was located in the interior of the parent grain (Figure 2(b)). These ends are hereafter referred to as free twin edges (FTEs). Finally, the relative frequencies of the various types of triple junctions in the microstructure before deformation are given in Figure 2(d). FTEs are included in this figure, because they develop into triple junctions upon deformation (see next paragraph). Junctions of one CSL boundary and two general HABs were dominant in the microstructure, followed by those of three general HABs (HABx3). Junctions of two HABs and one LAB were scarce, in line with the small number of LABs (~ 3 pct of all junctions).

Fig. 2
figure 2

(a) Microstructure of the Ni-30 wt pct Fe alloy before deformation. (b) Enlarged detail where the two black arrows point at two free twin edges (FTEs). In the maps, the color coding accounts for the inverse pole figure (IPF) parallel to the direction of compression. White lines indicate Σ3 and Σ9 CSL boundaries (i.e., twin boundaries). Black lines indicate boundaries with misorientations higher than 15 deg, and not identified as CSL boundaries (i.e., general HABs). Gray lines indicate boundaries with misorientations between 5 and 15 deg (i.e., LABs). (c) Length fraction of the different types of grain boundaries in the initial microstructure. (d) Number fraction of the different types of triple-junction nucleation sites in the initial microstructure. Error bars account for the random error in the measurements (Color figure online)

Full size image

The microstructure of the material after deformation can be seen in Figure 3(a). Grains became elongated in the direction perpendicular to the compression. Signs of grain division into deformation bands were occasionally present. Deformation around FTEs frequently induced the formation of LABs. Considering this, FTEs are hereafter classified as triple junctions. LABs produced by FTEs typically did not extend across the whole parent grain (Figure 4(a)). As previously described for this alloy,[20] twin boundaries were commonly found to have lost their CSL character during deformation. The reason for this is the absorption of gliding dislocations into the boundary, which gradually changes its character toward that of a general HAB.[33] As a result, the combined boundary fraction identified as ∑3 and ∑9 decreased to ~ 3 pct in the deformed microstructure. Therefore, deformed twin boundaries are hereafter referred to as former twin boundaries (FTBs). Similarly, their junctions with two general HABs are named HAB–FTB junctions. Deformed grains consistently exhibited higher KAM values around their boundaries than in the grain interiors. This can be ascribed to the local accumulation of dislocations, due to the role of grain boundaries as barriers to dislocation motion.[1]

Fig. 3
figure 3

EBSD maps obtained after deformation to a strain of 0.2 at 900 °C and a strain rate of 1 s.−1 and further annealing at 900 °C for (a) 1 s, (b) 2 s, (c) 5 s, (d) 10 s, (e) 50 s, and (f) 100 s. The direction of compression is the vertical direction of paper, as indicated in (a). Deformed and recrystallized grains are displayed in red and blue, respectively. Deformed and recrystallized grains were distinguished on the basis of internal misorientation as given by their average grain orientation spread (GOS). Yellow circles indicate evidence of strain-induced boundary migration (bulging). White lines indicate Σ3 and Σ9 CSL boundaries. Black lines indicate boundaries with misorientations higher than 15 deg, and not identified as CSL boundaries (i.e., general HABs). Gray lines indicate boundaries with misorientations between 5 and 15 deg (i.e., LABs) (Color figure online)

Full size image
Fig. 4
figure 4

(a) Examples of LABs created by deformation at FTEs (black arrows). Annealing time is 1 s. (b) Examples of SRX grains formed at a HAB–FTB junction (purple arrow) and a free twin edge (yellow arrow). Annealing time is 2 s. Deformed and recrystallized grains are displayed in red and blue, respectively. White lines indicate Σ3 and Σ9 CSL boundaries. Black lines indicate boundaries with misorientations higher than 15 deg, and not identified as CSL boundaries (i.e., general HABs). Gray lines indicate boundaries with misorientations between 5 and 15 deg (i.e., LABs) (Color figure online)

Full size image

3.2 Microstructural Evolution During SRX

The microstructures of the material after annealing during different times are shown in Figure 3. The resultant evolution of SRX fraction with annealing time is provided in Figure 5, together with that of nucleation rate. Nucleation rate was calculated from the increment in the number of SRX grains with respect to the previous annealing time. This neglects the effect of growth in the direction normal to the micrograph with annealing time, which is assumed to be small. On a logarithmic time scale, the increase rate of the SRX fraction was relatively low at first, becoming higher after 10 seconds. This is consistent with the sigmoidal shape typical in SRX kinetics curves, e.g., References 3,5,7, and 19. After 100 s, SRX was essentially complete (~ 99 pct SRX fraction), with an average SRX grain diameter of 37 µm (Figure 3(f)). The number of SRX grains increased sharply in the first 2 seconds (Figures 3(a) and (b)). This is reflected in a strong peak in nucleation rate, after which nucleation decayed sharply. However, the total number of SRX grains increased with annealing time up to 100 seconds (~ 400 grains/mm2 at 2 seconds against ~ 600 grains/mm2 at 100 seconds), albeit at much slower rate. An early peak in nucleation rate was also measured by Perryman for SRX in 20 pct cold-rolled aluminum, after comparing the number of grains in 2D-optical micrographs obtained for different annealing times.[17] Such an early peak was also predicted by Rehman and Zurob for SRX in austenite after fitting their model to SRX kinetics data.[15] As in the present case, the times for which the nucleation rate peaks were predicted/measured in References 15 and 17 were within 5 pct of the time for 99 pct SRX. In the model by Rehman and Zurob, the early peak occurred due to the early saturation of nucleation sites.[15] Nevertheless, the present results contradict this view: a significant fraction of the boundaries between deformed grains was still free of nuclei after the early peak. In particular, the aggregate length of general HAB and annealing twin boundaries in deformed grains was still ~ 60 and ~ 50 pct of the original one after 5 and 10 seconds (see e.g., Figures 3(c) and (d)). Consequently, other reasons must exist for the early peak of the SRX nucleation rate, instead of site saturation.

Fig. 5
figure 5

Evolution of SRX fraction (red) and nucleation rate (blue) with annealing time after deformation to a strain of 0.2 at a temperature of 900 °C and a strain rate of 1 s−1. Annealing time is given on a logarithmic scale. Nucleation rate is calculated from the increment in the number of SRX grains with respect to the previous annealing time, and normalized by the area analyzed in the EBSD scans. Error bars indicate the random error of the nucleation rate measurements (Color figure online)

Full size image

In the first 10 seconds, growth of the SRX grains was mainly observed parallel to the boundaries of the deformed grains (Figures 3(c) and (d)). In later stages, growth toward the interior of the deformed grains also occurred (Figure 3(e)). The boundaries of deformed grains exhibited frequent signs of SIBM, e.g., the regions encircled in yellow in Figure 3(a). Triple junctions were preferential sites for SIBM (Figures 6(a) and (b)). Bulging was also more pronounced at local orientation gradients such as pre-existent LABs (Figure 6(a)). Preferential formation of SRX nuclei was identified for the various types of triple junctions, including FTEs (Figure 4(b)).

Fig. 6
figure 6

(a) Strain-induced boundary migration (bulging) at the HABx3 triple junctions of a deformed grain. Annealing time is 1 s. (b) Strain-induced boundary migration (bulging) at a HAB–FTB triple junction of a deformed grain. Annealing time is 2 s. The black circles indicate the bulges formed at triple junctions. The black arrow indicates advanced bulging at a grain-boundary position, and into a LAB created by deformation. The color coding of the maps accounts for the inverse pole figure (IPF) parallel to the direction of compression. White lines indicate Σ3 and Σ9 CSL boundaries. Black lines indicate boundaries with misorientations higher than 15 deg, and not identified as CSL boundaries (general HABs). Gray lines indicate boundaries with misorientations between 5 and 15 deg (LABs). The text labels indicate the type of grain boundary: those which were general HABs before deformation are labeled as ‘HAB’; those which were annealing twin boundaries are labeled as ‘FTB’ (former twin boundaries) (Color figure online)

Full size image

3.3 SRX Nucleation Sites

The nuclei observed after different annealing times are classified per type of nucleation site in Table II. Five types of triple junctions (HABx3, HAB–FTB, HAB–LAB, FTB–FTB, and FTEs) and three types of boundaries (HABs, FTBs, and LABs) were considered. Nuclei which were not related to any of these features were considered as intragranular. The length of the various boundary types as quantified in the deformed microstructure is also presented in Table II. The length fractions of all three types lie within the random error of the quantification performed in the microstructure before deformation (Figure 2(c)). Similarly, the number of triple junctions of each type as quantified in the deformed microstructure is also indicated in Table II. The number fractions lie within the experimental uncertainty for all types (Figure 2(d)), except for HAB–LAB junctions (~ 8 pct against ~ 4 pct before deformation). This can be related to the occasional formation of deformation bands, as explained in Section III-B. Apart from this, the relative contribution of each type of site to nucleation (Figure 7) after each annealing time was quantified as the ratio between the number of nuclei at that type of site and the total number of nuclei present at that time. The “efficiency” of each type of site (Figure 8) was calculated as the ratio between the number of nuclei at that type of site and the number of sites of such type available in the deformed microstructure (for triple-junction sites), or the length of the corresponding type of boundary in the deformed microstructure (for boundary sites).

Table II Number of Nuclei Observed for the Various Types of Nucleation Sites at Annealing Times of 1, 2, and 5 s
Full size table
Fig. 7
figure 7

Relative contribution of each type of site to nucleation for annealing times of 1, 2, and 5 s. (a) Fraction of nuclei observed at three different types of nucleation sites normalized to the total number of nuclei. (b) Fraction of nuclei at each type of triple-junction site normalized to the total number of triple-junction nuclei. (c) Fraction of nuclei at each type of grain-boundary site normalized to the total number of grain-boundary nuclei. Error bars indicate the random error of the measurements

Full size image
Fig. 8
figure 8

(a) Efficiency of each type of triple-junction nucleation site as given by the number of nuclei corresponding to that type of site divided by the number of sites available of that type. (b) Efficiency of each type of grain-boundary nucleation site as given by the number of nuclei corresponding to that type of site divided by the length of that boundary type available. Data correspond to the accumulated efficiencies after annealing times of 1, 2, and 5 s. Error bars indicate the random error of the measurements

Full size image

The relative contributions of triple-junction, boundary, and intragranular sites to nucleation are given in Figure 7(a) for the different annealing times. The figure shows that triple-junction sites contributed to nucleation the most in the first second (~ 60 pct of all nuclei). Afterward, their contribution decreased slightly compared to the contribution of grain-boundary sites. This led to a roughly equal number of triple-junction and boundary sites (~ 50 pct) in the nuclei present at 2 seconds. This balance was maintained at 5 seconds. The number of intragranular nuclei was small irrespective of annealing time (less than 4 pct for 1 seconds, and less than 2 pct for 2 and 5 seconds). Figure 7(b) illustrates the relative contribution of the various types of triple-junction sites to the whole number of triple-junction nuclei present after the different annealing times. The majority of triple-junction nuclei (more than 90 pct) formed at either HABx3 or HAB–FTB junctions. However, the relative importance of these changed in a different way during annealing: the contribution of HABx3 junctions decreased, but that of HAB–FTB junctions increased. Moreover, while the contribution of HABx3 junctions decreased monotonically (from ~ 70 pct at 1 seconds to ~ 50 pct at 5 seconds), that of HAB–FTB junctions saturated at 2 seconds. The contribution of HAB–LAB junctions was small (~ 6 pct of triple-junction nuclei at 5 seconds), but increased with annealing time. The increase was sharper between 2 and 5 seconds. Finally, FTEs and FTB–FTB junctions played the smallest role in nucleation regardless of annealing time (~ 4 pct of triple-junction nuclei). Similarly, the relative contribution of the different boundary types to the whole number of nuclei present is displayed in Figure 7(c) for the various annealing times. General HABs produced the vast majority of boundary nuclei regardless of annealing time (~ 90 pct at 5 seconds). FTBs played a minor role (~ 15 pct of boundary nuclei, and less than 6 pct of all nuclei at 5 seconds), but their contribution increased with annealing time. Finally, no nuclei were found at LABs in the analyzed maps.

Sometimes, the location of nucleation events at grain-boundary sites coincided with a strong orientation gradient in one of the deformed grains. Strong orientation gradients were also observed to induce preferential SIBM (Figure 6(a)). This included the case of LABs produced by plastic deformation. On certain occasions, such LABs were short, and limited to the vicinity of the deformed boundary (Figure 9). Other times, they extended across a significant portion of the deformed grain. The latter included LABs separating deformation bands, which were preferential nucleation sites (Figure 10). Finally, when it was possible to distinguish which of the two grains had bulged into its neighbor, the pre-existent LAB was consistently located in the grain being consumed (e.g., Figure 6(a)).

Fig. 9
figure 9

SRX grain formed at a grain-boundary site in which an LAB created by deformation exists. The region surrounding the SRX grain is enlarged in detail I. Detail II contains another LAB created by deformation and intersecting the boundary of the same deformed grain. Both LABs created by deformation are indicated by black arrows. The SRX grain shown is the first one formed along that specific grain boundary, i.e., it is an initiator SRX grain. The color coding of the maps accounts for the inverse pole figure (IPF) parallel to the direction of compression. White lines indicate Σ3 and Σ9 CSL boundaries. Black lines indicate boundaries with misorientations higher than 15 deg, and not identified as CSL boundaries (general HABs). Gray lines indicate boundaries with misorientations between 2 and 15 deg (LABs). Annealing time is 1 s (Color figure online)

Full size image
Fig. 10
figure 10

Deformed grain containing deformation bands. The LABs separating the deformation bands are indicated by black arrows. The black squares enclose the two ends of one of the deformation bands, which are enlarged in the details labeled as I and II. Detail I shows that a nucleation event took place at one of the ends of the LAB. By contrast, no nucleation event occurred at the end shown in detail II. The color coding of the maps accounts for the inverse pole figure (IPF) parallel to the direction of compression. White lines indicate Σ3 and Σ9 CSL boundaries. Black lines indicate boundaries with misorientations higher than 15 deg, and not identified as CSL boundaries (general HABs). Gray lines indicate boundaries with misorientations between 4 and 15 deg (LABs). Annealing time is 5 s (Color figure online)

Full size image

Nevertheless, when more than one LAB intersected the boundaries of a grain, the nucleus was not necessarily found at the LAB with higher misorientation. One example can be seen in Figure 9, where the LAB in the detail labeled as I—whose position correlates with that of a nucleus—has an average misorientation of 3.2 deg. By contrast, the average misorientation across the LAB shown in the detail labeled as II—where a nucleus is not observed—is 3.4 deg. In both cases, the average LAB misorientation was measured along a boundary length of 2.5 µm. Similarly, in the case of LABs separating deformation bands, the nucleus was not always found at the end with the higher misorientation. For the case of Figure 10, the average misorientation of the LAB at the end where the nucleus lies is 6.8 deg. However, the average misorientation at the opposed end is 7.5 deg (as measured along a length of 4 µm in both cases). For the other deformation band highlighted in Figure 10, the average misorientation at the top end was only 2.9 deg.

3.4 Initiator SRX Nuclei

In this paper, initiator (primary) SRX nuclei are those accounting for the first nucleation event at a given boundary of the deformed microstructure, as delimited by two consecutive triple junctions. Hence, a grain-boundary nucleus was defined as initiator if no other SRX grain existed along the same boundary. Similarly, a triple-junction nucleus was defined as initiator if no other nuclei were present along any of the three boundaries meeting at the junction. Figure 11(a) represents the overall fraction of SRX grains classified as initiators as a function of annealing time. This fraction was considerably higher after 1 seconds than after 2 or 5 seconds, for which the value was similar. This indicates that the fraction of boundaries with only one nucleus was higher at 1 seconds. Later, a balance was reached between the number of nuclei initiating nucleation for a given boundary, and those forming at boundaries with SRX grains already present. Additionally, the type of nucleation site corresponding to the initiator SRX nuclei is given in Figure 11(b). The figure shows that most of initiator nuclei (~ 75 pct) formed at triple-junction sites rather than at grain-boundary sites for all annealing times. Therefore, it can be asserted that, for a given boundary between deformed grains, nucleation of SRX predominantly initiated at triple-junction sites irrespective of annealing time.

Fig. 11
figure 11

(a) Fraction of nuclei which were initiator normalized to the total number of nuclei. (b) Fraction of initiator nuclei that corresponded to triple-junction and grain-boundary nucleation sites normalized to the total number of initiator nuclei. Initiator SRX nuclei were those for which no other nucleation events were present along the same portion of boundary between deformed grains. Data are displayed for annealing times of 1, 2, and 5 s. Error bars indicate the random error of the measurements

Full size image

3.5 SRX Nucleation Potency Per Individual Boundary

The nucleation potency of a boundary in the deformed microstructure was defined as the total number of SRX grains formed at that boundary across recrystallization. Hence, it was quantified by counting the number of SRX grains present at boundaries fully consumed by SRX grains (i.e., saturated boundaries). An example of this quantification can be seen in Figure 12(a). Overall, the number of saturated boundaries observed in an area of 1.5 mm2 after annealing times of 2, 5, and 10 seconds was 11, 30, and 38, respectively. No saturated boundaries were found in an area of the same dimensions after 1 seconds. This increasing trend in the number of saturated boundaries with annealing time agrees with the expectation for recrystallizing microstructures with increasing recrystallized fractions. In addition, the average nucleation potency (as calculated over the number of saturated boundaries indicated above) decreased with annealing time (Figure 12(b)). This indicates a tendency for boundaries with higher nucleation potency to become saturated earlier in the SRX process.

Fig. 12
figure 12

(a) Example of saturated boundary between deformed grains with length 40 µm and nucleation potency of 4 SRX grains. Annealing time is 10 s. (b) Average nucleation potency of the saturated boundaries identified for annealing times of 2, 5, and 10 s. Error bars account for the standard error across the different boundaries considered for each annealing time. (c) Relative frequencies for the different values of nucleation potency per boundary measured for annealing times of 5 and 10 s. (d) Length of the saturated boundaries found for annealing times of 5 and 10 s as a function of their nucleation potency. (e) Example of boundary fully consumed by one SRX grain (boundary I) and two SRX grains (boundary II). Annealing time is 10 s. The color coding of the maps accounts for the inverse pole figure (IPF) parallel to the direction of compression. Only the boundaries of recrystallized grains have been drawn. White lines indicate Σ3 and Σ9 CSL boundaries corresponding to recrystallized grains. Black lines indicate boundaries between recrystallized grains, or between recrystallized and deformed grains, which have misorientations higher than 15 deg and have not been identified as CSL boundaries (general HABs) (Color figure online)

Full size image

In what follows, the gathered statistics of nucleation potency are examined in greater depth. The analysis is restricted to the saturated boundaries found after 5 and 10 seconds. The reason is that, while the average nucleation potency measured for both annealing times was similar, the potency measured for 2 seconds was significantly higher than for 10 seconds. Furthermore, Figure 12(b) suggests an asymptotic trend of nucleation potency with annealing time. Therefore, the statistics obtained for 5 and 10 seconds would be expected to be not only similar to each other, but also representative of the overall recrystallized microstructure (unlike those of 2 seconds). Accordingly, Figure 12(c) shows the distribution of nucleation potency across the saturated boundaries considered. The distribution is lognormal, centered on a value of three (which accounted for ~ 35 pct of all saturated boundaries). Interestingly, ~ 40 pct of boundaries exhibited only one or two nucleation events (e.g., Figure 12(e)). Following the results in Section III-D, this would typically correspond to boundaries where only triple-junction sites (one or both) could be thought to contribute to nucleation. On the other hand, boundaries with more than four nuclei (i.e., including more than two grain-boundary nucleation events, apart from two triple-junction nuclei) were rare (~ 5 pct).

In addition, Figure 12(d) represents the length of the saturated boundaries found after annealing for 5 and 10 seconds as a function of their nucleation potency. For a nucleation potency of up to four, the median boundary length increased with nucleation potency. Likewise, the range of boundary lengths across which a certain potency was measured extended with higher potency. In particular, the minimum boundary length remained approximately equal to the minimum value included in the quantification (i.e., 30 µm) irrespective of the nucleation potency (except for a potency of one, for which the amount of observations was limited). However, the maximum boundary length for boundaries with multiple nucleation events was greater than for those with only one or two. These results suggest that, while relatively short boundaries were able to produce multiple nucleation events, longer boundaries were more susceptible to those events. As a statistical check, a Kruskal–Wallis hypothesis contrast[30] was performed. For that purpose, the saturated boundaries were divided depending on their length into two groups with roughly equal number of boundaries (i.e., relatively short and long boundaries, see Table III). The equality of the median nucleation potency of both groups was tested, with the test resulting in a p-value of approximately 0.015 (Table III). This means that, with a confidence of 95 pct, the hypothesis that long and short boundaries had equal median nucleation potency can be rejected.

Table III Properties of the Two Groups of Boundaries Between Deformed Grains on Which a Kruskal–Wallis Hypothesis Contrast was Performed
Full size table

4 Discussion

4.1 Triple-Junction vs Grain-Boundary Nucleation

The analysis in Section III–C provided insight into the contribution of the different types of nucleation sites to SRX up to an annealing time of 5 s. The number of SRX grains at that time was roughly 80 pct of that at the end of SRX (100 s). Furthermore, the relative contribution of the various sites did not undergo significant changes between 2 and 5 s. Hence, the statistics gathered at 5 seconds are thought to provide a good representation of the role of nucleation sites throughout the whole process of SRX.

In particular, the data for 5 seconds demonstrate approximately equal contributions of triple-junction and grain-boundary sites to nucleation in the SRX of austenite (Figure 7(a)). This implies that, despite not being considered by current austenite SRX models,[15] triple-junction nucleation plays a distinct role. However, triple-junction nuclei are also not a majority in the recrystallized microstructure, as implied in former experimental studies.[7,19] In this sense, Figure 7(a) shows also a decrease in the contribution of triple-junction nucleation compared to the start of SRX (i.e., 1 s). This can explain why former experimental studies, which focused on the earliest recrystallization stages, ascribed a dominant role to triple junctions.[19] In turn, this greater initial contribution of triple-junction sites can be related to their tendency to start nucleation for a given boundary between deformed grains (Figure 11(b)). In fact, the evolution of the number of saturated boundaries with time as presented in Section III–E suggests that the fraction of boundaries at which nucleation was not yet complete was higher after 1 seconds than for longer annealing times. With nucleation within a given boundary typically starting by triple-junction nucleation, and ending with grain-boundary nucleation events, the fraction of triple-junction nuclei after 1 seconds would be expected to be higher than after longer times.

About the recrystallization mechanism at triple junctions, abundant evidence of SIBM (bulging) at such sites was found in this study (e.g., Figures 6(a) and (b)). Formation of a bulge implies an increase in the boundary area between deformed grains (Figure 13(a)) and, thus, an overall increase in boundary energy. However, following the theories of recrystallization,[14] bulging becomes thermodynamically feasible if the boundary energy increase is compensated by a reduction in the energy stored in the form of dislocations: a volume in a deformed grain (i.e., dislocation-rich) is replaced by a dislocation-poor nucleus. A smaller bulge implies a greater weight of the boundary energy term and, hence, less favorable nucleation.[14] In that sense, higher dislocation density can enable earlier bulging by reducing the critical subgrain size for nucleation. Moreover, higher dislocation density can also accelerate subgrain growth before that size is reached,[15] which would also contribute to earlier bulging. The EBSD maps in this study effectively display higher GND density around triple junctions than at positions around the same boundary, but away from the junctions. This can be seen in Figures 14(a) through (d) for different triple-junction types: HABx3, HAB–FTB, FTE, and HAB–LAB. The observation is in line with other EBSD studies, where higher GND densities around triple junctions were found after deformation at room temperature.[34,35] Accumulation of dislocations near triple junctions after room-temperature deformation has also been suggested by transmission electron microscopy.[36] The present results demonstrate that dislocations accumulate around triple junctions also during high-temperature deformation. This higher dislocation density around triple junctions as compared to grain-boundary sites would thus lead to earlier bulging at the former. Nevertheless, another effect may contribute to the earlier bulging: unlike for grain-boundary sites, nucleation at triple junctions involves the consumption of an ‘extra’ grain boundary (Figure 13(b)). The elimination of the energy corresponding to this boundary results in an energy decrease via bulging at the junction, additional to the reduction of stored energy, which does not occur for bulging at grain-boundary sites. Consequently, the earlier nucleation observed at triple junctions for a given boundary between deformed grains can be attributed to a combined effect of higher dislocation density and the ‘extra’ boundary energy which is eliminated by the nucleation.

Fig. 13
figure 13

Schematics showing the event of bulging at different types of nucleation sites: (a) grain boundary, (b) HABx3 junction, (c) HAB–FTB junction, and (d) FTE. Dotted lines indicate the position of the deformed boundaries before the bulge forms. Thick solid lines represent the position of the deformed boundaries after the bulge has formed. Dashed lines indicate the portion of the ‘extra’ deformed boundary that is consumed by the bulge. Thin solid lines represent the portion of the ‘extra’ deformed boundary that is not consumed by the bulge. Black lines account for general HABs, red lines correspond to FTBs, and gray lines represent LABs. The blue arrows show the increase in the area of the deformed boundaries resulting from the formation of the bulge (Color figure online)

Full size image
Fig. 14
figure 14

Distribution of GND density around different types of triple junctions after annealing for 1 s: (a) HABx3 junction, (b) HAB–FTB junction, (c) FTE, and (d) HAB–LAB junction. The color scale indicates values of GND density. Red lines indicate Σ3 and Σ9 CSL boundaries. Black lines indicate boundaries with misorientations higher than 15 deg, and not identified as CSL boundaries (i.e., general HABs). Gray lines indicate boundaries with misorientations between 5 and 15 deg (i.e., LABs). The text labels indicate whether each boundary was a general HAB before deformation (‘HAB’), or an annealing twin boundary (‘FTB,’ former twin boundary) (Color figure online)

Full size image

4.2 The Role of the Various Nucleation Site Types

Among the various types of triple-junction and grain-boundary nucleation sites, grain-boundary sites located at general HABs made the greatest contribution to nucleation (~ 45 pct of all nuclei). This implies a strong difference with respect to the other type of grain-boundary sites: FTBs only accounted for ~ 6 pct of all nuclei. With similar lengths of HABs and FTBs in the deformed microstructure (Table II), this different contribution is explained by the higher nucleation efficiency of HABs (Figure 8(b)). After HABs, HABx3 and HAB–FTB junctions were the greatest contributors to nucleation (~ 25 and ~ 20 pct of all nuclei). These similar contributions contrast with the higher density of HAB–FTB junctions in the deformed microstructure (Table II). Hence, the higher contribution of HABx3 junctions can also be associated to higher nucleation efficiency (Figure 8(a)). Finally, the other types of nucleation sites (FTE, HAB–LAB, FTB–FTB, intragranular) had a minor contribution only (less than 3 pct of all nuclei each), and displayed considerably lower nucleation efficiency than the four main types of nucleation sites.

The present results thus partly agree with the suggestion by Beladi et al. that FTBs scarcely contribute to nucleation in the SRX of austenite.[7] However, they indicate that this is true for the grain-boundary sites along FTBs only. On the other hand, the triple junctions of FTBs and the boundaries of their parent grains (HAB–FTB junctions) do play a relevant role. The low nucleation activity of FTBs was related by Beladi et al. to low intrinsic boundary mobility, reducing the tendency for FTBs to bulge.[7] The EBSD maps in this work agree with this view: whereas deformed general HABs display clear serrations, this is not the case of FTBs (at least, along their grain-boundary sites, see Figures 3(a) and (e)). Apart from the mobility, the scarce bulging of FTBs compared to HABs could also be explained by lower dislocation density around them. However, studies on fatigue behavior of nickel-based superalloys have found the greatest strain localization to precisely occur around annealing twin boundaries.[33,37,38] Similarly, higher boundary energy for FTBs would also hinder their bulging, since a higher dislocation density would be required to compensate for the boundary area increase produced by the bulge. However, twin boundaries in face-centered cubic (FCC) metals have consistently been ascribed lower boundary energies than general HABs.[39,40] Hence, lower intrinsic boundary mobility represents a plausible explanation for the slight bulging of FTBs.

Regarding HAB–FTB junctions, recurrent bulging was observed at such sites, in line with their higher nucleation activity (Figure 6(b)). Furthermore, bulging at HAB–FTB junctions most often occurred by consuming one of the general HABs. As shown in Figure 13(c), this means that the bulge was formed by both the FTB and the other general HAB, i.e., bulging at HAB–FTB junctions directly required bulging of the FTB itself. In turn, this implies that FTBs had a greater tendency to bulge at their junctions than along the boundaries. Again, this can be explained by higher dislocation density around HAB–FTB junctions than around grain-boundary sites along the same FTB (Figure 14(b)), and the elimination of an ‘extra’ boundary (Section IV-A). The increased bulging activity of FTBs at triple-junction positions can also explain the higher nucleation efficiency ratio between HAB–FTB and HABx3 junctions, compared to that between FTB and HAB grain-boundary sites (Section III-C). Additionally, the fact that bulging tended to occur by consuming one of the general HABs, and not the FTB, may be related to the low boundary energy of twin boundaries: the higher the energy of the ‘extra’ boundary consumed by the bulge, the more bulging will be favored (Section IV-A).

The efficiency of HAB–FTB junctions was lower than for HABx3 sites. The difference between bulges at HAB–FTB and HABx3 junctions is that bulges formed at HAB–FTB junctions include an FTB (Figures 13(b) and (c)). By contrast, bulges at HABx3 junctions are solely formed by general HABs. On the other hand, the ‘extra’ boundary consumed is a general HAB in both cases. Lower mobility of FTBs can explain this lower efficiency through the relative restriction of bulging at HAB–FTB junctions compared to HABx3 junctions.

HAB–LAB junctions also exhibited a lower nucleation efficiency than HABx3 sites. On the one hand, higher dislocation density was effectively observed around HAB–LAB junctions compared to other positions along the same HAB (Figure 14(d)). In addition, bulging at HAB–LAB junctions occurred along the LAB (e.g., Figure 6(a)). The lower boundary energy of LABs compared to general HABs[41,42] would retard bulging at HAB–LAB junctions compared to HABx3 junctions (where bulging occurs always at the expense of a general HAB). Apart from this, the elimination of an ‘extra’ LAB can explain why grain-boundary nucleation sometimes occurred preferentially at sites containing LABs (Figure 9), and the more advanced bulging at such sites (Figure 6(a)). The elimination of this ‘extra’ LAB energy provides an energy advantage for nucleation at those sites, compared to grain-boundary sites where no LABs are present. As LAB energy essentially increases with misorientation,[41,42,43] grain-boundary nucleation would be expected to be more likely for higher misorientation across the LAB. However, the results presented in Section III-C contradict this view: nuclei were not always found at the LABs with the higher misorientation. This suggests that, while the lower energy of LABs can explain the lower efficiency of HAB–LAB junctions compared to HABx3 junctions, the energy of the intersecting LAB does not suffice to explain at which HAB–LAB junctions the nuclei form.

Finally, the relatively low nucleation efficiency of FTEs as compared to e.g., HAB–FTB junctions remains to be explained. Like for the other types of junctions, higher dislocation density was observed around FTEs compared to other sites around the same boundary (Figure 14(c)). In addition, as in HAB–FTB junctions, bulging at FTEs involves the bulging of FTBs. By contrast, the ‘extra’ boundary consumed is an LAB for FTEs, instead of a HAB for HAB–FTB junctions (Figure 13(d)). Assuming the same level of dislocation density accumulation, the lower energy of the ‘extra’ boundary could thus explain the lower nucleation efficiency measured for FTEs.

5 Conclusions

Nucleation of static recrystallization (SRX) in austenite after hot deformation was systematically studied using a Ni-30 pct Fe model alloy. The following main conclusions can be drawn:

  1. 1.

    Nucleation takes place continuously during SRX. However, the rate of nucleation exhibits a strong peak at the beginning of SRX (less than 5 pct of the time required to achieve 99 pct SRX fraction). This cannot be explained by the saturation of nucleation sites, as proposed in the literature.

  2. 2.

    Nucleation at triple junctions starts via strain-induced boundary migration (SIBM). Triple-junction and grain-boundary nucleation make a quantitatively similar contribution to the nucleation of SRX. However, for a given boundary between deformed grains, nucleation predominantly starts at one of the triple junctions. This was attributed to the combined effect of higher dislocation density around the junction and the elimination of an ‘extra’ boundary which is not present at grain-boundary sites.

  3. 3.

    The contribution of grain-boundary sites along annealing twin boundaries to nucleation is minor. However, the contribution of the junctions of twin boundaries with the boundaries of their parent grains is significant. This was ascribed to the higher dislocation density around the junctions and the presence of an ‘extra’ general HAB, which can be consumed by the bulge.

  4. 4.

    Both the maximum and average number of nuclei formed per boundary between deformed grains (“nucleation potency”) increase with increasing boundary length.