1 Introduction

Duplex stainless steels (DSS) usually contain both austenite (fcc) and ferrite (bcc) phases in roughly equal proportions. These steels give an attractive combination of high strength and excellent corrosion resistance and are a natural material choice in applications such as pressurized equipment in the nuclear, chemical, and pulp and paper industries.[1,2,3,4,5,6] However, DSS are susceptible to embrittlement at virtually all temperatures.[7,8,9] Therefore, the service temperature of DSS is limited to ~ 250 °C.[10,11] At temperatures above 250 °C, a phase separation (PS) phenomenon renders the alloy susceptible to the “475 °C embrittlement” phenomenon.[4,12,13] This embrittlement in DSS leads to changes in mechanical properties such as the impact, tensile, and fatigue properties.[4,14]

During the PS phenomenon, alloying elements within the ferrite phase segregate into Fe-rich (α) and Cr-rich (α′) regions (domains), leading to increased hardness and a subsequent decrease in impact toughness.[15,16,17,18,19,20] Here, the mechanism for segregation depends on the Cr concentration of the alloy.[4,17,21,22] As the phase separation occurs within the ferrite phase, embrittlement of the steel is due to changes in mechanical properties of this phase. Consequently, the PS phenomenon has been extensively studied in ferritic grades for several decades.[15,23,24,25,26,27,28,29,30,31,32] With developments in both experimental and computational tools, it is now also more tangible to investigate the nanostructure evolution in duplex alloys quantitatively, even during the early stages of the PS phenomenon.[26,33]

Phase separation in commercial grade duplex alloys[9,14,17,22,34,35] has only been investigated to a limited extent, especially for test conditions emulating operando conditions, i.e., low temperatures where the embrittlement takes years.[17,36] Furthermore, there is a lack of comprehensive bulk characterization of PS and often measurements are made on a limited volume of the material using techniques such as atom probe tomography.[18,22,37] Recently, Small-Angle Neutron Scattering (SANS) has been applied for quantitative bulk characterization of PS during long-term isothermal aging of a commercial grade super-duplex stainless steels (SDSS) at 300 °C.[36] This manuscript expands on that work and reports quantitative information on the compositional fluctuations taking place during PS at the nano-length scale for two commercial alloys at various industrially relevant service temperatures. The two commercial grades studied were the 22Cr-5Ni (also referred to as 2205 or UNS S32205) grade DSS and 25Cr-7Ni (also referred to as 2507 or UNS S32750) grade super-duplex stainless steel (SDSS). The manuscript further correlates the nanostructural evolution during isothermal aging with the micro- and macro-hardness property response of both these alloys. A better understanding of the nanostructure-property evolution correlation at real service temperatures could pave the way to identify critical design parameters for novel grades of DSS. These DSS would be less susceptible to embrittlement in industrial applications. Furthermore, the reliability, i.e., service life time, of current commercial grade DSS may also be better predicted.

2 Experimental Methodology

2.1 Materials

Isothermal heat treatments were conducted on 6 mm thick plate material of 22Cr-5Ni (2205) DSS and 25Cr-7Ni (2507) SDSS which were delivered by Outokumpu Stainless AB. The chemical compositions of these two alloys are given in Table I.

Table I The Chemical Composition of the Commercial Grade Duplex Stainless Steels [Wt Pct]
Full size table

The representative microstructures of the 22Cr-5Ni grade DSS and 25Cr-7Ni grade SDSS are shown in Figure 1, with ferrite and austenite phase regions elongated in the rolling direction. In Figure 1, the ferritic phase appears dark, and the austenitic phase appears bright. The samples were etched using a modified Beraha II reagent consisting of 100 ml water, 50 ml HCl, and 0.5 g K2S2O5.

Fig. 1
figure 1

Optical photomicrographs of 22Cr-5Ni and 25Cr-7Ni grade duplex stainless steels, where austenite appears bright and ferrite dark

Full size image

2.2 Mechanical Testing

2.2.1 Hardness

Macro-hardness measurements were carried out on all the aged samples using a 30 kg load on the rolled surface after it had been wet ground with 1200 mesh grit paper. An average value of 5 hardness measurements was used, whereas, for the micro-hardness measurements, prior to performing measurements, the specimens were polished down to a 0.25 µm diamond finish. The test specimens were then lightly etched using a solution of 100 ml HCl, 10 ml HNO3, and 100 ml H2O. The micro-hardness measurements within the ferrite and austenite phases were performed using a Qness Q10 micro-hardness tester with small loads of 5 g on the transverse section of the test specimen. Here, for each condition, the average of at least 10 measurements were taken in both the austenite and ferrite phases.

2.2.2 Impact toughness

Impact toughness was evaluated using an Instron–350MPX-V2 model test rig. These tests were conducted at room temperature with sub-size Charpy-V specimens of 55 × 10 × 5 mm3 dimensions. Machining was done to align and position the sample V-notch in the rolling direction/transverse direction plane. Each specimen had a notch depth of 2 mm in accordance with the Swedish Standard.[38] Two specimens were tested for each condition, and the average was taken.

2.3 Small-Angle Neutron Scattering (SANS)

For the SANS studies, specimens were cut to dimensions ~ 10 × 10 × 1.5 mm3 using a Struers Accutom 5-disk cutter. The two large faces were then polished using standard metallographic sample preparation techniques down to a grit size of 2500 to remove any plastic deformation induced due to the cutting. This removed about 100 μm from each side and so also ensured that the polished surfaces were free of any surface oxide film that may have been present.

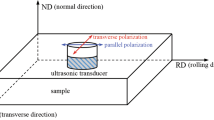
SANS experiments were conducted at the LOQ beamline at the ISIS Pulsed Neutron Source, United Kingdom. At LOQ, the ‘white’ beam of incident neutrons has wavelengths (λ) in the range of 2.2 to 10 Å. These are time sorted on arrival at the detectors to simultaneously measure scattering vectors (Q = 4πSin θ/λ, where 2θ is the scattering angle) in the range 0.006 to 1.4 Å−1.[39] Each sample was positioned between the poles of a water-cooled 1.5 T electromagnet (Goudsmit Magnetics) situated at about 11 m from the neutron moderator, with the neutron beam normally incident on the large faces. The applied magnetic field was then orthogonal to the axis of the neutron beam. This field was found to be sufficient to reach magnetic saturation for the samples.[40] Data were recorded on two detector banks, an in-house annular scintillator area detector at 0.5 m from the sample with 12 mm spatial resolution, and an ORDELA 3He-CF4 gas area detector (64 cm × 64 cm) with 5 mm resolution located 4.15 m from the sample. The incident neutron beam was collimated to 8 mm in diameter. Data were measured for at least 100 µamp hrs of proton current (approximately 1 hour) per sample at ambient temperature.

After SANS data collection, the Mantid framework (version 4.2).[41,42] was used to correct for the efficiency and spatial linearity of detectors, instrumental background scattering, the measured sample transmission, and the illuminated gage volume, to yield the macroscopic coherent differential scattering cross section (dΣ (Q)/dΩ), colloquially referred to as the intensity I (units: cm−1),[39] as a function of Q (refer Figure 2). These data were then placed on an absolute scale by reference to the scattering from a secondary calibration standard measured under the same experimental conditions in accordance with established procedures.[43] Due to the presence of a strong Bragg edge in the sample transmission data, neutrons with λ ≤ 4.3 Å were excluded from the data reduction. This had the effect of reducing the maximum accessible Q-value.

Fig. 2
figure 2

The 1D reduction of the azimuthally averaged (− 90 deg to 90 deg) total scattering data shows the evolution in correlation peak intensity following the isothermal aging of (upper) 22Cr-5Ni and (lower) 25Cr-7Ni duplex stainless steels at 250 °C, 275 °C, and 300 °C up to 48,000 h and 325 °C and 350 °C up to 6000 h. Note measurements for 22Cr-5Ni aged at 250 °C and 275 °C and 25Cr-7Ni aged at 250 °C were made without the 1.5T field

Full size image

For the investigated 22Cr-5Ni DSS and 25Cr-7Ni SDSS, only 48.7 and 40.6 pct of the illuminated volume of the steels, respectively, constituted the ferrite phase which was phase separated and which, therefore, contributed to the correlation peak in the SANS data.[44]

The total scattering (Itotal) obtained from SANS on these samples is a combination of scattering from nuclear (Inuclear) and magnetic (Imagnetic) contributions. When a saturating magnetic field is applied (see Figure 3), the total scattering becomes a function of the angle, Ψ, between the scattering vector and the direction of the applied field as follows:

$$ I\left( Q \right)_{{{\text{total}}}} = I\left( Q \right)_{{{\text{nuclear}}}} + I\left( {Q,H} \right)_{{{\text{magnetic}}}} {\text{Sin}}^{2} \Phi. $$
(1)
Fig. 3
figure 3

Evolution of the 2D SANS from (upper) 22Cr-5Ni DSS and (lower) 25Cr-7Ni super DSS in both (left to right) the as-cooled condition and after isothermal aging for 3000, 6000, 12,000, 24,000, and 48,000 h, respectively, at 300 °C. Measurements were made with a saturating 1.5 T magnetic field applied horizontally. The labels Nuclear and Magnetic denote the respective scattering contributions. The black lines denote the horizontal (\(\Psi =-20\mathrm{ to}+20)\) and vertical (\(\Psi =70\mathrm{ to}+110)\) sectors used for data reduction. In both cases, the mirror sectors were included

Full size image

Therefore, for the experimental geometry employed, the scattering along the horizontal (or equatorial) axis of the detector (where \(\Psi \sim 0\mathrm{ or }180\)) should give the pure nuclear scattering contribution, while the scattering along the vertical (or meridonal) axis (where \(\Psi \sim 90\mathrm{ or}-90\)) should give a combination of nuclear plus magnetic scattering. In practice, it is usual to integrate the scattering in narrow sectors on either side of the meridian or the equator to improve the statistics. Thus, the magnetic contribution may be estimated by a simple subtraction of the equatorial scattering from the meridonal scattering. This manuscript mainly presents and discusses results from analysis of the nuclear scattering (\(\Psi =-20\mathrm{ to}+20)\) contributions from 22Cr-5Ni DSS and 25Cr-7Ni super DSS isothermally aged at 250 °C to 350 °C for up to 48,000 hours. For the lower temperature aging experiments, i.e., 250 °C and 275 °C, where the phase separation is in the very early stage, measurements were made without an applied magnetic field for experimental expediency, as the magnetic scattering in these samples can be assumed to be negligible.[45]

The scattering data were analyzed using the SasView software (version 4.2.2)[46] by model fitting a combination of a power law[27,47] and a generalized spinodal function[48] to the sector-averaged data such that

$$ I\left( Q \right)_{{{\text{fit}}}} = I\left( Q \right)_{{{\text{spinodal}}}} + B_{{{\text{fit}}}}, $$
(2)

where \({B}_{\mathrm{fit}}={A}_{\mathrm{power}\_\mathrm{law}}{Q}^{-n}+{B}_{\mathrm{g}}\), the prefactor \({A}_{\mathrm{power}\_\mathrm{law}}\) determines the relative contribution of that term, \(n\) is a power law exponent (1.5 ≤ n ≤ 4), and \({B}_{\mathrm{g}}\) is the residual \(Q\)-independent background level. \({I(Q)}_{\mathrm{fit}}\), \({B}_{\mathrm{fit}},\) and \({I(Q)}_{\mathrm{spinodal}}\) have dimensions of inverse length (here cm-1), but the dimensions of \({A}_{\mathrm{power}\_\mathrm{law}}\) will vary with \(n\). The spinodal model used here is taken from the work of Furukawa[48] and is as follows:

$$ I\left( Q \right)_{{{\text{spinodal}}}} = I_{{{\text{peak}}}} \left( {1 + \frac{{\upgamma }}{2}} \right)x^{2} /\left( {\frac{{\upgamma }}{2} + x^{{2 + {\upgamma }}} } \right), $$
(3)

where \(x=Q/{Q}_{\mathrm{peak}}\), \({Q}_{\mathrm{peak}}\) is the peak position, and \({I}_{\mathrm{peak}}\) is the intensity at \({Q}_{\mathrm{peak}}\). The evolution of the phase separation may be obtained by fitting for the latter two parameters. The term \(\upgamma \) is equal to d+1 for off-critical concentration mixtures and 2d for critical concentration mixtures. Near the percolation threshold, a transition from \(\upgamma =\mathrm{d}+1\) to \(\upgamma =2\mathrm{d}\) is expected.[48] Here, d is the dimensionality (i.e., 1, 2, 3) of the system: 3 was used in this work. Good fits were obtained with \(\upgamma =6\).[[36]

Fits of Eq.2 to the SANS data (see Figure 4) are very good, and the fitting parameters give information on the physical parameters of interest. This approach can accurately identify the changes in the length scale and the concentration fluctuation amplitude during the phase separation process. To present the evolution of the scattering intensity clearly as shown later in Figure 8, the \(I{(Q)}_{\mathrm{fit}}\) in Figure 4 was normalized by the background function \({B}_{\mathrm{fit}}\) (i.e., \(\frac{I{\left(Q\right)}_{\mathrm{fit}}}{{B}_{\mathrm{fit}}})\) to reveal the shape of the underlying spinodal signal (In). This “In” was then fitted to a Gaussian function \({S(Q)}_{\mathrm{fit}}\).[23] Signals of phase separation were then obtained by removing the contribution of the background and normalizing it with respect to \({B}_{\mathrm{fit}}\) i.e., \(S(Q)={B}_{\mathrm{fit}}*({S\left(Q\right)}_{\mathrm{fit}}-{B}_{\mathrm{fit}}/{B}_{\mathrm{fit}})\).[36]

Fig. 4
figure 4

Illustration of fitting (a) the complete scattering data to (b) the background. Parameters obtained on fitting experimental data give wavelength and amplitude of phase separation. Data depict condition of 25Cr-7Ni super DSS isothermally aged at 300 °C for 48,000, fitting χ2 = 3.0. Qpeak position is highlighted by the dotted lines

Full size image

The wavelength of the α and α′ phase separation i.e., distance between the two α′ domains was obtained as follows[23,26,27,44,49,50]:

$$ {\Lambda } = 2{\uppi }/{\text{Q}}_{{{\text{peak}}}}. $$
(4)

Using the above expression, the evolution of the amplitude of the concentration fluctuations within the ferrite phase of the DSS and SDSS can then be extracted. The weighted ferrite fraction (48.7 pct for 22Cr-5Ni DSS and 40.6 pct for 25Cr-7Ni SDSS, respectively) was firstly accounted for. Following Hashimoto et al.[51] and Meier and Strobl,[52] and assuming the α′ precipitates are cubes, we then have

$$ I_{{{\text{peak}}}} = \varphi \left( {1 - \varphi } \right) \left( {\frac{\Lambda }{2}} \right)^{3} \left( {\Delta \rho } \right)^{2}, $$
(5)

where φ is the volume fraction of the α′ phase in the ferrite and \(\Delta \rho \) is the neutron scattering length density (SLD) difference between the α and α′ phases. Changes in the Cr concentration were then derived from changes in the SLD difference simplified to only consider Fe (8.02 × 10-6 Å−2) and Cr (3.03 × 10−6 Å−2) where SLD changes by ~0.5 × 10−6 Å−2 for every 10 at. pct increase in Cr concentration.[36] Thus, the fluctuation amplitude (A at. pct) is given by

$$ A \left( {{\text{at}}{.}\;{\text{pct}}} \right) = \Delta \rho \frac{{10\;{\text{at}}{.}\;{\text{pct}}}}{{0.5 \times 10^{ - 6} {\AA}^{ - 2} }}. $$
(6)

The above method was recently also successfully applied to a study of the amplitude and wavelength evolution in a binary Fe-Cr (35 at. pct Cr) alloy.[53] In our earlier work,[36] some of the nanostructural measurements obtained here were validated with atom probe measurements.[22] In the commercial DSS and SDSS, the other alloying elements such as Ni, Mn, etc. were found to have a minor effect on the SLD changes (owing to Cr signal being about 5 times that of the next most significant element Mn).

3 Results and Discussion

3.1 Hardness

The macro-hardness evolution during the isothermal aging for the 22Cr-5Ni DSS and 25Cr-7Ni grade SDSS is shown in Figure 5. In comparison to aging at the higher temperatures, the changes in hardness were observed to be negligible for both the alloys aged at 250 °C and 275 °C. Isothermal aging at 300 °C resulted in a gradual increase in hardness for the 22Cr-5Ni grade DSS and 25Cr-7Ni grade SDSS. This was evidenced by a very similar increase in hardness for both, where the 22Cr-5Ni data increased from ~290 > 316 (i.e., ~26) whereas the 25Cr-7Ni increased from ~320 > 346 (i.e., ~26). However, it should be noted that there is a smaller volume fraction of the ferrite phase in 25Cr-7Ni grade SDSS. With further increase in the isothermal aging temperatures, there was a rise in the hardness values measured. The only exception to this trend is the 25Cr-7Ni SDSS sample isothermally aged 325 °C for 3000 hours, which shows a higher hardness than the 25Cr-7Ni SDSS sample aged 350 °C for the same time.

Fig. 5
figure 5

Macro-hardness evolution following the isothermal aging of (left) 22Cr-5Ni DSS and (right) 25Cr-7Ni SDSS at 250 °C, 275 °C, 300 °C, 325 °C, and 350 °C

Full size image

Additional micro-hardness measurements were conducted on the samples isothermally aged at 250 to 350 °C to look at the hardness variation in the ferrite and austenite phases. From the micro-hardness measurements (see Figure 6) there was, in general, an observable increase in the ferrite hardness, with increases in isothermal aging time, for both 22Cr-5Ni DSS and 25Cr-7Ni grade SDSS. Whereas the hardness of the austenitic phase remained close to constant during aging for both alloys. Moreover, the change in the ferrite micro-hardness for the 25Cr-7Ni grade SDSS was more pronounced in comparison to the 22Cr-5Ni grade DSS. Furthermore, for both 22Cr-5Ni and 25Cr-7Ni, the micro-hardness of ferrite underwent larger increases when subjected to higher aging temperatures. For the 22Cr-5Ni grade DSS in Figure 5, it is shown that 48,000 hours of isothermal aging can result in a ~44 pct increase in the hardness of the ferrite phase when aged at 300 \(^\circ \)C. However, at 350 \(^\circ \)C for only 6000 hours aging can lead to 47.3 pct increase in the ferrite hardness. For the 25Cr-7Ni grade SDSS, this change in micro-hardness was rapid, especially during the first 12,000 hours of isothermal aging at 300 \(^\circ \)C (~56 pct increase after 12,000 hours), see Figure 5. A similar hardening phenomenon was observed by Yao and co-workers for cast DSS.[54] There was an observable increase in ferrite micro-hardness during the longer isothermal aging times, in which ferrite micro-hardness increased by ~66 pct after 48,000 hours of aging. When it was aged at higher temperature, the micro-hardness of ferrite increased to a maximum 73.6 pct at 350 \(^\circ \)C.

Fig. 6
figure 6

Micro-hardness evolution for (upper) 22Cr-5Ni DSS and (lower) 25Cr-7Ni SDSS, following isothermal aging at 250 °C, 275 °C, 300 °C, 325 °C, and 350 °C

Full size image

3.2 Toughness

The impact toughness results for 22Cr-5Ni grade DSS and 25Cr-7Ni grade SDSS are shown in Figure 7. For the 22Cr-5Ni DSS, isothermal aging at 250 °C and 275 °C does not significantly change the impact toughness. However, after isothermal aging at 300 °C, a significant change in impact toughness is observed for specimens aged for at least 12,000 hours. In contrast, for the 25Cr-7Ni grade SDSS, an observable change is seen after isothermal aging at 275 °C for 24,000 and 48,000 hours. Loss in impact toughness is more pronounced in both alloys with increases in isothermal aging temperature and aging time.

Fig. 7
figure 7

Impact toughness evolution of (left) 22Cr-5Ni DSS and (right) 25Cr-7Ni SDSS following isothermal aging at 250 °C, 275 °C, 300 °C, 325 °C, and 350 °C

Full size image

3.3 SANS

3.3.1 Evolution in normalized scattering intensity

The evolution in the normalized scattering intensity for samples aged between 250 °C and 350 °C for up to 48,000 hours was derived from the SANS data for both 22Cr-5Ni DSS and 25Cr-7Ni SDSS and is depicted in Figure 8. It can be seen that an increase in the isothermal aging temperature significantly accelerates the kinetics of the phase separation phenomenon. For isothermal aging at temperature 250 °C, the PS appears to be limited for both the alloys. For the 25Cr-7Ni SDSS, it is possible to clearly identify the scattering intensity evolution during the isothermal aging at 275 °C and above, whereas, for the 22Cr-5Ni alloy, it is difficult to distinguish this evolution for aging below 300 °C.

Fig. 8
figure 8

Evolution of the normalized scattering intensity following the isothermal aging of (upper) 22Cr-5Ni DSS and (lower) 25Cr-7Ni SDSS at 250 °C, 275 °C, 300 °C, 325 °C, and 350 °C

Full size image

In comparison to the lower temperatures, the amount of PS increases rapidly at the higher aging temperature of 325 °C. This PS is even more pronounced for samples isothermally aged at 350 °C. Here, even relatively short aging time of 1500 hours was found to be sufficient to cause more PS than specimen aged for 48,000 hours at 300 °C.

The changes in wavelength and amplitude derived from Figure 8 are presented in Figure 9. The minor wavelength fluctuations observed are indicative of the α and α′ phase separation being in the early stages when the main development of the nanostructure is related to an increased concentration amplitude.[51] Even during these early stages, there is often a significant development of the amplitude as a function of either time or temperature. For example, for a given isothermal aging temperature, the amplitude increases with time. This evolution is usually gradual in comparison to the change in amplitude for a given time as a function of temperature (compare the amplitude evolution in Figure 9 for 3000 and 6000 hours for both alloys).

Fig. 9
figure 9

(A) Schematic of wavelength and amplitude evolution during phase separation. (B) SANS quantification of evolution of the spinodal wavelength and amplitude following the isothermal aging of (left column) 22Cr-5Ni DSS and (right column) 25Cr-7Ni SDSS at 250 °C, 275 °C, 300 °C, 325 °C, and 350 °C

Full size image

4 Discussion

The long-term isothermal aging of both 22Cr-5Ni and 25Cr-7Ni grade duplex alloys, at 300 °C and above, leads to an evolution in Cr concentration fluctuations within the ferritic phase, i.e., the amplitude of phase separation. As the wavelength of the decomposition remained constant throughout the isothermal aging process, it is reasonable to assume that the phase separation process was still in the early stages for both the alloys. This variation in the Cr concentration of the α and α′ phases within the ferrite (refer Figure 9) has a pronounced effect on the mechanical properties of both the alloys investigated. During the isothermal aging at 300 °C, there was an increase in only the ferrite hardness for both materials (see Figure 6). Consequently, each material becomes embrittled with a measurable decrease in impact toughness (see Figure 7). Pettersson et al.[22] also observed a direct influence of the Cr fluctuations on the ferrite hardness during isothermal aging, and these results were similar to others in the literature.[18,20,55] As no other mechanism than α and α′ phase separation was observed in either alloy, it is a reasonable to assume the embrittlement is primarily due to this phenomenon in our investigation.

From the results presented here, and previous works from some of the present authors,[22] it is evident that even in the as-cooled samples of the 25Cr-7Ni SDSS, there was already some amount of decomposition. This decomposition was also observed in the as-cooled samples of the 22Cr-5Ni grade DSS. This is because of a positive Cr interaction in solution-treated materials.[22,27,56,57] The degree of phase separation would then primarily depend on the time spent within the miscibility gap, i.e., the cooling rate achieved.[49,58,59] Second, a positive short-range order (SRO) factor for Cr compositions above 10 at. pct may result in some Cr clustering above the miscibility gap.[22,60,61] Zhou et al.[62] showed that fast cooling in brine resulted in a tendency to clustering primarily due to positive Cr interactions above the miscibility gap, but it can also result from cooling through the miscibility gap. These clustering tendencies would manifest themselves as weak amplitudes.

There are several hardening models available in the literature that have been developed to describe hardening due to modulation of Cr fluctuations in ferrite.[63,64,65,66] For fcc crystal structures, Kato et al.[67] found that the yield strength was directly proportional to the amplitude of modulation. Later, Kato[65] proposed and developed a theory for spinodal modulated structures in bcc alloys. Both these models were based on the work of Cahn.[63] Kato[65] attributed the evolution in hardness to the misfit effect arising from the coherent internal stress and variation in elastic modulus in the modulated structure due to the phase decomposition, i.e., the Cr fluctuation between the α and α′ phase. He found slip was required to initiate deformation even in the later stages of deformation where twinning becomes the dominant deformation mode. This proposed mechanism predicted that the strengthening mechanism is directly proportional to the Cr amplitude and inversely proportional to its wavelength. The Kato[65] expression is as given below:

$$ \Delta \tau_{{{\text{CRSS}}}} = A\eta Y/2 + 0.65 \left( {\frac{\Delta G b}{{\Lambda }}} \right), $$
(7)

where \(\Delta {\tau }_{\mathrm{CRSS}}\) is the incremental change in critically resolved shear stress (CRSS) due to hardening by spinodal decomposition, A is the amplitude, η (4 × 10-3) is a measure of the lattice strains produced during spinodal decomposition (i.e., a dimensionless variation of the lattice constant with respect to the concentration of the secondary element), Y (3.5 × 1011 N/m2) is the elastic modulus resisting lattice deformation during spinodal decomposition, \(\Delta G\) (1.2 × 1010 N/m2) is the change in shear modulus, and b (2.47 Å) is the magnitude of the Burger’s vectors of dislocations.

Ardell[66] considered the Kato approach too primitive and proposed another hardening mechanism:

$$ \Delta \tau_{{{\text{CRSS}}}} = N\left( {A\eta Y} \right)^{\frac{5}{3}} \left( {\frac{{{\Lambda }b}}{}} \right)^{2/3}, $$
(8)

where Г (with units of Gb2) is the line tension of a dislocation. The values of Г can be calculated from Equation 54 in the work of Ardell.[66] For the DSS and SDSS, Γ was calculated to be 0.182, 0.591, and 0.284 for edge, screw, and mixed dislocations, respectively. The numerical coefficient N also varies depending on the characteristic dislocation as 0.122, 0.041, and 0.026 for edge, screw, or mixed type dislocations, respectively.[66]

Then, using the approach given by Pavlina and Van Tyne,[68] the increase critical resolved shear stress in ferrite may be converted to changes in ferrite hardness:

$$ \Delta HV = \frac{{M \times \Delta \tau_{{{\text{CRSS}}}} }}{2.876}, $$
(9)

where M is the Taylor factor for polycrystalline BCC metals and was found to be approximately equal to 2.733.[69] Using the amplitude and wavelength derived from the SANS data (refer Figure 8 and Figure 9) as input parameters, the predicted changes in hardness have been computed using both approaches outlined above and compared to the actual experimental measurements (as shown in Figure 10). From Figure 10, it was observed that the Kato approach and Ardell model for edge dislocations gave similar predictions for all conditions. These predictions overestimated the change in hardness at 350 °C by a factor of 2 for 22Cr-5Ni DSS and by a factor of 3 for 25Cr-7Ni SDSS, whereas at 325 °C, the predictions were in good agreement for 22Cr-5Ni DSS but overestimated the changes in 25Cr-7Ni by a factor of 2. For measurements at 300 °C, both Kato and Ardell edge model predictions were in good agreement with experimental changes in hardness. For lower temperature aging experiments, these models slightly overpredicted the hardness changes. However, all the Ardell models for screw type and mixed mode of dislocations underestimate the experimental hardness observations for 22Cr-5Ni grade DSS. For the 25Cr-7Ni grade SDSS, these Ardell models are in good agreement with the changes in hardness.

Fig. 10
figure 10

Comparison between the measured changes in hardness and model predictions based on the Kato [64] and Ardell [65] approaches following the isothermal aging of (upper) 22Cr-5Ni DSS and (lower) 25Cr-7Ni SDSS at 250 °C, 275 °C, 300 °C, 325 °C, and 350 °C

Full size image

During the isothermal aging of DSS, the resulting changes in hardness are because of the Cr concentration difference in the α and α′ phase, i.e., the development of the Cr amplitude. This development in Cr amplitude increases lattice resistance and renders dislocation propagation difficult in the ferrite phase. This lattice resistance is often referred to as coherency strain and arises due to the lattice misfit between the α and α′ phases.[70] These nanostructural features shift the deformation mode from a slip- to twin-type deformation mode.[71,72] From Figure 10, it is evident that the increases in hardness and subsequent embrittlement is more pronounced in the 25Cr-7Ni grade SDSS than it is in the 22Cr-5Ni grade DSS. The primary reason for this being that the 25Cr-7Ni grade SDSS is richer in Cr and Ni contents.[17,22,73]

Figure 11 shows the Cr amplitude from Figure 9 compared to the impact toughness from Figure 7 at corresponding aging times. For 22Cr-5Ni, the impact toughness decreases dramatically at 300 °C after aging for 12,000 hours. As for 25Cr-7Ni, an observable drop of impact toughness was seen even at 275 °C aging for 24,000 hours. From Figure 11, there is a clear trend observed, a reduction in impact toughness as Cr amplitude increases. Moreover, this increase in Cr amplitude corresponds to an increase in ferrite hardness.

Fig. 11
figure 11

Impact toughness and ferrite hardness compared to Cr amplitude (atomic pct) for 22Cr-5Ni DSS and 35Cr-7Ni SDSS at corresponding aging temperatures and times

Full size image

After the decomposition of the BCC phase into α and α′ phases, there is an increase in the resistance to dislocation propagation, and ultimately the twinning deformation mode becomes more prominent.[19,22,74,75] There are several slip systems possible within the ferritic phase and slip primarily occurs in the <111> direction for the {110}, {112}, or {123} planes.[35,74,76,77,78] Twinning may occur in any of the 12 {112} <111> planes but requires higher stress concentrations to be triggered in comparison to slip.[72,75,79,80] This implies that in the early stages of decomposition, the resolved shear stress is sufficient to initiate slip without twinning. However, with increases in isothermal aging time, the total stress required to initiate slip surpasses the stress required for twin propagation and therefore the twinning deformation mode is favored.[75] For the aged 25Cr-7Ni SDSS samples, Pettersson et al.[22] observed deformation twins on the fracture surface. These deformation twins may either assist failure by providing nucleation sites for micro-cracks to form or may provide obstacles to the propagation of these cracks during deformation.

During the prolonged isothermal aging at intermediate and low temperatures, in addition to hardening, Pettersson et al.[22] observed a transition in the deformation mode from a ductile to a cleavage one, by delamination observations in aged SDSS samples. The impact toughness was observed to be inversely proportional to the increase in Cr amplitude of α and α′ phase separation (see Figure 11). This relationship was also observed in the previous work by Pettersson and co-workers.[22] Chai and Stenvall[81] also observed that spinodal decomposition in DSS promoted the cleavage type failure mode, increasing the ductile to brittle transition temperature of the material. As discussed above, this is because the stress required for slip continuously increases with the increase in the isothermal aging of the alloy. Pilhagen and Sandström[82,83] have discussed the delamination phenomenon during the low-temperature testing of DSS. They found that austenite lamellae act as barriers for crack propagation, such that cleavage cracks are constrained in the direction of the austenite lamellae, thereby giving a predefined crack path. When a certain stress threshold is reached, the austenite lamellae are unable to constrain these cracks. These cracks may subsequently propagate over the complete cross section of the material causing cleavage type failure in the specimen.[82] These observations were made for 22Cr-5Ni DSS deformed at very low temperatures. A similar behavior would be expected to occur for room-temperature deformation in the long-term isothermally aged duplex alloys.

5 Conclusions

This manuscript discusses the effect of long-term isothermal aging at in operando low temperatures on embrittlement phenomenon in a commercial grade duplex and a super-duplex stainless steel. Embrittlement is due to an increase in the hardness of the ferrite phase during long-term exposure within the miscibility gap. This increase in hardness is caused by the nanostructural Cr fluctuations within the ferrite phase. These Cr fluctuations were evaluated using SANS and mechanical property testing using hardness and impact toughness experiments. Key findings are summarized as follows:

  1. 1.

    It is in the very early stages of phase separation process that a measurable change is observed in the micro- and subsequently macro-mechanical properties (i.e., hardness) of the duplex alloys. Embrittlement is a function of both the isothermal aging temperature and time.

  2. 2.

    The increase in hardness is driven by an increase in the Cr concentration of the α′ phase, i.e., by an increase its amplitude, and not influenced here by the almost unchanged length scale of the α and α′ phase separation, i.e., its wavelength, whereas the impact toughness drops with increase in Cr amplitude.

  3. 3.

    The hardness model predictions are in fair comparison with the experimental data for experiments up to 325 °C.

  4. 4.

    The embrittlement phenomenon in 25Cr-7Ni SDSS is more pronounced in comparison to the embrittlement of 22Cr-5Ni DSS. This is evidenced by the rapid evolution in the micro-hardness of the ferrite phase (see Figure 6) and the distinct reduction in Charpy impact toughness measurements (see Figure 7). The cause of this pronounced difference in properties is the higher Cr and Ni concentrations in the 25Cr-7Ni SDSS compared to the 22Cr-5Ni DSS.[9]