Abstract
The boundary region formed on the surface of nickel-based single-crystal turbine blades was investigated by high-resolution microscopy observation. There was a distinguishable intermediate layer with the size of about 2 to 5 μm between the matrix and surface defect grains such as stray grains, multiple grains, freckle grains, and even low-angle grain boundaries which were formed during the solidification of turbine blades. The intermediate layer was composed of many elongated γ′ as well as γ phases. In addition, only one side of the intermediate layer was coherent to the matrix grain or defect grain due to good orientation match. At the coherent interface, the γ′ (as well as γ) phase started to extend from the parent grain and coincidently, rhenium-rich particles were detected. Furthermore, the particles existed within both elongated gamma prime and gamma phases, and even at their boundary. Based on experimental observations, the formation mechanism of this intermediate layer was discussed.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
As superalloys have excellent mechanical strength, phase and surface stability, and resistance to creep, corrosion, and oxidation under relatively severe mechanical stresses at elevated temperatures close to their melting point,[1,2,3,4] they have found widespread application in gas turbine engines for jet propulsion and electricity generation. Newly developed superalloys are continually sought to be used in the hottest parts of the engine because the efficiency of the engine, fuel economy and reduction of emissions, can be improved by higher operation temperatures.[4] The strengthening mechanism for these superalloys is mainly by solid solution hardening and the precipitation of an intermetallic phase.[1] Solid solution hardening is achieved by the addition of different soluble elements, such as Cr, Mo, W, and Re via the inhibition of dislocation movement and the decrease of stacking fault energy in the crystal lattice, which leads to the inhibition of cross slip of dislocations.[3] Precipitation hardening is obtained through the additions of Al, Ti, and Nb which have limited solubility in the alloy matrix. During heat treatment, a supersaturated solid solution generates finely distributed precipitates of gamma prime (γ′) phase which inhibits dislocation movement.
Superalloys are one of the most compositionally complex alloys developed, sometimes containing more than ten alloying elements, and through their component manufacture they are subjected to multiple steps of melting, casting, and heat treatment. As a result, they are subject to numerous metallurgical phenomena, such as melting, solidification, homogenization, aging, precipitation, transformation, coarsening, microsegregation, and chemistry variation. Therefore, these complexities can make it difficult to understand exactly the strengthening mechanism of Re in superalloys. The distribution of Re clusters, about 1 nm across, in the γ phase, which was observed by field ion microscopy and atom probe, may induce this strengthening mechanism,[5,6] while there are other studies showing no clustering of Re in superalloys, which was confirmed by extended X-ray absorption fine structure (EXAFS), atom probing, and first-principles density functional theory calculations.[7,8] Depending on the analysis method or equipment, different interpretations can be made. In addition, as analysis techniques and equipments develop, new findings can be made even in these widely investigated alloy systems. One of these recent findings is the formation of an intermediate layer containing Re-rich particles in Ni-based single-crystal turbine blades along grain boundaries.[9] In single-crystal superalloys, the reintroduction of any grain boundaries can dramatically reduce the superior mechanical properties because grain boundary strengthening elements, such as boron, carbon, and zirconium, have been removed[3,4] and more importantly, creep rupture can occur along the boundary.[10] In addition, if Re-rich particles form, they lose their main role as a solid solution hardening element which distorts the atomic lattice of the gamma (γ) phase matrix and inhibits dislocation movement. Therefore, the existence of any boundary and this associated intermediate layer, and the formation of Re-rich particles in a single-crystal superalloy are undesirable. In this study, based on this previous reporting of the intermediate layer in turbine blades and the detection of Re-rich particles in a sample containing a stray grain,[9] the boundary regions between matrix grains and several other defect grains, such as stray grains, multiple grains, freckle grains, and even low-angle grain boundaries found in nickel-based single-crystal turbine blades have been investigated for better understanding of these materials. In addition, high-resolution analysis has been carried out from several other Ni-based single-crystal alloys, such as SRR99 and CMSX-4, as well as CMSX-10. Based on experimental observation, the formation mechanism of the intermediate layer, and the relationship between Re-rich particles and the layer have been also discussed.
2 Experimental
A commercially available Ni-based single-crystal alloy CMSX-10[11] containing a large amount of Re (Table I) was used to manufacture turbine blades at an aerospace production manufacturing facility, Rolls-Royce plc. As-cast turbine blades were removed from the runner system and underwent solution heat treatment in order to develop the required microstructure composed of cuboids of γ′ phase in a matrix of γ phase. The solution heat treatment for this material has been published as 1589 K (1316 °C) for 1 hour; followed by 2 hour steps at 1602 K, 1613 K, and 1619 K (1329 °C, 1340 °C, and 1346 °C), and then, 3 hour steps at 1625 K, 1630 K (1352 °C, 1357 °C), before slowing the heating rate to 5 hours at 1633 K (1360 °C), 10 hours at 1636 K (1363 °C), and finally 15 hours at 1638 K (1365 °C).[3] This slow ramp is due to the proximity of the γ′ solvus to the melting point.[12] To identify any grain defects which could be observed on the surface of the component, the blades were etched to allow visual inspection. The preferential attack into the boundary by the etchant enabled the inspection for secondary grains on the surface of the blades. The detailed explanation of sample preparation and inspection is available elsewhere.[3,4,9,13] The samples identified as containing a surface defect were cut out by wire-guided electro discharge machining (EDM). The cut sample was ultrasonic-cleaned in ethanol for 5 minutes.
For microstructural investigation, a field emission scanning electron microscope (FE-SEM, FEI Quant 3D dual beam FIB-SEM) was used in order to observe samples at ultra-high magnifications of 100,000 to 200,000 times and to perform chemical analysis using energy dispersive X-ray spectroscopy (EDX). Three different SEM imaging modes, i.e., secondary electron (SE) and back-scattered electron (BSE) using electron beam imaging, and ion-induced SE (IS) using gallium ion beam imaging were used throughout this study. The FE-SEM was also able to perform the cross-sectioning of regions of interest by cutting and thinning using a focused ion beam (FIB). After cross-sectioning, a TEM sample was fabricated by an in situ FIB lift-out technique.[14,15] However, as it was difficult to preserve the interface between two grains without critical damage during FIB cutting and thinning because the interested region was not flat (see Figures 2 through 4, and 6), a simple technique using the rotation of a thin lamellae was used as shown in Figure 1. A region of interest was selected, and a platinum layer was deposited on it for protection during FIB sampling. Top and bottom sides were fabricated by FIB (Figure 1(a)). Then, the thin lamella was lifted-out and put on a TEM copper grid (Figure 1(b)). This cutting and thinning procedure is typical in the conventional FIB lift-out technique. In this study, however, the thinning direction was changed by rotating the lamella 90 deg as shown in Figure 1(c). Therefore, further thinning could be done from one grain to the adjacent grain, left to right in Figure 1(a). Without the 90 deg rotation, the thinning would be done from the top surface platinum layer into the inside of the grains. After the rotation, the lamella was thinned by the conventional FIB thinning process as shown in Figures 1(d) through (f). Finally, a thin enough section for TEM observation was made and then observed by high-resolution transmission electron microscopy (FE-TEM, FEI Tecnai F20) equipped with a scanning mode (STEM) and an EDX system. As the close proximity of characteristic X-rays (M α, keV) of alloying elements, such as Hf (1.644), Ta (1.709), W (1.774), and Re (1.842), made it difficult to distinguish clearly each element through SEM-EDX analysis,[16,17] the chemical analysis of samples was simply checked by SEM-EDX and then performed by STEM-EDX with a nominal probe size of around 2 nm. The chemical composition was acquired from silicon drift detectors installed to the TEM and provided by a qualitative analysis software (Oxford AZtecTEM) which can perform a standardless analysis without need for any background fitting adjustment, and allow sample thickness and density to be taken into consideration and correction for pulse pile-up at high count.[9] The TEM sample was cooled with liquid nitrogen to avoid or minimize microstructural changes in the irradiated area during TEM observation.[15]
TEM sampling using a conventional FIB lift-out technique: (a) selected location marked with an arrow after trenching the top and bottom faces, (b) thin lamella placed on a Cu grid, (c) after the rotation of 90 deg, (d) top view after the rotation, (e) side view after thinning, (f) top view of a thin layer. Note that after the cleaning of the thin layer, a TEM sample was fully prepared
3 Results
Figure 2 is composed of typical images of an intermediate layer formed in a CMSX-10 turbine blade. A stray grain detected in the platform region by visual inspection was selected for further observation (Figure 2(a)). The stray grain is shown as dark contrast without any boundary region. However, an SEM image (Figure 2(b)) at a low magnification (100 times) clearly indicates that there is a distinguishable line between the stray grain and the matrix. The boundary line becomes clear at higher magnifications (3500 and 12,000 times) as shown in Figures 2(c) through (d). First of all, it is a boundary layer formed between two adjacent grains. To check whether the layer forms only between a stray grain and the matrix, boundary regions of several other surface defect grains were similarly observed. Figure 3 shows SEM images of the boundary layers detected in several different surface defect grains which formed during solidification of turbine blades.[9,18,19,20,21] The layer was also visible at the boundary of the matrix grain and a stray grain found on a shroud region (Figure 3(a)), an area of multiple grains (Figure 3(b)), and a freckle grain (Figure 3(c)). It should be emphasized that the layer is also found even in grain boundaries with low angles of mismatch (Figure 3(d)) where the mis-orientation angle between the adjacent grains was measured using a reflected Laue X-ray system at 6.1 deg. This result is important for the understanding of the formation mechanism of this boundary layer because it is known that the development of the discontinuous precipitation reaction, which forms similar microstructures to the layer observed in this study, can only occur along boundaries with mis-orientation greater than 10 deg.[22,23,24] From the observation, it is clear that there is a distinct boundary layer between a matrix and surface defect grains.
Photographs (a) and SEM images (b to d) showing an intermediate layer between a stray grain and a matrix grain: (b) low-magnification BSE image showing a whole stray grain, (c) SE image of a boundary layer between a stray grain and a matrix grain with an arrow, (d) magnified SE image clearly showing an intermediate layer
SEM images of an intermediate layer formed between a matrix grain and several different surface defect grains: (a) a stray grain formed in the shroud region of a turbine blade, (b) an area of multiple grains, (c) a freckle grain, and (d) low-angle grain boundary. Panels (a to c) are SE images and panel (d) is a BSE image
Figures 2 and 3 also show that the size of the boundary layer is about 2 to 5 μm, which means that it is a layer (not an independent grain boundary) formed between adjacent two grains because the size of effective grain boundaries in other systems is shown to be about 0.5 nm.[25] Most of all, the observation suggests that the intermediate layer can be detected in any grain boundary regions formed during the solidification of Ni-based single-crystal turbine blades even though the boundary width is slightly different. In addition, close observation of the intermediate layer formed between a stray grain and the matrix in the platform region (Figures 2 and 3(a)) shows that the stray grain is surrounded with the intermediate layer, and as a result, the boundary was easily distinguishable during observation. It is interesting to note that only one side of the layer marked with an arrow in Figure 3(a) has a coherent boundary. Most of all, the coherent interface could be found on both the sides of the stray grain or the side of the matrix separately, which means that there is no tendency to form the coherent interface in any particular grain. The observation suggests that one side of the intermediate layer has a coherent interface with one of the grains.
The previous observations were made of the intermediate layer on the casting surface. To observe the cross section, two intermediate layers were cross-sectioned, respectively, by the FIB milling process as shown in Figure 1. Figure 4 is two representative SEM images of the cross section. SEM tilting view images made by secondary electron imaging (SE, Figure 4(a)) and ion-induced secondary electron imaging (IS, Figure 4(b)) clearly indicated two important facts; firstly that the intermediate layer is composed of many elongated γ′ as well as γ phases (not pure γ′ phase), and secondly that at the interface which is coherent, γ′ (as well as γ) phase starts to extend from the parent grain. Most of all, the IS image (Figure 4(b)), using channeling contrast, also indicated clearly that the γ′ phase in the intermediate layer has the same {100} orientation as the γ′ phase in the stray grain, as a result, it has the same contrast, while at the non-coherent interface the contrast is changed dramatically due to the slightly different {100} orientation of γ′ phase in the matrix grain. Therefore, the non-coherent (sharp) interface is along the side of the intermediate layer where the orientation mismatch occurs.
To confirm the elongation of γ′ and γ phases, an intermediate layer was observed at a magnification of 100, 000 times. The sample in Figure 5(a) was etched away for visual inspection to find any surface defect grains. Even after the severe etching process, many tiny γ′ particles survived as shown in Figures 5(a) and (b), leaving the intermediate layer proud of the rest of the surface. As the etching solution attacked the γ phase preferentially, the γ′ particles in the intermediate layer have less surrounding γ phase to be etched away, leaving them attached and proud of the surface. To observe the detailed microstructure, a TEM sample was made exactly on the intermediate layer in Figure 5(a) using the aforementioned FIB lift-out technique (Figure 1). Figure 5(c) and (d) show STEM-HAADF images after TEM sampling. With conventional FIB sampling, i.e., without the rotation of 90 deg (Figure 1(c)), it was extremely difficult to make a sample preserving the whole intermediate layer because the layer was not flat, as shown in Figures 2,3 through 5, and most of all, a strong gallium ion beam could make deep scratches near or at the interfaces even though a protective platinum layer was deposited on it. In Figure 5(c), the dark contrast in the intermediate layer was caused by the pull-out of some particles during TEM sampling. Figure 5(d) clearly shows that a γ′ phase in the intermediate layer starts to be elongated from a γ′ particle in the stray grain as marked with an arrow. This observation suggests that the elongated γ′ phase forms from tiny γ′ precipitates adjacent to the boundary between two grains.
Figure 6(a) is an SEM image acquired in BSE mode on an intermediate layer. The BSE image as well as the cross-sectioned images in Figures 4(a) and (b) clearly show that there were many tiny particles along the interface between the intermediate layer and a stray grain (Figures 4(b) through 6(a)) or a matrix grain (Figure 4(a)). The BSE image indicated that the particles contained heavier elements, such as Mo, Hf, Ta, W, and Re than Ni. A STEM-EDX point analysis (Table I, also see Reference 9) carried out on a Re-rich particle using a nominal probe size of 2 nm suggested that the particles contained large amount of Re and they were probably Ni(Re,Cr,Co,Mo,W)3. It is necessary to emphasize that the Re-rich particles exist along only one side of the intermediate layer; that which the elongated γ and γ′ grow from and is coherent. On the contrary, it was observed that there were few Re-rich particles near the non-coherent interface. To confirm the distribution of the Re-rich particles along only one side of the intermediate layer, a layer was selected and cross-sectioned by FIB (Figure 6(b)). After FIB cutting and cleaning, tilting views of the cross section (Figures 6(c) and (d)) showed a remarkable distribution of Re-rich particles. The particles existed within the γ′ phase as well as in the γ phase, and even at their boundaries. It should be noted that the particles were not caused by contamination or re-deposition during milling. Therefore, the random distribution of Re-rich particles suggests that they exist from solidification from the melt, which is in good agreement with the observation that the Re-rich particles were experimentally detected in as-cast samples.[9]
4 Discussion
4.1 Possibility of Cellular Recrystallization or Formation of Columnar Zone of Elongated Grains
The elongated γ′ phase in the intermediate layer is similar to the lamellar microstructure formed by cellular recrystallization,[26,27,28,29,30] or the columnar zone of elongated grains formed in solidified alloy ingots.[25] The samples in this study were subjected to multiple steps of melting, casting, and heat treatment during manufacturing. The solution heat treatment process undertaken on these samples was intended to dissolve the γ/γ′ eutectics and reduce the chemical segregation resulting from the dendritic growth during the solidification process.[13] Therefore, even though the elongated γ′ phase might form during solidification, it would have been dissolved as the heat treatment was above the γ′ solvus, and as a result there was little possibility that the elongated γ′ phase was analogous to the columnar zone of elongated grains formed during solidification.
During the manufacturing and processing of new parts, plastic deformation may be induced in the component from many sources, such as contracting stresses during cooling of the solid metal in the shell mold, mechanically removing shell mold residue, removal of the part from the gating system and general handling,[26] and these can be concentrated on the surface of components or even extend into the bulk of the part. This concentrated deformation could be released by recrystallization during solution heat treatment and subsequent grain growth by strain-induced boundary migration.[31,32] As a result, cellular recrystallization which is similar to the elongated γ′ and γ phases has been observed in many specimens.[26,27,28,29,30,31,32] However, in order to initiate the recrystallization, a free surface as well as γ′-free zone must be available and this allows the recrystallization to occur on the surface and move into the bulk of the material. If these conditions do not exist, then a much higher amount of plastic deformation is required (e.g., more than about 10 pct).[26] After that, the cellular recrystallization moves a grain boundary into the deformed parent material. The reduction of free energy (ΔG T) by the cellular recrystallization can be expressed as ΔG T = ΔG m + ΔG γ + ΔG c, where ΔG m reflects the annihilation of dislocations, ΔG γ is related to the microstructural coarsening and creation of a high-angle grain boundary, and ΔG c is the chemical composition of phases in the recrystallized region.[26] As our previous study showed that the compositions of γ′ in the elongated region and the matrix or a stray grain are almost same, the last term is negligible.[9] The realistic strain values which can be imposed on the components are about 2 to 3 pct.[26] Therefore, the value of ΔG T is positive without any additional deformation, such as a hardness indentation or similar non-uniform deformation in excess of about 10 pct, which means that it is almost impossible to induce the recrystallization in the bulk materials without additional deformation. In the previous study[9] an investigation into a recrystallized grain showed that the elongated γ and γ′ were not present despite the boundary moving through the material to the final location during solution heat treatment. In addition, it should be emphasized that in the sample observed in this study, the top surface of the component (which plastic deformation was concentrated on) was etched away for visual inspection, and the elongated direction of the intermediate layer was nearly parallel to the surface through the thickness of the component. Therefore, the elongated γ′ phase in the intermediate was not formed either by the cellular recrystallization or by the formation of a columnar zone of elongated grains during solidification.
4.2 Formation Mechanism of Intermediate Layer
Before discussing the formation mechanism of the intermediate layer, it is necessary to clarify whether the sharp (non-coherent) interface is the starting point in the formation of the layer or the terminating one. To form the elongated phases, either γ′ or γ should be nucleated. For nucleation, the activation energy should be reduced through releasing some free energy (ΔG T) which can be expressed as ΔG T = Aγ−V(ΔG v−ΔG s), where A and V are area and volume, respectively, γ an interfacial energy, ΔG v a volume free energy, and ΔG s is a misfit strain energy per unit volume.[25] Therefore, to achieve a low interfacial energy, it is important to achieve a good lattice match through a small disregistry (δ = Δa 0/a o), where Δa 0 is the difference between the lattice parameters of the nucleating and the nucleated metal belonging to the same crystal structure along a specific direction, and having similar crystallography.[33,34,35] At this point, it should be emphasized that the sharp interface between the elongated phase and the matrix grain (or a stray grain) means that there was no specific orientation relationship between them. Therefore, the non-coherent interface was not energetically the starting point of the formation of the intermediate layer, which means that the formation of the layer started from the coherent interface and terminated at the topologically sharp one.
Then, the interface energy is significantly affected by many factors, such as grain size, crystal structure, misfit dislocations in the interface of substrate/nucleated metal, lattice mismatch, orientation relationship, chemical nature, and electrostatic potential between them.[25,35,36] Recently, however, it has been reported that if any nucleation occurs on the same base material, the interface energy is minimized and as a result, nucleation can occur easily.[37,38] Therefore, the formation of the elongated γ′ and γ phases in the intermediate layer may be explained basically by the nucleation mechanism on the same material, i.e., the formation of the elongated γ′ and γ phases (in the intermediate layer) from adjacent γ′ and γ phases in matrix, which is known as grain boundary precipitation or cellular precipitation. In this precipitation, the reaction can be written as follows:
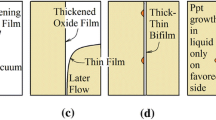
where γ sat is the supersaturated γ phase, γ i ′ is the γ′ phase in the intermediate layer, and γ i is the γ phase in the intermediate layer but with a lower thermo-dynamic excess of solute.[25] The first stage of the reaction is the nucleation of γ′ or γ as schematically shown in Figure 7. At this point, it should be remembered that the Re-rich particles probably existed from solidification of the melt and were experimentally detected in as-cast samples.[9] If the γ′ phase nucleates first, the activation energy barrier to nucleation can be minimized by nucleation on the same γ′ phase in an adjacent grain. The γ phase surrounding the nucleus will become rich in the elements which partition from the γ′ (Re, W, Ta, etc.) and then will increase the driving force for the formation of normal γ phase in the intermediate layer. This process can be repeated along the grain boundary. After the nucleation, the colony can grow edgewise by the movement of boundary changing the orientation of γ′ particles,[31] and then, finally, the observed elongation of γ′ and γ phases form in the intermediate layer.
4.3 Comparison of the Formation Mechanism with a Conventional Discontinuous Precipitation Reaction
In the formation mechanism of the intermediate layer, it should be emphasized that without pre-existing Re-rich particles, the nucleation mechanism of the intermediate layer is similar to a conventional discontinuous precipitation (DP) reaction which has been intensively and widely observed in over 500 binary and multicomponent systems even though it still remains a controversial issue.[39,40,41] To reduce the energy of the grain boundary, the DP reaction can easily occur from the following reaction[22,23,24,42]:
where P is a parent grain, I the intermediate layer, and TCP topologically close-packed phases. The driving force for the reaction is a reduction of the internal strain energy as well as the change in the γ′ precipitate size, reducing the surface area per unit volume of precipitation.[24] However, the DP reaction generally occurs along both sides of the boundary adjacent to grains which results in the formation of a wavy grain boundary. The boundary observed in this study is always straight on a microscopic scale. Also, when compared to the composition of the TCP phases reported in the DP reaction, such as the P phase with an amount of rhenium of about 20 at. pct,[43,44] that of the Re-rich particles reported here with over 60 at. pct are very different. Compared to other TCP phases, such as σ phase {Ni8(Cr,Mo)4(Cr,Mo,Ni)18}, δ phase (NiMo), Laves phase with formula A2B, μ phase (Co,Fe,Ni)7(MoWCr)6, and R phase (Mo31Cr18Co50),[1] the composition is also very different. In addition, TCP phases from the DP reaction form after a long aging time through grain boundary diffusion.[45] However, the Re-rich particles in this study were seen after relatively short solution heat treatment and subsequent aging. When TCP phases are precipitated from the DP reaction, the area surrounding the TCP phases becomes depleted of TCP-forming elements. However, the distribution of alloying elements near Re-rich particles in this study is uniform. Most of all, from the DP reaction, needle-like TCP phases are formed and usually aligned perpendicular to the growth interface,[46] while in this study, round-shaped Re-rich particles were randomly distributed along the interface. In addition, the Re-rich particles exist inside the elongated γ′ as well as γ phase in the intermediate layer, which means that it is difficult to explain this observation with the DP reaction and subsequent TCP precipitation as there is no previous observation showing these Re-rich particles which exist from the as-cast state. Most of all, the reported morphology and chemistry of the TCP phases is different to those seen in this study. Finally, it should be emphasized that our previous study showed that Re-rich particles were also detected in as-cast samples[9] and their existence in as-cast samples have been confirmed (not reported here). The pre-existence of Re-rich particles means that in the DP reaction, TCP phases formed from the reaction of \( \left( {\gamma + \gamma^{\prime } } \right)_{\text{p}} \to \gamma_{\text{I}} + \gamma^{\prime }_{\text{I}} + {\text{TCP}} \), while in the current study, Re-rich particles already existed before the elongated γ and γ′ phases formed from \( \gamma_{\text{sat}} \to \gamma^{\prime }_{i} + \gamma_{i} \), which is the main difference of the suggested formation mechanism in this study and the conventional discontinuous precipitation. However, as the cell front in the cellular precipitation passes, the composition of the matrix changes discontinuously and as a result, the cellular precipitation is also known as the discontinuous precipitation.[25] Therefore, in order to distinguish the formation mechanism of the intermediate layer in this study with the conventional discontinuous precipitation, the formation mechanism can be referred as the Re-rich particle-induced cellular precipitation or Re-rich particle-induced discontinuous precipitation.
4.4 Relationship Between the Intermediate Layer and Re-rich Particles
Until now, the formation mechanism for the intermediate layer containing Re-rich particles has been discussed in detail. However, with the aforementioned mechanism, it is not easy to explain the elongated γ′ and γ phases through the reaction \( \gamma_{\text{sat}} \to \gamma^{\prime }_{i} + \gamma_{i} \) because it cannot explain the reason for the elongation instead of forming cubic γ′ phase in the adjacent grain. It is known well that in the case of applying external uniaxial stress to the component, platelike γ′ can be formed and rod-shaped γ′ forms in biaxial stress fields. However, external stress was not applied to the samples in this study and the only stress in the area is the grain boundary mismatch stress. Therefore, the elongation of γ′ and γ phases in the intermediate layer could be influenced by the existence of Re-rich particles. In order to study the possibility of this relationship, a Re-free Ni-based superalloy (SRR99, Ni-5.5 pct Al-2.2 pct Ti-8 pct Cr-5 pct Co-3 pct Ta-10 pct W, wt pct) was investigated. single-crystal SRR99 turbine blades were manufactured at the same aerospace production manufacturing facility and a sample containing a high-angle defect grain was selected. Figure 8 is SEM images of a high-angle grain boundary in a Re-free SRR99 sample. It is clear that there is no intermediate layer between two grains.
The CMSX-10, which is one of Ni-based superalloys containing large amount of Re, clearly showed the intermediate layer, while no intermediate layer was found in the SRR99 alloy, containing no Re. Therefore, as it is necessary to observe a sample containing medium amount of Re, another Ni-based superalloy (CMSX-4) containing 3 wt pct Re was selected and manufactured at the same facility. Figure 9 is SEM images acquired in a CMSX-4 sample. Along the same boundary between a stray grain and matrix, two different microstructures were observed: one is the intermediate layer just like CMSX-10 samples, and the other no intermediate layer like SRR99 samples. It should be noted that the region showing the intermediate layer (Figure 9(a)) was not far from the region showing the sharp interface (Figure 9(c)). The cross section made from the region containing the intermediate layer shows several Re-rich particles marked with arrows in Figure 9(b), while there were no particles in the cross section at the sharp interface (Figure 9(d)). Therefore, this observation confirms that the elongation of γ′ and γ phases in the intermediate layer is definitely related to the pre-existence of Re-rich particles, and supports the formation mechanism of the intermediate layer via the Re-rich particle-induced cellular precipitation.
SEM images of two different boundaries in a single-crystal CMSX-4 turbine blade: (a) plain view of a boundary, (b) tilting view after cross-sectioning of the central region in panel (a), (c) plain view of another boundary, and (d) tilting view after cross-sectioning in (c). Note that the two boundary regions were not far from each other, which can be ascertained by the {100} directions of the cube edges of each γ′ phase
5 Summary and Conclusion
An intermediate layer with a width of about 2 to 5 μm containing fine Re-rich particles was detected between a matrix grain and several surface defect grains which formed during solidification. The intermediate layer was composed of many elongated γ′ as well as γ phases (not purely γ′ phase) and had two different interfaces: coherent and non-coherent sharp interfaces. From the side of the coherent interface, γ′ (as well as γ) phase initiated and grew in elongated form, not the cuboidal structure seen in the body of the grain. Most of all, the elongated γ′ phase formed from γ′ precipitates in an adjacent surface defect grain or matrix and retained the orientation of these initiating grains. This morphology of the intermediate layer was similar to an interfacial layer formed from the discontinuous precipitation. However, in the intermediate layer, some Re-rich particles existed along only one side which was coherent and they existed in both the γ′ phase and the γ phase, and even at their boundary. Most of all, the Re-rich particles existed from as-cast samples. Re-free or samples containing medium amount of Re clearly supported that the elongation of γ′ and γ phases in the intermediate layer was definitely related to the existence of Re-rich particles.
It is well known that grain boundaries are a source of weakness of turbine blades.[3,4] The existence of grain boundaries, exactly, the existence of the intermediate layer is probably detrimental to the superior mechanical properties of Ni-based turbine blades. Therefore, even though any direct measurements of mechanical properties was not done in this study, it is suggested that it is necessary to investigate the methods to minimize or avoid the formation of the intermediate layer as well as numerous Re-rich particles.
References
M. Durand-Charre, The Microstructure of Superalloys (OPA, Amsterdam, 1997), pp. 1–14
Y. Bar-Cohen, High Temperature Materials and Mechanisms (CRC Press, New York, 2014), pp. 41–43
B. Geddes, H. Leon, X. Huang, Superalloys: Alloying and Performance (ASM International, Materials Park, 2010), pp. 1–15
R.C. Reed, The Superalloys: Fundamentals and Applications (Cambridge University Press, Cambridge, 2006), pp. 1–211
J. Rüsing, N. Wanderka, U. Czubayko, V. Naundorf, D. Mukherji, J. Rösler, Scr. Mater. 46, 235–40 (2002)
N. Wanderka, U. Glatzel, Mater. Sci. Eng. A 203, 69–74 (1995)
A. Mottura, R.T. Wu, M.W. Finnis, R.C. Reed, Acta Mater. 56, 2669–75 (2008)
A. Mottura, N. Warnken, M.K. Miller, M.W. Finnis, R.C. Reed, Acta Mater. 58, 931–42 (2010)
K. Kim, P. Withey, W.D. Griffiths, Metall. Mater. Trans. A 46, 1024–29 (2015)
W.S. Walston, J.C. Schaeffer, W.H. Murphy, Superalloys 1996 (Minerals, Metals & Materials Soc, Warrendale, 1996), pp. 9–18
G.L. Erickson, Superalloys 1996 (Minerals, Metals & Materials Soc, Warrendale, 1996), pp. 35–44
R.W. Broomfield, D.A. Ford, H.K. Bhangu, M.C. Thomas, D.J. Frasier, P.S. Burkholder, K. Harris, G.L. Erickson, J.B. Wahl, J. Eng. Gas Turb. Power 120, 595–608 (1998)
T. Grosdidier, A. Hazotte, A. Simon, Mater. Sci. Eng. A 256, 183–96 (1998)
K. Kim, M. Watanabe, J. Kawakita, S. Kuroda, Scr. Mater. 59, 768–71 (2008)
K. Kim, Metall. Mater. Trans. A 45, 3650–60 (2014)
Energy table for EDS analysis (JEOL, 2013), http://www.jeol.co.jp. Accessed 28 Sept 2013.
P.J. Warren, A. Cerezo, G.D.W. Smith, Mater. Sci. Eng. A 250, 88–92 (1998)
J.P. Gu, C. Beckermann, A.F. Giamei, Metall. Mater. Trans. A 28, 1533–42 (1997)
N. Stanford, A. Djakovic, B.A. Shollock, M. McLean, N. D’Souza, P.A. Jennings, Scr. Mater. 50, 159–63 (2004)
Z.D. Long, W.H. Yang, K.M. Chang, Superalloys 718, 625, 706 and Various Derivatives (Minerals, Metals & Materials Soc, Warrendale, 2001), pp. 745–54
J.W. Aveson, P.A. Tennant, B.J. Foss, B.A. Shollock, H.J. Stone, N. D’Souza, Acta Mater. 61, 5162–71 (2013)
J.D. Nystrom, T.M. Pollock, W.H. Murphy, A. Garg, Metall. Mater. Trans. A 28, 2443–52 (1997)
A.C. Yeh, S. Tin, Metall. Mater. Trans. A 37, 2621–31 (2006)
R.B. Scarlin, Scr. Metall. 10, 711–15 (1976)
D.A. Porter, K.E. Eastering, M.Y. Sherif, Phase Transformations in Metals and Alloys, 2nd edn. (CRC Press, Boca Raton, 2009), pp. 322–25
R. Burgel, P.D. Portella, J. Preuhs, Superalloys 2000 (Minerals Metals & Materials Soc, Warrendale, 2000), pp. 229–38
B. Zhang, X.-G. Cao, D.-L. Liu, X.-L. Liu, Trans. Nonfer. Metals Soc. China 23, 1286–92 (2013)
J. Meng, T. Jin, X.-F. Sun, Z.-Q. Hu, Int. J. Miner. Metall. Mater. 18, 197–202 (2011)
L.-C. Zhuo, M. Huang, J.-C. Xiong, J.-R. Li, J. Zhu, Acta Metall. Sin. 28, 72–76 (2014)
X. Jichun, L. Jiarong, L. Shizhong, Chine. J. Aerona. 23, 478–85 (2010)
A. Porter, B. Ralph, J. Mater. Sci. 16, 707–13 (1981)
A.J. Porter, B. Ralph, Mater. Sci. Eng. 59, 69–78 (1983)
K. Nogita, S.D. McDonald, K. Tsujimoto, K. Yasuda, A.K. Dahle, J. Electron Microsc. 53, 361–69 (2004)
H.S. Dai, X.F. Liu, Mater. Sci. Tech. 25, 1183–88 (2009)
B. Bramfitt, Metall. Trans. 1, 1987–95 (1970)
R. Schweinfest, S. Köstlmeier, F. Ernst, C. Elsäser, T. Wagner, M.W. Finnis, Philos. Mag. A 81, 927–55 (2001)
J.A. Dantzig, M. Rappaz, Solidification (CRC Press, Boca Raton, 2009), pp. 261–75
K. Kim, Metall. Mater. Trans. A 45, 4538–48 (2014)
L. Zhuo, M. Huang, F. Wang, J. Xiong, J. Li, J. Zhu, Mater. Lett. 139, 232–36 (2015)
E.A. Brener, D.E. Temkin, Acta Mater. 51, 797–803 (2003)
I. Manna, S.K. Pabi, W. Gust, Int. Mater. Rev. 46, 53–91 (2001)
A. Heckl, S. Cenanovic, M. Goken, R.F. Singer, Metall. Mater. Trans. A 43A, 10–19 (2012)
J. Meng, T. Jin, X. Sun, Z. Hu, Mater. Sci. Eng. 527, 6119–22 (2010)
Z. Yu, X. Ding, Y. Zheng, L. Cao, Q. Feng, MATEC Web Conf. 14, 11006 (2014)
N. D’Souza, S. Simmonds, G.D. West, H.B. Dong, Metall. Mater. Trans. A 44, 4764–73 (2013)
W.S. Walston, K.S. O’Hara, E.W. Ross, T.M. Pollock, W.H. Murphy, Superalloys 1996 (Minerals, Metals & Materials Soc, Warrendale, 1996), pp. 27–34
Acknowledgments
The financial support and provision of evaluation test pieces by Rolls-Royce is acknowledged.
Author information
Authors and Affiliations
Corresponding author
Additional information
Manuscript submitted November 4, 2016.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Kim, K., Withey, P. Formation of an Intermediate Layer Between Grains in Nickel-Based Superalloy Turbine Blades. Metall Mater Trans A 48, 2932–2942 (2017). https://doi.org/10.1007/s11661-017-4044-7
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11661-017-4044-7