Concentration-Dependent Carbon Diffusivity in Austenite

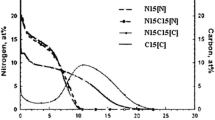
Abstract

The diffusion coefficient of carbon in austenite depends on the local carbon concentration. This concentration dependence is particularly noticeable during low-temperature “paraequilibrium” carburization. A critical review of the extensive literature on this topic reveals that an early paper by Asimow provides an excellent description of this substantial concentration dependence. The present analysis suggests that the marked concentration dependence of carbon diffusivity is most likely due to interstitial carbon decreasing the activation energy for carbon jumps from one interstitial site to its neighbor.

Appendices

Appendix 1

The expression of $f_{\text{u}}^{ 1}$ based upon cumulant–moment expansions is[32]

$$ f_{\text{u}}^{ 1} = \sum\limits_{i = 1}^{\infty } {\delta_{i} \frac{{\alpha^{i - 1} }}{{\left( {i - 1} \right)!}}} , $$

(A1)

where

$$ \delta_{i} = \frac{{\lambda_{i} }}{{N_{\text{u}} }} $$

(A2)

and

$$ \alpha = - \frac{{\Delta \varepsilon_{\gamma } }}{kT}. $$

(A3)

The calculation of the cumulants δ _i up to i = 4 in Eq. [A2] is as follows:

$$ \delta_{1} = 6Y_{\text{C}} , $$

(A4)

$$ \delta_{2} = 6Y_{\text{C}} \left( {1 - Y_{\text{C}} } \right)^{2} , $$

(A5)

$$ \delta_{3} = 6\left[ {Y_{\text{C}} \left( {1 - Y_{\text{C}} } \right)^{2} \left( {1 - 2Y_{\text{C}} } \right)^{2} + 8Y_{\text{C}}^{2} \left( {1 - Y_{\text{C}} } \right)^{3} } \right], $$

(A6)

$$ \delta_{4} = 6\left[ {Y_{\text{C}} \left( {1 - Y_{\text{C}} } \right)^{2} \left( {1 - 6Y_{\text{C}} + 6Y_{\text{C}}^{2} } \right)^{2} + 24Y_{\text{C}}^{2} \left( {1 - Y_{\text{C}} } \right)^{3} \times\left( {1 - 2Y_{\text{C}} } \right)^{2} + 126Y_{\text{C}}^{3} \left( {1 - Y_{\text{C}} } \right)^{4} } \right]. $$

(A7)

The expression of $\sigma^{\prime}$ based upon cumulant–moment expansions is[32]

$$\sigma^{\prime} = \sum\limits_{i = 1}^{\infty } {\frac{{\alpha^{i - 1} }}{{\left( {i - 1} \right)!}}} \left[ {\delta_{i} + \left( {1 + fY_{\text{C}} } \right)\frac{{{\text{d}}\delta_{i} }}{{{\text{d}}Y_{\text{C}} }}Y_{\text{C}} } \right] = \delta_{1} + \left( {1 + fY_{\text{C}} } \right)\frac{{{\text{d}}\delta_{1} }}{{{\text{d}}Y_{\text{C}} }}Y_{\text{C}} + \alpha \left\{ {\delta_{2} + \left( {1 + fY_{\text{C}} } \right)\frac{{{\text{d}}\delta_{2} }}{{{\text{d}}Y_{\text{C}} }}Y_{\text{C}} } \right\} + \frac{{\alpha^{2} }}{2}\left\{ {\delta_{3} + \left( {1 + fY_{\text{C}} } \right)\frac{{{\text{d}}\delta_{3} }}{{{\text{d}}Y_{\text{C}} }}Y_{\text{C}} } \right\} + \frac{{\alpha^{2} }}{6}\left\{ {\delta_{4} + \left( {1 + fY_{\text{C}} } \right)\frac{{{\text{d}}\delta_{4} }}{{{\text{d}}Y_{\text{C}} }}Y_{\text{C}} } \right\}. $$

(A8)

The calculation of the cumulants $\frac{{{\text{d}}\delta_{i} }}{{{\text{d}}Y_{\text{C}} }}$ up to i = 4 in Eq. [A8] is as follows:

$$ \frac{{{\text{d}}\delta_{1} }}{{{\text{d}}Y_{\text{C}} }} = 6, $$

(A9)

$$ \frac{{{\text{d}}\delta_{2} }}{{{\text{d}}Y_{\text{C}} }} = 6 - 24Y_{\text{C}} + 18Y_{\text{C}}^{2} , $$

(A10)

$$ \frac{{{\text{d}}\delta_{3} }}{{{\text{d}}Y_{\text{C}} }} = 6\left[ {1 + 4Y_{\text{C}} - 33Y_{\text{C}}^{2} + 48Y_{\text{C}}^{3} - 20Y_{\text{C}}^{4} } \right], $$

(A11)

$$ \frac{{{\text{d}}\delta_{4} }}{{{\text{d}}Y_{\text{C}} }} = 6\left[ {1 + 20Y_{\text{C}} + 93Y_{\text{C}}^{2} - 912Y_{\text{C}}^{3} + 1920Y_{\text{C}}^{4} - 1584Y_{\text{C}}^{5} + 462Y_{\text{C}}^{6} } \right]. $$

(A12)

Appendix 2

$$ I = \sum\limits_{j = 0}^{\infty } {\frac{{\alpha^{j} }}{j!}} \frac{{{\text{d}}\lambda_{j} }}{{{\text{d}}N_{u} }} = \alpha \frac{{{\text{d}}\lambda_{1} }}{{{\text{d}}N_{u} }} + \frac{{\alpha^{2} }}{2}\frac{{{\text{d}}\lambda_{2} }}{{{\text{d}}N_{u} }} + \frac{{\alpha^{3} }}{6}\frac{{{\text{d}}\lambda_{3} }}{{{\text{d}}N_{u} }} + \frac{{\alpha^{4} }}{24}\frac{{{\text{d}}\lambda_{4} }}{{{\text{d}}N_{u} }} = 12Y_{\text{C}} \alpha + 6Y_{\text{C}} \left( {1 + 2Y_{\text{C}}^{2} - 3Y_{\text{C}} } \right)\alpha^{2} + 2Y_{\text{C}} \left( {1 + 3Y_{\text{C}} - 22Y_{\text{C}}^{2} + 30Y_{\text{C}}^{3} - 12Y_{\text{C}}^{4} } \right)\alpha^{3} + \left( {{{Y_{\text{C}} } \mathord{\left/ {\vphantom {{Y_{\text{C}} } 2}} \right. \kern-0pt} 2}} \right)\left( {1 + 15Y_{\text{C}} + 62Y_{\text{C}}^{2} - 570Y_{\text{C}}^{3} + 1152Y_{\text{C}}^{4} - 924Y_{\text{C}}^{5} + 264Y_{\text{C}}^{6} } \right)\alpha^{4} , $$

(A13)

where λ _j are the cumulants and are functions of the Thiele moments.[33] The values of λ _j have been calculated up to j = 4,[33] and their derivatives with respect to N _u (N _u  = number of interstitial atoms) have been given in McLellan and Ko.[32] The parameter α is the same as in McLellan and Ko[32] and is shown in Appendix 1.

$$ \frac{{{\text{d}}\hat{I}}}{{{\text{d}}Y_{\text{C}} }} = \frac{{\exp \left( { - I} \right)}}{{\left( {1 - Y_{\text{C}} } \right)^{2} }} - \frac{{\exp \left( { - I} \right)}}{{1 - Y_{\text{C}} }} \cdot \frac{{{\text{d}}I}}{{{\text{d}}Y_{\text{C}} }}, $$

(A14)

$$ \frac{{{\text{d}}I}}{{{\text{d}}Y_{\text{C}} }} = 12\alpha + 6\left( {1 + 2Y_{\text{C}}^{2} - 3Y_{\text{C}} } \right)\alpha^{2} + 2\left( {1 + 3Y_{\text{C}} - 22Y_{\text{C}}^{2} + 30Y_{\text{C}}^{3} - 12Y_{\text{C}}^{4} } \right)\alpha^{3} + \left( {{{\alpha^{4} } \mathord{\left/ {\vphantom {{\alpha^{4} } 2}} \right. \kern-0pt} 2}} \right)\left( {1 + 15Y_{\text{C}} + 62Y_{\text{C}}^{2} - 570Y_{\text{C}}^{3} + 1152Y_{\text{C}}^{4} - 924Y_{\text{C}}^{5} + 264Y_{\text{C}}^{6} } \right). $$

(A15)

$$\phi = \frac{1}{{N_{v} Z}}\sum\limits_{j = 1}^{\infty } {\frac{{\lambda_{j} \alpha^{j - 1} }}{{\left( {j - 1} \right)!}}} = Y_{\text{C}}^{2} + Y_{\text{C}}^{2} \left( {1 - Y_{\text{C}} } \right)^{2} \alpha + \left( {{{\alpha^{2} } \mathord{\left/ {\vphantom {{\alpha^{2} } 2}} \right. \kern-0pt} 2}} \right)\left[ {Y_{\text{C}}^{2} \left( {1 - Y_{\text{C}} } \right)^{2} \left( {1 - 2Y_{\text{C}} } \right)^{2} + 8Y_{\text{C}}^{3} \left( {1 - Y_{\text{C}} } \right)^{3} } \right] + \left( {{{\alpha^{3} } \mathord{\left/ {\vphantom {{\alpha^{3} } 6}} \right. \kern-0pt} 6}} \right)\left[ {Y_{\text{C}}^{2} \left( {1 - Y_{\text{C}} } \right)^{2} \left( {1 - 6Y_{\text{C}} + 6Y_{\text{C}}^{2} } \right)^{2} + 24Y_{\text{C}}^{3} \left( {1 - Y_{\text{C}} } \right)^{3} \left( {1 - 2Y_{\text{C}} } \right)^{3} + 126Y_{\text{C}}^{4} \left( {1 - Y_{\text{C}} } \right)^{4} } \right],$$

(A16)

where N _v is the number of solvent atoms, Z counts the nearest-neighbor interstitial sites of a given vacancy (Z = 6 for octahedral sites), λ _j and α have the same meanings as in Eq. [A13].

$$ \frac{{{\text{d}}\left[ {g\left( {Y_{\text{C}} } \right)} \right]}}{{{\text{d}}Y_{\text{C}} }} = - 2 - \frac{\phi }{{Y_{\text{C}}^{2} }} + \frac{{\phi^{2} }}{{Y_{\text{C}}^{3} }} + \left( {\frac{1}{{Y_{\text{C}} }} + \frac{1}{2} - \frac{\phi }{{Y_{\text{C}}^{2} }}} \right)\frac{{{\text{d}}\phi }}{{{\text{d}}Y_{\text{C}} }}. $$

(A17)

Appendix 3

Symbols and variables employed in this manuscript:

a ₀ :

The lattice parameter of the austenite matrix (m), Eq. [11]

$\tilde{D}_{\text{C}}$ :

Concentration-dependent diffusion coefficient of carbon (m² s⁻¹)

D _C :

Diffusion coefficient of carbon at infinite carbon dilution (m² s⁻¹)

E :

Young’s modulus of the austenite matrix (Pa)

Exp:

Exponential function

f :

The ratio of molar volumes of carbon and iron, Eq. [24]

$f_{\text{u}}^{1}$ :

The fraction of all interstitial atoms located in the interstitial sites which have at least one neighboring solute atom, Eq. [24]

G :

Molar Gibbs free energy (J mol⁻¹)

$\hat{G}$ :

${{{\text{d}}G} \mathord{\left/ {\vphantom {{{\text{d}}G} {{\text{d}}Y_{\text{C}} }}} \right. \kern-0pt} {{\text{d}}Y_{\text{C}} }}$ (J mol⁻¹), Eq. [24]

G ⁰ :

The activation energy of the jump of a carbon atom with no nearest neighbor carbon atoms (J mol⁻¹)

ΔG _A :

The Gibbs free energy associated with carbon diffusion in austenite (J mol⁻¹), Eq. [12]

g(Y _C):

Transmission coefficient, Eq. [32]

h :

Planck constant (m² kg s⁻¹)

I :

Parameter calculated by cumulant–moment expansion[33]

$\hat{I}$ :

$\hat{I} = {{\exp \left( { - I} \right)} \mathord{\left/ {\vphantom {{\exp \left( { - I} \right)} {\left( {1 - Y_{\text{C}} } \right)}}} \right. \kern-0pt} {\left( {1 - Y_{\text{C}} } \right)}}$, Eq. [32]

K :

Asimow’s parameter representing concentration enhancement,[19] Eq. [13]

$K^{\prime}$ :

The probability that an activated complex from sites, which have at least one neighboring solute atom, will execute a diffusion jump, Eq. [27]

k _B :

Boltzmann constant (m² kg s⁻² K⁻¹)

k _i :

Calculated parameters to simplify the expression of the models

${}^{0}L_{\text{Fe:C,Va}}$ :

CALPHAD interaction parameter of interstitial carbon atoms and vacancies when substitutional sublattice comprises iron atoms only (J mol⁻¹), Eq. [14]

N ₀ :

Avogadro’s number

N _u :

Number of interstitial atoms, Eq. [A2]

N _v :

Number of lattice atoms, Eq. [A16]

R :

Gas constant (8.3145 J mol⁻¹ K⁻¹)

r ₀ :

The radius of an interstitial site in the austenite matrix (m), Eq. [19]

T :

Thermodynamic temperature (K)

ΔV _A :

The activation volume associated with carbon diffusion in austenite (m³ mol⁻¹), Eq. [19]

X _C :

Atomic fraction of carbon

x :

General distance (m)

Y _C :

Site fraction of carbon

Z :

The nearest-neighbor interstitial sites of a given vacancy

$Z^{\prime}$ :

Coordination number for octahedral interstitial sites

z :

Depth (m)

α :

$\alpha = - {{\Delta \varepsilon_{\gamma } } \mathord{\left/ {\vphantom {{\Delta \varepsilon_{\gamma } } {k_{\text{B}} T}}} \right. \kern-0pt} {k_{\text{B}} T}}$ [33]

β :

Simplified parameter in Liu et al. model,[37] Eq. [28]

χ :

Compressibility (Pa⁻¹), Eq. [20]

δ :

Elementary jump distance in the direction of diffusion (m)

δ _i :

$\delta_{i} = {{\lambda_{i} } \mathord{\left/ {\vphantom {{\lambda_{i} } {N_{\text{u}} }}} \right. \kern-0pt} {N_{\text{u}} }}$, Eq. [A2]

ɛ :

The volumetric elastic strain associated with the difference in radii between a carbon atom and an interstitial site in the austenite matrix, Eq. [19]

Δɛ _γ :

The carbon–carbon pairwise interaction energy (J mol⁻¹), Eq. [24]

ϕ :

Parameter calculated by cumulant–moment expansion[33]

$\phi^{\prime}$ :

$\phi^{\prime} = {{kT} \mathord{\left/ {\vphantom {{kT} {hN_{0} }}} \right. \kern-0pt} {hN_{0} }}$ (s⁻¹)

γ _C :

Activity coefficient of carbon

γ _M :

Activity coefficient of the activated complex

η :

Linear expansion per atomic fraction change of carbon in austenite matrix, Eq. [19]

$\left( {{\lambda \mathord{\left/ {\vphantom {\lambda {\lambda \left( 0 \right)}}} \right. \kern-0pt} {\lambda \left( 0 \right)}}} \right)^{2}$ :

A small factor related to the carbon jump distance, whose value can be calculated from the high-temperature X-ray data of Ridley and Stuart,[34] Eq. [32]

λ _i :

Cumulants (functions of the Thiele Moments)[33]

μ :

Grüneisen parameter, Eq. [12]

μ _C :

Chemical potential of carbon in austenite (J mol⁻¹)

ν :

Poisson’s ratio of austenite matrix

ρ ₀ :

Density of lattice sites in austenite matrix (mol m⁻³), Eq. [19]

ρ :

The factor that takes the uniform dilation of the lattice into account and is present whether there is a particle gradient or not,[32] Eq. [24]

σ :

The parameter related to the repulsive interaction between neighboring carbon atoms in the model of Siller and McLellan,[26,27] Eq. [16]

$\sigma^{\prime}$ :

The parameter related to $f_{\text{u}}^{1}$ and calculated using cumulant–moment expansions,[33] Eq. [24]

ψ :

$\psi = \exp \left( { - \frac{\delta }{kT}\frac{{{\text{d}}G}}{{{\text{d}}x}}} \right)$, Eq. [24], and ψ = 1[32]