1 Introduction

The availability of an analytical form for an orientation distribution function (ODF), which describes a distribution of crystal orientations, is fundamental to the field of texture analysis. Analytical forms of the ODF are used, for example, in extracting orientation statistics from diffraction measurements,[1] in studying the effect of processing history on the statistical evolution of microstructures,[2] as an input to crystal plasticity models that examine the effect of mechanical anisotropy during deformation,[3] and in the design of materials using spectral methods to identify a desired ODF on the basis of the properties of interest.[4] Despite the development of various direct methods for the calculation and representation of an ODF,[5–7] the prevailing mathematical treatment of the ODF continues to be by means of a series expansion over the generalized spherical harmonics, as introduced into the field of texture analysis more than 40 years ago for this purpose.[8,9] This situation appears to be principally due to the propagation of conventions followed by Bunge in his seminal contributions to the field of texture analysis.[10] These conventions notably include the description of an orientation by the Euler angles ϕ 1, Φ, and ϕ2, and the consequent series expansion of the ODF as a linear combination of generalized spherical harmonics T m′,m l (ϕ 1, Φ, ϕ 2) in the form

$$ f\left( {\phi_{1} ,\Upphi ,\phi_{2} } \right) = \sum\limits_{l = 0}^{\infty } {\sum\limits_{m^\prime = - l}^{l} {\sum\limits_{m = - l}^{l} {t_{l}^{m^\prime ,m} T_{l}^{m^\prime ,m} \left( {\phi_{1} ,\Upphi ,\phi_{2} } \right)} } } $$
(1)

where the coefficients of the expansion are determined by the inner product

$$ t_{l}^{m^\prime ,m} = {\frac{2l + 1}{{8\pi^{2} }}}\int\limits_{0}^{2\pi } {\int\limits_{0}^{\pi } {\int\limits_{0}^{2\pi } {f\left( {\phi_{1} ,\Upphi ,\phi_{2} } \right)T_{l}^{m^\prime ,m * } \left( {\phi_{1} ,\Upphi ,\phi_{2} } \right)\sin \Upphi d\phi_{1} d\Upphi d\phi_{2} } } } $$
(2)

Despite the utility of this expansion, the use of Euler angles as a parameterization of rotations is not necessarily ideal. For example, one inevitable difficulty with this method is the existence of certain singular orientations that do not correspond to a unique set of Euler angles.[11] These orientations correspond to an infinite number of points in the orientation space, and give rise to singularities in the equations of motion[11] and in the formulas used to determine the result of sequential rotations.[12,13] Furthermore, the description for the boundaries of the asymmetric domains in the orientation space is notably more complex for the Euler-angle parameterization[14] than for some of the alternatives.[15–17]

These disadvantages of Euler angles are certainly not inherent to the study of orientation information; to be convinced of this, one needs merely to consider the properties of the normalized quaternion parameterizationFootnote 1 of rotations.[18] A quaternion, in this context, is a normalized four-vector with components given by

$$ \begin{gathered} q_{0} = \cos \left( {{\omega \mathord{\left/ {\vphantom {\omega 2}} \right. \kern-\nulldelimiterspace} 2}} \right) \hfill \\ q_{1} = \sin \left( {{\omega \mathord{\left/ {\vphantom {\omega 2}} \right. \kern-\nulldelimiterspace} 2}} \right)\sin \theta \cos \phi \hfill \\ q_{2} = \sin \left( {{\omega \mathord{\left/ {\vphantom {\omega 2}} \right. \kern-\nulldelimiterspace} 2}} \right)\sin \theta \sin \phi \hfill \\ q_{3} = \sin \left( {{\omega \mathord{\left/ {\vphantom {\omega 2}} \right. \kern-\nulldelimiterspace} 2}} \right)\cos \theta \hfill \\ \end{gathered} $$
(3)

where ω is the angle of rotation and θ and ϕ are the polar and azimuthal angles of the rotation axis, respectively. The rotation corresponding to a quaternion is readily apparent from the final three components, which form a vector that points along the axis of rotation and scales monotonically in length with the rotation angle.[19] This close relationship of a quaternion with the axis and angle of a rotation further permits the construction of an orientation space that is substantially simpler to visualize and interpret than that of the Euler-angle parameterization.[20] With regard to the manipulation of the orientation information, the most familiar example of the advantage of quaternions is given by the formula for the multiplication of rotations, which involves only a bilinear combination of the quaternion components.[21] Other instances in which the use of quaternions simplifies calculations related to the analysis of orientation information appear throughout the literature.[11,15,22,23]

Despite these advantages, a significant portion of the crystallography community continues to use Euler angles instead of quaternions to describe crystallographic texture. While this preference for Euler angles may historically be attributed to the absence of a series expansion by which to represent an ODF in the quaternion group space, we have recently provided such an expansion.[20] The motivation for this expansion relies on the observation that normalized quaternions may be considered as vectors identifying points on S 3 (the unit sphere in four-dimensional space). Analogous to the expansion of a square-integrable function on S 2 (the unit sphere in three-dimensional space) as an infinite linear combination of the spherical harmonics, a square-integrable function on S 3 may be expanded as an infinite linear combination of the hyperspherical harmonics Z n l,m (ω, θ, ϕ), or

$$ f\left( {\omega ,\theta ,\phi } \right) = \sum\limits_{n = 0,2 {\ldots} }^{\infty } {\sum\limits_{l = 0}^{n} {\sum\limits_{m = - l}^{l} {z_{l,m}^{n} Z_{l,m}^{n} \left( {\omega ,\theta ,\phi } \right)} } } $$
(4)

where the coefficients of the expansion are found from the inner product

$$ z_{l,m}^{n} = \int\limits_{0}^{2\pi } {\int\limits_{0}^{\pi } {\int\limits_{0}^{\pi } {f\left( {\omega ,\theta ,\phi } \right)Z_{l,m}^{n} \left( {\omega ,\theta ,\phi } \right)\sin^{2} \left( {{\omega \mathord{\left/ {\vphantom {\omega 2}} \right. \kern-\nulldelimiterspace} 2}} \right)\sin \theta d\left( {{\omega \mathord{\left/ {\vphantom {\omega 2}} \right. \kern-\nulldelimiterspace} 2}} \right)d\theta d\phi } } } $$
(5)

and n is restricted to even integers by the trivial symmetry of three-dimensional space. This expansion is discussed in more detail elsewhere.[20]

Because the physical significance of orientation information does not depend on the means by which it is described, the expansions given in Eqs. [1] and [4] may in principle be used interchangeably. However, there is presently no means of converting an ODF expressed in the form of the generalized spherical harmonic expansion of Eq. [1] to one in the form of the hyperspherical harmonic expansion of Eq. [4]. With this in mind, the purpose of this article is principally to provide continuity with the existing literature by deriving a simple linear transformation to relate the coefficients of these two expansions. Our expectation is that this will allow extant published results in texture analysis formulated by means of the traditional series expansion to be converted to, and presented in, a more intuitive and readily accessible form. This result is then harnessed to apply a mathematical technique in common use with the generalized spherical harmonic expansion to the hyperspherical harmonic expansion.

2 Problem Formulation

The group of primary concern to the study of crystallographic orientations is SO(3), the group of rotations of three-dimensional space. While the importance of this group to the physical sciences has encouraged many authors to investigate its properties, the resulting treatments do not always follow a consistent set of conventions.[12,18,24,25] At least for the current authors, this situation has caused a certain degree of confusion and inconvenience, as the conventions used in deriving many of the results available in the literature are not always explicitly stated. To our knowledge, the results contained in this article do not appear anywhere else in the literature with a consistent set of conventions.

We follow the same conventions in the interpretation and use of a rotation matrix as does Altmann.[18] That is, a rotation operation is viewed as an active rotation of configuration space rather than as a passive rotation of the coordinate system, unless explicitly stated otherwise. A rotation matrix left-multiplies the column vector of the coordinates of a point, and right-multiplies the row vector of the components of a basis. This interpretation allows one to identify a crystal orientation with the rotation operation required to bring a reference crystal into coincidence with the actual crystal. The ODF is then interpreted as a function of rotations of three-dimensional space or, more often, as a function of some set of parameters that clearly define a rotation.

This article makes use of two parameterizations. The first of these is the Euler angles ϕ 1, Φ, and ϕ 2, which define a general rotation as the result of three consecutive active rotations by the angles −ϕ 1, −Φ, and −ϕ 2 about the z, x, and z axes, respectively (from the point of view of an observer attached to the coordinate system, this active rotation sequence is identical to the passive rotation sequence defining the Euler angles as described by Bunge[10]). The second rotation parameterization is by the axis-angle parameters ω, θ, and ϕ, as described earlier. The relationship of the Euler angles to the axis-angle parameters is visible from the explicit conversion formulas provided in Appendix A.

The analytical form of the ODF used by the majority of the crystallography community is provided in Eq. [1], in which rotations are parameterized as sets of Euler angles. This equation actually derives from one of the consequences of the Peter–Weyl theorem, namely that the matrix elements of the irreducible representations of SO(3) provide a complete, orthogonal basis for the expansion of a square-integrable function of three-dimensional rotations.[26] While many equivalent expressions for the irreducible representations of SO(3) appear in the literature, they often differ from one another by similarity transformations.[12,18,24,25] Once a set of conventions is specified and a consistent expression is found, the Peter–Weyl theorem allows the ODF to be written as an infinite linear combination of the matrix elements of these irreducible representations. For example, the expansion in Eq. [1] is found by following the phase convention of Bunge,[10] expressing the matrix elements of the irreducible representations of SO(3) as functions of the Euler angles, and denoting the matrix element in row m′ and column m of the (2l+1)-dimensional irreducible representation by T m′,m l (ϕ 1, Φ, ϕ 2).

The expansion provided in Eq. [4] follows more directly from a consideration of SO(4), the group of rotations of four-dimensional space, than from SO(3). A well-known result of group theory states that the basis elements of the irreducible representations of a group of operators provide a complete, orthogonal basis for the expansion of a function to which an operation of the group may be applied.[24] Because sets of the hyperspherical harmonics Z n l,m (ω, θ, ϕ) transform as the bases of the irreducible representations of SO(4), the hyperspherical harmonics form a complete, orthogonal basis for the expansion of a square-integrable function on S 3. Considering points on S 3 to correspond to normalized quaternions, Eq. [3] suggests that the axis-angle parameters identify points on S 3 in a manner analogous to that of the spherical angles on S 2. That is, exactly as a function on S 2 is more naturally written as a function of the spherical angles than of Cartesian coordinates, a function on S 3 is more naturally written as a function of the axis-angle parameters than of quaternion coordinates. The axis-angle parameterization is therefore entirely compatible with the interpretation of the ODF as a square-integrable function on S 3, which allows the ODF to be written as an infinite linear combination of the hyperspherical harmonics in Eq. [4].

Regardless of the different motivations for the generalized spherical harmonic and the hyperspherical harmonic expansions, they contain the same orientation information. As such, there must be a method to convert from one expansion to the other. This expansion is found by comparing the expressions for the matrix elements of the irreducible representations of SO(3) in the Euler-angle and axis-angle parameterizations. When written using the Euler angles, the expression for these matrix elements gives the formula for the generalized spherical harmonics. When written using the axis-angle parameters, the same expression becomes a linear combination of the hyperspherical harmonics. Equating these forms gives the conversion of the basis functions in Eq. [1] to the basis function in Eq. [4], and the conversion from the coefficients in Eq. [1] to the coefficients in Eq. [4] as well. We develop this approach further in Sections III to V.

3 Rotation Conventions and the Generalized Spherical Harmonics

There are many mathematical results in the literature that are useful and relevant for the present problem. However, incorporating or referring to them without establishing a consistent set of conventions is quite hazardous. In particular, the conversion from the generalized spherical harmonics to the hyperspherical harmonics is nonsensical unless a consistent set of conventions is used to derive the expressions for the matrix elements of the irreducible representations of SO(3) as functions of the Euler-angle and axis-angle parameters. We therefore devote a significant portion of this article to the consideration of this issue.

The definition of the generalized spherical harmonics most frequently used by the crystallography community is[10]

$$ T_{l}^{m^\prime ,m} \left( {\phi_{1} ,\Upphi ,\phi_{2} } \right) = e^{{im^\prime \phi_{2} }} P_{l}^{m^\prime ,m} \left( {\cos \Upphi } \right)e^{{im\phi_{1} }} $$
(6)

where the function P m′,m l (cos Φ) is defined as

$$ \begin{aligned} P_{l}^{m^\prime ,m} \left( {\cos \Upphi } \right) = & {\frac{{\left( { - 1} \right)^{l - m^\prime } i^{m - m^\prime } }}{{2^{l} }}}\sqrt {{\frac{{\left( {l + m} \right)!}}{{\left( {l - m^\prime } \right)!\left( {l + m^\prime } \right)!\left( {l - m} \right)!}}}} \left( {1 - \cos \Upphi } \right)^{{{{\left( {m^\prime - m} \right)} \mathord{\left/ {\vphantom {{\left( {m^\prime - m} \right)} 2}} \right. \kern-\nulldelimiterspace} 2}}} \left( {1 + \cos \Upphi } \right)^{{ - {{\left( {m^\prime + m} \right)} \mathord{\left/ {\vphantom {{\left( {m^\prime + m} \right)} 2}} \right. \kern-\nulldelimiterspace} 2}}} \\ & \quad \times {\frac{{d^{l - m} }}{{d\left( {\cos \Upphi } \right)^{l - m} }}}\left[ {\left( {1 - \cos \Upphi } \right)^{l - m^\prime } \left( {1 + \cos \Upphi } \right)^{l + m^\prime } } \right] \\ \end{aligned} $$
(7)

The generalized spherical harmonic may be considered as the matrix element in row m′ and column m of the (2l+1)-dimensional irreducible representation of SO(3). Therefore, Eq. [6] depends implicitly on the conventions adopted by Bunge[10] during the construction of the irreducible representations. Generally speaking, the range of conventions that must be specified include the selection of the basis elements, the choice of the active or passive rotation convention, and the parameterization used to write the formulas for the resulting matrix elements.

The vast majority of literature on the subject, including that by Bunge[10] and the current article, selects the set of spherical harmonics with a particular value of l as the basis elements of the (2l+1)-dimensional irreducible representation of SO(3). Because the basis is consistent throughout, the issue is not discussed further. As for the remaining conventions enumerated earlier, Bunge[10] uses the passive convention and the Euler-angle parameterization, while the current article uses the active convention and the axis-angle parameterization. The comparison of matrix elements apparently requires that the relationship of the representations constructed following these different conventions be clearly established. We address these differences individually for the sake of clarity, with the difference in rotation convention first and the difference in parameterization second.

Regarding the difference in rotation convention, consider that the elements of a rotation matrix depend only on the selection of an initial coordinate system and the apparent rotation of space from the perspective of an observer rigidly attached to that coordinate system. If two matrices that effect the same apparent transformation of space share a single basis, then corresponding matrix elements of the two matrices should be the same, independent of the rotation convention followed. In particular, sequential active rotations by −ϕ 1 about the z-axis, −Φ about the x-axis, and −ϕ 2 about the z-axis effect the same apparent transformation of space as sequential passive rotations by ϕ 1 about the z-axis, by Φ about the x′-axis, and by ϕ 2 about the z″-axis. Therefore, the elements of the matrix describing the active rotation sequence should be the same as the elements of the matrix describing the passive rotation sequence.

Define the function D l m′,m (ϕ 1, Φ, ϕ 2) as the matrix element in row m′ and column m of the (2l+1)-dimensional irreducible representation of SO(3), in which the representation is considered to describe the active rotation sequence referred to earlier, i.e., to follow the active convention. The explicit formula for this function is derived in Appendix B. Because the generalized spherical harmonic T m′,m l (ϕ 1, Φ, ϕ 2) apparently differs only in that the corresponding representation is considered to describe the passive rotation sequence referred to earlier, these functions should be identical, i.e., T m′,m l (ϕ 1, Φ, ϕ 2) = D l m′,m (ϕ 1, Φ, ϕ 2).

Unfortunately, this is not found to be the case. As indicated by Eq. [B6], the relationship between the two nominally equivalent matrix elements of the irreducible representations is found to be

$$ T_{l}^{m^\prime ,m} \left( {\phi_{1} ,\Upphi ,\phi_{2} } \right) = \left( { - 1} \right)^{m - m^\prime } D_{m^\prime ,m}^{l} \left( {\phi_{1} ,\Upphi ,\phi_{2} } \right) $$
(8)

where there is an unexpected difference of phase between the two functions. Furthermore, it is not possible to directly compare the derivations of these expressions in order to identify the source of the disparity, because Bunge[10] does not provide a derivation of the formula for the generalized spherical harmonics. Rather, he indicates that more detailed accounts of the representations and properties of the generalized spherical harmonics appear in Gelfand, Minlos, and Shapiro,[27] Vilenkin,[12] and Wigner.[24] The same ambiguity of conventions appears there as well, however; while functions related to the generalized spherical harmonics do appear in these references, none of these is identical to the generalized spherical harmonics. These authors indicate their assorted expressions for the matrix elements of the irreducible representations of SO(3) by T l m′,m (ϕ 1, θ, ϕ 2),[27] t l m′,m (ϕ, θ, ψ),[12] and D (l)({α, β, γ}) m′,m ,[24] respectively. Inserting ϕ 1, Φ, and ϕ 2 for the angles of the first, second, and third rotations, respectively, of these functions, we find that their relationships to the generalized spherical harmonics T m′,m l (ϕ 1, Φ, ϕ 2) are

$$ T_{l}^{m^\prime ,m} \left( {\phi_{1} ,\Upphi ,\phi_{2} } \right) = \left( { - 1} \right)^{m^\prime - m} T_{m^\prime ,m}^{l * } \left( {\phi_{1} ,\Upphi ,\phi_{2} } \right) = t_{m^\prime ,m}^{l * } \left( {\phi_{2} ,\Upphi ,\phi_{1} } \right) = i^{m - m^\prime } \user2{D}^{\left( l \right)} \left( {\left\{ {\phi_{2} ,\Upphi ,\phi_{1} } \right\}} \right)_{m^\prime ,m} $$
(9)

where * is the complex conjugate. Examining Eq. [9], we see that none of these expressions matches another, or the form provided by Bunge. The reason is that simply inserting ϕ 1, Φ, and ϕ 2 for the angles of the first, second, and third rotations, respectively, of these functions does not adequately address the conventions concerning the use of these functions. We therefore find that the question of consistency of conventions pervades the literature and that it is quite difficult to resolve the difference between T m′,m l (ϕ 1, Φ, ϕ 2) and D l m′,m (ϕ 1, Φ, ϕ 2) in Eq. [8] without clearly establishing the source of the generalized spherical harmonics.

Regardless of the conventions followed in deriving the traditional form of the generalized spherical harmonics, the expansion in Eq. [1] remains a valid expansion of the ODF; changing the generalized spherical harmonics by a constant factor amounts to pulling a constant factor out of the coefficients in the expansion. Because Bunge used the generalized spherical harmonics almost exclusively in the context of Eq. [1], the question of the constant factor appearing in Eq. [8] is virtually irrelevant to his subsequent results. For the purposes of the present article, however, a constant factor represents a change in the values of the matrix elements of the irreducible representations of SO(3). Equating expressions for the matrix elements in different parameterizations certainly gives nonsensical results when the expressions are not equal. Within this article, the functions D l m′,m (ϕ 1, Φ, ϕ 2) will therefore be considered as more fundamental from the standpoint of calculations, although the majority of our equations will be formulated using the functions T m′,m l (ϕ 1, Φ, ϕ 2) in order to relate our results more directly to the literature.

4 Rotation Conventions and Hyspherical Harmonics

While definitions of the hyperspherical harmonics may be found throughout the literature,[28–31] there is no general agreement on the phase. The definition and phase convention followed here is given by

$$ \begin{aligned} Z_{l,m}^{n} \left( {\omega ,\theta ,\phi } \right) = & \left( { - i} \right)^{l} {\frac{{2^{l + 1/2} l!}}{2\pi }}\sqrt {\left( {2l + 1} \right){\frac{{\left( {l - m} \right)!}}{{\left( {l + m} \right)!}}}{\frac{{\left( {n + 1} \right)\left( {n - l} \right)!}}{{\left( {n + l + 1} \right)!}}}} \left( {\sin \left( {{\omega \mathord{\left/ {\vphantom {\omega 2}} \right. \kern-\nulldelimiterspace} 2}} \right)} \right)^{l} C_{n - l}^{l + 1} \left( {\cos \left( {{\omega \mathord{\left/ {\vphantom {\omega 2}} \right. \kern-\nulldelimiterspace} 2}} \right)} \right) \\ \quad P_{l}^{m} \left( {\cos \theta } \right)e^{im\phi } \\ \end{aligned} $$
(10)

with integer indices 0 ≤ n, 0 ≤ l ≤ n, and −l ≤ m ≤ l. The C l+1 n−l is a Gegenbauer polynomial and P m l is an associated Legendre function.[32,33] Complex conjugation of Eq. [10] reveals one of the properties of the hyperspherical harmonics to be

$$ Z_{l,m}^{n * } \left( {\omega ,\theta ,\phi } \right) = \left( { - 1} \right)^{l + m} Z_{l, - m}^{n} \left( {\omega ,\theta ,\phi } \right) $$
(11)

With the definition of the hyperspherical harmonics in hand, the matrix element in row m′ and column m of the (2l+1)-dimensional irreducible representation of SO(3) may be written as a linear combination of the hyperspherical harmonics[34,35]

$$ U_{m^\prime ,m}^{l} \left( {\omega ,\theta ,\phi } \right) = \sum\limits_{\lambda } {\sum\limits_{\mu } {C_{l,m^\prime ,\lambda ,\mu }^{l,m} {\frac{{\sqrt {2\left( {2\lambda + 1} \right)} \pi }}{2l + 1}}Z_{\lambda ,\mu }^{2l} \left( {\omega ,\theta ,\phi } \right)} } $$
(12)

where C l,m l,m′,λ,μ is a Clebsch–Gordan coefficient, as defined in Appendix C, and vanishes unless the summation indices satisfy the conditions 0 ≤ λ ≤ 2l and μ = m − m′. The irreducible representation corresponding to U l m′,m (ω, θ, ϕ) is considered to describe an active rotation in the axis-angle parameterization.

The arrangement of indices on the hyperspherical harmonics as used here differs from that of Reference 20, in consideration that the index n identifies the set of hyperspherical harmonics that form a basis for the (n+1)2-dimensional irreducible representation of SO(4), while the indices l and m identify a single member of this set. The difference in the significance of these indices encourages that they be separated accordingly. The phase of the hyperspherical harmonic differs from that of our previous work as well;[20] some motivation for this departure will be given presently.

4.1 Phase of Hyperspherical Harmonics

A reasonable condition that the phase of the hyperspherical harmonics defined in Eq. [10] must satisfy is revealed by investigating the properties of SO(3). While not necessarily obvious, the irreducible representations of SO(3) as presented in the literature are entirely compatible with the canonical representation of three-dimensional rotations as three-by-three real orthogonal matrices of the determinant one. That is, there exists a similarity transformation that brings the three-by-three irreducible representation of SO(3) into the familiar canonical form. Furthermore, the linear transformation effecting this similarity transformation, when right-multiplying the row vector of the basis elements of the three-by-three irreducible representation, brings the basis into a form that behaves identically to the usual unit vectors of three-dimensional space. Although requiring that this similarity transformation exist places a certain constraint on the relationship of the irreducible representation to the basis elements, the ability to freely select the similarity transformation permits an infinite number of equivalent forms for the irreducible representations and the basis elements. The Condon–Shortley phase convention uniquely determines a standard similarity transformation, however, and allows the irreducible representations of SO(3) to be given in a consistent form throughout the literature.

The situation is rather different with irreducible representations of SO(4) and the hyperspherical harmonics. There does not appear to be any counterpart to the Condon–Shortley phase convention to uniquely specify the form of the irreducible representations of SO(4) and the phase of the hyperspherical harmonics, as is reflected in the variety of phases for the hyperspherical harmonics appearing in the literature.[28–31] Nevertheless, the requirement that the four-by-four irreducible representation of SO(4) and the four hyperspherical harmonics for which n = 1 be related in the manner described earlier is certainly reasonable. That is, we require that there exist an invertible linear transformation of the hyperspherical harmonics that makes the resulting basis behave identically to the orthogonal unit vectors along the w, x, y, and z axes of four-dimensional space and that simultaneously defines a similarity transformation of the four-by-four irreducible representation that brings the representation into the canonical form.

Of course, this raises the question of what the canonical form is for the representations of SO(4), which is, generally speaking, not as familiar as for SO(3). We consider the canonical form for these representations as deriving from the multiplication rule for normalized quaternions. Given a rotation represented by the quaternion q that is followed by a rotation represented by the quaternion g, there exists a single equivalent rotation represented by the quaternion u. One of the particularly convenient properties of the quaternion parameterization is that this multiplication rule is bilinear,[11] which means that there is a four-by-four real orthogonal matrix of determinant one, G, that, when left-multiplying the column vector of the components of the quaternion q, returns the column vector of the components of the quaternion u, or[21]

$$ \left[ {\begin{array}{*{20}c} {g_{0} } & { - g_{1} } & { - g_{2} } & { - g_{3} } \\ {g_{1} } & {g_{0} } & { - g_{3} } & {g_{2} } \\ {g_{2} } & {g_{3} } & {g_{0} } & { - g_{1} } \\ {g_{3} } & { - g_{2} } & {g_{1} } & {g_{0} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {q_{0} } \\ {q_{1} } \\ {q_{2} } \\ {q_{3} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {u_{0} } \\ {u_{1} } \\ {u_{2} } \\ {u_{3} } \\ \end{array} } \right] $$
(13)

Alternatively, given a rotation represented by the quaternion q that is preceded by a rotation represented by the quaternion h, there exists a single equivalent rotation represented by the quaternion v. There is then a four-by-four real orthogonal matrix of determinant one, H, that, when left-multiplying the column vector of the components of the quaternion q, returns the components of the quaternion v, or[21]

$$ \left[ {\begin{array}{*{20}c} {h_{0} } & { - h_{1} } & { - h_{2} } & { - h_{3} } \\ {h_{1} } & {h_{0} } & {h_{3} } & { - h_{2} } \\ {h_{2} } & { - h_{3} } & {h_{0} } & {h_{1} } \\ {h_{3} } & {h_{2} } & { - h_{1} } & {h_{0} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {q_{0} } \\ {q_{1} } \\ {q_{2} } \\ {q_{3} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {v_{0} } \\ {v_{1} } \\ {v_{2} } \\ {v_{3} } \\ \end{array} } \right] $$
(14)

While the matrices G and H separately perform distinct, constrained four-dimensional rotations, the matrix formed by their product is a general four-by-four real orthogonal matrix of the determinant one and performs a general four-dimensional rotation. Because G and H commute, the order of application of these matrices does not change the result. This provides a canonical form for four-dimensional rotations.

Define the irreducible representations of SO(4) by a similarity transformation of the direct product of irreducible representations of SO(3), that is,[20,34]

$$ R_{{\lambda^{\prime } ,\mu^{\prime } ,\lambda ,\mu }}^{2l} \left( {\omega_{2} ,\theta_{2} ,\phi_{2} ,\omega_{1} ,\theta_{1} ,\phi_{1} } \right) = \sum\limits_{{m^{\prime \prime \prime } }} {\sum\limits_{{m^{\prime \prime } }} {\sum\limits_{{m^{\prime } }} {\sum\limits_{m} {C_{{l,m^{\prime \prime } ,l,m^{\prime } }}^{{\lambda^{\prime } ,\mu^{\prime } }} U_{{m^{\prime \prime \prime } ,m^{\prime \prime } }}^{l * } \left( {\omega_{2} ,\theta_{2} ,\phi_{2} } \right)U_{{m^{\prime } ,m}}^{l} \left( {\omega_{1} ,\theta_{1} ,\phi_{1} } \right)C_{{l,m^{\prime \prime \prime } ,l,m}}^{\lambda ,\mu } } } } } $$
(15)

Indicate the four-by-four irreducible representation with rows ordered in increasing values of λ′ and in decreasing values of μ′ for a particular λ′, and with columns ordered similarly, by R. The basis of this representation is formed by the four hyperspherical harmonics for which n = 1. We require then that there exists an invertible linear transformation B of the hyperspherical harmonics that defines functions that behave analogously to the unit vectors along the w, x, y, and z axes, and that B simultaneously defines a similarity transformation that brings the matrix R into the canonical form. A suitable linear transformation exists, and is defined by the relation

$$ \left[ {\begin{array}{*{20}c} {Z_{0,0}^{1} } & {Z_{1,1}^{1} } & {Z_{1,0}^{1} } & {Z_{1, - 1}^{1} } \\ \end{array} } \right]B = \left[ {\begin{array}{*{20}c} {Z_{0,0}^{1} } & {{{i\left( { - Z_{1,1}^{1} + Z_{1, - 1}^{1} } \right)} \mathord{\left/ {\vphantom {{i\left( { - Z_{1,1}^{1} + Z_{1, - 1}^{1} } \right)} {\sqrt 2 }}} \right. \kern-\nulldelimiterspace} {\sqrt 2 }}} & {{{ - \left( {Z_{1,1}^{1} + Z_{1, - 1}^{1} } \right)} \mathord{\left/ {\vphantom {{ - \left( {Z_{1,1}^{1} + Z_{1, - 1}^{1} } \right)} {\sqrt 2 }}} \right. \kern-\nulldelimiterspace} {\sqrt 2 }}} & {iZ_{1,0}^{1} } \\ \end{array} } \right] $$
(16)

The basis functions on the right of Eq. [16] differ by a constant positive coefficient from w, x, y, and z, respectively. The matrix B −1 RB is equivalent to G when ω 2 = 0, and to H when ω 1 = 0, that is, this similarity transformation brings the irreducible representation into canonical form.

While these developments are not intended as a rigorous justification for the choice of phases for the hyperspherical harmonics, the hyperspherical harmonics defined in Eq. [10] and the irreducible representations of SO(4) defined in Eq. [15] appear to be reasonable inasmuch as they satisfy the compatibility condition outlined earlier.

4.2 Relationship of Basis Functions

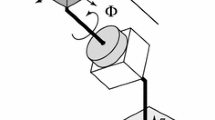
With the relationship of T m′,m l (ϕ 1, Φ, ϕ 2) and D l m′,m (ϕ 1, Φ, ϕ 2) established by Eq. [8], there remains the question of the relationship of D l m′,m (ϕ 1, Φ, ϕ 2) and U l m′,m (ω, θ, ϕ). For this, an inspection of the rotation operations corresponding to T m′,m l (ϕ 1, Φ, ϕ 2), D l m′,m (ϕ 1, Φ, ϕ 2) and U l m′,m (ω, θ, ϕ) is useful. According to Bunge,[10] T m′,m l (ϕ 1, Φ, ϕ 2) identifies a crystal orientation with the passive rotation that brings the sample coordinate system into coincidence with the crystal coordinate system, in which the crystal is in the actual orientation throughout. This operation is shown at the top of Figure 1. As discussed in Section III, D l m′,m (ϕ 1, Φ, ϕ 2) identifies a crystal orientation with the active counterpart to T m′,m l (ϕ 1, Φ, ϕ 2), i.e., with the active rotation that brings the crystal from the actual orientation into coincidence with the reference orientation, in which the coordinate system is aligned with the sample throughout. This operation is shown in the middle of Figure 1. By definition,[34] U l m′,m (ω, θ, ϕ) identifies a crystal orientation with the active rotation that brings the crystal from the reference orientation into coincidence with the actual orientation, in which the coordinate system is aligned with the sample throughout. This operation is shown at the bottom of Figure 1.

Fig. 1
figure 1

The physical interpretation and relationship of the quantities T m′,m l (ϕ 1, Φ, ϕ 2), D l m′,m (ϕ 1, Φ, ϕ 2), and U l m′,m (ω, θ, ϕ). The T m′,m l (ϕ 1, Φ, ϕ 2) is considered to passively bring the coordinate system into coincidence with an oriented crystal. The D l m′,m (ϕ 1, Φ, ϕ 2) is considered to actively bring an oriented crystal into coincidence with the coordinate system; this is identical to the effect of T m′,m l (ϕ 1, Φ, ϕ 2) from the perspective of an observer attached to the coordinate system. The U l m′,m (ω, θ, ϕ) is considered to actively bring a reference crystal into coincidence with the oriented crystal; this is the inverse of the effect of D l m′,m (ϕ 1, Φ, ϕ 2)

Full size image

Reference to Figure 1 clearly indicates that the active rotation corresponding to D l m′,m (ϕ 1, Φ, ϕ 2) is the inverse of the active rotation corresponding to U l m′,m (ω, θ, ϕ). That is, the unitary matrix constructed from D l m′,m (ϕ 1, Φ, ϕ 2) is the inverse of the unitary matrix constructed from U l m′,m (ω, θ, ϕ), or

$$ D_{{m^{\prime } ,m}}^{l} \left( {\phi_{1} ,\Upphi ,\phi_{2} } \right) = U_{{m,m^{\prime } }}^{l * } \left( {\omega ,\theta ,\phi } \right) $$
(17)

Applying Eq. [8] to Eq. [17] gives

$$ T_{l}^{{m^{\prime } ,m}} \left( {\phi_{1} ,\Upphi ,\phi_{2} } \right) = \left( { - 1} \right)^{{m - m^{\prime } }} U_{{m,m^{\prime } }}^{l * } \left( {\omega ,\theta ,\phi } \right) $$
(18)

This equation relates T m′,m l (ϕ 1, Φ, ϕ 2), formulated with the passive convention and the Euler-angle parameterization, to U l m′,m (ω, θ, ϕ), formulated with the active convention and the axis-angle parameterization, and is the basis for the conversion formulas presented in Section V.

5 Conversion Formulas

The conversion from the generalized spherical harmonics to the hyperspherical harmonics proceeds according to the prescription mentioned in Section IV–B; because the value of the matrix elements of the irreducible representations of SO(3) must be independent of the parameterization, the formulas for these matrix elements in the Euler-angle and axis-angle parameterizations may be equated. Inverting Eq. [18] and inserting Eq. [12] indicates that

$$ \left( { - 1} \right)^{{m - m^{\prime } }} T_{l}^{{m,m^{\prime } * }} \left( {\phi_{1} ,\Upphi ,\phi_{2} } \right) = \sum\limits_{\lambda } {\sum\limits_{\mu } {C_{{l,m^{\prime } ,\lambda ,\mu }}^{l,m} {\frac{{\sqrt {2\left( {2\lambda + 1} \right)} \pi }}{2l + 1}}Z_{\lambda ,\mu }^{2l} \left( {\omega ,\theta ,\phi } \right)} } $$
(19)

By relabeling the indices m and m′, complex-conjugating both sides and applying Eq. [11], this becomes

$$ T_{l}^{{m^{\prime } ,m}} \left( {\phi_{1} ,\Upphi ,\phi_{2} } \right) = \sum\limits_{\lambda } {\sum\limits_{\mu } {\left( { - 1} \right)^{{\lambda + \mu + m - m^{\prime } }} C_{l,m,\lambda ,\mu }^{{l,m^{\prime } }} {\frac{{\sqrt {2\left( {2\lambda + 1} \right)} \pi }}{2l + 1}}Z_{\lambda , - \mu }^{2l} \left( {\omega ,\theta ,\phi } \right)} } $$
(20)

Changing the summation over μ to a summation over −μ and applying the symmetry properties of the Clebsch–Gordan coefficients gives the result

$$ T_{l}^{{m^{\prime } ,m}} \left( {\phi_{1} ,\Upphi ,\phi_{2} } \right) = \sum\limits_{\lambda } {\sum\limits_{\mu } {\left( { - 1} \right)^{{\lambda + m - m^{\prime } }} C_{{l,m^{\prime } ,\lambda ,\mu }}^{l,m} {\frac{{\sqrt {2\left( {2\lambda + 1} \right)} \pi }}{2l + 1}}Z_{\lambda ,\mu }^{2l} \left( {\omega ,\theta ,\phi } \right)} } $$
(21)

This establishes the formula to convert from the generalized spherical harmonics to the hyperspherical harmonics.

The inverse expression is found by exploiting the unitarity relations of the Clebsch–Gordan coefficients. This procedure is simplified by initially applying the symmetry properties of the Clebsch–Gordan coefficients to obtain

$$ T_{l}^{{m^{\prime } ,m}} \left( {\phi_{1} ,\Upphi ,\phi_{2} } \right) = \sum\limits_{\lambda } {\sum\limits_{\mu } {\left( { - 1} \right)^{l + m} C_{{l, - m^{\prime } ,l,m}}^{\lambda ,\mu } {\frac{\sqrt 2 \pi }{{\sqrt {2l + 1} }}}Z_{\lambda ,\mu }^{2l} \left( {\omega ,\theta ,\phi } \right)} } $$
(22)

Multiplying through by C λ′,μ′ l,−m′,l,m , summing over the indices −m′ and m, and rearranging the summations then gives

$$ \begin{aligned} \sum\limits_{{ - m^{\prime } }} {\sum\limits_{m} {\left( { - 1} \right)^{ - l - m} C_{{l, - m^{\prime } ,l,m}}^{{\lambda^{\prime } ,\mu^{\prime } }} {\frac{{\sqrt {2l + 1} }}{\sqrt 2 \pi }}T_{l}^{{m^{\prime } ,m}} \left( {\phi_{1} ,\Upphi ,\phi_{2} } \right)} } = & \sum\limits_{\lambda } {\sum\limits_{\mu } {Z_{\lambda ,\mu }^{2l} \left( {\omega ,\theta ,\phi } \right)} } \\ & \quad \times \left[ {\sum\limits_{{ - m^{\prime } }} {\sum\limits_{m} {C_{{l, - m^{\prime } ,l,m}}^{{\lambda^{\prime } ,\mu^{\prime } }} C_{{l, - m^{\prime } ,l,m}}^{\lambda ,\mu } } } } \right] \\ \end{aligned} $$
(23)

The quantity in brackets is δ λ′,λ δ μ′,μ by the unitarity of the Clebsch–Gordan coefficients, simplifying the equation to

$$ Z_{\lambda ,\mu }^{2l} \left( {\omega ,\theta ,\phi } \right) = \sum\limits_{{ - m^{\prime } }} {\sum\limits_{m} {\left( { - 1} \right)^{ - l - m} C_{{l, - m^{\prime } ,l,m}}^{\lambda ,\mu } {\frac{{\sqrt {2l + 1} }}{\sqrt 2 \pi }}T_{l}^{{m^{\prime } ,m}} \left( {\phi_{1} ,\Upphi ,\phi_{2} } \right)} } $$
(24)

Applying the symmetry properties of the Clebsch–Gordan coefficients and replacing the summation over −m′ with a summation over m′ gives

$$ Z_{\lambda ,\mu }^{2l} \left( {\omega ,\theta ,\phi } \right) = \sum\limits_{{m^{\prime } }} {\sum\limits_{m} {\left( { - 1} \right)^{{\lambda + m^{\prime } - m}} C_{{l,m^{\prime } ,\lambda ,\mu }}^{l,m} {\frac{{\sqrt {2\lambda + 1} }}{\sqrt 2 \pi }}T_{l}^{{m^{\prime } ,m}} \left( {\phi_{1} ,\Upphi ,\phi_{2} } \right)} } $$
(25)

where the indices of summation satisfy the constraint m−m′ = μ. This is the counterpart to Eq. [21], and establishes the formula to convert from the hyperspherical harmonics to the generalized spherical harmonics.

The conversion of the basis functions in Eqs. [1] and [4] is not as useful as a direct conversion between the expansion coefficients. Calculation of these formulas requires one to account for the fact that the values of these ODFs are different, however. This is simplest to observe for the case of a uniform distribution, for which the value of the ODF in Eq. [1] is unity everywhere, while the value of the ODF in Eq. [4] is 1/2π 2 everywhere. As with the matrix elements of the irreducible representations of SO(3), equating expansions of the ODF when the values of the ODFs at corresponding points are not equal is nonsensical. This disparity is resolved by multiplying one of the expansions by the appropriate coefficient, or

$$ f\left( {\phi_{1} ,\Upphi ,\phi_{2} } \right) = 2\pi^{2} f\left( {\omega ,\theta ,\phi } \right) $$
(26)

Multiplying this by the complex conjugate of Eq. [21] and integrating by means of Eq. [A7] results in

$$ \begin{aligned} \int\limits_{0}^{2\pi } {\int\limits_{0}^{\pi } {\int\limits_{0}^{2\pi } {f\left( {\phi_{1} ,\Upphi ,\phi_{2} } \right)T_{l}^{{m^{\prime } ,m * }} \sin \Upphi d\phi_{1} d\Upphi d\phi_{2} } } } = & \sum\limits_{\lambda } {\sum\limits_{\mu } {\left( { - 1} \right)^{{\lambda + m - m^{\prime } }} C_{{l,m^{\prime } ,\lambda ,\mu }}^{l,m} {\frac{{8\pi^{3} \sqrt {2\left( {2\lambda + 1} \right)} }}{2l + 1}}} } \\ & \quad \times \int\limits_{0}^{2\pi } {\int\limits_{0}^{\pi } {\int\limits_{0}^{\pi } {f\left( {\omega ,\theta ,\phi } \right)Z_{\lambda ,\mu }^{2l * } \sin^{2} \left( {{\omega \mathord{\left/ {\vphantom {\omega 2}} \right. \kern-\nulldelimiterspace} 2}} \right)\sin \theta d\left( {{\omega \mathord{\left/ {\vphantom {\omega 2}} \right. \kern-\nulldelimiterspace} 2}} \right)d\theta d\phi } } } \\ \end{aligned} $$
(27)

where an additional factor of \( {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2} \) is introduced on the right side to account for the fact that every orientation is included in the integrated volume twice. The integrals in this expression may be evaluated using Eqs. [2] and [5]. Simplifying this gives

$$ t_{l}^{{m^{\prime } ,m}} = \sum\limits_{\lambda } {\sum\limits_{\mu } {\left( { - 1} \right)^{{\lambda + m - m^{\prime } }} C_{{l,m^{\prime } ,\lambda ,\mu }}^{l,m} \pi \sqrt {2\left( {2\lambda + 1} \right)} z_{\lambda ,\mu }^{2l} } } $$
(28)

The inverse expression may be found either by a similar integration, or by inverting Eq. [28] directly, with the result that

$$ z_{\lambda ,\mu }^{2l} = \sum\limits_{{m^{\prime } }} {\sum\limits_{m} {\left( { - 1} \right)^{{\lambda + m^{\prime } - m}} C_{{l,m^{\prime } ,\lambda ,\mu }}^{l,m} {\frac{{\sqrt {2\lambda + 1} }}{{\sqrt 2 \pi \left( {2l + 1} \right)}}}t_{l}^{{m^{\prime } ,m}} } } $$
(29)

Equations [28] and [29] provide the linear transformations to convert an ODF written in the form of Eq. [1] directly into the form of Eq. [4] and vice versa; the required Clebsch–Gordan coefficients are given in Appendix C.

6 Example

In this section, we validate the results of the previous sections by applying them to the ODF of a copper sample, as determined experimentally by electron backscatter diffraction (EBSD). For reference, the normal direction inverse pole figure map is given in Figure 2. We validate the conversion formulas by comparing the coefficients z n l,m of the hyperspherical harmonic expansion as calculated directly from fitting the experimental data with Eq. [5], and as calculated by first fitting for the coefficients t m′,m l of the generalized spherical harmonic expansion from Eq. [2] and then converting them to the z n l,m by means of Eq. [29]. The analytical expression for an ODF should be independent of the calculation method, so the equivalence of these sets of coefficients provides evidence for the accuracy of the formulas derived in the Section V.

Fig. 2
figure 2

The normal-direction inverse pole figure map of a copper sample, as measured experimentally by EBSD

Full size image

The expansion of the ODF given by the coefficients calculated directly from the experimental data appears in Figure 3(a), and that given by the coefficients calculated indirectly through conversion from the generalized spherical harmonics using Eq. [29] appears in Figure 3(b). The infinite summation in the hyperspherical harmonic expansion of Eq. [4] is limited to n ≤ 30, and the procedure used to display the hyperspherical harmonic expansions graphically is described elsewhere.[20] Blue and red regions correspond to positive and negative probability density, respectively. The presence of a few clearly distinguishable probability density peaks reflects that the observed region contained only a few grains, while the resemblance of Figure 3(a) to Figure 3(b) indicates that the directly calculated coefficients match well with those calculated by means of the conversion formulas. Although not practical to present in print, we have directly compared the numerical values of the 5456 coefficients in the two expansions as well, and they are equal to within one part per 108, i.e., to within the error of the numerical calculations. These results convincingly validate the mathematical conclusions in the Section V.

Fig. 3
figure 3

The ODF of the copper sample in Fig. 2, expressed via the hyperspherical harmonic expansion given in Eq. [4]. Here, a set of concentric spheres at prescribed values of rotation angle ω are presented in the area-preserving projection. Blue and red indicate regions of positive and negative probability density, respectively. (a) Coefficients of the expansion are calculated using Eq. [5]. (b) Coefficients of expansion are calculated using Eqs. [2] and [29], i.e., by means of the coefficient conversion formulas. Inspection of the figures reveals that the expansions are identical

Full size image

7 Positivity Constraint

We anticipate that the conversion formulas presented in Section V will allow existing texture information to be translated easily into the new hyperspherical harmonic-based representation. Beyond texture information, however, the conversion formulas carry the broader implication that mathematical methods and tools developed for use with the generalized spherical harmonics do not need to be rederived for the hyperspherical harmonics. One example is provided by the positivity method for the correction of the ghost error, which was handled in the context of the generalized spherical harmonic expansion by prior researchers.[36–38]

The regions of negative probability density appearing in Figure 3 are unphysical, and result from the truncation of the infinite expansion to a finite number of terms. Historically speaking, regions of negative probability density often appeared in the generalized spherical harmonic expansion of the ODF, although this phenomenon was generally attributed to the inherent limitations on the information obtained from conventional diffraction experiments (i.e., the so-called “ghost error”) rather than truncation error. Many of the same techniques developed in the literature to correct for the ghost error may be used to correct for the truncation error as well. Roughly, these include the positivity method,[36–38] the quadratic method,[39,40] and the maximum entropy method.[41–44] Of these, the positivity method is arguably the simplest to implement. This traditionally involves finding an approximation for the odd l coefficients in Eq. [1] by enforcing the non-negativity of the ODF.

Explicitly, given a reduced ODF f 0(g) that is calculated using only the even l coefficients, define a function

$$ \hat{f}_{i+1} \left( g \right) = \left\{ {\begin{array}{*{20}c} { - f_{i} \left( g \right)} & {f_{i} \left( g \right) < 0} \\ 0 & {\text{otherwise}} \\ \end{array} } \right. $$
(30)

Find the expansion coefficients of \( \hat{f}_{1} \left( g \right) \) from Eq. [2], and use the even l coefficients of f 0(g) and the odd l coefficients of \( \hat{f}_{1} \left( g \right) \) to define the function f 1(g). From this point on, the positivity method follows an iterative procedure. Insert f i (g) into Eq. [30] to define a function \( \hat{f}_{i+1} \left( g \right) \), and find the expansion coefficients of this function from Eq. [2]. Define the function f i+1(g) from the even l coefficients of f i (g) and the sum of the odd l coefficients of \( \hat{f}_{i+1} \left( g \right) \) and f i (g), and repeat the procedure until the magnitude of the negative probability density in f i+1(g) falls below a set threshold. The function f i+1(g) is called the complete ODF.

The same general principle, with minor modifications, may be used to reduce the extent of the truncation error in Figure 3. Indicate the hyperspherical harmonic expansion of the ODF by f 0(g). Insert this function into Eq. [30] to find \( \hat{f}_{1} \left( g \right) \), and calculate the expansion coefficients of \( \hat{f}_{1} \left( g \right) \) from Eq. [5]. Form the sum of every coefficient of f 0(g) with the corresponding coefficient of \( \hat{f}_{1} \left( g \right) \), and normalize the result by multiplying each coefficient by the constant that brings z 00,0 to the value \( {1 \mathord{\left/ {\vphantom {1 {\sqrt 2 \pi }}} \right. \kern-\nulldelimiterspace} {\sqrt 2 \pi }} \). This collection of coefficients defines the function f 1(g), which is a normalized approximation to \( f_{0} \left( g \right) + \hat{f}_{1} \left( g \right) \). This procedure is iteratively repeated, using Eq. [30] to find \( \hat{f}_{i+1} \left( g \right) \) from f i (g), until the magnitude of the negative probability density in f i+1(g) falls below a set threshold. (The difference between this method and the positivity method outlined earlier is the fact that EBSD measurements provide information about all the coefficients in the expansion; this removes the need to preserve the values of some coefficients while selectively changing others.)

This method is applied to the hyperspherical harmonic expansions appearing in Figure 3, with the result shown in Figure 4. The procedure markedly reduces the magnitude of the negative probability density regions, although it broadens the peaks in the probability distribution function as well.

Fig. 4
figure 4

ODF given in Fig. 3(a), constrained to positive values by the procedure described in Section VII. Apart from the removal of the regions of negative probability density and a slight broadening of the peaks, the distribution function is nearly identical

Full size image

8 Conclusions

While the importance of the generalized spherical harmonic expansion of an ODF to the historical development of texture analysis is undeniable, exclusive reliance on a single series expansion is inherently limiting. This is quite clear from an examination of the literature, in which discrete orientations are routinely manipulated with multiple parameterizations (rotation matrices, Rodrigues vectors, Euler angles, etc.) to leverage their complementary strengths, but series expansions of orientation distributions in the past were restricted to this single representation. The absence of an alternative to the generalized spherical harmonic expansion essentially required that every operation on the ODF be performed in the Euler-angle parameterization, regardless of its suitability. The hyperspherical harmonic expansion of an ODF provides the missing alternative, although the utility of this series expansion relies on the existence of a means by which to efficiently and easily convert from one representation to the other; this article provides the equations effecting this conversion for the first time.

The ramifications of these conversion formulas are expected to extend further than the ability to express a particular ODF by a series expansion in the axis-angle parameterization. Specifically, these formulas provide continuity of the hyperspherical harmonic expansion with the existing literature and allow mathematical results derived using the generalized spherical harmonic expansion (or programs written using this expansion) to be used with a minimum of modification. As a simple example, the fact that the conversion of the expansion coefficients is a linear transformation enables one of the procedures existing in the literature to enforce a positivity condition on the generalized spherical harmonic expansion of the ODF to be applied directly to the hyperspherical harmonic expansion of the ODF. We hope that these results significantly increase the accessibility and utility of the hyperspherical harmonic expansion in the field of texture analysis.