Abstract
As a result of recent investigations on nanocrystalline (nc) materials, extensive experimental data on the deformation behavior of these materials have become available. In this article, an analysis of these data was performed to identify the requirements that a viable deformation mechanism should meet in terms of accounting for the mechanical characteristics and trends that are revealed by the data. The results of the analysis show that a viable deformation mechanism is required to account for the following: (1) an activation volume the value of which is in the range 10 to 40 b 3; (2) an activation energy that is close to the activation energy for boundary diffusion but that decreases with increasing applied stress; (3) the magnitudes of deformation rates that cover wide ranges of temperatures, stresses, and grain sizes; (4) inverse Hall–Petch behavior; and (5) limited ductility. The validity of available deformation mechanisms for nc materials is closely examined in the light of these requirements.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
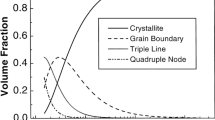
Nanocrystalline (nc) materials are characterized by grain sizes ≤100 nm. Because of the small grains of nc materials, grain boundaries, junction lines, and nodes have significant volume fractions, a characteristic that can influence properties far more strongly than in conventional materials.[1]
The nc materials offer interesting possibilities related to many structural applications. In order to explore some of these possibilities, an understanding of the origin and nature of deformation processes in nc materials is essential. Such understanding is important in two ways. First, when the origin of the deformation process is uncovered in sufficient detail, it should be possible to predict the mechanical behavior under a variety of conditions (stress, temperature, and grain size). Second, when the basic deformation process is known (successfully identified or developed), it is possible to introduce microstructural features that can improve the mechanical behavior of the materials in terms of ductility, toughness, etc.
As a result of recent investigations of nc materials, several deformation mechanisms have been proposed. These mechanisms are different in terms of concept and details. In addition, extensive experimental data on the mechanical behavior of nc materials such as nc Ni and nc Cu have become available. The availability of the experimental data on these two metals provides an opportunity to closely examine the validity of deformation mechanisms that were proposed to account for the characteristics of deformation in nc materials.
Accordingly, the objective of this article is twofold, as follows: (1) to identify the requirements that a deformation mechanism should meet in terms of accounting for the mechanical characteristics and trends that are revealed by the experimental data and (2) to assess available deformation mechanisms in the light of these requirements.
2 Analysis
2.1 Requirements for a Successful Deformation Mechanism
In order to identify or develop deformation processes, guiding information is needed. This guiding information can be obtained in part from experimental measurements. During the period 1990 to 2008, experimental measurements dealing with deformation behavior in nc materials were reported. These measurements have focused on items that characterize the deformation behavior of nc materials; these items are discussed in the following subsections.
2.1.1 Activation volume for deformation
The activation volume v is the rate of decrease of the activation enthalpy with respect to flow stress at constant temperature.[2] It provides useful insight into the nature of deformation mechanisms, because it is characterized by a definite value of stress dependence for each atomistic process. Measurements of the activation volume during deformation are made by the following: (1) making either a small change in applied stress and measuring the corresponding strain rate after the change, or a small change in strain rate and measuring the corresponding stress and (2) applying the following equation:
where k is the Boltzmann’s constant, T is the absolute temperature, τ is the shear stress, and \( \dot{\gamma } \) is the shear strain rate. Table I provides a summary of the values of the activation volume in materials that cover the nanocrystalline (nc), the ultrafine-grained (UFG), the micrograined (MG), and the coarsegrained (CG) ranges.[3–9] An examination of this table shows that the activation volumes for nc materials are much lower than those reported for UFG and MG counterparts. Because the value of the activation volume is a characteristic of the rate-controlling mechanism, consideration of this finding along with Table I reveals the following two important implications: (1) a proposed mechanism for nc materials should predict an activation volume in the range 10 to 40 b 3; and (2) if the proposed mechanism for nc materials involved some form of dislocation activity, these dislocations would sweep unimpeded through the lattice interiors. The latter implication is consistent with two experimental observations. First, results reported for nc Ni have shown[10] no evidence for the extensive dislocation debris that characterizes deformation in large-grained metals. Second, the results of an in-situ X-ray diffraction investigation of nc Ni that was tested in tension at room temperatures revealed no irreversible peak broadening.[11] This observation signifies that dislocations are not stored in the material as a result of deformation.
2.1.2 Activation energy
The apparent activation energy Q for deformation is defined as[12]
where R is the gas constant. Early experimental data[13,14] have indicated that the activation energy for deformation in nc Cu and nc Ni approximates that of boundary diffusion. However, very recent results[5] on nc Ni have shown that for stresses of 141, 165, and 188 MPa, the average apparent activation energies are 141, 134, and 126 kJ/mol, respectively. While the values of these energies are in the range of those anticipated for boundary diffusion in nc Ni, assuming the activation energy for boundary diffusion Q gb in fcc metals is of the order of 0.4 to 0.6[15] and that for lattice diffusion is Q L (Q L = 284 kJ/mol), it is clear that the activation energy for deformation decreases with increasing applied stress.
2.1.3 Magnitude of deformation rates
During the period 1990 to 2007, experimental measurements dealing with the deformation behavior of nc materials were reported. In particular, these investigations focused on nc Ni and nc Cu. As a result of these investigations, there exist several sets of data for these two metals[3,5,16–25] that are identified in Table II. All data are characterized in terms of shear stresses τ and shear strain rates \( \dot{\gamma }. \) To convert tensile data into shear data, the following relations were used:
where σ and \( \mathop \varepsilon \limits^{ \bullet } \) are the tensile stress and tensile strain rate, respectively. Also, Table II includes information that specifies the conditions under which the data were obtained. These conditions include the type of test, the grain size, the test temperature, the range of strain rate, and the range of stresses.
Any successful deformation mechanism is required not only to account for deformation characteristics, such as the activation volume and the activation energy for deformation, but also to predict the magnitudes of the deformation rates. The data given in Table I will permit examining whether a proposed deformation mechanism for nc materials meets this requirement.
2.1.4 Nanoscale softening
In general, as the grain size d is refined, the strength increases as \( 1/\sqrt d , \) according to the Hall–Petch relation[26,27] that can be represented by the following expression:
where τ 0 is a friction stress and c is a constant. Equation [4] is also valid when the yield strength is replaced by the hardness H or by the twin width. As reported elsewhere,[28] conventional Hall–Petch behavior for Cu and Ni can be described by Eqs. [5] and [6], respectively:
Experimental observations have indicated that when the grain sizes of nc Cu and nc Ni (and their alloys) fall below a critical value in the nanoscale range, the strength decreases, i.e., nanoscale softening (inverse Hall–Petch behavior) occurs. According to a very recent analysis,[28] the critical grain sizes for Cu and Ni are ~25 and 15 nm, respectively. The results of molecular dynamics (MD) simulations[29] have shown the presence of a maximum in the flow stress of Cu when its grain size becomes smaller than 15 nm.
2.2 Consideration of Proposed Deformation Mechanisms
According to the preceding discussion, a viable deformation mechanism is required to account for the following: (1) an activation volume in the range 10 to 40 b 3; (2) an activation energy that is close to the activation energy for boundary diffusion but that decreases with increasing stress; (3) the magnitudes of deformation rates that cover wide ranges of temperatures, stresses, and grain sizes; and (4) inverse Hall–Petch behavior.
Over the past two decades, several deformation mechanisms were proposed to account for the mechanical behavior of nc materials. In discussing the validity of these mechanisms, attention will be placed on rate-dependent deformation mechanisms, because experimental evidence certainly rules out the possibility of rate-controlling deformation mechanisms that are rate independent. These mechanisms are described in the following subsections.
2.2.1 Coble creep
Early theoretical considerations have indicated that under conditions of low homologous temperatures, very small normalized grain sizes, and small stresses, Coble creep[30] may control the creep behavior of fine-grained materials. Coble creep, in which creep strain is produced by the diffusion of vacancies along the grain boundaries, is represented by the following equation:
where A Co ~ 200 and D gb is the grain boundary diffusion coefficient. Although Coble creep is characterized by an activation energy that is equal to boundary diffusion, three factors indicate that this type of diffusional creep cannot be responsible for deformation in nc materials.
First, the activation volume associated with Coble creep is b 3. This value is much smaller than those reported for nc materials (10 to 40 b 3).
Second, deformation data reported for nc Ni and nc Cu (Table II) are plotted in the form of normalized creep rate \( \left( {{{\mathop \gamma \limits^{ \bullet } {\text{k}}T} \mathord{/ {\vphantom {{\mathop \gamma \limits^{ \bullet } {\text{k}}T} {D_{gb} Gb}}} \kern-\nulldelimiterspace} {D_{gb} Gb}}} \right)\left( {{d \mathord{\left/ {\vphantom {d b}} \right. \kern-\nulldelimiterspace} b}} \right)^{3} \) as a function of normalized stress (τ/G) on a logarithmic scale in Figure 1(a). The shear moduli for Ni and Cu were taken from Reference 31. Included in Figure 1(a) is the prediction of Eq. [7] that is given as a solid line at 45 deg. In plotting the deformation data, the following parameters were used: (1) for Ni, Q gb and D gb0 are equal[28] to 156.6 kJ/mole and 1.92 cm2/s, respectively; (2) for Cu, Q gb and D gb0 are equal[28] to 120 kJ/mole and 1.6 cm2/s, respectively; and (3) the Burgers vectors of Ni and Cu are 0.249 and 0.256 nm, respectively. An inspection of Figure 1(a) shows that the agreement between the prediction Coble creep and the data for nc Cu and nc Ni is poor in terms of trend and magnitude. This disagreement remains even if different values of Q gb and D gb0 reported by Frost and Ashby were used.[32] Figure 1(b) illustrates this point under the following conditions: (1) for Ni, Q gb and D gb0 are equal[32] to 115 kJ/mole and 0.1 cm2/s, respectively; and (2) for Cu, Q gb and D gb0 are equal[32] to 104 kJ/mole and 7 × 10−2 cm2/s, respectively.
(a) Plot of \( \left( {{{\mathop \gamma \limits^{ \bullet }{\text{k}}{{T}}}/{D_{gb} Gb}}} \right)(d/b)^3 \) against (τ/G) on a logarithmic scale showing the correlation between deformation data reported for nc Ni and nc Cu and prediction of Coble creep.[30] Grain boundary diffusivities for Ni and Cu were taken from Ref. 28. (b) Plot of \( \left( {{{\mathop \gamma \limits^{ \bullet }{\text{k}}{{T}}}/{D_{gb} Gb}}} \right)(d/b)^3 \) against (τ/G) on a logarithmic scale showing the correlation between deformation data reported for nc Ni and nc Cu and prediction of Coble creep.[30] Grain boundary diffusivities for Ni and Cu were taken from Ref. 32
Third, the Hall–Petch relations for Cu and Ni as described by Eqs. [5] and [6], respectively, are depicted as solid straight lines (labeled as Hall–Petch Equation) in Figures 2 and 3, respectively, where applied shear stress τ in the case of Cu and hardness, and H in the case of Ni, are plotted against \( 1/\sqrt d . \) In plotting Eq. [7] representing Coble creep in Figures 2 and 3 as τ or H against \( 1/\sqrt d \) (labeled as Coble creep), the following information and conditions in addition to the aforementioned data on Q gb and D gb0 were used: (1) the activation volumes v for Cu and Ni were taken[28] to be 12 and 10 b 3, respectively; and (2) the shear strain rate = 10−3 s−1[28] and T = 300 K. As shown by Figures 2 and 3, the curves representing Coble creep (Eq. [7]) for Cu and Ni intersect the straight lines representing the Hall–Petch behavior at 0.44 and 0.008 nm, respectively. It is clear that these values for the critical grain sizes are not realistic and that Coble creep cannot account for the transition from hardening (conventional Hall–Petch behavior) to softening (inverse Hall–Petch relation). The values of the critical grain size remain unrealistic even if different activation energies[32] were used. For example, the critical grain size for Cu becomes 1.6 nm when Q gb = 104 kJ/mole and D gb0 = 0.1 cm2/s. In addition, the critical grain size for Ni becomes 0.3 nm when Q gb = 115 kJ/mole and D gb0 = 7 × 10−2 cm2/s.
Finally, the results of investigations of nc materials have shown[33] that elongations to failure (ductility) are in the range 2 to 8 pct. These elongations to failure are too low to be attributed to the operation of Coble creep, the stress exponent of which is unity. As reported elsewhere,[34] ductility is a function of the reciprocal of the stress exponent. Accordingly, it is expected that elongations to failure arising from the Coble process (n = 1) will be much higher than those associated with the micrograin superplasticity process[35] (n = 2). For the latter process, elongations to failure are >500 pct.
2.2.2 Triple junction model
Wang et al.[36] derived a rate equation for triple junction creep that can be represented by the following equation:
where A tj is a dimensionless constant and D tj is the triple junction diffusion coefficient. It is not possible to examine quantitatively the correlation between the prediction of triple junction creep and the deformation behavior of nc materials for the following two reasons: (1) A tj is not known and (2) there is a lack of information on D tj . In addition, the equation for triple junction creep, similar to Coble creep, predicts Newtonian behavior. In view of this similarity, it is very doubtful that the triple junction creep will be responsible for the deformation behavior of nc materials. Moreover, available information has indicated that the triple junction process is likely to be important when the grain size is less than 10 nm.[37]
2.2.3 Atomic scale boundary sliding model
Hahn and Padmanabhan[38] developed a model for deformation in nc materials. The model is based on the concept that deformation in nc materials is controlled by atomic scale boundary sliding. The model, which is phenomenological in nature, involves many adjustable parameters, some of which cannot be evaluated with certainty. Accordingly, it is not possible to provide a comparison between the prediction of the model and present experimental data.
2.2.4 Modified Coble creep
In an attempt to explain nanoscale softening in Cu, Masumara et al.[39] has proposed a model involving Coble creep with a threshold stress τ 0 that is inversely related to grain size. The equation proposed by Masumara et al. is given as[39]
where τ 0 = A/d, A = Gb, \( B = {{{\text{k}}T\mathop \gamma \limits^{ \bullet } } \mathord{/ {\vphantom {{{\text{k}}T\mathop \gamma \limits^{ \bullet } } {42\pi \delta D_{gb} \Upomega }}} \kern-\nulldelimiterspace} {42\pi \delta D_{gb} \Upomega }}, \) δ is the grain boundary width, and Ω is the atomic volume. By taking δ = 2b and Ω = 0.7 b 3, Eq. [9a] can be written in the following normalized form as
Equation [9b] represents a modified form for Coble creep (Eq. [7]) under the condition of the operation of a threshold process. By combining Eq. [9a] with the equation representing conventional Hall–Petch behavior, Masumara et al.[39] predicted that for Cu, the average critical grain size for a transition from hardening to softening is approximately 20 nm. This value is in agreement with the value of 25 nm inferred from experimental data. In addition, there is evidence to support the presence of a threshold stress for diffusional creep, which is inversely proportional to grain size.[40]
Despite these merits, present attempts to provide a comparison between the prediction of Eq. [9a] and the experimental data given in Table II were not successful. The source for this problem was not initially clear. However, a careful consideration of the expression for the threshold stress in Eq. [9b] led to the identification of the most probable reason. It was found that for most of the experimental datum points given in Table II, the values of the normalized threshold stress were higher than those of the normalized applied stress. For example, the grain sizes used in investigations of nc Ni are in the range 25 to 100 nm. By using the value b for nc Ni (0.249 nm), the normalized threshold stress b/d in Eq. [9b] was estimated to be in the range 2.5 × 10−3 to 10−2. By normalizing applied stresses in Table II using the reported value of the shear modulus[31] for Ni, it was determined that most of the values of the normalized stresses used in testing nc Ni are in the range 7 × 10−4 to 4 × 10−3. Similar results were obtained for nc Cu. While the values of the normalized threshold stress are in the range 5 × 10−3 to 3 × 10−2, those of applied stress are in the range 2 × 10−3 to 4 × 10−3. These findings show that the expression of the threshold stress proposed by Masumara et al.[39] is not realistic, because it yields normalized threshold stresses higher than applied stresses.
In addition to this problem, which is related to the unrealistic nature of the expression for the threshold stress, another issue exists. The results of a very recent investigation of nc Ni have shown[5] that over several orders of magnitude of the strain rate, the stress exponent for creep in nc Ni at 393 K decreases from a value of 30 to a value of 4.5 with decreasing applied stress. This behavior cannot be explained by a modified Newtonian Coble process that incorporates a threshold stress τ 0, because the presence of τ 0 would lead to an increase in the stress exponent with decreasing applied stress, a trend that contrasts with the experimental behavior.
2.2.5 Grain boundary sliding with back stress
Langdon and Vastava[41] presented a model that deals with boundary sliding in conventional polycrystalline materials and that involves dislocation activity as an accommodation process. The model can be presented by the following expression:
where A 0 is a constant and D L is lattice diffusivity. Yi et al.[13] replaced D L by the effective diffusivity given by
where x is a constant.
Combining Eqs. [10a] and [10b] leads to
Yin et al.[13] extended this model for the case of nc materials. The extension was performed under the following two assumptions: (1) for nc materials, \( D_{L} \ll D_{gb} \delta_{gb} /d; \) and (2) the stress exponent of 4.5 reflects the operation of a back stress process and the true stress exponent is 2, not 4.5. By implementing these two assumptions, Yin et al.[13] rewrote Eq. [10a] in the form of Eq. [10d]. (We replaced δ with 2b.)
where A 1 is a constant and D gb0 is the frequency term for grain boundary diffusion.
There are two problems with this modified model, as represented by Eq. [10b]. First, a true stress exponent of approximately 2 is a characteristic of the superplastic flow that is associated with extensive ductility. However, as mentioned earlier, the results of investigations of nc materials have shown that these materials exhibit poor ductility.[33] Second, the presence of a back stress in Eq. [10b] leads to an increase in the apparent stress exponent with decreasing applied stress. This prediction contrasts with recent experimental evidence,[5] which shows that the stress exponent for creep over several orders of magnitude of the strain rate (10−9 s−1 to 10−3 s−1) in nc Ni at 393 K decreases with decreasing applied stress.
2.2.6 Boundary sliding under the condition of nonlinear-viscous behavior
Van Swygenhoven et al.[42,43] have proposed that during the deformation of nc Ni, plasticity arises from grains sliding against each other under the condition of nonlinear-viscous behavior. The equation representing such sliding behavior can be given by[42,43]
where d o is a rate constant, U is the activation energy, v is the activation volume, and τ is the applied stress. For a computer-modeled Ni,[42] v is approximately b 3 and U = 19.22 kJ/mol (0.2 eV). The model by Swygenhoven et al.[42,43] represents the first attempt to describe the deformation of nc materials in terms of a thermally activated process that incorporates the effect of grain size. However, there are three problems regarding the validity of this model, as represented by Eq. [11]. First, the rate constant d o is not defined in terms of material parameters. Accordingly, it is not possible to provide a direct comparison between the prediction of the model and experimental data that are given in Table II. Second, the values of v and U are not consistent with those experimentally measured. For example, the activation volume and the apparent activation energy for deformation in nc Ni that were recently reported[5] are 19.5 b 3 and 126 to 141 kJ/mol, respectively.
2.2.7 Thermally activated grain boundary shearing process
The results of atomistic simulations on Cu and Ni have shown that at very small grain sizes, grain boundary shear becomes a significant deformation process.[42,43] Conrad and Narayan[44] have used these results by proposing that during the deformation of nc materials, the controlling process is a stress-assisted thermally activated motion in the grain boundary in which the deformation rate is produced by independent atomic shear events (atomic jump processes). Under this condition, they developed the following rate-controlling equation:[44]
where ΔF is equal to the activation energy for grain boundary diffusion. The model is attractive, partly because Eq. [12a] does not include adjustable parameters and partly because the activation energy for deformation is equal to that for boundary diffusion.
The model predicts the activation volume to be b 3. This value contrasts with the experimental values of 10 to 30 b 3 that were reported for the activation volume for deformation in nc materials (Table I).
In order to provide a direct comparison between the prediction of the model and experimental data given in Table II, Eq. [12a] was rearranged in the following normalized form (multiplying both sides by b 2 and dividing by D gb ~ D gb0 exp (−ΔF/kT)):
In Figure 4(a), Eq. [11b] is depicted graphically by plotting \( {{\mathop \gamma \limits^{ \bullet } b^{2} } \mathord{/ {\vphantom {{\mathop \gamma \limits^{ \bullet } b^{2} } {D_{gb} }}} \kern-\nulldelimiterspace} {D_{gb} }} \) against \( {{b^{3} \upsilon_{D} } \mathord{\left/ {\vphantom {{b^{3} \upsilon_{D} } {dD_{gb0} }}} \right. \kern-\nulldelimiterspace} {dD_{gb0} }}\left[ {\sinh \left( {{{\tau \upsilon } \mathord{\left/ {\vphantom {{\tau \upsilon } {{\text{k}}T}}} \right. \kern-\nulldelimiterspace} {{\text{k}}T}}} \right)} \right] \) on a logarithmic scale. The solid line at 45 deg represents the prediction of the model. The experimental data given in Table II are plotted in the figure in terms of these two dimensionless parameters. It is clear that the experimental data, when normalized in terms of \( {{\mathop \gamma \limits^{ \bullet } b^{2} } \mathord{/ {\vphantom {{\mathop \gamma \limits^{ \bullet } b^{2} } {D_{gb} }}} \kern-\nulldelimiterspace} {D_{gb} }} \) and \( {{b^{3} \upsilon_{D} } \mathord{/ {\vphantom {{b^{3} \upsilon_{D} } {dD_{gb0} }}} \kern-\nulldelimiterspace} {dD_{gb0} }}\left[ {\sinh \left( {{{\tau \upsilon } \mathord{\left/ {\vphantom {{\tau \upsilon } {{\text{k}}T}}} \right. \kern-\nulldelimiterspace} {{\text{k}}T}}} \right)} \right], \) are not in agreement with the prediction of the model, as represented by the solid line at 45 deg. This disagreement remains even if different activation energies for the grain boundary[32] are used. Figure 4(b) demonstrates this point under the following conditions: (1) for Cu, Q gb , and D gb0 are equal[32] to 104 kJ/mole and 0.1 cm2/s, respectively; and (2) for Ni, Q gb and D gb0 are equal[32] to 115 kJ/mole and 7 × 10−2 cm2/s, respectively.
(a) Plot of \( {{\mathop \gamma \limits^{ \bullet } b^{2}}/{D_{gb} }} \) against \( {{b^{3} \upsilon_{D} } \mathord{/ {\vphantom {{b^{3} \upsilon_{D} } {dD_{gb0} }}} \kern-\nulldelimiterspace} {dD_{gb0} }}\left[ {\sinh \left( {{{\tau \upsilon } \mathord{/ {\vphantom {{\tau \upsilon } {{\text{k}}T}}} \kern-\nulldelimiterspace} {{\text{k}}T}}} \right)} \right] \) on a logarithmic scale showing the correlation between deformation data reported for nc Ni and nc Cu and prediction of the model of thermally activated grain boundary shearing process.[44] Grain boundary diffusivities for Ni and Cu were taken from Ref. 28. (b) Plot of \( {{\mathop \gamma \limits^{ \bullet } b^{2} } \mathord{\left/ {\vphantom {{\mathop \gamma \limits^{ \bullet } b^{2} } {D_{gb} }}} \right. \kern-\nulldelimiterspace} {D_{gb} }} \) against \( {{b^{3} \upsilon_{D} } \mathord{\left/ {\vphantom {{b^{3} \upsilon_{D} } {dD_{gb0} }}} \right. \kern-\nulldelimiterspace} {dD_{gb0} }}\left[ {\sinh \left( {{{\tau \upsilon } \mathord{\left/ {\vphantom {{\tau \upsilon } {{\text{k}}T}}} \right. \kern-\nulldelimiterspace} {{\text{k}}T}}} \right)} \right] \) on a logarithmic scale showing the correlation between deformation data reported for nc Ni and nc Cu and prediction of the model of thermally activated grain boundary shearing process.[44] Grain boundary diffusivities for Ni and Cu were taken from Ref. 32
Equation [12a] is plotted in Figure 5 as τ against \( 1/\sqrt d \) for Cu. Also, included in the figure is a solid line representing conventional Hall–Petch behavior for that metal, as described by Eq. [5]. As shown by the figure, the curves representing the model (Eq. [12a]) for Cu intersects the straight line representing conventional Hall–Petch behavior at 0.44 nm, a value that is not realistic. The behavior for Ni is illustrated in Figure 6, in which hardness H is plotted against \( 1/\sqrt d . \) Similarly, the intersection of the curve representing the model with the solid line representing the conventional Hall–Petch behavior results in a critical grain size the value of which is not realistic (0.16 nm). The values of the critical grain sizes remain, even if different activation energies[32] were used. For example, the critical grain size for Cu becomes 1.8 nm when Q gb = 104 kJ/mole and D gb0 = 0.1 cm2/s. Also, the critical grain size for Ni becomes 1.0 nm when Q gb = 115 kJ/mole and D gb0 = 7 × 10−2 cm2/s.
Yield strength as a function of the inverse square root of the grain size for Cu. Curve representing the model of thermally activated grain boundary shearing process[44] intersects the solid line representing conventional Hall–Petch behavior at approximately d c = 0.44 nm. Grain boundary diffusivity for Cu was taken from Ref. 28
Hardness as a function of the inverse square root of the grain size for Ni. Curve representing the model of thermally activated grain boundary shearing process[44] intersects the solid line representing conventional Hall–Petch behavior at approximately d c = 0.16 nm. Grain boundary diffusivity for Ni was taken from Ref. 28
The preceding discussion shows that although the model proposed by Conrad and Narayan has attractive features, it does not account for the deformation behavior of nc Cu and nc Ni in terms of the following: (1) the value of the activation volume, (2) the trend and position of the experimental data, and (3) the values of the critical grain sizes for a transition from hardening to softening (inverse Hall–Petch behavior) in nc Cu and nc Ni.
2.2.8 Composite model involving amorphous boundary layer
Fan et al.[45] have developed a new composite model that is different from other composite models in terms of concept and details. In developing the model, Fan et al.[40] have assumed that an nc material consists of a grain interior and an amorphous grain boundary layer and that upon stress application, the grain interior deforms elastically while the grain boundary layer deform viscoelastically according to a Maxwell’s equation. The rate-controlling equation in terms of shear strain rate and shear stress can be given by
where r is the radius of atoms at the grain boundary (~2 × 10−14 m), g is a geometric factor (=0.085), and w is the thickness of the boundary (3b).
Fan et al.[45] applied the equation of the model along with the Hall–Petch relations to fit the experimental data on Cu and Ni. On the basis of the best fit, the values of the critical grain size for Cu and Ni were estimated as 25 and 7.7 nm, respectively. The value of 25 nm for Cu fully agrees with that inferred from the experimental data for this metal,[28] but the value of 7.7 nm for Ni is smaller than that inferred from the experimental data (12 to 15 nm).
It is now necessary to examine whether Eq. [13a] can explain the trends in the positions of the experimental data for Cu and Ni. For this purpose, Eq. [13a] is re-expressed in the following normalized form:
In Figure 7(a), Eq. [13b] is depicted graphically by plotting \( {{\mathop \gamma \limits^{ \bullet } {\text{k}}T} \mathord{/ {\vphantom {{\mathop \gamma \limits^{ \bullet } {\text{k}}T} {D_{gb} Gb}}} \kern-\nulldelimiterspace} {D_{gb} Gb}} \) against \( {{{\text{R}}\tau } \mathord{/ {\vphantom {{{\text{R}}\tau } {bG}}} \kern-\nulldelimiterspace} {bG}}\left[ {1 + g\left( {{d \mathord{\left/ {\vphantom {d w}} \right. \kern-\nulldelimiterspace} w} - 1} \right)} \right]^{ - 1} \) on a logarithmic scale. The solid line at 45 deg represents the prediction of the model. The experimental data given in Table II are plotted in the figure in terms of these two dimensionless parameters. An examination of the figure indicates that the model as represented by the solid line at 45 deg cannot account for the trends and positions of the experimental data for nc Cu and nc Ni. This finding does change if different values for Q gb and D gb0 are used. Figure 7(b) demonstrates this behavior under the following conditions: (1) for Cu, Q gb and D gb0 are equal[32] to 104 kJ/mole and 0.1 cm2/s, respectively; and (2) for Ni, Q gb and D gb0 are equal[32] to 115 kJ/mole and 7 × 10−2 cm2/s, respectively.
(a) Plot of \( {{\mathop \gamma \limits^{ \bullet } {\text{k}}T}/{D_{gb} Gb}} \) against \( {{r\tau } \mathord{/ {\vphantom {{r\tau } {bG}}} \kern-\nulldelimiterspace} {bG}}\left[ {1 + g\left( {{d \mathord{\left/ {\vphantom {d w}} \right. \kern-\nulldelimiterspace} w} - 1} \right)} \right]^{ - 1} \) on a logarithmic scale showing the correlation between deformation data reported for nc Ni and nc Cu and prediction of the composite model involving amorphous boundary layer.[45] Grain boundary diffusivities for Ni and Cu were taken from Ref. 32. (b) Plot of \( {{\mathop \gamma \limits^{ \bullet } {\text{k}}T}/{D_{gb} Gb}}\) against \( {{r\tau } \mathord{\left/ {\vphantom {{r\tau } {bG}}} \right. \kern-\nulldelimiterspace} {bG}}\left[ {1 + g\left( {{d \mathord{\left/ {\vphantom {d w}} \right. \kern-\nulldelimiterspace} w} - 1} \right)} \right]^{ - 1} \) on a logarithmic scale showing the correlation between deformation data reported for nc Ni and nc Cu and prediction of the composite model involving the amorphous boundary layer.[45] Grain boundary diffusivities for Ni and Cu were taken from Ref. 32
There are three additional problems regarding the prediction of the composite model just discussed.[45] The first problem is related to the grain size dependence of the strain rate. As indicated by Fan et al.,[45] the grain exponent for deformation as predicted by Eq. [13b] is less than 1. This value is very low when compared with the experimentally reported value[5] of approximately 3. The second problem concerns ductility. The composite model, as represented by Eq. [13a], is characterized by a linear dependence of the strain rate on the applied stress (Newtonian behavior). As a result, the model predicts extensive ductility. This prediction is not consistent with present experimental evidence, which shows that ductility in nc material is very limited. Finally, grains in a real structure are not isolated but are surrounded by other grains. Accordingly, deformation in the boundary layer of one grain needs to be accommodated to relieve stress concentrations.
2.2.9 Model of strongest grain size
Argon and Yip[46] have proposed a composite model that can be represented by the following equation:
where ν D is the atomic frequency, m is equal to 30, γ T is a transformation shear strain, \( \hat{\tau }_{is} \) is the ideal shear resistance of the high-angle grain boundary material, ν G is a frequency factor, and α is a constant (=0.246). The development of Eq. [14] is based on the following.
-
(a)
Two competing but complementary deformation processes, dislocation plasticity and grain boundary shear, contribute to the overall deformation according to their volume fractions in the material in which they operate. Under this condition, the strain rate can be given as
$$ \mathop \gamma \limits^{ \bullet } = f{\mathop \gamma \limits^{\bullet }}_{{GB}} + \left( {1 - f} \right){\mathop \gamma \limits^{\bullet}}_{D} $$(15)where f = 6(b/d) is the volume fraction of the grain boundary material and \({ \mathop \gamma \limits^{ \bullet }}_{GB} \) and \({\mathop \gamma \limits^{ \bullet }}_{D} \) are the shear strain rates arising from the process of grain boundary shear and the process of dislocation plasticity, respectively.
-
(b)
The rate-dependent equation characterizing each deformation process is assumed to operate close to its athermal threshold level.
The model of Argon and Yi[46] appears to be attractive, because it is based on the idea that the deformation behavior of nc materials arises from the operation of grain boundary shear and dislocation plasticity.
At a constant strain rate, Eq. [14] leads to a maximum flow stress at a critical normalized grain size d c . For grain sizes <d c , the process of grain boundary shear controls the deformation and for grain sizes >d c , the process of dislocation plasticity controls the deformation. By selecting certain material parameters and by taking \( \dot{\gamma } = 10^{ 8} \,{\text{s}}^{ - 1} , \) Argon and Yip[46] plotted the variation in the normalized stress as a function of the normalized grain size. Such a plot exhibited a transition from hardening (conventional Hall–Petch behavior) to softening (inverse Hall–Petch behavior) at d c = 12.2 nm. Consideration of the analysis of Yip and Argon[46] indicates that the critical grain size is independent of the value of the shear strain rate. This indication is illustrated in Figure 8, in which Eq. [14] is plotted as applied shear stress τ against \( 1/\sqrt d , \) using a shear strain rate of 10−3 s−1. In addition, included in the figure is the prediction for 108 s−1. As shown by Figure 8, the value of the critical grain size remains as 12.2 nm, but the value of the maximum stress decreases with decreasing the shear strain rate. The critical grain size of 12.2 nm predicted by the model for Cu is close to that obtained from the results of MD simulations[29] performed on Cu (d c = 15 nm), but is smaller than that inferred from experimental data (d c = 25 nm). In addition, the peak stress predicted by the model is smaller than that inferred from experimental results and the left branch of the curve that represents hardening (Hall–Petch conventional behavior) extends to the origin. This trend is different from the real Hall–Petch behavior that intercepts the y-axis at τ 0 (Eq. [4]). Despite these differences, the model of Argon and Yip,[46] unlike other models discussed earlier,[30,44] predicts a transition from hardening to nanoscale softening at a realistic value for the grain size.
The next step is to examine whether Eq. [14] can account for the trends and positions of the experimental data for Cu and Ni. For the purpose of this examination, Eq. [14] is plotted as \( {{\mathop \gamma \limits^{ \bullet } }/{\left( {v_{D} {\cdot} F(d/b)} \right)}} \) vs τ/G on a logarithmic scale in Figure 9. The function F(d/b) under the condition that m = 30 is given by
where \( A = {{6\gamma^{T} } \mathord{/ {\vphantom {{6\gamma^{T} } {\left( {\hat{\tau }_{is} /\mu } \right)}}} \kern-\nulldelimiterspace} {\left( {\hat{\tau }_{is} /\mu } \right)}}^{m} \) and \( B = {{\left( {{{v_{G} } \mathord{/ {\vphantom {{v_{G} } {v_{D} }}} \kern-\nulldelimiterspace} {v_{D} }}} \right)} \mathord{\left/ {\vphantom {{\left( {{{v_{G} } \mathord{\left/ {\vphantom {{v_{G} } {v_{D} }}} \right. \kern-\nulldelimiterspace} {v_{D} }}} \right)} {\alpha^{m} }}} \right. \kern-\nulldelimiterspace} {\alpha^{m} }}. \) Included in Figure 9 are the data on nc Cu and nc Ni. An examination of the figure shows that Eq. [14] is represented by a solid line the slope of which is 30 (m = 30), that the agreement between experimental datum points and the positions of the solid line is poor with the exception of at very high stresses, and that the disagreement in position and trend between the experimental data and the prediction of the model is clearly evident at intermediate and low stresses; the data for these stresses fit short segments of straight lines the slopes of which are in the range 5 to 7. The origin of this disagreement is most likely related to two factors. First, Argon and Yip[46] have assumed that grain boundary shear and dislocation plasticity operate close to their athermal threshold level. This is reflected in the observation that Eq. [14] does not include a term related to thermal activation. The absence of this term is not consistent with the experimental results obtained on nc materials,[3,5,16–25] which clearly show that the deformation behavior of nc material is not athermal and that strain rates measured during the deformation depend on temperature according to the following expression:
Second, in order to simplify the analysis, Argon and Yip[46] assumed that the stress exponents characterizing both grain boundary shear and dislocation plasticity are not only the same (n = 30) but are also independent of temperature. There is no definitive experimental information that lends support for such a simplification. In addition, as acknowledged by Argon and Yip,[46] if deformation occurred at different temperatures other than room temperatures, m would be a function of temperature.
Plot of \( {{\mathop \gamma \limits^{ \bullet}}/{\left( {v_{D} {\cdot} F\left( {d/b} \right)} \right)}} \) against τ/G on a logarithmic scale showing the correlation between deformation data reported for nc Ni and nc Cu and the prediction of the model of strongest grain size[46]
2.2.10 Dislocation-accommodated boundary sliding
Very recently, it has been suggested[5,47] that plasticity in nc materials is the result of grain boundary sliding accommodated by the generation and motion of dislocations under local stresses, which are higher than applied stresses, due to the development of stress concentrations. The model was quantitatively developed using the following sequence of events: (1) as a result of the sliding of a group of grains, the shear stress becomes concentrated at any grain, triple point, or protrusion that obstructs the motion of this group; (2) this local high stress that is higher than applied can then generate dislocations in the blocking grain (or initiate voids); and (3) the generated dislocations move one by one to the opposite boundary, where they climb to their annihilation sites, i.e., no dislocation pileups occur. By considering the details of sliding and dislocation climb along the boundary, the following rate-controlling equation was derived:[5]
where D gb0 is the frequency factor for grain boundary diffusion and M is a stress concentration factor. The term 2Mb 3 in Eq. [18a] represents the activation volume v. Accordingly, Eq. [18a] can be written as
Also, Eq. [18b] can be rewritten in the following normalized form:
where \( D_{gb} = D_{gb0} \exp \left( {{\frac{{ - Q_{gb} }}{{{\text{R}}T}}}} \right). \)
Calculations[5] based on deformation characteristics in UFG ceramics and the value of the stress required to move a boundary dislocation into the interior of the grain have suggested that the value of M is the range 5 to 20. This range, in turn, results in an activation volume in the range 10 to 40 b 3, which is consistent with the reportedly experimental range; as mentioned earlier and shown by Table I, the activation volume measured during the deformation of nc materials is in the range 10 to 50 b 3.
The data on nc Ni and nc Cu that are given in Table II were plotted in Figure 10(a) in terms of the two normalized parameters: \( \mathop \gamma \limits^{ \bullet } \left( {{d \mathord{\left/ {\vphantom {d b}} \right. \kern-\nulldelimiterspace} b}} \right)^{3} \left( {{{b^{2} } \mathord{\left/ {\vphantom {{b^{2} } {D_{gb} }}} \right. \kern-\nulldelimiterspace} {D_{gb} }}} \right) \) and exp (τυ/kT) − 1. Also included in the figure is a solid straight line that represents the prediction of Eq. [18c]. It is clear that the data points cluster about the solid line, demonstrating the presence of good correspondence between the rate equation representing this deformation process and the experimental data for nc Ni and nc Cu, which were obtained at different conditions of temperature, grain size, and strain rates. If different values for diffusivities in Cu and Ni (for Cu, Q gb = 104 kJ/mole and D gb0 = 0.1 cm2/s; for Ni, Q gb = 115 kJ/mole and D gb0 = 7 × 10−2 cm2/s) are used,[32] most of the datum points cluster about a broken line that is parallel to the solid line representing the prediction of Eq. [18c]; the agreement is good between the prediction and experimental data in terms of trend. Figure 10(b) demonstrates this behavior.
(a) Plot of \( \mathop \gamma \limits^{ \bullet } \left( {{d \mathord{\left/ {\vphantom {d b}} \right. \kern-\nulldelimiterspace} b}} \right)^{3} \left( {{{b^{2} } \mathord{\left/ {\vphantom {{b^{2} } {D_{gb} }}} \right. \kern-\nulldelimiterspace} {D_{gb} }}} \right) \) against exp (τυ/kT) − 1 on a logarithmic scale showing the correlation between deformation data reported for nc Ni and nc Cu and prediction of the model of dislocation-accommodated boundary sliding.[5] Grain boundary diffusivities for Ni and Cu were taken from Ref. 28. (b) Plot of \( \mathop \gamma \limits^{ \bullet } \left( {{d \mathord{\left/ {\vphantom {d b}} \right. \kern-\nulldelimiterspace} b}} \right)^{3} \left( {{{b^{2} } \mathord{\left/ {\vphantom {{b^{2} } {D_{gb} }}} \right. \kern-\nulldelimiterspace} {D_{gb} }}} \right) \) against exp (τυ/kT) − 1 on a logarithmic scale showing the correlation between deformation data reported for nc Ni and nc Cu and prediction of model of dislocation-accommodated boundary sliding.[5] Grain boundary diffusivities for Ni and Cu were taken from Ref. 32
When Eq. [18b] was combined with the equation representing conventional Hall–Petch behavior, two findings were reported.[28] First, the variation in stress and hardness for Cu and Ni with \( 1/\sqrt d \) exhibits a transition from hardening to softening. Second, the critical grain sizes at this transition occur for Cu and Ni are 25 and 13 nm, respectively. These values agree well with those estimated by a recent analysis[28] of the experimental data reported for both metals.
Furthermore, this model provides explanations for two experimental observations. The first observation is related to the apparent activation energy for deformation. As stated earlier, the activation energy for deformation in nc Ni decreases with increasing applied stress. Applying the definition of the activation energy (Eq. [2]) to Eq. [18b] leads to the following expression that describes the dependence of the apparent activation energy on applied stress:
Equation [19] is depicted graphically in Figure 11 using T = 393 K and ν = 19 b 3. Included in the figure are the data on the variation of the activation energy for deformation in nc Ni (40 nm) with stress.[5] It is clear that there is good agreement between the prediction of Eq. [20] and the experimental data on nc Ni in terms of trend and magnitude.
The second observation is related to ductility. Experimental evidence indicates that ductility in nc materials is very limited. The model described earlier provides an explanation for this characteristic. The stress exponent for deformation n, as predicted from Eq. [18b], exhibits high and variable values; n > 5. Accordingly, it is expected that ductility in nc materials such as nc Ni would be low, because ductility depends on 1/n (n = 1/m), as indicated by the following expression:[34]
where the value of C = (1 − (1/n)) ln (400/n). In order to provide a close comparison between the values of ductility predicted from Eq. [20] and experimental data measured[25] for nc Ni at 393 K, three steps were carried out. First, the values of stresses at the imposed strain rates were calculated from Eq. [18b]. Second, the stress exponents characterizing these stresses were estimated using the following definition:
By applying this definition to Eq. [18b], the stress exponent for deformation can be given by
Finally, the values of stresses along with the values of the stress exponents estimated from Eq. [22] are combined with Eq. [20] for the purpose of plotting e f pct against the tensile strain rate at 393 K. This plot is shown in Figure 12. Included in the plot are the ductility data obtained for nc Ni (40 nm) at 393 K.[25] It is clear that the agreement between prediction and experiment is good in terms of the trend. However, the values of the predicted ductility are higher than those experimentally reported. Two possible factors may account for this discrepancy. First, the prediction is based on the value of the stress exponent estimated from Eq. [21]. However, ductility can be influenced by other factors such as impurities and the size of the tensile sample. Second, during the deformation of nc Ni, the occurrence of boundary sliding leads to the formation of voids and cavities the growth and linking of which result in premature failure. The process of cavitation and the linking of cavities and voids assumes significance at low strain rates. In this regard, it is interesting to notice that the separation between the predicted values and the experimental values of ductility at 393 K increases with decreasing strain rate.
3 Discussion
The nc materials are characterized by a unique substructural feature: Grain sizes are <100 nm. This characteristic, which signifies that grain boundaries, junction lines, and nodes have substantial volume fractions, plays a central role in defining the nature of possible deformation mechanisms for two reasons. First, with a grain size less than 100 nm, the intragrain Frank–Read dislocation sources become inoperable, because the grain size is too small to accommodate the size of the source. As a result, conventional dislocation mechanisms that produce plastic deformation in CG materials cease to be operational in nc materials. Second, grain boundary processes such as boundary sliding and grain boundary diffusion become relevant.
Two approaches have been adopted to shed light on the nature and origin of deformation processes that are active in nc materials in the absence of conventional Frank–Read sources and that involve boundary processes. In the first approach, MD computer simulations were extensively used.[48] The MD simulations involving nc materials have revealed that as the grain size decreases, boundary sliding dominates.[42,43] The results of MD simulations cannot be entirely applicable to the description of deformation in materials under typical experimental conditions, partly because simulations involve a limited number of grains and partly because they are performed at high strain rates (106 to 108 s−1) that are not typical of those associated with deformation experiments (10−9 s−1 to 10−2 s−1). However, recent analysis[48] has indicated that the results of MD have predicted several differences between CG and nc materials that are consistent with experimental evidence.
In the second approach, mechanical testing has been used to provide information on several deformation parameters. This information has resulted in the following findings.
-
(a)
Deformation is rate dependent. This finding precludes proposed deformation processes that are rate independent.[49–51] However, it should be emphasized that although rate-independent mechanisms are not applicable in light of the experimental evidence discussed in Section II, they have contributed to the process of providing guiding information on the details of deformation in nc materials. These contributions include, for example, providing insight into the process of generating partial or perfect dislocations from stress concentrations at grain boundaries, and the details of the role played by stacking fault energy.
-
(b)
The activation energy for deformation, as measured via conventional techniques (for example, temperature cycling) is close to that of boundary diffusion and decreases with increasing applied stress. This finding, which is illustrated in Figure 11, leads to two implications. First, deformation in nc materials not only entails a boundary process but also arises from a thermally activated process. Second, the driving force for this thermally activated process is given by
$$ \Updelta G = \Updelta F - \tau \nu $$(23)where ΔG is the Gibbs free activation energy and ΔF is the Holmholtz free energy. The usual expression for a thermally activated process may be represented as
$$ \mathop \gamma \limits^{ \bullet } \propto \exp \left( { - \left( {{\frac{{\Updelta G }}{{{\text{k}}T}}}} \right)} \right) $$(24)Replacing ΔF in Eq. [23] with Q gb leads to
$$ \mathop \gamma \limits^{ \bullet } \propto \exp \left( { - \left( {{\frac{{\mathop Q\nolimits_{gb} - \tau \upsilon }}{{{\text{k}}T}}}} \right)} \right) $$(25)As mentioned earlier, the apparent activation energy for deformation in nc Ni is dependent on stress. Accordingly, the exponential expression of τυ does not reduce to the linear case, i.e., \( \left[ {\exp \left( {{\raise0.7ex\hbox{${\tau v}$} \!\mathord{\left/ {\vphantom {{\tau v} {{\text{k}}T}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${{\text{k}}T}$}}} \right)} \right] \) does not reduce to \( 1 + \left( {{\raise0.7ex\hbox{${\tau v}$} \!\mathord{\left/ {\vphantom {{\tau v} {{\text{k}}T}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${{\text{k}}T}$}}} \right). \)
-
(c)
The experimental values of the activation volume measured during the deformation of nc materials are in the range 10 to 40 b 3. This finding eliminates any boundary process the activation volume of which is ~b 3.
-
(d)
The stress exponent is higher than unity and decreases with increasing applied stress. This finding precludes deformation mechanisms that are Newtonian in nature or that involve threshold stress.
-
(e)
The grain size dependence of the deformation rate is ~3.
Combining the aforementioned findings leads to the following suggestion: the most likely deformation process controlling deformation in nc materials involves boundary sliding that may be represented by the following empirical expression:
where B is a constant that has the units of nm3/s. The rate-controlling equation (Eq. [16b]) representing the model of dislocation-accommodated boundary sliding[5] is similar in form to this empirical expression and its predictions are consistent with mechanical characteristics noted for nc materials, as demonstrated in Section III.
As a result of the occurrence of an accommodation process that involves dislocation generation and motion, evidence for dislocation activity is expected to be monitored by microstructural techniques. This expectation contrasts with transmission electron microscopy (TEM) observations on deformed samples of nc Ni that have indicated the presence of few dislocations in grain interiors. However, the absence of evidence regarding dislocations in deformed nc Ni is not evidence of the absence of dislocation activity during deformation. First, during the unloading or subsequent specimen preparation for TEM examination, dislocations could be recovered under no stress and, thus, dislocations could disappear; dislocations only need to travel a very short distance, less than 100 b, to be lost at nearby grain boundaries. Second, the model of dislocation-accommodated boundary sliding does not predict dislocation activity in every grain; dislocations are only generated in the grain that blocks the sliding of a group of grains. The accommodation process involves the generation of dislocations at grain boundary triple points of the blocking grains and their subsequent motion in these grains to boundaries at which they are annihilated. In this context, it was reported that the microstructure of the superplastic MG Zn-22 pct Al alloy after deformation contained very limited isolated dislocations but that when nanoscale particles were very recently introduced in the alloy, an extensive level of dislocation activity was noted in some of the grains.[52,53]
4 Conclusions
The following conclusions are drawn from this study.
-
1.
There are several requirements that a successful deformation mechanism needs to satisfy in order to account for the mechanical characteristics of nc materials. These requirements include the following:
-
a.
an activation volume the value of which is in the range 10 to 40 b 3;
-
b.
an activation energy that is close to the activation energy for boundary diffusion but that decreases with increasing stress;
-
c.
the magnitudes of deformation rates that cover wide ranges of temperatures, stresses, and grain sizes;
-
d.
inverse Hall–Petch behavior; and
-
e.
limited ductility.
Satisfying one or two requirements is necessary but not sufficient.
-
a.
-
2.
Consideration of various proposed deformation mechanisms in the light of the requirements outlined here rules out Coble creep and a thermally activated grain boundary shearing process as viable mechanisms, not only because they predict an activation volume smaller than those experimentally reported but also because they yield unrealistic critical grain sizes for a transition from conventional Hall–Petch behavior (hardening with decreasing grain size) to inverse Hall–Petch behavior (softening with decreasing grain size).
-
3.
The composite model involving a grain boundary layer yields critical grain sizes for a transition from conventional Hall–Petch behavior (hardening with decreasing grain size) to inverse Hall–Petch behavior (softening with decreasing grain size) that agree well with those inferred from experimental results. However, the model has the following three problems.
-
a.
The model fails to account for the experimental data for nc Cu and nc Ni.
-
b.
The grain exponent for deformation as predicted by the rate-controlling equation is less than 1.
-
c.
No consideration is given to accommodating deformation in the grain boundary layer to relieve stress concentrations.
-
a.
-
4.
The model of the strongest grain size predicts a transition from hardening to nanoscale softening at a realistic value for the grain size. However, the model cannot account for the trends and positions of the experimental data for Cu and Ni at intermediate and low stresses.
-
5.
The predictions of the model of dislocation-accommodated boundary sliding are consistent with several deformation characteristics reported for nc materials, including the following:
-
a.
the range of the activation volume;
-
b.
the value of activation energy and its dependence on stress;
-
c.
the critical grain sizes for transitions from conventional Hall–Petch behavior to inverse Hall–Petch behavior in nc Cu and nc Ni; and
-
d.
the low values of elongation to fracture.
-
a.
References
H. Gleiter: Acta Mater., 2000, vol. 48, pp. 1–29.
U.F. Kocks, A.S. Argon, and M.F. Ashby: Thermodynamics and Kinetics of Slip: Progress in Materials Science, Pergamon Press, Oxford, United Kingdom, 1975, vol. 19, pp. 1–288.
F. Dalla Torre, P. Spätig, R. Schäublin, and M. Victoria: Acta Mater., 2005, vol. 53, pp. 2337–49.
E. Ma: Science, 2004, vol. 305, pp. 623–24.
F.A. Mohamed and M. Chauhan: Metall. Mater. Trans. A, 2006, vol. 37A, pp. 3555–67.
L. Lu, R. Schwaiger, Z.W. Shan, M. Dao, K. Lu, and S. Suresh: Acta Mater., 2005, vol. 53, pp. 2169–79.
P.S. Follansbee and U.F. Kocks: Acta. Metall., 1988, vol. 36, pp. 81–93.
R.P. Carrekar, Jr. and W.R. Hibbard, Jr.: Acta Metall., 1953, vol. 1, pp. 654–63.
Q. Wei, S. Cheng, K.T. Ramesh, and E. Ma: Mater. Sci. Eng., A, 2004, vol. 381A, pp. 71–79.
M. Legros, B.R. Elliott, M.N. Rittner, J.R. Weertman, and K.J. Hemker: Philos. Mag. A, 2000, vol. 80A, pp. 1017–26.
D. Farkas, S. Van Petegem, P.M. Derlet, and H. Van Swygenhoven: Acta Mater., 2005, vol. 53, pp. 3115–23.
O.D. Sherby, R.L. Orr, and J.E. Dorn: Trans. TMS-AIME, 1954, vol. 200, pp. 71–80.
W.M. Yin, S.H. Whang, and R.A. Mirshams: Acta Mater., 2005, vol. 53, pp. 383–92.
B. Cai, Q.P. Kong, P. Cui, L. Lu, and K. Lu: Scripta Mater., 2001, vol. 45, pp.1407–13.
P. Shewman: Trans. AIME, 1954, vol. 200, pp. 71–80.
I. Roy and F.A. Mohamed: unpublished data, University of California, Irvine, 2005.
F. Dalla Torre, H. Van Swygenhoven, and M. Victoria: Acta Mater., 2002, vol. 50, pp. 3957–70.
Y.M. Wang, A.V. Hamza, and E. Ma: Acta Mater., 2006, vol. 54, pp. 2715–26.
K.S. Kumar, H. Van Swygenhoven, and S. Suresh: Acta Mater., 2003, vol. 51, pp. 5743–74.
W.M. Yin, S.H. Whang, R. Mirshams, and C.H. Xiao: Mater. Sci. Eng., A, 2001, vol. 301A, pp. 18–22.
Y.J. Li, W. Blum, and F. Breutinger: Mater. Sci. Eng., A, 2004. vols. 387A–389A, pp. 585–89.
A.H. Chokshi, A. Rosen, J. Karch, and H. Gleiter: Scripta Metall., 1989, vol. 23, pp. 1679–83.
P.G. Sanders, J.A. Eastman, and J.R. Weertman: Acta Mater., 1997, vol. 45, pp. 4019–25.
F. Ebrahimi, G.R. Bourne, M.S. Kelly, and T.E. Matthews: Nanostruct. Mater., 1999, vol. 11, pp. 343–50.
H. Yang and F.A. Mohamed: Mater. Sci. Forum, 2009, vols. 633–634, pp. 411–20.
E.O. Hall: Proc. Phys. Soc., 1951, vol. B64, pp. 747–53.
N.J. Petch: J. Iron Steel Inst., 1953, vol. 174, pp. 25–28.
F.A. Mohamed: Metall. Mater. Trans. A, 2007, vol. 38A, pp. 340–47.
J. Schiøtz and K.W. Jacobsen: Science, 2003, vol. 301, pp. 1357–59.
R.L. Coble: J. Appl. Phys., 1963, vol. 34, pp. 1679–82.
J.E. Bird, A.K. Mukherjee, and J.E. Dorn: in Quantitative Relation between Properties and Microstructure, D.G. Brandon and A. Rosen, eds., Israel Universities Press, Jerusalem, 1969, pp. 255–342.
H.J. Frost and M.F. Ashby: Deformation-Mechanism Maps: The Plasticity and Creep of Metals and Ceramics, Pergamon Press, Oxford, United Kingdom, 1982. pp. 21–69.
R. Schwaiger, B. Moser, M. Dao, N. Chollacoop, and S. Suresh: Acta Mater., 2003, vol. 51, pp. 5159–72.
F.A. Mohamed: Scripta Metall., 1979, vol. 13, pp. 87–89.
F.A. Mohamed: Metall. Trans. A, 1977, vol. 8, pp. 933–38.
N. Wang, Z. Wang, K.T. Aust, and U. Erb: Acta Metall. Mater., 1995, vol. 43, pp. 519–28.
G. Palumbo, S.J. Thorpe, and K.T. Aust: Scripta Metall. Mater., 1990, vol. 24, pp. 1347–50.
H. Hahn and K.A. Padmanabhan: Philos. Mag. B, 1997, vol. 76B, pp. 559–71.
R.A. Masumura, P.M. Hazzledine, and C.S. Pande: Acta Mater., 1998, vol. 46, pp. 4527–34.
B. Burton: Diffusional Creep of Polycrystalline, Trans Tech Publications, Bay Village, OH, 1977, pp. 1–7.
T.G. Langdon and R.B.Vastava: in Mechanical Testing for Deformation Model Development: ASM STP 765, R.W. Rohde and J.C. Swearegen, eds., ASM, Metals Park, OH, 1982, pp. 435–51.
H. Van Swygenhoven and P.M. Derlet: Phys. Rev. B, 2001, vol. 64B, p. 224105-9.
H. Van Swygenhoven and A. Caro: Phys. Rev. B, 1998, vol. 58B, pp. 11246–11251.
H. Conrad and J. Narayan: Scripta Mater., 2000, vol. 42, pp. 1025–30.
G.J. Fan, H. Choo, P.K. Liaw, and E.J. Lavernia: Metall. Mater. Trans. A, 2005, vol. 36A, pp. 2641–49.
A.S. Argon and S. Yip: Philos. Mag. Lett., 2006, vol. 86, pp. 713–20.
F.A. Mohamed: Metall. Mater. Trans. A, 2007, vol. 39A, pp. 470–72.
D. Wolf, V. Yamakov, S.R. Phillpot, A.K. Mukherjee, and H. Gleiter: Acta Mater., 2005, vol. 53, pp. 1–40.
Y.J. Wei and L. Anand: J. Mech. Phys. Solids, 2004, vol. 52, pp. 2587–2616.
R.J. Asaro, P. Krysl, and D. Kad: Philos. Mag. Lett., 2003, vol. 83, pp. 733–43.
R.J. Asaro and S. Suresh: Acta Mater., 2005, vol. 53, pp. 3369–82.
Y. Xun and F.A. Mohamed: Philos. Mag. A, 2003, vol. 83A, pp. 2247–66.
Y. Xun and F.A. Mohamed: Acta Mater., 2004, vol. 52, pp. 4401–12.
Acknowledgments
This work was supported by National Science Foundation under Grant No. DMR-0702978. Thanks are due to Travis Van Den Vlekkert, an undergraduate student, for performing some of the calculations, and Shehreen Dheda and Khinlay Maung, FAM’s graduate students, for their assistance.
Open Access
This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
Author information
Authors and Affiliations
Corresponding author
Additional information
This article is based on a presentation given in the symposium entitled “Mechanical Behavior of Nanostructured Materials,” which occurred during the TMS Spring Meeting in San Francisco, CA, February 15–19, 2009, under the auspices of TMS, the TMS Electronic, Magnetic, and Photonic Materials Division, the TMS Materials Processing and Manufacturing Division, the TMS Structural Materials Division, the TMS Nanomechanical Materials Behavior Committee, the TMS Chemistry and Physics of Materials Committee, and the TMS/ASM Mechanical Behavior of Materials Committee.
Rights and permissions
Open Access This is an open access article distributed under the terms of the Creative Commons Attribution Noncommercial License (https://creativecommons.org/licenses/by-nc/2.0), which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
About this article
Cite this article
Mohamed, F.A., Yang, H. Deformation Mechanisms in Nanocrystalline Materials. Metall Mater Trans A 41, 823–837 (2010). https://doi.org/10.1007/s11661-009-0103-z
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11661-009-0103-z