Abstract
In view of single machine to infinite bus system with static synchronous compensator, which is affected by internal and external disturbances, a nonlinear adaptive robust controller is constructed based on the improved dynamic surface control method (IDSC). Compared with the conventional DSC, the sliding mode control is introduced to the dynamic surface design procedure, and the parameter update laws are designed using the uncertainty equivalence criterions. The IDSC method not only reduces the complexity of the controller but also greatly improves the system robustness, speed and accuracy. The derived controller cannot only attenuate the influences of external disturbances against system output, but also has strong robustness to system parameters variance because the damping coefficient is considered in the internal parameter uncertainty. Simulation result reveals that the designed controller can effectively improve the dynamic performances of the power system.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The static synchronous compensator (STATCOM) is one of the important flexible alternative current transmission systems (FACTS) devices and can be used for dynamic compensation of power systems to provide voltage support and stability improvement[1–3]. Over the past two decades, various kinds of linear controllers for STATCOM have been studied. The synthesized feedback controller was proposed to improve phase margin in inductive load[4], a linear quadratic regulator (LQR) control was proposed in [5], and the feedforward techniques and high gain full state feedback approach were used based on a linearization of the dq inverter model in [6]. But these linear feedback controllers cannot guarantee the uniform performance at all operating points. It is necessary to analyze the STATCOM system from the nonlinear control standpoint.
So far, some nonlinear controllers have been designed for STATCOM system, such as input-output feedback linearization[7–9]. The input-output feedback linearization method allows the reference tracking or regulating problems to be solved by linear output feedback controllers. However, although the stability and tracking performance of the system are ensured by feedback controller, the stability and transient behavior of internal dynamics cannot be guaranteed. In [10], the semi-global stability using Lya-punov stability method for the modified damping controller was proved. In [11–13], passivity-based control (PBC) was proposed and the effectiveness of the PBC methodology for STATCOM to achieve a robust performance was researched.
Based on the adaptive fuzzy sliding mode controller and the Nussbaum gain, a new power system stabilizer which enhances damping and improves transient dynamics of power system stabilizers was introduced in [14]. The Nussbaum gain was used to avoid the positive sign constraint and the problem of controllability of the system.
Although these existing nonlinear control methods are effective in some ways, one of the main problems of them is that the parameter uncertainty, unmodelled dynamic state and external disturbance have not been considered[15]. However, practical power systems are highly nonlinear, of large scale and multivariables, so they are inevitably subjected to the effects of external disturbances in the operation states, such as system faults, different hand operations and load variations. Besides, there are other general disturbances from different sources, for instance, the inaccurate description of system model, and errors of the controlled plant or the noise of measurement components. Therefore, it is a key point to tackle effectively these parameter uncertainties, unmodelled dynamic states and external disturbances in the controller design procedure.
In this paper, we extend the previous control methods for actual systems[16, 17]. Contribution made in this paper consists in an adaptive robust control scheme which incorporates the improved dynamic surface control method with disturbance attenuation techniques. Compared with the conventional backstepping and dynamic surface control (DSC)[18], for the single machine to infinite bus system (SMIB) with STATCOM including parametric uncertainties and exogenous disturbances, the sliding mode control is introduced into the dynamic surface design, and the parameters updated law is based on the uncertainty principle of equivalence[19]. As a result, the computation is reduced and system robustness is improved. In addition, the external disturbances are attenuated based on the Lyapunov stability theorem, and the robust stability and uniform ultimate boundedness are ensured for the controlled system. As the entire design process does not use any linearization processing, we can fully make use of the system nonlinearity to ensure the applicability of the proposed control law in the nonlinear systems. Further, simulation results are shown to verify the effectiveness of the proposed control law in an SMIB system.
The rest of the paper is organized as follows. Section 2 is devoted to the modelling of power system. The details of controller design and the main results are described in Section 3. Simulation studies are given in Section 4, and Section 5 concludes the work.
2 System model description
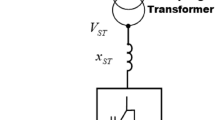
The configuration of an SMIB system equipped with a STATCOM is shown in Fig. 1.
In this system, the STATCOM is the parallel control which is based on power converter, and it is supposed that the components in it have no limitations of natural commutation and work as forced commutation. Then the STAT-COM could be modeled as a reactive flow resource, which could inject lead or lag current to the power system. If the mechanical input power of the generator is constant, then the generator is represented by the constant voltage source after transient reactance, and the STATCOM is described by a first-order inertial loop. The whole system model is expressed as follows.
where δ is the rotor angle of the generator, ω is the rotor speed of the generator, P m is the mechanical power of the prime motor, H is the inertial coefficient of the generator, T is the equivalent time constant of the STATCOM, D and E′ q are damping coefficient and transient EMF of generator q axis, respectively, X 1 is the reactance between the generator’s internal bus and STATCOM location bus, X 2 is the equivalent reactance between the middle bus and the infinite bus, V S is the infinite bus voltage, I q is the output reactive current of STATCOM, and u is the control input.
For system (1), we redefine the state variables as \({x_1} = \delta - {\delta _0},{x_2} = \omega - {\omega _0},{x_3} = {I_q} - {I_{q0}}\), where δ 0, ω 0, I q 0 are the initial values of corresponding variables. Then system (1) is rewritten as
Define \({k_1} = {{{\omega _0}} \over H},\,{k_2} = {{{\omega _0}{{E^{\prime}}_q}{V_S}} \over {H({X_1} + {X_2})}}\), and assume they are known constants. If D is an unknown constant parameter, then \({\theta _2} = - {D \over H}\) is also an unknown parameter.
Define a known nonlinear function as
We also consider the external disturbance w = [w 1 w 2]T, which is unknown bounded. Then system (2) is transformed into
At the same time, the following assumptions are made for system (3).
-
Assumption 1. x i ,(i = 1, ⋯, 3) is both measurable and bounded.
-
Assumption 2. w i ∈ R and satisfies w i ⩽ a i , where a i is a known positive constant, i = 1, 2.
-
Assumption 3. The reference trajectory x 1d and its first- and second-order derivatives are known and bounded.
For system (3) with parameter uncertainty and external disturbances, we can use the IDSC method to design the nonlinear robust controller. The control object is to construct a control law u such that the output y = x 1 of the controlled system tracks the reference trajectory x 1d , and the tracking error ∣x − x 1d ∣ converges to a small neighborhood of zero.
3 Design of nonlinear adaptive robust controller
For system (3), we first define the surface error as
where x 1d is the reference trajectory, x id (i = 2, 3) will be given later on by the first-order filter.
Define the boundary layer errors as
where \(x_{i + 1}^* (i = 1,2)\) is the stabilizing function which will also be designed later on.
Now we shall show a new dynamic surface control procedure of the robust adaptive controller for the system defined in (3).
Step 1. For the first subsystem of (3), viewing x 2 as the virtual control, we have
We select the first virtual stabilizing function as
where c 1 is a positive design constant. Substituting (7) into (6) yields
Let \(x_2^*\) be an input and pass through a first-order filter as
where τ 2 is a given time constant, and \({x_{2d}}(0) = x_2^* (0)\).
Step 2. For the second subsystem of (3), viewing x 3 as the virtual control, we have
where \(\hat \theta\) is the parameter estimation of θ, and z is the parameter estimation errors which is given by
Select the second virtual stabilizing function
where c 2, γ2 are positive design constants, and the adaptive law to the uncertain parameter is selected as follows based on the uncertainty equivalence criterion.
Therefore, the dynamics of the estimation error is
Substituting (11) and (12) into (10) yields
Let \(x_3^*\) be an input and pass through a first-order filter as
where τ 3 is a given time constant, and \({x_{3d}}(0) = x_3^* (0)\).
Step 3. For the third subsystem of (3), in light of (4), we have
Define the sliding mode s = d 1 e 1 + d 2 e 2 + e 3 = 0 which satisfies the asymptotic reaching condition, where d 1 and d 2 are positive design constants, and define the Lyapunov function of the whole system as
where ε >0 is a design constant. The time derivative of V is
Noting that (10) and \({\dot x_{(i + 1)d}} = {{x_{i + 1}^* - {x_{(i + 1)d}}} \over {{\tau _{i + 1}}}}\), we can get
From (7), we have \(\dot x_2^* = - {c_1}{\dot e_1} + {\ddot x_{1d}}\) based on Assumptions 1–3, we know \({D_2}\) is also bounded, i.e., there exists a positive constant D 2 such that sup \(|\dot x_2^* |\leqslant{D_2}\).
Besides, we can get from (12)
So \(\dot x_3^*\) can be written as the function form, i.e., \(\dot x_3^* = f({x_1},{\dot x_1},{\dot x_2},\hat \theta, {x_{2d}})\). By using Assumptions 1–3 and noting the system model (3), we can know that all the variables in \(\dot x_3^*\) are bounded, and there exists a positive constant D 3 such that sup \(|\dot x_3^* |\leqslant{D_3}\).
Then we have
Select the real control input u as
where β 1, β 2 and γ 3 are positive design constants. Substituting (22) into (17) yields
In the new coordinates defined by (6)–(23), we have an important theorem as follows.
Theorem 1. For the nonlinear systems (3) in the parameter feedback form with parameter uncertainty and external disturbances, the closed-loop error system will be globally and uniformly ultimately bounded if we apply the robust adaptive control law (22), the stabilizing functions (7), (12) and the parameter adaptive laws (13). Furthermore, given any constant \(e(t)\leqslant{\mu ^*}\), there exists T such that e(t) ⩽ µ * for all t ⩾ T.
Proof. The time derivative of V gives
where σ > 0 is a design constant, and g(x 1) = k 2 sin(δ 0 + x 1)f(x 1).
It follows that
where \({m_1} = - {\beta _1}d_1^2 + {\beta _1}{d_1}{d_2} + {\beta _1}{d_1},{m_2} = - {\beta _1}d_1^2 + 2{\beta _1}{d_1}{d_2} + {\beta _1}{d_1}\), and \({m_3} = - {\beta _1} + {\beta _1}{d_1} + {\beta _1}{d_2}\).
In the normal operation of power system, g(x 1) and w i are bounded, then we can suppose \(|g({x_1})|\leqslant{G_{\max }},|{w_i}|\leqslant{w_{\max }}\), and select \(\gamma = \max \{ \sqrt {\gamma _2^2 + {\textstyle{\varepsilon \over 2}}}, {\gamma _3}\}\). Then we get
Select \({c_1} > {m_1},{c_2} > {1 \over 2} + {m_2} + {G_{\max }},{m_3} + {{{G_{\max }}} \over 2} < 0,{\beta _2} > 0,\varepsilon > 1,{1 \over {{\tau _2}}} > {\sigma \over 2},{1 \over {{\tau _3}}} > {\sigma \over 2} + {{{G_{{\rm{max}}}}} \over 2},{a_0} = \min \left\{ {{c_i},{\beta _i},\varepsilon, {1 \over {{\tau _{i + 1}}}}} \right\}\), and \({b_0} = 2{\gamma ^2}d_{\max }^2 + \sum\nolimits_{i = 2}^n {{{D_i^2} \over {2\sigma }}}\). Then we have
If \(||E|| > \sqrt {{\textstyle{{{b_0}} \over {{a_0}}}}}\) and \(||Y|| > \sqrt {{\textstyle{{{b_0}} \over {{a_0}}}}}\), then \(\dot V\leqslant 0\) where E = [e 1, e 2, e 3]T and Y = [y 2, y 3]T. So the system errors are uniformly ultimately bounded. □
Remark 1. The above inequality guarantees that e i will converge to \({\textstyle{{{b_0}} \over {{a_0}}}}\) in an exponential rate, and when the external disturbances w i disappear, the whole system will still be globally uniformly ultimately bounded.
Remark 2. For the selection of designed constants, it seems that the value of G max needs to be decided. But in fact, this is not completely such. When the control gain g(x 1) is constant, we can know the real value of G max definitely. When g(x 1) is a bounded function, we only set c i and \({1 \over {{\tau _i}}}\) large enough to guarantee the stability and some performance of system by trial and error.
4 Simulation results
In this section, we simulate the closed-loop system under the designed controller. The used system parameters are in the following: H = 8, \(E_q^{\prime} = 1\), V s = 1, X 1 = 0.6, X 2 = 0.4, \({\delta _0} = {\pi \over 3}\), and ω 0 = 314.159 rad/s.
The relevant design parameters are taken as follows: d 1 = 0.6, d 2 = 0.1, d 3 = 2, β 1 = 80, β 2 = 2, c 1 = 2, c 2 = 30, ε = 4, σ = 10, γ = 0.2, and τ 2 = τ 3 = 0.01.
The closed-loop system is simulated in two cases: small-signal stability and large-disturbances stability.
Case 1. Small-signal stability.
The simulation results are shown in Figs. 2–4.
From the responding curves of the system states, we can see that the system has very good convergence performance though it is subjected to the influence of external disturbances and parameter uncertainty. The states of the closed loop system go into the steady states in no more than 0.5 seconds.
At the same time, the parameter estimation is also convergent to steady state, just like what the response curve depicted in Fig. 4. Thus, all of these do verify the conclusion of Theorem 1.
Case 2. Large-disturbances stability.
The system is in a pre-fault steady-state. Suppose that a symmetrical three-phase short-circuit fault occurs at the outlet of the transformer at t = 0.2 s. In order to show the effectiveness of the proposed IDSC controller, we compare it with the adaptive backstepping controller under the same initial condition and system parameters.
The corresponding results are shown in Figs. 5 and 6.
One can see that the rotor angle for the proposed IDSC in this paper approaches to the required operation points more quickly than the case of backstepping control, and that the local oscillation amplitudes of power angle and relative bus voltage under the IDSC are smaller. The simulation results show that the IDSC controller enhances the rotor angle and voltage stability in the presence of the fault.
5 Conclusions
A novel adaptive control strategy is presented in this paper based on the perturbed nonlinear mathematic model using the IDSC. The parameter uncertainty and the external disturbances are considered comprehensively, and finally the uniformly ultimately bounded is achieved. Compared with the conventional backstepping methods, this approach reduces the requirements of the controlled systems, such as matching condition and so on, while the robustness to model errors and external disturbances and the adaptability to uncertain parameters are reserved. Based on this approach, the robust adaptive controller has been designed and simulation studies are conducted. Simulation results demonstrate that the suggested controller can effectively improve the dynamic performances of the power systems.
References
S. Mori, K. Matsuno, T. Hasegawa, S. Ohnishi, M. Takeda, M. Seto, S. Murakami, F. Ishiguro. Development of a large static VAr generator using self-commutated inverters for improving power system stability. IEEE Transactions on Power Systems, vol. 8, no. 1, pp. 371–377, 1993.
C. Schauder, M. Gernhardt, E. Stacey, T. Lemak, L. Gyugyi, T. W. Cease, A. Edris. Operation of ± 100 MVAR TVA STATCOM. IEEE Transactions on Power Delivery, vol. 12, no. 4, pp. 1805–1811, 1997.
C. Schauder, H. Mehta. Vector analysis and control of advanced static VAR compensators. IEE Proceedings C: Generation, Transmission and Distribution, vol. 140, no. 4, pp. 299–306, 1993.
P. Rao, M. Crow, Z. Yang. STATCOM control for power system voltage control applications. IEEE Transactions on Power Delivery, vol. 15, no. 4, pp. 1311–1317, 2000.
P. W. Lehn, M. R. Iravani. Experimental evaluation of STATCOM closed loop dynamics. IEEE Transactions Power Delivery, vol. 13, no. 4, pp. 1378–1384, 1998.
P. Petitclair, S. Bacha, J. P. Ferrieux. Optimized linearization via feedback control law for a STATCOM. In Proceedings of the 32nd IAS Annual Meeting Conference Record of the 1997 Industry Applications Conference, IEEE, New Orleans, LA, USA, pp. 880–885, 1997.
T. S. Lee. Input-output linearization and zero dynamics control of three-phase AC/DC voltage source converters. IEEE Transactions Power Electronics, vol. 18, no. 1, pp. 11–22, 2003.
Y. S. Han, Y. O. Lee, C. C. Chung. A modified nonlinear damping of zero-dynamics via feedback control for a STATCOM. In Proceedings of IEEE Bucharest Power Tech Conference, IEEE, Bucharest, Romania, pp. 1–8, 2009.
Y. O. Lee, Y. S. Han, C. C. Chung. Output tracking control with enhanced damping of internal dynamics and its output boundedness. In Proceedings of the 49th IEEE Conference on Decision and Control, IEEE, Atlanta, USA, pp. 3964–3971, 2010.
H. Sira-Ramirez, R. A. Perez-Moreno, R. Ortega, M. Garcia-Esteban. Passivity-based controllers for the stabilization of DC-to-DC power converters. Automatica, vol. 33, no. 4, pp. 499–513, 1997.
G. E. Valderrama, P. Mattavelli, A. M. Stankovic. Reactive power and imbalance compensation using STATCOM with dissipativity-based control. IEEE Transactions on Control Systems Technology, vol. 9, no. 5, pp. 718–727, 2001.
T. S. Lee. Lagrangian modeling and passivity based control of three-phase AC/DC voltage-source converters. IEEE Transactions on Industrial Electronics, vol. 51, no. 4, pp. 892–902, 2004.
H. C. Tsai, C. C. Chu, S. H. Lee. Passivity-based nonlinear STATCOM controller design for improving transient stability of power systems. In Proceedings of IEEE/PES Transmission and Distribution Conference and Exhibition, IEEE, Dalian, China, pp. 1–5, 2005.
E. Nechadi, M. N. Harmas, N. Essounbouli, A. Hamzaoui. Adaptive fuzzy sliding mode power system stabilizer using Nussbaum gain. International Journal of Automation and Computing, vol. 10, no. 4, pp. 281–287, 2013.
F. Ding. System Identification — New Theory and Methods, Beijing: Science Press, 2013. (in Chinese)
W. L. Li, T. Lan, W.X. Lin.Nonlinear adaptive robust governor control for turbine generator. In Proceedings of the 8th IEEE International Conference on Control and Automation (ICCA 2010), IEEE, Xiamen, China, pp. 820–825, 2010.
W. Anna, S. Roman. Nonlinear backstepping ship course controller. International Journal of Automation and Computing, vol. 6, no. 3, pp. 277–284, 2009.
X. Y. Luo, Z. H. Zhu, X. P. Guan. Adaptive fuzzy dynamic surface control for uncertain nonlinear systems. International Journal of Automation and Computing, vol. 6, no. 4, pp. 385–390, 2009.
D. Karagiannis, A. Astolfi. Nonlinear adaptive control of systems in feedback form: An alternative to adaptive back-stepping. Systems & itControl Letters, vol. 57, no. 9, pp. 733–739, 2008.
Acknowledgements
The authors are grateful to anonymous referees for their constructive comments on this paper.
Author information
Authors and Affiliations
Corresponding author
Additional information
This work was supported by K. C. Wong Magna Fund in Ningbo University, Pivot Research Team in Scientific and Technical Innovative of Zhejiang Province (Nos. 2010R50004 and 2012R10004-03), Natural Science Foundation of Ningbo City (Nos. 2012A610005 and 201401A61009).
Rights and permissions
About this article
Cite this article
Li, WL., Li, MM. Nonlinear Adaptive Robust Control Design for Static Synchronous Compensator Based on Improved Dynamic Surface Method. Int. J. Autom. Comput. 11, 334–339 (2014). https://doi.org/10.1007/s11633-014-0797-2
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11633-014-0797-2