Tracking Control Design for Nonholonomic Mechanical Systems with Affine Constraints

Abstract

The trajectory tracking control is considered for nonholonomic mechanical systems with affine constraints and dynamic friction. A new state transformation is proposed to deal with affine constraints, and then an integral feedback compensation strategy is used to identify the dynamic friction. The proposed controller ensures that the output tracking errors converge to zero as t → ∞. As an application, a detailed example is presented to illustrate the effectiveness of the control scheme.

1 Introduction

Nonholonomic constraints arise in many mechanical systems when there is a rolling or sliding contact, such as wheeled mobile robots, n-trailer systems, space robots, underwater vehicles, multi-fingered robotic hands and so on. Control of these systems has received considerable attention[1–7] due to the demand for control of the above referred systems.

The tracking problem for nonholonomic systems, as a much more interesting issue in practice, is to make the state of the closed-loop system track a given desired trajectory. For example, Wang et al.[8] presented an adaptive robust control strategy for a class of mechanical systems with both holonomic and nonholonomic constraints. Based on physical properties, adaptive robust motion/force control for wheeled inverted pendulums is investigated in [9]. For mobile manipulators under both holonomic and non-holonomic constraints, the authors of [10] and [11] proposed state-feedback control strategies by introducing an appropriate state transformation, and adaptive robust outputfeedback force/motion control strategies, respectively. It is worth pointing out that tracking control of nonholonomic systems with linear constraints $(J(q)\dot q = 0)$ has been widely studied[8–14] to date. In fact, there is another large class of constraints which are affine in velocities, called affine constraints[15–17] $(J(q)\dot q = A(q))$, such as a boat on a running river with the varying stream, ball on rotating table with invariable angular velocity, under-actuated mechanical arm, etc. Kai[15] defined rheonomous affine constraints and explained a geometric representation method for them, then derived a necessary and sufficient condition for completing nonholonomicity of the rheonomous affine constraints. In [16], Kai et al. derived very good results about nonholonomic dynamic systems with affine constraints. To be specific, he got several preliminary properties of this system, investigated local accessibility and local controllability based on both Sussmann’s theorem and linear approximation approaches, and derived conditions for local asymptotic stabilizability by linear state feedback and nonlinear smooth state feedback at last. However, tracking control for such systems has not been investigated until now. Hence, researching tracking control for such mechanical systems is an innovatory and significative work.

A new continuous control mechanism compensated for uncertainty in a class of high-order, multiple-input multiple output nonlinear systems, was presented in [18]. Based on this control strategy, Makkar et al. considered modeling and compensation for parameterizable friction effects for a class of mechanical systems in [19]. In [20], Patre et al. developed a novel adaptive nonlinear control design which achieves modularity between the controller and the adaptive update law. Based on this compensatory strategy for the uncertainties and the asymptotic tracking idea for uncertain multi-input nonlinear systems, the trajectory tracking control for nonholonomic mechanical systems with affine constraints and dynamic friction is considered in this paper.

The rest of this paper is organized as follows. System description and control design are given in Section 2. Section 3 addresses the main results. For the application, a practical example is considered in Section 4. Section 5 gives some concluding remarks.

Notations. ∥x∥ denotes the Euclidean norm of x; sgn(·) denotes the standard signum function; we say that $x(t) \in {\mathcal{L}_\infty }$ when $||x|{|_\infty } \triangleq \over = {\sup _{t\geqslant 0}}|x(t)|$ exists; a continuous function h : R ⁺ − R ⁺ is said to be a $\mathcal{K}$ function if it is strictly increasing and vanishes at zero. For simplicity, sometimes the arguments of functions are dropped.

2 System description and control design

2.1 Dynamics model

In this paper, we consider a class of nonholonomic mechanical systems described by Euler-Lagrangian equation:

$$M(q)\ddot q + V(q,\dot q)\dot q + G(q) + F(q,\dot q) = \tau + f$$

(1)

where q = [q ₁, ⋯,q _n ]^T ∈ R ⁿ is the generalized coordinates, and $\dot q,\ddot q \in {{\bf{R}}^n}$ represent the generalized velocity vector and acceleration vector, respectively; M (q) ∈ R ^n×n is the inertia matrix; $V(q,\dot q)\dot q \in {{\bf{R}}^n}$ presents the centripetal, Coriolis forces; G(q) ∈ R ⁿ represents the gravitational force; $F(q,\dot q) \in {{\bf{R}}^n}$ represents the friction force; T ∈ R ⁿ is the vector of control input; f = J(q)λ ∈ R ⁿ denotes the vector of constraint force, where J (q) ∈ R ^n×m is constraint matrix, and λ ∈ R ^m is Lagrangian multiplier corresponding to m nonholonomic affine constraints which are represented by analytical relations between the generalized coordinates q and velocity vectors $\dot q$, and can be written as:

$${J^{\rm{T}}}(q)\dot q = A(q)$$

(2)

where J (q) = [j1(q), ⋯,j _m (q)] ∈ R ^n×m is of full rank, and A(q) = [a ₁ (q), ⋯,a _m (q)]^T ∈ R ^m is a known vector function.

Remark 1. It is worth emphasizing that the system studied in this paper is more general than that in some existing literatures such as [9, 12, 14], where dynamic equation satisfies the classical linear constraint. In fact, by taking A(q) = 0, (2) transforms to linear constraints, whose tracking problem has received considerable attention.

The subsequent development is based on the assumption that $M(q),V(q,\dot q),G(q)$ are known and bounded if their elements are all bounded. Moreover, in order to facilitate the subsequent design and analysis, the following assumptions will be exploited:

Assumption 1. If q and $\dot q$ are bounded, the inertia matrix M(q) satisfies ${{\partial M(q)} \over {\partial q}} \in {{\cal L}_\infty }$.

Assumption 2. The dynamic friction term $F(q,\dot q)$ satisfies $F(q,\dot q) \in {\mathcal{L}_\infty },\dot F(q,\dot q) \in {\mathcal{L}_\infty },\ddot F(q,\dot q) \in {\mathcal{L}_\infty }$, if their elements are bounded.

2.2 State transformation

This part mainly focuses on reducing the number of state variables which provide motion complying with the affine constraints.

It is easy to find a full-rank matrix S(q) ∈ R ^n×(^n−m) satisfying

$${J^{\rm{T}}}(q)S(q) = 0.$$

(3)

Define ξ(t) = [q,−t]^T, then(2) can be expressed concisely as

$$\left[ {{J^{\rm{T}}}(q)\quad A(q)} \right]\dot \xi (t) = 0.$$

(4)

Let

$$E(q) = \left[ {\matrix{{S(q)} \hfill & {\eta (q)} \hfill \cr 0 \hfill & { - 1} \hfill \cr } } \right] \in {{\bf{R}}^{(n + 1) \times (n - m + 1)}}$$

where η(q) ∈ R ⁿ satisfies J ^T(q)η(q) = A(q). One can deduce that E is a full-rank matrix and satisfies

$$\left[ {{J^{\rm{T}}}(q)\quad A(q)} \right]E(q) = 0.$$

(5)

From (4) and (5), we know that there exists a (n−m + 1)-dimensional vector $\dot \bar z = {[\dot \bar z_{n - m}^{\rm{T}},{\dot \bar z_{n - m + 1}}]^{\rm{T}}}$ such that $\dot \xi = E\dot \bar z$ that is

$$\left[ {\matrix{{\dot q} \hfill \cr { - 1} \hfill \cr } } \right] = \left[ {\matrix{{S(q)} \hfill & {\eta (q)} \hfill \cr 0 \hfill & { - 1} \hfill \cr } } \right]\left[ {\matrix{{\dot \bar z_{n - m}^{\rm{T}}} \hfill \cr {{{\dot \bar z}_{n - m + 1}}} \hfill \cr } } \right]$$

(6)

which implies ${\dot \bar z_{n - m + 1}} = 1$ For convenience, define $z \triangleq \Delta \over = {\bar z_{n - m}} \in {{\bf{R}}^{n - m}}$. In view of the relationship (6), the generalized velocity vectors can be written as

$$\dot q = S(q)\dot z + \eta (q).$$

(7)

It is clear that z corresponds to the internal state variable.

Substituting (7) into (1), pre-multiplying S ^T(q) on both sides of it, and using J ^T(q)S(q) = 0, the dynamics of the mechanical system made up by (1) and (2) can be described clearly as

$${M_1}(q)\ddot z + {V_1}(q,\dot q)\dot z + {G_1}(q,\dot q) + {F_1}(q,\dot q) = {\tau _1}$$

(8)

where ${M_1}(q) = {S^{\rm{T}}}(q)M(q)S(q),\quad {V_1}(q,\dot q) = {S^{\rm{T}}}(q)\left( {M(q)\dot S(q) + V(q,\dot q)S(q)} \right),\,\,{G_1}(q,\dot q) = {S^{\rm{T}}}(q)\left( {M(q)\dot \eta (q) + V(q,\dot q)\eta (q) + G(q)} \right),\,\,{\tau _1} = {S^{\rm{T}}}(q)\tau, \,\,{F_1}(q,\dot q) = {S^{\rm{T}}}(q)F(q,\dot q)$.

Property 1[21]. The matrix M ₁ is symmetric and satisfies

$$a||x|{|^2}\leqslant{x^{\rm{T}}}{M_1}(x)x\leqslant\bar a(||x||)||x|{|^2}$$

where a is a known positive constant, ā(x) is a known positive function.

Remark 2. The above transformations consist of (3) and (7) ensure that the transformed system (8) still satisfies constraint equation (2), and possesses the practical physical meaning, for further detail, see [8, 9]. This can also be confirmed by the practical example in Section 4.

Remark 3. The aforementioned transform method differs from the traditional ones in [8–11]. More specifically, when the affine constraints are imposed on the mechanical system, it is difficult to find linearly independent vector fields to proceed with a simple diffeomorphism transformation for canceling the constraint forces in dynamic equations. Hence, we present the aforementioned transform to achieve this goal.

2.3 Control design

The control objective of this paper can be specified as follows. Given the desired trajectories z _d (t) and ${\dot z_d}(t)$ which are assumed to be bounded and should satisfy constraint (2). In addition, ${\ddot z_d}(t)$ and are assumed to exist and be bounded. We determine a control law such that the internal state z(t) and $\dot z(t)$ are globally bounded and the output tracking error

$${e_1}(t) = {z_d}(t) - z(t).$$

(9)

And its time derivative ${\dot e_1}(t)$ converges to zero.

To achieve the desired control objective, the following filtered tracking errors[19, 20] are defined as

$$\left\{ {\matrix{{{e_2}(t) = {{\dot e}_1}(t) + {\alpha _1}{e_1}(t)} \hfill \cr {\rho (t) = {{\dot e}_2}(t) + {\alpha _2}{e_2}(t)} \hfill \cr } } \right.$$

(10)

where e ₂(t),ρ(t) ∈ R ^n–m, and α ₁ > 0, α ₂ > 0 are design constants. The filtered tracking error ρ(t) is not measurable because its expression depends on $\ddot z(t)$. In view of (8) and (9), pre-multiplying (10) by M ₁, the following expression can be obtained

$$\matrix{{{M_1}(q)\rho (t) = {M_1}(q){{\ddot z}_d}(t) + {V_1}(q,\dot q)\dot z(t) + } \hfill \cr {{G_1}(q,\dot q) + {F_1}(q,\dot q) - {\tau _1} + } \hfill \cr {{\alpha _1}{M_1}(q){{\dot e}_1}(t) + {\alpha _2}{M_1}{e_2}(t).} \hfill \cr }$$

(11)

Based on (11), the control torque input is designed as

$$\matrix{{{\tau _1} = {M_1}(q){{\ddot z}_d}(t) + {V_1}(q,\dot q)\dot z(t) + {G_1}(q,\dot q) + } \hfill \cr {{\alpha _1}{M_1}(q){{\dot e}_1}(t) + {\alpha _2}{M_1}{e_2}(t) + u(t)} \hfill \cr }$$

(12)

where u(t) ∈ R ^n−m denotes a subsequently designed control term. Substituting (12) into (11), one can get

$${M_1}(q)\rho (t) = {F_1}(q,\dot q) - u(t).$$

(13)

It is evident that if ρ(t) → 0, then u(t) will identify the friction model ${F_1}(q,\dot q)$. Hence, the next objective is to design the control term u(t) to ensure ρ → 0. To facilitate the design of u(t), differentiating (13) yields:

$${M_1}(q)\dot \rho (t) = {\dot F_1}(q,\dot q) - \dot u(t) - {\dot M_1}(q)\rho (t).$$

(14)

Similar to [19], u(t) is designed as

$$\matrix{{u(t) = ({k_s} + 1){e_2}(t) - ({k_s} + 1){e_2}(0) + } \hfill \cr {\int_0^t ( ({k_s} + 1){\alpha _2}{e_2}(\tau ) + \beta {\rm{sgn}}({e_2}(\tau ))){\rm{d}}\tau } \hfill \cr }$$

(15)

where k _s ∈ R is control gain, and β ∈ R is a positive constant which will be specified later. u(t) expressed in (15) does not depend on the unmeasurable filtered tracking error term ρ, but its time derivative of u(t) can be expressed as a function of ρ(t). Taking the time derivative of (15), one can get

$$\dot u(t) = ({k_s} + 1)\rho (t) + \beta {\rm{sgn}}({e_2}(t)).$$

(16)

Substituting (16) into (14), the following closed-loop error system can be obtained:

$$\matrix{{{M_1}(q)\dot \rho (t) = - {1 \over 2}{{\dot M}_1}(q)\rho (t) - ({k_s} + 1)\rho (t) - {e_2}(t) - } \hfill \cr {\beta {\rm{sgn}}({e_2}(t)) + \Theta (q,\dot q,t)} \hfill \cr }$$

(17)

where $\Theta (q,\dot q,t) = {\dot F_1}(q,\dot q) - {\textstyle{1 \over 2}}{\dot M_1}(q)\rho (t) + {e_2}(t)$. We define

$${\Theta _d} = {{\partial {F_1}({z_d},{{\dot z}_d})} \over {\partial {z_d}}}{\dot z_d}(t) + {{\partial {F_1}({z_d},{{\dot z}_d})} \over {\partial {{\dot z}_d}}}{\ddot z_d}(t).$$

In view of Assumption 2 and Remark 1, it is noted that ${\dot z_d},{\ddot z_d}$ and are all bounded. Hence, one can find known positive constants B ₁ and B ₂, such that

$$||{\Theta _d}||\leqslant {B_1},\quad ||{\dot \Theta _d}||\leqslant {B_2}.$$

Define $\tilde \Theta (t) = \Theta (t) - {\Theta _d}(t)$, then the closed-loop error system (17) can be rewritten as

$$\matrix{{{M_1}(q)\dot \rho (t) = - {1 \over 2}{{\dot M}_1}(q)\rho (t) - ({k_s} + 1)\rho (t) - {e_2}(t) - } \hfill \cr {\beta {\rm{sgn}}({e_2}(t)) + \tilde \Theta (t) + {\Theta _d}(t).} \hfill \cr }$$

(18)

3 Main results

Now, we are ready to present the following theorem, which summarizes the main results of the paper.

Theorem 1. Consider the nonholonomic mechanical system described by (1) and (2), subject to Assumptions 1 and 2, if we select parameter β satisfying $\beta > {B_1} + {1 \over {{\alpha _2}}}{B_2}$ then the controller given in (12) and (15) ensure that all the signals of closed-loop system are bounded and the tracking errors ${e_1}(t),{\dot e_1}(t) \rightarrow 0$.

Proof. Let D ∈ R ^3(n−m)+1 be a domain containing y(t) = 0, where y(t) ∈ R ^3(n−m)+¹ is defined as $y(t) = {[{x^{\rm{T}}}(t),\,\sqrt {P(t)} ]^{\rm{T}}},\,\,x(t) \in {{\bf{R}}^{3(n - m)}}$ is defined as $x(t) = {[e_1^{\rm{T}}(t),\,e_2^{\rm{T}}(t),\,{\rho ^{\rm{T}}}(t)]^{\rm{T}}}$, and the function P(t) ∈ R is defined as

$$P(t) = \beta ||{e_2}(0)|| - {e_2}{(0)^{\rm{T}}}{\Theta _d}(0) - \int_0^t L (\tau ){\rm{d}}\tau $$

where the auxiliary function L(t) is defined as

$$L(t) = {\rho ^{\rm{T}}}\left( {{\Theta _d}(t) - \beta {\rm{sgn}}({e_2}(t))} \right).$$

Then, if $\beta > {B_1} + {\textstyle{1 \over {{\alpha _2}}}}{B_2}$, with manipulations similar to Appendix A in [18], the following inequality can be obtained

$$\int_0^t L (\tau ){\rm{d}}\tau \leqslant \beta ||{e_2}(0)|| - {e_2}{(0)^{\rm{T}}}{\Theta _d}(0).$$

Hence, one can deduce P (t) ⩾ 0.

Choose a candidate Lyapunov function[19, 20] as

$$\matrix{{V(t) = e_1^{\rm{T}}(t){e_1}(t) + {1 \over 2}e_2^{\rm{T}}(t){e_2}(t) + } \hfill \cr {{1 \over 2}{\rho ^{\rm{T}}}(t){M_1}(q)\rho (t) + P(t).} \hfill \cr }$$

(19)

Taking the time derivative of V (t) along the solutions of (8), and substituting (9), (10) and (18) into it, we have

$$\matrix{{\dot V(t) = 2e_1^{\rm{T}}(t){{\dot e}_1}(t) + e_2^{\rm{T}}(t){{\dot e}_2}(t) + {\rho ^{\rm{T}}}(t){M_1}(q)\dot \rho (t) + } \hfill \cr {{1 \over 2}{\rho ^{\rm{T}}}(t){{\dot M}_1}(q)\rho (t) + \dot P(t) \leqslant } \hfill \cr { - 2{\alpha _1}||{e_1}(t)|{|^2} - {\alpha _2}||{e_2}(t)|{|^2} - ({k_s} + 1)||\rho (t)|{|^2} + } \hfill \cr {2e_1^{\rm{T}}(t){e_2}(t) + {\rho ^{\rm{T}}}(t)\tilde \Theta.} \hfill \cr }$$

(20)

Since Θ is continuously differentiable, according to the mean value theorem, we can get the upper bound of $\tilde \Theta$ as follows[18]:

$$||\tilde \Theta ||\leqslant\varphi (||x(t)||)||x(t)||$$

where φ(∥x(t)∥) is an appropriate $\mathcal{K}$ function. In view of $2e_1^{\rm{T}}(t){e_2}(t)\leqslant||{e_1}(t)|{|^2} + ||{e_2}(t)|{|^2},\dot V(t)$ can be simplified as

$$\dot V(t) - \lambda ||x(t)|{|^2} - \left( {{k_s}||\rho (t)|{|^2} - \varphi (||x(t)||)||\rho (t)||||x(t)||} \right)$$

where λ = min{2α ₁ − 1,α ₂ − 1, 1}, and α ₁,α ₂ satisfy α1 > ½, α ₂ > 1.

Completing the squares for third term in above inequality, one can easily get

$$\varphi (||x(t)||)||\rho (t)||||x(t)||\leqslant{k_s}||\rho (t)|{|^2} + {{{\varphi ^2}(||x(t)||)||x(t)|{|^2}} \over {4{k_s}}}.$$

With this inequality in mind, inequality (20) reduces to

$$\dot V(t)\leqslant - \lambda ||x(t)|{|^2} + {{{\varphi ^2}(||x(t)||)||x(t)|{|^2}} \over {4{k_s}}}.$$

(21)

Now we define a compact set:

$${N_1} = \left\{ {y(t) \in {{\bf{R}}^{3(n - m) + 1}}|||y(t)||\leqslant{\varphi ^{ - 1}}\left( {2\sqrt {\lambda {k_s}} } \right)} \right\}.$$

The inequality (21) can be used to show that V (t) ⩽ Vn N ₁, hence, all the the signals e ₁(t), e ₂(t), ρ(t) on the right-hand side of function (19) are bounded in N₁. From the definition of e ₁(t), e ₂(t) and ρ(t), we can further get ${\dot e_1}(t),{\dot e_2}(t) \in {\mathcal{L}_\infty }$ in N ₁. The assumption that ${z_d}(t),{\dot z_d}(t),{\ddot z_d}(t)$ are bounded can be used to conclude that $z(t),\dot z(t),\ddot z(t) \in {\mathcal{L}_\infty }$ are in N ₁. We know ${M_1}(q),{V_1}(q,\dot q),{G_1}(q)$ are all bounded in N ₁. Hence, ${\tau _1} \in {\mathcal{L}_\infty }$ is in N ₁.

Now, let N ₂ ⊂ N ₁ denote a set defined as follows:

$${N_2} = \left\{ {y(t) \subset {N_1}|{\delta _2}(y(t))||y(t)|{|^2} < {\delta _1}{{\left( {{\varphi ^{ - 1}}(2\sqrt {\lambda {k_s}} )} \right)}^2}} \right\}$$

where δ ₁ = ½min{l, a}, δ ₂(y(t)) = max{1, ½ā(y(t))}, and the definition of a and ā(y(t)) have been given in Property 1. From (21), one can obtain that there must exist a positive function U(y(t)) = c∥x(t)∥², such that

$$V(t)\leqslant - U(y(t)).$$

Invariance-like Theorem[22] can be used to show that

$$U(y(t)) = c||x(t)|{|^2} \rightarrow 0,\quad t \rightarrow \infty, \quad \forall y(0) \in {N_2}.$$

Based on the definitions of x(t), one has e ₁(t), e ₂(t) → 0 as t →∞, ∀y(0) ∈ N ₂. From (10), we finally get ${\dot e_1}(t) \rightarrow 0$ as t → ∞, ∀y(0) ∈ N ₂. □

4 Simulation

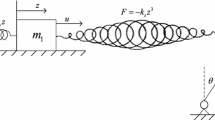
Consider a boat with payload on a running river [17] (see Fig. 1). The x-axis and y-axis denote the transverse direction and the downstream direction of the river, respectively. Here, we suppose the stream of the river only depends on transverse position x in the simulation. According to the motion of boat on the river, one can get the following kinematic equations:

$$\left\{ {\matrix{{\dot x = V\cos \theta - C(x)\cos \theta \sin \theta } \hfill \cr {\dot y = V\sin \theta + C(x){{\cos }^2}\theta } \hfill \cr } } \right.$$

where C(x) denotes the stream of the river. After some simple calculations, the affine constraints can be obtained as

$$\dot y\cos \theta - \dot x\sin \theta = C(x)\cos \theta $$

where C(x) cos θ corresponds to A(q) in (2).

Fig. 1

Boat on a running river

After imposing the constraint forces, and noting $V(q,\dot q)\dot q = 0,G(q) = 0$, one can get the following dynamic equation:

$$M(q)\ddot q + F(q,\dot q) = \tau + J(q)\lambda $$

(22)

where q = [y,x,θ]^T, M(q)= diag{m, m, I} and J ^T (q) = [cos q ₃, − sin q ₃, 0], m is the mass of the boat, and I is the inertia of the boat. For the sake of simplicity, select m = 1kg, I = 1kg · m², C(q2)= q2, F(q) = [cos q3, 0, 0]^T.

We select

It follows from the transformation (7) that

$$\left\{ {\matrix{{{{\dot q}_1} = {{\dot z}_1}\tan {q_3} + {q_2}} \hfill \cr {{{\dot q}_2} = {{\dot z}_1}} \hfill \cr {{{\dot q}_3} = {{\dot z}_2}.} \hfill \cr } } \right.$$

(23)

Substituting (23) into (22), pre-multiplying both sides of it by S ^T(q), and using J ^T(q)S(q) = 0, one can get

For the given J(q), S(q) and η(q), the desired trajectory ${q_d} = {[\sin t - \cos t,\sin t,{\textstyle{\pi \over 4}}]^{\rm{T}}}$ satisfies kinematic constraint ${J^{\rm{T}}}({q_d}){\dot q_d} = A({q_d})$ and transform ${\dot q_d} = S({q_d}){\dot z_d} + \eta ({q_d})$ with ${z_d} = {[\sin t,\,{\textstyle{\pi \over 4}}]^{\rm{T}}}$. The control objective is to determine a feedback controller so that z follows z _d and $\dot z$ follows ${\dot z_d}$, respectively.

Based on the previous control design (12) and (15), we get the actual controller as

where ${e_1} = {[{e_{11}},\,{e_{12}}]^{\rm{T}}} = {[\sin t - {z_1},\,{\textstyle{\pi \over 4}} - {z_2}]^{\rm{T}}},{e_2} = {[{e_{21}},\,{e_{22}}]^{\rm{T}}} = {[\sin t + \cos t - {z_1} - {\dot z_1},{\textstyle{\pi \over 4}} - {z_2} - {\dot z_2}]^{\rm{T}}}$.

In the simulation study, we chose ${\alpha _1} = 1,{\alpha _2} = 2,{k_s} = 1,\beta = 2$ and ${z_1}(0) = {\dot z_1}(0) = {z_2}(0) = {\dot z_2}(0) = 1$. Fig. 2 shows the position tracking errors of z(t) − z _d (t) converge to zero, and Fig. 3 shows the velocity tracking errors of $\dot z(t) - {\dot z_d}(t)$ converge to zero. At the end of the simulation, we should explain why the given signal z _2d is a constant. In fact, according to transformation (23), we know z ₂ = θ, so the control torques ensure asymptotical tracking all the time in the unchanged yaw angle with the different velocity of flow. Hence, the practical simulation example confirms the validity of the proposed algorithm.

Fig. 2

The trajectories of e ₁

Fig. 3

The trajectories of ${\dot e_1}$

5 Conclusions

In this paper, a systematic approach has been developed to design a tracking controller for the nonholonomic mechanical systems with affine constraints. The controller guarantees that the internal state tracks the desired trajectory.