1 Introduction

The phenomenon of time delay is frequently a source of instability and exists in various engineering systems. Time delay usually leads to unsatisfactory performance. Therefore, the problem of stabilization of time delay systems has received considerable attention over the past years[1–5]. To overcome this difficulty, the Lyapunov-Krasovskii functional is used for stability analysis and synthesis[6,7].

A typical approach for the analysis and synthesis of nonlinear system with time delay is the local linearization approach. First, a linearization model at the nominal operating point is obtained, and then a linear feedback control is designed for this linear model. In particular, some delay-independent stability conditions and stabilization approaches have been proposed for these linear delay differential equations[8,9]. It is known that each local model is valid only for a certain range of operating conditions and these results can only guarantee the local stability of nonlinear systems with time delays.

The adaptive neural controller was designed for a class of nonlinear time-delay systems[10–13]. However, these adaptive neural control methods require a large number of neural weights to be adapted online simultaneously. This makes the learning time unacceptably lengthy. Fuzzy logic systems are employed to approximate the unknown nonlinear functions, then the adaptive law of adjustable parameters is obtained. Adaptive fuzzy control approaches were developed in [14-16] for a class of nonlinear time delay systems to deal with the drawbacks of adaptive neural controllers. In [14], a novel systematic design procedure was developed for the synthesis of a stable adaptive fuzzy controller for a class of nonlinear time-delay systems. The Lyapunov-Krasovskii functional was constructed to compensate for the unknown delayed state uncertainties. However, almost all the existing approximator-based adaptive backstepping control schemes use function approximators as feedback compensators to model some suitable unknown functions in the controllers. In other word, approximators are used to model unknown functions depending on system states or outputs. It is well known that the universal approximation property of fuzzy system or neural network holds only over a compact set. The problem of globally stable adaptive backstepping output-feedback tracking control for a class of nonlinear systems was addressed in [17]. Adaptive fuzzy backstepping control work was extended to the design of a Mamdani fuzzy adaptive control for a class of strict-feedback single-input-single-output (SISO) nonlinear systems without backstepping[18].

On the other hand, the problem of observer design for reconstructing state variables is a more involved issue in systems with any kind of delay. In general, some sufficient conditions for the existence of an observer have been established, and computational algorithms for construction of the observers have been presented in [19, 20].

However, the previous work on adaptive fuzzy controller was limited to systems only with available measurement states for SISO[14–17]. Based on the initial results of SISO nonlinear systems, we intend to develop an observer-based adaptive fuzzy control for a class of SISO nonlinear systems[14]. Furthermore, the proposed scheme is constructed by integrating the feature of H ∞ tracking performance which can greatly attenuate disturbances, model uncertainties, and fuzzy approximation errors.

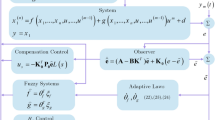
The main features of this paper are: 1) State observer is first designed, and the controller is designed via adaptive fuzzy control method based on the observed states. 2) Both the designed observer and controller are independent of the time delay.

The paper is organized as follows. The problem under investigation and the fuzzy system are introduced in Section 2. The observer-based adaptive fuzzy control design is introduced in Section 3. The main result is presented in Section 4. Simulation results are provided in Section 5. Conclusions are given in Section 6.

2 Problem formulation and fuzzy systems

Consider the SISO nonlinear time-delay dynamic system in the following form[14]:

$$\left\{ {\begin{array}{*{20}{l}} {{{\dot x}_i} = {x_{i + 1}},\quad \quad \quad \quad \quad i = 1,2, \cdots ,n - 1} \\ {{{\dot x}_n} = f(x) + g(x)u(t) + h(x(t - \tau ))} \\ {y = {x_1}} \end{array}} \right.$$
((1))

where x = [x 1,x 2,· · · ,x n ]T ∈ R n is the system state vector, u ∈ R and y ∈ R denote system control input and output, respectively. Functions f(·), g(·) and h(·) are unknown smooth functions, τ i is an unknown time delay of the state variables, i = 1, 2, · · · ,n. It is assumed that the desired output trajectory and its derivatives Y d = [y d , y d , · · ·, y d (n−1)]T are measurable and bounded and y d (n−1)denotes the (n−1)-th derivative of y d with respect to time.

Let \(\hat x = {[{\hat x_1},{\hat x_2}, \cdots ,{\hat x_n}]^{\text{T}}} \in {{\mathbf{R}}^n}\) be the estimation of the system state vector. Define error vector e, estimation error vector ê, and observation error \(\tilde e\), respectively as

((2))

The filtered tracking error e s , estimation error ê s , and observation error \({\tilde e_s}\) are defined respectively as

((3))
((4))
((5))

where \({\Lambda _i} = {[\lambda _i^{n - 1},\lambda _i^{n - 2}, \cdots ,{\lambda _i}]^{\text{T}}},i = 1,2,3\), and λ i > 0 are positive constants which can be specified by the designer.

The control objective is to design an observer-based adaptive fuzzy tracking controller for system (1) such that the system output y tracks a desired reference signal y d while all the signals in the closed-loop system remain bounded.

Remark 1. As stated in [21], equality (4) has the following properties: 1) When ê s = 0, it defines a time-varying hyperplane in R n on which the estimated tracking error ê 1 converges to zero eventually. 2) When ê s is bounded, the estimated tracking error vector ê s is also bounded. These properties are helpful for stability analysis.

We have the following assumptions for the system’s signals, unknown functions and reference signals.

Assumption 1. The desired trajectory vector \({\bar y_d}\) given by \({\bar y_d} = {[Y_d^{\text{T}},y_d^{(n)}]^{\text{T}}} \in {\Omega _d} \subset {{\mathbf{R}}^{n + 1}}\) with Ω d being a known compact set is continuous and available.

Assumption 2. The unknown time delay is bounded by a known constant, i.e., \({\tau _i}\; \leqslant \;{\tau _{{\text{max}}}},i = 1,2, \cdots ,n\).

The fuzzy system considered in this paper has center-average defuzzifier, product inference and singleton fuzzifier[21]. This type of fuzzy logic system is given by

$$q(x) = \frac{{\sum\limits_{l = 1}^M {{{\bar q}^l}} \prod\limits_{i = 1}^n {{\mu _{F_i^l}}{x_i}} }}{{\sum\limits_{l = 1}^M {\prod\limits_{i = 1}^n {{\mu _{F_i^l}}{x_i}} } }}$$
((6))

where M is the number of IF-THEN rules in the fuzzy rule base. The IF-THEN rules take the following form for ℓ = 1, 2,· · · ,M:

R ℓ: If x 1 is \(F_i^\ell \) and x 2 is \(F_2^\ell \) and ⋯ x n is \(F_n^\ell \), then q is G ℓ, where \(F_i^\ell \) and G ℓ are the fuzzy sets with membership functions \({\mu _{F_i^\ell }}\) and \({\mu _{{G^\ell }}}\), respectively, and q is the linguistic variable which can be considered as output of the fuzzy logic system.

Parameter \({\bar q^\ell }\) is the point at which \({\mu _{{G^\ell }}}({\bar q^\ell })\) achieves its maximum value and we assume that

$${\mu _{{G^l}}}\left( {{{\bar q}^l}} \right) = 1.$$
((7))

Equality (6) can be rewritten as

$$q(x) = {\psi ^{\rm T}}\zeta (x)$$
((8))

where ψ = [ψ 1, ψ 2,· · · ,ψM]T is a parameter vector, and ζ(x) = [ζ 1( x ), ζ 2(x),· · · ,ζ M(x)]T is a regressive vector with regressor ζ ℓ(x), which is defined as a fuzzy basis function (FBF) of the form

$${\zeta ^l}(x) = \frac{{\prod\limits_{i = 1}^n {{\mu _{F_i^l}}{x_i}} }}{{\sum\limits_{l = 1}^M {\prod\limits_{i = 1}^n {{\mu _{F_i^l}}{x_i}} } }}.$$
((9))

Two main reasons arise for using the fuzzy system (6) as the basic building block of adaptive fuzzy controllers. First, the fuzzy systems in the form of (6) were proven in [22] to be universal approximators, i.e., for any given real continuous function f on a compact set U, there exists a fuzzy system (6) such that it can uniformly approximate f over U to any arbitrary accuracy. Therefore, the fuzzy systems (6) are qualified for modeling nonlinear systems. Second, the fuzzy systems (6) are constructed from the fuzzy IF-THEN rules of (7) using some specific fuzzy inference, fuzzification, and defuzzification strategies. Therefore, linguistic information from a human expert can be directly incorporated into the controller.

3 Observer-based adaptive fuzzy control

In this section, the observer-based adaptive fuzzy controller is designed and the boundedness of the closed-loop signal is proved. The observer proposed in this paper takes the following form[4]:

$$\left\{ {\begin{array}{*{20}{l}} {{{\dot \hat x}_i} = {{\hat x}_{i + 1}} + {k_i}({x_1} - {{\hat x}_1}),\quad \quad i = 1,2, \cdots n - 1} \\ {{{\dot \hat x}_n} = g(\hat x)u(t) + f(\hat x) + {k_n}({x_1} - {{\hat x}_1})} \end{array}} \right.$$
((10))

where parameters k i (i ∈ [1, · · · ,n]) are the observer gains, which are selected to make sure that the characteristic polynomial s n + k n s n− 1 + k n− 1 s n− 2 + · · · + k 1 = 0 is Hurwitz.

Assumption 3. For \(1\; \leqslant \;i\; \leqslant \;n\), the signs of \(g(\hat x)\) are known, and there exist unknown positive constants b and c such that \(0\; < \;b\; \leqslant \;\left| {g(\hat x)} \right|\; \leqslant \;c\; < \infty ,\;\forall x \in {{\mathbf{R}}^i}\). Without loss of generality, it is assumed that \(g(\hat x)\; \geqslant \;b > 0\).

Remark 2. It should be emphasized that bounds b and c are only required for analytical purposes, their true values are not necessarily known since they are not used for controller design.

Assumption 4. The unknown functions f(·), i = 1, 2, · · · ,n can be expressed as a fuzzy logic system of the form (8), i.e.,

((11))

where \(\theta _f^{\text{T}}\) the estimation of the unknown parameter vector and \(\zeta (\hat x)\) is the associated fuzzy basis function.

From (1) and (3), we obtain

$${\dot e_s} = f(x) + g(x)u(t) + h(x(t - \tau x) + {v_1}$$
((12))

where \({v_1} = [0\;\;\Lambda _1^{\text{T}}]e - y_d^{(n)}\).

From (4) and (10), we also obtain

((13))

where \({v_2} = [0\;\;\Lambda _2^{\text{T}}]\hat e - y_d^{(n)} + {k_n}{e_1}\).

Subtracting (13) from (12) yields

$${\dot \tilde e_s} = (f(x) - f(\hat x) + (g(x) - g(\hat x))u + ({v_1} - {v_2}) + {h_n}(x(t - \tau )).$$
((14))

Define the minimum approximation error as

$$w = (f(x) - f(\hat x)) + (g(x) - g(\hat x))u.$$
((15))

Equality (14) can be rewritten as

$${\dot \tilde e_s} = {v_3} + w + {h_n}(x(t - \tau ))$$
((16))

where v 3 = v 1 − v 2.

If the smooth function is chosen as

$${V_{es}} = \frac{1}{2}(\hat e_s^2 + \tilde e_s^2)$$
((17))

then its time derivative along (13) and (14) is given by

((18))

By the triangular inequality, we have

$${\tilde e_s}{h_n}(x(t - {\tau _n})) \leqslant \frac{{\tilde e_s^2}}{2} + \frac{{h_n^2(x(t - \tau ))}}{2}.$$
((19))

Substituting (19) into (18) yields

((20))

In order to facilitate the procedure in the presence of the unknown time-delay, the following Lyapunov-Krasovskii functional is considered:

$${V_U} - \frac{1}{2}\int_{t - {\tau _n}}^t {h_n^2(x(\tau ))\operatorname{d} \tau } .$$
((21))

Then it follows from (20) and (21) that

((22))

where

$$L(Z) + {v_3} + \frac{{h_n^2(x)}}{{2{{\hat e}_s}}} + \frac{{{{\tilde e}_s}}}{{{{\hat e}_s}}}\left( {{v_3} + w + \frac{{{{\tilde e}_s}}}{2}} \right)$$
((23))

with \(Z = {[{\hat x^{\text{T}}},y_d^{\text{T}}]^{\text{T}}} \in {\Omega _Z} \subset {{\mathbf{R}}^{2n + 1}}\) and Ω Z being a compact set. Because of containing unknown function h(x(t)), the last two terms in (23) cannot be used directly to construct the control law u. In addition, the last two terms in (23) cannot be approximated by the fuzzy logic system because it is not well-defined when ê s = 0. To make the fuzzy approximation efficient, as done in [14], we define compact sets \(\Omega _Z^0\) and Ω Cs ⊂ Ω Z as

$$\Omega _Z^0 = {\Omega _Z} - {\Omega _{{C_s}}}$$
((24))
$${\Omega _{{C_s}}} = \{ {\hat e_s}:|{\hat e_s}| < {C_s}\} \subset {\Omega _Z}$$
((25))

where C s is a positive design constant that can be chosen arbitrarily small and the sign “–” in (24) denotes the complement of set ΩC s in set ΩZ. Moreover, it has been proven that \(\Omega _Z^0\) is a compact set on which the unknown function L(Z) is continuous. Therefore, the fuzzy logic system (8) can be used to approximate L(Z) over the compact set \(\Omega _Z^0\) such that

((26))

where δ(Z) is the approximation error and satisfies \(\left| {\delta (Z)} \right|\; \leqslant \) ε with ε being an arbitrarily small constant.

4 Main results

In this section, the boundedness of the closed-loop signals is proved using the Lyapunov function approach.

Theorem 1. For the nonlinear system (1), if the adaptive fuzzy control is chosen as

((27))

where α 1 > 0 is any positive constant, and the parameters are updated by

$${\dot \hat \theta _f} = \left\{ {\begin{array}{*{20}{l}} {{\gamma _1}\zeta (\hat x){{\hat e}_s},}&{{{\hat e}_s} \in \Omega _Z^0} \\ {0,}&{{{\hat e}_s} \in {\Omega _{{C_s}}}} \end{array}} \right.$$
((28))
$${\dot \hat \theta _L} = \left\{ {\begin{array}{*{20}{l}} {{\gamma _2}\zeta (Z){{\hat e}_s},}&{{{\hat e}_s} \in \Omega _Z^0} \\ {0,}&{{{\hat e}_s} \in {\Omega _{{C_s}}}} \end{array}} \right.$$
((29))

where ϒ1 and ϒ2 are positive design parameters, then for any initial conditions Z(0),\({\hat \theta _{{f_n}}}(0)\) and \({\hat \theta _L}(0)\), all the signals in the closed-loop system are bounded, and the estimated tracking error e s will stay in the compact set Ω Cs finally.

Proof. To show that \(\Omega _Z^0\) is a domain of attraction, we first find a Lyapunov function candidate V(t) > 0 such that \(\dot V(t)\; \leqslant \;0,\forall {\hat e_s} \notin \Omega _Z^0.\;{\text{For }}{\hat e_s} \notin \Omega _Z^0\), let us consider the following Lyapunov function candidate:

((30))

where r 1 and r 2 are positive constants, \({\bar \theta _f} = {\hat \theta _f} - \theta _f^ * \), and \({\bar \theta _L} = {\hat \theta _L} - \theta _L^ * \), where the “*” denotes the optimal estimations.

Assumption 5. The optimal estimations \(\theta _f^ * \) and \(\theta _L^ * \) of the parameters of θ f and θ L are assumed to have the forms ||θ f *|| = α ||θ f || and ||θ L *|| = β ||θ L ||, where α and β are arbitrary constants.

The time derivative of (30) is given by

((31))

Now, using (22), (28) and (29), we get

((32))

Using Assumption 2 and the following triangular inequality

$${\hat e_s}\delta (Z) \leqslant \frac{{b\hat e_s^2}}{2} + \frac{{{\varepsilon ^2}}}{{2b}}$$
((33))

it can be easily verified that

((34))

where the control law (27) has been substituted in (34).

Equality (34) can be reduced to

((35))

By using Assumption 5, (35) becomes

$$\dot V \leqslant - {\alpha _1}b\hat e_s^2 + \frac{{{\varepsilon ^2}}}{{2b}}.$$
((36))

As ε is a small positive constant representing the approximation error in L(Z), we conclude that V(t) is a Lyapunov function. Therefore, \({\hat e_s}(t),{\hat x_1}(t),\hat \theta _f^{\text{T}}\) and \(\hat \theta _L^{\text{T}}\) are bounded. In addition, the domain \(\Omega _Z^0\) is attractive in the sense that e s will be driven to \(\Omega _Z^0\) in a finite time, and then afterwards stays within it. For \({\hat e_s} \in {\Omega _{{C_s}}}\) since \({\hat e_1} = {\hat x_1} - {y_d},{\dot \hat \theta _f} = 0\), and \({\dot \hat \theta _L} = 0,{\hat x_1}\) is bounded, \(\hat \theta _f^{\text{T}}\) and \(\hat \theta _L^{\text{T}}\) are kept unchanged in bounded values. We can readily conclude that the tracking error ê s ∈ΩC s while all the other closed-loop signals are bounded.

5 Simulation results

In this section, we demonstrate the effectiveness of the proposed adaptive fuzzy control algorithm using the following illustrative example.

Example 1. To demonstrate the effectiveness of the proposed scheme, we consider the following second-order nonlinear time-delay system[14]:

$$\begin{array}{*{20}{l}} {{{\dot x}_1} = {x_2}} \\ {{{\dot x}_2} = {x_1} - 0.3\sin ({x_1}{x_2}) + (2 + \cos ({x_1}))u + h(x(t - \tau ))} \\ {y = {x_1}} \end{array}$$
((37))

where x 1and x 2 denote the state variables, u is the system control input, y is the system output, the time-delay term is h(x(t − τ)) = 2x 1(t − τ)x 2(t − τ). In this example, we choose τ = 2 with the bound τ max = 2 and the desired reference signal as y d = 0.5(sin(t) + sin(0.5t)).

The designed observer takes the following form:

$$\begin{array}{*{20}{l}} {{{\dot \hat x}_1} = {{\hat x}_2} + {k_1}({x_1} - {{\hat x}_1})} \\ {{{\dot \hat x}_2} = {x_1} - 0.3\sin ({x_1}{{\hat x}_2}) + (2 + \cos ({x_1}))u + } \\ {\quad \quad {k_2}({x_1} - {{\hat x}_1})} \end{array}$$
((38))

The control objective is to design an adaptive fuzzy tracking controller for system (37) such that the system output y tracks the desired reference signal y d while all the signals in the closed loop system remain bounded. Vector Z is defined as \(Z = {[{x_1},{\hat x_2},{y_d},{\dot y_d},{\ddot y_d}]^{\text{T}}}\).

Seven Gaussian membership functions with centers evenly spaced between [−1.5, 1.5] for variables \({x_1},{\hat x_2},{y_d},{\dot y_d}\) and ÿ d are chosen as

$$\begin{array}{*{20}{l}} {{\mu _{F_i^1}} = {\operatorname{e} ^{\frac{{ - 0.5{{({Z_i} + 1.5)}^2}}}{4}}}} \\ {{\mu _{F_i^2}} = {\operatorname{e} ^{\frac{{ - 0.5{{({Z_i} + 1)}^2}}}{4}}}} \\ {{\mu _{F_i^3}} = {\operatorname{e} ^{\frac{{ - 0.5{{({Z_i} + 0.5)}^2}}}{4}}}} \\ {{\mu _{F_i^4}} = {\operatorname{e} ^{\frac{{ - 0.5Z_i^2}}{4}}}} \\ {{\mu _{F_i^5}} = {\operatorname{e} ^{\frac{{ - 0.5{{({Z_i} - 0.5)}^2}}}{4}}}} \\ {{\mu _{F_i^6}} = {\operatorname{e} ^{\frac{{ - 0.5{{({Z_i} - 1)}^2}}}{4}}}} \\ {{\mu _{F_i^7}} = {\operatorname{e} ^{\frac{{ - 0.5{{({Z_i} - 1.5)}^2}}}{4}}}\quad \operatorname{for} \;i = 1,2,3,4,5.} \end{array}$$
((39))

For the nonlinear system, seven fuzzy rules in the following format are employed.

$$\begin{array}{*{20}{l}} {{R^l}:\operatorname{If} \;{x_1}\;\operatorname{is} \;F_1^l\;\operatorname{and} \;{{\hat x}_2}\;\operatorname{is} \;F_2^l\;\operatorname{and} \;{y_d}\;\operatorname{is} \;F_3^l} \\ {\quad \;\;\operatorname{and} \;{y_d}\;\operatorname{is} \;F_4^l\;\operatorname{and} \;{{\ddot y}_d}\;\operatorname{is} \;F_5^l,} \\ {\quad \;\;\operatorname{then} \;y\;\operatorname{is} \;{G^l},\;l = 1,2, \cdots ,7.} \end{array}$$
((40))

Denoting \({D_1} = \sum\limits_{\ell = 1}^7 {\prod\limits_{i = 1}^2 {{\mu _{F_i^\ell }}{{\hat x}_i}} } \) and \({D_2} = \sum\limits_{\ell = 1}^7 {\prod\limits_{i = 1}^5 {{\mu _{F_i^\ell }}{Z_i}} } \) we can then write the FBFs which are used to generate approximations for both \({f_i}({\bar x_i})\) and L(Z) as

((41))
((42))

Let k 1=10, k 2=5, α 1 = 25, γ1 = γ2 = 0.1, λ i = 5, C s = 1 × 10−4, the initial conditions be \({[{x_1},\quad {\hat x_2}]^{\text{T}}} = {[0.5,\quad 0]^{\text{T}}}\) and \({\hat \theta _{{f_2}}} = {\hat \theta _L} = 0\).

Simulation results are shown in Figs. 1–3, respectively. Fig. 1 shows the system states x 1 and x 2 and their estimations \({\hat x_1}\) and \({\hat x_2}\). Fig. 2 shows the system output y and the reference signal y d . From Fig. 2, we can see that the good tracking performance has been achieved. Fig. 3 shows the control input signal u. From the simulation results, it can be seen that the proposed controller not only guarantees the boundedness of all the signals in the closed-loop system, but also achieves the good tracking performance.

Fig.1
figure 1

System states and their estimations

Full size image
Fig.2
figure 2

System output y and its trajectory y d

Full size image
Fig.3
figure 3

Control input u

Full size image

6 Conclusions

Observer-based adaptive fuzzy control has been developed for a class of nonlinear systems with unknown time delays. Since the state variables of nonlinear systems are assumed to be unknown, the state observer is first designed to estimate state variables, via which fuzzy control schemes and the Lyapunov-Krasovskii functional are formulated. Based on the Lyapunov stability theorem, it is rigorously proved that the stability of the closed-loop system is assured and the tracking performance is achieved. The proposed control scheme guarantees the semi-global bound-edness of all the signals in the closed-loop system and the good tracking performance. Moreover, the suggested adaptive fuzzy controller contains only one adaptive parameter. This makes our design scheme easier to be implemented in practical applications. Simulation results show that the overall control system guarantees that all involved signals are uniformly ultimately bounded, and the tracking performance index is achieved.