1 Introduction

In many practical control problems, the physical state variables of systems are partially or fully unavailable for measurement, since the state variables are not accessible by sensing devices and transducers are not available or very expensive. In such cases, observer based control schemes should be developed to estimate the state. Therefore, observer design has been a very active field during the last decade and has turned out to be much more challenging than control problems[1]. Adaptive control techniques have received considerable attention over the past decades due to its power to successfully control uncertain systems[2–5]. However, conventional adaptive control theory can only handle the systems with known dynamic structure and unknown parameters (i.e., constant or slowly-varying). In addition, conventional adaptive control techniques cannot make use of human operators’ knowledge on process control, which usually contributes to the rough tuning of system dynamics.

The introduction of fuzzy systems led to a great success and provided effective approaches to handle nonlinear systems especially complex and illdefined dynamic systems. Being one of the efficient intelligent techniques, fuzzy systems have been applied to the modeling and control of uncertain nonlinear systems. Several stable adaptive fuzzy control schemes based on the universal approximation theorem[6] have been developed for unknown SISO nonlinear systems[7–9], multi-input multi-output (MIMO) nonlinear systems[10–12], and large-scale interconnected nonlinear systems[13–15]. These schemes provided an effective framework for incorporating the expert knowledge systematically and achieve stable performance criterion. The stability analysis in such schemes is performed by using the Lyapunov synthesis approach. However, these adaptive fuzzy control schemes are static in nature. The fact that most of physical systems are generally dynamic, suggests that one may introduce some sort of dynamics to these static fuzzy models in order to cope with the dynamic nature of the physical systems. This would provide a new tool in the control of dynamic systems. Hence, the dynamic fuzzy logic system (DFLS) was first introduced by Lee and Vukovich[16, 17]. They have successfully applied this concept to the identification of single-link robotic manipulator[16]. Stable identification and adaptive control based on DFLS were performed in [17]. This work was extended to design a DFLS based stable indirect adaptive control scheme for a class of SISO nonlinear systems[18] and a class of MIMO nonlinear systems[19].

However, the previous work on DFLS is limited to only systems with measurable states both for SISO and MIMO nonlinear systems[16–19]. Based on the initial results of SISO nonlinear systems[16–18], we intend to develop an observer based adaptive dynamic fuzzy control for SISO nonlinear systems. Furthermore, the proposed scheme is constructed by integrating the feature of H ∞ tracking performance which can greatly attenuate disturbances, model uncertainties, and fuzzy approximation errors.

The paper is organized as follows. A class of SISO nonlinear systems and control objectives are described in Section 2. Section 3 presents a brief description of static fuzzy systems and DFLS. The observer based DFLS control design is presented in Section 4. In Section 5, the proposed control algorithm is used to control an inverted pendulum. Section 6 concludes this paper.

2 System description

In this paper, we consider a class of SISO n-th order nonlinear systems represented by the following set of differential equations:

$$\begin{array}{*{20}{l}} {{x^{(n)}} = f(x,\dot x, \cdots .{x^{(n - 1)}}) + g(x,\dot x, \cdots .{x^{(n - 1)}})u + d(t)} \\ {\quad y = x} \end{array}$$
((1))

where f(⋅) and g(⋅) are smooth unknown nonlinear functions, \(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} = (x,\dot x, \cdots ,{x^{(n - 1)}}) \in {\operatorname{R} ^n}\) is the state vector which is assumed to be not available for measurements, u ∈ R and y ∈ R are the control input and the output of the system, respectively, and d denotes the unknown external disturbance. It is assumed that the desired output trajectory and its derivatives are measurable and bounded, where \({y_d^{(n - 1)}}\) denotes the (n - 1)-th derivative of y d with respect to time.

Let x 1 =x,\(\dot x, \cdots \) so that \(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} \) = (x 1,x 2,⋯ ,x n )T and (1) can be rewritten in the state space representation as

$$\begin{array}{*{20}{l}} {\;\;{{\dot x}_1} = {x_2}} \\ {\quad \;\;\; \vdots } \\ {{{\dot x}_{n - 1}} = {x_n}} \\ {\;\;{{\dot x}_n} = f(x) + g(x)u + d.} \end{array}$$
((2))

Let be the estination of system state vector. Define the error vector e, estimation error vector ê, and observation error \(\tilde e\), respectively, as

((3))
((4))
((5))

Control objectives. Develop a feedback control law u(t) (based on DFLS) which ensures the boundness of both variables in the closed-loop systems and the parameters of the DFLS, and guarantees output tracking of a specified desired trajectory . In addition, for a given disturbance attenuation level ρ > 0, the following H ∞ tracking performance index is achieved.

((6))

where e is the error vector, δ ∈ L 2 [0,T] is the combined disturbance and approximation error for T ∈ [0, ∞] , Q and P are positive matrices of proper dimensions, and Δ is parameter approximation error vector.

Throughout this paper, the following assumptions are considered on system (1).

Assumption 1. For 1 ⩽ i ⩽ n, the signs of \(g(\hat x)\) are known, and there exist unknown positive constants b and c such that \(0 < b \leqslant \left| {g(\hat x)} \right| \leqslant c < \infty ,\;\forall x \in {{\mathbf{R}}^i}\). Without losing generality, it is assumed that \(g(\hat x) \geqslant b > 0\).

Remark 1. It should be emphasized that the bounds b and c are only required for analytical purpose, their true values are not necessarily required to be known since they are not used for controller design.

Assumption 2. The reference trajectories Y d is a known bounded function of time with bounded known derivatives, and it is assumed to be r i -times differentiable.

3 Description of DFLS

The DFLS is composed of an ordinary fuzzy logic system (also referred to static fuzzy logic system) and a dynamic element[16,17]. The basic structure of the fuzzy logic system considered in this paper which has been widely used in identification and control of nonlinear systems is shown in Fig. 1. It is composed of four major components, namely, a fuzzification interface, a fuzzy rule base, a fuzzy inference engine, and a defuzzification interface.

Fig. 1
figure 1

The basic configuration of a fuzzy logic system

Full size image

For fuzzy logic systems, the fuzzy rule base is made up of the following inference rule:

$$\begin{array}{*{20}{l}} {{R^l}:\operatorname{If} \;{x_1}\;\operatorname{is} \;F_1^l\;\operatorname{and} \;{x_2}\;\operatorname{is} \;F_2^l\;\operatorname{and} \; \cdots \;{x_n}\;\operatorname{is} \;F_n^l} \\ {\quad \;\;\operatorname{Then} \;y\;\operatorname{is} \;{G^l}} \end{array}$$
((7))

where \(F_1^l\) and \(G_1^l\) are fuzzy sets in R, l = 1, 2, ⋯ , N, i = 1,2,⋯ ,n, j = 1,2,⋯ ,p.

Through center-average defuzzifier, product inference, and singleton fuzzifier[6], the output of the fuzzy logic system can be expressed as

$$y(x) = \frac{{\sum\limits_{l = 1}^N {{{\bar y}^l}(\prod\limits_i^n {{\mu _{F_i^l}}({x_i}))} } }}{{\sum\limits_{l = 1}^N {(\prod\limits_i^n {{\mu _{F_i^l}}({x_i}))} } }}$$
((8))

where \({\bar y^l}\) is the center of the fuzzy set G l at which \(\mu_G^l\) achieves its maximum value, and we assume that \(\mu _G^l({\bar y^l}) = 1\). Equality (3) can be written as

((9))

where is a vector of adjustable parameters, and ϕ(x) = [ϕ1, ⋯ , ϕ N ]T is a regression vector with each ϕ l defined as a fuzzy basis function (FBF)[6] as

$${\varphi _l} = \frac{{\prod\limits_i^n {{\mu _{F_i^l}}({x_i})} }}{{\sum\limits_{l = 1}^N {(\prod\limits_i^n {{\mu _{F_i^l}}({x_i}))} } }}.$$
((10))

The DFLS shown in Fig.2 can now be described by the following differential equations:

((11))
Fig. 2
figure 2

Dynamic fuzzy logic system

Full size image

The DFLS described by (3) was shown to possess universal approximating capabilities to a large class of nonlinear dynamic systems[17].

Our objective now is to develop an appropriate control law for input u in (1) and an adaptation law for the parameter matrix Ȳ of the DFLS (5), such that the closed loop system is stable in the sense that the tracking error e = y d − y is uniformly bounded, and the identification errors and identifier parameters are also uniformly bounded.

4 Observer based DFLS control

In this section, we develop an observer-based indirect adaptive fuzzy controller and its stability scheme for system (1) based on DFLS.

To begin with, take as the inputs of DFLS, and fuzzy rule base is

$$\begin{array}{*{20}{l}} {{R^l}:\operatorname{If} \;{{\hat x}_1}\;\operatorname{is} \;F_1^l\;\operatorname{and} \;{{\hat x}_2}\;\operatorname{is} \;F_2^l\;\operatorname{and} \;{{\hat x}_n}\;\operatorname{is} \;F_n^l,} \\ {\quad \;\;\operatorname{Then} \;y\;\operatorname{is} \;{G^l}.} \end{array}$$
((12))

The expression for \({\dot x_n}\) in (2) can be written as

$${\dot \hat x_n} = - \alpha \hat x + \bar Y\varphi (\hat x,u) - r(\hat x,u,\varphi ,\bar Y)$$
((13))

where \({r_i}(x,u,\varphi ,{\bar Y_i})\) represents the static modeling error of the DFLS identifier and can be expressed as

$$r(\hat x,u,\varphi ,\bar Y) = - \alpha \hat x + \bar Y\varphi (\hat x,u) - f(\hat x) - g(\hat x)u - d.$$
((14))

By Lemma 1 in [17], there exists an optimal parameter vector

$${\bar Y^*} = \mathop {\min }\limits_{\left\| {\bar Y} \right\|} \{ \bar Y:\left\| {\bar Y} \right\| \leqslant {M_{\bar Y}}\} $$
((15))

which minimizes the static modeling error r, such that

$$\mathop {\sup }\limits_{(x,u) \in \Omega } \left| {r(\hat x,u,\varphi ,{{\bar Y}^*})} \right| \leqslant {M^r}$$
((16))

where M Ȳ and M r are positive design constants. In the following, we develop an adaptive law for Ȳ. Replacing Ȳ by Ȳ* in (8) results in

$${\dot \hat x_n} = - \alpha \hat x + {\bar Y^*}\varphi (\hat x,u) - r(\hat x,u,\varphi ,{\bar Y^*}).$$
((17))

Subtracting (17) from (2) yields

$${\dot \tilde x_n} = - \alpha \tilde x + \Delta \varphi (\hat x,u) + r(\hat x,u,\varphi ,{\bar Y^*})$$
((18))

where Δ = Ȳ − Ȳ* is the parameter estimation error.

In this situation, we propose the following control law which is based on DFLS:

((19))

where \(\hat g(\hat x|{\theta _g})\) is a static fuzzy logic estimation of function \(\hat g(\hat x)\), it is also a nonlinear function of the state vector x and it can be approximated by a fuzzy logic system (4) as

((20))

The adaptive law for the parameter θ g , u r , and u s will be defined later. And ϕ(x, 0) = ϕ(x, u) | u=0 .

Substituting (19) into (2), after straight forward manipulations, it can be easily obtained as

((21))

where

$$\begin{array}{*{20}{l}} {A = \left[ {\begin{array}{*{20}{c}} 0&1& \cdots &0 \\ 0&0& \cdots &0 \\ \vdots & \vdots & \vdots & \vdots \\ { - {k_n}}&{ - {k_{(n - 1)}}}&{ - {k_{(n - 2)}}}&{ - {k_1}} \end{array}} \right],} \\ {B = \left[ {\begin{array}{*{20}{c}} 0 \\ 0 \\ \vdots \\ 1 \end{array}} \right],\;C = \left[ {\begin{array}{*{20}{c}} 1 \\ 0 \\ \vdots \\ 0 \end{array}} \right].} \end{array}$$

Using (21) with u = 0, we can write

((22))

The control gain functions g(x) can be approximated by a static fuzzy logic system (4). It follows that

$$g(x) = \hat g(\hat x|{\theta _g}) + \kappa = \varphi (x){\theta _g} + \kappa $$
((23))

where θ g is an adjustable parameter vector, ϕ(x) is a fuzzy basis function, and κ is the fuzzy approximation error. Define an optimal parameter estimate \(\theta _g^*\) such that it minimizes the approximation error. Therefore, we can write

$$g(x) = \varphi (x)\theta _g^* + {\kappa ^*}$$
((24))

where κ* is the minimum approximation error.

Design the error observer as

((25))

where \(K_0^T = \left[ {k_1^0,k_2^0, \cdots ,k_n^0} \right]\) is the observer gain vector, which is selected to make sure that the characteristic polynomial of A − K 0 C T is Hurwitz.

Subtracting (15) from (12) yields

((26))

where \({\Delta _g} = {\theta _g} - \theta _g^*\) and \(w = {k^*} + r(\hat x,u,0,{\bar Y^*})\). We define the robust compensator control terms u r and u s as

((27))
((28))

where λ and P are the solutions of the following Riccati-like equation:

((29))

It is noticed that Riccati equation (29) has a solution P = P T ⩾ 0 if and only if 2ρ 2 ⩾ λ i.

The adaptive laws are chosen as

((30))

and

((31))

Theorem 1. Consider system (1) that identifies by the DFLS (11) with its observer (25), and its controller (19), (27) and (28). Let the parameter vectors \(\bar Y\) and θ g be adjusted by the update law (30) and (31), respectively. Then, the closed loop system has the following properties:

  1. 1)

    All signals in the closed loop system are uniformly bounded.

  2. 2)

    For a given disturbance attenuation level, the proposed tracking performance index (6) is achieved.

Proof. Choose a Lyapunov function as

((32))

Differentiating V and using (18) and (21), we obtain

((33))

Using the adaptive laws (30) and (31), (33) can be simplified into

((34))

By the triangular inequality, we have

$$h\tilde er(\hat x,u,\varphi ,{\bar Y^*}) \leqslant \frac{{{h^2}{{\tilde e}^2}}}{{2{\rho ^2}}} + \frac{{{\rho ^2}}}{2}r_i^2(\hat x,u,\varphi ,\bar Y_i^*).$$
((35))

Substituting (35) and using Riccati-like equation (29), (34) becomes

((36))

Note that the third and fourth terms are negative in (36). So (36) can be rewritten as

((37))

The third term in (37) can be made negative by choosing h ⩽ 2αρ 2. So, (37) can be rewritten as

((38))

Since , from (38), we obtain

((39))

whereδ 2 = r 2(\(\hat Y\), u, ϕ, \(\bar Y^{*} \)) + w 2. After some straightforward manipulations, we can deduce

$$\dot V \leqslant - cV + \mu $$
((40))

where c= min\(\left\{ {\lambda ,\frac{1}{{{\eta _1}}},\frac{1}{{{\eta _2}}}} \right\}\) with λ =\(\frac{{\inf \;{\lambda _{\min }}(Q)}}{{\operatorname{sub} \;{\lambda _{\max }}(Q)}}\) and ¼ =\(\frac{1}{{2{\rho ^2}}}\sum {_{i = 1}^p} {\delta ^2}\)

From (40) and (33), we can obtain

$$\dot V \leqslant - cV + \mu $$
((41))

where c = \(\sum {_{i = 1}^p} {c_i}\) and ¼ = \(\sum {_{i = 1}^p} {\mu_i}\).

This implies that all signals in the closed loop system are bounded. Thus, the control objective 1) in Theorem 1 is realized.

Integrating (41) from t = 0 to t = T, we have

((42))

Since V(T) ⩾ 0, we can write (42) as

((43))

Then, from (43), we obtain

((44))

Thus, the control objective 2) in Theorem 1 is achieved.

For the sake of clarity of presentation, the overall design procedure of observer based DFLS scheme is summarized in the following steps:

Step 1. Select feedback gain and observer gain vectors K i and K o such that the matrices A - BK T i and A − K o C T are Hurwitz stable and meet the required transient response of tracking error dynamics.

Step 2. Specify a positive-definite matrix Q, desired attenuation level ρ, and the weighting factor λ such that 2ρ 2 ⩾ λ.

Step 3. Solve the Riccati equality (29) to obtain positive definite matrix P.

Step 4. Select membership functions \({\mu _{{F_i}}}( \cdot )\), and incorporate expert knowledge to the rule base if available to compute the fuzzy basis vectors \(\varphi (\hat x)\) and \(\varphi (\hat x,u)\).

Step 5. Apply the control law (19) with adaptive laws (30) and (31).

5 Simulation results

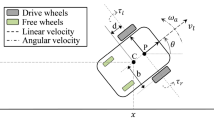
Consider the inverted pendulum system in Fig. 3. Let x 1 =θ and x 2 = \(\dot \theta \). The dynamic equations of the inverted pendulum system are

$$\begin{array}{*{20}{l}} {{{\dot x}_1} = {x_2}} \\ {{{\dot x}_2} = \frac{{g\;\sin \;{x_1} - \frac{{mlx_2^2\;\cos \;{x_1}\;\sin \;{x_1}}}{{{m_c} + m}}}}{{l\left( {\frac{4}{3} - \frac{{m\;{{\cos }^2}\;{x_1}}}{{{m_c} + m}}} \right)}} + \frac{{\frac{{\cos \;{x_1}}}{{{m_c} + m}}}}{{l\left( {\frac{4}{3} - \frac{{m\;{{\cos }^2}\;{x_1}}}{{{m_c} + m}}} \right)}}u} \\ {y = {x_1}} \end{array}$$
((45))

where g = 9.8 m/s2 is the acceleration due to gravity, m c is the mass of the cart, m is the mass of the pole, l is the half-length of the pole, and u is the applied force (control). The reference signal is assumed as \({y_d} = \frac{\pi }{{30(\sin (t))}}\). Also we choose m c = 10, m = 1, and l = 3.

Fig.3
figure 3

The inverted pendulum system

Full size image

The DFLS based control scheme design procedure for the inverted pendulum is described in some details in the following steps:

Step 1. Set k 1 =4,k 2 = 10, k 01 = 40, and k 2 = 200.

Step 2. Perform simulation with two different values of attenuation levels, ρ = 0.1. Select positive definite Q 1 = Q 2 = diag{10,10}. Select λ = 0.01 such that 2ρ 2 ⩾ λ.

Step 3. Solve Riccati equation for both values of attenuation level as

$$P = \left[ {\begin{array}{*{20}{c}} {11.75}&{ - 5} \\ { - 5}&{2.22} \end{array}} \right].$$

Step 4. In this simulation study, assuming that there are no linguistic rules, we choose M 1 = M 2 = 5. Since |x i| ⩽ \(\frac{\pi }{6}\) for i =1,2, we choose

$$\begin{array}{*{20}{l}} {\mu F_i^1({{\hat x}_i}) = \exp \left[ { - {{\left( {\frac{{{{\hat x}_i} + \frac{\pi }{6}}}{{\frac{\pi }{{24}}}}} \right)}^2}} \right],} \\ {\mu F_i^2({{\hat x}_i}) = \exp \left[ { - {{\left( {\frac{{{{\hat x}_i} + \frac{\pi }{{12}}}}{{\frac{\pi }{{24}}}}} \right)}^2}} \right],} \\ {\mu F_i^3({{\hat x}_i}) = \exp \left[ { - {{\left( {\frac{{{{\hat x}_i}}}{{\frac{\pi }{{24}}}}} \right)}^2}} \right],} \\ {\mu F_i^4({{\hat x}_i}) = \exp \left[ { - {{\left( {\frac{{{{\hat x}_i} - \frac{\pi }{{12}}}}{{\frac{\pi }{{24}}}}} \right)}^2}} \right],} \\ {\mu F_i^5({{\hat x}_i}) = \exp \left[ { - {{\left( {\frac{{{{\hat x}_i} - \frac{\pi }{6}}}{{\frac{\pi }{{24}}}}} \right)}^2}} \right].} \end{array}$$

Assuming that there is no available expert knowledge, we are going to consider the following fuzzy rules of inference.

R l : If x 1 is \(F_1^l\) and x 2 is \(F_2^l\), Then y is G l.

Now, we can construct the fuzzy basis vectors ϕ(x) and ϕ(x,u) as follows

$${\varphi _l}(x) = \frac{{{\mu _{F_1^1}}({x_1}){\mu _{F_2^1}}({x_2})}}{{\sum\limits_{l = 1}^7 {{\mu _{F_1^1}}({x_1}){\mu _{F_2^1}}({x_2})} }}$$
((46))
$${\varphi _l}(x,u) = \frac{{{\mu _{F_1^1}}({x_1}){\mu _{F_2^1}}({x_2}){\mu _{F_5^1}}(u)}}{{\sum\limits_{l = 1}^7 {{\mu _{F_1^1}}({x_1}){\mu _{F_2^1}}({x_2}){\mu _{F_5^1}}(u)} }}$$
((47))

Step 5. Using all the data from the previous steps, we can construct the control law (19) with adaptive laws (30) and (31). The parameters of the control and adaptive laws are selected as

$${\alpha _1} = 9,\quad {\alpha _2} = 5,\quad {h_1} = 100,\quad {h_2} = 50,\quad {\eta _1} = {\eta _2} = 1.$$

Choose initial condition as x 1(0) = 0.5,\({\hat x_2}\)(0) = 0, and initial conditions for the adaptive parameters are chosen to be zero. Simulation results are shown in Figs. 4-6, respectively. Fig. 4 shows the state estimation errors ê 1 and ê 2, Fig. 5 shows the system output y and the reference signal y d . From Fig. 5, we can see that a good tracking performance has been achieved. Fig. 6 displays the control input signal u. From the simulation results, it can be seen that the proposed controller guarantees the boundedness of all the signals in the closed-loop system, and also achieves a good tracking performance. The comparison results between the proposed method and that in [20] show that there is lesser maximum overshoot response, and low control energy cost as compared to the method given in [20].

Fig. 4
figure 4

The state estimation errors

Full size image
Fig.5
figure 5

The system output y

Full size image
Fig. 6
figure 6

Control input u

Full size image

6 Conclusions

In this paper, an observer based DFLS scheme is developed for a class of uncertain nonlinear SISO systems. Since the state variables of SISO nonlinear systems are assumed to be unknown, the state observer is first designed to estimate state variables, via which adaptive fuzzy controller is developed. The fuzzy control law is robustified by an H ∞ compensator to attenuate the effect of disturbances, model uncertainties, and fuzzy approximation errors. The design of the control scheme is developed by Lyapunov synthesize approach to guarantee the stability of the overall closed-loop system. The proposed approach guarantees that all signals in the closed loop system are uniformly bounded and tracking errors fall to a small neighborhood of the origin. Application of the proposed approach to an inverted pendulum system has a good performance. Simulation results show the effectiveness of the proposed scheme.