1 Introduction

Whether the 2008 financial crisis or the recent COVID-19 crisis have a massive impact on companies and industries, making the dramatic fluctuation and recession of the market. In order to safeguard the portfolio and its value, the portfolio risk management becomes particularly important. The global minimum variance portfolio model (GMV) [14] is widely used in a volatile market, which belongs to the Markowitz mean-variance (MV) portfolio framework [21]. Although the GMV model has a good performance in the out-of-sample tests, it still suffers from estimation error of the covariance matrix [8, 10, 16] and tends to highly concentrated portfolios on a few assets [22]. Indeed, diversifying risk according to the risk contributors plays an crucial role in modern portfolio risk management.

The marginal risk was first introduced by CreditMetrics [23] to measure the risk contribution of a given asset, which is defined as the difference between the risk of the portfolio and the risk of the portfolio without the given asset. Specifically, Zhu et al. [35] defined the marginal risk by decomposing the covariance matrix of the asset return, and proposed a portfolio selection model with marginal risk control. It has been found by empirical study the model with marginal risk control is a suitable analytical tool for active portfolio risk management. Li et al. [19] used a factor model to capture the systematic risk and proposed the concepts of marginal systematic risk and relative marginal systematic risk. Then these two concepts were integrated respectively into the (MV) formulation to construct portfolio optimization model for actively allocating the systematic risk. The above models were solved by the branch-and-bound method, which converges slowly when solving the large scale problems [28]. To overcome the challenge of computational cost, an optimal trade-off model was proposed for portfolio selection with the effect of systematic risk diversification, which can be solved by the efficient accelerated gradient algorithm [17]. Several other approaches on risk diversification are proposed in [20, 24,25,26,27].

Although integrating the marginal (systematic) risk into portfolio selection conducts risk diversification, there are still some drawbacks in practical applications. A important issues is the considerable transaction cost and managerial concerns by over diversifying portfolio risk. A directly approach is that introducing the cardinality constraint to limit the total number of positions. There are many efficient methods to solve the cardinality constraint portfolio selection problem such as branch-and-bound method [6] and nonmonotone projected gradient (NPG) method [31]. Another natural approach is to augment the objective function with a penalty on the portfolio weight vector. The most famous convex penalty approach is adding an \(\ell _{1}\) norm penalty to the Markowitz framework [1, 7], which encourages sparse and stable portfolios [1, 10]. While the \(\ell _{1}\) norm penalty is ineffective in inducing sparsity with the budget and no short selling constraints, an alternative is the use of weighted \(\ell _{1}\) norm penalty [11]. To promote sparsity and countervail the shortcomings of convex penalty related to large biased coefficient values [12], Fastrich et al. [11] apply non-convex penalties, including \(\ell _{q}\)-penalty [4, 5, 32], smoothly clipped absolute deviation [9], log-sum penalty [3] and minimax concave penalty [33], to identify sparse and stable portfolios with desirable out-of-sample properties. Recently, Li et al. [18] introduced the weighted piecewise quadratic approximation (PQA) function as a new penalty in the MV portfolio framework. By utilizing PQA penalty, one can not only promotes sparsity and has a good out-of-sample performance, but also design a more efficient large-scale optimization algorithm to achieve a local minimizer.

Motivated by the challenges of portfolio risk management and realistic investment, Zhao et al. [34] developed a robust conditional value at risk optimal portfolio rebalancing model with both embedded sparsity and diversification, and then proposed an effective ADMM algorithm to solve this model. In this paper, under the mean-variance framework, we jointly integrate asset selection, risk diversification and some other investment constrains into consideration. An efficient first-order large-scale algorithm based on the structure of optimization problem is presented. Empirical analysis is constructed on the historical market data. The main contributions of this paper are described as follows.

First, we propose an optimal portfolio selection model which jointly considering risk diversification and sparse asset selection, abbreviated as the JMV model. The weighted piecewise quadratic approximation is considered as a penalty promoting sparsity for the asset selection. On the other hand, the risk diversification is also formulated as a penalty based on the definitions of the marginal risk and variance. Besides, by exposing the special structure of the JMV model, we prove that the KKT point of JMV is the local minimizer if the regularization parameter satisfies a mild condition. The numerical tests demonstrate that this condition can be easily satisfied. Then, we introduce the accelerated proximal gradient (APG) algorithm [30] to solve the JMV model. Meanwhile, a algorithm depended on projection onto the probability simplex is presented to solve the subproblem in APG algorithm. Under some mild conditions, the APG algorithm is linearly convergent to a local minimizer of JMV model. Empirical analysis not only demonstrate the theoretical results, but also show that JMV model has a better out-of-sample performance and achieves a better balance among risk diversification, sparsity and some other practical investment factors when compared with the existing models. Furthermore, the efficiency of APG algorithm on JMV model is illustrated in numerical experiments.

The reminder of the paper is organized in this way. In Sect. 2, we review the background of risk diversification and sparsity penalty, which serve as the preliminaries for our optimization model. In Sect. 3, we present an optimal portfolio selection model which jointly considering risk diversification and sparse asset selection. Then, we prove that the KKT point of the JMV model is the local minimizer. In Sect. 4, we present an accelerated proximal gradient (APG) algorithm for solving the JMV model. The convergence property of APG algorithm for the JMV model is derived. To assess the investment performance of the JMV model, some empirical analysis is carried out in Sect. 5. We also conduct some numerical experiments in Sect. 6 to show the efficiency of the algorithm. Finally, a conclusion of this paper is in Sect. 7.

2 Preliminaries

In this section, we first recall some relevant portfolio selection models and review the background of risk diversification and sparsity penalty, which serve as the preliminaries for our optimization model.

Suppose there are n risky assets with the random returns \({r}=(r_{1},\ldots ,r_{n})^{\top }\) in the financial market. The mean vector and the covariance matrix of r are denoted as \({\mu }\) and \(\Sigma \), respectively. The Markowitz mean-variance portfolio selection model [21] is formulated as follows:

$$ \begin{gathered} {\text{MV}}\,\,\,\,\,\,\,\,\min \;\;x^{ \top } \Sigma x - \tau \mu ^{ \top } x\hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,s.t.\;\;e^{ \top } x = 1,~~x \ge 0. \hfill \\ \end{gathered} $$

where \(\tau \ge 0\) is the parameter to balance the risk and return of the portfolio and e is a vector in which all elements are ones. If \(\tau =0\), MV model reduces to the global minimum variance portfolio model, which always has a better performance than MV model in the out-of-sample test. To diversify the risk, the marginal risk is proposed so that the risk contribution of a specific asset can be quantified.

Definition 1

[35] The marginal risk of asset i in a portfolio \(x=(x_{1},x_{2},...,x_{n})^{T}\), denoted by \(MR_{i}(x)\), is defined as:

$$\begin{aligned} MR_{i}(x)=x^{T}\Sigma _{i}x=\sigma _{ii}x_{i}^{2}+2\sum _{j\ne i}^{n}\omega _{ij}x_{i}x_{j}\sigma _{ij}, \end{aligned}$$
(1)

where \(\omega _{ij}=\sigma _{ii}/(\sigma _{ii}+\sigma _{jj})\) for \(i\ne j\), \(\omega _{ii}=1\) and

$$\begin{aligned} \Sigma _{i}=\left( \begin{array}{ccccc} 0 &{} \cdots &{} \omega _{i1}\sigma _{i1} &{} \cdots &{} 0 \\ \vdots &{} &{} \vdots &{} &{} \vdots \\ \omega _{i1}\sigma _{i1} &{} \cdots &{} \sigma _{ii} &{} \cdots &{} \omega _{in}\sigma _{in} \\ \vdots &{} &{} \vdots &{} &{} \vdots \\ 0 &{} \cdots &{} \omega _{in}\sigma _{in} &{} \cdots &{} 0 \\ \end{array} \right) . \end{aligned}$$

Based on this definition, \(\Sigma _{i}\) is generally an indefinite matrix which have one positive and one negative eigenvalue since it can be decomposed as:

$$\begin{aligned}\Sigma _{i} = \alpha _{i}u_{i}u_{i}^{\top }-\gamma _{i}v_{i}v_{i}^{\top }\end{aligned}$$

where \(\alpha _{i}>0\) and \(-\gamma _{i}<0\) are the two non-zero eigenvalues, and \(u_{i}\) and \(v_{i}\) are the corresponding orthogonal unit eigenvectors. As we all know, there are various portfolio selection model with marginal risk control. We introduce

$$\begin{aligned}R(x) = \sum _{i=1}^{n}\left( MR_{i}(x)-\theta \right) ^{2}\end{aligned}$$

to measure the risk concentration, where \(\theta \) is a parameter to balance the average risk contributions of the selected assets. The smaller the quantity R(x) is, the more uniformly the risk is distributed among the selected assets. However, this portfolio type usually increases the number of nonzero weights, which implies high transaction cost and managerial concerns.

To control the transaction and monitor cost, sparsity plays an important role in the formulation of investment portfolios. Naturally, the cardinality constraint \(\Vert {x}\Vert _0\le K\) is introduced to limit the total number of positions, where \(0\le K \le n\). The cardinality constraint is always approximated as convex or non-convex regularization. The piecewise quadratic approximation function is proposed as a non-convex regularization to encourage sparse solutions which theoretical and numerical superiority are demonstrated in [18]. Based on the weighted \(\ell _{1}\) norm and the background of portfolio management, we introduce the non-convex weighted piecewise quadratic approximation function:

$$\begin{aligned} S({x})=-{x}^{\top }V^{\top }V{x}+2\Vert V{x}\Vert _{1} = -{x}^{\top }W{x}+2\Vert V{x}\Vert _{1}, \end{aligned}$$

where \(V= \mathrm{{diag}}(w_1, \cdots , w_n)\), \(w_i> 0\) is the individual regularization weight parameter of asset i. In practice, the investors can restrict the investment proportions of assets that are predicted to be more volatile or unfavorable. Fortunately, the weight parameter \(w_i\) can be used to control the investment proportion of asset i.

For simplicity, the support of \(x\in {\mathbb {R}}^{n}\) is \(\text {supp}(x):=\{i\mid x_{i}\ne 0, i=1, 2, \ldots , n\}\). \(\nabla f(x)\) is the gradient of f(x), \(\nabla ^{2} f(x)\) is the Hessian matrix of f(x). For any matrix \(A, B\in {\mathbb {R}}^{n\times n}\), \(A\succeq B\) if and only if \(A-B\) is a positive semidefinite matrix, \(A\succ B\) if and only if \(A-B\) is a positive definite matrix. For any index set \(S\subset \{1, 2, \ldots , n\}\), we denote \(A_{SS}\) as the sub-matrix of A with the rows and columns restricted to S. \(x_{S}\) represents the sub-vector consisting of only the components \(x_{i}, i\in S\).

3 JMV model and theory

In this section, we present an optimal portfolio selection model which jointly considering risk diversification and sparse asset selection. And then we develop the theoretical results on local optimality of the proposed model.

In this paper, we propose the following portfolio selection model which jointly considering risk diversification and sparsity:

$$ \begin{gathered} {\text{JMV}}\,\,\,\,\,\,\,\,\min \;\;x^{ \top } \Sigma x - \tau \mu ^{ \top } x + \lambda _{1} R(x) + \lambda _{2} S(x) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,s.t.\;\;e^{ \top } x = 1,~~x \ge 0. \hfill \\ \end{gathered} $$

where \(\lambda _{1}, \lambda _{2} \ge 0\) are the regularization parameters that control the degrees of risk diversification and sparsity, respectively.

If \(\lambda _{2}=0\), the JMV model is the risk diversification portfolio selection:

$$ \begin{gathered} {\text{RDMV}}\,\,\,\,\,\,\,\,\min \;\;x^{ \top } \Sigma x - \tau \mu ^{ \top } x + \lambda _{1} R(x)\hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,s.t.\;\;e^{ \top } x = 1,~~x \ge 0. \hfill \\ \end{gathered} $$

If \(\lambda _{1}=0\), the JMV model is the sparsity portfolio selection:

$$ \begin{gathered} {\text{SMV}}\,\,\,\,\,\,\,\,\min \;\;x^{ \top } \Sigma x - \tau \mu ^{ \top } x + \lambda _{2} S(x)\hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,s.t.\;\;e^{ \top } x = 1,~~x \ge 0. \hfill \\ \end{gathered} $$

Denoting \({q}=2\lambda _{2} V{e}-\tau {\mu }\), the JMV model can be rewritten as follows:

$$\begin{aligned} \min\;\;\;{x}^{\top }\Sigma {x}+{q}^{\top }{x}+ \lambda _{1}R(x)-\lambda _{2} {x}^{\top }W x\\ \mathrm{s.t.}\;\;\;{e}^{\top }{x}=1,~~{x}\ge {0}. \end{aligned}$$

Denote the objection function as F(x). The KKT conditions of this model are:

$$ \begin{gathered} e^{ \top } x = 1,~~~x \ge 0,~~~\phi _{i} x_{i} = 0,~~~\phi _{i} \ge 0,~~~i = 1, \cdots ,n, \hfill \\ 2\Sigma x + 4\lambda _{1} \sum\limits_{{i = 1}}^{n} M R_{i} (x)\Sigma _{i} x - 4\lambda _{1} \theta \Sigma x - 2\lambda _{2} Wx + q - \nu e - \phi = 0,~~\nu \in \mathbb{R}, \hfill \\ \end{gathered} $$

where \(\phi \) and \(\nu \) are Lagrange multipliers. Let \({x}^{*}\) be the stationary point of the JMV model, \(L=\{i\mid x_{i}=0, \phi _i=0, i=1, 2, \cdots , n\}\), E is the complement of L, \(\sigma \) denote the smallest eigenvalue of \(\Sigma _{EE}\), and \(\omega \) is the largest eigenvalue of \(W_{EE}\). In the following, we will show that the stationary point \({x}^{*}\) is a local minimizer of JMV under a suitable regularization parameter.

Theorem 1

Let \({x}^{*}\) be the stationary point of the JMV model. If the regularization parameters satisfy \(0\le 4\lambda _1 \le 1/\theta \) and \(0\le 2\lambda _2 \le \sigma /\omega \), then \({x}^*\) is a local minimizer of the JMV model.

Proof of Theorem 1

By the second-order optimality condition, to justify the theorem, we only need to show that there is a feasible direction h where \(e^{\top }h=0\), \(x^{*}+ h\ge 0\), \(\{h_i=0~\mid ~i\in L\}\) and \(\Vert h\Vert <\varepsilon , \varepsilon >0\), such that \(h^{\top }\nabla ^{2}F(x^{*})h>0\). For this purpose, we first get

$$ \begin{gathered} \nabla ^{2} F\left( {x^{*} } \right) = 2\Sigma - 2\lambda _{2} W + 4\lambda _{1} \sum\limits_{{i = 1}}^{n} {\left( {2\Sigma _{i} x^{*} x^{*{ \top }} \Sigma _{i} + x^{{*{ \top }}} \Sigma _{i} x^{*} \Sigma _{i} - \theta \Sigma _{i} } \right)} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \left( {\Sigma - 2\lambda _{2} W} \right) + \left( {8\lambda _{1} \sum\limits_{{i = 1}}^{n} {\Sigma _{i} } x^{*} x^{*{ \top }} \Sigma _{i} + 4\lambda _{1} \sum\limits_{{i = 1}}^{n} {x^{*{ \top }} } \Sigma _{i} x^{*} \Sigma _{i} + (1 - 4\lambda _{1} \theta )\Sigma } \right) \hfill \\ \end{gathered} $$

By h is a feasible direction, we have

$$\begin{aligned}h^{\top }\left( \Sigma -2\lambda _{2}W\right) h= h_{E}^{\top }\left( \Sigma _{EE} -2\lambda _{2}W_{EE}\right) h_{E}. \end{aligned}$$

If \(2\lambda _2 \le \sigma /\omega \), then \(h^{\top }\left( 2\Sigma -2\lambda _{2}W\right) h> 0\).

On the other hand,

$$\begin{aligned}\begin{aligned} ~&h^{\top }\left( 8\lambda _{1}\sum _{i=1}^{n}\Sigma _{i}x^{*}x^{*\top }\Sigma _{i}+ 4\lambda _{1}\sum _{i=1}^{n}x^{*\top }\Sigma _{i}x^{*}\Sigma _{i}+(1-4\lambda _{1}\theta )\Sigma \right) h\\&\quad \ge ~~ \frac{8\lambda _{1}}{n}(x^{*\top }\Sigma h)^2+(1-4\lambda _{1}\theta )h^{\top }\Sigma h-4\lambda _{1}\sum _{i=1}^{n}\left( x^{*\top }\Sigma _{i}x^{*}\right) ^2\sum _{i=1}^{n}\left( h^{*\top }\Sigma _{i}h^{*}\right) ^2\\&\quad \ge ~ ~\frac{8\lambda _{1}\sigma }{n}\Vert x^{*}\Vert ^2\Vert h\Vert ^2 + (1-4\lambda _{1}\theta )\sigma \Vert h\Vert ^2-4\lambda _{1}\sum _{i=1}^{n}\left( x^{*\top }\Sigma _{i}x^{*}\right) ^2\sum _{i=1}^{n}\alpha _{i}^{2}\Vert h\Vert ^{4}\\&\quad >~~0 \end{aligned} \end{aligned}$$

If \(0\le 4\lambda _1 \le 1/\theta \) and

$$\begin{aligned}\Vert h\Vert ^{2}< \frac{1}{4\lambda _{1}\sum _{i=1}^{n}\left( x^{*\top }\Sigma _{i}x^{*}\right) ^2\sum _{i=1}^{n}\alpha _{i}^{2}}\left( \frac{8\lambda _{1}\sigma }{n}\Vert x^{*}\Vert ^2 + (1-4\lambda _{1}\theta )\sigma \right) ,\end{aligned}$$

then the above last inequality hold.

In conclusion, if \(0\le 4\lambda _1 \le 1/\theta \) and \(0\le 2\lambda _2 \le \sigma /\omega \), \({x}^*\) is a local minimizer of the JMV model. \(\square \)

In numerical experiments, we will illustrate that setting \(0\le 4\lambda _1 \le 1/\theta \) and \(0\le 2\lambda _2 \le \sigma /\omega \) are reasonable and enough to get the desired optimal portfolios.

4 Accelerated proximal gradient algorithm

In this section, we present an accelerated proximal gradient (APG) algorithm for solving the JMV model.

4.1 APG algorithm for JMV

Denote \(f({x}) = {x}^{\top }\Sigma {x} + \lambda _{1}R(x)-\lambda _{2} {x}^{\top }W x\),

$$\begin{aligned}g(x)= {\left\{ \begin{array}{ll} q^{\top }x, &{} x\in X,\\ +\infty ~, &{} x\not \in X, \end{array}\right. }\end{aligned}$$

where \(X = \{{x}\in {\mathbb {R}}^n \mid ~{e}^{\top }{x}=1,~{x}\ge 0\}\). Then, the JMV model can be expressed as following:

$$\begin{aligned} \min _{{x}\in {\mathbb {R}}^n}&F(x) = f({x})+g({x}). \end{aligned}$$
(2)

Actually, X is equivalent to the feasible set of the above optimization problem. We use \({\mathcal {X}}\) to denote the set of stationary points of F(x). We choose a sufficiently large constant l such that

$$\begin{aligned} f_1(x) = f(x) + \frac{l}{2} \Vert x\Vert ^{2},~~~~f_2(x) = \frac{l}{2} \Vert x\Vert ^{2}\end{aligned}$$

are continuously differentiable and convex. On the feasible set X, \(\nabla f_1\) and \(\nabla f_2\) are Lipschitz continuous with modulus \(L>0\) and \(l>0\), respectively. Moreover, by taking a larger L if necessary, we assume throughout that \(L> l\). Thus, \(f(x)=f_1(x)-f_2(x)\) has Lipschitz continuous gradient, the Lipschitz continuity constants of \(\nabla f\) is L.

The accelerated proximal algorithm for solving the JMV model is as following:

figure a

By the definition of the proximal operator, we note that the Eq. (3) is equivalently given by

$$\begin{aligned} {x}^{k+1}= arg \min _{{x}\in {\mathbb {R}}^n} \left\{ \langle \nabla f({y}^{k}), {x}\rangle +\frac{L}{2}\Vert {x}-{y}^{k}\Vert ^{2}+g({x})\right\} . \end{aligned}$$
(3)

This subproblem is the key iteration of APG algorithm. Next, we first introduce how to solve the subproblem and then analysis the convergence of the APG algorithm for JMV model.

4.2 Solving the subproblem

The subproblem (3) can be expressed as the following optimization problem:

$$\begin{aligned}&\min \quad \frac{1}{2}\left\| {x}-B({y})\right\| ^2 \nonumber \\&\begin{array}{r@{\quad }r@{}l@{\quad }l} \mathrm{s.t.} &{}\quad {e}^{\top }{x}=1,~~{x}\ge {0},\\ \end{array} . \end{aligned}$$
(4)

where

$$\begin{aligned}B({y})=[I-\frac{1}{L}(2\Sigma + 4\lambda _{1}\sum _{i=1}^{n}MR_{i} (y)\Sigma _i - 4 \lambda _{1}\theta \Sigma -2\lambda _{2} W)]{y}-\frac{1}{L}{q}.\end{aligned}$$

This is to compute the Euclidean projection of a point B(y) onto the probability simplex. We adopt the algorithm in [29] to solve this problem.

4.3 Convergence of APG algorithm

By the convergence properties of the APG algorithm in [30], we can get that any accumulation point of the sequence \(\{{x}^{k}\}\) generated by APG algorithm is a stationary point of JMV model. Furthermore, under the following Assumption 1, the local linear convergence rate of the sequence \(\{{x}^{k}\}\) and \(\{F\left( {x}^{k}\right) \}\) are hold.

Assumption 1

[30]

  1. (i)

    For any \(\xi \ge \inf _{x\in {\mathbb {R}}^n} F(x)\), there exist \(\epsilon >0\) and \(\tau >0\) such that

    $$\begin{aligned}\text {dist}~(x, {\mathcal {X}})\le \nu \left\| \text {Prox}_{\frac{1}{L}g}\left( x-\frac{1}{L}\nabla f(x)\right) -x\right\| \end{aligned}$$

    whenever \(\left\| \text {Prox}_{\frac{1}{L}g}\left( x-\frac{1}{L}\nabla f(x)\right) -x\right\| <\epsilon \) and \(F(x)\le \xi \), where \(\text {dist}~(x, {\mathcal {X}})=\inf _{y\in {\mathcal {X}}}\Vert x-y\Vert \).

  2. (ii)

    There exists \(\delta >0\), such that \(\Vert x-y\Vert \ge \delta \) whenever \(x, y\in {\mathcal {X}}, F(x)\ne F(y)\)

Next, we first justify the above assumption is satisfied in the JMV model.

Lemma 1

If the regularization parameters satisfy \(0\le 4\lambda _1 \le 1/\theta \) and \(0\le 2\lambda _2 \le \sigma /\omega \), then the objective function F(x) of JMV model satisfies the Assumption 1.

Proof of Theorem 1

i) First, we prove that if there exists \(\epsilon >0\) such that, for any \(x\in X\) with \(\left\| \text {Prox}_{\frac{1}{L}g}\left( x-\frac{1}{L}\nabla f(x)\right) -x\right\| <\epsilon \), then it has a \(x^{*}\in {\mathcal {X}}\) such that \(\text {supp}({x})=\text {supp}({x^{*}})\). By contraction, if the claim does not hold, there would exist an \(S\subseteq \{1, 2, \cdots , n\}\) and a sequence of vectors \(\{x^1, x^2, \cdots \}\) satisfying \(\text {supp}(x^r)=S\) for all r and \(x^r - z^r\rightarrow 0\) where \(z^r=\text {Prox}_{\frac{1}{L}g}\left( x^r-\frac{1}{L}\nabla f(x^r)\right) \), and yet there is no \(x^{*}\in {\mathcal {X}}\) for \(\text {supp}(x^{*})=S\). By [29], the projection \(z^r\) can be easily determined through \(B(x^r)\). Denote

$$\begin{aligned}\rho =\max \{1 \le i \le n:\eta _i+\frac{1}{i}(1-\sum _{j=1}^{i}\eta _j)\},\end{aligned}$$

where \(\eta _1\ge \eta _2\ge \cdots \eta _n\) is the sorted sequence of the elements of \(B(x^r)\). The elements of the projection can be written as

$$\begin{aligned}z^{r}_i=\max \{B(x^r)_i+\delta ,~0\},~~~i=1,\ldots , n,~~~\mathrm{where}~\delta = \frac{1}{\rho }(1-\sum _{j=1}^{\rho }u_j).\end{aligned}$$

That is to say, only the dimensions corresponding to the largest \(\rho \) elements of \(B(x^r)\) are nonzero. Since \(\{({x}^{r},~{z}^{r})\}\) are bounded, then every one of its cluster points \(({\widehat{x}},~{\widehat{z}})\) satisfies

$$\begin{aligned}{\widehat{z}}={\widehat{x}}=\text {Prox}_{\frac{1}{L}g}\left( {\widehat{x}}-\frac{1}{L}\nabla f({\widehat{x}})\right) .\end{aligned}$$

As a result, the largest \(\rho \) elements of \(B(x^r)\) will be in the same dimensions as in \(B({\widehat{x}})\) when r is large enough,

$$\begin{aligned}\mathrm{{supp}}({x}^{r})=\mathrm{{supp}}({\widehat{x}})=S.\end{aligned}$$

Moreover, \({\widehat{x}}\) is a stationary point of JMV model, i.e. \({\widehat{x}}\in {\mathcal {X}}\), which contradicts our earlier hypothesis. Therefore, it has a \(x^{*}\in {\mathcal {X}}\) such that \(\text {supp}({x})=\text {supp}({x^{*}})\).

Next, we prove that the Assumption 1 i) holds. When \(\left\| z-x\right\| <\epsilon \), \(z=\text {Prox}_{\frac{1}{L}g}\left( x-\frac{1}{L}\nabla f(x)\right) \), there exists a \(x^{*}\in {\mathcal {X}}\) such that \(\text {supp}({x})=\text {supp}({x^{*}})\) and \(\text {dist}(x, {\mathcal {X}})=\Vert x-x^{*}\Vert \). Since

$$\begin{aligned} \Vert x-x^{*}\Vert \le \left\| x-z\right\| +\left\| z-x^{*}\right\| \end{aligned}$$
(5)

and

$$\begin{aligned}&\left\| z-x^{*}\right\| \le \left\| \left[ I-\frac{1}{L}(2\Sigma + 4\lambda _{1}\sum _{i=1}^{n}\left( 2\Sigma _{i}\xi \xi ^{\top }\Sigma _{i}\right. \right. \right. \\&\quad \left. \left. \left. + \xi ^{\top }\Sigma _{i}\xi \Sigma _{i}\right) - 4 \lambda _{1}\theta \Sigma -2\lambda _{2} W)\right] ({x} -x^{*})\right\| \end{aligned}$$

where \(\xi \) is between x and \(x^{*}\). By Theorem 1, we know that \(h^{\top }\nabla F(x^{*}) h>0\), where \(\text {supp}(h)=S\). So if \(\epsilon \) is small enough, we have

$$\begin{aligned}0\prec \left( 2\Sigma + 4\lambda _{1}\sum _{i=1}^{n}\left( 2\Sigma _{i}\xi \xi ^{\top }\Sigma _{i}+ \xi ^{\top }\Sigma _{i}\xi \Sigma _{i}\right) \right) _{SS}\prec LI.\end{aligned}$$

Thus

$$\begin{aligned} \left\| z-x^{*}\right\| \le c\left\| x-x^{*}\right\| ,~~~~0<c<1.\end{aligned}$$
(6)

Combining (5) and (6), we obtain that there exists \(\nu >0\) such that

$$\begin{aligned}\Vert x-x^{*}\Vert \le \nu \left\| x-z\right\| =\nu \left\| x-\text {Prox}_{\frac{1}{L}g}\left( x-\frac{1}{L}\nabla f(x)\right) \right\| .\end{aligned}$$

This proves i).

ii) Based on \(\nabla F(x^{*})\) is positive definite, it is easy to get that ii) holds. \(\square \)

In what follows, we can get the linear convergence rate of the APG algorithm for JMV model.

Theorem 2

Let \(\{{x}^{k}\}\) be the sequence generated by the APG algorithm, if \(0\le 4\lambda _1 \le 1/\theta \) and \(0\le 2\lambda _2 \le \sigma /\omega \), then \(\{{x}^{k}\}\) is linearly convergent to a local minimizer of the JMV model.

5 Empirical analysis

In this section, some empirical analysis are conducted on the proposed JMV, not only to evaluate its out-of-sample performance by employing real market data, but also to demonstrate the validity of our theoretical analysis on JMV.

5.1 Data and models

In the following empirical analysis, we compare the portfolio performance of the proposed JMV with these models:

  • MV: The Markowitz minimum-variance portfolio model [21].

  • EW: Equally-weighted risk contributions [20].

  • LMV: The weighted \(\ell _{1}\) regularized portfolio selection model [11].

  • SMV: The sparse portfolio selection model.

  • RDMV: The risk diversification portfolio selection model.

The optimal solutions of the MV and LMV models are computed by the optimization package CVX [13]. The equally-weighted risk contributions solution is solved as in [20]. The accelerated proximal gradient algorithm are used to solve the SMV, RDMV and JMV models, where we terminate the algorithms when an \(\epsilon \)-optimal solution is achieved or the number of iterations exceed 3000. The error precision is set to \(\epsilon = 10^{-5}.\)

To compare the above models, three different data sets are considered, including the weekly returns of the S &P 500, as well as the monthly returns of the 48 and 100 Fama French portfolios. The detail information of data set are list in Table 1. Note that the investment period includes the 2008 financial crisis, which is selected on purpose to test the portfolios performance in an unstable investment environment. Consequently, their ability to resist dramatic fluctuations can be compared.

Table 1 Information of data set
Full size table

We set \(\tau =0\) in the tested models. The weight parameters w in the LMV, SMV and JMV models are determined by considering specific financial time series properties, as suggested in [11]. The acceleration parameters in the APG algorithm are selected as

$$\begin{aligned}\beta _{k} \equiv 0.98\sqrt{\frac{L}{L+l}}.\end{aligned}$$

The parameter \(\theta \) is set as

$$\begin{aligned}\theta = \frac{{\overline{x}}^{\top }\Sigma {\overline{x}}}{{\overline{K}}},\end{aligned}$$

where \({\overline{x}}\) is the optimal portfolio solution of the MV model, \({\overline{K}}=\Vert {\overline{x}}\Vert _{0}\).

5.2 Performance measures

We demonstrate the theoretical results and evaluate the out-of-sample performance of the proposed JMV by the two tests included in-sample test on JMV and out-of-sample evaluation via realistic investment.

We use backtesting to compare the out-of-sample performances of the optimal portfolios generated by the tested models. The tests are performed in a rolling horizon fashion as follows: We choose a window with the size of \(\Gamma =100\) to construct the estimation. The tested models are then respectively solved to generate portfolio strategies for the following 10 weeks. At \(\Gamma + 11\), the estimation is updated using the data from 11 up to \(\Gamma +10\). The models are re-solved to produce new optimal portfolios for the following 10 weeks. The above procedure repeats until the end of the out-of-sample period.

We utilize the optimal portfolios generated by the tested models to compute the following performance measures. The out-of-sample mean (\({\overline{r}}\)), the out-of-sample risk (\(s^2\)) and the out-of-sample Sharpe ratio (Sh) are defined as:

$$\begin{aligned}{\overline{r}}= \frac{1}{T-\Gamma }\sum _{t=\Gamma }^{T-1}{r}_{t+1}^{\top }{x}_{t},~~~s=\sqrt{\frac{1}{T-\Gamma -1}\sum _{t=\Gamma }^{T-1}\left( {r}_{t+1}^{\top }{x}_{t}-{\overline{r}}\right) },~~~\mathrm{Sh}=\frac{{\overline{r}}}{s}.\end{aligned}$$

where \({r}_{t}\) is the random return vector at time t, \({x}_{t}\) is the optimal portfolio vector at time t. The number of selected assets for investment (No) is computed as:

$$\begin{aligned}\mathrm{No}=\frac{1}{\Gamma }\sum _{i=1}^{\Gamma }\mid \mathrm{supp}({x}_{i})\mid .\end{aligned}$$

The larger the value of the number, the more assets need to manage. Suppose that there are M selected assets and the maximum marginal risk (MMR) in selected assets is:

$$\begin{aligned}\text {MMR} = \max _{i=1, 2, \cdots , M} \text {MR}_i(x).\end{aligned}$$

The smaller the value of MMR, the better effect of risk diversification. The turnover (TO) represents the average weekly trading volume, which is defined as:

$$\begin{aligned}\mathrm{TO}=\frac{1}{T-\Gamma -1}\sum _{t=\Gamma }^{T-1}\left\| {x}_{t+1}-{x}_{t}\right\| _1.\end{aligned}$$

Taking the transaction fee into account, a large turnover will wipe out the gains of portfolios. Let \(W_0\) is the initial wealth, the cumulative profit (W) is

$$\begin{aligned}W=W_0\prod _{t=\Gamma }^{T-1}(1+{r}_{t+1}^{\top }{x}_{t}).\end{aligned}$$

Transaction cost is closely related to the turnover, in our empirical analysis, we consider that the transaction cost is 1% of the trading volume for each trade (selling and buying) of asset. Then the net profit can be computed as

$$\begin{aligned}\mathrm Net~Profit = Profit - Transaction~Cost.\end{aligned}$$

5.3 Empirical results

5.3.1 In-sample test on JMV

We consider a portfolio selection problem with historical data from the S &P 500, where the weekly returns of 50 randomly selected stocks from 5th, January 2006 to 27th, September 2010 are used to construct the test model. We set a grid of 90 ascending values from 8000 to 39600 and from \(8\times 10^{-5}\) to \(3.96\times 10^{-5}\) for the regularization parameter \(\lambda _{1}\) and \(\lambda _{2}\) in the JMV model, respectively.

Figure 1 shows how the sparsity, Sharpe ratio, risk and max marginal risk of the optimal portfolios generated by JMV vary with the regularization parameters \(\lambda _1\) and \(\lambda _2\). Unsurprisingly, we can see that when the value of \(\lambda _1\) increases, the max marginal risk is decreasing and the number of nonzero assets in the optimal portfolio is both decreasing. When the value of \(\lambda _2\) increases, the max marginal risk and the number of nonzero assets in the optimal portfolio are all increasing. Moreover, the values of the sparsity, Sharpe ratio, risk and max marginal risk are more sensitive to the parameter \(\lambda _1\). With the increase of \(\lambda _1\), the Sharpe ratio of the optimal portfolio decreases and the risk of the optimal portfolio increases. On the other hand, with the increase of \(\lambda _2\), the Sharpe ratio of the optimal portfolio increases and the risk of the optimal portfolio decreases.

Note that, in more than 50% area, the value of the Sharpe ratio is basically similar from 8.36 to 9.15, while the values of the sparsity and the max marginal risk are quite different. This illustrates that JMV model can generate a portfolio with a sufficient sparsity level, a good effect of risk diversification and a large Sharpe ratio.

Fig. 1
figure 1

No, Sh, \(s^2\) and MMR for Optimal Portfolios Generated by JMV

Full size image

Moreover, to demonstrate the theoretical guarantee of the local minimizer of JMV, Fig. 2 shows how the smallest eigenvalue of Hessian matrix for nonzero assets vary with \(\lambda _1\) and \(\lambda _2\) in this test. From Fig. 2, we can see that the smallest eigenvalue of Hessian matrix are lager than zero, which means the JMV model can achieve the local minimizer in numerical experiments.

Fig. 2
figure 2

The smallest eigenvalue of Hessian matrix for different \(\lambda _1\) and \(\lambda _2\)

Full size image

5.3.2 Out-of-sample evaluation via realistic investment

To further demonstrate the strength of JMV, we report the real market performances of different models via backtesting on the three data sets shown in Table 1. The initial wealth is set as 100 at the beginning of backtesting. For each rolling window, a sufficiently wide range of regularization parameter in tested models is implemented to produce an ensemble of portfolios containing different numbers of nonzero portfolios and effect of risk diversification. Among these, we select the best regularization parameters in tested models which produces a portfolio with the largest Sharpe ratio.

Fig. 3
figure 3

Evolution of portfolio values for S &P 500

Full size image
Fig. 4
figure 4

Evolution of portfolio values for FF 48

Full size image
Fig. 5
figure 5

Evolution of portfolio values for FF 100

Full size image

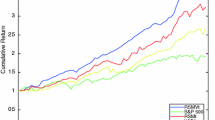
Fig. 3 illustrates the portfolio values from 6 December 2007 to 13 December 2011 for S &P 500. During the time period from December, 2007 to January, 2009, the portfolio values of all the tested models are decreasing, where the EW decreasing fastest. Notice that the period from December, 2007 to January, 2009 is mainly a period featured by financial crisis. Moreover, we set \(\tau =0\) in out-of-sample analysis which means that we focus on risk minimization in the MV model, so the performance of the JMV model is a little better than that of the MV model. The financial market begin growing in the beginning of 2009. From the beginning of 2009 to the end of 2010, the portfolio values of the JMV and RDMV models preform better than those of the EW, LMV, SMV and MV models, among which the performance of MV is the worst. At the end of 2010 the economy began to grow steadily, the performance of the EW, SMV and LMV models is getting better. Figures 4 and 5 illustrate the portfolio values from June 2008 to February 2020 for FF 48 and FF 100, respectively. They exhibit that the portfolio values of JMV perform the best during the whole period, compared with other tested models.

Table 2 Recovery results of a signal with different number of samples
Full size table

In addition, the results are shown in Table 2, including the number of nonzero portfolios, turnover and net profit of the optimal portfolios generated by all the tested models for S &P 500, FF 48, and FF 100. Looking at the number of nonzero portfolios in Table 2, we note that the risk of the portfolio generated by JMV model is neither concentrated on a few assets nor distributed to many assets. SMV model can produce optimal portfolios with the fewest number of nonzero portfolios for FF48 and FF100, and fewer number than MV, EW, RDMV and JMV for S &P 500. With regard to the turnover, equally-weighted risk contributions portfolio is the lowest. Because equally-weighted risk contributions portfolio assigns the capital equally to all stocks, which making it difficult to manage. JMV is comparatively similar with RDMV in the aspect of turnover. However, in the terms of profit, the JMV model generates the largest net profit.

6 Numerical experiments

In this section, we compare the computational results of APG algorithm on JMV with the other two important first-order algorithms, including the proximal gradient algorithm [15] and the fast iterative shrinkage-thresholding algorithm (FISTA) [2]. The APG algorithm and FISTA are the accelerated first-order algorithms, the difference is that the acceleration parameters are different. The numerical experiments are carried out using MATLAB 2018(a) on a PC with 2.50GHZ CPU processor and 8GB of RAM.

The randomly generated problems are used to test these algorithms. The test probelms are randomly generated by the same method mentioned in Li et al. [19]: The mean vector \(\mu =(\mu _{1}, \mu _{2}, \ldots ,\mu _{n})^{\top }\). The variance matrix

$$\begin{aligned}\Sigma = \left( \sum _{l=1}^{m}\sum _{k=1}^{m}\eta _{ik}\sigma _{kl}\eta _{jl}\right) _{n\times n}+ \mathrm{{diag}}(\sigma _{\epsilon _{1}}, \sigma _{\epsilon _{2}}, \cdots , \sigma _{\epsilon _{n}}).\end{aligned}$$

  • \(\mu _{i}\in [0, 0.03]\) and \(\sigma _{\epsilon _{i}}\in [0, 0.002]\) are generated by the uniform distribution, \(i=1, 2, \ldots , n\).

  • \(\sigma _{ij}\) is calculated with randomly sampled series from [0, 0.03], \(i=1, 2, \ldots ,m,\) \(j=1, 2, \ldots ,m\), \(m=n/10\).

  • \(\eta _{ij}\in [0.3, 2]/m\) is randomly generated by the uniform distribution, \(i=1, 2, \ldots ,n,\) \(j=1, 2, \ldots , m\).

In this part, the regularization parameters are set as \(\lambda _1=100\), \(\lambda _2=0.00001\). The weighted parameters are set as \(w_i=1/2,~i=1, 2, \ldots , n\), while the error precision is set as \(\epsilon = 10^{-5}\).

Fig. 6
figure 6

Comparisons of iterations of three first-order algorithms

Full size image

The comparison results of three first-order algorithms are summarized in Fig. 6, where n is the dimension of the problem and “Iteration” is the average number of iterations consumed to solve the ten randomly generated test problems. We can see that the accelerated first-order algorithms outperform the PG algorithm. Moreover, the APG algorithm is always the fastest one.

7 Conclusion

In this paper, we have utilized the weighted piecewise quadratic approximation function as a penalty term to promote sparsity, and the variance associated with the marginal risk as another penalty term to diversify the risk. Then, the optimal portfolio selection model which jointly considering risk diversification and sparse asset selection have been proposed. By exposing the feature of the JMV model, it is proved that the KKT point of JMV is the local minimizer under a mild condition. To solve this model, we have introduced the accelerated proximal gradient (APG) algorithm and presented the linear convergence rate of APG algorithm for solving JMV.

To demonstrate the validity and usefulness of this model, empirical analysis have been constructed on the historical datas of the S &P 500, FF48 and FF100. In-sample test is shown that JMV can attain portfolios with a sufficient sparsity level, a good effect of risk diversification and a large Sharpe ratio. Compared with the MV, EW, LMV, SMV, and RDMV models, JMV has a better out-of-sample performance and achieves a better balance among risk diversification, sparsity and some other practical investment factors. Numerical experiments also illustrate the superiority of APG algorithm on JMV model.