Model Dynamics and Optimal Control for Intervention Policy of COVID-19 Epidemic with Quarantine and Immigrating Disturbances

Abstract

A dynamic model called SqEAIIR for the COVID-19 epidemic is investigated with the effects of vaccination, quarantine and precaution promotion when the traveling and immigrating individuals are considered as unknown disturbances. By utilizing only daily sampling data of isolated symptomatic individuals collected by Mexican government agents, an equivalent model is established by an adaptive fuzzy-rules network with the proposed learning law to guarantee the convergence of the model’s error. Thereafter, the optimal controller is developed to determine the adequate intervention policy. The main theorem is conducted to demonstrate the setting of all designed parameters regarding the closed-loop performance. The numerical systems validate the efficiency of the proposed scheme to control the epidemic and prevent the overflow of requiring healthcare facilities. Moreover, the sufficient performance of the proposed scheme is achieved with the effect of traveling and immigrating individuals.

1 Introduction

At the end of 2019, a new disease caused by the virus severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) or COVID-19 has been discovered in Wuhan, China. Thereafter, an outbreak of COVID-19 continued to spread around the world and affected economic, education, food security and health issues (Worldometers 2022). Several preventive measures such as social distancing, locking down, vaccination and so on have been recommended and utilized to counteract the epidemic (Giordano et al. 2020). Therefore, the negative effects have been notified such that businesses shunting down, unemploying, the ineffectiveness of online education and limited vaccination and healthcare facilities (Wei et al. 2020; Ourworldindata 2022). To minimize those effects, the development of a sufficient intervention policy with model dynamics for forecasting the epidemic is imperative (Deka et al. 2020; Aghdaoui et al. 2021).

Fig. 1

Infected cases of Mexico’s COVID-19 epidemic: Data from CONACyT (Government of Mexico 2021a) (Color figure online)

Moreover, the epidemic of COVID-19 has already spread to Mexico in four waves from January 2020 until 23 February 2022. Figure 1 shows the record of daily infected cases recorded by COVID-19 DataLab CONACyT, Mexico (Government of Mexico 2021a). Causing by the omicron variant, the fourth wave has been detected since November 2021 and the peak has been observed as 70,000 cases approximately. Obviously, this peak is very higher than the previous three waves. As a result, the healthcare facilities have been over demanded (Government of Mexico 2021b, c). Thus, an effective intervention policy is rigidly required to control the epidemic according to the limited resources.

By the formulations of nonlinear ODEs (ordinary differential equations), the dynamics of epidemics have been utilized by mathematic models for sufficient information to design the adequate intervention strategies (Leonardo and Xavier 2021; Giordano et al. 2021; Sun and Wang 2020; Liu 2021). The set of equations has been established by the developed SEIR model (Engbert et al. 2021; Jia and Chen 2021) when the individuals have been classified by the following states: Susceptible (S), Exposed (E), Infectious (I) and Recovered (R). By detailing classification, the mathematical model called SIDARTHE (Giordano et al. 2020) has been developed under the distinction between non-diagnosed and diagnosed individuals. Thereafter, the investigations to design the sufficient policy have been conducted such as the next–generation matrix optimization (Perkins and Guido 2020; Xie et al. 2020), the fuzzy fractional derivatives optimal control (Dong et al. 2020), threshold dynamics vaccination (Al-Darabsah 2020), optimal sliding mode control (Amiri-Mehra et al. 2019) and so on. Even so, the performance of those schemes is strictly related to the model’s accuracy and the intensive measurement of state variables.

As a matter of fact, all state variables can not be easy to be obtained or monitored at all times under the concept of continuous-time ODEs (Auger and Moussaoui 2021). Thus, from the practical point of view, only some states are available at a daily interval (Zhan et al. 2021; Sooknanan and Mays 2021). Furthermore, immigration and traveling can be considered as a factor that causes the spread of COVID-19 according to the advanced air-traveling business (Government of Mexico 2021d; Abbasi et al. 2020). Thus, the impulsive disturbances caused by traveling people can lead the epidemic dynamics to be a class of impulsive control systems (ICS) when the disturbances are considered occurring on the impulsive axis (Villa-Tamayo and Rivadeneira 2020; Bachar et al. 2016; Ren et al. 2020).

For a class of discrete-time systems, ICS schemes have been proposed by some works such that (Gao et al. 2011; Liguang and Shuzhi 2016). It is worth mentioning that those controllers for ICS have focused on linear systems with well-defined models (He and Xu 2015; Nieto et al. 2011). By considering optimal-control approaches with ICS, only limited schemes have been recently proposed such as a linear-quadratic (LQ) controller (Cacace et al. 2020), an adaptive dynamic programming (ADP) (Wei et al. 2020) and Pontryagin’s maximum principle (Abbasi et al. 2020). The performance of those schemes is promptly related to the model’s accuracy and data-fitting to select the model’s parameters. Furthermore, for the model-free approach, the neural optimal controller (Hernandez-Mejia et al. 2018) and the optimal control based on passivity (Hernandez-Mejia et al. 2020) have been developed but the full state observer has been strongly required.

The focus of this work is to derive the intervention policy including vaccination, quarantine and precaution promotion with the optimal control aspect by utilizing only the daily data of isolated symptomatic infectious. Firstly, the conventional SEIR is redesigned as the SqEAIIR epidemic model which includes quarantined individuals and subgroups of infected individuals. By considering SqEAIIR as a class of discrete-time controlled plants, the control effort $u \in {\mathbb {R}}_{\ge 0}^3$ denotes the intervention policy and the output is the number of daily isolated infected individuals. Therefore, the parameters of SqEAIIR are determined by data-fitting with the fourth wave of the Mexico COVID-19 epidemic. Secondly, the affine equivalent model is established by an adaptive fuzzy-rules emulated network (FREN) (Treesatayapun and Uatrongjit 2005; Treesatayapun 2020) to represent the discrete-time manner of the epidemic by using only the daily data (Government of Mexico 2021a). The learning law is developed to improve the equivalent model’s performance with the convergence analysis. The proposed optimal controller is derived by the affine equivalent model which is linear with respect to the observed individual. Finally, the intervention policy is determined when the impulsive immigrating and traveling issues are considered as the unknown disturbances. Moreover, the limitations of resources such that vaccines, promotion budget and healthcare facilities are deliberated.

The structure of this paper is organized as follows. The problem formulation and SqEAIIR epidemic model are given in Sect. 2 with a general class of non-affine discrete-time systems. In Sect. 3, an adaptive network FREN is utilized to establish the affine equivalent model by using only the daily data of isolated symptomatic individuals. The optimal intervention policy is formulated in Sect. 4 with the closed-loop analysis. In Sect. 5, numerical systems are provided to validate the proposed scheme altogether with the impulsive immigrating and traveling. In Sect. 6, the work is concluded and summarized.

Fig. 2

SqEAIIR flow diagram and controlled plant concept (Color figure online)

2 Problem Formulation

2.1 Mathematical Model of SqEAIIR Epidemic

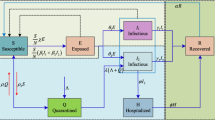
In this section, a formulation of the extended SEIAR model called SqEAIIR is derived by integrating state variables of quarantined people and vaccinated individuals. The total population is categorized into seven groups as follows: susceptible S(t), exposed E(t), symptomatic infectious $I_\mathrm{s}(t)$, asymptomatic infectious A(t), symptomatic infectious who isolated in hospitals and health-care facilities $I_\mathrm{i}$, recovered R(t) and quarantined Q(t) individuals.

The flow diagram between individual groups of SqEAIIR is depicted in Fig. 2. Therefore, the dynamic model is mathematically governed as the following:

$$\begin{aligned} \dot{S}(t)= & {} \varLambda _\mathrm{o}-[\beta \lambda (t)+\varepsilon _\mathrm{v}u_\mathrm{v}(t)+u_\mathrm{q}(t)+\mu ]S(t), \nonumber \\ \dot{Q}(t)= & {} u_\mathrm{q}(t)S(t)-[z_\mathrm{Q}+\mu ]Q(t), \nonumber \\ \dot{E}(t)= & {} \beta \lambda (t)S(t)-[\delta _\mathrm{E}+\mu ]E(t), \nonumber \\ \dot{A}(t)= & {} (1-\rho )\delta _\mathrm{E}E(t)-[z_\mathrm{A}+\phi _\mathrm{A}+r_\mathrm{A}+m_\mathrm{A}+\mu ]A(t), \nonumber \\ \dot{I}_\mathrm{s}(t)= & {} \rho \delta _\mathrm{E}E(t)+z_\mathrm{A}A(t)-[\phi _\mathrm{s}+r_\mathrm{s}+m_\mathrm{s}+\mu ]I_\mathrm{s}(t), \nonumber \\ \dot{I}_\mathrm{i}(t)= & {} \phi _\mathrm{A}A(t)+\phi _\mathrm{s}I_\mathrm{s}(t)-[r_\mathrm{i}+m_\mathrm{i}+\mu ]I_\mathrm{i}(t), \nonumber \\ \dot{R}(t)= & {} \varepsilon _\mathrm{v}u_\mathrm{v}(t)S(t)+r_\mathrm{A}A(t)+r_\mathrm{i}I_\mathrm{i}(t)+r_\mathrm{s}I_\mathrm{s}(t)+z_\mathrm{Q}Q(t)-\mu R(t), \end{aligned}$$

(1)

and the infection force is defined as

$$\begin{aligned} \lambda (t)=\frac{[1-u_\mathrm{m}(t)][I_\mathrm{s}(t)+n_\mathrm{A}A(t)]}{S(t)+E(t)+A(t)+I_\mathrm{s}(t)+R(t)}. \end{aligned}$$

(2)

Table 1 Parameters for SqEAIIR dynamics

All SqEAIIR’s parameters are described by Table 1 and $\varLambda _\mathrm{o}$ denotes the recruitment rate.

The parameters $u_\mathrm{v}(t)$, $u_\mathrm{q}(t)$ and $u_\mathrm{m}(t)$ are non-negative control efforts $\in [0,1]$ or the interventional policy including vaccination, quarantine and precaution promotion such as social distancing and the use of face masks, respectively. It’s worth remarking that the main objective of SqEAIIR in (1) is used to validate the proposed interventional policy within the per-unit such that the works in Xie et al. (2020), Dong et al. (2020), Amiri-Mehra et al. (2019). Therefore, the controlled plant is considered as the unknown dynamics described by the block diagram in Fig. 2. Unlike the previous works such as Dong et al. (2020), Abbasi et al. (2020), Perkins and Guido (2020), in this work, the policy is determined by a model-free adaptive control without any requirement of the dynamics in (1).

2.2 Discrete-Time Equivalent Model and Immigrating Disturbance

The aim of this work is to determine the optimal intervention policy including vaccination: $u_\mathrm{v}$, quarantine: $u_\mathrm{q}$ and precaution promotion: $u_\mathrm{m}$. In this work, the dynamics of SqEAIIR are considered as a class of non-affine discrete-time systems depicted in Fig. 3 when the control inputs are $u_\mathrm{v}(k)$, $u_\mathrm{q}(k)$ and $u_\mathrm{m}(k)$ and the observed output is $I_\mathrm{i}(k+1)$. k denotes the sampling time index with the interval 1-day. It’s worth emphasizing that from the practical point of view, $I_\mathrm{i}(k)$ can be daily obtained from the official databases such as CONACYT (Government of Mexico 2021a) and the immigrant population can be considered as the disturbance $d(k=\kappa _j)$ when $\kappa _j$ indicates the date of immigration occurring.

Fig. 3

SqEAIIR as a class of unknown discrete-time systems and immigrating disturbance (Color figure online)

To simplify, the equivalent model for the discrete-time system in Fig. 3 can be established as

$$\begin{aligned} I_\mathrm{i}(k+1)=F_\mathrm{d}(I_\mathrm{i}(k),u_\mathrm{v}(k),u_\mathrm{q}(k),u_\mathrm{m}(k),d(k)), \end{aligned}$$

(3)

where $F_\mathrm{d}(-)$ is the unknown nonlinear function and

$$\begin{aligned} d(k)=0 \; \mathrm{when} \; k \ne \kappa _j. \end{aligned}$$

(4)

By generalizing the problem formulation mentioned above, the discrete-time system in (3) is reformulated as

$\varSigma _1$: $k\ne \kappa _j$

$$\begin{aligned} I_\mathrm{i}(k+1)=F_\mathrm{d}(I_\mathrm{i}(k), U(k)), \end{aligned}$$

(5)

where $U(k)=[u_\mathrm{v}(k) \, u_\mathrm{q}(k)\, u_\mathrm{m}(k)]^\mathrm{T}$ and

$\varSigma _2$: $k =\kappa _j$

$$\begin{aligned} I_\mathrm{i}(k+1)=F_\mathrm{d}(I_\mathrm{i}(k), U(\kappa _j),d(\kappa _j)). \end{aligned}$$

(6)

In this work, the disturbance $d(\kappa _j)$ is considered as the unknown signal but its effect can be monitored through $I_\mathrm{i}(k+1)$ at ${\varSigma _2}$ which can be obtained by the database. By this motivation, the data-driven equivalent model will be established by using only the daily data of $I_\mathrm{i}(k)$. Thereafter, the approximated optimal controller will be designed by using the data-driven equivalent model.

3 Adaptive Data-Driven Affine Equivalent Model

3.1 Equivalent Model and Learning Laws

By utilizing the compact form dynamic-linearization (Hou et al. 2017; Treesatayapun 2017), it exists functions $f_\mathrm{o}(I_\mathrm{i}(k)) \in {\mathbb {R}}_{\ge 0}$ and $g_\mathrm{o}(I_\mathrm{i}(k)) \in {\mathbb {R}}_{\ge 0}^3$ for the affine dynamics which are equivalent with the system in (6) such that

$$\begin{aligned} I_\mathrm{i}(k+1)=f_\mathrm{o}(k)+g_\mathrm{o}^\mathrm{T}(k)U(k). \end{aligned}$$

(7)

According to the universal function approximation of FREN (Treesatayapun and Uatrongjit 2005; Treesatayapun 2020), it exists the affine model based on the analytic functions $f_\mathrm{m}(I_\mathrm{i}(k)) \in {\mathbb {R}}_{\ge 0}$ and $g_\mathrm{m}(I_\mathrm{i}(k)) \in {\mathbb {R}}_{\ge 0}^3$ such that

$$\begin{aligned} \hat{I}_\mathrm{i}(k+1)=f_\mathrm{m}(k)+g^\mathrm{T}_\mathrm{m}(k)U(k), \end{aligned}$$

(8)

where $\hat{I}_\mathrm{i}(k+1)$ denotes the estimated $I_\mathrm{i}(k+1)$. Without loss of generality, $g_\mathrm{m}(k)$ can be expressed as

$$\begin{aligned} g_\mathrm{m}(k)=[g_{m1}(k) \, g_{m2}(k) \, g_{m3}(k)]^\mathrm{T}. \end{aligned}$$

(9)

Thus, the equivalent model in (8) is rearranged as

$$\begin{aligned} \hat{I}_\mathrm{i}(k+1)=f_\mathrm{m}(k)+g_{m1}(k)u_\mathrm{v}(k)+g_{m2}(k)u_\mathrm{q}(k)+g_{m3}(k)u_\mathrm{m}(k). \end{aligned}$$

(10)

Therefore, functions $f_\mathrm{m}(k)$ and $g_{\mathrm{m}i}(k)$ for $i=1, 2, 3$ are utilized by FRENs as the following:

$$\begin{aligned} f_\mathrm{m}(k)=\beta ^\mathrm{T}_\mathrm{f}(k)\phi (k), \end{aligned}$$

(11)

and

$$\begin{aligned} g_{\mathrm{m}i}(k)=\beta ^\mathrm{T}_{\mathrm{g}i}(k)\phi (k), \end{aligned}$$

(12)

respectively, where $\phi (k) \in {\mathbb {R}}^{N_\mathrm{f}}$ is the basis vector of x(k) membership functions and $\beta _\mathrm{f}(k) \in {\mathbb {R}}^{N_\mathrm{f}}$ and $\beta _{\mathrm{g}i}(k) \in {\mathbb {R}}^{N_\mathrm{f}}$ are adjustable weights. $N_\mathrm{f}$ is the number of membership functions of FREN when the network architecture is illustrated in Fig. 4.

Fig. 4

Data-driven affine equivalent model (Color figure online)

To improve the model performance by tuning all adjustable weights, the learning laws are established with the estimation error $\hat{e}(k+1)$ given as

$$\begin{aligned} \hat{e}(k+1)=I_\mathrm{i}(k+1)-\hat{I}_\mathrm{i}(k+1). \end{aligned}$$

(13)

In order to establish the learning laws, the cost function $\hat{E}(k+1)$ over the k-iteration is defined as

$$\begin{aligned} \hat{E}(k+1)=\frac{1}{2}\hat{e}^2(k+1). \end{aligned}$$

(14)

Firstly, by applying the gradient search, the learning law of $\beta _\mathrm{f}(k)$ is obtained as

$$\begin{aligned} \beta _\mathrm{f}(k+1)=\beta _\mathrm{f}(k)-\eta _\mathrm{f}\frac{\partial {\hat{E}(k+1)}}{\partial {\beta _\mathrm{f}(k)}}, \end{aligned}$$

(15)

where $\eta _\mathrm{f}$ denotes as the learning rate. Therefore, let’s apply the chain rule along (8) to (14), it leads to

$$\begin{aligned} \frac{\partial {\hat{E}(k+1)}}{\partial {\beta _\mathrm{f}(k)}}= & {} \frac{\partial {\hat{E}(k+1)}}{\partial {\hat{e}(k+1)}} \frac{\partial {\hat{e}(k+1)}}{\partial {\hat{I}_i(k+1)}}\frac{\partial {\hat{I}_i(k+1)}}{\partial {\beta _\mathrm{f}(k)}}, \nonumber \\= & {} -\hat{e}(k+1)\phi (k). \end{aligned}$$

(16)

Thus, the learning law in (15) becomes

$$\begin{aligned} \beta _\mathrm{f}(k+1)=\beta _\mathrm{f}(k)+\eta _\mathrm{f}\hat{e}(k+1)\phi (k). \end{aligned}$$

(17)

Secondly, let’s repeat the same procedure as (15) to (17) with $\beta _{\mathrm{g}i}(-)$ for $i=1,2,3$, we obtain

$$\begin{aligned} \beta _{\mathrm{g}i}(k+1)=\beta _{\mathrm{g}i}(k)-\eta _{\mathrm{g}i}\frac{\partial {\hat{E}(k+1)}}{\partial {\beta _{\mathrm{g}i}(k)}}, \end{aligned}$$

(18)

where $\eta _{\mathrm{g}i}$ is the ith learning rate. Thereafter, by applying the chain rule, we have

$$\begin{aligned} \frac{\partial {\hat{E}(k+1)}}{\partial {\beta _{\mathrm{g}i}(k)}}= & {} \frac{\partial {\hat{E}(k+1)}}{\partial {\hat{e}(k+1)}} \frac{\partial {\hat{e}(k+1)}}{\partial {\hat{I}_\mathrm{i}(k+1)}}\frac{\partial {\hat{I}_i(k+1)}}{\partial {\beta _{\mathrm{g}i}(k)}}, \nonumber \\= & {} -\hat{e}(k+1)\phi (k)U_\mathrm{i}(k). \end{aligned}$$

(19)

Thus, the learning law in (18) is rewritten as

$$\begin{aligned} \beta _{\mathrm{g}i}(k+1)=\beta _{\mathrm{g}i}(k)+\eta _{\mathrm{g}i}\hat{e}(k+1)U_\mathrm{i}(k)\phi (k). \end{aligned}$$

(20)

It’s worth denoting that the learning rates $\eta _\mathrm{f}$ and $\eta _{\mathrm{g}i}$ can play an important role in the model performance. Therefore, the selection of the proper learning rates will be discussed next.

3.2 Performance Analysis

The performance of the learning laws can be guaranteed by setting $\eta _\mathrm{f}$ and $\eta _{\mathrm{g}i}$ according to the following theorem.

Theorem 1

For the equivalent model proposed by (8) with the learning laws (17) and (20), the estimation error (13) is a convergent sequence when the learning rates $\eta _\mathrm{f}$ and $\eta _{\mathrm{g}i}$ are designed by the following conditions:

$$\begin{aligned} 0\le \eta _\mathrm{f} < \frac{\gamma _\mathrm{f}}{\phi _M}, \end{aligned}$$

(21)

and

$$\begin{aligned} 0\le \eta _{\mathrm{g}i} < \frac{\gamma _\mathrm{g}}{U_{\mathrm{i}M}^2\phi _M}, \end{aligned}$$

(22)

where $0<\gamma _\mathrm{f}<2$, $0<\gamma _\mathrm{g}<2$, $U_{\mathrm{i}M}=\max {|U_\mathrm{i}(k)|}, \forall k=1,2, \ldots$ and

$$\begin{aligned} \phi _M=\sup _{\forall I_\mathrm{i}\ge 0}\{||\phi (I_\mathrm{i}(k))||^2 \}. \end{aligned}$$

(23)

Proof

Let’s define the Lyapunov function $L_\mathrm{m}(k)$ as

$$\begin{aligned} L_\mathrm{m}(k)=\frac{1}{2}\hat{e}^2(k). \end{aligned}$$

(24)

Therefore, the change of $L_\mathrm{m}(k)$ is derived as

$$\begin{aligned} \Delta L_\mathrm{m}(k)= & {} L_\mathrm{m}(k+1)-L_\mathrm{m}s(k), \nonumber \\= & {} \frac{1}{2}[\hat{e}^2(k+1)-\hat{e}^2(k)], \nonumber \\= & {} \frac{1}{2}\big [\hat{e}(k)+\Delta \hat{e}(k)]^2-\hat{e}^2(k)\big ], \nonumber \\= & {} \frac{1}{2}\Delta \hat{e}(k)[2\hat{e}(k)+\Delta \hat{e}(k)]. \end{aligned}$$

(25)

For the proof thereafter, the analysis is conducted by two parts for $\eta _\mathrm{f}$ and $\eta _{\mathrm{g}i}$ as the following:

Part I ($\eta _\mathrm{f}$): According to the weight parameter $\beta _\mathrm{f}(k)$, $\Delta \hat{e}(k)$ is estimated as $\Delta \hat{e}_\mathrm{f}(k)$ such that

$$\begin{aligned} \Delta \hat{e}_\mathrm{f}(k)\approx \Big [\frac{\partial {\hat{e}(k)}}{\partial {\beta _\mathrm{f}(k-1)}}\Big ]^\mathrm{T}\Delta \beta _\mathrm{f}(k-1). \end{aligned}$$

(26)

By recalling (8), (11) and (17) with one step backward, we obtain

$$\begin{aligned} \Delta \hat{e}_\mathrm{f}(k)\approx -\eta _\mathrm{f}\hat{e}(k)||\phi (k-1)||^2. \end{aligned}$$

(27)

Substitute (27) into (25), it yields

$$\begin{aligned} \Delta L_\mathrm{m}(k)\doteq & {} -\frac{1}{2}\eta _\mathrm{f}\hat{e}(k)||\phi (k-1)||^2[2\hat{e}(k) -\eta _\mathrm{f}\hat{e}(k)||\phi (k-1)||^2], \nonumber \\= & {} -\frac{1}{2}\eta _\mathrm{f}\hat{e}^2(k)||\phi (k-1)||^2[2-\eta _\mathrm{f}||\phi (k-1)||^2]. \end{aligned}$$

(28)

For the convergence of the sequence $\hat{e}(k)$ or $\Delta L_\mathrm{m}(k)\le 0$, it requires that

$$\begin{aligned} 2-\eta _\mathrm{f}||\phi (k-1)||^2\ge 0, \end{aligned}$$

(29)

or

$$\begin{aligned} \eta _\mathrm{f} \le \frac{2}{||\phi (k-1)||^2}. \end{aligned}$$

(30)

It’s clear that the condition in (30) is fulfilled as

$$\begin{aligned} \eta _\mathrm{f} < \frac{\gamma _\mathrm{f}}{\phi _M} \le \frac{2}{||\phi (k-1)||^2}. \end{aligned}$$

(31)

Thus, the proof of (21) is completed.

Part II ($\eta _{\mathrm{g}i}$): For the weight parameters $\beta _{\mathrm{g}i}(k)$, the change of Lyapunov function $\Delta \hat{e}(k)$ is approximated as $\Delta \hat{e}_{\mathrm{g}i}(k)$ as

$$\begin{aligned} \Delta \hat{e}_{\mathrm{g}i}(k)\approx \Big [\frac{\partial {\hat{e}(k)}}{\partial {\beta _{\mathrm{g}i}(k-1)}}\Big ]^\mathrm{T}\Delta \beta _{\mathrm{g}i}(k-1). \end{aligned}$$

(32)

Let’s recall (8), (12) and (20) with one step backward, we have

$$\begin{aligned} \Delta \hat{e}_{\mathrm{g}i}(k)\approx -\eta _{\mathrm{g}i}\hat{e}(k)U^2_\mathrm{i}(k)||\phi (k-1)||^2. \end{aligned}$$

(33)

Substitute (33) into (32), we obtain

$$\begin{aligned} \Delta L_\mathrm{m}(k)\doteq & {} -\frac{1}{2}\eta _{\mathrm{g}i}\hat{e}(k)U^2_\mathrm{i}(k)|| \phi (k-1)||^2[2\hat{e}(k)-\eta _{\mathrm{g}i}\hat{e}(k)U^2_\mathrm{i}(k)||\phi (k-1)||^2], \nonumber \\= & {} -\frac{1}{2}\eta _{\mathrm{g}i}\hat{e}^2(k)U^2_\mathrm{i}(k)||\phi (k-1)||^2 {[}2-\eta _{\mathrm{g}i}U^2_\mathrm{i}(k)||\phi (k-1)||^2]. \end{aligned}$$

(34)

With negative semi-define $\Delta L_\mathrm{m}(k)$, it leads to

$$\begin{aligned} \eta _{\mathrm{g}i} \le \frac{2}{U^2_\mathrm{i}(k)||\phi (k-1)||^2}. \end{aligned}$$

(35)

Considering (22) with (35), it’s clear that

$$\begin{aligned} \eta _{\mathrm{g}i} < \frac{\gamma _\mathrm{g}}{U_{\mathrm{i}M}^2\phi _M} \le \frac{2}{U^2_\mathrm{i}(k)||\phi (k-1)||^2}, \end{aligned}$$

(36)

for $i=1,2,3$. Thus, the proof is completed here. $\square$

4 Model-Free Optimal Preventative Policy

To prevent the inundation of $I_\mathrm{i}$ individuals according to the limited resources of hospitals or medical institutions, the optimal interventional policy including vaccination, quarantine and precaution promotion is derived by the optimal control scheme. It’s worth emphasizing that the daily data of $I_\mathrm{i}(k)$ is only required and utilized in this approach.

The long term cost function V(k) is firstly defined as

$$\begin{aligned} V(k)=\sum _{i=k}^{\infty }\gamma ^{i-k}[qI_\mathrm{i}^2(i)+U^\mathrm{T}(i)HU(i)], \end{aligned}$$

(37)

where $0<\gamma \le 1$ is a discount parameter, q is a positive constant and $H\in {\mathbb {R}}^{3\times 3}$ is a positive diagonal matrix such that $H_i>0$ for $i=1,2,3$.

By rearranging the cost function (37), it yields

$$\begin{aligned} V(k)= & {} qI_\mathrm{i}^2(k)+U^\mathrm{T}(k)HU(k)+\gamma \sum _{i=k+1}^{\infty } \gamma ^{i-(k+1)}[qI^2(i)+U^\mathrm{T}(i)HU(i)], \nonumber \\= & {} qI^2(k)+u^\mathrm{T}(k)Hu(k)+\gamma V(k+1). \end{aligned}$$

(38)

Considering the cost function in (38) in the quadratic form, the following Lemma is conducted.

Lemma 1

If the general formulation of the control law U(k) in (38) can be rearranged by the vector K(k) as

$$\begin{aligned} U(k)=-K(k)I_\mathrm{i}(k), \end{aligned}$$

(39)

then the cost function V(k) in (38) can be reformulated as a quadratic form such that

$$\begin{aligned} V(k)=PI_\mathrm{i}^2(k), \end{aligned}$$

(40)

where P is a positive time-varying parameter.

Proof

Let’s recall (37), thus, we have

$$\begin{aligned} V(k)= & {} \sum _{i=k}^{\infty }\gamma ^{i-k}[qI_\mathrm{i}^2(i)+U^\mathrm{T}(i)HU(i)], \nonumber \\= & {} \sum _{i=0}^{\infty }\gamma ^{i}[qI_\mathrm{i}^2(i+k)+U^\mathrm{T}(i+k)HU(i+k)]. \end{aligned}$$

(41)

Using (39) with (41), it yields

$$\begin{aligned} V(k)=\sum _{i=0}^{\infty }\gamma ^{i}[qI_\mathrm{i}^2(i+k)+K^\mathrm{T}(i+k)HK(i+k)I_\mathrm{i}^2(k)]. \end{aligned}$$

(42)

Substituting (39) into (7), we obtain

$$\begin{aligned} I_\mathrm{i}(k+1)= & {} [\acute{f}_\mathrm{o}(k)-g_\mathrm{o}^\mathrm{T}(k)K(k)]I_\mathrm{i}(k), \nonumber \\= & {} a_\mathrm{o}(k)I(k), \end{aligned}$$

(43)

where

$$\begin{aligned} a_\mathrm{o}(k)=\acute{f}_\mathrm{o}(k)-g^\mathrm{T}(k)K(k), \end{aligned}$$

(44)

and

$$\begin{aligned} f_{rm o}=\acute{f}_\mathrm{o}(k)I_\mathrm{i}(k). \end{aligned}$$

(45)

By utilizing the dynamics in (43), it leads to

$$\begin{aligned} I_\mathrm{i}(i+k)= & {} [a_\mathrm{o}(k+i-1)a_\mathrm{o}(k+i-2)\cdots a_\mathrm{o}(k)]I_\mathrm{i}(k), \nonumber \\= & {} a_{\prod _\mathrm{o}}(k+i-1)I_\mathrm{i}(k), \end{aligned}$$

(46)

where $a_{\prod _\mathrm{o}}(k+i-1)=a_\mathrm{o}(k+i-1)a_\mathrm{o}(k+i-2)\cdots a_\mathrm{o}(k)$. Substituting (43) into (42), we have

$$\begin{aligned} V(k)= & {} \sum _{i=0}^{\infty }\gamma ^{i}[qa^2_{\prod _\mathrm{o}}(k+i-1) +K^\mathrm{T}(i+k)HK(i+k)]I_\mathrm{i}^2(k),\nonumber \\= & {} PI_\mathrm{i}^2(k), \end{aligned}$$

(47)

where $P=\sum _{i=0}^{\infty }\gamma ^{i}[qa^2_{\prod _\mathrm{o}} (k+i-1)+K^\mathrm{T}(i+k)HK(i+k)]$. Thus, the proof is completed. $\square$

Remark 1

It’s worth to emphasize that the parameter P is a time-varying one comparing with the other quadratic value functions and optimization schemes (Abbasi et al. 2020).

According to the result of Lemma 1, it’s clear that the relation in (38) can be rearranged with the parameter P such that

$$\begin{aligned} PI_\mathrm{i}^2(k)=qI_\mathrm{i}^2(k)+U^\mathrm{T}(k)HU(k)+\gamma PI_\mathrm{i}^2(k+1). \end{aligned}$$

(48)

Thus, Hamiltonian equation $H_\mathrm{m}(I_\mathrm{i},U)$ can be obtained as

$$\begin{aligned} H_\mathrm{m}(k)=qI_\mathrm{i}^2(k)-PI_\mathrm{i}^2(k)+U^\mathrm{T}(k)HU(k)+\gamma PI_\mathrm{i}^2(k+1). \end{aligned}$$

(49)

By utilizing (49) and the equivalent model (7), it leads to

$$\begin{aligned} \frac{\partial {H_\mathrm{m}(k)}}{\partial {U_k}}=2HU(k)+2\gamma P[\acute{f}_\mathrm{o}(k)I_\mathrm{i}(k)+g_\mathrm{o}^\mathrm{T}(k)U(k)]g_\mathrm{o}(k). \end{aligned}$$

(50)

Considering $\frac{\partial {H(k)}}{\partial {U_k}}=0$, the control law can be derived as

$$\begin{aligned} U(k)= & {} -\Big [H+\gamma Pg_\mathrm{o}(k)g_\mathrm{o}^\mathrm{T}(k)\Big ]^{-1} \gamma P\acute{f}_\mathrm{o}(k)g_\mathrm{o}(k)I_\mathrm{i}(k), \nonumber \\= & {} -K(k)I_\mathrm{i}(k), \end{aligned}$$

(51)

where

$$\begin{aligned} K(k)=\Big [H+\gamma Pg_\mathrm{o}(k)g_\mathrm{o}^\mathrm{T}(k)\Big ]^{-1}\gamma P\acute{f}_\mathrm{o}(k)g_\mathrm{o}(k). \end{aligned}$$

(52)

Therefore, the performance analysis of the closed loop system under the proposed control law (51) is conducted by the following theorem.

Theorem 2

For a class of discrete-time systems satisfied the equivalent model (7), thus, the convergence of closed-loop systems under the control law (51) is guaranteed when $I_\mathrm{i}(k)\ge 0$ and

$$\begin{aligned} \acute{f}_\mathrm{o}(k)-\frac{1}{\sqrt{\gamma }}\le \acute{f}_\mathrm{o}(k)-1< g_\mathrm{o}^\mathrm{T}(k)K(k) < \acute{f}_\mathrm{o}(k)+1 \le \acute{f}_\mathrm{o}(k)+\frac{1}{\sqrt{\gamma }}. \end{aligned}$$

(53)

Proof

By recalling (48) with the control law (51) and the equivalent model (7), we have

$$\begin{aligned} PI_\mathrm{i}^2(k)= & {} qI_\mathrm{i}^2(k)+[K(k)I_\mathrm{i}(k)]^\mathrm{T}H[K(k)I_\mathrm{i}(k)] \nonumber \\&+\gamma P[\acute{f}_\mathrm{o}(k)I_\mathrm{i}(k)+g_\mathrm{o}^\mathrm{T}(k)U(k)]^2, \nonumber \\= & {} qI_\mathrm{i}^2(k)+[K(k)I_\mathrm{i}(k)]^\mathrm{T}H[K(k)I_\mathrm{i}(k)] \nonumber \\&+\gamma P[\acute{f}_\mathrm{o}(k)I_\mathrm{i}(k)-g_\mathrm{o}^\mathrm{T}(k)K(k)I_\mathrm{i}(k)]^2. \end{aligned}$$

(54)

For the case of infected individual $I_\mathrm{i}(k)>0$, it leads to

$$\begin{aligned} P= & {} q+K^\mathrm{T}(k)HK(k) \nonumber \\&+\gamma P\Big [\acute{f}_\mathrm{o}^2(k)-2 \acute{f}_\mathrm{o}(k)g_\mathrm{o}^\mathrm{T}(k)K(k)+[g_\mathrm{o}^\mathrm{T}(k)K(k)]^2\Big ] \nonumber \\= & {} q+K^\mathrm{T}(k)HK(k)+\gamma P\lambda _P(k), \end{aligned}$$

(55)

where

$$\begin{aligned} \lambda _P(k)=\acute{f}_\mathrm{o}^2(k)-2\acute{f}_\mathrm{o}(k)g_\mathrm{o}^\mathrm{T}(k)K(k)+[g_\mathrm{o}^\mathrm{T}(k)K(k)]^2. \end{aligned}$$

(56)

By considering

$$\begin{aligned} 1-\gamma \lambda _P(k)>0, \end{aligned}$$

(57)

it requires that

$$\begin{aligned} \lambda _P(k)< & {} \frac{1}{\gamma }, \nonumber \\ \big [\acute{f}_\mathrm{o}(k)-g_\mathrm{o}^\mathrm{T}(k)K(k)\big ]^2< & {} \frac{1}{\gamma }, \end{aligned}$$

(58)

or

$$\begin{aligned} \big |\acute{f}_\mathrm{o}(k)-g_\mathrm{o}^\mathrm{T}(k)K(k)\big | < \frac{1}{\sqrt{\gamma }}. \end{aligned}$$

(59)

Therefore, we have

$$\begin{aligned} \acute{f}_\mathrm{o}(k)-\frac{1}{\sqrt{\gamma }}< g_\mathrm{o}^\mathrm{T}(k)K(k) < \acute{f}_\mathrm{o}(k)+\frac{1}{\sqrt{\gamma }}. \end{aligned}$$

(60)

Next, let’s recall the closed-loop system in (43). It’s clear that I(k) is a convergence sequence when

$$\begin{aligned} |a_\mathrm{o}(k)| \le 1. \end{aligned}$$

(61)

That leads to

$$\begin{aligned} |\acute{f}_\mathrm{o}(k)-g_\mathrm{o}^\mathrm{T}(k)K(k))| \le 1, \end{aligned}$$

(62)

or

$$\begin{aligned} \acute{f}_\mathrm{o}(k)-1 \le g_\mathrm{o}^\mathrm{T}(k)K(k)) \le \acute{f}_\mathrm{o}(k)+1. \end{aligned}$$

(63)

By the setting of $\gamma$ mentioned in (37), it yields

$$\begin{aligned} 1\le \frac{1}{\sqrt{\gamma }}, \end{aligned}$$

(64)

and

$$\begin{aligned} -\frac{1}{\sqrt{\gamma }} \le -1. \end{aligned}$$

(65)

By utilizing (63–65) with (60), it leads to (53). Thus, the proof is completed. $\square$

For the practical point of view here, $\acute{f}_\mathrm{o}(k)$ and $g_\mathrm{o}(k)$ are unknown. Therefore, the affine equivalent model proposed in Sect. 3 is utilized. Thus, the gain vector K(k) in (52) can be employed as

$$\begin{aligned} K(k)=\Big [R+\gamma Pg_\mathrm{m}(k)g_\mathrm{m}^\mathrm{T}(k)\Big ]^{-1}\gamma Pf_\mathrm{m}(k)g_\mathrm{m}(k). \end{aligned}$$

(66)

Remark 2

For the conclusion, in this work, the equivalent model (8) is firstly established by utilizing the actual data. Secondly, the interventional policy is appointed by the optimal controller in Lemma 1: (39) when the gain vector K(k) is determined by (66).

5 Numerical Results

5.1 Parameters Setting and Model Accuracy

To validate the accuracy of SqEAIIR, the raw data from the Mexican government CONACyT (Government of Mexico 2021a) is utilized for the fourth wave of epidemic according to the omicron variant from November 2021 to 23 February 2022. By using the initial values given by Table 2 and the parameters represented by Table 3, Fig. 5 illustrates the plots of raw data and model’s results including $I_\mathrm{i}$, $I_\mathrm{s}$ and A individuals. As a result, SqEAIIR’s dynamics (1) can predict and mimic the epidemic behavior. Furthermore, according to the data from healthcare institutes in Mexico such as IMSS (Government of Mexico 2021b) and ISSSTE (Government of Mexico 2021c), the maximum capacity of COVID-19 cases who need hospital facilities is displayed by the red dashed line in Fig. 5. The over-demand has occurred for the fourth wave of the epidemic caused by the omicron variant.

Table 2 Initial values of individuals (Government of Mexico 2021a)

Table 3 Values of parameters for SqEAIIR dynamics

Fig. 5

SqEAIIR fitting with raw data according to 4th wave of omicron variant (Color figure online)

5.2 Optimal Control and Intervention

By utilizing SqEAIIR and its parameters in Sect. 5.1, the proposed equivalent model (8) and the controller (39) and (66) are constructed and validated. Thereafter, the parameters of the equivalent model and the upper bound of control efforts are designed by using the following information: $\phi _M=9$, $U_{1M}=0.07$, $U_{2M}=0.2$ and $U_{3M}=0.5$ according to Auger and Moussaoui (2021), Abbasi et al. (2020), Government of Mexico (2021b, 2021c). According Theorem 1, let’s select $\gamma _\mathrm{f}=\gamma _\mathrm{g}=1$, thus, the learning rates are determined as

$$\begin{aligned}&\eta _\mathrm{f} = \frac{1}{9}=0.11, \end{aligned}$$

(67)

$$\begin{aligned}&\eta _\mathrm{g1} = \frac{1}{0.07^2\times 9}=22.67, \end{aligned}$$

(68)

$$\begin{aligned}&\eta _\mathrm{g2} = \frac{1}{0.2^2\times 9}=2.78, \end{aligned}$$

(69)

and

$$\begin{aligned} \eta _\mathrm{g3} = \frac{1}{0.5^2\times 9}=0.44. \end{aligned}$$

(70)

Secondly, all controller’s parameters are given according to Theorem 2 as followings: $\gamma =$, $P(1)=10$, $H_1=0.04$, $H_2=0.07$ and $H_3=0.1$.

Fig. 6

Policy intervention response without and with applying controller with maximum capacity of hospitals (Government of Mexico 2021a, b, c) (Color figure online)

Fig. 7

Controlled $I_\mathrm{i}(k)$ and $\hat{I}_\mathrm{i}(k)$ (Color figure online)

Fig. 8

Control efforts or policy intervention (Color figure online)

The control effort $U(k)=[u_\mathrm{m}(k) \; u_\mathrm{q}(k) \; u_\mathrm{v}(k)]^\mathrm{T}$ is determined by (39) and (66). Thus, the response is depicted by the plot in Fig. 6 as the black line when the policy is initiated at Day 1st. For a case of delay, the blue line in Fig. 6 represents the response when the policy is initiated at Day 7th. As a result, the infected patients who require healthcare facilities are still under capacity. Figure 7 illustrates the equivalent model performance with the plots of $I_\mathrm{i}(k)$ and its estimated $\hat{I}_\mathrm{i}(k)$. Thereafter, the policy intervention is displayed in Fig. 8.

Fig. 9

Immigrating pattern (Color figure online)

5.3 Immigrating Disturbance

Next, the immigrating disturbance is considered for individuals. In this test, let’s define the immigrating pattern by the plots in Fig. 9 according to the data from Government of Mexico (2021a, 2021d). That leads to the immigration of four individual groups as $d_\mathrm{S}(\kappa _j)$, $d_\mathrm{E}(\kappa _j)$, $d_\mathrm{A}(\kappa _j)$ and $d_\mathrm{R}(\kappa _j)$ for disturbances of susceptible, exposed, asymptomatic infectious and recovered individuals, respectively. It’s worth to remark that the impulsive index is denoted as $\kappa _j$ for $j=1, 2, \ldots 9$ such that $\kappa _1=10: [@k=10]$.

Fig. 10

Policy intervention response without and with applying controller with populations immigration (Color figure online)

Fig. 11

Control efforts or policy intervention with populations immigration (Color figure online)

The uncontrolled response of SqEAIIR with the immigration effect is plotted by the solid-blue line in Fig. 10 when the response without immigrating is shown by the dash-dotted line in Fig. 10. Therefore, by applying the proposed policy intervention, the response is depicted by the black line in Fig. 10. Figure 11 shows the plots of the optimal intervention policy.

It’s worth emphasizing that only $I_\mathrm{i}(k)$ is utilized for the controller and all impulsive disturbances are considered as unknown signals. Thus, the proposed controller can respond to the impulsive disturbances or immigration of individual groups

6 Conclusions

The dynamic model called SqEAIIR has been proposed to mimic the dynamics of the COVID-19 epidemic. The accuracy of SqEAIIR has been validated by the raw data collected by CONACyT, Mexico for the fourth wave caused by the omicron variant from Nov. 2022 until 23 Feb. 2022. From the practical point of view, only the daily data of patients who require the medication and hospital facilities are appropriately recorded and collected. For that reason, the discrete-time equivalent model has been established by an adaptive network FREN by utilizing only the daily data of symptomatic infectious who isolated in hospitals and healthcare facilities $I_\mathrm{i}(k)$. Thereafter, the intervention policy including vaccination, quarantine and precaution promotion has been developed by the aspect of model-free optimal control. The proposed policy has reduced the number of infected individuals to prevent the overrun of healthcare’s capacity. Moreover, the effect of traveling on migrating has been studied by considering the immigration of each individual as an unknown disturbance. As a result, the proposed scheme has presented a sufficient policy to control the number of infected individuals.

For the note of this work, the proposed intervention policy may be used as a guideline for the authority to control the epidemic.