1 Introduction

Coronaviruses are a group of viruses that are widespread in nature, so named because it looks like a crown under electron microscopy. So far it has been found that coronaviruses have multiple hosts and can infect a variety of mammals such as pigs, cattle, cats, dogs, mink, camels, bats, rats, hedgehogs, and many species of birds in addition to humans, causing respiratory, gastrointestinal, and neurological diseases in humans and animals (National Institute of Allergy and Infectious Disease 2022). Thankfully not all coronaviruses are fatal, except for SARS (severe acute respiratory syndrome coronavirus) and MERS (middle east respiratory syndrome coronavirus). And, of course, there is also the famous SARS-CoV-2 (severe acute respiratory syndrome coronavirus 2) which caused a pandemic of novel coronavirus disease (named COVID-19 by the World Health Organization). In December 2019, the first case of COVID-19 in China is diagnosed in Wuhan. For the moment (May 3, 2021), a total of 103,694 cases of novel coronavirus pneumonia have been confirmed in China, with a total of 4858 death. There are cumulative total of 152,534,452 cases and the cumulative total of 3,198,528 death in the world (World Health Organization 2021).

In the past year, lots of mathematical models are proposed to describe the transmission of SARS-CoV-2 and to estimate the basic reproduction number, the effective reproduction number or the control reproduction number of this disease, etc. These research results not only explain the effectiveness of prevention and control strategies in certain countries or regions, but also predict the development trend of this disease and provide suggestions for the prevention and control. For example, Li et al. (2020a) proposed three-phase models to simulate and explain how the Fangcang shelter hospitals (rapidly built temporary hospitals) and the group isolation strategy helped to prevent the epidemic in Wuhan. Their theoretical results show that if family isolation or social distancing is not enough to suppress the spread of this virus, and then effective group isolation of a large number of lightly infected humans in Fangcang-type facilities can suppress the epidemic of COVID-19. Britton et al. (2020) introduced a mathematical model to reveal the effect of human heterogeneity on the herd immunity to SARS-CoV-2. Consider that South Africa is currently the epicenter for COVID-19 in Africa, Garba et al. (2020) established a compartmental model to simulate the transmission dynamics of this disease and assessed the effects of various control and mitigation strategies. For other related research results, see Refs. (Asamoah et al. 2021; Chen et al. 2020; Ho 2021; Hu and Nie 2021; Perkins and Espa\(\ddot{\mathrm{n}}\)a 2020; Sadun 2020; Tang et al. 2020; Wu et al. 2020; Zu et al. 2020; Zhao et al. 2020a) and the references therein, to just a few.

As we all know, many countries and regions in the world have implemented lockdowns to curb the rapid spread of SARS-CoV-2 and achieved phased victory at the early stage of the outbreak. From the perspective of mathematical modeling, Sun et al. (2020) proposed a two-patches model to reflect the mobility of humans between Hubei and regions outside Hubei, and estimated the effective reproduction numbers for two patches, and also discussed the impact of the resumption of work and production in Wuhan and the lifting of lockdown on the spread of COVID-19. Glass (2020) introduced a two-stage SEIR with different basic reproduction numbers pre- and post-lockdown to investigate the effects of lockdowns and relax the lockdown on the spread of SARS-CoV-2 in France, Germany, Italy, Spain, the UK. And author pointed out that the current levels of relaxation in these countries may lead to a second wave of epidemics and the duration may also exceed the first wave. Zhao and Feng (2020) devised a modified SEIR epidemic model with stage structured to discuss the risk from lockdown and social distancing measures and suggested that taking reasonable measures to lift restrictions on specific groups of people would stimulate economic recovery without affecting the prevention and control of COVID-19. Other investigations on the impact of lockdowns on the spread of COVID-19 or other infectious disease can be found in Refs. (Acuña-Zegarra et al. 2020; Bagal et al. 2020; Boulmezaoud 2020; Buaglia et al. 2020; Gao 2020; Gressman and Peck 2020; Sun et al. 2020; Lalwani et al. 2020), and related studies are still continuous.

On the other hand, the sudden outbreak of COVID-19 and the rapid increase of cases in a short period of time have made medical resources in various countries urgently, especially in developing states and underdeveloped regions. The shortage of protective clothing, nucleic acid kit, oxygen, the emergency of hospital beds, are all problems that have to be faced in the process of epidemic prevention and control. Limited medical resources have increased the difficulty of epidemic prevention and control, especially the treatment of patients. Based on the above considerations, Li et al. (2020b) proposed a mathematical model to assess the impact of the heavy pressure on the medical system caused by people’s excessive panic about COVID-19 and the arrival of flu season, where two saturated functions are introduced to describe the effect of cross-infection of influenza and COVID-19 patients, and the limitation of medical resources. Salman et al. (2021) used a SIRS model with half-saturation coefficient to describe the effects of the shortage of medical resources and mimicked the trend of infection cases of COVID-19 in Malaysia. Authors also pointed out that in developing countries like Malaysia, which faces the question of limited medical resources, there may be a long-lasting epidemic or the risk of another outbreak. Other research works on the impact of limited medical resources on the transmission and control of infectious diseases can be found in Refs. (Abdelrazec et al. 2016; Sepulveda-Salcedo et al. 2020; Saha and Samanta 2019; Wang et al. 2018; Zhao et al. 2020a).

In this work, we propose a two-patches mathematical model to study the effects of limited medical resources and humans migration between two regions on the transmission dynamics of SARS-CoV-2. The rest of this paper is organized as follows. In Sect. 2, we derive a two-patches epidemic model with half-saturation coefficient to describe the effect of limited medical resources for the screening of asymptomatic infected humans. In Sect. 3, the dynamics of patch-i without migration are discussed, which includes the non-negative and boundedness of solutions, the existence of multi-endemic equilibria and forward/backward bifurcation. The dynamics of the full model are studied in Sect. 4, and some numerical simulations are carried to explain the main results in Sect. 5. A brief discussion and conclusion are provided in the last section.

2 Model Formulation and Preliminaries

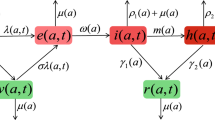
Taking into account the spread of SARS-CoV-2 and the prevention and control measures in various places, the total human population \(N_i\) in patch \(i\ (i=1,2)\) at time t is split into five classes: susceptible class \(S_i(t)\), asymptomatic infected class \(A_i(t)\), symptomatic infected class \(I_i(t)\), hospital isolation treatment class \(Q_i(t)\) and recovered class \(R_i(t)\). Assuming that susceptible persons are likely to be infected after contact with infected humans, one part becomes asymptomatic infection and the other part becomes symptomatic infection. Due to the nucleic acid screening measures adopted by the government, asymptomatic infected humans became hospital isolation treatment class, where the saturation phenomenon of the limited medical resources is considered (see Refs. Qin et al. 2013; Zhou and Fan 2012 for more detail). According to the assumptions above, a two-patches SARS-CoV-2 transmission model reads

$$\begin{aligned} \left\{ \begin{aligned} \frac{\mathrm {d}S_1(t)}{\mathrm {d}t}=&\Lambda _1-\beta _1S_1(t)(I_{1}(t)+ \theta _1 A_1(t))-\mu _1S_1(t)-mS_1(t),\\ \frac{\mathrm {d}A_{1}(t)}{\mathrm {d}t}=&(1-\varepsilon _1)\beta _1S_1(t)(I_{1}(t)+\theta _1 A_1(t))-(\mu _1+p_1+\omega _1+m\rho )A_1(t)\\&\quad -\frac{q_1A_1(t)}{k_1+A_1(t)},\\ \frac{\mathrm {d}I_1(t)}{\mathrm {d}t}=&\varepsilon _1\beta _1S_1(t)(I_1(t)+\theta _1 A_1(t))-\mu _1I_1(t)-c_1I_1(t)+p_1A_1(t),\\ \frac{\mathrm {d}Q_1(t)}{\mathrm {d}t}=&\frac{q_1A_1(t)}{k_1+A_1(t)}+c_1I_1(t)-\gamma _1Q_1(t)-\mu _1Q_1(t)-\alpha _1Q_1(t),\\ \frac{\mathrm {d}R_1(t)}{\mathrm {d}t}=&\gamma _1Q_1(t)-\mu _1R_1(t)+\omega _1A_1(t)-mR_1(t),\\ \frac{\mathrm {d}S_2(t)}{\mathrm {d}}=&\Lambda _2-\beta _2S_2(t)(I_2(t)+\theta _2 A_2(t))-\mu _2S_2(t)+mS_1(t),\\ \frac{\mathrm {d}A_2(t)}{\mathrm {d}t}=&(1-\varepsilon _2)\beta _2S_2(t)(I_2(t)+\theta _2 A_2(t))-(\mu _2+p_2+\omega _2)A_2(t)\\&\quad -\frac{q_2A_2(t)}{k_2+A_2(t)}+m\rho A_1(t),\\ \frac{\mathrm {d}I_2(t)}{\mathrm {d}t}=&\varepsilon _2\beta _2S_2(t)(I_2(t)+\theta _2 A_2(t))-\mu _2I_2(t)-c_2I_2(t)+p_2A_2(t),\\ \frac{\mathrm {d}Q_2(t)}{\mathrm {d}t}=&\frac{q_2A_2(t)}{k_2+A_2(t)}+c_2I_2(t)-\gamma _2Q_2(t)-\mu _2Q_2(t)-\alpha _2Q_2(t),\\ \frac{\mathrm {d}R_2(t)}{\mathrm {d}t}=&\gamma _2Q_2(t)-\mu _2R_2(t)+\omega _2A_2(t)+mR_1(t), \end{aligned} \right. \nonumber \\ \end{aligned}$$
(1)

with the initial value \((S_1(0),\cdots ,R_1(0),S_2(0),\cdots ,R_2(0))\!\in \!\mathbb {R}_+^{10}\!:=\!\{(x_1,x_2,\cdots , x_{10}):x_i\geqslant 0,i=1,2,\cdots ,10\}\). Other parameters of model (1) are non-negative constants, and their biological interpretations are given in Table 1.

Table 1 The biological interpretations of the basic parameters for model (1)
Full size table

On the non-negative and boundedness of solutions for model (1), the following result is obvious.

Lemma 1

Solution for model (1) with the initial value in the interior of \(\mathbb {R}_+^{10}\) at time \(t_0=0\) is globally exist and non-negative for all \(t\in [0,\infty )\). Further, the region

$$\begin{aligned} \Omega= & {} \left\{ (S_1,\cdots ,R_2)\in \mathbb {R}_+^{10}:0\leqslant S_1+\cdots +R_1\leqslant \frac{\Lambda _1}{\mu _1},0\leqslant S_2\right. \\&\quad \left. +\cdots +R_2 \leqslant \frac{\Lambda _2\mu _1+m\Lambda _1}{\mu _1\mu _2}\right\} \end{aligned}$$

is positively invariant set with respect to model (1).

Following Lemma 2 is given by Castillon-Charez and Song (2004), which is usually used to determine the existence forward or backward bifurcation of the general differential system with a parameter

$$\begin{aligned} \frac{\mathrm {d}x(t)}{\mathrm {d}t}=f(x,\varphi ), \end{aligned}$$
(2)

where \(f(x,\varphi ):\mathbb {R}^n\times \mathbb {R}\rightarrow \mathbb {R}^n\) with \(f\in \mathbb {C}^2(\mathbb {R}^n\times \mathbb {R})\), and \(f(\mathbf {0},\varphi )\equiv 0\) for all \(\varphi \in \mathbb {R}\). Denote that \(\mathcal {J}=D_xf(\mathbf {0},0)=(\partial f_i(\mathbf {0},0)/\partial x_j)\) is the linearization matrix of system (2) around the equilibrium \(\mathbf {0}\) with \(\varphi =0\). Further, 0 is a simple eigenvalue of matrix \(\mathcal {J}\) and all other eigenvalues of \(\mathcal {J}\) have negative real parts. In addition, matrix \(\mathcal {J}\) has a non-negative right eigenvector u and a left eigenvector v corresponding to the zero eigenvalue.

Lemma 2

(Castillon-Charez and Song 2004) Let \(f_k\) be the k-th component of function f and

$$\begin{aligned} \mathbf {a}=\sum _{k,i,j=1}^{n}v_ku_iu_j\frac{\partial ^2f_k}{\partial x_i\partial x_j}(\mathbf {0},0),\qquad \mathbf {b}=\sum _{k,i=1}v_ku_i\frac{\partial ^2f_k}{\partial x_i\partial \varphi }(\mathbf {0},0), \end{aligned}$$

then, the local dynamics of system (2) around \(\mathbf {0}\) are totally determined by \(\mathbf {a}\) and \(\mathbf {b}\).

  1. (i)

    \(\mathbf {a}>0\) and \(\mathbf {b}>0\). If \(\varphi <0\) with \(\mid \varphi \mid \ll 1\), then \(\mathbf {0}\) is locally asymptotically stable, and there exists a positive unstable equilibrium; if \(0<\varphi \ll 1\), \(\mathbf {0}\) is unstable and there exists a negative and locally asymptotically stable equilibrium.

  2. (ii)

    \(\mathbf {a}<0\) and \(\mathbf {b}<0\). If \(\varphi <0\) with \(\mid \varphi \mid \ll 1\), then \(\mathbf {0}\) is unstable; if \(0<\varphi \ll 1\), then \(\mathbf {0}\) is locally asymptotically stable, and there exists a positive unstable equilibrium.

  3. (iii)

    \(\mathbf {a}>0\) and \(\mathbf {b}<0\). If \(\varphi <0\) with \(\mid \varphi \mid \ll 1\), then \(\mathbf {0}\) is unstable, and there exists a locally asymptotically stable negative equilibrium; if \(0<\varphi \ll 1\), then \(\mathbf {0}\) is stable, and a positive unstable equilibrium appears.

3 Dynamics of Model in Patch-i Without Migration

We discuss, in this section, the dynamics of the spread of SARS-CoV-2 in patch-i \((i=1,2)\). Since the state variables \(Q_i\) and \(R_i\) do not appear in the first to third (or sixth to eighth) equations of model (1), the dynamical model of the transmission of SARS-CoV-2 in patch-i can be decoupled into the following three-dimensional system

$$\begin{aligned} \left\{ \begin{aligned} \frac{\mathrm {d}S_i(t)}{\mathrm {d}t}=&\Lambda _i-\beta _iS_i(t)(I_{i}(t)+ \theta _i A_i(t))-\mu _iS_i(t),\\ \frac{\mathrm {d}A_{i}(t)}{\mathrm {d}t}=&(1-\varepsilon _i)\beta _iS_i(t)(I_{i}(t)+\theta _i A_i(t))-(\mu _i+p_i+\omega _i)A_i(t)-\frac{q_iA_i(t)}{k_i+A_i(t)},\\ \frac{\mathrm {d}I_i(t)}{\mathrm {d}t}=&\varepsilon _i\beta _iS_i(t)(I_i(t)+\theta _i A_i(t))-\mu _iI_i(t)-c_iI_i(t)+p_iA_i(t). \end{aligned} \right. \end{aligned}$$
(3)

Following Theorem 1 is on the existence, uniqueness and boundedness of solution of model (3), which is obvious.

Theorem 1

Solution for model (3) with the initial value in the interior of \(\mathbb {R}_+^{3}\) at time \(t_0=0\) is globally exist and non-negative for all \(t\in [0,\infty )\), and the region \(\Omega =\{(S_i,A_i,I_i)\in \mathbb {R}_+^{3}:0\leqslant S_i+A_i+I_i\leqslant {\Lambda _i}/{\mu _i}\} \) is positively invariant set \((i=1,2)\).

3.1 The Stability of the Disease-Free Equilibrium

Obviously, model (3) admits a disease-free equilibrium \(\mathcal {E}_{0i}(\Lambda _i/\mu _i,0,0)\). Further, by using the next generation matrix formulated in Refs. (Diekmann et al. 1990; van den Driessche and Watmough 2002, 2008), the basic reproduction number of model (3) is defined by

$$\begin{aligned} \mathcal {R}_{0i}=\left[ \frac{(1-\varepsilon _i)\beta _i\theta _i}{\mu _i+p_i+\omega _i+q_i/k_i}+\frac{(1-\varepsilon _i)p_i\beta _i}{(\mu _i+p_i+\omega _i+q_i/k_i)(\mu _i+c_i)}+\frac{\varepsilon _i\beta _i}{\mu _i+c_i}\right] \frac{\Lambda _i}{\mu _i}. \end{aligned}$$

Following Theorem 2 is on the local asymptotical stability of model (3).

Theorem 2

If \(\mathcal {R}_{0i}<1\), then the disease-free equilibrium \(\mathcal {E}_{0i}\) of model (3) is locally asymptotically stable. If \(\mathcal {R}_{0i}>1\), then \(\mathcal {E}_{0i}\) is unstable.

Proof

According to the proof of Theorem 2 in Ref. (van den Driessche and Watmough 2002), the local asymptotical stability of the disease-free equilibrium \(\mathcal {E}_{0i}\) is determined by the following characteristic equation

$$\begin{aligned} (\lambda +\mu _i)(\lambda ^2+a_1\lambda +a_2)=0, \end{aligned}$$
(4)

where

$$\begin{aligned} a_1=&\left( \mu _i+p_i+\omega _i+\frac{q_i}{k_i}\right) \left( 1-\frac{(1-\varepsilon _i)\beta _i\theta _i\Lambda _i}{(\mu _i+p_i+\omega _i+q_i/k_i)\mu _i}\right) \\&\quad + (\mu _i+c_i)\left( 1-\frac{\varepsilon _i\beta _i\Lambda _i}{(\mu _i+c_i)\mu _i}\right) ,\\ a_2=&\left( \mu _i+p_i+\omega _i+\frac{q_i}{k_i}\right) (\mu _i+c_i)(1-\mathcal {R}_{0i}). \end{aligned}$$

This is easy to verify that \(a_1>0\), \(a_2>0\) for \(\mathcal {R}_{0i}<1\) and \(a_2<0\) for \(\mathcal {R}_{0i}>1\). Therefore, all eigenvalues of Eq. (4) have negative real parts for \(\mathcal {R}_{0i}<1\) and (4) has a positive root for \(\mathcal {R}_{0i}>1\). Thus, the disease-free equilibrium \(\mathcal {E}_{0i}\) is stable for \(\mathcal {R}_{0i}<1\) and unstable for \(\mathcal {R}_{0i}>1\). The proof is complete. \(\square \)

Remark 1

For patch-i, if we consider the effect of population migration, this can also obtain the expression of the basic reproduction number \(\mathcal {R}_{01}^m\) as follows

$$\begin{aligned} \mathcal {R}_{01}^m&=\left[ \frac{(1-\varepsilon _i)\beta _i\theta _i}{\mu _i+p_i+\omega _i+m\rho +q_i/k_i}+\frac{(1-\varepsilon _i)p_i\beta _i}{(\mu _i+p_i+\omega _i+m\rho +q_i/k_i)(\mu _i+c_i)}\right. \\&\quad \left. +\frac{\varepsilon _i\beta _i}{\mu _i+c_i}\right] \frac{\Lambda _i}{\mu _i+m} \end{aligned}$$

by the next-generation matrix formulated. It is also easy to see from this expression that \(\mathcal {R}_{01}^m\) is inversely proportional to m or \(m\rho \) (the migration rate of population) and \(q_1\) (maximal medical resources supplied per unite time in patch-i and positively proportional to \(k_1\)) (half-saturation constant in patch-1).

On the global asymptotical stability of the disease-free equilibrium \(\mathcal {E}_{0i}\), we have the following result.

Theorem 3

If \(\check{\mathcal {R}}_{0i}=\max \left\{ \mathcal {R}_{0i}^a,\mathcal {R}_{0i}^b\right\} <1\), where

$$\begin{aligned} \mathcal {R}_{0i}^a=\frac{\beta _i\Lambda _i}{(\mu _i+c_i)\mu _i},\qquad \mathcal {R}_{0i}^b=\frac{\beta _i\theta _i\Lambda _i}{(\mu _i+\omega _i+q_i/(k_i+\Lambda _i/\mu _i))\mu _i}, \end{aligned}$$

then the disease-free equilibrium \(\mathcal {E}_{0i}\) of model (3) is global asymptotical stable.

Proof

We choose a positive differentiable function \(V(t)=A_i(t)+I_i(t)\) and calculate its total derivative directly along model (3) to get that

$$\begin{aligned} \frac{\mathrm {d}V(t)}{\mathrm {d}t}=&\beta _iS_i(t)(I_i(t)+\theta _iA_i(t))-(\mu _i+\omega _i)A_i(t)-\frac{q_iA_i(t)}{k_i+A_i(t)}-\mu _iI_i(t)-c_iI_i(t)\\ \leqslant&\left( \beta _i\frac{\Lambda _i}{\mu _i}-\mu _i-c_i\right) I_i(t)+\left( \frac{\beta _i\theta _i\Lambda _i}{\mu _i}-(\mu _i+\omega _i)-\frac{q_i}{k_i+{\Lambda _i}/{\mu _i}}\right) A_i(t)\\ =&(\mu _i+c_i)\left( \mathcal {R}_{0i}^a-1\right) I_i(t)+\left( \mu _i+\omega _i+\frac{q_i}{k_i+{\Lambda _i}/{\mu _i}}\right) \left( \mathcal {R}_{0i}^b-1\right) A_i(t). \end{aligned}$$

Obviously, the LaSalle’s invariance principle implies that the disease-free equilibrium \(\mathcal {E}_{0i}\) is global asymptotical stability in \(\Omega \) for \(\check{\mathcal {R}}_{0i}<1\). The proof is complete. \(\square \)

Remark 2

Theorem 3 gives the criterion for quickly determining the extinction of the disease which does not depend on the initial state for the disease outbreak.

3.2 The Existence and Stability of the Endemic Equilibria

Now, we deal with the existence of endemic equilibrium of model (3). Let the derivatives with time t in model (3) equal to zero, we obtain the following algebraic equations

$$\begin{aligned} \left\{ \begin{aligned}&0=\Lambda _i-\beta _iS_i(I_{1}+\theta _i A_i)-\mu _iS_i,\\&0=(1-\varepsilon _i)\beta _iS_i(I_{i}+\theta _i A_i)-(\mu _i+p_i+\omega _i )A_i-\frac{q_iA_i}{k_i+A_i},\\&0=\varepsilon _i\beta _iS_i(I_i+\theta _i A_i)-\mu _iI_i-c_iI_i+p_iA_i. \end{aligned} \right. \end{aligned}$$
(5)

From the first equation of (5), one has

$$\begin{aligned} S_i=\frac{\Lambda _i}{\beta _i(I_i+\theta _i A_i)+\mu _i}. \end{aligned}$$
(6)

This yields from the third equation of (5) that

$$\begin{aligned} I_i=\left[ \frac{(\mu _i+p_i+\omega _i)\varepsilon _i}{(1-\varepsilon _i)(\mu _i+c_i)}+\frac{\varepsilon _iq_i}{(1-\varepsilon _i)(\mu _i+c_i)(k_i+A_i)}+\frac{p_i}{\mu _i+c_i}\right] A_i. \end{aligned}$$
(7)

Substituting (6) and (7) into the second equation of (5) and simplifying it, we can get

$$\begin{aligned}&(1-\varepsilon _i)\beta _i\Lambda _i\bigg \{\bigg [\frac{(\mu _i+p_i+\omega _i)\varepsilon _i(k_i+A_i)^2}{(1-\varepsilon _i)(\mu _i+c_i)}+\frac{\varepsilon _iq_i(k_i+A_i)}{(1-\varepsilon _i)(\mu _i+c_i)} +\frac{p_i(k_i+A_i)^2}{\mu _i+c_i}\bigg ]\nonumber \\&\quad +\theta _i(k_i+A_i)^2\bigg \}\nonumber \\&=\big [(\mu _i+p_i+\omega _i)(k_i+A_i)+q_i\big ] \bigg \{\beta _i\bigg [\bigg (\frac{(\mu _i+p_i+\omega _i)\varepsilon _i(k_i+A_i)}{(1-\varepsilon _i)(\mu _i+c_i)}+\frac{\varepsilon _iq_i}{(1-\varepsilon _i)(\mu _i+c_i)}\nonumber \\&\qquad +\frac{p_i(k_i+A_i)}{\mu _i+c_i}\bigg )A_i+\theta _i A_i(k_i+A_i)\bigg ]+\mu _i(k_i+A_i)\bigg \}. \end{aligned}$$
(8)

For \(\varepsilon _i>0\), from (8), the existence of endemic equilibrium of model (3) is determined by the positive roots of the following cubic equation

$$\begin{aligned} aA_i^3+bA_i^2+cA_i+d=0, \end{aligned}$$
(9)

where

$$\begin{aligned} a&=\beta _i(\mu _i+p_i+\omega _i)\left[ \frac{(\mu _i+p_i+\omega _i)\varepsilon _i}{(1-\varepsilon _i)(\mu _i+c_i)}+\frac{p_i}{\mu _i+c_i}+\theta _i\right] ,\\ b&=[(\mu _i+p_i+\omega _i)k_i+q_i]\bigg [\frac{(\mu _i+p_i+\omega _i)\beta _{i} \varepsilon _i}{(1-\varepsilon _i)(\mu _i+c_i)}+\frac{\beta _{i}p_ik_i}{\mu _i+c_i}+\beta _{i}\theta _i\bigg ]\\&\qquad + (\mu _i+p_i+\omega _i)\bigg [\frac{\beta _{i}(\mu _i+p_i+\omega _i)\varepsilon _ik_i+\beta _{i}\varepsilon _iq_i}{(1-\varepsilon _i)(\mu _i+c_i)}+\frac{\beta _{i}p_ik_i}{\mu _i+c_i}+\beta _{i}\theta _ik_i+\mu _i\bigg ]\\&\qquad -(1-\varepsilon _i)\beta _i\Lambda _i\bigg [\frac{(\mu _i+p_i+\omega _i)\varepsilon _i}{(1-\varepsilon _i)(\mu _i+c_i)}+\frac{p_i}{\mu _i+c_i}+\theta _i\bigg ],\\ c&=[(\mu _i+p_i+\omega _i)k_i+q_i]\bigg [\beta _ik_i\frac{(\mu _i+p_i+\omega _i)\varepsilon _i}{(1-\varepsilon _i)(\mu _i+c_i)}+\frac{\beta _i\varepsilon _iq_i}{(1-\varepsilon _i) (\mu _i+c_i)}+\frac{\beta _ik_ip_i}{\mu _i+c_i}\\&\qquad +\beta _ik_i\theta _i+\mu _i\bigg ]+k_i(\mu _i+p_i+\omega _i)\mu _i-(1-\varepsilon _i) \beta _i\Lambda _i\\&\qquad \times \bigg (\frac{2k_i\varepsilon _i(\mu _i+p_i+\omega _i)}{(1-\varepsilon _i)(\mu _i+c_i)} +\frac{\varepsilon _iq_i}{(1-\varepsilon _i)(\mu _i+c_i)}+\frac{2k_ip_i}{\mu _i+c_i} +2\theta _ik_i\bigg ),\\ d&=\big [k_i(\mu _i+p_i+\omega _i)+q_i\big ]\mu _ik_i-(1-\varepsilon _i)\beta _i\Lambda _i \bigg [\frac{(\mu _i+p_i+\omega _i)\varepsilon _ik_i^2}{(1-\varepsilon _i)(\mu _i+c_i)}\\&\qquad +\frac{\varepsilon _iq_ik_i}{(1-\varepsilon _i)(\mu _i+c_i)}+\frac{k_i^2p_i}{\mu _i+c_i} +\theta _ik_i^2\bigg ]\\&=\big [k_i(\mu _i+p_i+\omega _i)+q_i\big ]\mu _ik_i\left( 1-\mathcal {R}_{0i}\right) . \end{aligned}$$

Obviously, \(a>0\) and \(d\leqslant 0\Leftrightarrow \mathcal {R}_{0i}\leqslant 1\). Let \(f(A_i)=aA_i^3+bA_i^2+cA_i+d\), \(\Delta =4b^2-12ac\) and

$$\begin{aligned} \bar{x}_1=\frac{-2b-\sqrt{4b^2-12ac}}{6a},\qquad \bar{x}_2=\frac{-2b+\sqrt{4b^2-12ac}}{6a} \end{aligned}$$

According to the relationship between the real roots and coefficients of cubic equation (9), we have following Table 2 about the existence of the various possibilities for the roots of equation \(f(A_i)=0\).

Table 2 Numbers of possible positive real roots of \(f(A_i)=0\) for \(\mathcal {R}_{0i}<1\), \(\mathcal {R}_{0i}=1\) and \(\mathcal {R}_{0i}>1\), respectively
Full size table

Combining all the possibilities enumerated in Table 2, we have the following results.

Theorem 4

On the existence of endemic equilibria of model (3), one of the following statements is valid.

  • \((\mathrm {I})\) \(\mathcal {R}_{0i}<1\)

    • If one of the following conditions holds

        \(\mathbf{(i)}\) \(b>0\), \(c<0\) and \(f(\bar{x}_2)=0\);   \(\mathbf (ii)\) \(b<0\), \(c>0\), \(\Delta >0\) and \(f(\bar{x}_2)=0\);   \(\mathbf (iii)\) \(b<0\) and \(c<0\);

      then model (3) has a unique endemic equilibrium.

    • If one of the following conditions holds

        \(\mathbf{(i)}\) \(b>0\) and \(c<0\);   \(\mathbf (ii)\) \(b<0\), \(c>0\) and \(\Delta >0\);    \(\mathbf (iii)\) \(b<0\), \(c<0\) and \(f(\bar{x}_2)<0\);

      then model (3) has two endemic equilibria.

  • \((\mathrm {II})\) \(\mathcal {R}_{0i}=1\)

    • If one of the following conditions holds

        \(\mathbf{(i)}\) \(b>0\) and \(c<0\);   \(\mathbf (ii)\) \(b<0\), \(b>0\) and \(b^2-4ac=0\);    \(\mathbf (iii)\) \(b<0\) and \(c<0\);

      then model (3) has a unique endemic equilibrium.

    • If \(b<0\), \(c>0\) and \(b^2-4ac>0\), then model (3) has two endemic equilibria.

  • \((\mathrm {III})\) \(\mathcal {R}_{0i}>1\)

    • If one of the following conditions holds

      \(\mathbf{(i)}\) \(b>0\) and \(c>0\);    \(\mathbf (ii)\) \(b>0\) and \(c<0\);   \(\mathbf (iii)\) \(b<0\), \(c>0\), \(\Delta >0\), \(f(\bar{x}_1)<0\) (or, \(f(\bar{x}_1)>0\) and \(f(\bar{x}_2)>0)\);   \(\mathbf (iv)\) \(b<0\) and \(c<0\);

      then model (3) has a unique endemic equilibrium.

    • If \(b<0\), \(c>0\), \(\Delta >0\) and \(f(\bar{x}_1)=0\) (or, \(f(\bar{x}_1)>0\), \(f(\bar{x}_2)=0)\), then model (3) has two endemic equilibria.

    • If \(b<0\), \(c>0\), \(\Delta >0\), \(f(\bar{x}_1)>0\) and \(f(\bar{x}_2)<0\), then model (3) has three endemic equilibria.

Remark 3

From Table 2 or Fig. 1, we can easily find that the existence of positive roots of characteristic equation (9) becomes more complicated, whether the basic reproduction number \(\mathcal {R}_{0i}\) is greater than 1 or less than 1. This is also cased by the limited medical resources.

Fig. 1
figure 1

The existence of multiple positive roots of equation (9): a \(\mathcal {R}_{0i}=0.9934<1\); b \(\mathcal {R}_{01}=19.4510>1\)

Full size image

Noting that the existence of the endemic equilibria of model (3) is very complicated, whether the basic reproduction number \(\mathcal {R}_{0i}\) is greater than 1 or less than 1. Therefore, we only discuss the existence of the endemic equilibrium and backward bifurcation of model (3) for a special case \(\varepsilon _i=0\). That is, assume that all infected humans will experience asymptomatic stage first, and then asymptomatic infected humans will produce symptoms and become symptomatic infected humans. This situation is also consistent with the current spread of COVID-19. It is easy to calculate that the basic production number of model (3) with \(\varepsilon _i=0\) is

$$\begin{aligned} \mathcal {R}_{0i}^0=\left[ \frac{\theta _i}{\mu _i+p_i+\omega _i+q_i/k_i}+\frac{p_i}{(\mu _i+p_i+\omega _i+q_i/k_i)(\mu _i+c_i)}\right] \frac{\beta _i\Lambda _i}{\mu _i}. \end{aligned}$$

Further, for \(\varepsilon _i=0\), by simplifying Eq. (8) and merging similar terms, we can get a quadratic equation of one variable about \(A_i\) as

$$\begin{aligned} a_2A_i^2+a_1A_i+a_0=0, \end{aligned}$$

where

$$\begin{aligned} a_2&=\beta _i(\mu _i+p_i+\omega _i)\left( \frac{p_i}{\mu _i+c_i}+\theta _i\right) ,\\ a_1&=\beta _i[k_i(\mu _i+p_i+\omega _i)+q_i]\left( \frac{p_i}{\mu _i+c_i}+\theta _i\right) +\mu _i(\mu _i+p_i+\omega _i)\\&\qquad \qquad -\beta _i\Lambda _i\left( \frac{p_i}{\mu _i+c_i}+\theta _i\right) \\&=\beta _i\Lambda _i\left( \frac{p_i}{\mu _i+c_i}+\theta _i\right) \left[ \frac{k_i(\mu _i+p_i+\omega _i)+q_i}{\beta _{i}\Lambda _i}+\frac{\mu _i(\mu _i+p_i+\omega _i)}{\beta _i\Lambda _i\left( \frac{p_i}{\mu _i+c_i}+\theta _i\right) }-1 \right] \\ a_0&=\mu _i[k_i(\mu _i+p_2+\omega _i)+q_i]-\beta _i\Lambda _ik_i\left( \frac{p_i}{\mu _i+c_i}+\theta _i\right) \\&=\mu _i[k_i(\mu _i+p_i+\omega _i)+q_i]\left( 1-\mathcal {R}_{0i}^0\right) . \end{aligned}$$

Obviously, \(a_2\) is always greater than zero, and \(\mathcal {R}_{0i}^0<1\) if and only if \(a_0>0\). Further, it yields from \(\Delta =a_1^2-4a_2a_0=0\) that

$$\begin{aligned} \mathcal {R}_{0i}^{0c}=1-\frac{a_1^2}{4\omega _i\mu _i[k_i(\mu _i+p_i+\omega _i)+q_i]}. \end{aligned}$$

Based on the above discussion, we have the following conclusions about the existence of positive equilibrium for model (3) with \(\varepsilon _i=0\).

Theorem 5

For model (3) with \(\varepsilon _i=0\), there always exists a disease-free equilibrium \(\mathcal {E}_{0i}\) and

  1. (a)

    If \(\mathcal {R}_{0i}^{0}<\mathcal {R}_{0i}^{0c}\), or \(\mathcal {R}_{0i}^{0}\leqslant 1\) and \(a_1>0\), then there is no endemic equilibrium;

  2. (b)

    If \(\mathcal {R}_{0i}^{0}>1\), or \(\mathcal {R}_{0i}^{0}=\mathcal {R}_{0i}^{0c}\leqslant 1\) and \(a_1<0\), then there is a unique endemic equilibrium \(\bar{\mathcal {E}}_{i}^{0}(\bar{S}_{i}^{0},\bar{A}_{i}^{0},\bar{I}_{i}^{0})\);

  3. (c)

    If \(\mathcal {R}_{0i}^{0c}<\mathcal {R}_{0i}^{0}<1\) and \(a_1<0\), then there are two distinct endemic equilibria \(\tilde{\mathcal {E}_{i}^0}(\tilde{S}_{i}^{0},\tilde{A}_{i}^{0},\tilde{I}_{i}^{0})\) and \(\hat{\mathcal {E}_{i}^0}(\hat{S}_{i}^{0},\hat{A}_{i}^{0},\hat{I}_{i}^{0})\).

Remark 4

The conditions of conclusion (a) of Theorem 5 require that both \(\mathcal {R}_{0i}^0\leqslant 1\) and \(a_1>1\). From their expressions, we can obtain

$$\begin{aligned} \mathcal {R}_{0i}^0<1&\iff \beta _i\Lambda _i[\theta _i(\mu _i+c_i)+p_i]\leqslant \mu _i(\mu _i+c_i)(\mu _i+p_i+\omega _i)+\mu _i(\mu _i+c_i)q_i/k_i,\\ a_1>0&\iff \beta _i\Lambda _i[\theta _i(\mu _i+c_i)+p_i]<\mu _i(\mu _i+c_i)(\mu _i+p_i+\omega _i)\\&\quad +\beta _ik_i(\mu _i+p_i+\omega _i+q_i/k_i)[\theta _i(\mu _i+c_i)+p_i]. \end{aligned}$$

Obviously, the above two inequalities can hold simultaneously. Similarly, for the condition of conclusion (b) (or (c)) of Theorem 5, \(\mathcal {R}_{0i}\leqslant 1\) (or \(\mathcal {R}_{0i}<1\)) and \(a_1<0\) are, respectively, equivalent to

$$\begin{aligned} \mathcal {R}_{0i}^0<1&\iff \beta _i\Lambda _i[\theta _i(\mu _i+c_i)+p_i]\leqslant \mu _i(\mu _i+c_i)(\mu _i+p_i+\omega _i)\\&\qquad \qquad +\mu _i(\mu _i+c_i)q_i/k_i,\\ a_1<0&\iff \beta _i\Lambda _i[\theta _i(\mu _i+c_i)+p_i]>\mu _i(\mu _i+c_i)(\mu _i+p_i+\omega _i)\\&\qquad \qquad +\beta _ik_i(\mu _i+p_i+\omega _i+q_i/k_i)[\theta _i(\mu _i+c_i)+p_i]. \end{aligned}$$

In fact, the above two inequalities can also hold simultaneously for some specific parameters.

Now, we consider the stability of the endemic equilibria for \(\varepsilon _i=0\). To do this, linearizing model (3) with \(\varepsilon _i=0\) around a point \(\mathcal {E}^*_i(S_i^*,A_i^*,I_i^*)\) yields the Jacobian matrix

$$\begin{aligned} \mathcal {J}_{\mathcal {E}^*_i}= \begin{pmatrix} -\beta _i(I_i^*+\theta _iA_i^*)-\mu _i &{} -\beta _iS_i^*\theta _i &{} -\beta _iS_i^*\\ \beta _i(I_i^*+\theta _iA_i^*)&{} \beta _i\theta _iS_i^*-\mu _i-p_i-\omega _i-\frac{q_ik_i}{(k_i+A_i^*)^2} &{} \beta _iS_i^*\\ 0 &{} p_i &{} -\mu _i-c_i \end{pmatrix}. \end{aligned}$$

Further, through a series of calculations, we can get the corresponding characteristic equation is

$$\begin{aligned} \lambda ^3+b_2(A_i^*)\lambda ^2+b_1(A_i^*)\lambda +b_0(A_i^*)=0, \end{aligned}$$
(10)

where

$$\begin{aligned} b_2(A_i^*)&=3\mu _i+c_i+p_i+\omega _i+\frac{q_ik_i}{(k_i+A_i^*)^2}+\beta _i\bigg (\frac{p_i}{\mu _i+c_i}+\theta _i\bigg )A_i^*\\&\qquad -\frac{\beta _i\theta _i\Lambda _i}{\beta _i(p_i/(\mu _i+c_i)+\theta _i )A_i^*+\mu _i},\\ b_1(A_i^*)&=\mu _i\bigg (2\mu _i+c_i+p_i+\omega _i+\frac{q_ik_i}{(k_i+A_i^*)^2}\bigg ) +(\mu _i+c_i)\bigg (\mu _i+p_i+\omega _i\\&\qquad +\frac{q_ik_i}{(k_i+A_i^*)^2}\bigg ) +\beta _i\left( \frac{p_i}{\mu _i+c_i}+\theta _i\right) \bigg (2\mu _i+c_i+p_i+\omega _i+\frac{q_ik_i}{(k_i+A_i^*)^2}\bigg )A_i^*\\&\qquad -\big [\mu _i\beta _i\theta _i+(\mu _i+c_i)\beta _i\theta _i+\beta _ip_i\big ]\frac{\beta _i\theta _i\Lambda _i}{\beta _i(p_i/(\mu _i+c_i)+\theta _i )A_i^*+\mu _i},\\ b_0(A_i^*)&=(\mu _i+c_i)[\mu _i+\beta _i(I_i+\theta _iA_i)]\left( \mu _i+p_i+\omega _i+\frac{q_ik_i}{(k_i+A_i^*)^2}\right) \\&\qquad \times \bigg [1-\mathcal {R}_{0i}^0\frac{(\mu _i+p_i+\omega _i+q_i/k_i)\mu _i^2}{(\mu _i+p_i+\omega _i+{q_ik_i}/{(k_i+A_i^*)^2})\big [\mu _i+\beta _i({p_i}/{(\mu _i+c_i)}+\theta _i)A_i^*\big ]^2}\bigg ]. \end{aligned}$$

By using Routh-Hurwitz criterion, it is easy to get that all roots of equation of (10) have negative real parts if and only if the following conditions satisfy

$$\begin{aligned} b_1(A_i^*)>0\ (i=0,1,2), \qquad b_1(A_i^*)b_2(A_i^*)-b_0(A_i^*)>0. \end{aligned}$$
(11)

Based on the above discussion, we have the following result on the stability of the endemic equilibrium for model (3) with \(\varepsilon _i=0\).

Theorem 6

If model (3) with \(\varepsilon _i=0\) admits a endemic equilibrium \(\mathcal {E}^*(S_i^*,A_i^*,I_i^*)\) and \(A_i^*\) satisfies conditions (11), then \(\mathcal {E}^*\) is locally asymptotically stable.

Following Theorem 7 is on the existence of the forward/backward bifurcation for model (3) with \(\varepsilon _i=0\).

Theorem 7

For \(\varepsilon _i=0\) and \(\mathcal {R}_{0i}^{0}=1\), one of the following statements is valid.

  1. (a)

    If \(1-4(\mu _i+p_i+\omega _i) k_i<0\), then model (3) exhibits a forward bifurcation for all \(q_i>0\).

  2. (b)

    If \(1-4(\mu _i+p_i+\omega _i) k_i=0\), then model (3) admits a forward bifurcation for all \(q_i\in (0,1/4)\cup (1/4,+\infty )\).

  3. (c)

    If \(1-4(\mu _i+p_i+\omega _i) k_i>0\), then model has a backward bifurcation for \(q_i\in (\hat{q}_i,\breve{q}_i)\) and has a forward bifurcation for all \(q_i\in (0, \hat{q}_i)\cup (\breve{q}_i,+\infty )\), where

    $$\begin{aligned} \begin{aligned}&\hat{q_i}=\frac{1-2(\mu _i+p_i+\omega _i) k_i-\sqrt{1-4(\mu _i+p_i+\omega _i) k_i}}{2},\\&\breve{q_i}=\frac{1-2(\mu _i+p_i+\omega _i) k_i+\sqrt{1-4(\mu _i+p_i+\omega _i)k_i}}{2}. \end{aligned} \end{aligned}$$
    (12)

Proof

Let \(S_i(t)=x_1(t)\), \(A_i(t)=x_2(t)\) and \(I_i(t)=x_3(t)\), then model (3) can be rewritten as

$$\begin{aligned} \left\{ \begin{aligned}&\frac{\mathrm {d}x_1}{\mathrm {d}t}=\Lambda _i-\beta _i(x_3+\theta _ix_2)x_1-\mu _ix_1:=f_1,\\&\frac{\mathrm {d}x_2}{\mathrm {d}t}=\beta _i(x_3+\theta _ix_2)x_1-(\mu _i+p_i+\omega _i) x_2-\frac{q_ix_2}{k_i+A_i}:=f_2,\\&\frac{\mathrm {d}x_3}{\mathrm {d}t}=p_ix_2-\mu _ix_3-c_ix_3:=f_3. \end{aligned} \right. \end{aligned}$$
(13)

Further, the Jacobian matrix of the disease-free equilibrium \(\mathcal {E}_{0i}^0\) for model (13) is

$$\begin{aligned} \mathcal {J}_{\mathcal {E}_{0i}^0}= \begin{pmatrix} -\mu _i &{} -\beta _i\theta _i\frac{\Lambda _i}{\mu _i} &{} -\beta _i\frac{\Lambda _i}{\mu _i}\\ 0&{} \beta _i\theta _i\frac{\Lambda _i}{\mu _i}-\mu _i-p_i-\omega _i-\frac{q_i}{k_i} &{} \beta _i\frac{\Lambda _i}{\mu _i}\\ 0 &{} p_i &{} -\mu _i-c_i \end{pmatrix}. \end{aligned}$$

Therefore, the corresponding characteristic equation of \(\mathcal {J}_{\mathcal {E}_{0i}^0}\) with \(\mathcal {R}_{0i}^0=1\) is as follows

$$\begin{aligned} \lambda (\lambda +\mu _i)(\lambda +a_i)=0, \end{aligned}$$
(14)

where

$$\begin{aligned} a_i=\left( \mu _i+p_i+\omega _i+\frac{q_i}{k_i}\right) \left( 1-\frac{\beta _i\theta _i\Lambda _i}{(\mu _i+p_i+\omega _i+q_i/k_i)\mu _i}\right) +\mu _i+c_i>0 \end{aligned}$$

due to the fact \(\mathcal {R}_{0i}^0=1\). Obviously, all eigenvalues of equation (14) are \(\lambda _1=0\), \(\lambda _2=-\mu _i\) and \(\lambda _3=-a_i\). Therefore, \(\lambda _1=0\) is a simple zero eigenvalue and all other eigenvalues of \(\mathcal {J}_{\mathcal {E}_{0i}^0}\) are real and negative. Thus, the center manifold theory in Guckenheimer and Holmes (1983) can be used to discuss the occurrence of bifurcations.

Now, we choose the transmission rate \(\beta _i\) as the bifurcation parameter. It is obvious to calculate that \(\mathcal {R}_{0i}^0=1\) is equivalent to

$$\begin{aligned} \beta _i=\beta _i^*=\frac{(\mu _i+p_i+\omega _i+q_i/k_i)(\mu _i+c_i)}{\theta _i(\mu _i+c_i)+p_i}\frac{\mu _i}{\Lambda _i}. \end{aligned}$$

Hence, if \(\beta _i=\beta _i^*\) the disease-free equilibrium \(\mathcal {E}_{0i}^0\) is a non-hyperbolic equilibrium and the assumption \((\mathrm {H}_1)\) of Lemma 2 is satisfied.

Denote that \(U=(u_1,u_2,u_3)^T\) a right eigenvector associated with the zero eigenvalue \(\lambda _1=0\), which is formulated by \(\mathcal {J}_{\mathcal {E}_{0i}^0}U=0\). That is,

$$\begin{aligned} \left\{ \begin{aligned}&-\mu _iu_1-\frac{\beta _i^*\theta _i\Lambda _i}{\mu _i}u_2 -\frac{\beta _i^*\Lambda _i}{\mu _i}u_3=0,\\&\left( \frac{\beta _i^*\theta _i\Lambda _i}{\mu _i} -\mu _i-p_i-\omega _i-\frac{q_i}{k_i}\right) u_2+\frac{\beta _i^*\Lambda _i}{\mu _i}u_3=0,\\&p_iu_2-(\mu _i+c_i)u_3=0. \end{aligned} \right. \end{aligned}$$

It can be obtained by direct calculation and simplification that

$$\begin{aligned} \left\{ \begin{aligned} u_1=&\left[ \frac{\theta _i}{\mu _i}\frac{(\mu _i+p_i+\omega _i+q_i/k_i)(\mu _i+c_i)}{(\mu _i+c_i)\theta _i+p_i}-\frac{\theta _i\Lambda _i}{\mu _i^2} -\frac{\mu _i+p_i+\omega _i+q_i/k_i}{\mu _i}\right] \\&\times \frac{(\mu _i+p_i+\omega _i+q_i/k_i) (\mu _i+c_i)}{(\mu _i+c_i)\theta _i+p_i},\\ u_2=&\frac{(\mu _i+p_i+\omega _i+q_i/k_i)(\mu _i+c_i)}{(\mu _i+c_i)\theta _i+p_i},\\ u_3=&\mu _i+p_i+\omega _i+\frac{q_i}{k_i}-\theta _i\frac{(\mu _i+p_i+\omega _i+q_i/k_i)(\mu _i+c_i)}{(\mu _i+c_i)\theta _i+p_i}. \end{aligned} \right. \end{aligned}$$
(15)

Similarly, a left eigenvector associated with the zero eigenvalue \(\lambda _1=0\) is given by \(V=(v_1,v_2,v_3)\), where

$$\begin{aligned} v_1=0,\quad v_2=p_i,\quad v_3\!=\!\mu _i+p_i\!+\!\omega _i+\frac{q_i}{k_i}-\theta _i\frac{(\mu _i+p_i+\omega _i+q_i/k_i)(\mu _i+c_i)}{(\mu _i+c_i)\theta _i+p_i}.\nonumber \\ \end{aligned}$$
(16)

Next, we compute the partial derivatives at the disease-free equilibrium \(\mathcal {E}_{0i}^0\). From model (13), it can be obtained that

$$\begin{aligned}&\frac{\partial ^2f_1}{\partial x_1^2}=\frac{\partial ^2f_1}{\partial x_2^2}=\frac{\partial ^2f_1}{\partial x_3^2}=\frac{\partial ^2f_1}{\partial x_2\partial x_3}=\frac{\partial ^2f_1}{\partial x_3\partial x_2}=0,\nonumber \\&\frac{\partial ^2f_1}{\partial x_1\partial x_3}=\frac{\partial ^2f_1}{\partial x_3\partial x_1}=-\beta _i^*,\quad \frac{\partial ^2f_1}{\partial x_1\partial x_2}=\frac{\partial ^2f_1}{\partial x_2\partial x_1}=-\theta _i\beta _i^*,\nonumber \\&\frac{\partial ^2f_2}{\partial x_1^2}=\frac{\partial ^2f_2}{\partial x_3^2}=\frac{\partial ^2f_2}{\partial x_2\partial x_3}=\frac{\partial ^2f_2}{\partial x_3\partial x_2}=0,\quad \frac{\partial ^2f_2}{\partial x_2^2}=\frac{2q_ik_i}{(k_i+x_2)^3},\\&\frac{\partial ^2f_2}{\partial x_1\partial x_2}=\frac{\partial ^2f_2}{\partial x_2\partial x_1}=\theta _i\beta _i^*,\quad \frac{\partial ^2f_2}{\partial x_1\partial x_3}=\frac{\partial ^2f_2}{\partial x_3\partial x_1}=\beta _i^*,\nonumber \\&\frac{\partial ^2f_3}{\partial x_i^2}=\frac{\partial ^2f_3}{\partial x_2^2}=\frac{\partial ^2f_3}{\partial x_3^2}=\frac{\partial ^2f_3}{\partial x_1\partial x_2}=\frac{\partial ^2f_3}{\partial x_2\partial x_i}=0,\nonumber \\&\frac{\partial ^2f_3}{\partial x_1\partial x_3}=\frac{\partial ^2f_3}{\partial x_3\partial x_1}=\frac{\partial ^2f_3}{\partial x_2\partial x_3}=\frac{\partial ^2f_3}{\partial x_3\partial x_2}=0.\nonumber \end{aligned}$$
(17)

Further, from (15), (16), (17), and some tedious symbolic calculations, we can get that

$$\begin{aligned} \mathbf{a}=&\sum _{k,i,j=1}^{3}v_ku_iu_j\frac{\partial ^2f_k}{\partial x_i\partial x_j}(\mathcal {E}_{0i}^0)\\ =&2v_i(-\theta _i\beta _i^*u_iu_2-\beta _i^*u_iu_3)+2v_2\left( \theta _i\beta _i^*u_iu_2 +\beta _i^*u_iu_3+\frac{q_i}{k_i^2}u_2^2\right) \\ =&2p_i\left( u_iu_2\theta _i\beta _i^*+u_iu_3\beta _i^*+u_2^2\frac{q_i}{k_i^2}\right) \\ =&2\frac{p_ik_i}{Q^2}h_i(q_i^*), \end{aligned}$$

and

$$\begin{aligned} \mathbf{b}=\sum _{k,i=1}^3v_ku_i\frac{\partial ^2f_k}{\partial x_i\partial b}(\mathcal {E}_{0i}^0)=p_i\left( \theta _i\frac{\Lambda _i}{\mu _i}u_2+\frac{\Lambda _i}{\mu _i}u_3\right) =p_i\frac{\Lambda _i}{\mu _i}\left( \alpha +\frac{q_i}{k_i}\right) , \end{aligned}$$

where

$$\begin{aligned}&Q\!=\!\frac{\theta _i(\mu _i+c_i)+p_i}{(\mu _i+p_i+\omega _i+q_i/k_i)(\mu _i+c_i)},\ h_i(q_i)\!=\!-q_i^2+(1-2(\mu _i+p_i+\omega _i) k_i)q_i\\&\quad \quad -(\mu _i+p_i+\omega _i)^2k_i^2. \end{aligned}$$

Obviously, the coefficient \(\mathbf{b}\) is always positive and the sign of \(\mathbf{a}\) is determined by the sign of function \(h_i(q_i)\). Note that the image of function \(h_i(q_i)\) is a parabola with an opening downward, and the maximum value is obtained at \(q_i^*=(1-2(\mu _i+p_i+\omega _i) k_i)/2\) and the maximum value is \(h_i(q_i^*)=(1-4(\mu _i+p_i+\omega _i)k_i)/4\). Therefore, there are three cases to consider:

  1. (a)

    If \(h_i(q_i^*)<0\), that is, \(1-4(\mu _i+p_i+\omega _i)k_i<0\), we have \(\mathbf{a}<0\) for all \(q_i>0\);

  2. (b)

    If \(h_i(q_i^*)=0\), that is, \(1-4(\mu _i+p_i+\omega _i)k_i=0\), it yields that \(\mathbf{a}<0\) for all \(q_i\in (0,1/4)\cup (1/4,+\infty )\), where we use the fact \(q_i^*=(1-2(\mu _i+p_i+\omega _i)k_i)/2=1/4\);

  3. (c)

    If \(h_i(q_i^*)>0\), that is, \(1-4(\mu _i+p_i+\omega _i)k_i>0\), it follows that the quadratic equation of one variable \(h_i(q_i)=0\) has two unequal positive real roots \(\hat{q}_i\) and \(\breve{q}_2\), which are given by (12). Thus, we have \(\mathbf{a}<0\) for all \(q_i\in (0,\hat{q_i})\cup (\breve{q}_i,+\infty )\), and \(\mathbf{a}>0\) for all \(q_i\in (\hat{q}_i,\breve{q}_i)\).

Based on the above discussion and Lemma 2, it is not difficult to find that the model has backward bifurcation if the coefficient \(\mathbf{a}\) is positive and admits a backward bifurcation if the coefficient \(\mathbf{a}\) is positive. The proof is complete. \(\square \)

4 Dynamics of Full Model

In this section, we discuss the dynamics of the spread of COVID-19 in patch-1 and patch-2. Since the state variables \(Q_{i}\) and \(R_{i}\) (\(i=1,2\)) are decoupled from other variables, model (1) reduces to the following six-dimensional system

$$\begin{aligned} \left\{ \begin{aligned} \frac{\mathrm {d}S_1(t)}{\mathrm {d}t}&=\Lambda _1-\beta _1S_1(t)(I_{1}(t)+ \theta _1 A_1(t))-\mu _1S_1(t)-mS_1(t),\\ \frac{\mathrm {d}A_{1}(t)}{\mathrm {d}t}&=(1-\varepsilon _1)\beta _1S_1(t)(I_{1}(t)+\theta _1 A_1(t))-(\mu _1+p_1+\omega _1+m\rho )A_1(t)\\&\quad -\frac{q_1A_1(t)}{k_1+A_1(t)},\\ \frac{\mathrm {d}I_1(t)}{\mathrm {d}t}&=\varepsilon _1\beta _1S_1(t)(I_1(t)+\theta _1 A_1(t))-\mu _1I_1(t)-c_1I_1(t)+p_1A_1(t),\\ \frac{\mathrm {d}S_2(t)}{\mathrm {d}}&=\Lambda _2-\beta _2S_2(t)(I_2(t)+\theta _2 A_2(t))-\mu _2S_2(t)+mS_1(t),\\ \frac{\mathrm {d}A_2(t)}{\mathrm {d}t}&=(1-\varepsilon _2)\beta _2S_2(t)(I_2(t)+\theta _2 A_2(t))-(\mu _2+p_2+\omega _2)A_2(t)\\&\quad -\frac{q_2A_2(t)}{k_2+A_2(t)}+m\rho A_1(t),\\ \frac{\mathrm {d}I_2(t)}{\mathrm {d}t}&=\varepsilon _2\beta _2S_2(t)(I_2(t)+\theta _2 A_2(t))-\mu _2I_2(t)-c_2I_2(t)+p_2A_2(t). \end{aligned} \right. \end{aligned}$$
(18)

Obviously, full model (18) admits a disease-free equilibrium \(\mathcal {E}_{0}(\widehat{S}^{0}_{1},0,0,\widehat{S}^{0}_{2},0,0)\), where

$$\begin{aligned} \widehat{S}^{0}_{1}=\frac{\Lambda _{1}}{\mu _{1}+m},\qquad \widehat{S}^{0}_{2}=\frac{\Lambda _{2}(\mu _{1}+m)+m\Lambda _{1}}{\mu _{2}(\mu _{1}+m)}. \end{aligned}$$

Further, by using the next-generation matrix approach, the basic reproduction number of model (18) is defined by

$$\begin{aligned} \mathcal {R}_{0} = \max \{\mathcal {\widetilde{R}}_{01},\mathcal {\widetilde{R}}_{02}\}, \end{aligned}$$

where

$$\begin{aligned} \mathcal {\widetilde{R}}_{01}&= \left[ \frac{(1-\varepsilon _{1})\beta _{1}\theta _{1}}{\mu _{1}+p_{1}+\omega _{1}+m\rho +q_{1}/k_{1}} + \frac{(1-\varepsilon _{1})p_{1}\beta _{1}}{(\mu _{1}+p_{1}+\omega _{1}+m\rho +q_{1}/k_{1})(\mu _{1}+c_{1})}\right. \\&\quad \left. + \frac{\varepsilon _{1}\beta _{1}}{\mu _{1}+c_{1}} \right] \widehat{S}^{0}_{1},\\ \mathcal {\widetilde{R}}_{02}&= \left[ \frac{(1-\varepsilon _{2})\beta _{2}\theta _{2}}{\mu _{2}+p_{2}+\omega _{2}+q_{2}/k_{2}} + \frac{(1-\varepsilon _{2})p_{2}\beta _{2}}{(\mu _{2}+p_{2}+\omega _{2}+q_{2}/k_{2})(\mu _{2}+c_{2})} + \frac{\varepsilon _{2}\beta _{2}}{\mu _{2}+c_{2}} \right] \widehat{S}^{0}_{2}. \end{aligned}$$

Remark 5

In particular, if there is no migration between patches 1 and 2, that is, the migration rate \(m=0\), then \(\mathcal {\widetilde{R}}_{0i}=\mathcal {R}_{0i}\), \(i=1,2\).

Following Theorem 8 is on the local asymptotical stability of \(\mathcal {E}_0\) for model (18).

Theorem 8

The disease-free equilibrium \(\mathcal {E}_{0}\) of model (18) is locally asymptotically stable for \(\mathcal {R}_{0}<1\) and is unstable for \(\mathcal {R}_{0}>1\).

Proof

According to the proof of Theorem 2 in Ref. (van den Driessche and Watmough 2002), the local asymptotical stability of the disease-free equilibrium \(\mathcal {E}_{0}\) is determined by the following characteristic equation

$$\begin{aligned} (\lambda +\mu _{1}+m)(\lambda ^{2}+a_{11}\lambda +a_{12})(\lambda +\mu _{2})(\lambda ^{2}+a_{21}\lambda +a_{22})=0, \end{aligned}$$
(19)

where

$$\begin{aligned} a_{11}&= \left( \mu _{1}+p_{1}+\omega _{1}+m\rho +\frac{q_{1}}{k_{1}} \right) \left( 1-\frac{(1-\varepsilon _{1})\beta _{1}\theta _{1}\widehat{S}^{0}_{1}}{\mu _{1}+p_{1}+\omega _{1}+m\rho +q_{1}/k_{1}} \right) \\&\qquad \qquad +(\mu _{1}+c_{1})\left( 1- \frac{\varepsilon _{1}\beta _{1}\widehat{S}^{0}_{1}}{\mu _{1}+c_{1}} \right) ,\\ a_{12}&= \left( \mu _{1}+p_{1}+\omega _{1}+m\rho +\frac{q_{1}}{k_{1}} \right) (\mu _{1}+c_{1}) \left( 1-\mathcal {R}_{01} \right) ,\\ a_{21}&= \left( \mu _{2}+p_{2}+\omega _{2}+\frac{q_{2}}{k_{2}} \right) \left( 1-\frac{(1-\varepsilon _{2})\beta _{2}\theta _{2}\widehat{S}^{0}_{2}}{\mu _{2}+p_{2}+\omega _{2}+q_{2}/k_{2}} \right) \\&\qquad \qquad +(\mu _{2}+c_{2})\left( 1-\frac{\varepsilon _{2}\beta _{2}\widehat{S}^{0}_{2}}{\mu _{2}+c_{2}} \right) ,\\ a_{22}&= \left( \mu _{2}+p_{2}+\omega _{2}+\frac{q_{2}}{k_{2}} \right) +(\mu _{2}+c_{2}) \left( 1-\mathcal {R}_{02} \right) . \end{aligned}$$

This is easy to verify that \(a_{i1}>0, a_{i2}>0\) for \(\mathcal {R}_{0i}<1\) and \(a_{i2}<0\) for \(\mathcal {R}_{0i}>1\), \(i=1,2\). Therefore, all eigenvalues of Eq. (19) have negative real parts for \(\mathcal {R}_{0}<1\) and (19) has at least one positive root for \(\mathcal {R}_{0}>1\). Thus, the disease-free equilibrium \(\mathcal {E}_{0}\) is stable for \(\mathcal {R}_{0}<1\) and is unstable for \(\mathcal {R}_{0}>1\). The proof is complete. \(\square \)

On the global asymptotical stability of \(\mathcal {E}_{0}\), we have the following result.

Theorem 9

If \(\check{\mathcal {R}}_{0}=\max \{\check{\mathcal {R}}_{01}, \check{\mathcal {R}}_{02}\}<1\), then the disease-free equilibrium \(\mathcal {E}_{0}\) of model (18) is global asymptotical stable, where \(\check{\mathcal {R}}_{0i}\) \((i=1,2)\) is given in Theorem 3.

Proof

Choosing a positive differentiable function \(V(t) = \sum _{i=1}^{2}(A_{i}(t)+I_{i}(t))\) and calculating its total derivative directly along model (18), one has

$$\begin{aligned} \frac{{\mathrm {d}}V(t)}{{\mathrm {d}}t}&=\sum \limits _{i=1}^{2} \left[ \beta _{i}S_{i}(t)(I_{i}(t)+\theta _{i}A_{i}(t))-(\mu _{i}+\omega _{i})A_{i}(t)-\frac{q_{i}A_{i}(t)}{k_{i}+A_{i}(t)}-\mu _{i}I_{i}(t)-c_{i}I_{i}(t) \right] \\&\le \sum \limits _{i=1}^{2} \left[ \left( \beta _{i}\frac{\Lambda _{i}}{\mu _{i}}-\mu _{i}-c_{i} \right) I_{i}(t)+\left( \frac{\beta _{i}\theta _{i}\Lambda _{i}}{\mu _{i}}-(\mu _{i}+\omega _{i})-\frac{q_{i}}{k_{i}+\Lambda _{i}/\mu _{i}} \right) A_{i}(t) \right] \\&\le \sum \limits _{i=1}^{2} \left[ (\mu _{i}+c_{i})(\mathcal {R}^{a}_{0i}-1)I_{i}(t)+\left( \mu _{i}+\omega _{i}+\frac{q_{i}}{k_{i}+\Lambda _{i}/\mu _{i}} \right) (\mathcal {R}^{b}_{0i}-1)A_{i}(t) \right] , \end{aligned}$$

where \(\mathcal {R}^{a}_{0i}\) and \(\mathcal {R}^{b}_{0i}\) are given in Theorem 3. Obviously, the LaSalle’s invariance principle implies that the disease-free equilibrium \(\mathcal {E}_{0}\) is global asymptotical stability in \(\Omega \) for \(\check{\mathcal {R}}_{0} < 1\). The proof is complete. \(\square \)

Remark 6

From Theorem 7, it is also not difficult to find that when the basic reproduction numbers of both patches are less than 1, full model (18) also exists backward bifurcation. In other words, the persistence or extinction of the disease is no longer dependent on the basic reproduction but on the initial size of the infected population.

Regarding the existence and stability of other equilibria of model (18), the following conclusions are clearly valid.

Theorem 10

If \(\mathcal {\widetilde{R}}_{01}<1\) and \(\mathcal {\widetilde{R}}_{02}>1\), then model (18) admits a boundary equilibrium \((\widehat{S}^{0}_1,0,0,S_2^*,A_2^*,I_2^*)\). That is, the disease in patch-1 is extinct and disease is endemic in patch-2.

Theorem 11

If \(\mathcal {\widetilde{R}}_{01}>1\) and \(m\rho >0\), then model (18) exists an endemic equilibrium \((S_1^*,A_1^*,I_1^*,S_2^*,A_2^*,I_2^*)\) and disease is endemic in patch-1 and patch-2.

5 Numerical Simulation

In this section, some numerical simulations are carried to explain the effect of migration and limited medical resources for the transmission of SARS-CoV-2 using the Runge–Kutta method in the software MATLAB. We consider, firstly, the transmission dynamics of disease in patch-1 without migration. To do so, we choose basic model parameters as follows: \(\Lambda _{1}=750\), \(\mu _1=1/(65\times 365)\), \(\beta _1=5.22\times 10^{-9}\), \(\varepsilon _1=0.25\), \(m=0\), \(p_1=0.001\), \(\theta _1=0.35\), \(q_1=0.35\), \(k_1=4500\). Further, according to the biological significance of other model parameters in Table 1, as well as the current treatment cycle and nucleic acid testing cycle for SARS-CoV-2, we choose \(\omega _1=1/20\), \(c_1=1/14\), \(\gamma _1=1/14\). By the direct calculation, one has \(\mathcal {R}_{01}\approx 0.9025<1\); therefore, the disease-free equilibrium \(\mathcal {E}_{01}\) is stable. This also implies that the disease is extinct and is shown in Fig. 2a and b.

Fig. 2
figure 2

The stability of the disease-free equilibrium \(\mathcal {E}_{01}\) of model (3) with \(\Lambda _{1}=750\), \(\mu _1=1/(65\times 365)\), \(\omega _1=1/20\), \(p_1=0.001\), \(\theta _1=0.35\), \(q_1=0.35\), \(k_1=4500\), \(c_1=1/14\), \(\beta _1=5.22\times 10^{-9}\) and \(\varepsilon _1=0.25\), where \(\mathcal {R}_{01}\approx 0.9025<1\)

Full size image

Further, if we just change the values of parameters as \(q_1=0.015\), \(\beta _1=5.22\times 10^{-8}\) and other model parameters are fixed as Fig. 2. Through direct calculation, the basic reproduction number \(\mathcal {R}_{01}\approx 9.0322>1\). Therefore, from Theorems 2 and 3, the disease-free equilibrium is unstable and model (3) has an endemic equilibrium. This is shown in Fig. 3a and b. Additionally, numerical simulations in Fig. 3c and d show that the solutions with differential values converge to the same endemic equilibrium, where the initial values are \(A_1(0)=I_1(0)=500\), \(A_1(0)=I_1(0)=500500\), \(A_1(0)=I_1(0)=1500500\), \(A_1(0)=I_1(0)=3500500\) and \(A_1(0)=I_1(0)=10500500\), respectively. Perhaps, the endemic equilibrium is stable under this set of parameters. So far, we have an interesting question: if \(\mathcal {R}_{0i}>1\), then model (3) without migration admits an endemic equilibrium which is locally asymptotically stable.

Fig. 3
figure 3

The existence and stability of the endemic equilibrium of model (3) with \(\Lambda _{1}=750\), \(\mu _1=1/(65\times 365)\), \(\omega _1=1/20\), \(p_1=0.001\), \(\theta _1=0.35\), \(q_1=0.015\), \(k_1=4500\), \(c_1=0.07\), \(\beta _1=5.22\times 10^{-8}\), \(\varepsilon _1=0.25\), where \(\mathcal {R}_{01}\approx 9.0322>1\)

Full size image

Next, we discuss the effect of migration rate m on the transmission of SARS-CoV-2 in the two patches. To this end, we fixed the parameters of model (18) as follows: \(\Lambda _{i}=950\), \(\mu _{i}=1/(65\times 365)\), \(p_{i}=0.3\), \(\varepsilon _i=0.015\), \(\theta _{i}=0.6\), \(\omega _{i}=0.03\), \(q_{i}=0.1\), \(c_{i}=0.05\), \(\beta _{1}=2.97\times 10^{-8}\), \(\beta _{2}=2.002\times 10^{-9}\), \(k_1=4000\), \(k_2=6000\) and \(\rho =0.0002\), \(i=1,2\). Further, we choose \(m=0\), 1/50000, 1/30000, 1/10000, 1/7000 and 1/4000, respectively. Correspondingly, one can calculate the basic reproduction numbers in six case as shown in following Table 3.

Table 3 The effects of migration rate m on the basic reproduction numbers \(\mathcal {\widetilde{R}}_{01}\) and \(\mathcal {\widetilde{R}}_{02}\) of full model (18)
Full size table

Numerical calculations are shown that the basic reproduction number \(\mathcal {\widetilde{R}}_{01}\) decreases and \(\mathcal {\widetilde{R}}_{02}\) increases as the migration rate m increases. Further, the numerical simulations in Fig. 4a and b also show that when \(m=0\), the disease is endemic in the patch-1 and extinct in patch-2. With the increase of m, the disease spreads in the two patches at the same time, although the migration rate \(m\rho \) of asymptomatic infection is very small. In addition, numerical simulations also show that the time and peak of this disease outbreak in the patch-1 are delayed and decreased with the increase of m, while the situation in patch-2 is just the opposite. Both theoretical results and numerical simulations show that the prevalence of SARS-CoV-2 between different regions is closely related to the migration rate m. The control of COVID-19 is the common responsibility of different countries and regions around the world. After all, in the context of economic globalization, it is impossible for countries and regions to be completely lockdown.

Fig. 4
figure 4

The effect of migration rate m on the transmission of SARS-CoV-2 in the two patches

Full size image

Finally, we discuss the sensitivity of the main parameters of full model (18) to the basic reproduction numbers \(\mathcal {\widetilde{R}}_{01}\) and \(\mathcal {\widetilde{R}}_{02}\). It is not difficult to see from Fig. 5a–d, the infection rates of \(\beta _{1}\) and \(\beta _{2}\) are positively correlated with \(\mathcal {\widetilde{R}}_{01}\) and \(\mathcal {\widetilde{R}}_{02}\), while other parameters, such as \(m\rho \), \(c_1\), \(c_2\) and \(q_2\), are negatively correlated. More specifically, susceptible humans wear masks and keep a safe social distance, and the relevant institutions can provide enough medical materials to quickly screen out asymptomatic infected people and take effective isolation measures for the infected humans, which can greatly reduce the basic reproduction number, so as to achieve the purpose of disease control.

Fig. 5
figure 5

Sensitivity of the main parameters of full model (18) on the basic production numbers \(\mathcal {\widetilde{R}}_{01}\) and \(\mathcal {\widetilde{R}}_{02}\)

Full size image

6 Conclusion and Discussion

Since the worldwide outbreak of SARS-CoV-2, the human lifestyles and frequency of travel have changed considerably. However, some necessary migration of the population is inevitable, such as working across regions, studying, visiting relatives, traveling. In addition, due to the rapid spread of the epidemic, countries around the world are experiencing varying degrees of medical resource scarcity, which greatly restricts the screening of patients with SARS-CoV-2 and the treatment of this disease, which poses a great problem for the prevention and control of the disease. From the perspective of mathematical modeling, we construct, in this paper, a dynamical model to describe the transmission of SARS-CoV-2 between two patches, where asymptotic infected class, isolation treatment class and limited medical resources are introduced. Among them, limited medical resources are described by the saturation function. Firstly, the dynamics of the model without migration in patch-i are studied, which includes the stability of the disease-free equilibrium, the existence of multi-endemic equilibria and forward/backward bifurcation. This means that the basic reproduction number is no longer the threshold condition for determining the prevalence of this disease, and the persistence or extinction of disease may depend more on the initial state of infected classes. Further, the local/global asymptotical stability of the disease-free equilibrium of the full model is obtained. In addition, the prevalence of disease is also discussed when the reproduction numbers of two patches are larger than or less than one. Finally, numerical simulations are carried to explain the main theoretical results, especially the effect of migration rate on the spread of SARS-CoV-2 in two patches.

In addition, some interesting findings are obtained from the theoretical results of this paper. Since we apply a saturation function to portray the limited medical resources, which complicates the existence of the endemic equilibria of our model. The model may have multiple endemic equilibria even in the case where the basic reproduction number is less than one (see Theorem 7). This makes the persistence and extinction of the disease no longer dependent on the basic reproduction number of our model but on the size of the infected population at the initial moment. Thus, it is not difficult to imagine a scenario in which the basic reproduction numbers in both patches are less than 1 and the disease is extinct in both patches, but the basic reproduction number in patch-2 is closer to 1 and the population migrating from patch-1 to patch-2 has infected individuals, which causes the initial size of infected population in patch-2 to jump from the attraction domain of the disease-free equilibrium to the attraction domain of the endemic equilibrium. This leads to the persistence of the disease in patch-2, where the basic reproduction number is less than 1. Even if this population migration is a one-time event. From these interesting results, it is easy to see that the control of the current COVID-19 is not sufficient to control the basic reproduction of this disease in a region or country to less than 1, but to make it much less than 1. Even if the basic reproduction number of the disease in all regions is less than 1, local outbreaks may occur with limited medical resources. In addition, in the case of international epidemics, strict quarantine and testing measures for population migration, especially those imported from medium and high risk regions, are in place. Therefore, “to prevent the coronavirus from entering and spreading within the cit/regio” remains an effective measure for the prevention and control of the new epidemic. These imply that, in the context of economic globalization, the control of COVID-19 is the common responsibility of different countries and regions around the world since it is impossible for countries and regions to be completely lockdown. No one or country can be left alone in the face of an epidemic.

Of course, there are many factors that are not reflected in our model. For example, if the migration of humans in two patches is two way, how about the spread of this disease? In the process of the transmission of disease, there are many uncertain factors. What impact do these factors have on the prevention and control of disease? The effectiveness and coverage of vaccine have an impact on disease, and so on. These are all issues that need further discussion.