Effect of Non-homogeneous Mixing and Asymptomatic Individuals on Final Epidemic Size and Basic Reproduction Number in a Meta-Population Model

Abstract

To uncover the effective interventions during the pandemic period, a novel mathematical model, which incorporates separate compartments for incubation and asymptomatic individuals, has been developed in this paper. On the basis of a general mixing, final size relation and next-generation matrix are derived for a meta-population model by introducing the matrix blocking. The final size (${\mathcal {F}}$) and the basic reproduction number (${\mathcal {R}}_{0}$) are no longer a simple monotonous relationship. The analytical results of heterogeneity illustrate that activity is more sensitive than the others. And the proportion of asymptomatic individuals is a key factor for final epidemic size compared to the regulatory factor. Furthermore, the impact of preferential contact level on ${\mathcal {F}}$ and ${\mathcal {R}}_{0}$ is comparatively complex. The isolation can effectively reduce the final size, which further verifies its effectiveness. When vaccination is considered, the mixing methods maybe influence the doses of vaccination used and its effective. Moreover, using the present predictive model, we can provide the valuable reference about identifying the ideal strategies to curb the pandemic disease.

1 Introduction

Epidemic dynamic is an important method to study the transmission rules of infectious diseases. The research purpose of epidemic model is to reveal the epidemic law of diseases, predict their development trend and harm degree. Another purpose is to determine sensitivity of parameters to provide theoretical basis for seeking effective control measures and optimal intervention strategies (Ma et al. 2004).

Epidemic model includes the homogeneous and heterogeneous model. A common conclusion of the existing research is that ${\mathcal {F}}$ and ${\mathcal {R}}_{0}$ are positively related in homogeneous model. Homogeneous model is popular in the study of infectious diseases because of its simple form. However, due to the over-simplification and idealization of the model, sometimes the analytical results deviate from the reality. With the outbreak of emerging diseases such as MERS, SARS and COVID-19, homogeneous model cannot meet the requirement. Actually, heterogeneity is a common phenomenon among biological species, which can directly affect the spread scope and harm degree of infectious diseases. Therefore, it is vital to introduce the heterogeneous factors into the infectious disease model in order to solve the practical issue.

Some progress has been made in the research of the final scale relationship in heterogeneity epidemic model. This relation had been extensively discussed in Brauer (2008a, 2008b, 2017) using different models to predict how serious an epidemic could be during a disease outbreak. Andreasen (2011) studied the effect of heterogeneity on final epidemic size for the case of proportionate mixing and discussed the relationship between ${\mathcal {F}}$ and ${\mathcal {R}}_{0}$. Cui et al. (2019) analyzed the role of heterogeneity on final epidemic size and discussed the relationship between ${\mathcal {F}}$ and ${\mathcal {R}}_{0}$ for preferential mixing, which concluded that ${\mathcal {F}}$ and ${\mathcal {R}}_{0}$ are monotonous negatively correlated. Sattenspiel and Dietz (1995) proposed the model incorporating geographic mobility among regions for the case of foot-and-mouth disease. Feng et al. (2016) evaluated targeted interventions via meta-population models with multi-level mixing and generalized this function by including preferential contacts between grandparents and grandchildren. David (2018) analyzed the influences of heterogeneous mixing and indirect transmission on the basic reproduction number and used the final size relation to analyze the ability of disease to invade over a short period of time. Research related to heterogeneity can be seen in other literature (Annett 1980; Arino et al. 2007; Glasser et al. 2016; Rodríguez and Torres-Sorando 2001; Wang and Zhao 2004). In addition, incubation and asymptomatic individuals are critical factors to the outbreak of infectious disease. Calculation of the average incubation period will help to determine the time of exposure. However, determinants of variation may be related to the early clinical outcome or pathogenic procedures of infection (Dhouib et al. 2021). None of the above studies have been considered the influences of heterogeneous factors on final epidemic size or relationship between ${\mathcal {F}}$ and ${\mathcal {R}}_{0}$ in a meta-population model, in which we introduce incubation period and asymptomatic infected individuals in the case of consideration a general mixing and isolated mixing.

In this paper, in the case of general mixing method, the effect of heterogeneity on the final epidemic size, basic reproduction number and the relationship between ${\mathcal {F}}$ and ${\mathcal {R}}_{0}$ will be discussed with the SEIAR model, which introduces incubation period and asymptomatic infected individuals. Moreover, the sensitivity of heterogeneous factors is also analyzed. The present research is the improvement and generalization of the results in Cui et al. (2019).

However, in this paper, we will conclude that ${\mathcal {F}}$ and ${\mathcal {R}}_{0}$ are the opposite or some other irregular relationship and the amount of vaccine used is minimal to the same immune effect in the case of combination of proportional mixing and preferential mixing. Moreover, ${\mathcal {F}}$ and ${\mathcal {R}}_{0}$ are not just monotonous negatively relationship anymore in the case of isolated mixing. The sensitivity of activity is higher than other heterogeneous factors.

The paper is organized as follows: Sect. 2 includes the establishment of the model with n subpopulations and non-homogeneous mixing, and the derivations of the reproduction number and a final epidemic size relation. Section 3 investigates the effects of heterogeneity in various subpopulation factors and mixing on the final epidemic size during an outbreak. Section 4 includes discussion and conclusion remarks.

2 Dynamical Model

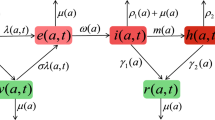
The present model comprises n subpopulations, the population in group i includes $S_{i}$ (susceptible), $E_{i}$ (exposed), $I_{i}$ (symptomatic), $A_{i}$ (asymptomatic), $R_{i}$ (recovered). Let ${N_i} = {S_i} + {E_i} + {I_i} + {A_i} + {R_i}(1 \le i \le n)$ be the total population number of group i. Because we mainly focus on the final epidemic size of a single disease outbreak, births and deaths are ignored. The dynamic model with n subpopulations consists of the following ordinary differential equations:

$$\begin{aligned} \left\{ \begin{aligned} S_{i}'(t)&=-a_{i}\beta _{i}S_{i}\sum \limits _{j=1}^{n}c_{ij}\frac{I_{j}+\delta _{A}A_{j}}{N_{j}},\\ E_{i}'(t)&=a_{i}\beta _{i}S_{i}\sum \limits _{j=1}^{n}c_{ij}\frac{I_{j}+\delta _{A}A_{j}}{N_{j}}-qE_{i},\\ I_{i}'(t)&=pqE_{i}-\gamma _{I}I_{i},\\ A_{i}'(t)&=(1-p)qE_{i}-\gamma _{A}A_{i},\\ R_{i}'(t)&=\gamma _{A}A_{i}+\gamma _{I}I_{i},\\ \end{aligned} \right. \end{aligned}$$

(1)

with the nonnegative initial condition:

$$\begin{aligned} \begin{aligned}&{S}_{i}(0)={N}_{i}-{E}_{i0}-{I}_{i0}-{A}_{i0},\\&{E}_{i}(0)={E}_{i0}, {I}_{i}(0)={I}_{i0}, {A}_{i}(0)={A}_{i0}, {R}_{i}(0)=0. \end{aligned} \end{aligned}$$

(2)

In model (1), $a_{i}$ is the average contact rate (referred to as activity). $\beta _{i}$ is the probability of infection upon contacting an infectious person. $\gamma _{I}$, $\gamma _{A}$ are denoted as the recovery rate. $\delta _{A}$ is the regulatory factor. $(1-p)$ is proportion of the asymptomatic. The contact between subpopulations is described by $c_{ij}$, where $c_{ij}$ is the proportion of the ith subpopulation’s contacts that is with members of the jth subpopulation. ${I_{j}}/{N_{j}}$ is the probability that a proportionally encountered member of subpopulation j is symptomatic infectious. ${\delta _{A}A_{j}}/{N_{j}}$ is the probability that a proportionally encountered member of subpopulation j is asymptomatic infectious and n is the number of subpopulations. The mixing function needs to satisfy the following basic conditions (Stavros and Carlos 1991):

$$\begin{aligned} \left\{ \begin{aligned} c_{ij}\ge&0,\\ \sum \limits _{j=1}^{n}c_{ij}&=1,\\ a_{i}N_{i}c_{ij}&=a_{j}N_{j}c_{ji}.\\ \end{aligned} \right. \end{aligned}$$

The preferential mixing function has the following form:

$$\begin{aligned} c_{ij}=\varepsilon _{i}\delta _{ij}+(1 -\varepsilon _{i})f_{j},~~\text {where}~~ f_{j}=\frac{(1-\varepsilon _{j})a_{j}N_{j}}{\sum \limits _{k=1}^{n}(1-\varepsilon _{k})a_{k}N_{k}}. \end{aligned}$$

In the preferential mixing function, $\varepsilon _{i}$ is the fraction of preferential contacts for one’s own group, and $\delta _{ij}$ is the Kronecker function (1 when $i=j$ and 0 otherwise). $f_{j}$ is the proportional mixing for other groups. Assume that all parameters are nonnegative.

2.1 The Basic Reproduction Number

By using the next-generation matrix approach (van den Driessche and Watmough 2002), the following isolated basic reproduction number for group i can be obtained:

$$\begin{aligned} {\mathcal {R}}_{0i}=a_{i}\beta _{i}\left[ \frac{p}{\gamma _{I}}+\frac{\delta _{A}(1-p)}{\gamma _{A}}\right] ,(1\le i \le n). \end{aligned}$$

We derive the next-generation matrix for the meta-population in “Appendix,” and the next-generation matrix for the meta-population is:

$$\begin{aligned} F{V^{-1}}\mathrm{{=diag}}\left( {\mathop {{f_{11}}}\limits ^*{v^{-1}_{11}},\mathop {{f_{22}}}\limits ^*{v^{-1}_{22}},\cdots ,\mathop {{f_{nn}}}\limits ^*{v^{-1}_{nn}}}\right) \left[ {\begin{array}{cccc} {{C_{11}}}&{}{{C_{12}}}&{}\cdots &{}{{C_{1n}}}\\ {{C_{21}}}&{}{{C_{22}}}&{}\cdots &{}{{C_{2n}}}\\ \vdots &{}\vdots &{}\vdots &{}\vdots \\ {{C_{n1}}}&{}{{C_{n2}}}&{}\cdots &{}{{C_{nn}}} \end{array}}\right] . \end{aligned}$$

(3)

The basic reproduction number for the meta-population is:

$$\begin{aligned} {\mathcal {R}}_{0}=\rho (FV^{-1}), \end{aligned}$$

where ${\mathcal {R}}_{0}=\rho (FV^{-1})$ denotes the dominant eigenvalue of $FV^{-1}$.

Two special mixing ways are proportionate (i.e., when $\varepsilon _{i}=0$) and isolated (i.e., when $\varepsilon _{i}=1$). In two cases, the basic reproduction numbers are, respectively, given by:

$$\begin{aligned} {\mathcal {R}}_{0}=\sum \limits _{i=1}^{n}{\mathcal {R}}_{0i}c_{ii}(\varepsilon _{i}=0), ~\text {and}~ {\mathcal {R}}_{0}=\max \limits _{1\le i \le n}\{{\mathcal {R}}_{0i}\}(\varepsilon _{i}=1). \end{aligned}$$

If the susceptible individuals were vaccinated before the epidemic starts, a certain level of population immunity can be achieved via vaccination. Let $p_{i}$ denote the vaccination coverage for subpopulation i at time $t=0(0\le p_{i} \le 1)$. Then, the modified initial conditions have the following forms:

$$\begin{aligned} \begin{aligned} S_{i}(0)&=(1-p_{i})({N_i}-E_{i0}-I_{i0}-A_{i0}),E_{i}(0)=E_{i0},I_{i}(0)={I_{i0}},\\ A_{i}(0)&=A_{i0},R_{i}(0)=p_{i}(N_{i}-E_{i0}-I_{i0}-A_{i0})(1 \le i \le n). \end{aligned} \end{aligned}$$

Accordingly, the isolated effective reproduction number for group i is:

$$\begin{aligned} {\mathcal {R}}_{ei}=(1-p_{i}){\mathcal {R}}_{0i}. \end{aligned}$$

The next-generation matrix for the meta-population is:

$$\begin{aligned} F_{e}V_{e}^{-1}{=}\mathrm{{diag}}\left( {{{\mathop f\limits ^*}_{11}}v_{11}^{-1},\mathop {{f_{22}}}\limits ^*v_{22}^{-1},\cdots ,\mathop {{f_{nn}}}\limits ^* v_{nn}^{-1}}\right) \left[ {\begin{array}{ccc} {{C_{11}}\left( {1-{p_1}}\right) }&{} \cdots &{}{{C_{1n}}\left( {1-{p_1}}\right) }\\ \vdots &{} \vdots &{} \vdots \\ {{C_{n1}}\left( {1-{p_n}}\right) }&{} \cdots &{}{{C_{nn}}\left( {1-{p_n}}\right) } \end{array}}\right] . \end{aligned}$$

The whole effective reproduction number for the meta-population is:

$$\begin{aligned} {\mathcal {R}}_{e}=\rho (F_{e}V_{e}^{-1}). \end{aligned}$$

As a special case, when the influences of incubation period and asymptomatic individuals are ignored, the whole basic reproduction number is same as formula (3) in Cui et al. (2019).

2.2 The Final Epidemic Size

Next, we use model (1) with the initial condition (2) to derive the relation for the final epidemic size.

Adding the equations from $S_{i}'(t)$ to $A_{i}'(t)$ in model (1), we can achieve

$$\begin{aligned} (S_{i}'(t)+E_{i}'(t)+I_{i}'(t)+A_{i}'(t))=-\gamma _{A}A_{i}-\gamma _{I}I_{i}. \end{aligned}$$

(4)

It is not difficult to know $S_{i}(t)\ge 0,E_{i}(t)\ge 0,I_{i}(t)\ge 0,A_{i}(t)\ge 0$; we can show that$(S_{i}'(t)+E_{i}'(t)+I_{i}'(t)+A_{i}'(t))$ is uniformly continuous. And then $\lim _{t\rightarrow \infty }(S_{i}'(t)+E_{i}'(t)+I_{i}'(t)+A_{i}'(t))=0$. Thus, $I_{i}(\infty )=A_{i}(\infty )=0$ and $E_{i}(\infty )=0$ as $t\rightarrow \infty$ by a similar approach in Lv et al. (2020). Hence, we can conclude that $S_{i}(\infty )$ exists.

Integrating equation (4) from 0 to $\infty$, we get

$$\begin{aligned} N_{i}-S_{i}(\infty )=\gamma _A\int _0^\infty {A_{i}(t)}\mathrm{d}t+\gamma _I\int _0^\infty {I_{i}(t)}\mathrm{d}t. \end{aligned}$$

(5)

Next, we claim that $S_{i}(t)>0$ and then $S_{i}(\infty )>0$. In fact, (5) hints that

$$\begin{aligned} \gamma _A\int _0^\infty {A_{i}(t)}\mathrm{d}t+\gamma _I\int _0^\infty {I_{i}(t)}\mathrm{d}t. \end{aligned}$$

is convergent. Therefore,

$$\begin{aligned} S_{i}(t)&=S_{i}(0)e^{ -a_{i}\beta _{i}\sum \limits _{j=1}^n \frac{1}{N_{j}}(\int _0^{t}{I_{j}(\theta )}\mathrm{d}\theta +\delta _{A}\int _0^{t}{A_{j}(\theta )}\mathrm{d}\theta )}>0,\\ S_{i}(\infty )&=S_{i}(0)e^{ - (\gamma _A\int _0^\infty {A_{i}(t)}\mathrm{d}t+\gamma _I\int _0^\infty {I_{i}(t)}\mathrm{d}t)}>0. \end{aligned}$$

Adding and integrating the equations of $I'_{i}(t), A'_{i}(t), R'_{i}(t)$, we can obtain

$$\begin{aligned} \int _0^\infty {E_{i}(t)}\mathrm{d}t=\frac{(S_{i}(0)-S_{i}(\infty ))+E_{i0}}{q}. \end{aligned}$$

Adding and integrating the equations of $S'_{i}(t),E'_{i}(t),A'_{i}(t)$ and substitution into (4), we can obtain

$$\begin{aligned} \int _0^\infty {I_{i}(t)}\mathrm{d}t&=\frac{p(S_{i}(0)-S_{i}(\infty )+E_{i0})+I_{i0}}{\gamma _{I}},\\ \int _0^\infty {A_{i}(t)}\mathrm{d}t&=\frac{(1-p)(S_{i}(0)-S_{i}(\infty )+E_{i0})+A_{i0}}{\gamma _{A}}. \end{aligned}$$

Dividing both sides of the first equation of model (1) by $S_{i}(t)$, we get

$$\begin{aligned} \frac{S_{i}'(t)}{S_{i}(t)}=-a_{i}\beta _{i}\sum \limits _{j=1}^nc_{ij}\frac{I_{j}+\delta _AA_{j}}{N_{j}}. \end{aligned}$$

(6)

Integrating equation (6) from 0 to $\infty$, we obtain

$$\begin{aligned} \ln \frac{S_{i}(\infty )}{S_{i}(0)}=-\sum \limits _{j=1}^n{\mathcal {R}}_{0i}c_{ij}\frac{(S_{j}(0)-S_{j}(\infty ))+E_{j0}+\frac{\gamma _{A}I_{j0}+\gamma _{I}\delta _AA_{j0}}{p\gamma _{A}+(1-p)\gamma _{I}}}{N_{j}}. \end{aligned}$$

(7)

Let $Z_{i}=S_{i}(0)-S_{i}(\infty )$ denote the final epidemic size for the isolated group,

$$\begin{aligned} Z_{i}\!=\!S_{i}(0)\left( 1\!-\!\exp \left( -\sum \limits _{j=1}^{n}{\mathcal {R}}_{0i}c_{ij}\frac{1}{N_{j}}(Z_{j}\!+\!E_{j0})\!+\!\frac{\gamma _{A}I_{j0}\!+\!\delta _{A}\gamma _{I}A_{j0}}{p\gamma _{A}\!+\!(1-p)\gamma _{I}}\right) \right) . \end{aligned}$$

(8)

Let $N=\sum \nolimits _{i=1}^{n}N_{i}$ denote the total population size and ${\mathcal {F}}_{i}=Z_{i}/N_{i}$ is the proportion of infected individuals for group i. We define the final epidemic size ${\mathcal {F}}$ by

$$\begin{aligned} {\mathcal {F}}=\sum \limits _{i=1}^n{\mathcal {F}}_{i}=\sum \limits _{i=1}^n\frac{Z_{i}}{N}. \end{aligned}$$

In the special case that the population is homogeneous mixing, i.e., the parameter values are identical for all subpopulations ($a_{i}=a,\beta _{i}= \beta ,\varepsilon _{i}=0,N_{i}=N/n,S_{i}(0)=S(0)/n,E_{i}(0)=E(0)/n,I_{i}(0)=I(0)/n,A_{i}(0)=A(0)/n$), the final size relation is simplified as:

$$\begin{aligned} Z=S(0)\left( {1-\exp \left( {-{\mathcal {R}}_{0}\frac{1}{N}(Z+E_{0})+\frac{\gamma _{A}I_{0}+\delta _{A}\gamma _{I}A_{0}}{p\gamma _{A}+(1-p)\gamma _{I}}}\right) } \right) , \end{aligned}$$

(9)

where $Z=\sum \nolimits _{i=1}^nZ_{i}$ and ${\mathcal {R}}_{0}={\mathcal {R}}_{0i}=a\beta (\frac{p}{\gamma _{I}}+\frac{\delta _{A}(1-p)}{\gamma _{A}})$. If we vary ${\mathcal {R}}_{0}$ by changing $\beta$ and the other parameters remain unchanged, the final size relation (9) is shown in line with Fig. 1 in reference Cui et al. (2019), which shows that ${\mathcal {F}}$ is an increasing function of ${\mathcal {R}}_{0}$.

As can be seen, ${\mathcal {F}}$ and ${\mathcal {R}}_{0}$ are positively related, which shows that ${\mathcal {F}}$ is an increasing function of ${\mathcal {R}}_{0}$. Furthermore, it has the conclusion (7) of Cui et al. (2019) when incubation period and asymptomatic individuals are ignored, i.e., $E_{0}=0,A_{0}=0,p= 0,\delta _{A}=0,\gamma _{A}=\gamma _{I}=\gamma$.

As shown in reference Cui et al. (2019), ${\mathcal {F}}$ can be influenced by the pattern of mixing in a significant way. Heterogeneity in various subpopulation characteristics may have the opposite or complex effect on ${\mathcal {F}}$ and ${\mathcal {R}}_{0}$. Furthermore, the relationship of ${\mathcal {F}}$ and ${\mathcal {R}}_{0}$ may not be illustrated in Fig. 1 in reference Cui et al. (2019). In the following sections, we will investigate how population heterogeneity in model with preferential mixing may influence ${\mathcal {F}}$, the relationship between ${\mathcal {F}}$ and ${\mathcal {R}}_{0}$ and evaluation of intervention measures.

2.3 The Relationship of ${\mathcal {F}}$ and ${\mathcal {R}}_{0}$

${\mathcal {F}}$ is an increasing function of ${\mathcal {R}}_{0}$ in the case of homogeneous mixing. Moreover, the change of ${\mathcal {R}}_{0}$ is mainly caused by altering $\beta _{i}$. And the heterogeneous factors include activity ($a_{i}$), preferential contact ($\varepsilon _{i}$), proportion of asymptomatic individuals ($1-p$), regulatory factor ($\delta _{A}$). When the heterogeneity factors are introduced in meta-population model, ${\mathcal {F}}$ and ${\mathcal {R}}_{0}$ will vary in a complicated way (8).

Due to the high dimension of heterogeneity model and complexity of analysis, it is difficult to figure out the specific expression of final epidemic size. In order to simplify the analysis process, we first study the case of $n=2$ groups, which can be easily extended to the case of $n>2$. To explore the dependence of $Z_{i}$ on other parameters numerically, we rewrite equation (8) as

$$\begin{aligned} F(Z_{1},Z_{2})=1,\quad G(Z_{1},Z_{2})=1, \end{aligned}$$

where

$$\begin{aligned} \begin{aligned} F({Z_1},{Z_2})&= \frac{{{S_1}(0)}}{{{Z_1}}}\left( {1 - {e^{ - \sum \limits _{j = 1}^2 {{{{{\mathcal {R}}}}_{01}}{c_{1j}}\frac{1}{{{N_j}}}({Z_j} + {E_{j0}}) + \frac{{{\gamma _A}{I_{j0}} + {\gamma _I}{\delta _A}{A_{j0}}}}{{p{\gamma _A} + (1 - p){\delta _A}{\gamma _I}}}} }}} \right) ,\\ G({Z_1},{Z_2})&= \frac{{{S_2}(0)}}{{{Z_2}}}\left( {1 - {e^{ - \sum \limits _{j = 1}^2 {{{{{\mathcal {R}}}}_{02}}{c_{2j}}\frac{1}{{{N_j}}}({Z_j} + {E_{j0}}) + \frac{{{\gamma _A}{I_{j0}} + {\gamma _I}{\delta _A}{A_{j0}}}}{{p{\gamma _A} + (1 - p){\delta _A}{\gamma _I}}}} }}} \right) . \end{aligned} \end{aligned}$$

(10)

In the following section, we will conduct numerical simulation to analyze the effect of various heterogeneities on the final epidemic size.

3 Influence of Heterogeneous Factors and Mixing Methods

To investigate the impact of various heterogeneous factors and mixing methods on model prevention, we fixed the parameter values $N_{1}= N_{2}=5000,E_{i}(0)=A_{i}(0)=I_{i}(0)=1,\beta _{1}=\beta _{2}=0.035,q=0.3,\gamma _{A}=1/7,\gamma _{I}=1/5$. The values of other parameters vary according to the applications. Heterogeneous characteristics include activity ($a_{i}$), regulatory factor ($\delta _{A}$), asymptomatic individuals $(1-p)$, preferential contact level ($\varepsilon _{i}$), vaccine coverage ($p_{i}$).

3.1 Heterogeneity of Activity ($a_{i}$)

In the case of preferential mixing $(\varepsilon _{1}=0.4,\varepsilon _{2}=0.3)$, we discuss the effect of heterogeneity and variability in activity on the final epidemic size. We fixed $\delta _{A}=0.2, p=0.9$. By simulating equation (10) and model (1), Fig. 1 is obtained, in which the activity is $(a_{1},a_{2})=(10,10), (a_{1},a_{2})=(14,6),(a_{1},a_{2})=(18,2)$, respectively. Accordingly, the basic reproduction numbers are ${\mathcal {R}}_{0}=1.624,1.963,2.734$, respectively, while the final epidemic sizes are ${\mathcal {F}}= 0.654,0.636,0.554$, respectively. Combined with the data of three different activities, we can conclude that

• ${\mathcal {F}}$ decreases;

• ${\mathcal {R}}_{0}$ increases;

• The peak size of an outbreak increases;

• The time of epidemic peak decreases.

Fig. 1

Comparison of ${\mathcal {F}}$, ${\mathcal {R}}_{0}$ peak, peak time when activities vary from homogeneous to heterogeneous. The left column shows the final epidemic size, as the intersection of $F=1$ and $G=1$ (marked by the dot). The right column shows the epidemic curves based on the simulations of model (1) (Color figure online)

In order to illustrate the effect of $a_{i}$ on ${\mathcal {F}}$, ${\mathcal {R}}_{0}$ and the relationship between them, Figs. 2 and 3 show ${\mathcal {F}}$, ${\mathcal {R}}_{0}$ for several different sets of activities $(a_{1},a_{2})$ with different preferential contact level $(\varepsilon _{1},\varepsilon _{2})$.

Fig. 2

Effects of $(a_{1},a_{2})$ on ${\mathcal {F}}$ and ${\mathcal {R}}_{0}$ when $(a_{1},a_{2})$ varies from (10,10) to (18,2) with the same mean activity 10. Mixing is preferential $(\varepsilon _{1},\varepsilon _{2})=(0.4,0.3)$ (Color figure online)

Figure 2 indicates that the homogeneous activity $(a_{1},a_{2})=(10,10)$ corresponds to the smallest ${\mathcal {R}}_{0}\!=\!1.624$ and the largest ${\mathcal {F}}=0.654$. While the heterogeneity activity $(a_{1},a_{2})\!=\!(18,2)$ to the largest ${\mathcal {R}}_{0}\!=\!2.734$ and the smallest ${\mathcal {F}}=0.554$. Thus, it confirms that ${\mathcal {F}}$ and ${\mathcal {R}}_{0}$ are not a positive correlation, which is consistent with conclusion of the reference Cui et al. (2019). Controlling disease outbreak by reducing activity in one group, it may lead to a sharp increase in infection in another group. Most of the contribution of ${\mathcal {R}}_{0}$ come from the group with high activity, and the increase in the number of infected individuals is less than the decrease in the other group. It results in ${\mathcal {F}}$ decreases and ${\mathcal {R}}_{0}$ increases. This conclusion may have an important impact on public health policy-making.

In order to reveal the effects of activity on ${\mathcal {F}}$ and ${\mathcal {R}}_{0}$ in different mixing methods, Fig. 3 exhibits ${\mathcal {F}}$ and ${\mathcal {R}}_{0}$ for several sets of activities $(a_{1},a_{2})$ in case of preferential contact level $(\varepsilon _{1}=\varepsilon _{2}=1)$.

Fig. 3

Effects of $(a_{1},a_{2})$ on ${\mathcal {F}}$ and ${\mathcal {R}}_{0}$ when $(a_{1},a_{2})$ varies from (10,10) to (18,2) with the same mean activity 10. Mixing is preferential $(\varepsilon _{1},\varepsilon _{2})=(1,1)$ (Color figure online)

In Fig. 3, the change rule of ${\mathcal {F}}$ and ${\mathcal {R}}_{0}$ is not consistent with the previous conclusion. ${\mathcal {F}}=0.434$ is the lowest point when activity is $(a_{1},a_{2})=(14,6)$. Furthermore, it is obviously ${\mathcal {F}}_{(12,8)}>{\mathcal {F}}_{(15,5)}>{\mathcal {F}}_{(14,6)}$. Reducing the activity of individual population can reduce the epidemic final size. If $(\varepsilon _{1},\varepsilon _{2})=(1,1)$, Fig. 3 shows that the values of ${\mathcal {F}}$ are smaller than that in Fig. 2, but ${\mathcal {R}}_{0}$ is the opposite. Therefore, we can conclude that isolation is an effective way to reduce the final epidemic size and control the outbreak of disease by comparing Figs. 2 and 3.

Interestingly enough, there is a turning point about ${\mathcal {F}}$ at activity value of $(a_{1},a_{2})=(14,6)$. The implement of isolation measures should be combined with the activity gap between groups. Otherwise, the isolation effect will rebound due to rapid outbreak of single group. If the increase in the number of infected individuals in the high-activity group is greater than the decrease in the other group, ${\mathcal {F}}$ will rise up again. The isolation effect is obvious, while the activity gap is kept in reasonable limits.

3.2 Heterogeneity in Regulatory Factor ($\delta _{A}$) and Asymptomatic Individuals ($1-p$)

The influence of $\delta _{A}$ and $(1-p)$ on ${\mathcal {F}}$ and ${\mathcal {R}}_{0}$ can be examined by fixing the other parameter values $(\varepsilon _{1},\varepsilon _{2})= (0.4,0.3),(a_{1},a_{2})=(15,5)$. For example, Fig. 4a illustrates the effect of $\delta _{A}$ on ${\mathcal {F}}$ and ${\mathcal {R}}_{0}$ when $p=0.9$. Figure 4b shows the impact of $(1-p)$ on ${\mathcal {F}}$ and ${\mathcal {R}}_{0}$ when $\delta _{A}=0.2$.

Fig. 4

Effect of $\delta _{A}$, $(1-p)$ on ${\mathcal {F}}$, ${\mathcal {R}}_{0}$. The red line shows the basic reproduction number(${\mathcal {R}}_{0}$). The blue line shows the final size(${\mathcal {F}}$) (Color figure online)

It can be seen from Fig. 4a that ${\mathcal {F}}$ and ${\mathcal {R}}_{0}$ vary with $\delta _{A}$ positively and slightly. The main reason is that the proportion of asymptomatic infected is very small and the change of regulatory factor does not cause a big variation on ${\mathcal {F}}$ and ${\mathcal {R}}_{0}$. The pharmaceutical measures to reduce the regulatory factor can modestly decrease the final size, while the effect is not obvious.

To further explore the influence of asymptomatic individuals $(1-p)$ on ${\mathcal {F}}$ and ${\mathcal {R}}_{0}$, Figure 4b also plots ${\mathcal {F}}$, ${\mathcal {R}}_{0}$ by fixing the parameter values $\delta _{A}=0.2$. And Fig. 4b indicates that ${\mathcal {F}}$, ${\mathcal {R}}_{0}$ both decrease with the increasing of $(1-p)$. ${\mathcal {R}}_{0}$ changes with $(1-p)$ linearly. And ${\mathcal {R}}_{0}$ reduces to 1 when $(1-p)$ approaches to 0.65. But ${\mathcal {F}}$ changes with $(1-p)$ nonlinearly. ${\mathcal {F}}$ declines slowly when $(1-p)$ is between 0.2 and 0.5. While $(1-p)$ is greater than 0.5, ${\mathcal {F}}$ decreases fast.

This shows that asymptomatic individuals will affect the final size and basic reproduction number. In the choice of prevention and control measures, asymptomatic individuals can be reduced to achieve the purpose of disease control by early detection and early isolation. It is further verified that the influence of asymptomatic individuals on the outbreak of disease is related to the asymptomatic proportion in meta-population.

Fig. 5

Effect of $\delta _{A}$, p on ${\mathcal {F}}$, ${\mathcal {R}}_{0}$. We fixed parameter value $\delta _{A}\in (0.1,0.8), p\in (0.1,0.8)$. The left figure is the effect on ${\mathcal {F}}$. The right figure is the effect on ${\mathcal {R}}_{0}$ (Color figure online)

Figure 5 illustrates the effect of $\delta _{A}$ and p on ${\mathcal {F}}$, ${\mathcal {R}}_{0}$. From Fig. 5, we can conclude that the effect of $\delta _{A}$ on ${\mathcal {F}}$, ${\mathcal {R}}_{0}$ is linear, while the effect of p on ${\mathcal {F}}$, ${\mathcal {R}}_{0}$ is nonlinear. The effect of p is greater than $\delta _{A}$, which further verifies the results of Fig. 4. Therefore, the main strategy to control the outbreak of disease is to reduce the number of asymptomatic infected individuals. The pharmaceutical and non-pharmaceutical interventions can reduce the morbidity of asymptomatic and effectively reduce the final epidemic size (Fig. 6).

Fig. 6

Effect of p on ${\mathcal {F}}$ and ${\mathcal {R}}_{0}$. The left column shows ${\mathcal {F}}$ and ${\mathcal {R}}_{0}$ increase with p when $\delta _{A}$ is fixed as 0.7. The right column shows that ${\mathcal {F}}$ and ${\mathcal {R}}_{0}$ decrease with p when $\delta _{A}$ is fixed as 0.8 (Color figure online)

3.3 Heterogeneity in Preferential Contact ($\varepsilon _{i}$)

The mixing method of meta-population is reflected in $c_{ij}$. There are mainly activity ($a_{i}$), preferential contact level ($\varepsilon _{i}$), subpopulation size ($N_{i}$). And the preferential contact level ($\varepsilon _{i}$) is a significant influence factor for the final epidemic size. The other parameter values are fixed the same as Sect. 3, including $(a_{1},a_{2})=(12,8)$. The effect of $\varepsilon _{i}$ on ${\mathcal {F}}$ and ${\mathcal {R}}_{0}$ can be found in Fig. 7.

Fig. 7

Influence of $\varepsilon _{i}(i=1,2)$ on ${\mathcal {F}}$ and ${\mathcal {R}}_{0}$. The preferential $\varepsilon _{i}$ varies from 0.01 to 0.99 and the case of $\varepsilon _{i}=1$ is not considered here (Color figure online)

Fig. 8

Influence of $\varepsilon _{i}(i=1,2)$ on ${\mathcal {F}}$ and ${\mathcal {R}}_{0}$. The blue figures show the influence of $\varepsilon _{i}$ on ${\mathcal {F}}$. The green figures show the influence of $\varepsilon _{i}$ on ${\mathcal {R}}_{0}$. The variation of ${\mathcal {F}}$ and ${\mathcal {R}}_{0}$ is nonlinear with $\varepsilon _{i}$. The ${\mathcal {F}}$ and ${\mathcal {R}}_{0}$ are positively related (Color figure online)

Figure 7 shows that the variation of ${\mathcal {F}}$ and ${\mathcal {R}}_{0}$ with $\varepsilon _{i}$ is nonlinear. Figure 8 illustrates that ${\mathcal {F}}$ and ${\mathcal {R}}_{0}$ have a negative correlation when $(\varepsilon _{1},\varepsilon _{2})$ is fixed in twopopulations. In fact, Fig. 8 is a partial graph of Fig. 7, which explains the conclusions of Fig. 7 in more detail. And it further verifies the results of Fig. 2. Furthermore, ${\mathcal {F}}$ increases with $\varepsilon _{1}$ when $0.4<\varepsilon _{1}<0.8$, while ${\mathcal {F}}$ decreases with $\varepsilon _{1}$ in the case of $\varepsilon _{1}>0.8$ under any case of $\varepsilon _{2}$. This proves that activity and preferential contact level in subpopulations are the key factors affecting the final size. The significant factor about the final size will transform from activity into mixing method when preferential contact level is higher than a certain value. This change may reduce the final size, which confirms the results of Fig. 3. Additionally, Figs. 7 and 8 verify the conclusion of Fig. 9 simultaneously.

Fig. 9

Influence of various preferential contact levels $\varepsilon _{i}(i=1,2)$ and activity variability $(a_{i},a_{j})$ on ${\mathcal {F}}$ and ${\mathcal {R}}_{0}$. The variation of ${\mathcal {F}}$ is nonlinear but ${\mathcal {R}}_{0}$ is linear with the increase in $\varepsilon _{i}$ and $(a_{i},a_{j})$. The sapphire bar charts verify the results of Fig. 7 (Color figure online)

It can be seen that isolation is an effective way to control the disease outbreak, but too strong isolation measure will only delay the process of disease outbreak and present a temporary safe period. Thus, excessive isolation will lead to the factors that affect disease outbreak change.

Figure 9 shows the influences of $(a_{i},a_{j})$ on ${\mathcal {F}}$ and ${\mathcal {R}}_{0}$ when the preferential contact level increases in the same proportion, i.e., $(\varepsilon _{1}=\varepsilon _{2})$. The sapphire bar charts illustrate that ${\mathcal {F}}$ first increases and then decreases with the increase in $\varepsilon _{i}$. Actually, this is the case for the diagonal in Fig. 7. The saffron bar charts show the opposite conclusion with the sapphire bar charts. And the saffron and army green bar charts declare that ${\mathcal {F}}$ monotonously decreases with the increase in $\varepsilon _{i}$. The only difference is that ${\mathcal {R}}_{0}$ is always monotonously increasing under the various cases of $(a_{i},a_{j})$ and $\varepsilon _{i}$.

It is widely known that activity and preferential contact level are the significant heterogeneity factors on the final size. To control the outbreak of disease, reducing the activity of population and taking appropriate quarantine measures are effective ways.

3.4 Heterogeneity in Vaccine Coverage ($p_{i}$)

The initial condition in model changes when the vaccine coverage is considered. Assume that the vaccine efficacy is 100% so that the vaccination coverage in group i is the same as the immunity $p_{i}$, and the total number of vaccine dose is $p_{1}+p_{2}$. Thus, we can examine the effect of heterogeneity in vaccine allocation $(p_{1},p_{2})$ on ${\mathcal {F}}$ and ${\mathcal {R}}_{0}$ for a fixed number of vaccinations $p_{1}+p_{2}=1.2$. The values of other parameters are the same as before, except for $(\varepsilon _{1},\varepsilon _{2})=(0.4,0.3)$.

3.4.1 Shortages of Vaccine Stockpiles

Consider the case of the general mixing. The effects of vaccine coverage on ${\mathcal {F}}$, ${\mathcal {R}}_{0}$, I(t), A(t) are illustrated in Figs. 10, 11 and 12. The activity is fixed $(a_{1},a_{2})=(14,6)$.

Fig. 10

Change of ${\mathcal {F}}$ and ${\mathcal {R}}_{0}$ with the vaccine coverage $p_{i}$. The blue line shows ${\mathcal {F}}$. The red line shows ${\mathcal {R}}_{0}$. The solid line shows vaccinated. The dot-dashed line shows non-vaccinated (Color figure online)

Fig. 11

Effect of vaccine allocation $p_{1}$ on cumulative infections (the values of $p_{1}$ for different curves are marked in the legend) (Color figure online)

Fig. 12

The epidemic curves I(t) and A(t) for various vaccine allocations with $p_{1}+p_{2}=1.2$ (the values of $p_{1}$ for different curves are marked in the legend) (Color figure online)

From Fig. 10, it can be seen that the solid line of the corresponding color is lower than dot-dashed line, which illustrates that vaccination can reduce the final epidemic size effectively. In the case of $p_{1}<0.25$, ${\mathcal {F}}$ and ${\mathcal {R}}_{0}$ both decrease as $p_{1}$ increases. However, as $p_{1}$ continuously increases from 0.25 to 0.35, ${\mathcal {F}}$ increases and ${\mathcal {R}}_{0}$ decreases. And ${\mathcal {F}}$ and ${\mathcal {R}}_{0}$ both decrease as $p_{1}>0.3$. Thus, $p_{1}^{0.35}<p_{1}^{0.25}<p_{1}^{0.3}$. A vaccine coverage of $p_{1}=0.3$ does not reach the immunity threshold of vaccination. On the contrary, the final size of the disease outbreak rises up again.

Figures 11 and 12 illustrate that ${\mathcal {F}}$, I(t) and A(t) all nonlinearly decrease with the increase in $p_{1}$. Additionally, it further demonstrates the conclusion of Fig. 10.

3.4.2 Sufficient of Vaccine Stockpiles

National support and the development of medical standards have made the vaccines no longer exist in the limited stocks. However, for the sake of saving resources, it is important to find the best vaccination strategies for controlling the disease outbreak. Based on this idea, Fig. 13 shows the result of numerical simulation of ${\mathcal {R}}_{0}$ when the other parameter values for model (1) are fixed as before expect for $(a_{1},a_{2})=(12,8)$.

Fig. 13

Effect of mixing methods on the dose of vaccine. The isolated mixing (a), proportional mixing (b) and general mixing (c) are three differential mixing methods (Color figure online)

Figure 13 plots that different doses of vaccine are used in the different diverse mixing patterns to achieve the same effect, i.e., ${\mathcal {R}}_{0}\le 1$. The plane of ${\mathcal {R}}_{0}=1$ and the region below the intersection of the inclined plane are feasible regions. Obviously, the feasible region of proportional mixing is larger than general mixing. Meanwhile, the dose of vaccine used is also more than that when the effectiveness of vaccine is the same.

Thus, public health institutions can choose the best vaccination strategy by taking into account key factors such as the feasible region and dose of vaccine. In order to achieve the goal of disease control, the most critical step is to select the suitable model, which is in accord with the dynamics of disease transmission. Furthermore, for the infectious diseases with heterogeneity factors, the mixing methods of (a) and (b) overestimate the value of ${\mathcal {R}}_{0}$. And if we use the vaccine coverage of (a) and (b), a certain amount of vaccine will be wasted to control the outbreak of disease, i.e., ${\mathcal {R}}_{0}\le 1$. Therefore, it is critical to build a model that is more consistent with the real dynamics of disease transmission.

4 Discussion and Conclusion Remarks

In this paper, we introduce a novel epidemiological model which includes the explicit separate compartments for incubation and asymptomatic individuals, taking into account the effect of population heterogeneity and mixing methods on the final epidemic size. The purpose of modelling and evaluation is to reduce the final epidemic size, decline the basic reproduction number, minimize the peak, and maximize the time to reach the peak, so as to avoid the early surge of potential transmission cases. The novel model can well describe the dynamic process of disease transmission and provide many important insights for disease transmission dynamics and related effective control strategies.

The main contributions and conclusions are described below:

• Based on the incubation and asymptomatic infectious individuals, a subpopulation dynamic model has been established, which can provide a theoretical basis for the study of some diseases with asymptomatic. And it further illustrates the effect of asymptomatic individuals on the outbreak of disease.

• Taken into account the characteristic of population heterogeneity, it mainly includes asymptomatic proportion, regulatory factor, mixing methods and other factors. The model is aimed to analyze the sensitivity of heterogeneous factors and provide a number of valuable references for the optimizing control strategies.

• The relationship of ${\mathcal {F}}$ and ${\mathcal {R}}_{0}$ is explicitly calculated. The expression of the next-generation matrix and threshold value of ${\mathcal {R}}_{0}$ are proposed.

• The conclusions are as follows:

  • 1. In Fig. 1, the ${\mathcal {R}}_{0}$ increases but ${\mathcal {F}}$ decreases with the variation of activity in the left column. Moreover, the peak size of an outbreak shows a rising trend and the time to the peak is postponed with the increasing of activity in the right column. We conclude that ${\mathcal {F}}$ and ${\mathcal {R}}_{0}$ are negatively correlated, and inhibition of the activity of population is a effective measure to control the disease outbreak.

  • 2. The relationship of final epidemic size (${\mathcal {F}}$) and basic reproduction number (${\mathcal {R}}_{0}$) is negative or other complicated with various heterogeneities. ${\mathcal {F}}$ decreases but ${\mathcal {R}}_{0}$ increases with the increase in $|a_{1}\!-\!a_{2}|$ in Fig. 2, which further verifies the results of Fig. 4 in reference Cui et al. (2019), while the variation of ${\mathcal {F}}$ and ${\mathcal {R}}_{0}$ is rather complex in Fig. 3, not a simple monotonous relationship. For the numerical of ${\mathcal {F}}$, Fig. 3 is generally lower than Fig. 2, while ${\mathcal {R}}_{0}$ in Fig. 3 is higher than that in Fig. 2. And it is a new finding in our study. Furthermore, it shows that isolation can reduce the final epidemic size.

  • 3. Another interesting finding of this study is that ${\mathcal {F}}$ rises up with the increasing of $|a_{1}\!-\!a_{2}|$ due to the preferential mixing. The excessive isolation will make the disease present a temporary safe period and rapidly increase the ${\mathcal {R}}_{0i}$ in a meta-population group, which results in the devastating damage to the high-active group and the increasing of ${\mathcal {F}}$ again.

  • 4. The relationship of ${\mathcal {F}}$ and ${\mathcal {R}}_{0}$ as well as heterogeneous analysis demonstrates how the heterogeneity and mixing methods effect ${\mathcal {F}}$ and ${\mathcal {R}}_{0}$. The influence of preferential contact level is very complex on ${\mathcal {F}}$ and ${\mathcal {R}}_{0}$, which shows the different pattern of variation in Figs. 7, 8 and 9.

  • 5. Whether asymptomatic infection causes a big variation in the final epidemic size mainly depends on the asymptomatic proportion. Therefore, this factor is more sensitive than regulatory factor, and its activity has the highest sensitivity among the heterogeneity. The vaccination can also decrease the final epidemic size effectively, and the different mixing methods change the amount of vaccination used and feasible region with the sufficient of vaccine stockpiles.

  • 6. When considering the influence of heterogeneity, we should evaluate not only the effect of measures on ${\mathcal {R}}_{0}$, but also the impact of measures on ${\mathcal {F}}$. In this paper, the results show that ${\mathcal {F}}$ and ${\mathcal {R}}_{0}$ are not a simple monotonous relationship as the same conclusion we got before.

We acknowledge several limitations of our study. The predictions are dependent on the model assumptions, and there are several assumptions that could be worth revisiting in future iterations of the model. Additionally, some of the assumptions in the simplified model might not be realistic in all settings, necessitating the analysis of the full model. However, the conclusions of this study should be considered in policy-making and measure selection.

In addition to the above limitations, further expansion is needed. The epidemiological data are used to estimate the parameters to increase the accuracy of the model prediction as far as possible. Another consideration for future modeling work is that since all individuals transmit through the asymptomatic compartments, those who continue to develop symptoms in our model are more infectious than asymptomatic individuals. Elasticity of the implementation of control measures and cognition degree of population about disease are what we need to think about.

Appendix

In the following, we introduce the idea of block matrix to calculate the basic reproduction number ${\mathcal {R}}_{0}$ of the meta-population.

The increasing rate of secondary infection and disease progress in disease compartment i are denoted by ${\mathcal {F}}_{i}$ and ${\mathcal {V}}_{i}$, respectively.

$$\begin{aligned} \begin{aligned} {\mathcal {F}}_{i}&= \begin{bmatrix} a_{i}\beta _{i}S_{i}\left( c_{i1}\frac{I_{1}+\delta _{A}A_{1}}{N_{1}}+c_{i2} \frac{I_{2}+\delta _{A}A_{2}}{N_{2}}+\ldots +c_{in}\frac{I_{n}+\delta _{A}A_{n}}{N_{n}}\right) \\ 0\\ 0 \end{bmatrix},\\ {\mathcal {V}}_{i}&= \begin{bmatrix} qE_{i}\\ -pqE_{i}+\gamma _{I}I_{i}\\ (p-1)qE_{i}+\gamma _{A}A_{i} \end{bmatrix}. \end{aligned} \end{aligned}$$

The Jacobian matrices of ${\mathcal {F}}_{i}$ and ${\mathcal {V}}_{i}(1 \le$i$\le n)$ at $(N_{1},0,0,\cdots ,N_{i},0,0,\cdots ,N_{n},0,0,)$ are

$$\begin{aligned} \begin{aligned} F_{i}&=\begin{bmatrix} 0&{}a_{i}\beta _{i}N_{i}c_{i1}\frac{1}{N_{1}}&{}a_{i}\beta _{i}N_{i}c_{i1}\frac{1}{N_{1}}\delta _{A}&{} \cdots &{}0&{}a_{i}\beta _{i}N_{i}c_{in}\frac{1}{N_{n}}&{}a_{i}\beta _{i}N_{i}c_{in}\frac{1}{N_{n}}\delta _{A}\\ 0&{}0&{}0&{} \cdots &{}0&{}0&{}0\\ 0&{}0&{}0&{} \cdots &{}0&{}0&{}0 \end{bmatrix}, \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} V_{i}&=\begin{bmatrix} 0&{}0&{}0&{} \cdots &{}q&{}0&{}0 \cdots &{}0&{}0&{}0\\ 0&{}0&{}0&{} \cdots &{}-pq&{}\gamma _{I}&{}0 \cdots &{}0&{}0&{}0\\ 0&{}0&{}0&{} \cdots &{}(p-1)q&{}0&{}\gamma _{A} \cdots &{}0&{}0&{}0 \end{bmatrix}, \end{aligned} \end{aligned}$$

respectively. Let

$$\begin{aligned} \begin{aligned} \begin{array}{c} f_{ij}\!=\!\begin{bmatrix} 0&{}a_{i}\beta _{i}N_{i}\frac{c_{ij}}{N_{j}}&{}a_{i}\beta _{i}N_{i}\delta _{A}\frac{c_{ij}}{N_{j}}\\ 0&{}0&{}0\\ 0&{}0&{}0 \end{bmatrix},~~ v_{ii}=\begin{bmatrix} q&{}0&{}0\\ -pq&{}\gamma _{I}&{}0\\ (p-1)q&{}0&{}\gamma _{A} \end{bmatrix},~~ v_{ij}\!=\!0(i\ne j). \end{array} \end{aligned} \end{aligned}$$

The above matrix can be converted into the following simple forms

$$\begin{aligned} \begin{aligned} \begin{array}{c} F_{i}=\begin{bmatrix} f_{i1} \cdots f_{in} \end{bmatrix},~~ V_{i}=\begin{bmatrix} 0 \cdots v_{ii} \cdots 0 \end{bmatrix}(v_{ij}=0(i\ne j)). \end{array} \end{aligned} \end{aligned}$$

Furthermore, ${\mathcal {F}}$, ${\mathcal {V}}$ are defined as the increasing rate of secondary infection and disease progress in meta-population, respectively.

$$\begin{aligned} \begin{aligned} {\mathcal {F}}=\begin{bmatrix} {\mathcal {F}}_{1}\\ \vdots \\ {\mathcal {F}}_{n} \end{bmatrix},~~ {\mathcal {V}}=\begin{bmatrix} {\mathcal {V}}_{1}\\ \vdots \\ {\mathcal {V}}_{n} \end{bmatrix}. \end{aligned} \end{aligned}$$

In order to reveal the relationship of the basic reproduction number and the next-generation matrix, the following isolated basic reproduction number for group i is defined as: ${\mathcal {R}}_{0i}$. Let

$$\begin{aligned} \mathop {f_{ij}}\limits ^*= \begin{bmatrix} 0&{}a_{i}\beta _{i}N_{i}&{}a_{i}\beta _{i}N_{i}\delta _{A}\\ 0&{}0&{}0\\ 0&{}0&{}0 \end{bmatrix},~ C_{ij}=\begin{bmatrix} \frac{c_{ij}}{N_{j}}&{}0&{}0\\ 0&{}\frac{c_{ij}}{N_{j}}&{}0\\ 0&{}0&{}\frac{c_{ij}}{N_{j}} \end{bmatrix}.\\ \end{aligned}$$

Then, it is easy to see that $f_{ij}=\mathop {{f_{ij}}}\limits ^*C_{ij}$, $\mathop {{f_{ij}}}\limits ^*=\mathop {{f_{ii}}}\limits ^*$, $i,j=1,2,\cdots ,n$. Consequently, we have

$$\begin{aligned} \begin{aligned} F=\left[ {\begin{array}{*{20}{c}} {{F_1}}\\ \vdots \\ {{F_n}} \end{array}}\right] =\left[ {\begin{array}{*{20}{c}} {{f_{11}}}&{} \cdots &{}{{f_{1n}}}\\ \vdots &{} \vdots &{} \vdots \\ {{f_{n1}}}&{} \cdots &{}{{f_{nn}}} \end{array}}\right] ,~ V=\left[ {\begin{array}{*{20}{c}} {{V_1}}\\ \vdots \\ {{V_n}} \end{array}}\right] =\left[ {\begin{array}{*{20}{c}} {{v_{11}}}&{} \cdots &{}0\\ \vdots &{} \vdots &{} \vdots \\ 0&{} \cdots &{}{{v_{nn}}} \end{array}}\right] ,\\ \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} FV^{-1}&={\left[ {\begin{array}{*{20}{c}} {\mathop {{f_{11}}}\limits ^*v_{11}^{-1}{C_{11}}}&{}\cdots &{}{\mathop {{f_{1n}}}\limits ^*v_{nn}^{-1}{C_{1n}}}\\ \vdots &{} \vdots &{}\vdots \\ {\mathop {{f_{n1}}}\limits ^*v_{11}^{-1}{C_{n1}}}&{}\cdots &{}{\mathop {{f_{nn}}}\limits ^*v_{nn}^{-1}{C_{nn}}} \end{array}}\right] }. \end{aligned} \end{aligned}$$

Note that $v^{-1}_{ii}=v^{-1}_{jj}$, $i,j=1,2,\cdots ,n$, the next-generation matrix can be written as:

$$\begin{aligned} F{V^{-1}}\mathrm{{=diag}}\left( {\mathop {{f_{11}}}\limits ^*{v^{-1}_{11}},\mathop {{f_{22}}}\limits ^*{v^{-1}_{22}},\cdots ,\mathop {{f_{nn}}}\limits ^*{v^{-1}_{nn}}}\right) \left[ {\begin{array}{*{20}{c}} {{C_{11}}}&{}{{C_{12}}}&{}\cdots &{}{{C_{1n}}}\\ {{C_{21}}}&{}{{C_{22}}}&{}\cdots &{}{{C_{2n}}}\\ \vdots &{}\vdots &{}\vdots &{}\vdots \\ {{C_{n1}}}&{}{{C_{n2}}}&{}\cdots &{}{{C_{nn}}} \end{array}}\right] , \end{aligned}$$

where

$$\begin{aligned} \mathop {f_{ii}}\limits ^*v_{ii}^{-1}= \begin{bmatrix} {\mathcal {R}}_{0i}N_{i}&{}*&{}*\\ 0&{}0&{}0\\ 0&{}0&{}0 \end{bmatrix}. \end{aligned}$$