Abstract
There has been a rapidly growing number of studies of the geographical aspects of happiness and well-being. Many of these studies have been highlighting the role of space and place and of individual and spatial contextual determinants of happiness. However, most of the studies to date do not explicitly consider spatial clustering and possible spatial spillover effects of happiness and well-being. The few studies that do consider spatial clustering and spillovers conduct the analysis at a relatively coarse geographical scale of country or region. This article analyses such effects at a much smaller geographical unit: community areas. These are small area level geographies at the intra-urban level. In particular, the article presents a spatial econometric approach to the analysis of life satisfaction data aggregated to 1,215 communities in Canada and examines spatial clustering and spatial spillovers. Communities are suitable given that they form a small geographical reference point for households. We find that communities’ life satisfaction is spatially clustered while regression results show that it is associated to the life satisfaction of neighbouring communities as well as to the latter's average household income and unemployment rate. We consider the role of shared cultural traits and institutions that may explain such spillovers of life satisfaction. The findings highlight the importance of neighbouring characteristics when discussing policies to improve the well-being of a (small area) place.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
There have been many research efforts aimed at adding a spatial dimension in the examination of happinessFootnote 1 data (Ferrer-i-Carbonell & Gowdy, 2007; Brereton et al., 2008; Bernini & Tampieri, 2019; Ala-Mantila et al., 2018; for a recent review see Ballas, 2021). However, there have been very limited research studies involving small area level analysis and in particular of spatial clustering and spatial spillover effects between small area level spatial units. The studies that do consider spatial clustering and spatial spillover effects of subjective measures of well-being use a relatively coarse geographical scale of analysis usually aggregated at the country or regional level (Lin et al., 2014, 2017; Okulicz-Kozaryn, 2011; Stanca, 2010). A key limitation of these studies is exactly the level of the analysis. The high level of aggregation is likely to conceal the “true” pattern that subjective well-being measures display compared to when looking at finer geographical scales. The advantage of moving further down to geographical scale is that we find forms of aggregation that are closer to the actual communities that households form. The use of small area level subjective well-being data can provide a new perspective in the investigation of spatial clustering and spatial spillover effects as such effects are scale dependent and they are likely to change as we change the geographical level of the analysis. Access to small area data allows us to revisit previous studies that attempted to add a geographical dimension to happiness research pertaining to urban and rural differences in terms of happiness between places and to the relationship between happiness and happiness inequality. Past research also highlights the need for better data collection with emphasis on the geographical scale as well as the necessity to investigate the spatial effects of various factors of subjective well-being at various spatial scales (Hong & Park, 2021; Okulicz-Kozaryn, 2011).
The objective of the research presented in this article is to analyse subjective well-being and its socio-spatial, economic and demographic determinants at small area levels. To that end, we employ suitable geographic and spatial statistical analysis techniques and apply them to the literature of well-being at small area level for an entire country in order to unveil the spatial pattern and the geographical spillover effects between communities in terms of their life satisfaction while taking into account other relevant socio-economic characteristics. This is important because, as the results confirm, life satisfaction is not randomly distributed in space while this time the scale of the analysis is small area level communities that has not been examined before. Apart from the spatial clustering, we also observe spillover effects between communities. In addition, we provide new insights both in the urban–rural divide at the community level and to the relationship between happiness and happiness inequality. We do that by using high-quality intra-urban level data at the community level in Canada provided by a recent relevant study by Helliwell et al. (2019). This study combined suitable social survey and health survey microdata with small area data to build a new public use dataset for community-level life satisfaction in Canada and identified important intercommunity differences. This new dataset apart from covering the entire country of Canada, making it the only dataset that covers an entire country at such a small geographical scale, also opens up new possibilities for further comprehensive analysis that can provide insights regarding the importance of place and space in happiness research.
In this article we examine possible spatial interdependencies and spillovers of life satisfaction at the community level between neighbouring communities that happen to share a common border (Anselin, 1988) while contributing to the literature of small area geographical scale comparisons. Furthermore, we consider whether a more homogenous group of areas displays higher spillover effects between them. Previous research has shown that between countries, spillovers of happiness are higher in more homogenous groups of countries (Lin et al., 2014). In this article, we examine the homogeneity of communities in terms of similar institutions. Knowing the distribution of life satisfaction among spatial units and the strength of interdependencies between them is useful for policy makers in order to identify the regions that lag behind in this regard. Policy makers can also examine the extent to which a spatial equilibrium of happiness exists (Goetzke & Islam, 2017). If such an equilibrium is present, it implies that there are no differences between communities in terms of happiness. In addition, by knowing the factors that are related to life satisfaction levels of spatial units, governments and policy makers can take initiatives that either aim to increase life satisfaction of such communities or to protect them from the (neighbouring) factors that are negatively related to their own life satisfaction. In particular, we present a methodological framework aimed at addressing the following questions: Are the variables under examination spatially clustered at the community level? Does the collective sense of life satisfaction of a community affect that of a neighbouring community suggesting an equilibrium of life satisfaction? Does the level of income and other socio-economic indicators, such as unemployment rate, in one community are associated with life satisfaction of neighbouring communities? The results indicate that life satisfaction displays a spatial clustering at the community level while we further observe spatial spillover effects between communities both in terms of their life satisfaction as well as in terms of their income and unemployment level. Regarding the homogeneity of the areas, we confirm that in more homogenous areas the (indirect) spillover effects are indeed higher compared to the analysis that uses the entire sample. On the other hand, the spillover effects of happiness are either lower or insignificant when we examine more homogenous areas. This is the first paper, to the best of our knowledge, that examines clustering and spillover effects of life satisfaction at the intra-urban community level for an entire country which is one of the lowest aggregated spatial scales that individuals form. It is arguably a closer representation of actual communities compared to other relatively coarse spatial scales where they consist of many possibly heterogeneous communities resulting in balancing out the spatial pattern that would otherwise emerge.
The remainder of this article is organised as follows: the second section uses relevant literature to provide a theoretical and empirical framework for the empirical research that follows. Section three presents the data that we used and the methodological approach (spatial econometrics). Section “Results” presents the results of our empirical analysis and Section “Discussion and Conclusion” discusses them in more detail, also highlighting links to possible policy implications. This is the last section of the article and it also offers some concluding comments, including a consideration of the limitations of our study as well as possibilities for follow-up research.
Literature Review and Conceptual Framework
There have long been efforts to theorise, conceptualise and analyse happiness from a wide range of different disciplinary perspectives, dating to at least as early as the work of Aristotle entitled Nicomachean Ethics (Lear, 1988) during the fourth century BC. In recent years happiness has been systematically examined by research scholars in the fields of psychology (Diener et al., 1999, 2017, 2018) as well as economics and sociology (e.g. see seminal contributions of Easterlin, 1974, 1995; Veenhoven, 1988, 1996; Clark & Oswald, 1994, 1996). More recently, there have been studies in geography and regional science (Aslam & Corrado, 2012; Ballas & Tranmer, 2012; Morrison, 2011) and recent reviews of the state-of-the-art relevant work to this article in Economics (Nikolova & Graham, 2022) and in Economic Geography (Ballas, 2021). The work presented in this article aims to contribute to the literature that involves an economic and geographic approach in examining happiness. The brief literature review that follows focuses on these two fields, providing a theoretical context for the empirical analysis that follows.
The majority of empirical happiness research to date has been conducted either at the individual or at the country level. Most studies tend to focus on the individual characteristics that affect one’s happiness. These studies examine the role of personal and household income, age, gender, marital status and employment status among other things (Blanchflower & Oswald, 2004, 2008; Clark, 2003; Clark et al., 2019; Layard & Ward, 2020; Luttmer, 2005; Stutzer & Frey, 2006). Some other studies examine the role of aggregated country level characteristics such as income inequality, inflation and unemployment on people’s happiness (Alesina et al., 2004; Di Tella et al., 2001, 2003). More recent work has considered the impact of well-being inequality at the country and regional level upon individual well-being. The measure of well-being inequality most often used is the standard deviation of the subjective measure of well-being. The main finding is that higher inequality is associated with lower levels of well-being (Burger et al., 2020, 2022; Dickinson & Morrison, 2022; Goff et al., 2018; Morrison, 2020; Okulicz-Kozaryn, 2011). On the other hand, the studies that focus on aggregated level happiness either use annual rankings between countries when it comes to similar measures (Veenhoven et al., 1993; Veenhoven, 1995; Inglehart et al., 2000; OECD Better Life Index 2011; Helliwell et al., 2022Footnote 2) or they examine factors related to aggregated happiness (Di Tella et al., 2003; Easterlin, 2001; Schyns, 1998; Steptoe et al., 2015; Stevenson & Wolfers, 2013). There has also been an increasing number of studies concentrated on the subnational level examining regional correlates of happiness and well-being (Ferrara et al., 2022; Lawless & Lucas, 2011) as well as efforts to combine individual and country or regional level data with the use of multilevel modelling (Rampichini & Schifini d'Andrea 1998; Pittau et al., 2010; Aslam & Corrado, 2012; Ballas & Tranmer, 2012; Neira et al., 2018; Weckroth et al., 2022). Kubiszewski et al. (2019), on the other hand, using a local scale dataset for Australia examine the spatial variation of life satisfaction while employing geographically weighted regressions which estimate the relationships of interest separately for each region. The limitation with all the aforementioned studies is that they do not consider spatial interactions between the units of the analysis. Multilevel modelling, for example, accounts for contextual characteristics of countries and regions by exploring the hierarchical nature of data where individuals are nested within regions and regions are nested within countries. This approach though ignores any spatial spillovers between the units of the analysis by treating the areas as containers that the interactions between them are not directly considered. Similarly, geographically weighted regressions allow us to explore variations between different regions when the relationship between variables changes from area to area but they do not account for interactions and interdependencies between the areas (Mennis, 2006). This non-spatial approach fails to take into account the spatial spillover effects and spatial clustering that are present in the data.
More recently, there have been some research efforts aimed at adding a geographical dimension in the analysis of happiness. The so-called urban happiness penalty literature examines whether there are differences in well-being measures between urban and rural areas. The evidence shows that urban areas experience lower levels of subjective well-being (Berry & Okulicz-Kozaryn, 2011; Morrison, 2011; Okulicz-Kozaryn, 2017; Morrison & Weckroth, 2018; Helliwell et al., 2019; Burger et al., 2020; Weckroth et al., 2022). GIS related analysis and geographically environmental and climate characteristics have also been examined like pedestrian and car-oriented zones or wind speed and temperature (Ala-Mantila et al., 2018; Brereton et al., 2008). Regarding spatial clustering and spillover effects in studying happiness data, different geographical levels have been examined that identify spatial patterns and spillover effects between neighbouring countries, regions and cities. Amongst the first notable contributions is the work of Stanca (2010) where he uses country level data and examines the spatial dependence of 94 countries. This study, however, does not directly examine happiness spatial spillovers. Instead, it explores the spillovers of the country-specific sensitivities of happiness (i.e. income and unemployment) between the countries. Other studies that employ spatial econometric techniques with country level data examine either the effect of globalisation of the spatial dependency and spillover effects between countries (Lin et al., 2017) or how different groups of countries based on characteristics that range from economic (income inequality) to political (democracies and socialist countries) interact with each other and how this grouping affects their happiness spillovers (Lin et al., 2014). At the subnational level, the work of Okulicz-Kozaryn (2011) explores geographies of life satisfaction in Europe at the regional level and attempts to identify possible geographical patterns and the extent to which areas with high levels of life satisfactions are spatially clustered with the measurement of relevant indexes of spatial autocorrelation. The work of Hong and Park (2021) acknowledges the limitations of the coarse spatial scale used in previous studies and examines the interdependencies and spatial spillover effects between cities in South Korea. Nevertheless, as the authors of these studies pointed out, there is a need for more local area data and for detailed and sophisticated analysis. Spatial clustering is scale dependent and there is a need for more spatially disaggregated data in order to best approximate the scale at which individuals form communities and use them as their reference point of belonging (Helliwell & Wang, 2010; Messacar, 2022). In addition, there is a lack of suitable data at small area levels that would enable the examination of spatial clustering and spatial interdependencies at the community level. One way to measure the happiness of a community (defined as all people living a relatively small area or neighbourhood) is to calculate the average of the happiness or life satisfaction of individuals within this communityFootnote 3 (in the same way that, for example, area unemployment is calculated) (Helliwell & Barrington-Leigh, 2010).
One might question why happiness and life satisfaction data should display a spatial pattern and clustering in the first place. It is difficult, however, to identify the underlying mechanisms that generate this spatial clustering. Most of the previous literature provides arguments about income comparison effects, cultural exchange and institutional framework of the units of analysis (Lin et al., 2014). Other studies attribute the clustering of happiness on unobserved factors (Pierewan & Tampubolon, 2014). Florida et al. (2011) argue that the aesthetic quality of a place is important for the satisfaction of individuals in such areas while Seresinhe et al. (2019) using a novel dataset find that individuals experience more happiness when they spend more time in scenic environments, either natural or built-up. Subsequently, we can assume that the aesthetic quality of a place is related to the wealth of the place itself. For example, richer places have the capacity to invest in infrastructure, better protect the natural environment and provide better facilities in general. All of these factors have been found to contribute to happiness. Given the evidence that wealth is spatially clustered within countries (Putnam et al., 1992), we would expect that life satisfaction measures will have a similar pattern. However, as the results we provide later show, this is not the case for Canada as the spatial distributions and the hot-spots of clusters for happiness and income differ between the two variables. Nevertheless, and to the best of our knowledge there have been very limited efforts aimed at analysing possible spatial interactions, spillovers or interdependencies between geographical units at the community level that would also lead to a spatial equilibrium of happiness. The theoretical foundations of equilibrium posit that after optimization, all markets will reach an equilibrium resulting in equalized life satisfaction across space (Goetzke & Islam, 2017). The literature of spatial equilibrium or disequilibrium has mostly been focused on the labour and real-estate markets through the mechanism of amenities and migration (Graves & Mueser, 1993; McCann, 2013). Furthermore, there are only few peer-reviewed studies to date that explicitly involved analysis of spatial relationships and equilibrium between small areas regarding labour market in-migration (Rijnks et al., 2018). There is a study directly examining the existence of (long-run) spatial equilibrium in happiness using data from U.S regions (Goetzke & Islam, 2017) while other studies have slightly touched upon the concept of equilibrium in happiness (Ballas & Tranmer, 2012; Mishra et al., 2015; Oswald & Wu, 2011) without, however, directly examining it. The paucity of studies considering geography, space, place, socio-economic characteristics and happiness is to some extent due to the lack of publicly available data for geographical units smaller than the region.
Data and Methodology
We adopt a new public use cross-sectional dataset for community life satisfaction in Canada which was made available by Helliwell et al. (2019). This data was built by combining the 2009–2014 waves from the Canadian Community Health Survey (CCHS) and the 2009–2013 waves from the General Social Survey (GSS) in order to construct a cross-sectional life satisfaction estimates for each of 1,215 Canadian communities based on more than 500,000 individuals in total. This is a high-resolution dataset on life satisfaction with the coordinates of the communities being attached. Based on this approach, Canada is divided into 1,215 geographic communities, both urban and rural. These communities are formed on the basis of a mixture of natural, built and administrative boundaries combined with a minimum sampling threshold of 250 individuals in each geographical unit to minimise the idiosyncratic component at the individual level (Helliwell et al., 2019).Footnote 4 The surface area of the communities is unevenly distributed as is evident from Fig. 1. This reflects the uneven geographical dimensions in Canada with sparsely populated communities in the North and centre of the country and more densely populated areas on the coasts and around the cities. For example, the North-West territories (comprising an area of 1,173,793 km2) are divided in three communities in our sample whereas Guelph covers an area of just 593.51 km2 and is divided into 5 distinct communities in the dataset. The different sizes of the communities likely affect the interdependencies between them. The same holds true when we look at cultural characteristics like the language which differs between some of the provinces further implying that interdependencies may be affected. For this reason, in the robustness section we restrict our analysis in a subsample of communities that are more homogenous in terms of both institutions and units’ size.
The measure of a communities’ life satisfaction is based on aggregated individual measurements. Given that the life satisfaction questions asked in surveys are always bounded in well-defined scales (e.g. Likert scales of 4, 7 or 10 units), there are no concerns that the mean value of areas will be influenced by outliers that might be present in the original responses of individuals as it is the case for the average income. We should still be cautious though and avoid the ecological fallacy. As a result, we cannot make any claims about the individuals of these communities. What we do instead in this article is to discuss life satisfaction in a collective sense at the community level in relation to the life satisfaction of other communities as has been before using regional data (Hong & Park, 2021; Okulicz-Kozaryn, 2011). As such, changes in life satisfaction can be attributed to changes in the community context as well as changes in the composition of the population following migration. In our empirical setup this is not expected to influence results as migration flows are relatively modest and we also adopt a cross-sectional approach which is not sensitive to migration over time.
Regarding the Life Satisfaction variable per se, in both surveys, the question that individuals had to answer in order to record their scores was of the form “Taking all things considered, how satisfied you are currently with your life on a scale ranging from 0 to 10” with 10 being the highest level of satisfaction. Acknowledging some shortcomings of these subjective evaluations, there have been many high impact evidence-based studies that confirm their validity and reliability (Krueger & Schkade, 2008; Layard, 2011; Oswald & Wu, 2010). We use such measures given that they can provide insights into the debate about “What makes communities better-off?” and particularly “Whether the interactions between communities spur any spatial spillovers in subjective life satisfaction?”. Nevertheless, it should be noted that the likely mechanisms underpinning possible spatial interactions and interdependencies are very much dependent on the scale of spatial units. Our research focuses on the spatial level of community as defined above, which is currently the smallest area level at which we have available data on life satisfaction. In addition to Life Satisfaction of each community, the dataset also contains various community area variables. Table 1 summarises the variables used in the empirical analysis and provides descriptive statistics. The variables represent confounders in explaining community life satisfaction, similar to those used in studies using individual level data and include both socio-economic characteristics of the population such as income (Latif, 2016), unemployment, educational level (Jongbloed, 2018) and contextual information such as commuting (Dickerson et al., 2014; Stutzer & Frey, 2008), density (Mouratidis, 2019) and religiosity (Ferriss, 2002; Rizvi & Hossain, 2017). Life Satisfaction is the only dependent variable used in the regression models while the rest of the variables serve as control variables. The same control variables will be used in explaining intercommunity spillovers (indirect effects). Importantly, the data allow for including the variance in life-satisfaction in the form of standard deviation (Std Dev. of Life Satisfaction). Given the evidence suggesting a negative relationship between individual well-being and well-being inequality, we use the latter as a control for community life satisfaction in order to examine whether the collective sense of well-being is related to well-being inequality within a community. We argue that the inequality of life satisfaction in a community exerts an (negative) effect upon the general level of life satisfaction given the evidence of the detrimental effects of various forms of inequality on health and well-being (Wilkinson & Pickett, 2009, 2020). Hence, the inequality of life satisfaction can be considered a community area characteristic. Lastly, we consider whether rural or urban communities are related to the happiness of a community.
Spatial Weights Matrix
The empirical approach we adopt originates from a spatial economics perspective. The conceptualization of neighbouring communities is based on a spatial weights matrix denoted by W. Such a weights matrix describes the spatial arrangement of units in a sample (Anselin, 1988; Elhorst, 2014; Lin et al., 2014). It is always a non-negative squared N × N (WN×N) matrix that reflects the spatial connectivity among spatial units, where N denotes the number of the unique spatial units. Specifically, the dimensions of the matrix we are using are 1,215 × 1,215, as the number of the communities (N = 1,215).Footnote 5 Among the weights matrices that are most often used in empirical research are the p-orderFootnote 6 Binary Contiguity (B.C.) matrix (Queen or Rook) and the inverse distance matrix (Inverse Distance). Within B.C. matrices, where they take the value of 1 each time two communities share a common border (line or edge) and 0 otherwise. The difference between Queen and Rook is how common edges are treated (the queen criterion is more encompassing). On the other hand, the Inverse Distance matrix has as its elements the inverse of the distance between each pair of communities (distance from the centroids of each community). Given that the communities in our dataset are quite uneven in terms of size, we do not use inverse distance matrices. For example, if we try to formulate the location similarity using an inverse distance matrix in this dataset, we will end up having many locations that their connectivity will be virtually zero, no matter whether we are using a cut-off point or not, because of the uneven size of our communities. In addition, the formulation of the weights matrix using an inverse distance framework will result in a structure of the covariance matrix that produces local spillovers. In this study, we examine the spatial equilibrium of happiness among other things. The notion of equilibrium implies that there should not be differences in life satisfaction between the communities across the entire country. If there are differences though, the strength of spillovers will suggest the speed or the intensity that needs for the equilibrium to take place. Hence, we prefer models that can produce global spillover effects and that allow us to examine the spatial equilibrium across the entire country. For those reasons, we use only B.C. weight matrices. For all the empirical analysis, the weights matrices (Queen 1st order B.C., Queen 2nd order B.C., Rook 1st order B.C. and Rook 2nd order B.C.) have been normalised. Specifically, we have row normalised the B.C. weights matrices (Queens or Rook) and as a result the sum of each row equals to one (Vega & Elhorst, 2015). We are using all aforementioned matrices when we explore the data in order to examine the sensitivity of the results to the formulation of the weight matrix. Descriptive statistics regarding the weight matrices can be found in the Appendix (Table 8 and Fig. 7).
Spatial Autocorrelation
We use the spatial weights matrices discussed above in order to examine spatial autocorrelation or spatial clustering of the variables. The two variables of interest that we focus our analysis on for the spatial autocorrelation are the life satisfaction and the household income of the communities. We mentioned in a previous section that there might be a relationship between the two variables resulting in a similar spatial clustering. Since communities with high income often cluster together, someone would expect that life satisfaction would do the same given the evidence that within regions life satisfaction and income are positively related. If this expectation is true, we would see a similar spatial clustering between the two variables with the same direction, i.e. positive or negative clustering. Namely, communities with positive clustering in terms of life satisfaction would also have a positive clustering in terms of income and vice versa. For that reason, we separately apply the Moran’s I test to the raw variables and examine the sign and the level of the spatial autocorrelation across the 1,215 communities. The values that the Moran’s I test can take range from -1 to + 1, where a positive value indicates positive spatial autocorrelation (similar values of a variable between neighbouring spatial units) and a negative value indicates negative spatial autocorrelation (contrasting values of a variable between neighbouring spatial units). In addition, suitable maps using the Local Indicators of Spatial Autocorrelation (LISA) proposed by Anselin (1995) help us to detect whether there are clusters of high-high (hot-spots), low-low or mixed in life satisfaction and average income communities. That is, whether communities are surrounded by other communities with fairly similar levels of life satisfaction and average income using a map. The pattern that these maps reveal, and we present in the next section, suggest that despite the clustering that we observe in both variables, the clustered communities differ between the two variables implying that life satisfaction and average income are not positively related between communities. This finding is further supported in the spatial regression analysis. Lastly, in order to proceed in the spatial regression analysis in the first place, we use the Moran’s I test with the same spatial weights matrices to the residuals of the OLS regressions in order to examine whether the residuals are independently distributed.
Spatial Econometrics
Spatial econometrics is a set of methods which aim at modelling cross-sectional dependence and clustering within an econometric specification. Previous research has shown that geographical factors and spatial interactions should be included in the examination of well-being (Pierewan & Tampubolon, 2014; Stanca, 2010). In essence, we include spatial interactions using the weights matrix Wij described before in order to control for spatial dependence and to examine spatial spillover effects (Elhorst, 2014). The general specification in vectors/matrix formation is as follows:
Equation (1) includes spatial interactions with the dependent variable (ρWY) and independent variables (WXθ). This model that includes only these two spatial interaction terms is known as the Spatial Durbin Model (SDM). Equation (1) together with Eq. (2) i.e. the inclusion of the interaction with the error term (\(\lambda We\)), is known as the General Nesting Spatial model (GNS) (Vega & Elhorst, 2015). We do not use the GNS that includes all possible spatial interactions due to the difficulty in obtaining the estimated coefficients because of the overparameterization, namely the tendency of the estimated coefficients to become insignificant when many variables are added in the model (Burridge et al., 2016). However, different combinations of spatial interactions give rise to different spatial econometric models where each spatial interaction tries to model the spatial component of the data generating process. Given our concerns regarding the spatial clustering of the variables of interest, we first compare the results from the standard OLS model with the results produced from models where we include only spatial interaction with the error term (Spatial Error Model: SEM model). Subsequently, we empirically examine the spillover effects of the dependent variable (SAR model) and that of the dependent along with some of the independent variables (SDM model). These last models enable us to consider whether spatial equilibrium of life satisfaction (LS) can be found by measuring the strength of coefficient rho (ρ). An equilibrium of happiness would imply that there are no differences and hence, there are no spillovers between communities in terms of their happiness. Our intention is to estimate spatial interdependencies and spillovers in life satisfaction by using suitable models. We are interested in the coefficient ρ from Eq. (1) that gives the spatial spillovers between communities’ life satisfaction. That is why for the spatial spillovers of well-being we consider both the SAR and the SDM models. Following Vega and Elhorst (2015), we also argue that only models that include a spatial lag of X (WXθ) are able to produce flexible spatial spillover effects. Spatial spillovers of the independent variables are of interest as they show how a change in an explanatory variable in community j, impacts the dependent variable in community i (i ≠ j). The definition of a spatial spillover is the marginal impact of a change to one independent variable in a one cross-sectional unit on the dependent variable in another unit. This is known as the indirect effect. Direct effects on the other hand, measure the impact of a change of an explanatory variable of spatial unit i on the dependent variable of the same unit i. A synopsis of the models used is included in Table 2 while we formally estimateFootnote 7 the following structural equation using the various spatial interactions (resulting in different models) discussed above.
The estimation of these models is derived from the reduced form of the spatial econometric model at hand. The estimation is usually carried out using maximum likelihood or spatial two-stage least-squares. Due to concerns regarding the endogeneity of the spatial interaction with the dependent variable (ρWY), we carry out the estimation using spatial two-stage least squares. For an illustration, Eq. (7) presents the reduced form for the SDM model only from Eq. (1):
Results
Descriptive Analysis
The main variable of interest is the Life Satisfaction observed at community area level in Canada. We start by presenting some descriptive statistics that provide insights for the regression analysis employed later in the article. The left panel of Fig. 2 presents the distribution of Life Satisfaction. as well as the normal and kernel function distributions. The mean of Life Satisfaction in our sample is 8.04 (vertical line) on a 0 to 10 scale. This is in line with the results in the World Happiness Report and OECD better life index, which rank Canada very high in the list of countries. We proceed by first exploring the geographical aspects of the communities under examination. It has often been suggested in the literature that rural areas tend to have higher levels of life satisfaction than urban ones (Berry & Okulicz-Kozaryn, 2011) and especially that this is the case in more affluent countries (Helliwell et al., 2019; Burger et al., 2020). Our descriptive results are consistent with this. The right panel of Fig. 2 shows the difference in Life Satisfaction between urban and rural areas. It seems that the distribution of rural areas is located to the right of that of urban distribution and the rural spike is larger than the urban one suggesting that the Life Satisfaction is on average higher in rural areas compared to urban ones. The vertical lines for the mean value of Life Satisfaction between rural and urban communities are 8.15 and 7.97 respectively.
An important observation is the negative association found between Life Satisfaction and the Std Dev. of Life Satisfaction. It could be argued that higher levels of inequality in happiness in a community would be associated with decreasing levels of life satisfaction, given relevant arguments pertaining to socio-spatial cohesion (Wilkinson & Pickett, 2009). Figure 3 graphically depicts this observation both for the full sample and for the rural and urban subsamples. The negative association is more intense in urban areas (steeper red line). Hence, we observe that urban areas have generally lower levels of life satisfaction and at the same time the dispersion of happiness within those areas is higher, suggesting that greater life satisfaction inequality can be found in urban places. This is consistent with relevant recent research presented in the 2020 World Happiness Report (Burger et al., 2020). A possible explanation for this result is the difference in how densely populated those two areas are. The mean value of the logarithm of population density in urban areas is 6.92 while for rural areas is 2.29.
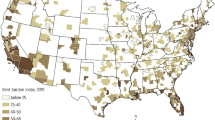
On the left side of Fig. 4 there is the spatial distribution of Life Satisfaction across Canadian communities. Life Satisfaction appears to be spatially dependent since the high and low satisfied communities appear to be clustered together. In particular, there are many communities in the east of the country (Quebec) with high levels of life satisfaction. This observation suggests that cultural or institutional characteristics may be in place in these communities that can explain this pattern (Veenhoven, 2009). On the other hand, the right side of Fig. 4 shows the spatial distribution of mean household income in Canada. The difference we notice between the two maps is that the communities with high levels of Life Satisfaction are mostly located to the east side of the country while the communities with high levels of average household income are mostly on the west. These maps, however, are simply the spatial distribution of the variables and they do not formally examine the clustering of the communities. Spatial statistics can further explore the data and shed light to the underlying mechanisms governing these observations (see next subsection).
The information provided by the correlation matrix is valuable as it provides us with some intuitive indications and insights about the relationship between our variables. A general comment is that the majority of the correlations in Table 3 are statistically significant. First of all, there is a positive and significant correlation at 1% significance level between Life Satisfaction and the Household Income. In contrast, there is a negative correlation between Life Satisfaction and Unemployment Rate as well as with Std Dev. of Life Satisfaction. The former correlation is statistically significant at 10% level while the latter at 1% level. Apart from that, it is also interesting to note that there is a positive correlation between Urban areas, Commute Duration and Population Density as one might expect. The explanation for that is straightforward since the majority of economic activity is often concentrated in urban areas which leads to overpopulation resulting in traffic jams and increased commute duration. Finally, a thought-provoking correlation is observed between the community-level education attainment (Proportion of 4y degree) and community income (Household Income) on the one hand, which is positive and significant, and between the former and community level of Unemployment Rate (negative and significant) on the other.
Spatial Analysis
In Fig. 5 we present the results from the Moran’s I test and LISA indicators for Life Satisfaction and household income using the Queen 1st B.C. spatial weights matrix. Both variables display a positive value of Moran’s I test for spatial autocorrelation (0.361 and 0.523 respectively). This result alone indicates that in both variables individually there are neighbouring communities with similar values of life satisfaction and income i.e. either high or low values. That means that a positive spatial autocorrelation is obtained either from similar large values of a variable being close together or from similar low values of a variable being clustered together. However, Moran’s I graph does not say anything about the specific communities that cluster and especially about the level of the value of these variables (high or low). We get a more detailed picture about this clustering by looking at the cluster maps from LISA as shown below in Fig. 5. We notice that there is not an overlap in the spatially clustered communities between the two variables based on the level of their values. For example, despite the fact that both variables appear to be spatially clustered in the communities in the east side of the country, the clustering is based on high values for life satisfaction and on low values for income. This is an indication that the clustering of life satisfaction between the communities is probably not due to the same communities being clustered based on high income. In the Appendix Fig. 9, one can find the Moran’s I graphs and LISA cluster maps for Life Satisfaction and Household Income for all the spatial weights matrices used.
Turning now to the regression analysis, Table 4 presents the results from the OLS regressions. The three non-spatial models presented in Table 4 differ only in that Model 2 expands Model 1 in order to include a geographical dummy variable for urban communities (reference group is rural communities) while Model 3 expands Model 2 by adding provincial dummies in the specification.Footnote 8 In all three models the pattern is similar and in accordance with the correlation matrix from before. For example, we see that household income is positively associated with life satisfaction while commute duration and population density are negatively associated with life satisfaction. Towards the end of the table, we observe that the magnitude of the inequality of life satisfaction is the strongest as it has a coefficient that ranges from 0.548 to 0.556 in absolute values. Finally, the dummy variable for urban communities displays the negative sign in Model 2 and 3. Interestingly, the coefficient of unemployment rate is neither negative nor significant as one would expect. In general, almost all of our coefficients are rather statistically significant and in accordance with previous findings. However, the spatial dependence and clustering that is present in the dataset may drive the results. We apply the Moran’s I test for spatial autocorrelation in the residuals from the three OLS regression in Table 4. The test rejects the null hypothesis that the residuals are independently distributed in space under all four specifications of the weights matrices (the chi-square values from Model 3 for the Queen 1st, Queen 2nd, Rook 1st and Rook 2nd weights matrices are 9.07, 7.81, 8.32 and 8.81 respectively). For that reason, we expand the previous specification by adding a spatial interaction in the error term in order to account for the spatial autocorrelation in the residuals.
Table 5 shows the results from the spatial error model (SEM) that accounts for spatial autocorrelation in the residuals using the four spatial weight matrices we discussed in a previous section. There are no major differences in the estimated coefficients (marginal effects) compared to the Model 3 of Table 4, however, we notice that the spatial coefficient lambda (λ) is positive and statistically significant in all of our weights matrices which means that there is still a spatial structure in the data.
Spatial Spillovers
The models presented so far do not show any spatial spillover effects. The next step in our investigation is to include spatial interactions with the dependent and independent variables in our model allowing for flexible spatial spillover effects (Vega & Elhorst, 2015). In addition, given that we are interested in the spillovers not only of the independent variables but also of life satisfaction, we employ a series of models that include spatial interaction with the dependent variable. Such models are the pure SAR, SAR and SDM that can produce global spillover effects. Results from these models are presented in Table 6. In the upper panel of Table 6 we present the direct effects, namely the impact community characteristics have upon its life satisfaction levels, while the middle panel presents the indirect effect (only SDM includes indirect effects). The latter is the average impact of the characteristics of neighbouring communities, as defined according to the weights matrix used, upon the life satisfaction of the community. Finally, the bottom panel presents the spatial regression coefficient ρ. All direct effects, regardless of the weights matrix used, have the expected signs and are statistically significant for most of the variables. An exception is the coefficient of Unemployment Rate which is insignificant. Specifically, there is a positive relationship between Household Income and Life Satisfaction while Commute Duration, Population Density and Proportion of Foreign Born are negatively associated with community’s Life Satisfaction as we saw in the correlation matrix and the OLS regressions before. Finally, the proxy we used for the inequality of happiness, the Std Dev. of Life Satisfaction, is negative and highly statistically significant (1% level). Again, it is clear that inequality hurts the satisfaction found in communities.
For the indirect effects as well as for the spatial coefficient, ρ, some of the results differ depending on the spatial weight matrix employed. In Table 6 we see that the Life Satisfaction level of a community is negatively associated with the income of the neighbouring communities (indirect Household Income) as opposed to the direct effect which is positive, irrespective of the matrix. However, the results are statistically significant only under the second order B.C. matrices, either queen or rook. Regarding the indirect Unemployment Rate, we observe that the results are positive and significant when the first order B.C. weight matrices are used. Interestingly, we notice that the coefficients of the indirect effects switch signs compared to the direct effects, possibly reflecting the feeling of “relief” that a community can experience from the economic situation of neighbouring communities (Lin et al., 2014). Finally, we should highlight that the coefficient ρ has a positive and significant sign regardless of the model,Footnote 9 while its effect is even higher when the second order B.C. matrices are used (either queen or rook). This finding means that there is a positive association between neighbouring spatial units’ life satisfaction. Hence, the estimations we get for the coefficients of spillovers between communities’ Life Satisfaction range from 0.113 to 0.714. These findings suggest that there are spillover effects of Life Satisfaction among the communities suggesting that communities can influence each other in terms of life satisfaction and can potentially lead to a spatial equilibrium of life satisfaction once all communities reach the same level of life satisfaction.
Robustness
Given the large area of some of the communities in Canada, especially in the northern part of the country, we repeat the analysis by using the communities of an urban area where spatial units are smaller and hence are assumed to be more connected. The reason for this distinction is the geographical surface of the northern regions. The problem that arises in those large communities is that their centres are quite distant from each other and hence the interaction between the communities is probably less intense. In other words, individuals that reside in those large areas may rarely cross the borders of their own communities resulting in less interaction with neighbouring communities. On the contrary, the interactions between neighbouring communities in urban areas are expected to be higher. Thus, in this exercise, we examine whether the results remain qualitatively robust when we restrict the analysis to smaller geographical units where interactions are likely to happen more often between the spatial units.
In Fig. 6 we present the map of the communities included in the robustness check. We use 270 communities, all belonging to the province of Ontario. Ontario consists of 399 communities in the dataset, however, we are using only 270 after having removed the “island” spatial units and the remote areas.Footnote 10 Another advantage of this exercise is that a more homogenous sample of communities in terms of surface area is achieved. Furthermore, Canada has both English and French speaking communities and hence, there may be differences that could be attributed to cultural or linguistic effects (Ballas & Dorling, 2013). By focusing on the communities of Ontario, we eliminate the cultural differences that might be responsible for results we found before. Furthermore, given the different provinces in the entire sample, by focusing on just one province, we achieve a more homogenous sample in terms of institutions. The institutional differences that might have played a role before are now eliminated.
Table 7 presents the results for the new restricted sample with the 270 communities. The same spatial econometric models are examined using the four B.C. spatial weights matrices as before (Queen 1st, Queen 2nd, Rook 1st and Rook 2nd). The structure of Table 7 is the same as in Table 6. The direct effects are qualitatively the same in both tables, however, in Table 7 fewer direct effects are now statistically significant such as Household Income, Commute Duration, Population Density and Std Deviation of Life Satisfaction among others. Specifically, we observe that the association between Life Satisfaction and Household Income is positive and significant at the 1% level for all spatial regressions, however, the magnitude of the coefficients has on average been increased compared to the entire sample as they range from 0.129 to 0.203. Interestingly, the direct effect of Unemployment Rate is still insignificant regardless of the weight matrix used. Insignificant predictors are the Permanent Location and Proportion of 4y degree as well. Regarding the indirect effects, we observe again the same changes as we witnessed in the direct effects compared to Table 6. For example, the indirect effect of Household Income in the models that use the second order queen or rook weight matrix is negative and statistically significant. In contrast, Unemployment Rate exhibits insignificant coefficients under those two weights matrices while it is positive and significant under the first order B.C. weights matrices. These findings suggest that apart from a community's own characteristics, neighbours matter to some extent for a community’s life satisfaction as neighbours’ effects are both significant and occasionally greater in magnitude compared to those found from the direct effects. In the bottom panel, the spatial coefficients ρ are not as significant as they were in Table 6. We see some positive and significant results under pure SAR and SDM models while we even get two negative and significant estimations for SAR models. The negative ones though have a small coefficient in absolute values. Despite that, the findings suggest that the spillovers of Life Satisfaction among more homogenous communities are also taking place but they are less intense compared to the entire sample. The estimations we get for the ρ coefficient range from -0.022 to 0.460. One limitation of this exercise, however, is the relatively small sample size that leads to higher standard errors of the coefficients compared to the entire sample resulting in less reliable results.
Discussion and Conclusion
As we pointed out in the introduction, the work presented in this article aims at analysing subjective well-being and its socio-spatial, economic and demographic determinants at small area levels. To that end, we adopt a spatial econometrics approach (Anselin, 1988; Elhorst, 2014) to the analysis of an innovative dataset presented and made available by Helliwell et al. (2019). This dataset includes life satisfaction data in Canada and relevant socio-economic and demographic data at small area (community) level in Canada. Our analysis investigates possible spatial clustering, interdependencies and spillover effects between communities. We first explore the spatial correlation of life satisfaction and income, and we confirm some of the previous findings regarding clustering. Both variables exhibit spatial clustering, however, the income clustering does not seem to be the driving force of the life satisfaction clustering. Then we examine the spillover effects of life satisfaction between the communities using regression analysis.
It is interesting and relevant to note that although there have been theoretical and empirical arguments for the analysis of social comparisons of happiness between people and places, there has been a relative paucity of relevant empirical studies at the local geographical level. It can be argued that our analysis considers (at least implicitly) possible social comparisons (at the community area level), making an empirical contribution to knowledge regarding possible socio-spatial comparison effects between communities in terms of life satisfaction. The empirical framework we adopt allows us to examine our standard life satisfaction specification by taking into account the spatial dependence and spatial clustering of the communities. In addition, it allows us to explore the extent to which characteristics of one community (e.g. Household Income and Unemployment Rate in the area) are associated with the life satisfaction levels of a neighbouring community. Furthermore, using this framework we assess the relation of a community’s life satisfaction with the life satisfaction of neighbouring communities. Last but not least, we control for the urbanity of the community using a dummy variable as well as for the happiness inequality using the standard deviation of life satisfaction.
Our results demonstrate that on average urban communities are less satisfied with life compared to rural communities and that happiness inequality is harmful for the collective sense of well-being within small area communities as there is a negative relationship between happiness and happiness inequality. Focusing on the spatial regressions we observe that aggregate levels of Life Satisfaction in communities are associated with characteristics of neighbouring communities. Apart from the Household Income level and Unemployment Rate, the level of Life Satisfaction of a community is related to the life satisfaction levels of its neighbouring communities. These findings suggest that there is evidence of spatial interdependencies between communities. Hence, the findings can inform and support local and regional policy decision making pertaining to the well-being and life satisfaction in rural and urban places (Ferrara et al., 2022).
The most persistent result from our spatial regressions is the significance of the spatial coefficients λ and ρ and the opposing signs between direct and indirect (income and unemployment) effects. This means that at the community area level, the Life Satisfaction of one community can be used as a predictor for the Life Satisfaction of neighbouring communities. Given that spatial spillovers occur, it suggests that there are communities with different levels of life satisfaction. These results imply the absence of a spatial equilibrium of happiness. However, the fact that we observe such spatial spillover effects further implies that eventually a spatial equilibrium in happiness may occur since interdependencies and comparisons between communities will most likely continue. Regarding the indirect effects of the Household Income as well as of the Unemployment Rate, they can also be used as predictors for neighbouring communities’ life satisfaction. Although the direction is not clear, the fact that we observe associations can be seen as an alerting sign that the level of income as a geographical area phenomenon can exert an influence on life satisfaction in the immediate vicinity as well as neighbouring areas at a global scale. Particularly interesting is the finding that in more homogenous communities, both in terms of size and institutional characteristics, the indirect spillover effects are more intense compared to the entire sample while the life satisfaction spillovers effects are less intense compared to the entire sample. Hence, policy makers that are interested in improving the life satisfaction of a community should take into account both the level of life satisfaction, the income level and the unemployment rate in neighbouring communities among other things. In particular, the findings suggest a socio-spatial comparison effect, a possible sense of ‘relief’ or in other words a possible ‘it could be worse’ effect regarding income level and the rate of unemployment of the neighbours. These results highlight the important role of income in shaping the life satisfaction, not only of individuals but also of communities and even of neighbouring communities. It would possibly imply that income needs to be more evenly distributed across communities for such effects to be absent, although more research is needed in this direction in order to establish a causal relationship. This finding also illustrates the potential of our methodological approach to make a contribution to debates about socio-spatial comparisons and life satisfaction between places. Nevertheless, we should acknowledge the limitations of using a cross-sectional dataset instead of panel data. If panel data become available, we could examine the dynamics in the relationships we are interested in and we could draw causal relationships between our variables. Having only contemporaneous relations may be misleading but they still provide the interdependencies we would have expected between communities’ life satisfaction. We should be cautious when we interpret such results and further research is needed with more disaggregated regional and panel data.
Overall, the work reported in this article presents a framework that can be used to explore and quantify the extent to which the collective sense of community’s well-being, measured by individuals’ measures of subjective life satisfaction, may be related to neighbouring communities. The work further implies some policy implications as the cooperation that should exist between local governments. The spillover effects between communities in terms of their life satisfaction and other variables suggest that policies in one community will reach neighbouring communities as well. Local governments should take that into account when making their decisions and further foster cooperation between them. Similar patterns could be explored regarding other variables and considering issues pertaining to other economic variables (e.g. economic growth in neighbouring communities) but also (and especially given the current Covid-19 crisis) health-related variables (e.g. how the high prevalence of Covid-19 in an small area may affect subjective happiness or sense of anxiety in neighbouring areas). The methodological framework specified in this article can be used and adapted to explore a wide range of regional and sub-regional socio-spatial interdependencies. Furthermore, recent methodological advances allow researchers to combine the hierarchical structure of survey and registered data, commonly examined with the use of multilevel modelling, with the spatial econometrics literature that allows for interactions and spatial spillovers effects between the units of analysis (Savitz & Raudenbush, 2009; Dong et al., 2015; Ma et al., 2018). These developments incorporate spatial dependence, spatial interactions and spatial autoregressive processes into the standard multilevel modelling. There have been some research efforts in examining travel satisfaction in an urban context using this empirical framework (Dong et al., 2016) but there is no study examining subjective well-being measures of individuals at a small area level. Pierewan and Tampubolon (2014) attempted to explain happiness data using a spatial multilevel model, however, the level of their analysis was NUTS2 regions in Europe. There is great potential for further research aimed at building on the framework and analysis presented here at an even smaller and micro-level for countries and regions that have suitable high-quality level. In particular, the methodological framework presented here can potentially be extended for the analysis of individuals that are nested within small area neighbourhoods and communities, and examine the spillover effects between individuals’ happiness while taking into account the hierarchical structure of the data.
Data Availability
The data replicating the findings of this article is openly available from the personal website of John F. Helliwell. https://blogs.ubc.ca/helliwell/publications/.
Notes
The words happiness, life satisfaction and well-being are used interchangeably for the purposes of this article.
Other approaches include the creation of composite indexes of well-being, however, there is no consensus on how to create one (Dialga & Le Giang, 2017).
In the robustness section where we examine communities within and around Toronto, the sample size decreases to N = 270. Hence, the W for the robustness is 270 × 270.
p-order binary contiguity (B.C.) matrices are defined as follows: if p = 1 only first-order neighbours are included, if p = 2 first and second order neighbours are considered (my neighbours’ neighbours are also my own neighbours), and so on. See the Appendix Fig. 8, for a visualisation using maps.
All data analysis, modelling and mapping of the data presented in this article was carried out using GeoDa 1.14.0 and Stata 17.
The 1,215 communities in our sample are spatially distributed among the 13 provinces and territories of Canada, namely: Alberta, British Columbia, Manitoba, New Brunswick, Newfoundland and Labrador, Nova Scotia, Northwest Territories, Nunavut, Ontario, Prince Edward Island, Quebec, Saskatchewan and Yukon.
It is only insignificant when first order queen and rook spatial weights matrices are used under SAR model.
Islands and remote areas are called those communities that even though they are located in the mainland, they do not share any borders with other core communities from the same province. Hence, they are surrounded by communities belonging to a different province.
References
Ala-Mantila, S., Heinonen, J., Junnila, S., & Saarsalmi, P. (2018). Spatial nature of urban well-being. Regional Studies, 52(7), 959–973.
Alesina, A., Di Tella, R., & MacCulloch, R. (2004). Inequality and happiness: Are Europeans and Americans different? Journal of Public Economics, 88(9–10), 2009–2042.
Anselin, L. (1988). Spatial econometrics: methods and models (Vol. 4). Springer Science & Business Media.
Anselin, L. (1995). Local indicators of spatial association—LISA. Geographical Analysis, 27(2), 93–115.
Aslam, A., & Corrado, L. (2012). The geography of well-being. Journal of Economic Geography, 12(3), 627–649.
Ballas, D. (2021). The economic geography of happiness. In: Zimmermann, K.F. (eds) Handbook of labor, human resources and population economics. Springer, Cham. https://doi.org/10.1007/978-3-319-57365-6_188-1
Ballas, D., & Dorling, D. (2013). The geography of happiness. In Ilona Boniwell, Susan A. David, and Amanda Conley Ayers (eds). Oxford handbook of happiness (2013; online edn, Oxford Academic, 1 Aug. 2013). https://doi.org/10.1093/oxfordhb/9780199557257.013.0036
Ballas, D., & Tranmer, M. (2012). Happy people or happy places? a multilevel modeling approach to the analysis of happiness and well-being. International Regional Science Review, 35(1), 70–102.
Bernini, C., & Tampieri, A. (2019). Happiness in Italian cities. Regional Studies, 53(11), 1614–1624.
Berry, B. J., & Okulicz-Kozaryn, A. (2011). An urban-rural happiness gradient. Urban Geography, 32(6), 871–883.
Blanchflower, D. G., & Oswald, A. J. (2004). Well-being over time in Britain and the USA. Journal of Public Economics, 88(7–8), 1359–1386.
Blanchflower, D. G., & Oswald, A. J. (2008). Is well-being u-shaped over the life cycle? Social Science & Medicine, 66(8), 1733–1749.
Brereton, F., Clinch, J. P., & Ferreira, S. (2008). Happiness, geography and the environment. Ecological Economics, 65(2), 386–396.
Burger, M. J., Morrison, P. S., Hendriks, M., & Hoogerbrugge, M. M. (2020). Urban-rural happiness differentials across the world. World Happiness Report, 2020, 66–93.
Burger, M., Hendriks, M., & Ianchovichina, E. (2022). Happy but unequal: Differences in subjective well-being across individuals and space in Colombia. Applied Research in Quality of Life, 17(3), 1343–1387.
Burridge, P., Elhorst, J. P., Zigova, K. (2016). Group interaction in research and the use of general nesting spatial models, Spatial Econometrics: Qualitative and limited dependent variables (advances in econometrics, vol. 37), Emerald Group Publishing Limited, Bingley, pp. 223–258. https://doi.org/10.1108/S0731-90532016000003701
Clark, A. E. (2003). Unemployment as a social norm: Psychological evidence from panel data. Journal of Labor Economics, 21(2), 323–351.
Clark, A. E., & Oswald, A. J. (1994). Unhappiness and unemployment. The Economic Journal, 104(424), 648–659.
Clark, A. E., & Oswald, A. J. (1996). Satisfaction and comparison income. Journal of Public Economics, 61(3), 359–381.
Clark, A., Fleche, S., Layard, R., Powdthavee, N., & Ward, G. (2019). The origins of happiness. Princeton University Press.
Di Tella, R., MacCulloch, R. J., & Oswald, A. J. (2001). Preferences over inflation and unemployment: Evidence from surveys of happiness. American Economic Review, 91(1), 335–341.
Di Tella, R., MacCulloch, R. J., & Oswald, A. J. (2003). The macroeconomics of happiness. Review of Economics and Statistics, 85(4), 809–827.
Dialga, I., & Le Giang, T. H. (2017). Highlighting methodological limitations in the steps of composite indicators construction. Social Indicators Research, 131(2), 441–465.
Dickerson, A., Hole, A. R., & Munford, L. A. (2014). The relationship between well-being and commuting revisited: Does the choice of methodology matter? Regional Science and Urban Economics, 49, 321–329.
Dickinson, P. R., & Morrison, P. S. (2022). Aversion to local wellbeing inequality is moderated by social engagement and sense of community. Social Indicators Research, 159(3), 907–926.
Diener, E., Suh, E. M., Lucas, R. E., & Smith, H. L. (1999). Subjective well-being: Three decades of progress. Psychological Bulletin, 125(2), 276.
Diener, E., Heintzelman, S. J., Kushlev, K., Tay, L., Wirtz, D., Lutes, L. D., & Oishi, S. (2017). Findings all psychologists should know from the new science on subjective well-being. Canadian Psychology/psychologie Canadienne, 58(2), 87.
Diener, E., Oishi, S., & Tay, L. (2018). Advances in subjective well-being research. Nature Human Behaviour, 2(4), 253–260.
Dong, G., Harris, R., Jones, K., & Yu, J. (2015). Multilevel modelling with spatial interaction effects with application to an emerging land market in Beijing, China. Plos One, 10(6), e0130761.
Dong, G., Ma, J., Harris, R., & Pryce, G. (2016). Spatial random slope multilevel modeling using multivariate conditional autoregressive models: A case study of subjective travel satisfaction in Beijing. Annals of the American Association of Geographers, 106(1), 19–35.
Easterlin, R. A. (1995). Will raising the incomes of all increase the happiness of all? Journal of Economic Behavior & Organization, 27(1), 35–47.
Easterlin, R. A. (1974). Does economic growth improve the human lot? some empirical evidence. In Nations and households in economic growth, eds David, P.A, & Reder M. W. (pp. 89–125). Academic Press. https://doi.org/10.1016/B978-0-12-205050-3.50008-7
Easterlin, R. A. (2001). Income and happiness: Towards a unified theory. The Economic Journal, 111(473), 465–484.
Elhorst, J. P. (2014). Spatial econometrics from cross-sectional data to spatial panels. Springer.
Ferrara, A. R., Dijkstra, L., McCann, P., & Nisticó, R. (2022). The response of regional well-being to place-based policy interventions. Regional Science and Urban Economics, 97, 103830. https://doi.org/10.1016/j.regsciurbeco.2022.103830
Ferrer-i-Carbonell, A., & Gowdy, J. M. (2007). Environmental degradation and happiness. Ecological Economics, 60(3), 509–516.
Ferriss, A. L. (2002). Religion and the quality of life. Journal of Happiness Studies, 3(3), 199–215.
Florida, R., Mellander, C., & Stolarick, K. (2011). Beautiful places: The role of perceived aesthetic beauty in community satisfaction. Regional Studies, 45(1), 33–48.
Goetzke, F., & Islam, S. (2017). Testing for spatial equilibrium using happiness data. Journal of Regional Science, 57(2), 199–217.
Goff, L., Helliwell, J. F., & Mayraz, G. (2018). Inequality of subjective well-being as a comprehensive measure of inequality. Economic Inquiry, 56(4), 2177–2194.
Graves, P. E., & Mueser, P. R. (1993). The role of equilibrium and disequilibrium in modeling regional growth and decline: A critical reassessment. Journal of Regional Science, 33(1), 69–84.
Helliwell, J. F., & Barrington-Leigh, C. P. (2010). Measuring and understanding subjective well-being. Canadian Journal of Economics/Revue Canadienne d’économique, 43(3), 729–753.
Helliwell, J. F., & Wang, S. (2010). Trust and well-being. Technical report. National Bureau of Economic Research. https://doi.org/10.5502/ijw.v1i1.3
Helliwell, J. F., Shiplett, H., & Barrington-Leigh, C. P. (2019). How happy are your neighbours? variation in life satisfaction among 1200 Canadian neighbourhoods and communities. PLoS ONE, 14(1), e0210091.
Helliwell, J. F., Layard, R., Sachs, J. D., De Neve, J.-E., Aknin, L. B., & Wang, S. (Eds.). (2022). World happiness report 2022. New York: Sustainable development solutions network, available from: https://worldhappiness.report/ed/2022/. Accessed 8 Feb 2023.
Hong, Z., & Park, I. K. (2021). Is the well-being of neighboring cities important to me? analysis of the spatial effect of social capital and urban amenities in south Korea. Social Indicators Research, 154(1), 169–190.
Inglehart, R., Basanez, M., Diez-Medrano, J., Halman, L., & Luijkx, R. (2000). World values surveys and European values surveys, 1981–1984, 1990–1993, and 1995–1997. Ann Arbor-Michigan, Institute for Social Research, ICPSR version.
Jongbloed, J. (2018). Higher education for happiness? investigating the impact of education on the hedonic and eudaimonic well-being of Europeans. European Educational Research Journal, 17(5), 733–754.
Krueger, A. B., & Schkade, D. A. (2008). The reliability of subjective well-being measures. Journal of Public Economics, 92(8–9), 1833–1845.
Kubiszewski, I., Jarvis, D., & Zakariyya, N. (2019). Spatial variations in contributors to life satisfaction: An Australian case study. Ecological Economics, 164, 106345.
Latif, E. (2016). Happiness and comparison income: Evidence from Canada. Social Indicators Research, 128(1), 161–177.
Lawless, N. M., & Lucas, R. E. (2011). Predictors of regional well-being: A county level analysis. Social Indicators Research, 101(3), 341–357.
Layard, R. (2011). Happiness: Lessons from a new science. Penguin UK.
Layard, R., & Ward, G. (2020). Can we be happier?: Evidence and ethics. Penguin UK.
Lear, J. (1988). Aristotle: The desire to understand. Cambridge University Press.
Lin, C.-H.A., Lahiri, S., & Hsu, C.-P. (2014). Happiness and regional segmentation: Does space matter? Journal of Happiness Studies, 15(1), 57–83.
Lin, C.-H.A., Lahiri, S., & Hsu, C.-P. (2017). Happiness and globalization: A spatial econometric approach. Journal of Happiness Studies, 18(6), 1841–1857.
Luttmer, E. F. (2005). Neighbors as negatives: Relative earnings and well-being. Quarterly Journal of Economics, 120(3), 963–1002.
Ma, J., Chen, Y., & Dong, G. (2018). Flexible spatial multilevel modeling of neighborhood satisfaction in Beijing. The Professional Geographer, 70(1), 11–21.
McCann, P. (2013). Modern urban and regional economics. Oxford University Press.
Mennis, J. (2006). Mapping the results of geographically weighted regression. The Cartographic Journal, 43(2), 171–179.
Messacar, D. (2022). Community attachment, job loss and regional labour mobility in Canada: Evidence from the great recession. Canadian Journal of Economics/Revue Canadienne d’économique, 55(3), 1404–1430.
Mishra, T., Parhi, M., & Fuentes, R. (2015). How interdependent are cross-country happiness dynamics? Social Indicators Research, 122(2), 491–518.
Morrison, P. S. (2011). Local expressions of subjective well-being: The New Zealand experience. Regional Studies, 45(8), 1039–1058.
Morrison, P. S., & Weckroth, M. (2018). Human values, subjective well-being and the metropolitan region. Regional Studies, 52(3), 325–337.
Morrison, P. S. (2020). Wellbeing and the region. In: Fischer, M., Nijkamp, P. (eds) Handbook of regional science. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-36203-3_16-1
Mouratidis, K. (2019). Compact city, urban sprawl, and subjective well-being. Cities, 92, 261–272.
Neira, I., Bruna, F., Portela, M., & Garcia-Aracil, A. (2018). Individual well-being, geographical heterogeneity and social capital. Journal of Happiness Studies, 19(4), 1067–1090.
Nikolova, M., Graham, C. (2022). The economics of happiness. In: Zimmermann, K.F. (eds). Handbook of labor, human resources and population economics. Springer, Cham. https://doi.org/10.1007/978-3-319-57365-6_177-2
Okulicz-Kozaryn, A. (2011). Geography of European life satisfaction. Social Indicators Research, 101(3), 435–445.
Okulicz-Kozaryn, A. (2017). Unhappy metropolis (when American city is too big). Cities, 61, 144–155.
Organisation for Economic Co-operation and Development OECD, O. E. C. (2011). How’s life?: measuring well-being. OECD Paris.
Oswald, A. J., & Wu, S. (2010). Objective confirmation of subjective measures of human well-being: Evidence from the USA. Science, 327(5965), 576–579.
Oswald, A. J., & Wu, S. (2011). Well-being across America. Review of Economics and Statistics, 93(4), 1118–1134.
Pierewan, A. C., & Tampubolon, G. (2014). Spatial dependence multilevel model of well-being across regions in Europe. Applied Geography, 47, 168–176.
Pittau, M. G., Zelli, R., & Gelman, A. (2010). Economic disparities and life satisfaction in European regions. Social Indicators Research, 96(2), 339–361.
Putnam, R. D., Leonardi, R., & Nanetti, R. Y. (1992). Making democracy work: Civic traditions in modern Italy. Princeton University Press.
Rampichini, C., & Schifinid’Andrea, S. (1998). A hierarchical ordinal probit model for the analysis of life satisfaction in Italy. Social Indicators Research, 44(1), 41–69.
Rijnks, R. H., Koster, S., & McCann, P. (2018). Spatial heterogeneity in amenity and labor market migration. International Regional Science Review, 41(2), 183–209.
Rizvi, M. A. K., & Hossain, M. Z. (2017). Relationship between religious belief and happiness: A systematic literature review. Journal of Religion and Health, 56(5), 1561–1582.
Savitz, N. V., & Raudenbush, S. W. (2009). 5. Exploiting spatial dependence to improve measurement of neighborhood social processes. Sociological Methodology, 39(1), 151–183.
Schyns, P. (1998). Cross national differences in happiness: Economic and cultural factors explored. Social Indicators Research, 43(1), 3–26.
Seresinhe, C. I., Preis, T., MacKerron, G., & Moat, H. S. (2019). Happiness is greater in more scenic locations. Scientific Reports, 9(1), 1–11.
Stanca, L. (2010). The geography of economics and happiness: Spatial patterns in the effects of economic conditions on well-being. Social Indicators Research, 99(1), 115–133.
Steptoe, A., Deaton, A., & Stone, A. A. (2015). Subjective wellbeing, health, and ageing. The Lancet, 385(9968), 640–648.
Stevenson, B., & Wolfers, J. (2013). Subjective well-being and income: Is there any evidence of satiation? American Economic Review, 103(3), 598–604.
Stutzer, A., & Frey, B. S. (2006). Does marriage make people happy, or do happy people get married? The Journal of Socio-Economics, 35(2), 326–347.
Stutzer, A., & Frey, B. S. (2008). Stress that doesn’t pay: The commuting paradox. Scandinavian Journal of Economics, 110(2), 339–366.
Veenhoven, R. (1988). The utility of happiness. Social Indicators Research, 20(4), 333–354.
Veenhoven, R. (1995). World database of happiness. Social Indicators Research, 34(3), 299–313.
Veenhoven, R. (1996). Developments in satisfaction-research. Social Indicators Research, 37(1), 1–46.
Veenhoven, R. (2009). Well-being in nations and well-being of nations. Social Indicators Research, 91(1), 5–21.
Veenhoven, R., Ehrhardt, J., Ho, M. S. D., & de Vries, A. (1993). Happiness in nations: Subjective appreciation of life in 56 nations 1946–1992. Erasmus University Rotterdam.
Vega, S. H., & Elhorst, J. P. (2015). The SLX model. Journal of Regional Science, 55(3), 339–363.
Weckroth, M., Ala-Mantila, S., Ballas, D. et al. (2022). Urbanity, neighbourhood characteristics and perceived quality of life (QoL): Analysis of individual and contextual determinants for perceived QoL in 3300 postal code areas in Finland. Social Indicators Research, 164, 139–164. https://doi.org/10.1007/s11205-021-02835-z
Wilkinson, R. G., & Pickett, K. (2009). The spirit level: Why more equal societies almost always do better (Vol. 6). Allen Lane London.
Wilkinson, R., & Pickett, K. (2020). The inner level: How more equal societies reduce stress, restore sanity and improve everyone’s well-being. Penguin.
Acknowledgements
The authors are grateful to John Helliwell, Hugh Shiplett and Christopher P. Barrington-Leigh for the public use dataset they created (https://wellbeing.research.mcgill.ca/publications/2019PLOS-CanadaSWB/).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of Interest
There is no conflict of interest. All responsibility for the analysis and interpretation of the data presented in this article lies with the authors.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
Table 8
a Moran’s I test for Life Satisfaction using Queen 1st order B.C. b Moran’s I test for Household Income using Queen 1st order B.C. c LISA cluster map for Life Satisfaction using Queen 1st order B.C. d LISA cluster map for Household Income using Queen 1st order B.C. e Moran’s I test for Life Satisfaction using Queen 2nd order B.C. f Moran’s I test for Household Income using Queen 2nd order B.C. g LISA cluster map for Life Satisfaction using Queen 2nd order B.C. h LISA cluster map for Household Income using Queen 2nd order B.C. i Moran’s I test for Life Satisfaction using Rook 1st order B.C. j Moran’s I test for Household Income using Rook 1st order B.C. k LISA cluster map for Life Satisfaction using Rook 1st order B.C. l LISA cluster map for Household Income using Rook 1st order B.C. m Moran’s I test for Life Satisfaction using Rook 2nd order B.C. n Moran’s I test for Household Income using Rook 2nd order B.C. o LISA cluster map for Life Satisfaction using Rook 2nd order B.C. p LISA cluster map for Household Income using Rook 2nd order B.C.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ziogas, T., Ballas, D., Koster, S. et al. Happiness, Space and Place: Community Area Clustering and Spillovers of Life Satisfaction in Canada. Applied Research Quality Life 18, 2661–2704 (2023). https://doi.org/10.1007/s11482-023-10203-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11482-023-10203-x