Introduction

The optical properties of nanoshells have been studied since the works of Kerker [1], Wu and Yang [2], and others [3,4,5], using Mie theory [6,7,8]. The approach presented in this work is a surprisingly simple alternative for obtaining the dipole polarizability of nanoshells using the long-wavelength approximation (LWA) of Maxwell’s equations, also known as the quasi-static limit [6]. Hence, the formulae proposed herein have the usual assumptions associated with the LWA. In the LWA, we will show that if the electrostatic polarizability is considered the physical quantity of interest instead of the ubiquitous approach that is based on scattering coefficients [9,10,11,12,13,14,15], a generalized analytical form of the dipole polarizability can be derived for the nth nanoshell given a multilayer nanoshell (MNS) with n number of concentric layers. In addition, a function that predicts the localized surface plasmon resonances (LSPRs) supported by the nth nanoshell, which we will refer to as the Fröhlich function, can be derived using this general form of the dipole polarizability of the nth nanoshell when the Fröhlich condition [7, 16, 17] is applied to the polarizability.

Several authors have shown that the dipole polarizability of a MNS can be calculated using the LWA—an approximation that leads to the de-coupling of the electric and magnetic field intensities and allows retardation effects such as radiation damping and dynamic depolarization to be ignored, as long as the sizes of the nanoparticles being considered are within the Rayleigh regime [6, 10, 12, 14, 15, 18,19,20]. This regime considers particle sizes that are small compared to the excitation wavelength, usually within one-tenth of the excitation wavelength or less [6, 7, 16, 17, 21]. However, at such sub-100 nm particle sizes, usually around 10 nm or less, metal nanoparticles (MNPs) have been shown to display non-local effects [16, 17, 22]. These effects, which are mostly due to increased scattering of the quasi-free electrons near the metal surface, lead to a dependence of the dielectric function of the metal on the longitudinal wavevector of the incident field [16, 17]. In most studies, this dependence is ignored via the introduction of the local response approximation (LRA) [11, 21, 23]. While the non-local response leads to spectral broadening and suppression of the scattered intensity due to the increased plasmon damping as well as size-induced LSPR shift, it predicts the same number of LSPRs supported by a given MNP when compared to the LRA [16, 17, 22].

Dielectric-metal/semiconductor or metal/semiconductor-dielectric core-shell nanostructures that are cylindrically or spherically symmetric [6, 9, 14, 19, 24,25,26] are the building blocks of MNSs—nanoshells with two or more layers [11,12,13, 15, 23, 27,28,29,30]. These nanoshells can be concentric or non-concentric depending on whether the core and shell(s) share a common centre [11, 27] or not [10, 18, 31]. Nanoshells can support one or more LSPRs in their scattering or absorption spectra depending on the material composition [12, 23, 29], sizes of the core and shells [13, 30, 32], or via geometrical symmetry-breaking [10, 18, 31]. In a MNS, each of the LSPR is either due to a bonding, an anti-bonding, or a non-bonding mode, formed due to the plasmon hybridization of the solid or cavity plasmons of the core with the nanoshell plasmons [10, 13, 27, 32].

Previously, Daneshfar and Bazyari [9] had proposed a generalized electrostatic dipole polarizability for an \(n-\)layer nanoshell that depends on the scattering coefficients of the electric fields in the core, shell, and medium regions of the nanoshell, given the material properties and sizes of the core and shells, which they used to calculate the spectral properties of a MNS with \(n=3\) shells. However, Wu and Yang [2] were the first to propose and implement a recursive algorithm for calculating the multipole optical response of an n-layered sphere in terms of the scattering coefficients of the electric and magnetic field intensities in the core, shell, and host regions of the nanoshell, based on Mie theory [8], following the works of Kerker [1]. Pal et al. [3,4,5] improved Yang’s work and have used it to predict the dipolar extinction efficiencies of a MNS with \(n=3\) layers [5]. The approach by Wu and Yang [2], Pal et al. [3,4,5], and more recent work [33,34,35,36,37] should always be the standard, especially because they account for retardation effects and multipolar response. However, in the LWA, these approaches [9, 10, 12, 14, 19]—where the dipole polarizability of the nth nanoshell is obtained from scattering coefficients—are not necessary if the polarizability of the preceding \((n-1)\)th nanoshell is known, as we will show by reproducing the usual LWA results using the proposed formula. Our model is less complicated to work with, and also very insightful, especially when it is used to predict LSPRs via the proposed Fröhlich function.

Given the electrostatic dipole polarizability of a MNP, its imaginary part is proportional to the absorption efficiency of the MNP [18, 25]. We will show that the dipole polarizability of a MNS with n shells can be calculated from the dipole polarizability of the preceding \((n-1)\)th shell and the material properties and size of the nth shell. Here, we will employ both the LWA and the LRA to predict the dipolar LSPRs and the absorption spectra of concentric MNS with n layers or shells up to \(n = 6\) shells. We will show that the formula is more straightforward to work it and that it reduces to the dipole polarizability of a spherical MNP when there are no shell(s), i.e., when \(n = 0\). We will also show that the implemented iterative algorithm for predicting the dipole polarizability of the MNS reproduces the usual LWA results by comparing our model to Mie theory-based simulations using the open source python software, scattnlay [3,4,5], as well as finite-element method-based, classical electrodynamics simulations in 3D using Comsol Multiphysics\(^{\circledR }\) [38, 39].

Theory and Simulations

Electrostatic Dipole Polarizability

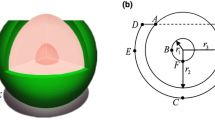
An \(x-\)polarized electric field, \(\textbf{E} = E_{0}e^{-ikz}\hat{e}_{x}\), with amplitude, \(E_{0}\), is incident on the MNS as shown in Fig. 1. The magnitude of the wavevector is \(k = 2\pi \sqrt{\epsilon _{n+1}}/\lambda\), where \(\varepsilon _{n+1}\) is the permittivity of the medium surrounding the nth shell, and \(\lambda\) is the excitation wavelength. Since \(z = r\cos \theta\), given that \(r_{n}\) is the radius of the nth shell, and \(\theta\) is the polar angle, the electric field in each region of a MNS depends on the size parameter, \(kr_{n}\), as shown in Refs. [3, 5]. However, in the LWA, this is not the case, since \(r_{n}<< \lambda\), and \(kr_{n} \longrightarrow 0\), leading to the following electrostatic dipole polarizability of a sphere (i.e., no shells, \(n = 0\)) [6, 7]:

$$\begin{aligned} \alpha _{0} = r_{0}^{3} \left( \frac{\epsilon _{0} - \epsilon _{1} }{\epsilon _{0} + 2\epsilon _{1} } \right) , \end{aligned}$$
(1)

where Eq. (1) is the dipole polarizability normalized by \(4\pi \epsilon _{1}\), and \(\epsilon _{0}\) and \(\epsilon _{1}\) are the permittivities of the sphere and the medium surrounding the sphere, respectively, and \(r_{0}\) is the sphere radius. When there is only one concentric shell (\(n = 1\)), the dipole polarizability of the nanoshell in the LWA, derived in Ref. [6], and normalized by \(4\pi \epsilon _{2}\), is obtained as

$$\begin{aligned} \alpha _{1} = r_{1}^{3} \frac{\beta _{1} }{\varrho _{1} }, \end{aligned}$$
(2)

where

$$\begin{aligned} \beta _{1}&= (\epsilon _{1} - \epsilon _{2})(\epsilon _{0} + 2\epsilon _{1}) + (r_{0}/r_{1})^{3}(\epsilon _{0} - \epsilon _{1})(\epsilon _{2} + 2\epsilon _{1}), \end{aligned}$$
(3a)
$$\begin{aligned} \varrho _{1}&= (\epsilon _{1} + 2\epsilon _{2})(\epsilon _{0} + 2\epsilon _{1}) + 2(r_{0}/r_{1})^{3}(\epsilon _{1} - \epsilon _{2})(\epsilon _{0} - \epsilon _{1}). \end{aligned}$$
(3b)
Fig. 1
figure 1

2D schematic of the model geometries of a MNS with a 5 layers and b 6 layers, in the presence of an \(x-\)polarized incident electric field, \(\textbf{E}\), propagating along the z-direction with a wavevector \(\textbf{k}\). The permittivity of the core is \(\epsilon _{0}\), that of the medium surrounding the a 5th shell is \(\epsilon _{6}\), and b 6th shell is \(\epsilon _{7}\), and \(\epsilon _{n}, n = 1, 2, 3,..., 6\), are the shell permittivities. The radius of the core is \(r_{0}\), and \(r_{n}, n = 1, 2, 3,..., 6\), are the nanoshell radii. As we will explain in detail in "Results and Discussion" section, we only consider two kinds of MNSs—in a, the core is a dielectric, and in b, the core is a metal. These are the two most common MNS configurations based on material composition, but the model is also valid when semiconductors are used

Full size image

Equation (2) can be re-written as follows:

$$\begin{aligned} \alpha _{1} = r_{1}^{3} \left( \frac{\epsilon _{1} - f_{0}\epsilon _{2} }{\epsilon _{1} + 2f_{0}\epsilon _{2} } \right) , \end{aligned}$$
(4)

where \(r_{1}\) is the nanoshell radius, \(\epsilon _{1}\) is the permittivity of the shell, \(\epsilon _{2}\) is the permittivity of the medium surrounding the shell, and

$$\begin{aligned} f_{0} = \left( 1 - \frac{\alpha _{0}}{r_{1}^{3}} \right) \left( 1 + 2 \frac{\alpha _{0}}{r_{1}^{3}} \right) ^{-1}. \end{aligned}$$
(5)

When there are two concentric shells (\(n = 2\)), the dipole polarizability of the nanoshell in the LWA, as derived in Refs. [10, 12, 40], and normalized by \(4\pi \epsilon _{3}\), is

$$\begin{aligned} \alpha _{2} = r_{2}^{3}\;\left[ \frac{\epsilon _{2} \Big (\varrho _{1} + 2(r_{1}/r_{2})^{3}\beta _{1} \Big ) - \epsilon _{3}\Big (\varrho _{1} - (r_{1}/r_{2})^{3}\beta _{1} \Big ) }{\epsilon _{2}\Big (\varrho _{1} + 2(r_{1}/r_{2})^{3}\beta _{1} \Big ) + 2\epsilon _{3}\Big (\varrho _{1} - (r_{1}/r_{2})^{3}\beta _{1} \Big ) }\right] , \end{aligned}$$
(6)

and can be re-written as follows:

$$\begin{aligned} \alpha _{2} = r_{2}^{3} \left( \frac{\epsilon _{2} - f_{1}\epsilon _{3} }{\epsilon _{2} + 2f_{1}\epsilon _{3} } \right) , \end{aligned}$$
(7)

where \(r_{2}\) is the nanoshell radius, \(\epsilon _{2}\) is the permittivity of the shell, \(\epsilon _{3}\) is the permittivity of the medium surrounding the shell, and

$$\begin{aligned} f_{1} = \left( 1 - \frac{\alpha _{1}}{r_{2}^{3}} \right) \left( 1 + 2 \frac{\alpha _{1}}{r_{2}^{3}} \right) ^{-1}. \end{aligned}$$
(8)

By inspection, there is a common pattern which \(\alpha _{1}\) and \(\alpha _{2}\) follow, and so do \(f_{0}\) and \(f_{1}\). We can utilize these patterns to obtain \(\alpha _{3}\) and \(f_{2}\) by induction, for a MNS with three concentric shells (\(n = 3\)), as follows:

$$\begin{aligned} \alpha _{3}&= r_{3}^{3} \left( \frac{\epsilon _{3} - f_{2}\epsilon _{4} }{\epsilon _{3} + 2f_{2}\epsilon _{4} } \right) , \end{aligned}$$
(9a)
$$\begin{aligned} f_{2}&= \left( 1 - \frac{\alpha _{2}}{r_{3}^{3}} \right) \left( 1 + 2 \frac{\alpha _{2}}{r_{3}^{3}} \right) ^{-1}, \end{aligned}$$
(9b)

where \(\alpha _{3}\) is the dipole polarizability of the nanoshell, \(\epsilon _{3}\) is the permittivity of the shell, \(\epsilon _{4}\) is the permittivity of the medium surrounding the shell, and \(r_{3}\) is the radius of the nanoshell. Hence, by induction, we can re-write Eqs. (9a) and (9b) for the nth shell to obtain the following:

$$\begin{aligned} \alpha _{n}&= r_{n}^{3} \left( \frac{\epsilon _{n} - f_{n-1}\epsilon _{n+1} }{\epsilon _{n} + 2f_{n-1}\epsilon _{n+1} } \right) , \end{aligned}$$
(10a)
$$\begin{aligned} f_{n-1}&= {\left\{ \begin{array}{ll} 1, &{} n = 0\\ \left( 1 - \frac{\alpha _{n-1}}{r_{n}^{3}} \right) \left( 1 + 2 \frac{\alpha _{n-1}}{r_{n}^{3}} \right) ^{-1}, &{} n \ge 1 \end{array}\right. }, \end{aligned}$$
(10b)

where \(r_{n}\) is the radius of the nth nanoshell, \(\epsilon _{n}\) is the permittivity of the nth shell, \(\epsilon _{n+1}\) is the permittivity of the medium surrounding the nth shell, \(\alpha _{n-1}\) is the normalized (normalized by \(4\pi \epsilon _{n}\)) dipole polarizability of the \((n-1)\)th shell, and \(\alpha _{n}\) is the normalized (normalized by \(4\pi \epsilon _{n+1}\)) dipole polarizability of the nth shell. An iterative algorithm proposed for calculating \(\alpha _{n}\) can be found in Algorithm 1 of the Appendix section. Although substituting \(n = 0, 1, 2,...\), in Eqs. (10a) and (10b) will reproduce \(\alpha _{0}, \alpha _{1}, \alpha _{2},...\), we now need to use these equations to calculate the spectral properties of a given MNS and compare our results to simulations, in order to ascertain their validity. One such property is absorption. In the LWA, the absorption efficiency of a MNS in the presence of an incident electric field can be calculated using the equation [6, 10, 12, 16]:

$$\begin{aligned} Q_{abs} = \frac{k\Im [4\pi \epsilon _{n+1} \alpha _{n} ]}{\pi r_{n}^{2}}. \end{aligned}$$
(11)

The Fröhlich Function

Given a MNP with a certain polarizability, the Fröhlich condition [6, 7, 19] states that the LSPRs supported by the MNP are the poles of the polarizability. In other words, the LSPRs correspond to frequencies where the real part of the denominator of the polarizability vanishes. Let us call this real part of the denominator of the polarizability of the Fröhlich function. Starting with Eq. (2), the dipole polarizability of a spherical nanoshell with \(n = 1\), the denominator of \(\alpha _{1}\) simplifies to the following:

$$\begin{aligned} D[ \alpha _{1} ] =&\; \epsilon _{1}\left[ (\epsilon _{0} + 2\epsilon _{1}) + 2(r_{0}/r_{1})^{3}(\epsilon _{0} - \epsilon _{1}) \right] \\&+ 2 \left[ (\epsilon _{0} + 2\epsilon _{1})- (r_{0}/r_{1})^{3}(\epsilon _{0} - \epsilon _{1}) \right] \epsilon _{2}. \end{aligned}$$
(12)

We can re-write Eq. (12) as follows:

$$\begin{aligned} D[ \alpha _{1} ] = \epsilon _{1}D_{1}^{r} + 2 N_{1}^{r} \epsilon _{2}. \end{aligned}$$
(13)

with

$$\begin{aligned} D_{1}^{r}&= D_{0} + 2N_{0}/r_{1}^{3}, \end{aligned}$$
(14a)
$$\begin{aligned} N_{1}^{r}&= D_{0} - N_{0}/r_{1}^{3}, \end{aligned}$$
(14b)

and

$$\begin{aligned} D_{0}&= \epsilon _{0} + 2\epsilon _{1}, \end{aligned}$$
(15a)
$$\begin{aligned} N_{0}&= r_{0}^{3}(\epsilon _{0} - \epsilon _{1}), \end{aligned}$$
(15b)

so that the Fröhlich function for the \(n=1\) nanoshell is:

$$\begin{aligned} \mathcal {F}_{1} = \Re [ \epsilon _{1}D_{1}^{r} + 2 N_{1}^{r} \epsilon _{2} ]. \end{aligned}$$
(16)

For the MNS with \(n = 2\), the denominator of \(\alpha _{2}\) given in Eq. (6) simplifies to the following:

$$\begin{aligned} D[ \alpha _{2} ] = \epsilon _{2}[D_{1} + 2N_{1}/r_{1}^{3} ] + 2[D_{1} - N_{1}/r_{1}^{3} ] \epsilon _{3}, \end{aligned}$$
(17)

with

$$\begin{aligned} N_{1}&= r_{1}^{3} \beta _{1}, \end{aligned}$$
(18a)
$$\begin{aligned} D_{1}&= \varrho _{1}. \end{aligned}$$
(18b)

We can re-write Eqs. (18a) and (18b) in terms of \(N_{0}\) and \(D_{0}\) to obtain the following:

$$\begin{aligned} D_{1}&= \epsilon _{1}(D_{0} + 2N_{0}/r_{1}^{3}) + (D_{0} - N_{0}/r_{1}^{3})\epsilon _{2} = \epsilon _{1}D_{1}^{r} + N_{1}^{r}\epsilon _{2} , \end{aligned}$$
(19a)
$$\begin{aligned} N_{1}&= r_{1}^{3}[\epsilon _{1}(D_{0} + 2N_{0}/r_{1}^{3}) - (D_{0} - N_{0}/r_{1}^{3})\epsilon _{2}] = r_{1}^{3}[\epsilon _{1}D_{1}^{r} - N_{1}^{r}\epsilon _{2}], \end{aligned}$$
(19b)

so that with \(D_{2}^{r} = D_{1} + 2N_{1}/r_{1}^{3}\) and \(N_{2}^{r} = D_{1} - N_{1}/r_{1}^{3}\), we obtain the Fröhlich function for the \(n=2\) nanoshell:

$$\begin{aligned} \mathcal {F}_{2} = \Re [ \epsilon _{2}D_{2}^{r} + 2 N_{2}^{r} \epsilon _{3} ]. \end{aligned}$$
(20)

Hence, by induction, the Fröhlich function for the nth shell is as follows:

$$\begin{aligned} \mathcal {F}_{n} = \Re [ \epsilon _{n}D^{r}_{n} + 2N^{r}_{n}\epsilon _{n+1} ]. \end{aligned}$$
(21)

In Eq. (21),

$$\begin{aligned} D^{r}_{n}&= {\left\{ \begin{array}{ll} 1, &{} n = 0\\ D_{n-1} + 2\frac{N_{n-1}}{r_{n}^{3}} , &{} n \ge 1 \end{array}\right. },\end{aligned}$$
(22a)
$$\begin{aligned} N^{r}_{n}&= {\left\{ \begin{array}{ll} 1, &{} n = 0\\ D_{n-1} - \frac{N_{n-1}}{r_{n}^{3}} , &{} n \ge 1 \end{array}\right. }, \end{aligned}$$
(22b)

where, for \(n \ge 0\),

$$\begin{aligned} D_{n}&= \epsilon _{n}D^{r}_{n} + 2N^{r}_{n}\epsilon _{n+1} ,\end{aligned}$$
(23a)
$$\begin{aligned} N_{n}&= r_{n}^{3}(\epsilon _{n}D^{r}_{n} -N^{r}_{n}\epsilon _{n+1}) . \end{aligned}$$
(23b)

The zeroes of the Fröhlich function for the nth shell, i.e., frequencies (or excitation wavelengths) where \(\mathcal {F}_{n} = 0\), correspond to the LSPRs supported by the MNS. An iterative algorithm proposed for calculating \(\mathcal {F}_{n}\) can be found in Algorithm 2 of the Appendix section.

Simulations

The first set of simulations were based on the finite-element method (FEM). These FEM-based simulations were performed in the Wave Optics module of COMSOL Multiphysics\(^{\circledR }\) software [38] using a spherically symmetric perfectly matched layer (PML) and scattering boundary conditions applied in the internal PML surface. An \(x-\)polarized incident electric field, as described earlier, was applied to the MNS. The absorption efficiency of the nanoshell is calculated through the following expression [10, 39]:

$$\begin{aligned} Q_{abs} = \frac{1}{P_{0}A} {\int \!\!\!\int \!\!\!\int } P_{diss}dV . \end{aligned}$$
(24)

The integral in Eq. (24) is a volume integral of the total power dissipation density of the nanoshell, \(P_{diss}\), where \(P_{0}\) is the power density of the incident electric field, and A is the area of the nanoshell obtained from a surface integral over the nanoshell surface [39].

In the second set of simulations, we used scattnlay [5]—an open source code for investigating the scattering of electromagnetic radiation by a multilayered sphere—developed by Pal et al. [3,4,5] based on Mie theory (MT) [1, 6, 8]. In these MT-based simulations, the absorption efficiency of a given MNS is calculated from the extinction efficiency, \(Q_{ext}\), and the scattering efficiency, \(Q_{sca}\), using the following equation [3]:

$$\begin{aligned} Q_{abs} = Q_{ext} - Q_{sca}, \end{aligned}$$
(25)

where [3, 4]

$$\begin{aligned} Q_{ext}&= \frac{2}{x^{2}_{n}}\sum _{l=1}^{\infty }(2l+1)\Re \Big (a_{l} +b_{l}\Big ) , \end{aligned}$$
(26a)
$$\begin{aligned} Q_{sca}&= \frac{2}{x^{2}_{n}}\sum _{l=1}^{\infty }(2l+1)\Big (|a_{l}|^{2} +|b_{l}|^{2}\Big ) . \end{aligned}$$
(26b)

In Eqs. (26a) and (26b), \(l = 1, 2,3,...\) is an angular momentum number, denoting the number of multipoles over which the summation is done, \(a_{l}\) and \(b_{l}\) are scattering coefficients, and \(x_{n}\) is the size parameter of the nth layer [3].

As an example, we investigated nanoshells containing only one type of metal as well as one type of dielectric, as illustrated in Fig. 1. To account for both intra- and inter-band electron damping in the metal, we used the Drude-Lorentz model for the permittivity of metals, given in Ref. [41] as follows:

$$\begin{aligned} \varepsilon (\omega ) = \varepsilon _{\infty } - f_{0}\frac{\omega ^{2}_{0}}{\omega (\omega -i\gamma _{0})} +\sum _{s=1}^{5}f_{s}\frac{\omega ^{2}_{0}}{\omega ^{2}_{s}-\omega ^{2}+i\omega \gamma _{s}}, \end{aligned}$$
(27)

where \(\varepsilon (\omega )\) in the case of Fig. 1 is the permittivity of the metallic core (or shell), \(\omega\) is the frequency of the incident field, \(\varepsilon _{\infty }\) is the high-frequency permittivity of the positive ion core in the metal, \(f_{0}, \omega _{0}\), and \(\gamma _{0}\) are the oscillator strength, plasma frequency, and damping rate of the intra-band electrons in the metal, respectively, and s is the number of Lorentz oscillators with oscillator strength \(f_{s}\), damping rate \(\gamma _{s}\), and frequency \(\omega _{s}\), associated with inter-band electrons in the metal. The values of these parameters for the most common metals used in plasmonics are given in Ref. [41].

Table 1 List of the nanoshell configurations we investigated. The letter “D" stands for dielectric and “M" stands for metal. The starting configurations differ, but we have kept the motif uniform. For the nanoshells in Fig. 1a, the number of layers, n, is odd, i.e., \(n = 1, 3, 5\), while for the nanoshells in Fig. 1b, the number of layers, n, is even, i.e., \(n = 2, 4, 6\)
Full size table

Results and Discussion

Table 1 shows the material compositions of the MNS we investigated using the proposed dipole polarizability formula. Here, we will consider glass, with a permittivity of 2.25 as the dielectric as well as the medium surrounding the outermost nanoshell, and gold, modelled with the Drude-Lorentz parameters given in Ref. [41], as the metal. We chose to use only two materials for simplicity and ease of analysis of the results, but the formula is also valid when different material compositions are used. The radius of the core of the nanoshell in each of the nanoshell configurations in Table 1 (or in Fig. 1) is kept constant at 15 nm. The shells were modelled as equidistant shells, each of thickness, 5 nm.

Absorption Spectra

Using the MT-based results as the benchmark—since it is based on exact multipole expansion of the field intensities in the core, shell, and host mediums of the nanoshell—the usual limitations of the LWA, i.e., under-prediction of the absorption efficiencies (and other efficiency factors [16]) and under-prediction of the LSPR shift [16, 17] (less redshift), can be seen in Fig. 2. However, in the MNS configurations in Fig. 2, the LWA does not under-predict all the absorption peaks—it appears that one of the absorption peaks is always in good agreement with the MT-based simulations. For instance, as can be seen in Fig. 2, their absorption peaks are comparable at 693 nm (for \(n=1\)), 644 nm (for \(n=3\)), and 628 nm (for \(n=5\)), for the MNS with a dielectric core, and at 958 nm (for \(n=2\)), 835 nm (for \(n=4\)), and 784 nm (for \(n=6\)), for the MNS with a metallic core—under-going a blueshift as the number of shells increases. The FEM-based simulations also follow a similar trend as the LWA except that it over-predicts some of the absorption peaks. Though the most redshifted peaks (Fig. 2e and f) are more suppressed in the MT-based results, the number of peaks is always the same when compared to the LWA results, unlike the FEM-based simulations, showing that the LWA model is in good agreement with the MT-based simulations.

Fig. 2
figure 2

Normalized absorption efficiencies (normalized by the maximum value of \(Q_{abs}\) in each data set) of the MNS. Nanoshells with a \(n = 1\), b \(n = 2\), c \(n = 3\), d \(n = 4\), e \(n = 5\), and f \(n = 6\). Our approach (via LWA): red curves. COMSOL Multiphysics (via FEM): blueviolet curves. scattnlay (via MT): green curves

Full size image

On the other hand, when compared to the MT-based simulations, the FEM-based simulations are very accurate in predicting the LSPR shift, as shown by the agreement in the wavelengths corresponding to the absorption peaks in Fig. 2. This is because the FEM-based simulations account for phase retardation effects between oscillating modes of the scattered fields in the MNP [39]. We therefore attribute the under-prediction of the LSPRs by the LWA to mostly retardation effects. The difference in the absorption peaks of the FEM-based and MT-based simulations most likely stems from the approximation of the spherical Bessel functions in the former while the latter uses the exact functions. It is likely that these approximations accumulate as the number of shells increases causing a noticeable discrepancy between the two simulations. The accuracy of the FEM-based simulations depends largely on the properties of the mesh elements used as well as on the PML features, so that in principle, the simulation can be improved. However, this work is the first to compare comsol multiphysics and scattnlay simulations, using MNSs as the target nanostructure, to the best of our knowledge.

As we will show in "Plasmon Resonances" section using near-field intensity plots, the LSPRs in Fig. 2 (green curves) all have a dipole character, which means that their origin is most likely to have been dominated by dipolar modes, due to the small particle size of the nanoshells we studied. In addition, Eq. (10a), which we used to calculate the absorption spectra of the MNS in Fig. 2 (red curves), is a dipole polarizability. Thus, the LSPRs in the LWA spectra are all due to dipole hybridization between the core and shell plasmons of the MNS. Hence, in the LWA, these LSPRs all have a dipole character.

A noticeable difference between the absorption spectra of the nanoshells with a dielectric core (Fig. 2a, c, and e with \(n = 1,3\), and 5, respectively) and those with a metallic core (Fig. 2b, d, and f, with \(n = 2, 4\), and 6, respectively) is the enhancement versus suppression of the leading absorption peak. This can be attributed to the presence of cavity plasmons in the core (in the case of Fig. 2a, c, and e) and solid plasmons in the core (in the case of Fig. 2b, d, and f). In the MNS in Fig. 2a, c, and e, hybridization of the cavity plasmons of the core with the solid plasmon of the innermost shell results in the formation of the leading LSPR, while in the MNS in Fig. 2b, d, and f, the solid plasmons of the core hybridize with the cavity plasmon of the innermost shell to form the leading LSPR. Previous studies have reported similar trends for \(n = 2\) [4, 10] and \(n = 3\) [4, 9]. As we will discuss in the next section, any one of the LSPRs supported by the MNS is either due to a bonding mode, an anti-bonding mode, or a non-bonding mode [25, 42,43,44].

Plasmon Resonances

The LSPRs supported by the nth nanoshell can be further investigated using graphical solutions of the Fröhlich function given in Eq. (21). Electric field enhancement plots produced from simulations in scattnlay [5] reveal the hybridized nature of these LSPRs, in agreement with plasmon hybridization theory (PHT) [42]. We will also characterize the LSPRs as either due to a bonding, an anti-bonding, or a non-bonding dipole mode, using the behaviour of the electric field distributions in the core and shell regions of the MNS.

Figure 3a shows the plasmon spectrum of the MNS produced by plotting the Fröhlich function. There are more LSPRs located at shorter wavelengths (between 400 and 1200 nm) than at longer wavelengths (between 1200 and 2400 nm), which can be attributed to particle size effects. The number of LSPRs increases with an increase in the number of metallic shells in the MNS. This is due to an increase in the number of wavelength-dependent permittivity terms in the polarizability. Also, the spacing between the LSPRs increases as the number of shells increases. For \(n=1, 2\), and \(n=4\), the number of LSPRs predicted by the Fröhlich function agrees with the absorption spectra (Fig. 2a, b, and d, respectively). However, for \(n = 3, 5\), and 6, respectively, the Fröhlich function predicts an extra LSPR in each case compared to the absorption spectra (Fig. 2c, e, and f, respectively). This is most likely due to the dipole moment of the extra LSPR being too weak to contribute to the absorption spectra in Fig. 2, making it appear invisible in the spectra. According to Fig. 3a and b, the extra LSPR is located at a shorter wavelength than the leading LSPR in the absorption spectra in Fig. 2c, e, and f, respectively.

Fig. 3
figure 3

a A plot of the Fröhlich function showing the plasmon spectrum of the MNSs. The LSPRs correspond to wavelengths at which \(\mathcal {F}_{n}(\lambda ) = 0\). The Fröhlich function is either an n degree polynomial or an \((n-1)\) degree polynomial in \(\lambda\). The plot has been zoomed in to show only the parts of the polynomials that pass through \(\mathcal {F}_{n}(\lambda ) = 0\). b Natural logarithm of the Fröhlich function, \(\ln [\mathcal {F}_{n}(\lambda )]\), showing a more detailed version of the plasmon spectrum of the MNSs. The paired and/or unpaired LSPRs are respectively due to the convex and/or concave curves in the Fröhlich function of each MNS

Full size image

The \(n = 1\) nanoshell supports two LSPRs—a bonding dipole (BD) LSPR and an anti-bonding dipole (ABD) LSPR, according to PHT [42, 25]. The BD LSPR (\(\omega _{-}\)) is a longer-wavelength mode formed due to the symmetric coupling between solid sphere plasmons of the shell and cavity sphere plasmons of the core while the ABD LSPR (\(\omega _{+}\)) is a shorter-wavelength mode formed as a result of anti-symmetric coupling between cavity sphere plasmons of the core and the solid sphere plasmons of the shell. In the BD mode, solid plasmons contribute more than cavity plasmons while the opposite is the case in the ABD mode [25]. However, the dipole moment of the ABD mode is very weak, and therefore, it can only be visible in spectral calculations when inter-band damping is ignored [25, 43], which is not the case in this work. Figure 4a shows that the LSPR at 685 nm is the BD mode since the incident electric field experiences the most enhancement outside the nanoshell in contrary to the ABD mode, where the electric field has been shown to be more enhanced inside the nanoshell (see Ref. [43], Fig. 1). Hence, the LSPR in Fig. 3 (red line/curve), for \(n = 1\), is a BD mode.

The \(n=2\) nanoshell supports three LSPRs—a BD LSPR, an ABD LSPR, and a non-bonding dipole (NBD) LSPR [27, 44]. The NBD LSPR (\(\omega _{+}^{-}\)) is a short-wavelength mode formed by symmetric coupling between the solid sphere plasmon of the core and the ABD mode (\(\omega _{+}\)) of the nanoshell. Due to its weak dipole moment, it is only visible in the spectra of silver nanoshells [29], where plasmon damping is significantly lower, or in the absence of inter-band effects. Hence, in our case, the two LSPRs supported by the \(n=2\) MNS, as shown in Fig. 3, are an ABD mode (\(\omega _{-}^{+}\)) and a BD mode (\(\omega _{-}^{-}\)). The longer wavelength, BD (\(\omega _{-}^{-}\)) mode, is due to anti-symmetric coupling between the BD (\(\omega _{-}\)) nanoshell plasmon and the solid sphere plasmon of the core, while the shorter wavelength, ABD (\(\omega _{-}^{+}\)) mode, is due to symmetric coupling between the BD (\(\omega _{-}\)) nanoshell plasmon and the solid sphere plasmon of the core [27, 29, 44]. As shown in Fig. 4b, for \(n = 2\), the enhanced electric field is situated entirely in the dielectric shell at 952 nm (the BD mode) compared to the electric field distribution at 548 nm (the ABD mode), in agreement with previous work [44].

Fig. 4
figure 4

Contour plots of the electric field enhancement, \(|\textrm{E}|/|\textrm{E}_{0}|\), inside and outside the MNS, in the xy-plane, using scattnlay [3, 5], where \(|\textrm{E}|\) is the magnitude of the incident and scattered fields and \(|\textrm{E}_{0}|\) is the magnitude of the incident field. The contour plots were obtained at the LSPRs supported by each MNS in the LWA via the Fröhlich function: a \(n = 1\), b \(n=2\), c \(n = 3\), d \(n=4\), e \(n=5\), and f \(n=6\). These LSPRs are indicated (in nm units) in the core of each nanoshell

Full size image

In Fig. 3b, a plot of the natural logarithm of the Fröhlich function is shown. Here, the positions of the LSPRs are much more visible, and the plot also reveals an intricate detail about the plasmonic behaviour of the LSPRs—the pairing of certain LSPRs beyond \(n=1\) due to the convex curves in the Fröhlich function. We propose that this pairing behaviour can be used in determining whether a given LSPR supported by the MNS has a BD or an ABD character. For instance, when \(n=2\), we have the blueviolet curve in Fig. 3b which contains a pair of LSPRs corresponding to an ABD mode at 548 nm and a BD mode at 952 nm, in agreement with Fig. 2b. However, we will use the rest of this section to show that any given pair of LSPRs in the Fröhlich function does not always consist of an ABD and a BD mode. On the other hand, subsequent analysis of the unpaired LSPRs shows that a shorter-wavelength LSPR (the leftmost LSPR in the Fröhlich function) that does not participate in the pairing behaviour is always an ABD mode, while a longer-wavelength LSPR (the rightmost LSPR in the Fröhlich function) that does not form a pair has a BD character. These results are summarized in Table 2.

To support the above claim, consider the rest of the electric field intensity plots shown in Fig. 4c–f. The \(n=3\) MNS supports up to four LSPRs in the absence of inter-band damping in gold, according to PHT [25]. These LSPRs are formed as a result of hybridization between the inner- and outer-nanoshell BD and ABD modes. They include \(\omega _{-}^{-}\), a BD mode due to symmetric coupling between the inner- and outer-nanoshell BD modes; \(\omega _{-}^{+}\), an ABD mode due to anti-symmetric coupling between the inner- and outer-nanoshell BD modes; \(\omega _{+}^{-}\), a NBD mode due to anti-symmetric coupling between the inner- and outer-nanoshell ABD modes; and \(\omega _{+}^{+}\), a NBD mode due to anti-symmetric coupling between the inner- and outer-nanoshell ABD modes. The dipole moment of the \(\omega _{+}^{+}\) mode is very weak, and thus, it can only be visualized with a Drude model for gold. Likewise, the \(\omega _{+}^{-}\) mode is also a dark mode, since its contribution is not visible in the absorption spectra in Fig. 2c, but it does appear in the Fröhlich function at 482 nm (green line/curve in Fig. 3). The weak dipole moment explanation for the absence of \(\omega _{+}^{-}\) (NBD) mode in Fig. 2c is also supported by Fig. 4c, where the electric field is weakly distributed in the core and inside the second shell at 482 nm. On the other hand, the \(\omega _{-}^{+}\) and \(\omega _{-}^{-}\) modes are visible in Fig. 2c due to their large dipole moments. This gave rise to the electric field distributions shown in Fig. 4c, where at 637 nm, the electric field is distributed in both the dielectric core and metallic shells, compared to the field distribution at 1227 nm, where the field is only enhanced inside one of the dielectric shells. Therefore, compared to Fig. 3 (green curve), we have a LSPR pair corresponding to an ABD mode at 482 nm and another ABD mode at 637 nm, as well as a rightmost LSPR corresponding to the BD mode at 1227 nm.

To characterize the rest of the LSPRs in Figs. 2 and 3, we utilized the electric field enhancement plots in Fig. 4d–f. Using the same analogy as above, for \(n = 4\) (Fig. 4d), we assigned the LSPRs at both 823 nm and 1530 nm a BD character, since the enhanced electric field is mostly distributed in the dielectric shells, i.e., the electric field enhancements in the metallic regions are negligible compared to the LSPR at 560 nm, which we assigned an ABD character. Thus, for \(n=5\), the LSPRs at both 1050 nm and 1830 nm were assigned a BD character while the LSPRs at both 506 nm and 623 nm, where some significant field enhancement exists in the metallic regions, were assigned an ABD character. Similarly, for \(n=6\), the LSPRs at 767 nm, 1295 nm, and 2204 nm were assigned a BD character, while those at both 483 nm and 571 nm were assigned an ABD character. As shown in Table 2, a LSPR pair located in the short-wavelength region of the plasmon spectrum is most likely an ABD-ABD pair, while a pair located in the long-wavelength region consists of a BD-BD pair. However, a LSPR pair in between the short- and long-wavelength regions is most likely an ABD-BD pair.

Table 2 List of the nanoshell configurations we investigated and the LSPRs they support, according to the Fröhlich function. Here, “  – ” stands for a LSPR pair in the plasmon spectrum
Full size table

Conclusion

The dipole polarizability formula we have proposed for spherical MNSs is straightforward to implement. It is an alternative for obtaining the dipole polarizability of MNSs in the LWA without going through the conventional approach based on scattering coefficients. The formula works well especially when used to predict the LSPRs supported by a MNS via the proposed Fröhlich function. We have shown that the LSPRs correspond to the zeroes of the Fröhlich function for the nth shell and that a pairing behaviour by some of the LSPRs identified in the Fröhlich function might be useful for mode characterization. However, we maintain that it is an approximate formula strictly valid in the LWA and should not be used otherwise. The limit of validity of the formula was revealed by comparison with numerical simulations, showing that it reproduces the usual LWA results. Therefore, for the analytical modelling of the optical response of MNSs, the proposed formula is neither meant to replace the standard non-LWA approaches nor to eliminate the limitations of the LWA, but rather to highlight its simplicity and applicability when compared to conventional LWA.