Abstract
The surface plasmon resonances of silver nanoshell particles are studied by Green’s function. The nanoshell system of plasmon resonances results from the coupling of the inner and outer shell surface plasmon. The shift of the nanoshell plasmon resonances wavelength is plotted against with different dielectric environments, several different dielectric cores, the ratio of the inner and outer radius, and also its assemblies. The results show that a red- and blue-shifted localized surface plasmon can be tuned over an extended wavelength range by varying dielectric environments, the dielectric constants and the radius of nanoshell core respectively. In addition, the separation distances, the distribution of electrical field intensity, the incident directions and its polarizations are also investigated. The study is useful to broaden the application scopes of Raman spectroscopy and nano-optics.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Due to the quantum size and surface effects, noble metal nanoparticles have different optical, electromagnetic and chemical properties from bulk materials [1–4]. The intense optical absorption and scattering effects induced by surface plasmon resonances have attracted particularly strong study in recent years [5–7]. Plasmon resonances are electromagnetic modes associated with the excitation of collective oscillations of the electronic charge density in metals. When plasmon is under certain electromagnetic disturbance, according to metallic electrical theory, charge density may not be zero in some regions, and a restoring force will be generated to induce oscillating charge distribution [8]. When frequencies of the electromagnetic disturbance and the plasmon oscillation match each other, resonance will happen. The oscillation frequency is determined by four factors: the density of electrons, the electron mass, the size and the shape of the charge distribution. The metal surface plasmon resonances is the main factor in determining the optical properties of metal nanoparticles. Many unique optical properties can be achieved when adjusting the structure, morphology, size, nanoshell and composition of the metal nanoparticles [9–16]. Consequently, manufacturing and application of metallic nanoparticles have become very active topics in materials science. Furthermore, the strong optical field generated in these systems could be used in surface enhancement Raman scattering [17, 18], devise new configuration for chemical and material science [19, 20]. As all these devices are strongly sensitive to the light frequency, it could be interesting to dispose tunable nanoparticles to modify their frequency range.
This paper is organized as follows. In Section Theoretical Background and Numerical Method, we describe our numerical simulation method based on Green’s function. In Section Numerical Simulation: Results and Analysis, we present spectrum calculations for silver nanoshell particles in different dielectric environments, the ratio of the inner and outer radius, its assemblies, the separation distances, the distribution of electrical field intensity, the incident directions and also its polarizations. In Section Conclusions, we summarize our study.
Theoretical Background and Numerical Method
Generally, there are some numerical simulation methods to study the interaction between the light and metal spheres such as FDTD (Finite-difference Time-domain) [21], FEM (Finite Element Method) [22], DDA (Discrete-dipole Approximation) [23] and Green’s function [24] or called CDA (Coupled-dipole Approximation) [25]. In this paper, Green’s function is used to study the optical properties of silver nanoshell particles. First, let’s briefly outline the main features of the theoretical scattering formalism with the Green’s function on which the numerical simulation is based and associated numerical method. Given a scattering object with a dielectric function \(\varepsilon_{s}(\textbf{\textit{r}},\omega)\) embedded in an infinitely homogenous background medium with a dielectric parameter of \(\varepsilon_{m}(\textbf{\textit{r}},\omega)\), we can assume that the electric and magnetic fields have a harmonic time dependence exp( − iω t) in Maxwell’s equations. When this system is illuminated by an incident field in the background medium, the vectorial wave equation for electric field can be expressed as:
Where ε s and ε m are the scattering dielectric constant and system dielectric constant respectively, and k 0 is the wave number in vacuum.
The method of solving scattering field is based on the Lippmann-Schwinger equation \(\textbf{\textit{E}}=\textbf{\textit{E}}_{inc}+\textbf{\textit{E}}_{s}\), where \(\textbf{\textit{E}}_{inc}\) and \(\textbf{\textit{E}}_{s}\) are the incident field and the scattering field respectively. Taking the Dirac delta function into account, Eq. 1 can be resolved to the following three-dimension vector Lippmann-Schwinger integral equation:
\(\textbf{\textit{G}}_{0}(\textbf{\textit{r}},\textbf{\textit{r}}',\omega)\) is the Green’s tensor for an infinitely homogeneous background medium ε m , which is expressed as:
Where \(\textbf{\textit{I}}\) is the unit dyadic, \(\textbf{\textit{R}}=\textbf{\textit{r}}-\textbf{\textit{r}}'\), \(R=|\textbf{\textit{r}}-\textbf{\textit{r}}'|\) and \(\Delta\varepsilon(\textbf{\textit{r}}',\omega)=\varepsilon_{s}-\varepsilon_{m}\). There is a singularity in Eq. 2 when \(\textbf{\textit{r}}=\textbf{\textit{r}}'\), which have been solved by Yaghjian in detail [26]. The implicit Eq. 2 can be solved via numerical simulation based on discretization, which results in:
V j is the volume of the scattering particle. Since the scalar Green’s tensor is dependent only on the absolute relative distance \(\textbf{\textit{R}}\), and is reciprocal, i.e., \(\textbf{\textit{G}}(\textbf{\textit{r}}_{i},\textbf{\textit{r}}_{j}) =\textbf{\textit{G}}(\textbf{\textit{r}}_{j},\textbf{\textit{r}}_{i})\), or written as \(\textbf{\textit{G}}(\textbf{\textit{r}}_{i},\textbf{\textit{r}}_{j})=\textbf{\textit{G}}_{i-j}\). We can generate the following equation by substituting \(\textbf{\textit{G}}(\textbf{\textit{r}}_{i},\textbf{\textit{r}}_{j})=\textbf{\textit{G}}_{i-j}\) into Eq. 4 and rearranging terms:
\(\textbf{\textit{E}}_{j}\) and \(\textbf{\textit{E}}_{inc}\) are 3N-dimensional vector, while \(\textbf{\textit{G}}_{i-j}\) is a 3N×3N matrix. The total electric field can be derived, along with spectral and optical parameters, after solving these 3N complex linear equations. The researchers could obtain magnetic field \(\textbf{\textit{H}}\) and Poynting vector \(\textbf{\textit{S}}\) with the similar method [27]. The optical efficiencies [28] (i.e., extinction cross section, absorption cross section and scattering cross section) are defined as:
Where * means complex conjugate, \(\textbf{\textit{P}}_{i}=\alpha_{i}\cdot\textbf{\textit{E}}_{loc}\), \(\textbf{\textit{E}}_{loc}=[(\varepsilon_{s}+2\varepsilon_{m})/3]\textbf{\textit{E}}\) with \(\alpha_{i}=\frac{(\varepsilon_{s}(\textbf{\textit{r}}_{i},\omega)-\varepsilon_{m}(\textbf{\textit{r}}_{i},\omega))} {(\varepsilon_{s}(\textbf{\textit{r}}_{i},\omega)+2\varepsilon_{m}(\textbf{\textit{r}}_{i},\omega))}\frac{3V}{4\pi}\), and scattering cross section can be obtained by C sca = C ext − C abs . The extinction and absorption efficiency are Q ext = C ext /S and Q sca = C sca /S respectively, S is the effective area of scattering particles.
In order to achieve desired simulation accuracy, it is necessary to use a large number of dipoles, to model features properly with the Green’s function. In this paper, depending on the error in the calculation for silver nanoshell particles, the cube size of each dipole is lesser than 1.5 nm, and the number of dipoles (N) is between 1.7×104 and 5.8×104. For the linear equations Eq. 5, we could solve them effectively with CCGM (Complex-conjugate Gradient Method) [29]. But during each iterative process, the product between the matrix and the vector is very time consuming. Thanks to the product which satisfies the convulsion, we can use FFT (Fast Fourier Transform Algorithm) to accelerate it [30]. Our results confirm that CPU run time with FFT method is reduced significantly comparing to case without FFT [31].
Numerical Simulation: Results and Analysis
In this section, the optical properties of silver nanoshell particles are studied, the numerical simulation system is given in Fig. 1. The optical constants for silver are taken from reference [32]. Spectroscopic effects occur when the dielectric response of the particles shows a strong dispersion as a function of the incident wavelength. It is well known that the dielectric response of metals displays this behavior which is associated with the phenomenon of local plasmon resonances of small metallic particles for the variation wavelengths. The physical and chemical properties of metallic nanoshell have been studied in recent years due to their attractive features which make them used in nanoscale optical regions [33–36].
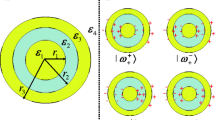
Numerical simulation system, where yellow one denotes silver, while blue one is dielectric, R is radius (R1 and R2 are inner and outer radius) and gap denotes separation gap, \(\textbf{\textit{K}}\) is incident wave propagate direction. a, b, c and d denote a solid silver sphere, a dielectric core-silver shell, a silver core-dielectric shell and two interacted silver nano-shell spheres respectively.
Firstly, to get resonance behaviors, the influences of the mediums surrounding to the extinction efficiency of a solid silver sphere are studied with radius 25 nm (see Fig. 1 case of a, R = 25 nm) as a function of the incident wavelength by plane wave. Spectroscopes are given with infinite homogeneous medium in vacuum (n = 1.00), water (n = 1.33) and SiO2 (n = 1.50) respectively. We can see an increase intensity which is materialized by a peak in its variation with the incident wavelength at about λ = 370 nm in vacuum, λ = 400 nm in water and λ = 410 nm in SiO2. The peak in SiO2 is shifted to higher wavelength and broader width compared with silver sphere in vacuum and water, which can be seen in Fig. 2. The peak corresponding to the localized plasmon resonance depended on the refractive index of the surround medium [8]. The influences of the surround mediums are agree with DDA (Discrete-dipole Approximation) simulation by Pileni [37], who gave an interesting equation to calculate the new position of plasmon resonance for the particle in new medium, it is:
Where λ 0 is the common point of all the spectra calculated, i.e. the minimum corresponds to the wavelength at which the dielectric constant of silver, both the real and imaginary parts almost vanish. λ 1 is the wavelength position of a resonance peak for the particle embedded in a medium with refractive index n 1 , and λ 2 the new position of plasmon resonance for the particle in a new medium n 2. We can use this formulation to calculate the corresponding peak’s position in new medium. It is worth noticing that Eq. 7 is only valid for the usual solvent media and not suitable for absorbing one where charge transfer should be taken into account in the plasmon bands shift. Considering the cures of Fig. 2, we can observe that all the efficiencies have a local minimum at about 315 nm; moreover, its spectral feature is inherent to the silver materials, independent to the particle geometries [8, 17, 18].
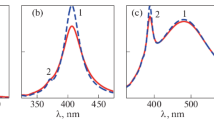
Secondly, in a system that consist of a dielectric core-silver shell nanoparticle is considered with inner and outer radius 15 nm and 25 nm respectively (see Fig. 1 case of b, R1 = 15 nm and R2 = 25 nm). We compare the extinction efficiency of a solid silver sphere (see Fig. 1 case of a) with the different dielectric cores-silver shell (see Fig. 1 case of b), a core filled with the refractive index n = 1.00, 1.33, 1.50 and 1.75 respectively, which are illuminated by plane wave. It shows that increasing the value of refraction cores results in a longer red-shifted and narrower width of peak, which are good agreement with experiments [38–40]. Figure 3 shows that the peak’s position shifts from 370 nm for a solid sphere to 440 nm for dielectric core with n = 1.75. It is interesting to find out that there is only one single peak for both a solid silver sphere and dielectric core with n = 1.00; while a second or more smaller peak for dielectric core with n>1 modes. This is due to the symmetries of the charge distributions for dielectric core-silver shell nanoparticles [41–42]. The dipole and quadrupolar (or higher-order) resonance of the nanoshell particles could be used to explain the phenomenon of this system. The dipole moments of the inner and outer surfaces are arranged. A stronger coupling effect could be gotten when dielectric core-silver shell is much smaller compared with the nanoparticle radius, it will lead to a new scheme of polarization and result in a thin metallic layer, which could be described as symmetric and asymmetric modes. For case with n = 1.00, the mode is air-silver-air, which is very symmetric, while for another three modes n > 1, the geometry for silver film is asymmetric, i.e. dielectric-silver-air, there will be two independent single-interface modes and not any mode-splitting phenomenon. The nanoshell structure is reconciled with the plasmon hybridization model, which was developed by Halas [19] for explaining of the physical origin of the tunable plasmon resonance in metal nanoshells. The nanoshell is a two-surface system, which gets two distinct plasmon modes: an inner shell-surface and an outer shell-surface mode, which couple or hybridize with each other, result in splitting into more new modes. In addition, there are two quadrupolar modes, one is at about 340 nm and does not change with dielectric constants of dielectric-core; the other is at about 450 nm with n = 1.33, which seems to liner red-shift with increasing the constants of dielectric core.
On the other hand, the outer shell coated by different dielectric value with silver core (see Fig. 1 case of c) is also considered, and the corresponding parameters are the same as the above mode, i.e. the inner and outer radius are 15 nm and 25 nm respectively. We can see that increasing the value of dielectric shell results in a higher red-shifted in Fig. 4, which is similar to the case of dielectric core-silver shell. And a trend to the broader width of peak with increasing the dielectric constant in shell [39, 40], which is contrary to the above dielectric core-silver shell mode. There are two smaller peaks due to quadrupolar contributions at about 360 nm and 455 nm with n = 1.33, which are seem to liner red-shift with increasing the value of dielectric constant for silver core-dielectric shell compared with dielectric core-silver shell at about 340 nm and 450 nm. In summary, the plasmon resonance peak’s position could be tuned over an extended wavelength by varying the value of dielectric- core and shell.
In order to gain a deeper insight into the optical properties of silver nanoshell, we set the silver nanoshell with the refractive index n = 1.50, and its outer radius 25 nm, while varying the inner silver core radius from 9 nm to 21 nm. The results are given in Fig. 5. It can be seen that the peak’s position is red-shifted with increasing the inner silver core radius from 9 nm to 18 nm, and the intensity enhance firstly and then attenuate. There are more peaks when the inner radius reaches 15 nm or more larger, these are due to quadrupolar contributions. And the peak’s position is blue-shifted when the inner radius reach to 21 nm or more larger, these optical properties were found in some experiments [43–45]. It is easy to imagine that when the inner radius reaches 25 nm, thus the silver core-dielectric shell is equal to a solid silver sphere whose peak position is at about 370 nm. Silver-core SiO2-shell nanoparticles have been used for probing spatial distribution of electrical field enhancement via surface-enhanced Raman scattering [46]. In addition, the SiO2 core-silver shell with different inner radius are also reported with the outer radius 25 nm, seen in Fig. 6. It shows that the peak’s position is blue-shifted with increasing inner radius, and there is a second smaller peak when radius is smaller, while only one single peak for bigger radius and the intensity seems to enhance straightly. It is worth noting that the plasmon resonance is quiet sensitive to the thickness of silver shell and dielectric core. It means that the plasmon resonance peak’s position also could be tuned over an extended wavelength by varying the ratio of the inner and outer radius. In fact, the dipole resonance condition for a core-shell structure in the quasi-static limit is defined by [28]
Where ε c , ε s and ε m are the dielectric constants of the core, shell, and medium, respectively, and \(\emph{f}\) is the fraction of the volume of the core in the composite structure. It is interesting to note that \(\emph{f}\) is essentially \((\emph{t/R}+1)^{-3}\), where \(\emph{t}\) is the nanoshell thickness and \(\emph{R}\) is the core radius. In other words, a larger core has a larger polarizability and a thin shell gets stronger near-field coupling, thus leading to a larger fractional plasmon shift. This analogy serves to qualitatively explain the similarity of the distance dependence and scaling behavior of plasmon coupling in the nanoshell structure to that in the particle-pair structure. The cores in the nanoparticles can be considered as truncated waveguide; the core or cavity between the nanoshell is open to the free space and forms a low-Q-cavity resonator [36, 41].
Thirdly, the coupling silver nanoshell spheres are also studied. A solid silver sphere has only one plasmon resonance due to its symmetry, but new resonances may appear when they are collected in assemblies, which are depend on the symmetry of its assemblies. Figure 7 shows the extinction efficiency for SiO2 core-silver shell spheres collected by small coupling spheres with two, three, and four nanoparticles in vacuum (n = 1.00) illuminated by plane wave with polarization parallel to the inter-spheres. The parameters of silver nanoshell sphere are the same as the above mode, with a SiO2 core of inner radius R1 = 15 nm and an outer radius R2 = 25 nm, thus a silver shell of thickness 10 nm. Two, three and four silver nanoshell spheres are touched but not interpenetrated, seen in the top of Fig. 7. It can be observed that there are new resonance modes and are red-shifted with increasing the number of silver nanoshell spheres from 2 to 4 compared with one single solid silver sphere. And the position of plasmon resonance peak are new red-shifted bands and there are more small peaks due to adding more sharp corners or singularities for touching interfaces with more spheres, which play an important role to scattering intensity [33].
Fourtly, the influences of polarization modes (see Fig. 1 case of d) to the plasmon resonance are also investigated. We give the extinction efficiency of four linear chains of SiO2 core-silver shell particles illuminated by two polarization modes, one parallel to intersphere axis direction i.e. the chain’s parallel axis of Ex, and the other perpendicularly to intersphere axis direction Ez. Figure 8 shows that there is only a very weak blue-shift with polarization perpendicularly to intersphere axis direction, whose spectra is similar to one single SiO2 core-silver shell particle, while the intensity may be influenced by its numbers, the more nanoparticles, the less intensity. We also find out that the peak position of plasmon resonance is independent to the numbers of nanoshell spheres in the array and also with different gaps distances, the peak’s position is almost the same as the single particle case. Conversely, the peak’s position is strongly red-shifted with the polarization direction along intersphere axis. It denotes that touching silver spheres could get “hot spots” only when the wave polarization direction is parallel to the intersphere axis compared with other polarization directions. The numerical simulations are agree well with EI-Sayed groups in experiments, DDA (Discrete-dipole Approximation) and FEM (Finite Element Method) simulations [42, 47, 48]. The optical properties were previously found in experiment by Nakano [49]. These phenomenons could be explained as, due to the properties of the boundary conditions of Maxwell’s equations [31, 50], the discontinuity of the electric field component at normal to the surface are proportional for surface’s polarized charge densities, only Ex-polarized light can excite plasmon resonances between the gap of silver nanoshell particles. Taking account of the Ez-polarized light, the boundary conditions are continuous for polarization parallel to the z-axis. These near-field optical signals of silver nanospheres corresponded to the nonlinear near-field optical properties. The presence of parallel mode instead of perpendicular one could be due to the presence of the dielectric spacer between the silver shells. This could explain why the second is present only when the array is perpendicular to the direction of incident wave. The plasmon resonance shift results from the electromagnetic coupling of the single particle plasmon, the polarization dependence of which is based on the single dipole-dipole coupling model. Parallel polarization is a attractive the dipole-dipole interaction, which results in lower-energy or reduction of plasmon frequency (red-shift of the plasmon band), while it is repulsive with the perpendicularly polarization, resulting in higher-energy or increasing in the plasmon frequency (blue-shift of the plasmon band). The interactions are stronger for parallel polarization, as seen from the larger wavelength shifts compared with perpendicular one. Therefore, the interparticle spacing cause the red-shifted band, and represent a collective plasmon mode [36, 47, 51] which is similar to those observed in a great number of assembled silver nanoparticles. The red-shifted plasmon excitation has been enhanced by the dielectric core or silver core nanoshell through a “waveguide effect”. And then, the role plays of the separation distances between silver nanoshell and nanoshell sphere pairs are also studied. Figure 9 shows the spectra of extinction efficiency for a single silver nanoshell sphere and nanoshell sphere pairs with radius 50 nm of different gap distances from 0 to 20 nm as a function of wavelengths with polarization parallel to intersphere. It shows that when the gap distance g increases, the peak’s position of extinction efficiency shows red-shifted for very smaller g firstly, while blue-shifted for larger g in visible light region, and the intensity enhanced firstly and then decreases as the gap distance larger [33, 51]. In addition, the silver nanoshell spheres with the ration of different distance gap and radius are considered (the radius/gap ratio remains constant), silver nanoshell sphere pairs radius varied from 20 to 50 nm as a function of wavelengths. It shows that the peak’s position of extinction efficiency shows red-shifted with distance gap and radius increasing in visible light region (the result is not given here). The new plasmon modes are likely due to oscillations along the intersphere axis or interface plane. It is also found that the peak’s position is red-shifted with increasing the numbers of silver nanoshell spheres in a linear chains of two, three, four and more SiO2 core-silver shell particles [42].
At last, in order to study the properties of the silver nanoshell, the distribution of total electrical field intensity inside two touched SiO2 core-silver shell nanoparticles (see Fig. 1 case of d, R1 = 15 nm and R2 = 25 nm, g = 0) with polarization mode (λ = 430 nm) parallel to intersphere axis direction is presented in Fig. 10. It is clear to find that the highest symmetry of electrical field intensity and the electrical field in the central gap differs clearly from those in other gaps; it also shows that there is a highest electrical field enhancement or called “hot spot” within the central gap region, which could be seen in Fig. 10. The enhanced intensity in the central gap between two SiO2 core-silver shell nanoparticles are due to the surface plasmon resonance and the concentration of energy flow [42, 51]. It is worth noting that the electrical field intensity of local field in the gaps between silver shell nanoparticles is quite sensitive to the separation distance, the intensities of electrical field reduce monotonically as the separation distance becomes larger, becoming extremely small at large interparticle distances. More detailed discussions on the distributions of electrical field intensity will be studied in the future.
Conclusions
In this paper, the optical properties of silver nanoshell particles have been studied. The results exhibit tunable plasmon resonances red- and blue-shifted by varying the dielectric environments, the constants of dielectric core, the separation distances and the ratio between the outer and inner radius respectively, which are accessible to various sensing and spectroscopy applications at the nanometer scale. It is also found out that a strongly red-shift of the plasmon peak position could be gotten only with the polarized light parallel to its interspheres, but much weaker blue-shift with polarized light perpendicularity to its interspheres. As obtained from the above numerical simulations, the main features can be qualitatively understood from a simple silver nanoshell to its assembly model. The unique properties of this nanostructure are highly attractive for serving as resonant nanocavities to hold and probe smaller nanostructures, such as quantum dots. Due to their strong and tunable plasmon resonance, nanoshells may be useful applications in nano-optical devices, surface-enhanced Raman spectroscopy, chemical and biological sensors. Furthermore, the strong frequency sensitivity of these coupled resonances could be used to produce frequency-selective devices in the future.
References
Nie S, Enmory SR (1997) Probing single molecules and single nanoparticles by surface-enhanced Raman scattering. Science 275:1102
Barnes WL, Dereux A, Bobesen TW (2003) Surface plasmon subwavelength optics. Nature 424:824
Schatz GC (1984) Theoretical studies of surface enhanced Raman scattering. Acc Chem Res 17:271
Moskovits M (1985) Surface-enhanced spectroscopy. Rev Mod Phys 57:783
Murray WA, Barnes WL (2007) Plasmonic materials. Adv Mater 19:3771
Shuford KL, Ratner MA, Schatz GC (2005) Multipolar excitation in triangular nanoprisms. J Chem Phys 123:114713
Su K H, Wei QH, Zhang X (2006) Tunable and augmented plasmon resonances of Au/SiO2 /Au nanodisks. Appl Phys Lett 88:063118
Kelly KL, Coronado E, Zhao LL, Schatz GC (2003) The optical properties of metal nanoparticles: the influence of size, shape, and dielectric environment. J Phys Chem B 107:668
Zhang Q, Tan YN, Xie J, Lee JY (2009) Colloidal synthesis of plasmonic metallic nanoparticles. Plasmonics 4:9
Sun Y, Xia Y (2002) Shape-controlled synthesis of gold and silver nanoparticles. Science 298:2176
Nehl CL, Liao H, Hafner JH (2006) Optical properties of star-shaped gold nanoparticles. Nano Lett 6:683
Talley CE, Jackson JB, Oubre C, Grady NK, Hollars CW, Lane SM, Huser TR, Nordlander P, Halas NJ (2005) Surface-enhanced Raman scattering from individual Au nanoparticles and nanoparticle dimer substrates. Nano Lett 5:1569
Zhang ZY, Zhao YP (2007) Optical properties of helical Ag nanostructures calculated by discrete dipole approximation method. Appl Phys Lett 90:221501
Wu DJ, Xu XD, Liu XJ (2008) Tunable near-infrared optical properties of three-layered metal nanoshells. J Chem Phys 129:074711
Hoflich K, Gosele U, Christiansen S (2009) Near-field investigations of nanoshell cylinder dimmers. J Chem Phys 131:164704
Kottmann JP, Martin OJF (2000) Field polarization and polarization charge distributions in plasmon resonant nanoparticles. New J Phys 2:271
Maier SA (2007) Plasmonics: fundamentals and application. Springer
Novotny L, Hecht B (2006) Principles of nano-optics. Cambridge University Press, Cambridge
Prodan E, Radloff C, Halas NJ, Nordlander P (2003) A hybridization model for the plasmon response of complex nanostructures. Science 302:419
Haes AJ, Zou S, Schatz GC, Van Duyne RP (2004) Nanoscale optical biosensor: short range distance dependence of the localized surface plasmon resonance of noble metal nanoparticles. J Phys Chem B 108:6961
Taflove A (2000) Computational electrodynamics: the finite difference time domain method. MA: Artech House, Norwood
Jin JM (2002) The finite element method in electromagnetics, 2nd edn. Wiley, New York
Draine BT, Flatau PJ (1994) Discrete-dipole approximation for scattering calculations. J Opt Soc Am A 11:1491
Martin OJF, Girard C, Dereux A (1998) Electromagnetic scattering in polarizable backgrounds. Phys Rev E 58:3909
Piller NB, Martin OJF (1998) Increasing the performance of the coupled-dipole approximation: a spectral approach. IEEE Trans Antennas Propag 46:1126
Yaghjian AD (1980) Electric dyadic Green’s functions in the source region. Proc IEEE 68:248
Girard C, Weeber JC, Dereux A (1997) Optical magnetic near-field intensities around nanometer-scale surface structures. Phys Rev B 55:16487
Bohren CF, Huffman DR (1983) Absorption and scattering of light by small particles. Wiley-Interscience, New York
Petravic M, Petravic GK (1979) An ILUCG Algorithm which minimizes in the Euclidean norm. J Comp Phys 32:263
Press WH (1986) Numerical recipes. Cambridge University Press, Cambridge
Ma YW, Zhang Y, Wu ZW, Zhang J, Jian GS, Wu SF (2009) Theoretical studies of the optical properties of plasmon resonance on silver nanoparticles in the near-field optics. J Appl Phys 105:103101
Johnson PB, Christy RW (1972) Optical constants of the noble metals. Phys Rev B 12:4370
Lassiter JB, Aizpurua J, Hernandez LI, Brandlet DW, Romero I, Surbhi L, Hafner JH, Nordlander P, Halas NJ (2008) Close encounters between two nanoshells. Nano Lett 8:1212
Jain PK, El-Sayed MA (2007) Universal scaling of plasmon coupling in metal nanostructures: extension from particle pairs to nanoshells. Nano Lett 7:2854
Jackson JB, Westcott SL, Hirsch LR, West JL, Halas NJ (2003) Controlling the surface enhanced Raman effect via the nanoshell geometry. Appl Phys Lett 82:257
Ruan Z, Qiu M (2006) Enhanced transmission through periodic arrays of subwavelength holes: the role of localized waveguide resonances. Phys Rev Lett 96:233901
Brioude A, Pileni MP (2005) Silver nanodisks: optical properties study using the discrete dipole approximation method. J Phys Chem B 109:23371
Kalele S, Gosavi SW, Urban J, Kulkarni SK (2006) Nanoshell particles: synthesis, properties and applications. Current Science 91:1038
Baida H, Billaud P, Marhaba S, Christofilos D (2009) Quantitative determination of the size dependence of surface plasmon resonance damping in single Ag@SiO2 nanoparticles. Nano lett 9:3463
Maceira V, Caruso F, Luis M (2003) Coated colloids with tailored optical properties. J Phys Chem B 107:10990
Amendola V, Bakr OM, Stellacci F (2010) A study of the surface plasmon resonance of silver nanoparticles by the discrete dipole approximation method: effect of shape, size, structure, and assembly. Plasmonics 5:85
Chen MW, Chau YF, Tsai DP (2008) Three-dimensional analysis of scattering field interactions and surface plasmon resonance in coupled silver nanospheres. Plasmonics 3:157
Xu K, Wang JX, Kang XL, Chen JF (2009) Fabrication of antibacterial monodispersed Ag–SiO2 core–shell nanoparticles with high concentration. Mat Lett 63:31
Aslan K, Wu M, Lakowicz JR, Geddes CD (2007) Fluorescent core-shell Ag@SiO2 nanocomposites for metal-enhanced fluorescence and single nanoparticle sensing platforms. J Am Chem Soc 129:1524
Xu HX, Aizpurua J, Mikael K, Pell P (2000) Electromagnetic contributions to single-molecule sensitivity in surface-enhanced Raman scattering. Phy Rev E 62:4318
Wang W, Li ZP ,Gu BH, Zhang ZY, Xu HX (2009) Ag@SiO2 core–shell nanoparticles for probing spatial distribution of electromagnetic field enhancement via surface-enhanced raman scattering. ACS Nano 3:3493
Jain PK, Huang W, El-Sayed MA (2007) On the universal scaling behavior of the distance decay of plasmon coupling in metal nanoparticle pairs: a plasmon ruler equation. Nano Lett 7:2080
Huang W, Qian W, Jain PK, El-Sayed MA (2007) The effect of plasmon field on the coherent lattice phonon oscillation in electron-beam fabricated gold nanoparticle pairs. Nano Lett 7:3227
Nakano T, Schmidt B, Plessen G (2007) Radiation damping in metal nanoparticle pairs. Nano Lett 7:318
Jackson JD (1998) Classical electrodynamics, 3rd edn. Wiley, Hoboked
Chau YF (2009) Surface plasmon effects excited by the dielectric hole in a silver-shell nanospherical pair. Plasmonics 4:253
Acknowledgements
We thank the financial support from the Scientific Research Fund of Anhui Provincial Education Department under Grant Nos. (2005KJ232, KJ2008B83ZC and KJ2011Z234) and the Young Fund of Anqing Teachers College (KJ201008).
Open Access
This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This is an open access article distributed under the terms of the Creative Commons Attribution Noncommercial License (https://creativecommons.org/licenses/by-nc/2.0), which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
About this article
Cite this article
Ma, YW., Zhang, J., Zhang, LH. et al. Theoretical Analysis the Optical Properties of Multi-coupled Silver Nanoshell Particles. Plasmonics 6, 705–713 (2011). https://doi.org/10.1007/s11468-011-9254-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11468-011-9254-z