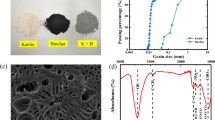
Abstract
Hydrochar is an urban soil amender that supports plant growth on slopes. It is a biomass-derived carbon-rich material produced by the hydrothermal carbonation process; thus, it has a different pore structure from biochar produced by pyrolysis. The effects of hydrochar on the hydraulic properties of unsaturated compacted soils and the underlying pore-level soil-hydrochar interaction mechanisms are unclear. In this study, silty-clay sand was amended by grass-derived hydrochars produced at two hydrothermal carbonisation temperatures (180 and 240 °C, denoted as H-180 and H-240, respectively) with different mass proportions (\({f}_{{\text{H}}}\)). The pore and throat size distributions, water retention curves (WRCs) and hydraulic conductivity functions (HCFs) of the soils with and without amendment were measured. The results showed that hydrochar improved the soil water retention capability as the smaller hydrochar particles filled the soil pores with diameters larger than 290 μm. Compared with the increase in air-entry value made by H-180, the one made by H-240 was more substantial as this type of hydrochar altered the soil pores to be smaller in size. Hydrochar also increased the hydraulic conductivity of the soil by half to one order of magnitude due to the increase in the throat frequency and the presence of hydrochar intra-pores. One exception was the amendment by H-180 at \({f}_{{\text{H}}}\) of 2.5%, wherein the HCF was reduced due to pore clogging at throat diameters less than 90 μm and more than 250 μm. Finally, amending the soil with either H-180 or H-240 at \({f}_{{\text{H}}}\) of 5% always improved the WRC and HCF, thereby benefiting plant water uptake.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Nature-based solutions using vegetation are an environmentally and ecologically friendly means to improve the stability of earthen infrastructure, such as slopes, embankments and landfills [58]. Plants provide mechanical root reinforcement [2, 34, 35, 67] and hydrological reinforcement through root water uptake upon which the effects of soil drying would increase the soil matric suction and potentially enhance the strength of unsaturated soil [12, 39]. The effectiveness of using this kind of nature-based solution to stabilise soil slopes heavily counts on the survival of vegetation, which could be a problem to certain plant species when they are exposed to a harsh environment without frequent maintenance. Indeed, the reduction of root biomass due to decomposition and plant death may create macro-pore channels and accelerate preferential water flow to depths, which could be detrimental to the soil stability [24, 25, 54]. The soil used to construct roadside slopes in urban areas is typically heavily compacted (e.g. 95% maximum dry density in Hong Kong; CEDD [15]) to satisfy the engineering requirements of stability. However, the resulting quality of urban soil from landscape perspective is often low and is unfavourable to plant growth.
To improve the soil quality and to support plant growth, various types of soil amenders, including inorganic fertilisers and organic materials, such as biochar, fibre, biopolymer and compost, have been used [52]. Amongst these amenders, biochar—a carbon-rich, porous material produced by the pyrolysis of biomass waste at controlled high temperatures of up to 700 °C—has been increasingly used, because it is a sustainable material [53] and has a promising ability to improve the soil water retention and drainage properties (through the measurements of water retention curve, WRC) for plant water uptake [45, 46, 66]. Previous studies have shown that the porous nature of biochar can effectively improve the soil water retention capability of compacted soils [16, 23, 30, 46]. However, the effects of biochar on the hydraulic conductivity function (HCF, i.e. relation between hydraulic conductivity and matric suction) of unsaturated soils appear to be contradictory. Thus far, only a few studies have focused on the effect of biochar on the HCF of loose soils used in agriculture [i.e. 0.72–1.5 kg/m3; 33, 59, 63, 65] and compacted soils used in engineering [30]. In particular, Kameyama et al. [33] and Villagra-Mendoza and Horn [63] attributed the observed increase in HCF of the respective test soils (clay and sand) to the increase in soil porosity due to the biochar addition. On the contrary, Uzoma et al. [59], Wanniarachchi et al. [65] and Hussain and Ravi [30] reported a reduction in HCF of sand, loamy sand and silty sand soils, respectively. The results of Hussain and Ravi [30] indicated that the addition of hard wood of mesquite-derived biochar reduced the HCF of both sand and silty sandy soils; furthermore, the amount of reduction was greater at a higher \({f}_{{\text{H}}}\). They postulated that the reduction in the HCFs was attributed to the increase in the smaller-sized pores and the increase in tortuosity by biochar addition (though PSD data were not available to support the finding, and the compaction dry densities of unamended and biochar-amended soils varied). Although it is well-known that the WRC and HCF of a soil are controlled by pore morphology, the fundamental pore-level soil-biochar interaction and how the biochar alters the soil pore structure and pore-size distribution are rarely studied.
Hydrochar is another soil amender alternative to biochar and is produced by a process called hydrothermal carbonisation (HTC). In this process, a feedstock is submerged in water and heated in a closed system under a temperature of 180–260 °C with an autogenous pressure between 2 and 6 MPa for a residence time of 5–240 min [32, 40]. Compared with the pyrolysis used to produce biochar, the HTC does not require any pre-drying of the feedstock (which could be initially wet like most of the yard and food wastes) and produce minimal toxic gases (2–5%). Previous studies have shown that hydrochar could improve the WRCs and plant growth [1, 9, 21]. To the best of our knowledge, only one study has measured the effects of woodchip-derived hydrochar on the HCF of a loamy sand [21]. This study found that the HCF was almost unaffected when amending the soil with 2% of hydrochar (by mass). Evidently, more studies are needed to investigate the effects of hydrochar on both the soil’s WRC and HCF and the fundamental soil-hydrochar interaction at the pore level. Owing to differences in production methods and biochemical reactions between the processes of HTC and pyrolysis, hydrochar would have different physiochemical properties and pore structure from biochar [40, 73]. In this case, the knowledge derived from existing studies of soil amendment by biochar may not be directly transferred to the case of hydrochar.
Therefore, the current study aims to investigate the effects of grass-derived hydrochar at two different HTC temperatures on the drying WRCs and HCFs of a compacted silty-clay sand using the simplified evaporation method. To interpret the data, comprehensive and systematic microstructural investigations, including scanning electron microscopy (SEM), mercury intrusion porosimeter (MIP) and X-ray computed tomography (CT) scanning, were carried out to assist in the interpretation of the test results.
2 Test materials
2.1 Soil
The soil tested in this study was completely decomposed volcanic (CDV) sample obtained from a construction site in Hong Kong. This soil type is commonly found in Hong Kong and is typically used as backfill in engineering projects. The specific gravity (Gsi) of soil is 2.604. Based on the particle size distribution, the soil has 83.6% sand content, 16.2% silt content and 0.2% clay content. The liquid limit and the plasticity index are 36.5% and 12.1%, respectively. According to the Unified Soil Classification System [4], the soil can be classified as SC-SM (silty, clay sand). The soil has a maximum dry density (ρdmax) of 1705 kg/m3 with an optimum water content (wopt) of 21.1%, according to the results of the standard proctor tests [6]. Some basic properties of the soil (after sieving to a particle diameter less than 2 mm) are summarised in Table 1.
2.2 Hydrochar
Clippings of a grass species, Axonopus compressus, a type of yard waste commonly found in Hong Kong, were collected as feedstock to produce hydrochar. The feedstock has hemicellulose, cellulose and lignin contents of 238.2 ± 19.7 mg/g (mean ± standard deviation), 134.1 ± 16.9 mg/g and 10.0 ± 0.3%, respectively, which were determined by the methods outlined by Wu et al. [67]. The grass feedstock (G-F) collected was processed as follows: (1) rinsed with deionised water to remove the soil particles attached, impurities and other contaminants; (2) oven-dried at 105 °C for 12 h; and finally (3) milled to pass through the 2 mm sieve. The feedstock was then stored in a freezer at − 22 °C before use [11].
To produce hydrochar, approximately 200 g of grass and 1 L of deionised water were placed in a 2 L stirred pressure reactor (Parr 4524 Model; Parr Instrument Company in Moline, Illinois, USA). The mixture was heated to the desired temperature for 30 min and then cooled down. Given that the reaction temperature governs the HTC reaction mechanism and the physiochemical properties of the derived hydrochar products [32], in the current study, two temperatures (180 and 240 °C) were chosen to study its effects on the soil properties. After production, the solid yield (i.e. hydrochar) was filtered, oven-dried at 105 °C for 12 h and then milled to a particle size of less than 2 mm. The two derived hydrochars were respectively denoted as H-180 and H-240 herein. Grass and grass-derived hydrochars were light materials with much smaller values of GHs (1.551 ± 0.041 and 1.629 ± 0.036 for H-180 and H-240, respectively, Table 2) than the test soil. The differences in GHs amongst G-F, H-180 and H-240 were thought to be associated with the HTC reaction process and were investigated via the surface morphology discussed later. The surface morphologies of G-F, H-180 and H-240 were observed by a scanning electron microscopy (SEM, JSM-6390; JEOL Ltd. in Akishima, Tokyo, JAPAN). The pore-size distributions (PSDs) of G-F, H-180 and H-240 were measured by using a mercury intrusion pore size analyser (MIP; Pore Master 33, Anton Paar QuantaTec Inc. in Boynton Beach, Florida, USA) for a pore diameter D ranging from 340 to 0.005 μm (or 5 nm). To further investigate the nanoscaled pore differences of these materials, nitrogen adsorption isotherms (NAI) tests were carried out by using a surface area and pore size analyser (BELSORP-miniX, MicrotracBEL Corp. in Osaka, Japan) for a D ranging from 0.6 to 0.001 μm. In these tests, the oven-dried G-F and hydrochar samples (H-180 and H-240) were degassed under vacuum at 150 °C for 6 h and absorbed by nitrogen gas at a temperature of − 196.15 °C. The specific surface area (SSA) and PSD of the hydrochar samples were determined by the Brunauer–Emmett–Teller (BET) and Barrett-Joyner-Halenda (BJH) methods, respectively [10, 13]. To quantify the difference of PSD of hydrochar from that of biochar derived from the same grass species (A. compressus), biochar was also produced using a tube furnace at a pyrolysis temperature of 500 °C (denoted as B-500). The PSD of B-500 was then measured by the MIP and NAI tests.
To measure other physiochemical properties of the hydrochar, including the volatile matter, ash and fixed carbon contents, the oven-dried hydrochar samples were grounded by an ultra-centrifugal mill fitted with a 250 μm ring sieve (Model ZM200, Retch GmbH in Nordrhein-Westfalen, Germany), which is the requirement for physicochemical analysis. The volatile matter content was determined by measuring the weight loss of the hydrochar in a muffle furnace at 950 °C for 7 min [8]. Finally, the ash content was determined by measuring the weight loss of the hydrochar in a muffle furnace at 750 °C for 3 h [5]. The elemental composition (i.e. nitrogen, carbon, hydrogen, sulphur and oxygen contents) analysis was measured by a NCHS elemental analyser (FlashSmart, Thermo Scientific in Rodano, Milan, Italy). Thermogravimetric analysis was performed to assess the thermal oxidation stability of the hydrochar samples by a thermogravimetric analyser (UNIX/TGA7, Perkin Elmer Corp. in Waltham, MA, USA). In this test, the samples were placed in a crucible and then heated up to 800 °C at a constant heating rate of 15 °C/min in an inert nitrogen atmosphere (i.e. with a supply of nitrogen flow rate at 60 ml/min). Three replicates were examined for each type of tests to capture any natural variability of the feedstock.
2.3 Sample preparation methods
Samples of amended soils that were used for testing their hydraulic properties were prepared by mixing the hydrochar with oven-dried soil at different proportions (\({f}_{{\text{H}}}\)) of 0, 2.5, 5 and 10% by mass (i.e. ratio of the mass of hydrochar [\({m}_{{\text{H}}}\)] to the mass of soil [\({m}_{{\text{si}}}\)]). De-aired water was then added to the soil-hydrochar mixtures to reach 21.1% by mass (i.e. the optimal moisture content of unamended soil; Table 1). The wet mixtures were passed through a 2 mm sieve to reduce the formation of clods and then stored in a sealed plastic bag for 24 h for moisture equalisation. Each mixture was statically compacted to the identical target dry density (\({\rho }_{{\text{d}}}\)) of 1.340 g/cm3 (i.e. 80% degree of compaction of the unamended soil), which was suitable for facilitating plant growth [43]. The samples were compacted in six layers into an acrylic column (70 mm diameter and 90 mm height) using different compaction efforts (Table 3). During compaction, the two holes drilled on the mould for inserting sensors at the depths of 22.5 and 67.5 mm away from the column surface were sealed by a pair of O rings and screws. Each compacted specimen was sandwiched by a pair of filter paper and a pair of porous stones using a clamp, after which the assembly was placed inside a desiccator filled with de-aired water for saturation. Each specimen was submerged in water for 8 h and then a vacuum pressure of approximately − 80 kPa was applied to the desiccator for at least 24 h. Each specimen was weighted to check its degree of saturation, and the saturation process was considered to be completed when the specimen weight no longer changed. The final degree of saturation of all the compacted specimens were higher than 98%. The as-compacted properties of all the specimens are summarised in Table 3.
3 Test methods
3.1 Evaporation tests
By the simplified evaporation method [51], a series of evaporation tests was conducted to determine the hydraulic properties of the compacted samples. This is a transient-state method in the laboratory to simultaneously measure changes in volumetric water content (VWC) and matric suction of soil samples during evaporation. Figure 1 shows the schematic diagram and a photo of the test setup. After saturation, each specimen was placed on an electronic balance (with a resolution of 0.1 g). The bottom of the specimen was covered by an acrylic plate and sealed with an O ring to achieve a zero-flux boundary condition. Two miniature tensiometers (6.4 mm diameter and 11.4 mm length, model: MEAS EPB-PW, manufactured by Measurement Specialties) were inserted to the specimen at the depths of 22.5 and 67.5 mm from the soil surface. Each tensiometer was equipped with a 1 bar ceramic tip; hence any negative pore water pressure (PWP) or matric suction between 0 and 100 kPa can be measured directly with an accuracy of 1 kPa. The surface of the specimen was left for natural evaporation in the laboratory (temperature of 23 ± 1 °C and relative humidity of 65 ± 5%). Variations of PWP with time were recorded by both the tensiometers, while the mass change of the specimens (hence the gravimetric water content) was measured by the balance. The evaporation test was considered completed when the upper tensiometer recorded a negative PWP of around 80 kPa before cavitation occurred.
Assuming that the PWP distribution between the two tensiometers was linear at each measurement interval and hence the hydraulic gradient was constant, the WRC can be determined by relating the water content of the specimen with the average suction (i.e. averaging the measurements made by the two tensiometers) recorded at the same elapsed time t. According to the Darcy’s law, the unsaturated hydraulic conductivity of the soil at the middle of the two tensiometers (i.e. mid-height of the specimen) at the average elapsed time of evaporation, \({t}_{{\text{ave}}}\)(\({t}_{{\text{ave}}}=\left({t}_{{\text{i}}-1}+{t}_{{\text{i}}}\right)/2\)), can be calculated as follows:
where \({q}_{{\text{m}}, {t}_{{\text{ave}}}}\) and the \(\nabla {H}_{{\text{m}},{t}_{{\text{ave}}}}\) are the water flux and the hydraulic gradient at the middle of the two tensiometers at \({t}_{{\text{ave}}}\), respectively. The water flux at the mid-height of the specimen is considered as half of the total water flux of the specimen (\({q}_{0, {t}_{{\text{ave}}}}\)) and can be calculated as follows:
where \({\Delta t}_{{\text{ave}}}\) is taken as (\({t}_{{\text{i}}}-{t}_{{\text{i}}-1})\); \(\Delta {V}_{{t}_{{\text{ave}}}}\) is the volume of water evaporated during \({\Delta t}_{{\text{ave}}}\), and \(A\) is the cross-sectional area of the specimen (i.e. 3848.45 mm2). Meanwhile, the hydraulic gradient can be approximated using the following equation:
where \({\psi }_{u,{\text{i}}}\) and \({\psi }_{u,{\text{i}}-1}\) are the values of matric suction measured by the upper tensiometer at time \({t}_{{\text{i}}}\) and \({t}_{{\text{i}}-1}\), respectively;\({\psi }_{l,{\text{i}}}\) and \({\psi }_{l,{\text{i}}-1}\) are the values of matric suction measured by the lower tensiometer at time \({t}_{{\text{i}}}\) and \({t}_{{\text{i}}-1}\), respectively; and \(\Delta z\) is the vertical distance between the two tensiometers (i.e. 45 mm). Therefore, the HCF can be obtained by relating the hydraulic conductivity determined by Eq. (1) with the average suction measured at the same time intervals. The results indicated that no significant volume change was observed from the specimens within the suction change of concerned during the process of evaporation.
After each evaporation test, three to four subsamples of different values of water content were sliced from the top, middle and bottom parts of each specimen. To extend the WRC to a higher suction range, a dew point hygrometer (WP4C) was used to measure the total suction of these subsamples. Osmotic suction was considered negligible.
3.2 Microstructure tests
Microstructure investigation was conducted to visualise the changes in pore morphology and quantify the PSDs of the soil after being amended by different types and amounts of hydrochar. This investigation aimed to assist in the interpretation of the measurements of WRCs and HCFs. Seven specimens (unamended soil and soil samples amended with H-180 and H-240 at \({f}_{{\text{H}}}\) of 2.5, 5 and 10%) were prepared, following the identical methods and procedures as those used in the evaporation tests. Small cubic samples with a size of 20 mm were trimmed from each specimen and then dehydrated by the freeze-drying method [20]. Each freeze-dried cube was taken for non-destructive X-ray computer tomography (CT) scanning and then followed by MIP tests.
Each cubic sample was scanned by a nanovoxel-3000 Microfocus X-ray 3D scanner (Sanying Precision Instruments). The voltage and current of the scanner were set at 140 kV and 200 μA, respectively. For each scan, a total of 1080 projections were obtained for three-dimensional (3D) image reconstruction and a pixel resolution of 8.09 μm was achieved, indicating that pores with \(D\) larger than 8.09 μm in the CT images can be identified. A cylindrical region of interest (ROI) with a diameter of 6 mm and a height of 6 mm was randomly extracted from different locations of each sample for investigation. The pores in the selected ROI were segmented using the Otsu thresholding algorithm [47]. Figure 2a and b respectively present two examples of the ROI (in plane) and the corresponding segmented pores of the unamended soil (i.e. the control, C), as well as the soil amended with H-240 at the mix proportion of 10% (i.e. H-240–10%). Figure 2c–f illustrate the steps followed to construct the pore network model (PNM [26];) from the reconstructed 3D CT images. Following phase segmentation, all the pores were labelled and separated (Fig. 2d and e). Hence, a PNM consisting of balls and sticks was generated (Fig. 2f). The maximum inscribed balls centred in each pore voxel were identified as pores, whilst the narrowest channels connecting the centres of these balls were represented by sticks and were regarded as pore throats [56]. Following this procedure, the number, size and volume of equivalent pores and throats can be used to calculate PSDs, pore throat size distributions (PTSDs) and pore connectivity.
Steps to obtain the pore network model (PNM) from an X-ray CT image for an arbitrarily selected region of interest (ROI): a CT images of unamended (C) soil and soil amended with H-240 at the mix proportion of 10% (H-240–10%); b segmented images of C and H-240–10% (pore phase in dark blue and hydrochar in light blue); c 3-D microstructure of CT images; d pore segmentation; e pore labelling; and f the product of PNM
After X-ray CT scanning, the same cubic samples were trimmed into smaller cylindrical samples (6 mm diameter and 6 mm height). These smaller samples were then sent for MIP tests to measure the PSDs in a smaller pore range, specifically for D ranging between 1000 and 0.007 μm, using a mercury intrusive porosimeter (MIP; Pore Master 33, Quantachrome Corp.). The MIP test aimed to complement the measurements made by the X-ray CT for D > 8.09 μm.
4 Results and discussion
4.1 Physiochemical properties of hydrochar
The physiochemical properties of the feedstock (G-F) and grass-derived hydrochar at two different HTC temperatures (H-180 and H-240) are summarised in Table 2. As can be seen, all of them were acidic. G-F had an average ash content of 8.80% and volatile matter content of 86.43%. As the HTC temperature increased from 180 to 240 °C, the ash content increased from 9.73 to 16.40%, whilst the volatile matter content decreased from 82.67 to 72.66%. The degradation of some organic components and the loss of some weak oxygen and hydrogen bonds were responsible for the observed reduction in the unstable volatile matter and the increase in fix carbon content [22]. Meanwhile, the increase in ash content may be attributed to the increase in the porosity of hydrochar, which absorbed more inorganic contents on the particle surface [71]. Based on the elemental composition analysis, HTC temperature increased the carbon (C) content from 40.45 to 50.58% and reduced the oxygen (O) content from 51.43 to 42.21%. However, the nitrogen (N), hydrogen (H) and sulfur (S) contents remained largely unchanged. The changes in the elemental composition were further investigated using van Krevelen’s diagram [62], which related the atomic H/C with O/C ratios (Fig. 3a). The atomic H/C and O/C ratios both decreased with an increase in HTC temperature mainly accompanied by the dehydration and decarboxylation reactions. Reductions in the H/C and O/C ratios indicated a higher degree of aromaticity and a lower polarity of the hydrochar, respectively. Spokas [57] suggested that the half-life of biochar (produced by pyrolysis) with a O/C ratio ranging from 0.2 to 0.6 would be between 100–1000 years, whereas that with a O/C > 0.6 would be less than 100 years. Based on the test results, the hydrochar, especially for H-240, may be suitable for intermediate carbon sequestration. Schimmelpfennig and Glaser [50] recommended that biochar with thresholds of O/C ratio less than 0.4 and H/C ratio less than 0.6 is desirable for long-term carbon sequestration. In this regard, hydrochar had less condensed aromatic structure and lower stability than biochar produced at high pyrolysis temperature (i.e. > 500 °C). Thus, the hydrochar could not be considered a suitable candidate for long-term carbon sequestration (> 2000 years).
Figure 3b and c respectively reveal the thermo-gravimetric (TG) (i.e. weight loss as a function of temperature) and the derivative thermo-gravimetric (DTG) (i.e. weight loss per minute as a function of temperature) curves for G-F, H-180 and H-240. In general, there were three stages of thermal degradation. (1) When the temperature was smaller than 200 °C, approximately 3–5% of the total weight was lost due to water evaporation. Although the samples were oven-dried at 105 °C before testing, there was still a small amount of water absorbed on the particle surface that required higher energy to evaporate. (2) Significant weight loss was observed between 200 and 600 °C, following the decomposition of lignocellulosic components. (3) Beyond 600 °C, no significant weight loss was observed. The weight loss rates of G-F, H-180 and H-240 were 93.26, 92.26 and 86.53%, respectively, as the temperature increased to 800° C. H-240 had the smallest amount of weight loss, indicating that it had the highest thermal stability. From Fig. 3c, evident peaks of maximum weight loss per minute can be seen at 363, 384 and 380 °C for G-F, H-180 and H-240, respectively. Moreover, the absolute value of the peak of the DTG curve appeared to increase with increasing HTC temperature. During HTC, the degradation of hemicellulose, cellulose and lignin started from approximately 180, 220 and 250 °C, respectively [73]. Specifically, hemicellulose and cellulose decomposed rapidly between 200 and 300 °C and between 300 and 400 °C, respectively, whilst lignin devolatilised at temperatures ranging between 150 and 1000 °C [70]. Therefore, the peaks observed from the DTG curves were likely due to the decomposition of cellulose in the feedstock and both types of hydrochar. In particular, the absolute value of the peak for H-240 was smaller than that of H-180, indicating that there was less cellulose left in the former. The larger area bounded by the DTG curve of H-240 at the temperature range of 500–800 °C in Fig. 3c indicated the presence of lignin in H-240. A recalcitrance index R50 [28] is defined as the ratio of the temperature value of char corresponding to the 50% weight loss in the TG curve after correcting for the water and ash contents (T50,char) to that of graphite at 50% weight loss (T50,graphite). If T50,graphite = 886 °C was used as suggested by Harvey et al. [28], then G-F, H-180 and H-240 (classified as Class C, R50a < 0.5) would have comparable carbon sequestration capacities (Table 2). By contrast, when using T50,graphite = 844 °C as suggested by Yang et al. [69], H-240 (Class B, 0.5 ≤ R50b < 0.7) would have an intermediate carbon sequestration potential.
4.2 Microstructures and pore characteristics of hydrochar
Figure 4a–f present the SEM images of G-F, H-180 and H-240, respectively. The G-F had an elongated particle shape (Fig. 4a) and a flat and smooth surface (Fig. 4b). For H-180 (Fig. 4c and d), some of the original microstructure of G-F appeared to have been destroyed during the HTC process, and irregular microplate-like fragments (size of 1–3 μm) emerged on the surface. These fragments were formed by the destruction of the grass cell wall due to the degradation of the lignocellulosic components and the recombination of the degraded products [68]. As the HTC temperature increased from 180 to 240 °C (Fig. 4e and f), the hydrochar surface became more ruptured and rougher with the presence of some small sponge-like pores. Furthermore, H-240 began to have more plate-like fragments on the surface than H-180 due to the stronger polymerisation reaction.
SEM images of G-F ((a) at × 200 and zoomed-in view at × 5000 in (b)), H-180 ((c) at × 200 and zoomed-in view × 5000 in (d)); and H-240 ((e) at × 200 and zoomed-in view × 5000 in (f)); (g) PSDs of G-F, H-180, H-240 and B-500 measured by MIP; and (h) their zoomed-in view for smaller D range measured by NAI
The PSDs of G-F, H-180, H-240 and B-500 are given in Fig. 4g and h. G-F has a pore peaking at D of 119 μm, corresponding to the most probable pore size of the original grass cells. According to the Soil Science Society of America [55], pore sizes can be classified into macropores (> 75 μm), mesopores (30–75 μm), micropores (5–30 μm), ultra-micropores (0.1–5 μm) and cryptopores (< 0.1 μm). According to the test results, H-180 had abundant macropores, whilst H-240 had abundant mesopores. When turning G-F into H-180, the pore volume of > 75 μm macropores increased, and the dominant D showed a corresponding increase from 119 to 177 μm. However, the pore volume of < 10 μm micropores reduced, which can be attributed to the emergence of the microplate-like fragments (Fig. 4d) and the change in the particle contacts caused by the change in the particle shape (Fig. 4a and c). As the HTC temperature increased further to 240 °C (H-240), the intensification of the HTC reactions led to significant pore volume reduction of macro- and meso-pores and the reduction in D from 177 to 36 μm (Fig. 4g). The slight increase in pore volume for D ranging from 5 to 36 μm can be attributed to the appearance of sponge-like fragments (Fig. 4f) and to the change in the particle contacts (Fig. 4e). When pyrolysing G-F to B-500, the pore peak reduced from 119 to 40 μm. The B-500 has a pore volume more than H-240 but less than H-180, as a result of the two completely different chemical reactions involved in the two production processes.
Based on the MIP results presented by Lu and Zong [42], biochars derived from ten herbaceous species often had a bimodal PSD with two pore peaks at D of 4–14 and 1–4 μm. Compared with these biochars, the hydrochar tested in the present study had a larger D, in which the pore peaked (119 μm for H-180 and 36 μm for H-240) and had a larger pore volume (Table 2), which may be favourable to the storage and transport of free water. The smaller peak at D of 1–4 μm that was identified by Lu and Zong [42] was absence in the hydrochar of the present study (Fig. 4g). Compared with the pyrolysis temperature (i.e. 550 °C) used to produce the biochars, the HTC temperature used to produce the hydrochar (i.e. 180 °C and 240 °C) was lower, resulting in less intense decomposition and volatilisation reactions of the lignocellulosic components.
Figure 4h shows a zoomed-in view of the PSDs for the smaller range of D from 0.001–1 μm). The nano-scale intrapores of G-F were considered negligible with a pore peaking at D of 0.106 μm and a relatively small pore volume of 0.012 mL/g (Table 2). H-180, H-240 and B-500 had pores peaking at D of 0.163, 0.106 and 0.106 μm, respectively. Compared with G-F, the total pore volume increased by 1.2 and three times for H-180 and H-240, respectively (Table 2). The increase in those nano-scale intrapores was probably due to the loss of hydroxyl (–OH) and aliphatic functional groups upon HTC [36]. The pore volume of B-500 was less than that of H-180 and H-240, probably because the pores of B-500 were filled by the condensed volatiles (i.e. tars) following the decomposition of G-F during the pyrolysis process [74]. To sum up, the pore structures developed in H-180 and H-240 were beneficial for adsorption, microbial activity, retaining of soil nutrients and the improvement of water holding capacity [29].
4.3 Pore characteristics of hydrochar-amended soils
Figure 5a–d present the PSDs of the soils amended by H-180 and H-240. The PSDs were obtained by the X-ray CT scanning. The bottom x-axis is the equivalent pore diameter (Dep). The corresponding range of equivalent matric suction (calculated by the Young–Laplace equation (\(\psi =\frac{4{T}_{{\text{s}}}}{{D}_{{\text{ep}}}}\), where \({T}_{{\text{s}}}\) represents the water surface tension equal to 0.0723 N/m at 20 °C) is expressed in the top x-axis. Furthermore, the left y-axis shows the number of pores in the range of Dep divided by the number of total pores (pore frequency), whilst the right y-axis is the pore volume in the range of Dep divided by the solid volume (void ratio). The resolved void ratio are summarised in Table 4. Considering the pixel resolution (i.e. 8.09 μm) of the X-ray CT images and the smallest Dep (i.e. 10 μm) that can be obtained from the PNM, the following discussion focused only on the pore characteristics for Dep > 8.09 μm. First, the PSDs were divided into three zones with different ranges of Dep. The unamended soil (Fig. 5a) had 91.8% pores at Dep ranging from 10 to 50 μm in Zone I, and the frequency of the rest of the pores varied from 0.6 to 2% (Fig. 5b). Although the pore frequency with Dep > 290 μm in Zone III was only 1.3%, it had the largest void ratio of 0.236. When replacing 2.5% of the soil mass with H-180 (H-180–2.5%; whilst maintaining the same dry density, the void ratio at Dep in Zone II slightly increased, whilst that in other zones had negligible changes. The increase in the void ratio could be due to the presence of the hydrochar particles’ macropores (Fig. 4g). As \({f}_{{\text{H}}}\) of H-180 increased from 2.5% to 5% (i.e. H-180–5%), both the pore frequency and void ratio in Zones I and III reduced, whilst the void ratio in Zone II increased further (Fig. 5a and b, respectively). Given that hydrochar had a much smaller GHs than soil (Table 2), a higher compaction energy was needed (Table 3) to produce the samples of higher hydrochar contents with the same as-compacted state. As a result, the void ratio in Zone III to decreased, whilst that in Zone II increased. When the \({f}_{{\text{H}}}\) increased further to 10% (i.e. H-180–10%), the void ratio in Zone III remained largely unchanged. The increase in the compaction energy and the resulting particle rearrangement might be responsible for the increase in frequency in Zone II but led to the reduction in Zone I. Similar phenomena (i.e. the compression of large pores in Zone III, the expansion of median pores in Zone II and the slight decrease in the frequency of small pores in Zone I) were also observed in the soils amended with H-240 at different values of \({f}_{{\text{H}}}\) (Fig. 5c and d), except H-240–10%. In this case, the relatively large pores in Zone III were further compressed, and the pore frequency and void ratio in Zone I and II both increased, unlike what was found from H-180–10% in Fig. 5a and b. The observed differences in the changes in the pore characteristic may be attributed to the differences in the PSDs of the H-180 and the H-240 (Fig. 4g). Indeed, H-240 had abundant mesopores at D of 36 μm, which was different from the case of H-180 that was rich in macropores at D of 119 μm. In other words, the different pore characteristics may have contributed to the increase in the small pores in Zone I and the decrease in the large pores in Zone III.
Figure 6a and b show the PTSDs of the soils amended with H-180 and H-240. As can be seen, the unamended soil displayed a unimodal throat frequency distribution with the most abundant pore throats at the equivalent pore throat diameter (Det) ranging from 10 to 50 μm (Fig. 6a). The addition of H-180 of 2.5% caused an increase in the throat frequency at most of the Det in Zone II, consistent with the increase in the pore frequency shown in Fig. 5a and b. However, although the pore frequency in Zone I was increased, the throat frequency in this zone reduced. Thus, replacing soil by 2.5% of hydrochar content by mass (i.e. H-180–2.5%) led to the formation of more median pores and median throats in Zone II (called the ‘pore expansion effect’). However, this also led to the reduced connectivity of the smaller pores in Zone I and the larger pores in Zone III (called the ‘pore clogging effect’). Previous studies [1, 27, 30] have also observed these effects in biochar- and hydrochar-amended soils, although they did not quantify their respective contributions to the changes in the corresponding soil pore and throat structures. In the current study, as the hydrochar content increased further (H-180–5% and H-180–10%), the large pores formed were compressed by the higher compaction energy (Table 3), leading to the reduction in the pore throats of Det > 90 μm and the simultaneous increase in the throats of Det < 90 μm.
For the case of H240 (Fig. 6b), the soil amended at \({f}_{{\text{H}}}\) of 2.5% showed an increase in the throat frequency mainly in the Det range from 50 to 170 μm in Zone II and a reduction for Det > 170 μm. These phenomena suggest that the addition of H-240 at this \({f}_{{\text{H}}}\) was not enough to form larger throats of Det from 170 to 250 μm in Zone II similar to H-180–2.5% (Fig. 6a). The observed differences between H-180 and H-240 at this \({f}_{{\text{H}}}\) was probably due to the latter having a smaller pore peak (Fig. 4g). For H-240–5%, the addition of H-240 increased the throats of Det > 170 μm in Zones II and III. As the \({f}_{{\text{H}}}\) increased further to 10%, the large throats of Det > 170 μm were again compressed, accompanied by an increase in the throats of Det ranging from 50 to 90 μm.
The PSDs of hydrochar-amended soils for D ranging from 1000 to 0.007 μm were measured by MIP, with the results shown in Fig. 7. As depicted in Fig. 7a and c, the addition of hydrochar increased the cumulative pore volume and the intruded void ratio (eMIP, Table 5) when the \({f}_{{\text{H}}}\) exceeded 2.5%. From Fig. 7b and d, it can be seen that all the specimens displayed bimodal PSDs (except H-240–5% and H-240–10% which were tri-modal) with a macro-pore peak (Dma) ranging from 50 to 150 μm and a micro-pore peak (Dmi) ranging from 0.2 to 0.5 μm. Both H-240–5% and H-240–10% showed a first macro-pore peak (Dma1) larger than 150 μm and a second macro-pore peak (Dma2) ranging from 10 to 100 μm. The value of D, where the minimum value of incremental pore volume (< 0.001 mL/g) was attained between the Dma (Dma2 for H-240–5% and H-240–10%) and Dmi, can be defined as the delimiting pore diameter Dd separating the macro- and micro-pores. The resolved Dd and the corresponding macro-void ratio (ema) and micro-void ratio (emi) are summarised in Table 5. The differences in the void ratio resolved from the X-ray CT and that measured by MIP for all the specimens are also compared in Table 5. As can be seen, in the overlapping range of D between 8.09 and 1000 μm, the void ratio difference (Δe) obtained by the two methods was negligible, thus verifying the accuracy of the X-ray CT scanning study, especially for the large pores beyond the capability of MIP (i.e. > 1000 μm).
From Fig. 7b, it can be observed that the unamended soil (C) had a Dma of 80.2 μm and a Dmi of 0.37 μm. The addition of H-180–2.5% slightly decreased the emi from 0.368 to 0.340 (Table 5), which might be due to the micro-pores being filled by the small hydrochar particles. As the \({f}_{{\text{H}}}\) of H-180 increased from 2.5% to 5% (i.e. H-180–5%), both the Dmi and emi increased (Fig. 7b, Table 5), which could be attributed to the < 1 μm pores of H-180 (Fig. 4h). However, the emi decreased as the \({f}_{{\text{H}}}\) increased further to 10% (H-180–10%), which can be attributed to particle rearrangement and the resultant pore compression due to the much higher compaction energy required to reach the same dry density as H-180–5%.
In accordance with the observation in the current study, a previous work [41] also found that the increase in the compaction energy would not affect the pores with D smaller than 0.1 μm. Interestingly, for the soil amended with H-240 in the current study, the bimodal PSD became trimodal with two values of Dma due to the addition of H-240 at \({f}_{{\text{H}}}\) of 5% and 10% to the soil (Fig. 7d, Table 5). The second peak at the Dma of 61.75 μm (H-240–5%) and 34.90 μm (H-240–10%) might be associated with the dominant pore peak of H-240 at D of 36 μm (Fig. 4g).
4.4 Changes in matric suction and water content
Figure 8 shows the respective temporal variations of matric suction ((a) and (c)) and VWC ((b) and (d)) of the unamended and hydrochar-amended soils. Note that the data were taken every 10 min and were presented in lines for clarity, whilst the data points were marked to ease the referencing to the legend. As expected, following the evaporation of pore water through the top soil surface, suction in all the specimens increased exponentially, whilst the VWC reduced linearly. In all cases, the suction recorded from the upper tensiometer was always higher than that from the lower one due to the relatively large hydraulic gradient developed at the soil-atmosphere interface upon evaporation. Consistently, during the initial stage of evaporation, all the specimens did not show significant suction increases until the magnitude of suction reached certain levels. Thus, it is evident that irrespective to the production temperature, the addition of hydrochar made the suction responses quicker for a given duration of evaporation. Moreover, it appears that the higher the \({f}_{{\text{H}}}\), the faster the suction response would be.
Notably, the reduction in VWC accompanied the suction increase during evaporation (Fig. 8b), which appeared to be linear throughout the test period. Before soil drying, the saturated VWC (θsat), or porosity, of C, H-180–2.5%, H-180–5% and H-180–10% were 0.474, 0.467, 0.460 and 0.444, respectively. Evidently, the addition of hydrochar reduced the porosity. Indeed, at the same as-compacted dry density, replacing soil by hydrochar reduced the GHs, thereby causing a reduction in the porosity (Table 3). Here, evaporation rate is defined as the gradient of the relationship between the mass of water evaporated from the specimen and elapsed time. The evaporation rate was almost constant during the tests for all the specimens (Table 7), suggesting that water phase remained continuous, and the water transported from the depths to the soil surface may be driven by capillary pressure differences between pores [3, 31]. It has been reported that the capillary difference required to maintain a constant evaporation rate is not determined by one single pore size, but the difference in the size of the small and large pores [38, 64]. Indeed, the pore analysis by the CT suggested that the addition of hydrochar increased the median pore frequency and void ratio in Zone II (Fig. 5a and b) and the cumulative pore throat frequency (Fig. 6a) through the ‘pore expansion effect’. Given that the Dmi and Dma from the biomodal PSDs (Fig. 7a and b, Table 5) were the most abundant micro- and macro-pore diameters in the specimens, the ratio of Dmi and Dma may be taken as the size difference between the small and large pores. For trimodal PSDs of H-240–5% and H-240–10%, the average value of Dma1 and Dma2 may be approximated as the Dma. The calculated ratios of Dmi/Dma are summarised in Table 5. As can be seen, for the soils amended with H-180 and H-240, the Dmi/Dma reduced with an increase in \({f}_{{\text{H}}}\), thereby explaining the observed increase in the evaporation rate with \({f}_{{\text{H}}}\). Zhang et al. [72] also found an increase in the evaporation rate of biochar-amended clay soils as \({f}_{{\text{H}}}\) increased beyond 4%, suggesting that this may be due to the increase in the connectivity of water migration channels.
The temporal variations of suction and VWC for the case of H-240 amendment (Fig. 8c and d) were similar to those found for the case of H-180. However, for a given \({f}_{{\text{H}}}\), the rate of increase in the suction and evaporation rates in the soils amended by H-240 were both smaller (Fig. 8a and c, Table 7). Although the values of eMIP of H-180–2.5% and H-240–2.5% were similar, the smaller evaporation rate found in the latter may be due to its larger Dmi/Dma (Table 5). When the \({f}_{{\text{H}}}\) increased to 5% and 10%, the values of Dmi/Dma for the H-240 amendment became smaller than those for the H-180 amendment, which could not explain the smaller evaporation rates found in the cases of H-240. It is hypothesised that the water existing in the intra-pores of H-240 could not easily evaporate compared with that of H-180 due to its smaller pore peak diameter (36 μm for H-240 and 177 μm for H-180, Fig. 4g).
4.5 WRC
Figure 9a and b show the WRCs of unamended soil and soils amended with the hydrochar produced at 180 and 240 °C. To assist in the interpretation, each WRC was fitted by using van Genuchten model [61]. The fitting parameters are summarised in Table 6. The air-entry value (AEV), defined as the minimum suction beyond which air starts to enter the largest soil pores to make the soil unsaturated, was determined using the Casagrande method [60]. The results indicated that adding a small amount of H-180 (i.e. 2.5%) to the soil increased the AEV marginally from 0.3 to 0.7 kPa, given the limited accuracy of the tensiometers. Increasing \({f}_{{\text{H}}}\) further did not appear to increase the AEV much. The noticeable increase in AEV could be explained by the decrease in the magnitude of the pore throat frequency at Det > 290 μm (corresponding to the suction of < 1.0 kPa; Fig. 6a) due to the addition of the hydrochar particles. A similar phenomenon may be found from other studies that also showed an increase in AEV after amending soil with materials that have substantially smaller GHs (e.g. biochar and fibres) than the soil samples themselves [17, 19]. For the soils amended by H-240 (Fig. 9b), the observed increase in AEV due to the increase in \({f}_{{\text{H}}}\) was attributable to the reduction in the throat frequency at Det > 130 μm (Fig. 6b) and the pore volume for D larger than 100 μm (Fig. 7c). The more significant increase in the AEV made by the amendment of H-240 (compared with that by H-180) may be due to the soils having smaller pores (pore peak at 36 μm; Fig. 4g), when compared with the case of H-180 (pore peak at 119 μm), leading to the soil’s greater retention capability.
The desorption rate of the WRCs, defined as the amount of VWC drop upon an increase in suction beyond the AEV, may be represented by the shape parameter n of van Genuchten model [61]. This parameter is known to empirically relate to the PSDs of the specimens [44]. Adding 2.5% of H-180 to the soil caused an increase in n from 1.125 (unamended soil) to 1.149; however, the value of n subsequently dropped to 1.109 and 1.059 as the \({f}_{{\text{H}}}\) increased to 5 and 10%, respectively (Fig. 9a, Table 6). When the \({f}_{{\text{H}}}\) was relatively small (2.5%), the hydrochar mainly filled the large pores and throats in the soil (Zone III; Figs. 5b and 6a), and changed the size of the pores to a median size (see the increase in frequencies for the pores in Zone II; Figs. 5b and 6a), thus causing the increase in n. As the \({f}_{{\text{H}}}\) was increased to 5 and 10%, the large and median pores and throats were compressed by the higher compaction energy applied, leading to the simultaneous reduction in the pore throats at Det > 90 μm and the increase in the throats at Det < 90 μm (Fig. 6a). This explains the drops of n for the cases of H-180–5% and H-180–10%. Hussain and Ravi [30] also observed the reduction in n for biochar-amended soils and postulated that this phenomenon was associated with the reduction in pore size after biochar amendment (yet PSD was not provided). A similar trend can be found for the soils amended with H-240 (Fig. 9b, Table 6), except that adding a \({f}_{{\text{H}}}\) of 10% returned a larger value of n (i.e. a faster desorption rate). This may be because H-240–10% had the largest throat frequency at Det 50–90 μm, corresponding to the suction of 3.2–5.8 kPa in Fig. 6b). The amendment of H-180 and H-240 at the \({f}_{{\text{H}}}\) of 5% was more significant than that at 10%, especially in terms of both the increase in the AEV and the reduction in the desorption rate.
The data obtained from the independent measurements of relatively high suction (> 500 kPa) by the WP4C exhibited consistent findings with those found in lower suction by the evaporation tests; the addition of hydrochar generally improved the water retention capacity of the soils at the same dry density, especially for the case of H-180 (Fig. 9a). To evaluate the effects of hydrochar on the efficiency of plant water use, field capacity (FC; i.e. the amount of water content held in soil after draining excess water, referring to the value of VWC at 33 kPa suction; [18]) and permeant wilting point (i.e. the amount of water content below which the plant starts to wilt, referring to the value of VWC at suction of 1500 kPa; [49]) were used. As a result, plant available water content (PAWC) was determined by the difference between the FC and permeant wilting point [14]. The values of FC, permeant wilting point and PAWC are summarised in Table 7. Evidently, both the FC and PWP increased with the increase in \({f}_{{\text{H}}}\). Relatively speaking, the soils amended by H-180 increased both the FC and PWP more substantially than that amended by H-240. The addition of hydrochar of 5% \({f}_{{\text{H}}}\) increased the PAWC, yet a further increase in \({f}_{{\text{H}}}\) to 10% had either no influence (e.g. H-180–10%) or even reduced (e.g. H-240–10%) the PAWC. These observations suggest that there exists a threshold \({f}_{{\text{H}}}\) (5% in this case), beyond which a further addition of hydrochar to the soil would become uneconomical in terms of water availability for plants.
4.6 HCF
Figure 10 relates the hydraulic conductivity with the suction of the unamended soil and the soils amended with the hydrochar produced at different HTC temperatures. The saturated hydraulic conductivity (ks) of the unamended and amended soils prepared at the same initial dry density and water content as those used for the evaporation tests were measured by the falling-head tests [7]. The results are shown at 0.1 kPa suction for reference. Before interpreting the test results, it is important to evaluate and filter any errors associated with the estimation of the hydraulic gradient (\(\nabla {H}_{{{\text{m}},t}_{{\text{ave}}}}\)) and, therefore, the hydraulic conductivity (\({k}_{{\text{m}},{t}_{{\text{ave}}}}\)). According to the law of error propagation [37] and Eq. (3), assuming the measurements of water flux \({q}_{{\text{m}},{t}_{{\text{ave}}}}\) by a high-accuracy, high-resolution balance to be error-free, the error of \({k}_{{\text{m}},{t}_{{\text{ave}}}}\) may be evaluated as follows:
where \({Uk}_{{\text{m}},{t}_{{\text{ave}}}}\) is the uncertainty of\({k}_{{\text{m}},{t}_{{\text{ave}}}}\), and \(U\nabla {H}_{{\text{m}},{t}_{{\text{ave}}}}\) is the uncertainty of\(\nabla {H}_{{\text{m}},{t}_{{\text{ave}}}}\). Notably, the calculation of \(\nabla {H}_{{\text{m}},{t}_{{\text{ave}}}}\) is not based on a single measurement, but from two tensiometers in a test (Eq. (3)). Therefore, although the accuracy of the tensiometers was known (1 kPa), the effects of the errors from the tensiometer measurements on \({k}_{{\text{m}},{t}_{{\text{ave}}}}\) cannot be directly evaluated using Eq. (4) [30]. Given that \({k}_{{\text{m}},{t}_{{\text{ave}}}}\) is inversely proportional to \(\nabla {H}_{{\text{m}},{t}_{{\text{ave}}}}\) (Eq. (1)), a small hydraulic gradient could lead to a substantial error in the estimation of\({k}_{{\text{m}},{t}_{{\text{ave}}}}\). Thus, Peters and Durner [48] proposed a rejection criterion on\(\nabla {H}_{{\text{m}},{t}_{{\text{ave}}}}\le 6\frac{{\sigma }_{{\text{h}}}}{\Delta z}\), where \({\sigma }_{{\text{h}}}\) is the measurement error of the tensiometer (i.e. 1 kPa), and \(\Delta z\) is the vertical distance between the two tensiometers (i.e. 45 mm). Correspondingly, the calculated data of hydraulic conductivity were filtered, and any value of \({k}_{{\text{m}},{t}_{{\text{ave}}}}\ge \frac{\Delta {V}_{{t}_{{\text{ave}}}}}{2\cdot {\text{A}}\cdot {\Delta t}_{{\text{ave}}}\cdot \left(6\frac{{\sigma }_{{\text{h}}}}{\Delta z}\right)}=\frac{\Delta {V}_{{t}_{{\text{ave}}}}}{2\cdot {\text{A}}\cdot {\Delta t}_{{\text{ave}}}\cdot 13.33}\)were removed from Fig. 10. For clarity, the filtered data are presented in lines, with several data points added on top to ensure ease of reference to the legend.
The addition of hydrochar produced at different HTC temperatures increased the ks by more than an order of magnitude. Adding 2.5% of H-180 (i.e. H-180–2.5%) and 5% of H-240 (i.e. H-240–5%) generated the most significant increase in ks, beyond which the increase became less effective. The hydrochar affected the ks mainly through the change in the ema of the amended soils. From Table 5, it can be seen that ks had a positive correlation with ema when \({f}_{{\text{H}}}\) was smaller than a respective threshold value. As expected, as air entered the soil pores accompanying the evaporation of the pore water, the hydraulic conductivity of both unamended and amended soils reduced significantly upon suction increase beyond the AEV. The air bubbles trapped in the pores made the water flow path more tortuous, thereby reducing the hydraulic conductivity.
Amending the soil with H-180 (Fig. 10a) to the \({f}_{{\text{H}}}\) of 2.5% reduced the unsaturated hydraulic conductivity of the soil. Based on the PNM obtained from the X-ray CT scanning image, the connected and isolated porosities can be calculated, and the results are summarised in Table 4. Based on the analysis, the reduction in the HCF may be related to the increase in the tortuosity due to the pore clogging effects in Zones I and III (Fig. 6a). On the contrary, amending the soil with H-180 to higher \({f}_{{\text{H}}}\) of 5% and 10% made the unsaturated hydraulic conductivity higher than that of the unamended soil at any given suction. This may be due to the particle rearrangement being accompanied by higher compaction energy, causing an increase in the cumulative throat frequency (Fig. 6a). In turn, the increase in the cumulative throat frequency may contribute to the creation of more water flow path and hence reduce the tortuosity.
When amended with the H-240 (Fig. 10b), the HCF at any suction consistently increased. Indeed, unlike the effect of H-180–2.5%, which reduced the hydraulic conductivity, H-240 at the same \({f}_{{\text{H}}}\) of 2.5% (H-240–2.5%) increased the value of the hydraulic conductivity. Although the throat frequency in Zone III (Fig. 6b) was reduced, the resolved eCT of H-240–2.5% was larger than that of H-180–2.5%, implying an increase in water flow path. The greater amount of intra-pores available in H-240–2.5% than that in H180-2.5% (Fig. 4h) may also explain the increase in the HCF. Careful inspection of the data suggests that at suctions less than 10 kPa, the HCF of H-240–5% was less than H-240–2.5% and H-240–10%, consistent with the variations of the cumulative throat frequency of the soils amended by the H-240 (Fig. 6b). Beyond 10 kPa of suction, the hydraulic conductivity, irrespective of the \({f}_{{\text{H}}}\) considered, appeared to converge to the same HCF. This phenomenon could be attributed to their similar throat frequencies at Det < 10 μm (i.e. corresponding to the suction of > 29.2 kPa; Fig. 6b).
The increases in the WRCs and HCFs of the soil due to the hydrochar amendment are favourable for root water uptake and root growth. Indeed, the greater amount of suction retrained in the hydrochar-amended soil, under a given water content or degree of saturation, could be beneficial to increasing soil shear strength and improving the stability of bioengineered slopes, embankments and landfills. However, the increase in the hydraulic conductivity due to the hydrochar amendment entails the promotion of preferential water flow to certain depths, which could be detrimental to soil stability. Related to this, a more thorough seepage-stability analysis should be carried out in the future to evaluate the overall effects of hydrochar on the seepage characteristics and the implication of the resulting pore-water pressure distribution to soil stability. Further investigations are also needed to focus on any soil shear strength changes due to the amendment of different types of hydrochar. Also, a previous study [75] has shown that only approximately 5% hydrochar would be decomposed after seven days of incubation; this observation suggests that any effects of hydrochar decomposition on the WRCs and HCFs during the 7 day evaporation experiment conducted in the present study might be negligible. Future work should focus on how the hydrochar decomposition in longer term would affect the soil hydro-mechanical properties.
5 Conclusions
This study quantified and investigated the effects of grass-derived hydrochar on the microstructural changes of a compacted silty-clay sand and their influences on the unsaturated hydraulic properties, including WRCs and HCFs of the soil. Compared to H-180, H-240 had a higher carbon content and higher thermal stability but a lower pore volume. Despite using the same feedstock, the derived hydrochar and biochar had remarkably different PSDs due to their different production conditions. Notably, the pore peak of H-180, H-240 and B-500 was 177, 36 and 40 μm, respectively. Hydrochar amendment made the water evaporation rate higher because the addition of hydrochar increased the amounts of the pores and throats (mainly in the pore diameter range of 50–250 μm) and the pore size differences between the peak diameters of micro- (Dmi) and macro-pores (Dma). The addition of hydrochar also enhanced the soils’ water retention capability by increasing the AEV and reducing the desorption rate. The enhancement can be attributed to the pore filling effect of the larger soil pores by the hydrochar, especially those with diameters larger than 290 μm. In particular, at \({f}_{{\text{H}}}\) of 2.5%, the filling of hydrochar in these larger pores (> 290 μm) changed them into median-sized pores of pore throat diameter (Det) ranging from 90 to 290 μm, causing an upward shift of the WRC. As the \({f}_{{\text{H}}}\) exceeded 2.5% (i.e. 5% and 10%), the pores of Det > 90 μm were further compressed by the higher compaction energy required to reach the same dry density of the amended soils. This process was accompanied by an overall reduction in the macro-void ratio, which caused an increase in AEV and a further reduction in the desorption rate. In general, the hydrochar produced at the HTC temperatures of 180 and 240 °C (i.e. H-180 and H-240) introduced a similar change in the WRC for any given \({f}_{{\text{H}}}\), following the same underlying mechanisms to affect the WRC. The two cases only differed in terms of the range of pore diameters being affected due to the difference in the PSDs of the types of hydrochar. Nevertheless, the addition of either H-180 or H-240 increased the plant available water content as long as the \({f}_{{\text{H}}}\) was less than 5%.
The HCFs of compacted soil was increased by half to one order of magnitude by the hydrochar addition (except H-180–2.5%), which was attributed to the increased throat frequency and the contribution of hydrochar intrapores, thus creating more water flow path and reducing the tortuosity. Furthermore, the addition of H-180–2.5% reduced the HCF by approximately half an order of magnitude, which was probably because of the pore clogging effects accompanied by the reduced pore throat frequencies at Det of < 90 μm and > 250 μm, which weakened the pore connections and the increase in the tortuosity. Although the throat frequencies at Det of < 90 μm and > 250 μm were reduced in H-240–2.5%, the HCF was increased because there were more intra-pores in the soil created by H-240 than that by H-180. Based on the test results, the \({f}_{{\text{H}}}\) of 5% may be an optimal mass fraction of hydrochar for soil amendment, as the resulting increases in the WRC, HCF and PAWC are favourable for root water uptake and plant growth.
References
Abel S, Peters A, Trinks S, Schonsky H, Facklam M, Wessolek G (2013) Impact of biochar and hydrochar addition on water retention and water repellency of sandy soil. Geoderma 202:183–191
Alam M, Jiang YJ, Umar M, Su LJ, Rahman M, Ullah F (2021) Influence of drainage and root biomass on soil mechanical behavior in triaxial tests. Acta Geotech 17:1–19
An N, Tang CS, Xu SK, Gong XP, Shi B, Inyang HI (2018) Effects of soil characteristics on moisture evaporation. Eng Geol 239:126–135
ASTM D 2487 (2011) Standard Practice for Classification of Soils for Engineering Purposes (unified soil classification system). West Conshohocken, PA: ASTM
ASTM D3174 (2012a). Standard Test Method for Ash in the Analysis Sample of Coal and Coke from Coal. West Conshohocken, PA: ASTM
ASTM D698 (2012b) Standard Test Methods for Laboratory Compaction Characteristics of Soil using Standard Effort (12400 ft-lbf/ft3(600 kN-m/m3)). West Conshohocken, PA: ASTM
ASTM D5084 (2016) Standard Test Methods for Measurement of Hydraulic Conductivity of Saturated Porous Materials Using a Flexible Wall Permeameter. West Conshohocken, PA: ASTM
ASTM D3175 (2017) Standard Test Method for Volatile Matter in the Analysis Sample of Coal and Coke. West Conshohocken, PA
Bargmann I, Rillig MC, Kruse A, Greef JM, Kücke M (2014) Effects of hydrochar application on the dynamics of soluble nitrogen in soils and on plant availability. J Plant Nutr Soil Sci 177(1):48–58
Barrett EP, Joyner LG, Halenda PP (1951) The determination of pore volume and area distributions in porous substances. I. Computations from nitrogen isotherms. J Am Chem Soc 73(1):373–380
Basso D, Weiss-Hortala E, Patuzzi F, Castello D, Baratieri M, Fiori L (2015) Hydrothermal carbonization of off-specification compost: a byproduct of the organic municipal solid waste treatment. Bioresour Technol 182:217–224
Boldrin D, Leung AK, Bengough AG (2020) Hydro-mechanical reinforcement of contrasting woody species: a full-scale investigation of a field slope. Geotechnique 71(11):970–984
Brunauer S, Emmett PH, Teller E (1938) Adsorption of gases in multimolecular layers. J Am Chem Soc 60(2):309–319
Cassel DK, Nielsen DR (1986) Field capacity and available water capacity. Methods soil anal Part 1 Phys Mineral Methods 5:901–926
CEDD. General specification for civil engineering works (GS) (2006) Civil Engineering and Development Department, the HKSAR Government; Volume 1
Chen B, Cai W, Garg A (2023) Relationship between bioelectricity and soil–water characteristics of biochar-aided plant microbial fuel cell. Acta Geotech 18:1–14
Chen Z, Chen C, Kamchoom V, Chen R (2020) Gas permeability and water retention of a repacked silty sand amended with different particle sizes of peanut shell biochar. Soil Sci Soc Am J 84(5):1630–1641
Colman EA (1947) A laboratory procdure for determining the field capacity of soils. Soil Sci 63(4):277–284
de Gusmão LRC, Jucá JFT (2021) Influence of green’s coconut fibers in the unsaturated behavior of compacted clayey soil. In: MATEC Web of Conferences, Vol. 337, p 01017. EDP Sciences
Delage P, Audiguier M, Cui YJ, Howat MD (1996) Microstructure of a compacted silt. Can Geotech J 33(1):150–158
Eibisch N, Durner W, Bechtold M, Fuß R, Mikutta R, Woche SK, Helfrich M (2015) Does water repellency of pyrochars and hydrochars counter their positive effects on soil hydraulic properties? Geoderma 245:31–39
Fang J, Gao B, Chen J, Zimmerman AR (2015) Hydrochars derived from plant biomass under various conditions: characterization and potential applications and impacts. Chem Eng J 267:253–259
Garg A, Wani I, Zhu H, Kushvaha V (2022) Exploring efficiency of biochar in enhancing water retention in soils with varying grain size distributions using ANN technique. Acta Geotech 17:1–12
Ghestem M, Sidle RC, Stokes A (2011) The influence of plant root systems on subsurface flow: implications for slope stability. Bioscience 61(11):869–879
Glendinning S, Hughes P, Helm P, Chambers J, Mendes J, Gunn D, Uhlemann S (2014) Construction, management and maintenance of embankments used for road and rail infrastructure: implications of weather induced pore water pressures. Acta Geotech 9:799–816
Hapca SM, Houston AN, Otten W, Baveye PC (2013) New local thresholding method for soil images by minimizing grayscale intra-class variance. Vadose Zone J. https://doi.org/10.2136/vzj2012.0172
Hardie M, Clothier B, Bound S, Oliver G, Close D (2014) Does biochar influence soil physical properties and soil water availability? Plant soil 376(1):347–361
Harvey OR, Kuo LJ, Zimmerman AR, Louchouarn P, Amonette JE, Herbert BE (2012) An index-based approach to assessing recalcitrance and soil carbon sequestration potential of engineered black carbons (biochars). Environ Sci Technol 46(3):1415–1421
Hong Z, Zhong F, Niu W, Zhang K, Su J, Liu J, Wu F (2020) Effects of temperature and particle size on the compositions, energy conversions and structural characteristics of pyrolysis products from different crop residues. Energy 190:116413
Hussain R, Ravi K (2021) Investigating unsaturated hydraulic conductivity and water retention characteristics of compacted biochar-amended soils for potential application in bioengineered structures. J Hydrol 603:127040
Hussary J, Alowaisy A, Yasufuku N, Ishikura R, Abdelhadi M (2022) Pore structure and falling rate stage of evaporation in homogeneous sandy soil profiles. Soils Found 62(2):101108
Kambo HS, Dutta A (2015) A comparative review of biochar and hydrochar in terms of production, physio-chemical properties and applications. Renew Sust Energ Rev 45:359–378
Kameyama K, Miyamoto T, Shiono T, Shinogi Y (2012) Influence of sugarcane bagasse-derived biochar application on nitrate leaching in calcaric dark red soil. J Environ Qual 41(4):1131–1137
Karimzadeh AA, Leung AK, Hosseinpour S, Wu Z, Fardad Amini P (2021) Monotonic and cyclic behaviour of root-reinforced sand. Can Geotech J 99(999):1915–1927
Karimzadeh AA, Kwan Leung A, Amini PF (2022) Energy-based assessment of liquefaction resistance of rooted soil. J Geotech Geoenviron Eng 148(1):06021016
Kloss S, Zehetner F, Dellantonio A, Hamid R, Ottner F, Liedtke V, Soja G (2012) Characterization of slow pyrolysis biochars: effects of feedstocks and pyrolysis temperature on biochar properties. J Environ Qual 41(4):990–1000
Ku HH (1966) Notes on the use of propagation of error formulas. J Res Natl Bur Stand 70(4):263–273
Lehmann P, Assouline S, Or D (2008) Characteristic lengths affecting evaporative drying of porous media. Phys Rev E 77(5):056309
Leung AK, Kamchoom V, Ng CWW (2017) Influences of root-induced soil suction and root geometry on slope stability: a centrifuge study. Can Geotech J 54(3):291–303
Libra JA, Ro KS, Kammann C, Funke A, Berge ND, Neubauer Y, Emmerich KH (2011) Hydrothermal carbonization of biomass residuals: a comparative review of the chemistry, processes and applications of wet and dry pyrolysis. Biofuels 2(1):71–106
Lloret A, Villar MV, Sanchez M, Gens A, Pintado X, Alonso EE (2003) Mechanical behaviour of heavily compacted bentonite under high suction changes. Géotechnique 53(1):27–40
Lu S, Zong Y (2018) Pore structure and environmental serves of biochars derived from different feedstocks and pyrolysis conditions. Environ Sci Pollut Res 25(30):30401–30409
Ng CWW, Leung AK, Woon KX (2014) Effects of soil density on grass-induced suction distributions in compacted soil subjected to rainfall. Can Geotech J 51(3):311–321
Ng CWW, Sadeghi H, Hossen SB, Chiu CF, Alonso EE, Baghbanrezvan S (2016) Water retention and volumetric characteristics of intact and re-compacted loess. Can Geotech J 53(8):1258–1269
Ng CWW, Liao JX, Bordoloi S (2022) Relationship between matric suction and leaf indices of Schefflera arboricola in biochar amended soil. Can Geotech J 59(2):191–202
Ni JJ, Chen XW, Ng CWW, Guo HW (2018) Effects of biochar on water retention and matric suction of vegetated soil. Geotech Lett 8(2):124–129
Otsu N (1979) A threshold selection method from gray-level histograms. IEEE Trans Syst Man Cybern 9(1):62–66
Peters A, Durner W (2008) Simplified evaporation method for determining soil hydraulic properties. J Hydrol 356(1–2):147–162
Richards LA, Weaver LR (1943) Fifteen-atmosphere percentage as related to the permanent wilting percentage. Soil Sci 56(5):331–340
Schimmelpfennig S, Glaser B (2012) One step forward toward characterization: some important material properties to distinguish biochars. J Environ Qual 41(4):1001–1013
Schindler U, Müller L (2006) Simplifying the evaporation method for quantifying soil hydraulic properties. J Plant Nutr Soil Sci 169(5):623–629
Sekharan S, Gadi VK, Bordoloi S, Saha A, Kumar H, Hazra B, Garg A (2019) Sustainable geotechnics: a bio-geotechnical perspective. In: Madhavi Latha G (ed) Frontiers geotechnical engineering. Springer, Berlin, pp 313–331
Seow YX, Tan YH, Mubarak NM, Kansedo J, Khalid M, Ibrahim ML, Ghasemi M (2022) A review on biochar production from different biomass wastes by recent carbonization technologies and its sustainable applications. J Environ Chem Eng 10(1):107017
Sharma RH, Konietzky H, Kosugi KI (2010) Numerical analysis of soil pipe effects on hillslope water dynamics. Acta Geotech 5:33–42
Soil Science Society of America (1997) Glossary of Soil Science Terms Madison, WI
Silin D, Patzek T (2006) Pore space morphology analysis using maximal inscribed spheres. Phys A Stat Mech Appl 371(2):336–360
Spokas KA (2010) Review of the stability of biochar in soils: predictability of O: C molar ratios. Carbon Manag 1(2):289–303
Stokes A, Atger C, Bengough AG, Fourcaud T, Sidle RC (2009) Desirable plant root traits for protecting natural and engineered slopes against landslides. Plant soil 324:1–30
Uzoma KC, Inoue M, Andry H, Zahoor A, Nishihara E (2011) Influence of biochar application on sandy soil hydraulic properties and nutrient retention. J Sci Food Agric Environ 9(¾ part 2):1137–1143
Vanapalli SK, Fredlund DG, Pufahl DE (1999) The influence of soil structure and stress history on the soil–water characteristics of a compacted till. Geotechnique 49(2):143–159
Van Genuchten MT (1980) A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci Soc Am J 44(5):892–898
Van Krevelen DW (1950) Graphical-statistical method for the study of structure and reaction processes of coal. Fuel 29:269–284
Villagra-Mendoza K, Horn R (2018) Effect of biochar on the unsaturated hydraulic conductivity of two amended soils. Int Agrophys, 32(3)
Vorhauer N, Metzger T, Tsotsas E, Prat M (2012) Experimental investigation of drying by pore networks: influence of pore size distribution and temperature. In: 4th International Conference on Porous Media and its Applications in Science, Engineering and Industry
Wanniarachchi D, Cheema M, Thomas R, Kavanagh V, Galagedara L (2019) Impact of soil amendments on the hydraulic conductivity of boreal agricultural podzols. Agriculture 9(6):133
Wong JTF, Chen Z, Wong AYY, Ng CWW, Wong MH (2018) Effects of biochar on hydraulic conductivity of compacted kaolin clay. Environ Pollut 234:468–472
Wu Z, Leung AK, Boldrin D, Ganesan SP (2021) Variability in root biomechanics of Chrysopogon zizanioides for soil eco-engineering solutions. Sci Total Environ 776:145943
Xiao LP, Shi ZJ, Xu F, Sun RC (2012) Hydrothermal carbonization of lignocellulosic biomass. Bioresour Technol 118:619–623
Yang F, Zhao L, Gao B, Xu X, Cao X (2016) The interfacial behavior between biochar and soil minerals and its effect on biochar stability. Environ Sci Technol 50(5):2264–2271
Yang H, Yan R, Chen H, Lee DH, Zheng C (2007) Characteristics of hemicellulose, cellulose and lignin pyrolysis. Fuel 86(12–13):1781–1788
Zhang B, Heidari M, Regmi B, Salaudeen S, Arku P, Thimmannagari M, Dutta A (2018) Hydrothermal carbonization of fruit wastes: a promising technique for generating hydrochar. Energies 11(8):2022
Zhang Y, Gu K, Li J, Tang C, Shen Z, Shi B (2020) Effect of biochar on desiccation cracking characteristics of clayey soils. Geoderma 364:114182
Zhang Z, Zhu Z, Shen B, Liu L (2019) Insights into biochar and hydrochar production and applications: a review. Energy 171:581–598
Lehmann J, Joseph S (eds) (2009) Biochar for environmental management (Vol. 1). Earthscan, London
Eibisch N, Helfrich M, Don A, Mikutta R, Kruse A, Ellerbrock R, Flessa H (2013) Properties and degradability of hydrothermal carbonization products. J Environ Qual 42(5):1565–1573
Acknowledgements
This research work was supported by the grants funded by the Hong Kong Research Grants Council (CRF/C6006-20G and GRF/16207521), a grant provided by the Joint NSFC/RGC Joint Research Scheme (N_HKUST603/22) and a grant from the initiative on the Sustainable Smart Campus as Living Lab, from the Hong Kong University of Science and Technology.
Funding
Open access funding provided by Hong Kong University of Science and Technology.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Dong, H., Leung, A.K., Liu, J. et al. Microstructural investigation of the unsaturated hydraulic properties of hydrochar-amended soils. Acta Geotech. 19, 833–853 (2024). https://doi.org/10.1007/s11440-024-02254-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11440-024-02254-7