A novel DEM-based pore-scale thermal-hydro-mechanical model for fractured non-saturated porous materials

Abstract

For fracture propagation, a novel DEM-based pore-scale thermal-hydro-mechanical model of two-phase fluid flow with heat transfer in non-saturated porous materials with low porosity was developed. Numerical computations were performed for bonded granular specimens, using a DEM fully coupled with CFD (based on a fluid flow network) and heat transfer, which integrated discrete mechanics with fluid mechanics and heat transfer at the meso-scale. Both the fluid (diffusion and advection) and bonded particles (conduction) were involved in heat transfer. The numerical findings of the coupled thermal-hydraulic-mechanical (THM) model were first compared to the analytical solution of the classic 1D heat transport problem. The numerical and analytical outcomes were in perfect agreement. Advection's impacts on the cooling of a bonded particle assembly were next numerically demonstrated for low and high Peclet numbers. Finally, the THM model's utility was proved in a thermal contraction test employing a bonded particle assembly during cooling, which resulted in the creation of a macro-crack. The effects of a macro-crack on the distribution of fluid pressure, density, velocity, and temperature were studied.

1 Introduction

The majority of physical phenomena in engineering challenges happen in non-isothermal environments. Furthermore, even if the physical system is initially in thermodynamic equilibrium, physical processes or chemical reactions may cause local temperature fluctuations, resulting in heat transfer. Only in a few circumstances may the engineering problem under investigation be reduced to isothermal conditions. As a result, numerous scientific disciplines and technical applications, such as environmental science, chemical and food processing, powder metallurgy, energy management, geomechanics, and geological engineering, are interested in understanding heat transfer in particle systems. In the analysis of many multi-field issues in porous and fractured materials, the requirement to address the effect of heat transfer becomes crucial. Diffusion, advection, and radiation are examples of heat transmission mechanisms. Many nonlinear processes affect complex coupled thermal–hydraulic–mechanical (THM) systems, which include heat transfer, fluid flow, and material deformation.

The most popular technique in THM models is a continuum approach, which is based on a mathematical framework linking sets of differential equations to explain thermodynamic, solid, and fluid mechanics laws, such as finite element [19, 26, 31, 36, 39, 52], or finite difference implementations [37]. Even though they are appealing for macro-scale applications, continuum modelling approaches based on the finite element method (FEM) or the finite volume method (FVM) have significant computational and continuity limitations when applied to discontinuous and highly deformable media like packed or fluidized beds and fractured granular porous materials. Classical approaches have tremendous numerical challenges generating suitably fine meshes in porous media with low porosity (less than around 15%), such as concrete or rocks [1]. When modelling the crack initiation and propagation in porous materials with low porosity, the problem is amplified dramatically (e.g. concrete or rocks). Discrete techniques, such as the discrete element method (DEM) [13] or the finite-discrete element method (FDEM) [49, 50], on the other hand, have proven to be successful in modelling the behaviour of particulate systems. The capacity to directly capture and predict fracture and micro-crack evolution through particulate materials is a benefit of DEM. Yan and Zheng [50] created a 2D thermo-mechanical model based on the FDEM (finite-discrete element technique) for modelling thermal rock cracking, while Yan et al. [49] created a 2D coupled thermal-hydro-mechanical model for simulating rock hydraulic fracturing. The ability to anticipate coupled THM processes at the meso-scale has recently been expanded because of DEM's strength in realistic simulations of the behaviour of fragmented particle systems. Various methods were adopted to combine DEM with fluid flow and heat transfer methodologies, to connect TH processes with DEM, direct numerical simulations (DNS) could be used. Different numerical approaches (for example, FEM and FVM) were applied to solve governing equations. Deen et al. [14] suggested a method for implementing submerged boundaries that did not require the use of an effective diameter. THM processes in dense fluid-particle systems were the subject of the approach. The proposed approach was confined to invariant geometries, topologies, and porosities of relatively high values (porosities greater than those of concrete or rock). DNS-DEM models, in reality, are limited to systems with fewer particles than CFD models. The lattice Boltzmann methods (LBMs) [10, 18, 51] rely heavily on the precise depiction of solid–fluid interfaces and have the same numerical and computational restrictions as DNS-DEM models.

To decrease computing costs and overcome numerical restrictions when utilizing DEM to THM processes in very dense fluid–particle systems with very low porosity (even below 5%), the fluid flow and heat transfer models must be reduced. Recently, most DEM-based THM models separated fluid flow within reservoirs (pores, macro-pores, pre-existing cracks, etc.) from the flow between reservoirs. According to the assumption, the fluid in the reservoirs is compressible, but the fluid flowing between the reservoirs is incompressible. Cundall [11], Hazzard et al. [16], and Al-Busaidi et al. [2] were the first to introduce and explore the concept of simplification. In addition to highlighting fluid characteristics, fluid flow regimes are separated. To estimate the mass flow rates at the reservoirs' boundaries, the fluid flow regime in the reservoirs is stationary or close to stagnation, while the fluid flow between the reservoirs is laminar. In most cases, a Poiseuille flow model in pipes or between two parallel plates is utilized to predict mass flow rates. The pressure in the pore is calculated using either the assumed equation of state [2, 16] or the Stokes equation [7, 32]. All models assume a pure liquid or mixture flowing in a single-phase barotropic fluid flow (without tracking phase fractions). Different heat transfer models are combined with coupled DEM–CFD models in this technique. For each reservoir (cell) volume, Tomac and Gutierrez [46] computed the energy conservation equation. The selected energy conservation equation was related to energy transport in an incompressible fluid's laminar flow. Caulk et al. [8] proposed a more advanced 3D DEM-based THM model based on the framework of the pore-scale finite volume (PFV) scheme, which was first proposed by Chareyre et al. [9] and later extended by Scholtès et al. [38] for up-scaling compressible viscous flow and oriented towards saturated dense grain packing applications in geomechanics.

The purpose of this work is to show a new DEM-based pore-scale hydro-mechanical model of two-phase fluid flow in non-saturated porous materials with very low porosity that is enhanced by heat transfer (e.g. for concrete or rocks). Both the fluid (diffusion and advection) and the bonded particles (conduction) were involved in heat transfer. THM calculations were carried out numerically using a 3D DEM in conjunction with 2D CFD (based on a fluid flow network made up of channels) and 2D heat transfer, which connected discrete mechanics, fluid mechanics, and heat transfer at the meso-scale. Previously, a coupled DEM/CFD model based on the fluid flow network without heat transfer (formulated by the authors [24, 25]) was used to describe hydraulic fracturing in unsaturated rock masses with one- or two-phase laminar viscous two-phase fluid flow containing a liquid and gas.

This paper's DEM-based THM mesoscopic technique for modelling fluid flow and heat transfer has substantial advantages over other existing ones in the literature. Some of the advantages are as follows:

• 1. the precise tracking of water/gas fractions in pores, taking into account their variable geometry, size, and position,

• 2. an effective algorithm for automatically meshing and remeshing particle and fluid domains to account for changes in their geometry and topology,

• 3. the use of a coarse mesh of solid and fluid domains to generate a virtual fluid flow network (VPN) and to solve the energy conservation equation,

• 4. using FVM to solve the energy conservation equation in both domains on a very coarse mesh of cells,

• 5. to examine supercritical fluid flow, the corrected Peng–Robinson equation of state [34] was adopted for both fluid phases (necessary e.g. for studying THM processes in hydraulic fracturing problems),

• 6. calculating varying heat fields in pores and particles,

• 7. tracking virtual thermal deformation of discrete elements to precisely compute fluid volume changes over time, and

• 8. two-phase flow.

There are no coupled DEM-based thermal-hydro-mechanical models of multi-phase supercritical fluid flow in rocks that can be used to mimic THM processes during hydraulic fracturing. The numerical findings in the current paper are first compared to the analytical solution of the classic 1D heat transfer issue to validate the innovative fully coupled THM model. The numerical and analytical results are found to be perfectly in agreement. A numerical representation of the effects of advection on the cooling of a bonded granular bar specimen is also provided. Finally, the THM model's utility is proved in a thermal contraction test employing a bonded particle assembly during cooling, which results in the creation of a macro-crack. The effects of a macro-crack on fluid pressure, density, velocity, and temperature are investigated. The findings of this study can be directly applied to a variety of geothermal applications.

The structure of the current study is outlined below. Following Sect. 1, a mathematical model of the DEM-based linked thermal-hydro-mechanical method is provided in Sect. 2. The calibration of the model is detailed in Sect. 3. The validation of the THM model is described in Sect. 4. The influence of advection on the cooling of a bonded granular assembly is examined in Sect. 5. A damage process in a bonded granular assembly during a thermal contraction test is discussed in Sect. 6. Finally, in Sect. 7, some closing remarks are made. The THM model has been incorporated by the authors into the YADE DEM code, which is an opensource software [20, 41].

2 Thermo-hydro-mechanical model

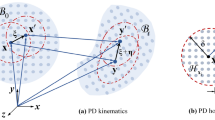
The THM model's original concept is based on the notion that in a physical system, two domains coexist: the 3D discrete (solid) domain and the 2D continuous (fluid) domain. The solid domain is made up of a single layer of discrete 3D elements (spheres), whereas the fluid domain was two-dimensional (Fig. 1a). Discrete elements are placed so that their centres of gravity are in the middle of the plane (2D surface). They are projected next onto the plane to form circles (Fig. 1b). As a result, discrete element equations of motion are solved in the 3D discrete domain, whereas fluid flow equations are solved in the 2D fluid continuous domain (red colour in Fig. 1), and heat transfer equations are solved in the 2D fluid and solid continuous domains (red and grey colours in Fig. 1b). Despite the use of a 3D DEM solver, the entire DEM-based THM model is two-dimensional.

Fig. 1

Two domains coexisting in one physical system: a coexisting domains before projection and discretization and b solid and fluid domains after discrete elements projection and discretization (fluid domain is in red colour and solid domain is in grey colour)

2.1 DEM for cohesive-frictional materials

DEM calculations were performed with the 3D spherical explicit discrete element open code YADE [20, 41] that allows for a small overlap between two contacted bodies (soft-particle model). Utilizing an explicit time-stepping scheme, particles in DEM interact with one another during translational and rotational motions using a contact law and Newton's 2nd law of motion [13]. A cohesive bond at the grain contact is postulated in the model, with brittle failure beneath the critical normal tensile force. Under normal compression, shear cohesion failure causes contact slip and sliding, which follows the Coulomb friction law. The mechanical response of DEM is presented in Fig. 2. The DEM equations are below

$$\vec{F}_{n} = K_{n} U\overrightarrow {N,}$$

(1)

$$\vec{F}_{s} = \vec{F}_{{s,{\text{prev}}}} + K_{s} \Delta \vec{X}_{s} ,$$

(2)

$$K_{n} = E_{c} \frac{{2R_{A} R_{B} }}{{R_{A} + R_{B} }}\;{\text{and}}\;K_{s} = v_{c} E_{c} \frac{{2R_{A} R_{B} }}{{R_{A} + R_{B} }},$$

(3)

$$\left\| {\vec{F}_{s} } \right\| - F_{\max }^{s} - \left\| {\vec{F}_{n} } \right\| \times \tan \mu_{c} \le 0\quad ({\text{before contact breakage}}),$$

(4)

$$\left\| {\vec{F}_{s} } \right\| - \left\| {\vec{F}_{n} } \right\| \times \tan \mu_{c} \le 0\quad \left( {\text{after contact breakage}} \right),$$

(5)

$$F_{\max }^{s} = CR^{2} \;{\text{and}}\;F_{\min }^{n} = TR^{2} ,$$

(6)

$$\vec{F}_{{{\text{damp}}}}^{k} = \vec{F}^{k} - \alpha_{d} \cdot {\text{sgn}} \left( {\vec{v}_{p}^{k} } \right)\vec{F}^{k} .$$

(7)

where ${\overrightarrow{F}}_{n}$-the normal contact force, U-the overlap between discrete elements, $\overrightarrow{N}$-the unit normal vector at contact point, ${\overrightarrow{F}}_{s}$-the tangential contact force, ${\overrightarrow{F}}_{s,\mathrm{prev}}$-the tangential contact force in the previous iteration, ${\overrightarrow{X}}_{s}$-the relative tangential displacement increment, K_n-the normal contact stiffness, K_s-the tangential contact stiffness, E_c-the elastic modulus of the particle contact, v_c-the Poisson’s ratio of particle contact, R-the particle radius, R_A and R_B contacting particle radii, μ_c-the Coulomb inter-particle friction angle, ${F}_{\mathrm{max}}^{s}$-the critical cohesive contact force, ${F}_{\mathrm{min}}^{n}$-the minimum tensile force, C-the cohesive contact stress (maximum shear stress at pressure equal to zero), and T-the tensile normal contact stress, ${\overrightarrow{F}}_{\mathrm{damp}}^{k}$-the dampened contact force, ${\overrightarrow{F}}^{k}$ and ${\overrightarrow{v}}_{p}^{k}$-kth-the components of the residual force and translational particle velocity v_p and α_d-the positive damping coefficient smaller than 1 (sgn(·) that returns the sign of the kth component of velocity) [12]. Non-viscous damping was applied [12] to accelerate convergence in quasi-static simulations (Eq. 7).

Fig. 2

Mechanical response of DEM: a tangential contact model, b normal contact model, c loading and unloading path in tangential contact model and d modified Mohr–Coulomb model [20, 41]

The following material constants: E_c, υ_c, μ_c, C and T are required for DEM simulations. In addition, R, ρ, (mass density) and α_d are needed. The C/T-ratio is crucial to adequately simulate the failure type of specimens (brittle or quasi-brittle), the distribution of shear and tensile cracks, and the ratio between the uniaxial compressive and tensile strength. The material constants are usually identified by running a series of DEM simulations and comparing them with experimental results of simple tests (e.g. uniaxial compression, triaxial compression, simple shear) [28]. The damping parameter is always α_d = 0.08. For this value, the loading velocity v does not affect the results [28]. Damage occurs if a cohesive joint between spheres (Eq. 6) disappears after reaching a critical threshold. If any contact between spheres after failure re-appears, the cohesion does not appear more (Eq. 5). Note that material softening is not considered in the DEM model. Although bonds can break by shear, the essential micro-scale mechanism for damage in the pre-failure regime is bond damage in tension. An arbitrary micro-porosity might be achieved in DEM since the particles may overlap. The fracture is not allowed to propagate through aggregate, i.e. the particle breakage is not taken into account. The model was successfully used by the authors for describing the behaviour of different engineering materials with a granular structure (mainly of granular materials [21,22,23, 48] and concrete materials [29, 30, 40, 42–44] by taking shear localization and fracture into account).

2.2 Fluid flow model

The general concept of a fluid flow algorithm using DEM and a channel network is adopted from [2, 11, 16]. In this concept, fluid flow is simulated by assuming that each particle contact is an artificial flow channel (between two parallel plates in 2D or along a duct in 3D) and those artificial channels connect real reservoirs in the particulate medium (pores, fractures, and pre-existing cracks) that store fluid pressures. Thus, the pressure in reservoirs depends both on the mass transported along channels from/to other reservoirs and the volume changes of reservoirs. Since the volume of reservoirs changes due to the material deformation (described by discrete elements in DEM), the fluid density must also change (the fluid in reservoirs is compressible). Thus, the fluid moves in channels while the reservoirs solely store pressure. The artificial channels create a fluid flow network. The fluid flow in those artificial channels is characterized by a simplified laminar flow of an incompressible fluid as opposed to the compressible fluid model in real reservoirs.

The fluid model in the current paper significantly differs from the general concept [2, 11, 16]. The reservoirs (pores, cracks, pre-existing cracks, etc.) store now not only pressures but also phase fractions, fluids densities, energy, and temperature. The continuity equation is employed to compute the density of fluid phases stored in reservoirs. The fluid-phase fractions in reservoirs are computed by applying the equation of state for each phase assuming that fluid phases share the same pressure (as in the Euler model of multi-phase flow). The mass flow rate in artificial channels of a fluid flow network is now estimated by solving continuity and momentum equations for the laminar flow of incompressible fluid. The gravity centres of the 3D spheres are located on the XOY plane. The 3D spherical particles are projected onto the 2D mid-plane and next discretized into the 2D polygons [24]. To get a more realistic distribution of the unknown variables (pressure, fluid-phase fractions, and densities), a remeshing procedure discretizes the overlapping circles, determines the contact lines, and deletes the overlapping areas [24]. As a result, each reservoir is discretized into a number of triangles (in 2D problems). Each triangle in the fluid domain is called the Virtual Pore (VP) (Fig. 3). The artificial channels connect the gravity centres of triangles (VPs) to create a fluid flow network called the Virtual Pore Network (VPN). The displacements of discrete elements in the perpendicular direction OZ and the rotations around the axes OX and OY are fixed. All forces converted from pressure and shear stress are applied to the spheres. The forces are computed, based on the pressure and shear stress for the specimen thickness (in the OZ direction) equal to the largest diameter of spheres. All numerical parameters might be used without the necessity of re-calibration. VPs accumulate pressure and store both fluid-phase fractions and densities, energy, and temperature. The mass change in VPs is related to the density change in a fluid phase that results in pressure variations. The equation of momentum conservation is neglected in triangles but the mass is still conserved in the entire volume of triangles. The numerical algorithm can be divided into five main stages:

• a) estimating the mass flow rate for each phase of fluid flowing through the cell faces (in channels surrounding VP) by employing continuity and momentum equations,

• b) computing the phase fractions and their densities in VP by employing equations of state and continuity,

• c) computing pressure in VP by employing the equation of state,

• d) solving the energy conservation equation in fluid and solids,

• e) updating material properties.

Fig. 3

Fluid flow network in material matrix with triangular discretization of pores (in blue): A channel type ‘S2S’ (red colour) and B channel type ‘T2T’ (red colour) [24]

This algorithm is repeated for each VP in VPN and each solid cell (stage ‘d’) using an explicit formulation. According to the above algorithm, incompressible laminar two-phase fluid (liquid/gas) flow under non-isothermal conditions is assumed in the channels of the fluid flow network. The liquid and gas initially exist in the material matrix and pre-existing discontinuities. Two types of channels are introduced in the Virtual Pore Network [24] (Fig. 3): (A) the channels between discrete elements of the material matrix in contact (called the ‘S2S’ channels) and (B) the channels connecting grid triangles in pores that touch each other by a common edge (called the ‘T2T’ channels). The channel length is assumed to be equal to the distance between the gravity centres of adjacent grid triangles. In real 3D problems, the fluid flows around the spheres in contact. However, in 2D problems, there is no free space for fluid flow. Therefore, the concept of virtual S2S channels is introduced [24]. The hydraulic aperture h of the channels ‘S2S’ is related to the normal stress at the particle contact by a modified empirical formula of Hökmark et al. [35]:

$$h = \beta \left( {h_{\inf } + \left( {h_{0} - h_{\inf } } \right)e^{{ - 1.5 \times 10^{ - 7} \sigma_{n} }} } \right),$$

(8)

where ${h}_{\mathrm{inf}}$ is the hydraulic aperture for the infinite normal stress, ${h}_{0}$-the hydraulic aperture for the zero normal stress, ${\sigma }_{n}$-the effective normal stress at the particle contact and β-the aperture coefficient. The hydraulic aperture of the channel type ‘T2T’ is directly related to the geometry of the adjacent triangles as

$$h = \gamma e\cos \left( {90^{^\circ } - \omega } \right).$$

(9)

where e-the edge length between two adjacent triangles, ω-the angle between the edge with the length e and the centre line of the channel that connects two adjacent triangles and γ-the reduction factor, necessary to fit the fluid flow intensity to real complex fluid flow conditions in materials. The reduction factor γ is determined in parametric studies to keep the maximum Reynolds number R_e along the main flow path always lower than the critical one for laminar flow.

2.2.1 Mass flow rate in channels

Three flow regimes in the VPN channels are distinguished: (a) single gas-phase flow with gas-phase fraction α_p = 1, (b) single liquid-phase flow with liquid phase fraction α_q = 1 and (c) two-phase flow (liquid and gas) with 0 < α_q < 1. For single-phase flow in channels (flow regime ‘a’ and ‘b’), the fluid moves in channels through a thin film region separated by two closely spaced parallel plates according to a classical lubrication theory [35], based on the Poiseuille flow law [5]. As a result, the mass flow rate of the single-phase flow along channels is

$$M_{x} = \rho \frac{{h^{3} }}{12\mu }\frac{{P_{i} - P_{j} }}{L},$$

(10)

where ${M}_{x}$-the mass fluid flow rate (per unit length) across the film thickness in the x-direction [kg/(m s)], h-the hydraulic channel aperture (its perpendicular width) [m], ρ-the fluid density [kg/m³], t-the time [s], μ-the dynamic fluid (liquid or gas) viscosity [Pa s] and P-the fluid pressure [Pa] (${P}_{i}$ and ${P}_{j}$ are the pressures in the adjacent VPs).

A two-phase flow of two immiscible and incompressible fluids in a channel (Fig. 4) is assumed to simulate a two-phase fluid flow (flow regime ‘c’), driven by a pressure gradient in adjacent VPs. The liquid–gas interface is parallel to the channel plates and constant along the channel. Gravity forces are neglected. The interface between the fluids, labelled as j = q, p (q-the lower liquid phase and p-the upper gas phase), is assumed to be flat in the undisturbed flow state. Under this assumption, the model allows for a plane-parallel solution. The interface position is known and is related to fractions of fluid phases in adjacent VPs while the volumetric flow rates of fluid phases are unknown.

Fig. 4

Two-layer fluid flow in channels ‘S2S’ and ‘T2T’ (h-channel aperture, L-channel length, ‘q’-liquid and ‘p’-gas) [25]

Continuity and momentum equations characterize the flow in each phase. The time and pressure are scaled by ${h}_{p}/{u}_{i}$ and ${\rho }_{p}{u}_{i}^{2}$ (h_p-the height of the upper layer and u_i-the interfacial velocity). The dimensionless continuity and momentum equations are [3]

$$div {\mathbf{u}}_{j} = 0,$$

(11)

$$\frac{{\partial u_{j} }}{\partial t} + \left( {{\mathbf{u}}_{j} \cdot \nabla } \right){\mathbf{u}}_{j} = - \frac{{\rho_{q} }}{{r\rho_{j} }}\nabla p_{j} + \frac{1}{{{\text{Re}}_{p} }}\frac{{\rho_{q} }}{{r\rho_{j} }}\frac{{mu_{j} }}{{\mu_{q} }} \cdot {\mathbf{u}}_{j} ,$$

(12)

where ${\text{u}}_{j}=\left({u}_{j},{v}_{j}\right)$ and ${p}_{j}$ are the velocity and pressure of the fluid phase j, ${\rho }_{j}$ and ${\mu }_{j}$ are the corresponding density and dynamic viscosity. The Reynolds number is ${\text{Re}}_{p}={\rho }_{p}{u}_{i}{h}_{p}/{\mu }_{p}$ and the density and viscosity ratios are $r={\rho }_{q}/{\rho }_{p}$ and $m={\mu }_{q}/{\mu }_{p}$. In the dimensionless formulation, the lower and upper phases occupy the regions $-{n}_{d}\le y\le 0$ and $0\le y\le 1$, where ${n}_{d}={h}_{q}/{h}_{p}$. At the channel walls, the velocities meet the no-slip boundary condition

$$u_{q} \left( {y = - n_{d} } \right) = 0\;{\text{and}}\;u_{p} \left( {y = 1} \right) = 0.$$

(13)

The boundary conditions at the interface $y=0$ require the continuity of velocity components and tangential stresses [3]

$$u_{q} \left( {y = 0} \right) = u_{p} \left( {y = 0} \right)$$

(14)

and

$$\mu_{q} \left. {\frac{{\partial u_{q} }}{\partial y}} \right|_{y = 0} = \mu_{p} \left. {\frac{{\partial u_{p} }}{\partial y}} \right|_{y = 0} .$$

(15)

The solution details are presented in [25]. Solving Eqs. 11 and 12 with boundary conditions (Eqs. 13–15), the mass flow rates ${M}_{q,x}$ and ${M}_{p,x}$ for both fluid phases are calculated (as well as the shear stress ${\tau }_{f0}$ at the channel surfaces for $y=-{n}_{d}$ and $y=1$).

2.2.2 Fluid flow in virtual pores

VPs, in contrast to the channel flow model, assume that the fluid is compressible. The fluid pressure can reach 70 MPa in specific situations, such as during the hydraulic fracturing process. The gas phase exceeds the critical point and becomes a supercritical fluid under these conditions. For both fluid phases in VPs, the Peng–Robinson equation of state [34] is used to describe fluid behaviour above the critical point

$$P = \frac{RT}{{\left( {V_{q/p} - b_{q/p} } \right)}} - \frac{{a_{q/p} }}{{\left( {V_{q/p}^{2} + 2b_{q/p} V_{q} - b_{q/p}^{2} } \right)}},$$

(16)

where P is the pressure [Pa], R denotes the gas constant (R = 8314, 4598 J/(kmol K)), ${V}_{q/p}$ is the molar volume of liquid (q) and gas (p) fraction [m³/kmol] and T denotes the temperature [K]. The parameters in Eq. 16 are:

$$a_{q/p} \left( T \right) = a_{q/p,0} \left[ {1 + n_{q/p} \left( {1 - \left( {\frac{{T_{i}^{n} }}{{T_{q/p,c} }}} \right)^{0.5} } \right)} \right]^{2} ,$$

(17)

$$n_{q/p} = 0.37464 + 1.54226\omega_{q/p} - 0.26992\omega_{q/p}^{2} ,$$

(18)

$$a_{q/p,0} = a_{c,q/p} \beta \left( T \right),$$

(19)

$$a_{c,q/p} = \frac{{0.457247R^{2} T_{q/p,c}^{2} }}{{P_{q/p,c} }},$$

(20)

$$b_{q/p} = \frac{{0.07780RT_{q/p,c} }}{{P_{q/p,c} }},$$

(21)

$$\beta = \left[ {1 + c_{1} \left( {1 - T_{r}^{\frac{1}{2}} } \right) + c_{2} \left( {1 - T_{r}^{\frac{1}{2}} } \right)^{2} + c_{3} \left( {1 - T_{r}^{\frac{1}{2}} } \right)^{3} } \right]^{2} ,$$

(22)

where ${T}_{q/p,c}$ is the critical temperature of phase [K], ${P}_{q/p,c}$ denotes the critical pressure of phase [Pa], ${\omega }_{q/p}$ is the acentric factor of phase [–] and T_r denotes the reduced temperature$\frac{T}{{T}_{c}}$. When c₁ = c₂ = c₃ = 0, the original model is obtained. The extra factors help connect vapour pressure data from highly polar liquids like water and methanol. For most substances, Eqs. 17–22 provide a good fit for the vapour pressure, however predicting molar volumes can be very inaccurate. The forecast of saturated liquid molar quantities might deviate by l0–40% [27]. Peneloux and Rauzy [33] proposed an effective correction term

$$V_{q}^{{{\text{corr}}}} = V_{q} + s,$$

(23)

where s is the small molar volume correction term that is component dependent; ${V}_{q}$ is the molar volume predicted by Eq. 16 and ${V}_{q}^{\mathrm{corr}}$ refers to the corrected molar volume. The value of s is negative for higher molecular weight non-polar and essentially for all polar substances. The molar volume correction term is considered to be 0.0 m³/kmol and − 0.0034 m³/kmol for the gas phase and liquid phase (water), respectively. The Peng–Robinson equation of state has the advantage of being able to describe the behaviour of supercritical fluids at extremely high fluid pressures and temperatures. For each phase, the mass conservation equation is used. The mass transfer between phases and the grid velocity is ignored when there is no internal mass source. The discretized form of the mass conservation equation for the liquid phase is

$$\frac{{\alpha_{q,i}^{n + 1} \rho_{q,i}^{n + 1} V_{i}^{n + 1} - \alpha_{q,i}^{n} \rho_{q,i}^{n} V_{i}^{n} }}{\Delta t} + \mathop \sum \limits_{f} \left( {\rho_{q,f}^{n} U_{f}^{n} \alpha_{q,f}^{n} } \right) = 0$$

(24)

with

$$V_{i}^{n + 1} = V_{i}^{n} + \frac{{{\text{d}}V}}{{{\text{d}}t}}\Delta t,$$

(25)

where f is the face (edge) number, ${U}_{f}^{n}$ denotes the volume flux through the face [m³/s], based on the average velocity in the channel, ${\alpha }_{q,f}^{n}$ is the face value of the fluid-phase volume fraction [–], t is the time step [s], n denotes the time increment and i is the VP number [–]. The explicit formulation is used instead of an iterative solution of the transport equation during each time step since the volume fraction at the current time step is directly computed from known quantities at the previous time step. Similarly, the mass conservation equation for a gas phase is introduced. The product ${\rho }_{q}{U}_{f}^{n}{\alpha }_{q,f}^{n}$ in Eq. 24 is the mass flow rate ${M}_{q,f}$ of the liquid phase flowing through the face f (edge of a triangle) of VP_i. The density of the liquid phase can be calculated by solving the mass conservation equation for both phases

$$\rho_{i,q}^{n + 1} = \frac{{\alpha_{q,i}^{n} \rho_{q,i}^{n} V_{i}^{n} + \Delta t\mathop \sum \nolimits_{f} M_{q,f} }}{{\left( {V_{i}^{n} + \Delta V_{i} \Delta t} \right)\alpha_{q,i}^{n + 1} }}.$$

(26)

The density of the gas phase can also be computed in the same way. It should be noted that the molar volume V (q/p) is related to the gas density.

$$V_{i,p}^{n + 1} = \frac{{w_{p} }}{{\rho_{i,p}^{n + 1} }},$$

(27)

and to the liquid density

$$V_{i,q}^{n + 1} = \frac{{w_{q} }}{{\rho_{i,q}^{n + 1} }} - s.$$

(28)

Due to the fact that the fluid phases share the same pressure

$$\frac{{RT_{i}^{n} }}{{\left( {V_{i,p}^{n + 1} - b_{p} } \right)}} - \frac{{a_{p} }}{{\left( {V_{i,p}^{n + 12} + 2b_{p} V_{i,p}^{n + 1} - b_{p}^{2} } \right)}} = \frac{{RT_{i}^{n} }}{{\left( {V_{i,q}^{n + 1} - b_{q} } \right)}} - \frac{{a_{q} }}{{\left( {V_{i,q}^{n + 12} + 2b_{q} V_{i,q}^{n + 1} - b_{q}^{2} } \right)}},$$

(29)

the fluid-phase fractions are computed. Inserting Eq. 27 for the gas phase and Eq. 28 for the liquid phase into Eq. 29, a polynomial equation is obtained with respect to the liquid fraction ${\alpha }_{q,i}^{n+1}$. The gas-phase fraction is computed as ${\alpha }_{p,i}^{n+1}=1-{\alpha }_{q,i}^{n+1}$. Equation 16 is used to calculate the new pressure ${P}_{i}^{n+1}$ in VP_i. Table 1 lists the material constants required for THM simulations.

Table 1 Basic material constants assumed for solid, fluid and gas in coupled THM-DEM calculations

2.3 Heat transfer

Heat must be transferred in both the fluid and solid domains. When it comes to heat transfer in multi-phase fluid flow, the temperature is shared, but enthalpy is transferred. The heat transfer model is simplified in the same way that the fluid flow model is simplified. As a result, a homogeneous heat transfer model is assumed in multi-phase flow (mass transfer between phases is not supposed to be taken into account). The multi-phase fluid is homogenized to a single-phase fluid. The effective fluid properties and velocity are calculated using volume averaging over the phases. The numerical solution uses the same very coarse mesh of both domains (Fig. 1b) that is used to create the fluid flow network to solve the governing equations.

2.3.1 Heat transfer in fluid

In multi-phase fluid flow, we assume homogenous heat transfer. The fluid is incompressible and homogeneous. The viscous dissipation of energy is not taken into account. The energy conservation equation is shared by all phases in the homogeneous model and is expressed in integral form

$$\mathop \int \limits_{V} \frac{{\partial \rho_{{{\text{eff}}}} E}}{\partial t}{\text{d}}V + \oint {\rho_{{{\text{eff}}}} } \mathop{v}\limits^{\rightharpoonup} E \cdot {\text{d}}\vec{A} = \oint {\lambda_{{{\text{eff}}}} } \nabla T \cdot {\text{d}}\vec{A} + \mathop \smallint \limits_{V} S_{h} ,$$

(30)

where ${\rho }_{\mathrm{eff}}$ is the effective density of the fluid [kg/m³], $E$ denotes the total energy [J], t is the time [s], $\mathop{v}\limits^{\rightharpoonup}$ is velocity vector [m/s], $T$ is the temperature [K], ${\lambda }_{\mathrm{eff}}$ denotes the effective thermal fluid conductivity [W/(mK)] and ${S}_{h}$ represents the energy source term. Assuming an incompressible and laminar flow of the homogeneous fluid, the enthalpy h equation of state is

$$h = \mathop \int \limits_{{T_{{{\text{ref}}}} }}^{T} c_{p} \,{\text{d}}T,$$

(31)

where ${T}_{\mathrm{ref}}$ is the reference temperature [K] and ${c}_{p}$ denotes the specific heat for constant pressure [J/(kg K)]. The effective fluid properties and velocity are computed by volume averaging over the phases

$$\rho_{{{\text{eff}}}} = \mathop \sum \limits_{k = 1}^{2} \alpha_{k} \rho_{k} ,$$

(32)

$$\mathop{v}\limits^{\rightharpoonup} _{{{\text{eff}}}} = \frac{1}{{\rho_{{{\text{eff}}}} }}\mathop \sum \limits_{k = 1}^{2} \alpha_{k} \rho_{k} \mathop{v}\limits^{\rightharpoonup} _{k} ,$$

(33)

$$\lambda_{{{\text{eff}}}} = \mathop \sum \limits_{k = 1}^{2} \alpha_{k} \lambda_{k} ,$$

(34)

$$\mu_{{{\text{eff}}}} = \mathop \sum \limits_{k = 1}^{2} \alpha_{k} \mu_{k} .$$

(35)

The specific heat capacity is assumed to be independent of composition and pressure:

$$c_{p} = \mathop \sum \limits_{i} \alpha_{i} c_{pi} = {\text{const}}.$$

(36)

Equation 30 is applied to each fluid cell (triangle) in the computational domain. The finite volume method is used to solve Eq. 30. The discretization of Eq. 30 on a given cell produces

$$\frac{\partial \rho E}{{\partial t}}V + \mathop \sum \limits_{f}^{{N_{{{\text{faces}}}} }} \rho_{f} \mathop{v}\limits^{\rightharpoonup} _{f} E_{f} \cdot \vec{A}_{f} = \mathop \sum \limits_{f}^{{N_{{{\text{faces}}}} }} \lambda_{{{\text{eff}}}} \nabla T_{f} \cdot \vec{A}_{f} + S_{h} V,$$

(37)

where ${N}_{\mathrm{faces}}$ is the number of faces enclosing the cell, ${E}_{f}$ is the value o E on the face f of the cell, ${T}_{f}$ is the value of T on the face f, $\rho_{f} \mathop{v}\limits^{\rightharpoonup} _{f} \cdot \vec{A}_{f}$ denotes the mass flux through the face f, ${\overrightarrow{A}}_{f}$ is the area vector of the face f, $\left|A\right|=\left|{A}_{x}\widehat{i}+{A}_{y}\widehat{j}\right|$ in 2D, $\nabla {T}_{f}$ denotes the gradient of T at the face f and V is the cell volume. If the time derivative is discretized using backward differences, the first-order accurate temporal discretization is given by

$$\frac{{\rho^{n + 1} E^{n + 1} - \rho^{n} E^{n} }}{\Delta t}V + \mathop \sum \limits_{f}^{{N_{{{\text{faces}}}} }} \rho_{f}^{n} \mathop{v}\limits^{\rightharpoonup} \,_{f}^{n} E_{f}^{n} \cdot \vec{A}_{f} = \mathop \sum \limits_{f}^{{N_{{{\text{faces}}}} }} \lambda_{{{\text{eff}}}} \nabla T_{f}^{n} \cdot \vec{A}_{f} + S_{h} V,$$

(38)

where n + 1 is the value at the next time step t + Δt and n is the value in the current time t. The energy conservation equation can be expressed in terms of temperature T by assuming that total energy E equals enthalpy h and applying the enthalpy equation of state to Eq. 38

$$\begin{aligned} T^{n + 1} & = T_{{{\text{ref}}}} + \frac{{c_{{p,{\text{eff}}}}^{n} \left( {T^{n} - T_{{{\text{ref}}}} } \right)}}{{c_{{p,{\text{eff}}}}^{n + 1} }} + \frac{\Delta t}{{V\rho^{n} c_{{p,{\text{eff}}}}^{n + 1} }}\mathop \sum \limits_{f}^{{N_{{{\text{faces}}}} }} \lambda_{{{\text{eff}}}} \nabla T_{f}^{n} \cdot \vec{A}_{f} \\ & \quad - \frac{\Delta t}{{V\rho^{n} c_{{p,{\text{eff}}}}^{n + 1} }}\mathop \sum \limits_{f}^{{N_{{{\text{faces}}}} }} \rho_{f}^{n} \mathop{v}\limits^{\rightharpoonup} \,_{f}^{n} c_{{p,{\text{eff}}}}^{n} \left( {T_{f}^{n} - T_{{{\text{ref}}}} } \right) \cdot \vec{A}_{f} + \frac{\Delta t}{{\rho^{n + 1} c_{{p,{\text{eff}}}}^{n + 1} }}S_{h} , \\ \end{aligned}$$

(39)

where ${S}_{h}$ is related to the internal enthalpy source of the diffusive energy [W/m³] of heat transported by diffusion along the channel “S2S”

$$S_{h} = - \lambda_{{{\text{eff}}}} \frac{{T_{i}^{n} - T_{j}^{n} }}{{L_{k} }}A_{k} \frac{1}{V},$$

(40)

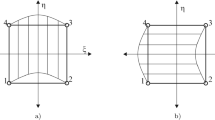
where L_k is the length [m] of the channel S2S and ${A}_{k}$ is the area of the channel cross section [m²]. The total energy can be calculated using the enthalpy equation of state $E={c}_{p}\left(T-{T}_{\mathrm{ref}}\right)$ since total energy equals enthalpy. The Green-Gauss theorem is utilized to generate a scalar value at cell faces and compute secondary diffusion terms and velocity derivatives. To obtain the gradient of the scalar T at the cell centre c0 (Fig. 5), the following discrete form is stated as

$$\left( {\nabla T} \right)_{c0} = \frac{1}{V}\mathop \sum \limits_{f} \overline{T}_{f} \vec{A}_{f} ,$$

(41)

where ${\overline{T} }_{f}$ represents the value of T at the cell face centroid. The face value ${\overline{T} }_{f}$ in Eq. 41 is derived from the arithmetic average of values at neighbouring cell centres using Green-Gauss Cell-based gradient assessment

$$\overline{T}_{f} = \frac{{T_{c0} + T_{c1} }}{2}.$$

(42)

Fig. 5

Control volume illustrating discretization of scalar transport equation

The cell grid is assumed to be very coarse, therefore when the surface f is at the domain boundary or at the liquid–solid interface, the temperature ${\overline{T} }_{f}$ is analytically calculated. Several scenarios may be considered: case I: the temperature ${T}_{f,bc}\left(t\right)$ on the boundary is known (constant or variable) ${\overline{T} }_{f}={T}_{f,bc}\left(t\right)$, case II: the heat flux ${q}_{f,bc}\left(t\right)$ on the boundary is known (constant or variable) ${\overline{T} }_{f}={T}_{c0}+\frac{{d}_{r}{q}_{f,bc}\left(t\right)}{{\lambda }_{\mathrm{eff}}}$, where ${d}_{r}$ is the distance between the pore c0 centroid and centre of the face f. For the adiabatic boundary condition ${T}_{f}={T}_{c0}$, case III: the convective heat flux on the boundary ${\overline{T} }_{f}=\frac{\frac{{d}_{r}{h}_{e}{T}_{e}}{{\lambda }_{\mathrm{eff}}}-{T}_{c0}}{\left(\frac{{d}_{r}{h}_{e}}{{\lambda }_{\mathrm{eff}}}-1\right)}$, where ${h}_{e}$ is the convective heat transfer coefficient in the surroundings (${T}_{e}$ is the temperature of surroundings), case IV: if the fluid cell face is adjacent to the solid cell, the interface is assumed as ${q}_{f,\mathrm{pore}}={q}_{f,\mathrm{cell}}$, where ${q}_{f,\mathrm{pore}}={h}_{f}\left({T}_{f}-{T}_{c0}\right)$ is the heat flux in the fluid transferred from the pore cell through the interface to the solid; ${q}_{f,\mathrm{cell}}={\lambda }_{s}\frac{\left({T}_{c1}-{T}_{f}\right)}{{d}_{r,c}}$ denotes the heat flux in the solid transferred from the fluid cell through the interface to solid, ${d}_{r,c}$ is the distance between the cell centre c1 and face centre f and ${\lambda }_{s}$ is the heat transfer coefficient of the solid and ${h}_{f}$ is the convective heat transfer coefficient of the fluid. The convective heat transfer coefficient ${h}_{f}$ is calculated using the Nusselt number ${\mathrm{Nu}}_{k}$, which may be empirically obtained using the macroscopic porosity of the particle assembly and Reynolds number (0 < Re < 102) (according to Tavassoli et al. [45])

$${\text{Nu}}_{k} = \left( {7 - 10\varepsilon + 5\varepsilon^{2} } \right)\left( {1 + 0.1{\text{Re}}_{k}^{0.2} \Pr_{k}^{1/3} } \right) + \left( {1.33 - 2.19\varepsilon + 1.15\varepsilon^{2} } \right){\text{Re}}_{k}^{0.7} \Pr_{k}^{1/3} ,$$

(43)

where $\varepsilon$ is the porosity, ${\mathrm{Re}}_{k}$ denotes the Reynolds number and ${\mathrm{Pr}}_{k}$ is the Prandtl number. For the Reynolds number Re > 102, an empirical formula proposed by Wakao and Kaguei [47] is used

$${\text{Nu}} = 2 + 1.1{\text{Re}}_{k}^{0.6} \Pr_{k}^{\frac{1}{3}} .$$

(44)

After that, the convective heat transfer coefficient ${h}_{ik}$ is calculated

$$h_{ik} = \frac{{Nu_{k} \lambda_{{{\text{eff}}}} }}{{2r_{i} }}.$$

(45)

The diffusive flux D_f in Eq. 39 across the face f is given by

$$D_{f} = \lambda_{{{\text{eff}}}} \nabla T_{f}^{n} \cdot \vec{A}_{f} .$$

(46)

The parameter ${D}_{f}$ may be approximated as

$$D_{f} = \lambda_{{{\text{eff}}}} \frac{{\left( {T_{1} - T_{0} } \right)}}{ds}\frac{{\vec{A}_{f} \cdot \vec{A}_{f} }}{{\vec{A}_{f} \cdot \overrightarrow {{e_{s} }} }} + \lambda_{{{\text{eff}}}} \left( {\overline{\nabla }T \cdot \vec{A}_{f} - \overline{\nabla }T \cdot \overrightarrow {{e_{s} }} \frac{{\vec{A}_{f} \cdot \vec{A}_{f} }}{{\vec{A}_{f} \cdot \overrightarrow {{e_{s} }} }}} \right),$$

(47)

where the first term on the right-hand side represents the primary gradient oriented along the vector $\overrightarrow{{e}_{s}}$ and the second term represents the ‘cross’ diffusion term. In Eq. 47, the parameter ${\overrightarrow{A}}_{f}$ is the area normal vector of the face f directed from the cell c0 to c1, ds is the distance between cell centroids and $\overrightarrow{{e}_{s}}$ is the unit normal vector in this direction (Fig. 6) and $\overline{\nabla }T$ is the average of gradients at two adjacent cells. Discrete values of the scalar are stored at the cell centres. However, face values are required for convection terms in Eq. 39 and must be interpolated from cell centre values. This is accomplished through the use of an upwind scheme. As a result, the second-order upwind scheme is used to compute face values. A multidimensional linear reconstruction method is used to calculate quantities at cell faces. Thus, the face value ${\varphi }_{f}$ is computed using the expression below

$$\varphi_{f} = \varphi + \nabla \varphi \cdot \vec{r},$$

(48)

where $\varphi$-the cell-centred value in the upstream cell, $\nabla \varphi$-the cell-centred gradient of the value in the upstream cell, $\overrightarrow{r}$-the displacement vector from the upstream cell centroid to the face centroid (Fig. 5).

Fig. 6

Adjacent cells c₀ and c₁ with fluid velocity vector V (coloured in blue)

The gradient in each cell must be determined for this formula to work. Finally, the gradient must be limited to prevent the introduction of additional maxima or minima. As a result, the concept of gradient limiters [4] is introduced.

2.3.2 Heat transfer in solid

The energy conservation equation has the following integral form if there is no convective energy transfer, no internal heat sources, and constant density in solid regions

$$\rho_{s} \mathop \smallint \limits_{V} \frac{\partial E}{{\partial t}} \cdot {\text{d}}V = \oint {\left( {\lambda_{s} \nabla T} \right)} \cdot {\text{d}}\vec{A},$$

(49)

where E is the total energy, equal to enthalpy $h={\int }_{{T}_{\mathrm{ref}}}^{T}{c}_{p}\mathrm{d}T$, ${\rho }_{s}$ denotes the solid density [kg/m³], ${\lambda }_{s}$ is the thermal conductivity of solid [W/(mK)], ${T}_{\mathrm{ref}}$ denotes the reference temperature and ${c}_{p}$ is the specific heat in constant pressure. Equation 49 is applied to each cell (triangle) in the solid domain. On a given cell, the discretization of Eq. 49 produces

$$T^{n + 1} = T^{n} + \frac{\Delta t}{{V\rho_{s} c_{p} }}\mathop \sum \limits_{f}^{{N_{{{\text{faces}}}} }} \lambda_{s} \nabla T_{f}^{n} \cdot \vec{A}_{f} .$$

(50)

The gradients and face values are computed in the same way that the fluid gradients and face values are computed (Sect. 2.3). The total energy is calculated using the enthalpy equation of the state

$$E = c_{p} \left( {T - T_{{{\text{ref}}}} } \right).$$

(51)

2.4 Coupling scheme

The discretization algorithm is based on the Alfa Shapes theory [6]. The triangular pore mesh deforms extensively and even affects the geometry topology in specific problems (e.g. in hydraulic fracturing when the fracture begins to propagate). Equation 25's volume changes are transmitted to CFD. When the topological features of the grid geometry change, the grid is automatically re-meshed [24]. Even though the mesh is coarse, the re-mesh procedure takes a relatively long computational time. Therefore, an algorithm that tracks configuration changes of discrete elements is developed and implemented in the model. The algorithm tracks displacements, overlaps, and size changes of discrete elements in each iteration (time increment). The remeshing procedure runs when the configuration changes are large enough. The criterion for triggering the re-mesh procedure is arbitrarily defined but is based on the results of a parametric study. As a result, the repeated remeshing procedure is run on average every several hundred or even several thousand iterations and slightly increases the total computation time. However, the total number of times the remeshing procedure is repeated strongly depends on the problem studied.

The calculation outputs (e.g. pressures, fluid fractions) are accurately converted from the old mesh to the new mesh in this scenario, providing that the mass is a topological invariant [24]. Equation 29 is used to determine the new fluid-phase fractions by using mass quantities rather than mass flow rates. In the VPs, Eq. 16 is utilized to calculate the new pressure after transformation.

The coupling scheme of DEM with CFD and heat transfer (Fig. 7) involves three sets of discrete equations to be solved: the fluid flow equations for all VPs in the fluid domain, the law of motion in DEM for all discrete elements (e.g. spheres) and heat transfer equations for all grid cells in the fluid and particle (solid) domain. The two-way coupling scheme is based on a transfer of pressures, shear stress forces, and temperatures from CFD to DEM and the time derivative of VP volumes from DEM to CFD. The pressure and shear forces from the fluid cause displacements of discrete elements (e.g. spheres) in DEM that change coordinates and triangle volumes in VPN. Temperature changes the diameters of spheres and, as a result, the volume of the solid and fluid. The VP volume's time derivative, dV/dt, is computed in DEM and then transmitted to CFD (Eq. 25, which includes the term dV/dt, takes into account the volume change). As a result, pressure and temperature changes in the fluid are affected by volume changes in DEM. The forces acting on spheres are then transformed into fluid pressures in VPs and channels. CFD calculates the pressures and shear stresses in the 'S2S' channels as well as the temperature in each time step $\Delta {t}_{\mathrm{C}}$. They are transferred from CFD to DEM in each time step $\Delta {t}_{\mathrm{D}}$. They are next utilized to compute fluid forces, which are added to the contact forces F before time integration to update discrete element displacements. The fluid pressures in VPs and ‘S2S’ channels are converted into the forces ${\overrightarrow{F}}_{P,j}$ acting on spheres

$$\vec{F}_{P,j} = - P_{i} \vec{n}A_{k} ,$$

(52)

where $\overrightarrow{n}$ is the unit vector normal to the discretized sphere’s edge, ${P}_{i}$-the pressure in VP, i-the VP number, j-the sphere number and ${A}_{k}$-the contact area between the fluid in VP_i and sphere

$$A_{k} = 2r_{j} e_{k} ,$$

(53)

where ${r}_{j}$ is the maximum sphere radius and ${e}_{k}$-the sphere edge length. The shear stresses are converted into the forces acting on spheres in ‘S2S’ channels as

$$\vec{F}_{S,j} = \tau_{f0,i} \vec{I}A_{k} \;\;{\text{with}}\;\;A_{k} = 2r_{j} L_{k} ,$$

(54)

where $\overrightarrow{I}$ denotes the unit vector parallel to the channel wall and oriented in the fluid flow direction, ${\tau }_{f0,i}$-the shear stress in the channel, i-the channel number, j-the sphere number and ${A}_{k}$-the contact area between the channel fluid and sphere and ${L}_{k}$-the channel length. The new sphere radii are computed through a thermal (linear) expansion coefficient

$$r^{n + 1} = r^{n} \left( {1 + \alpha_{\exp } \left( {T_{{{\text{avg}}}}^{n + 1} - T_{{{\text{avg}}}}^{n} } \right)} \right),$$

(55)

where ${r}^{n+1}$-the new radius [m], ${r}^{n}$-the previous value of radius [m], ${\alpha }_{\mathrm{exp}}$-the thermal (linear) expansion coefficient [1/K], ${T}_{\mathrm{avg}}^{n+1}$-the new volume average sphere temperature [K], ${T}_{\mathrm{avg}}^{n}$-the previous volume average sphere temperature [K] and n-the time increment [–].

Fig. 7

DEM-TH (thermo-hydro model) coupling schema (${\overrightarrow{F}}_{P,j}$-force converted from pressure in VP, ${\overrightarrow{F}}_{S,j}$-force converted from shear stress in channels, $\Delta {V}_{i}^{n}$-volume change in VP, ${T}_{j}^{n+1}$-temperature in cell j of solid domain, ${r}_{j}^{n+1}$-sphere radius and n-time increment)

The DEM-based THM model was implemented by the authors into the open-source software package YADE [41] which is already parallelized by computer cluster nodes using the OpenMPI library. Technically, the DEM-based THM model (called VPNengine) is a native YADE plugin. However, VPNengine is parallelized with the use of the OpenMP library (by single computer threads) and only a few loops are parallelized. Overall, VPNengine only uses one CPU core, while several loops can use a certain number of threads. Therefore, the plugin's performance is limited. The calculation time of bar specimen thermal contraction during cooling (Sect. 6, case ‘a’) is about 1 day using a processor Intel Xeon 2.7 GHz. However, in simulations of short-term processes, e.g. hydraulic fracturing, a specimen of about 1100 spheres is processed in a very similar computer runtime. To overcome this limitation, the authors began developing a 3D DEM-based THM model to be parallelized by the cluster computer nodes using the OpenMPI library. This will greatly increase the efficiency of the software and enable 2D and 3D simulations to be performed on samples containing thousands of spheres within a reasonable computer runtime.

3 Calibration of DEM and CFD

DEM and CFD were separately calibrated, based on mechanical tests (DEM) and a permeability test [24] (CFD), respectively. For calibration, a simple bonded granular specimen in the form of a bar was used (Fig. 8). A random distribution of spheres was employed with a 20 × 80 mm² bar specimen approximating artificial porous material with a porosity of roughly p = 10%. The pores represented the empty area between the spheres. The sphere diameter ranged from 4 to 8 mm with a mean diameter of d₅₀ ≅ 6 mm. Along the depth of the specimen, one layer of spheres was applied.

Fig. 8

Bonded granular specimen in DEM used for THM simulations

3.1 DEM results

Pure DEM was used during uniaxial tension of a bonded granular bar specimen of Fig. 8. To maintain quasi-static conditions during uniaxial tension, the smooth bottom and top of the specimen (Fig. 8) were moved at a constant opposing vertical velocity of 1 mm/s. Based on early calculations, DEM simulations used a time step of 2 × 10^–7 s. In DEM simulations with spheres, the following material constants were assumed: E_c = 3.36 GPa and υ_c = 0.30, C = 150 MPa and T = 30 MPa (C/T = 5), μ_c = 18° and ρ = 2 600 kg/m³, based on quasi-static uniaxial compression and splitting tests on shale specimens [24]. The DEM results were in agreement with the corresponding experimental results [15]. The greatest compressive normal stress was 47 MPa, while the maximum tensile stress was 8 MPa.

Figure 9 depicts the deformed specimen, broken normal contact distribution at the failure, and sphere displacement vectors (before the stress peak and at the failure) during uniaxial tension. The red and blue colours in Fig. 9c denote the displacements > 0.08 mm and < − 0.08 mm, and the orange and green colours the displacements between 0 and 0.08 mm, and − 0.08 mm to 0 mm.

Fig. 9

Pure DEM simulations of uniaxial tension for cohesive granular specimen of Fig. 8: a deformed specimen (sphere displacements were 10-times enlarged), b distribution of normal sphere contacts in non-deformed specimen at failure (broken contacts are in colour) and c particle displacement vectors before peak and at failure in non-deformed specimen (displacement vectors were 50-times enlarged)

A nearly horizontal macro-crack appeared at the top specimen region due to the neighbourhood of the top boundary (Fig. 9a). In the major macro-crack, six normal contacts were broken, for a total of twelve contacts broken in the specimen (Fig. 9b). The sequence of damage was the following: first red contacts, then orange and finally green ones. Due to boundary conditions assumed, the sphere displacements were mostly vertical (Fig. 9c). The mean resultant spheres' displacement was 0.061 mm with a maximum value of 0.11 mm at boundaries.

The behaviour of the specimen was elastic-brittle due to a low number of spheres and 2D conditions [28]. The specimen’s tensile strength was 8.8 MPa for the vertical displacement/strain of 0.22 mm/0.28% and the elastic modulus was 3.5 GPa [15, 24]. Before the peak, the mean tensile normal contact force between spheres was 20.58 N with a maximum tensile contact force equal to 69.20 N (= TR², Eq. 6). The coordination number was 6.53 (initially) and 4.17 (at the failure).

3.2 CFD results

A basic Darcy permeability test was performed on a bonded granular specimen of Fig. 8 to calibrate the fluid flow model regarding the macroscopic permeability. Simulated was single-phase water flow (the specimen was fully saturated). The top edge was subjected to a constant water pressure of 0.1 MPa, while the bottom edge was subjected to a constant water pressure of 5 MPa. On the side edges, zero mass flow rate requirements were imposed (Fig. 10a). The macroscopic permeability coefficient was determined using Darcy's law, assuming that the volumetric flow rate at horizontal edges was the same at equilibrium

$$\kappa = \frac{Q}{A}\mu_{q} \frac{L}{\Delta P},$$

(56)

where Q is the volumetric flow rate at the equilibrium state [m³/s], A is the specimen cross section [m²], L denotes the specimen height and $\Delta P$ is the pressure difference between the bottom and top edges [Pa]. The simulation was carried out until the mass flow rate of the fluid along the lower and the upper boundary stopped changing. The fluid pressure isolines were almost parallel to each other, which confirmed that the fluid flow at the macro-level was one-dimensional (Fig. 10b). The volumetric flow rate at the equilibrium state reached 3.5.31 × 10⁻⁵ m³/s. Hence, the cohesive granular bar specimen had an estimated permeability coefficient of $\kappa =2.47\times {10}^{-16}$ m².

Fig. 10

Pure CFD simulations concerning permeability test for bonded granular specimen of Fig. 8: a boundary and initial conditions (P-pressure and q-mass flow rate) and b fluid pressure distribution

The basic mechanical, fluid and heat material constants for the solid, water and gas are summarized in Table 1.

4 Validation of THM model for 1D heat transfer problem

The THM model was validated by comparing the numerical findings with the analytical solution for the classic 1D heat transfer problem (diffusion) in the cohesive granular bar specimen

$$\frac{\partial T}{{\partial t}} = \alpha_{{{\text{eqv}}}} \frac{{\partial^{2} T}}{{\partial x^{2} }},$$

(57)

where ${\alpha }_{\mathrm{eqv}}$ is the effective thermal diffusivity [m²/s] and t is the time [s]. The initial and boundary conditions for the analytical solution of the 1D heat equation are as follows

$$T\left( {x, 0} \right) = 323.16\;\left[ {\text{K}} \right]\quad x \in \left\langle {0,L} \right\rangle ,$$

(58)

$$T\left( {0, t} \right) = T\left( {L, t} \right) = 293.16\;\left[ {\text{K}} \right]\quad t \ge 0$$

(59)

where L is the length of the bar. Using the Fourier series, the unsteady solution becomes

$$T\left( {x, t} \right) = \mathop \sum \limits_{n = 1}^{\infty } D_{n} \sin \frac{n\pi x}{L}e^{{\alpha \frac{{n^{2} \pi^{2} t}}{{L^{2} }}}} ,$$

(60)

where

$$D_{n} = \frac{2}{L}\mathop \int \limits_{0}^{L} T\left( {x, 0} \right)\sin \frac{n\pi x}{L}{\text{d}}x.$$

(61)

The calculations were performed using a bonded granular bar specimen with a random distribution of spheres (Fig. 8). The effective thermal diffusivity ${\alpha }_{\mathrm{eqv}}$ was calculated for the volume-averaged phase properties

$$\alpha_{{{\text{eqv}}}} = \frac{{\lambda_{{{\text{eff}}}} }}{{c_{{p,{\text{eff}}}} \rho_{{{\text{eff}}}} }},$$

(62)

where

$$\lambda_{{{\text{eff}}}} = \frac{1}{{V_{r} }}\mathop \sum \limits_{k} \lambda_{k} V_{k} ,\quad c_{{p,{\text{eff}}}} = \frac{1}{{V_{r} }}\mathop \sum \limits_{k} c_{p,k} V_{k} ,\quad \rho_{{{\text{eff}}}} = \frac{1}{{V_{r} }}\mathop \sum \limits_{k} \rho_{k} V_{k}$$

(63)

and V_r-the total volume of the bar specimen [m³], k-the phase index, ${V}_{k}$-the k-phase volume [m³], ${\lambda }_{k}$-the heat conductivity of the phase k [W/(m K)], ${c}_{p,k}$ is the specific heat in constant pressure of the phase k [J/(kg K)] and ${\rho }_{k}$ is the phase density k [kg/m³]. The initial and boundary conditions are shown in Fig. 11 (the bar specimen was cooled down by 30 K). The effective thermal diffusivity and boundary conditions imitated heat transfer by diffusion only in the equivalent solid bar, made of a fictitious homogeneous material with effective thermal properties (Eq. 63). The single-phase flow of water was assumed.

Fig. 11

Initial and boundary conditions for bonded granular bar specimen of Fig. 8 during diffusion simulations (q-fluid mass flow rate and q_h-heat transfer rate)

The numerical results of cooling the bar specimen with a random distribution of spheres (Fig. 8) were compared to an analytical solution of the one-dimensional diffusion problem in an equivalent solid bar. In general, all properties of a fluid flowing under non-isothermal conditions are more or less temperature-dependent. If the problem requires consideration of the temperature dependence of the fluid properties, any relationship can be used in the DEM-based THM model. The most important property of a fluid is density. The DEM-based THM model uses the corrected Peng–Robinson equation of state to calculate the fluid-phase density. Hence, the density depends on temperature and pressure. In this study, it was assumed for the sake of simplicity that other fluid properties were independent of temperature since most of the simulations presented were performed for a maximum temperature difference of 30 K. In that temperature range, the dynamic viscosity of the fluid slightly changes only. Therefore, we neglected the temperature dependence of viscosity in the current paper and the thermal properties of the fluid.

From the phase properties (Table 1), the effective material properties of the equivalent solid were determined using Eq. 63: λ_eff = 3.357 W/m K, c_p,eff = 929.51 J/kg K, and ρ_eff = 2422.74 kh/m³. For four different time values (100 s, 200 s, 300 s, and 400 s) and the corresponding Fourier numbers F_o, the comparison results in Fig. 12 are shown.

Fig. 12

Temperature along vertical centre line of cohesive granular bar specimen of Fig. 8 during cooling after time: a t = 100 s (F_o = 0.0227), b t = 200 s (F_o = 0.0453), c t = 300 s (F_o = 0.0680) and d) t = 400 s (F_o = 0.0907) (F_o-Fourier number)

The numerical results agree with the analytical solution. After 400 s of cooling, the largest difference between numerical and analytical values was 0.52 K. Figure 13 shows the temperature distribution and liquid density in the bar after 400 s of cooling. The density ranged from 1000.02 to 1014.28 kg/m³ after 400 s of cooling. In the estimation of the water density, the Peng–Robinson equation of state (Eq. 16) with a correction (Eq. 23) generated very little inaccuracy (less than 1.3%). The fluid density was slightly overestimated. For single-phase fluids and flow regimes near stagnant flows, the Peng–Robinson equation of state offers no significant advantages over other models (e.g. IAPWS for water and steam). The same findings were obtained by distributing the spheres in an structured manner.

Fig. 13

Cohesive granular bar specimen with random distribution of spheres (Fig. 8) during cooling after t = 400 s: a temperature distribution and b liquid density distribution

5 Effect of advection on cooling of bar specimen

A random distribution of spheres (Fig. 8) was used to evaluate the effect of advection on the cooling of the cohesive granular bar specimen. Two simulation types were carried out: for a low Peclet (Pe) number (case ‘a’) and a high Peclet Pe number (case ‘b’). The assumption was that water flowed in a single phase. Heat transfer in the bar specimen was simulated by diffusion (due to temperature differences) and advection (due to fluid mass movement) using the initial and boundary conditions in Fig. 14. The bar specimen was cooled down again by 30 K. The two various pressure differences between the two edges of the bar specimen were defined: 0.9 MPa (low Peclet number) and 9.9 MPa (high Peclet number). Table 1 lists the properties of the liquid (water) and solid. The numerical results are demonstrated in Figs. 15, 16 and 17.

Fig. 14

Initial and boundary conditions in cohesive granular bar specimen during diffusion and advection (q-fluid mass flow rate and q_h-heat transfer rate)

Fig. 15

Temperature distribution in cohesive granular bar specimen after cooling time t = 400 s due to diffusion and advection (low Peclet number): a in entire specimen and b along vertical centreline of bar

Fig. 16

Cohesive granular bar specimen after cooling time of t = 400 s due to diffusion and advection: a pressure distribution, b density distribution and c velocity vectors

Fig. 17

Temperature distribution in cohesive granular bar specimen after cooling time t = 300 s due to diffusion and advection along vertical centreline for small and large Peclet numbers

In the case ‘a’ after t = 400 s of cooling, the temperature difference between diffusion without advection and diffusion with advection reached 1.14 K (Fig. 15). The maximum Peclet number in the fluid domain was 24. The advection helped to speed up the cooling process. The fluid velocity was small; it did not exceed a velocity of 8.92·10^–5 m/s. The velocity vectors were almost parallel to the vertical sides (Fig. 16c), indicating that the fluid flow in the bar specimen was 1D. From the bottom to the top, the fluid pressure varied approximately linearly along the bar specimen (Fig. 16a). After 400 s of cooling, the fluid density ranged from 995.7 to 1012.5 kg/m³ (Fig. 16b). In the density estimation, the Peng–Robinson equation of state (Eq. 16) with a correction (Eq. 23) produced an insignificant error (less than 1.3%) (the fluid density was again slightly overestimated). In comparison with diffusion-only heat transfer, the temperature change along the vertical centreline was not symmetric. As a result of a colder fluid flowing (advection) in the same direction as the temperature shift, a very minor spatial shift of the temperature (e.g. temperature about 298 K or 303 K) was seen in the fluid flow direction (Fig. 16b). The temperature of the bar fluctuated very little along its horizontal cross-section. The largest temperature difference in the bar's middle cross-section was only 0.008 K.

The comparison of the results between cases ‘a’ and ‘b’ with different Peclet numbers is presented after t = 300 s of cooling of the bar specimen (Fig. 17). An increase in the pressure difference between the two edges of the bar specimen significantly increased the Peclet number from 24 to 179. The difference in the maximum temperature in the specimen reached 2 K between Pe = 24 and Pe = 179. A higher mass flow rate for Pe = 179 resulted in a significant right shift of the temperature distribution along the vertical centreline of the bar.

6 Bar specimen thermal contraction during cooling

A thermal contraction test during cooling of the cohesive granular bar specimen with a random distribution of spheres was performed (Fig. 8). To eliminate advection at the start of the cooling process and keep the fluid beyond the phase change conditions, the boundary and initial conditions of Fig. 18 were used. The flow of two-phase fluid was studied. The bar specimen was composed of 80% water and 20% air. Two cases were investigated: (a) sphere displacements and rotations were fixed only at both ends of the specimen and (b) sphere displacements and rotations were fixed in all spheres of the specimen. As a result, temperature variations had an impact on mechanical properties.

Fig. 18

Initial and boundary conditions in cohesive granular bar specimen of Fig. 8 in thermal contraction test (q-fluid mass flow rate and q_h-heat transfer rate)

In contrast to earlier simulations, the thermal properties of the solid and fluid were changed to accelerate the heat transfer process and its effect on the damage mechanism in the specimen. As a result, the water and air heat transfer coefficients indicated in Table 1 were multiplied by 10, and the solid heat transfer coefficient of 420 W/(m K) (typical for silver) was adopted. Solids were assumed to have a thermal (linear) expansion coefficient of 0.00083 1/K. Table 1 summarizes the material properties of water, air, and solids. The bar specimen's initial temperature (solid and fluid) was rather high (368.16 K), although it was still below the boiling point. The bar specimen was then cooled by setting a constant temperature of 278.16 K at both ends (bottom and top) (the temperature difference was 90 K).

6.1 Case ‘a’

Figure 19 depicts the temperature distribution in the bar specimen after 17 s. A deformed bar specimen with macro-crack, broken normal sphere contacts, and sphere displacement vectors after 17 s of cooling is illustrated in Fig. 19. The distribution of grain diameter changes during cooling is presented in Fig. 21. Figures 22 and 23 show the distribution of the fluid pressure and fluid temperature in the macro-crack zone.

Fig. 19

Temperature distribution in cohesive granular bar specimen in thermal contraction test after time t = 17 s: a in entire specimen and b along vertical centre line

The temperature was the highest (333.44 K) in the specimen near the macro-crack edge (Fig. 19a). A macro-crack occurred in the bar specimen due to tension (Fig. 20). It was created at the bar specimen's weakest zone near the top edge in a slightly different location than during pure uniaxial tension (Fig. 9a). The greatest normal contact tensile force before breakage was 29.313 N. Five normal contacts were broken in the macro-crack zone (34 in the entire bar specimen) (Fig. 20b). There was a noticeable vertical movement of spheres in the specimen mid-region (Fig. 20c). The mean diameter of spheres d₅₀ reduced from 6.032 to 5.837 mm (by around 3%) with the smallest changes in the bar’s mid-region (Fig. 21). In the damaged location, the fluid pressure dropped to 0.0116 MPa (by 0.0884 MPa below the original pressure) (Fig. 22). Once the normal contacts broke and the macro-crack began to expand, the pressure drop was produced by an increase in fluid volume in the damaged area due to tensile strain.

Fig. 20

Final damage (t = 17 s) of fixed cohesive granular bar specimen in thermal contraction test: a deformed specimen (black spheres are fixed), b normal contact distribution (broken contacts are in red) and c sphere displacement vectors (10-times enlarged)

Fig. 21

Grain diameter reduction in bonded granular bar specimen during thermal contraction test after time t = 17 s (largest diameter reduction is in black, smallest diameter reduction is in white)

Fig. 22

Pressure distribution in macro-crack region during thermal contraction test after time t = 17 s

The increasing width of the macro-crack generated temperature variations (Fig. 23). Between the particles on both sides of the macro-crack, the temperature in the macro-crack area was reduced by as much as 20.9 K. The particle mobility and deformation had, thus, a significant impact on fluid pressure and temperature. Heat transfer in the bar specimen caused fluctuations in fluid pressure, temperature, and density, which resulted in fluid flow, even though the pressure differential between the bottom and upper specimen borders was initially 0 kPa. The fluid's velocity, on the other hand, was still very low, measuring only 0.0057 m/s.

Fig. 23

Thermal contraction test in bonded granular bar specimen (after time t = 17 s): a temperature in macro-crack area of bar specimen and b temperature variations along vertical cross-section of bar specimen (macro-crack area-red colour)

6.2 Case ‘b’

An additional simulation was performed to show a decoupling effect between the deformation of the cohesive granular bar specimen and fluid flow and heat transport. In the DEM–CFD simulations, the same specimen was used (Fig. 8) with the same initial and boundary conditions (Fig. 18). A decoupling effect was obtained by an assumption that the granular assembly was unmovable (the displacements and rotations of all spheres were fixed). Thus, the bar cooling did not cause a crack. The temperature distribution in the specimen (Fig. 24) was similar to the simulation results in Sects. 4 and 5, and completely different from case ‘a’ (Fig. 19).

Fig. 24

Temperature distribution in cohesive granular bar specimen in thermal contraction test after time t = 17 s (decoupled model): a in entire specimen and b along vertical centreline

Due to temperature differences along the specimen height, the fluid began to flow. This caused fluid pressure changes (Fig. 25). After 17 s of cooling, the maximum fluid pressure dropped in the specimen to about 73.0 kPa (below the initial conditions of 100 kPa). The maximum specimen temperature decreased to 328.1 K (case ‘a’), while in case ‘b’, the maximum temperature reduced to 333.3 K. The temperature difference was due to fluid volume changes in case ‘a’, while in case ‘b’, the DEM model was decoupled from the fluid flow and heat transfer model and thus the changes of sphere diameters did not occur, and also the changes of fluid volumes.

Fig. 25

Pressure distribution in cohesive granular bar specimen during thermal contraction test after time t = 17 s (decoupled model)

7 Summary and conclusions

The research proposes a new DEM-based pore-scale thermal-hydro-mechanical model of two-phase fluid flow in unsaturated porous materials with low porosity that was coupled with heat transfer. The numerical findings were compared to the analytical solution of the 1D heat transfer problem in an analogous bar specimen to validate the model. The effect of advection was also investigated. In addition, the thermal contraction of the bar specimen during cooling was carefully studied, associated with the creation of a macro-crack. Based on meso-scale simulations, the following conclusions can be offered:

• During the 1D heat transfer problem, the largest temperature difference between numerical and analytical findings was just 0.52–0.64 K.

• Advection increased the cooling of the specimen. The highest temperature difference between cooling by diffusion and cooling by diffusion with advection was 2.26 K after 400 s of cooling with a pressure decrease of 0.5 MPa at the specimen height. The increase in the pressure difference between the two edges of the specimen increased the Peclet number from 24 to 179 and the maximum temperature difference from 1 to 2 K and caused a significant right shift of the temperature distribution along the vertical centreline of the specimen.

• In the thermal contraction of the bar specimen after cooling, the tensile failure mechanism was comparable to that of purely mechanical uniaxial tension.

• During specimen thermal contraction, the fluid pressure in the macro-crack dropped to 0.0116 MPa, which was 88.4% lower than the initial pressure.

• During specimen thermal contraction, the propagating macro-crack created temperature differences. The temperature difference between particles on both sides of the macro-crack was 20.9 K.

• Fluid pressure was affected more by particle displacement changes than by temperature changes during bar thermal contraction.

• Heat transfer in the cooled bar specimen during bar thermal contraction resulted in pressure and fluid density discrepancies, causing the fluid to flow at a very low velocity of less than 0.0057 m/s.