1 Introduction

Peridynamics (PD), as a nonlocal reformulation of classical continuum mechanics (CCM) [1], unites the modeling of continuous media, cracks and particles within a single framework [2]. It concerns the nonlocal effects of material particles within a certain cutoff distance named horizon [3], which functions as a fundamental length scale indicating the extent of nonlocality [4, 5]. The bond-based PD (BB-PD) theory replaces the classical partial differential equations (PDEs) with integro-differential equations (IDEs) to overcome the intrinsic incapability of CCM in describing discontinuities [1]. Furthermore, the “state” based PD establishes a new general version of continuum mechanics [6], making CCM a special case of PD theory when the value of internal length scale equals zero [5]. Compared with other nonlocal methods such as smoothed particle hydrodynamics (SPH), reproducing kernel particle method (RKPM) and lattice model (LM) [7,8,9,10], PD theory applies a single consistent set of field equations in the absence or presence of discontinuities [2] without any special treatments to accommodate the evolving discontinuity or significant nonlocality. In 2016, the peridynamic differential operator (PDDO) was proposed by Madenci et al. [11, 12].The PDDO enables numerical differentiation through PD integration and unifies the solution of differential and integral equations regardless of their intrinsic behavior and the presence of singularity. Internal length scale is hereby introduced to local partial differential equations as well, contributing to a paradigm shift in computational mechanics.

With theoretical advantages, the PD theory has been widely applied in the failure analysis of rocks, metals, polymers and composites under static and dynamic conditions [13, 14]. The numerical implementation of PD equations has been realized in various formats such as Peridigm [15], Finite Element Method (FEM) [16, 17] and PDLAMMPS [18, 19]. However, numerical simulations with fully non-local formats are computationally more demanding than local ones [20,21,22], especially in a fully 3D analysis where 2D idealization is not valid. Concerning the effectiveness and computational robustness of FEM, the coupling between PD and FEM can retain the salient features of both local and nonlocal methods. PD models can be used for problems where non-local effects strongly influence the solution, while FEM being used for general deformation without damage. However, due to the differences between local and nonlocal approaches in energy computation, the energy mismatch along interface presents a major difficulty for FEM-PD coupling.

Multiple coupling schemes have been proposed to mitigate the mismatch of the FEM and PD solutions without introducing large numerical artifacts. Macek and Silling [16] implemented PD into FEM scheme using ABAQUS truss element with surface correction and then coupled PD with FEM by using embedded element technique for overlap region. Coupling schemes with overlap regions have further been developed by Kilic and Madenci [21], Liu and Hong [23], Sun and Fish [24], Wang and Kulkarni [25], Yu and Bargos [26], etc. Blending approaches [27, 28], morphing strategy [20] and splice method [29,30,31] are also prevailing. In 2018, Madenci et al. [32] presented a variational approach to couple PD and FEM without an overlap region and later generalized it to a seamless coupling method for all PD models without nonphysical displacement kinks and stress concentrations near boundaries [33]. Existing coupling schemes can be further classified into two main classes concerning constant horizons (CH) class and varying horizon (VH) class according to the review article of D’Elia [34].

To describe material behavior in a practical 3D manner, plane strain and plane stress idealizations are commonly accepted in describing fracture [20, 24, 33] and shear-band evolution [35]. However, in the presence of material inclusions or a transverse crack, 3D models are required to conduct failure analysis. Most 3D coupling methods available in the literature couple PD and FEM domains of consistent dimensionality, where 3D FEM is coupled with 3D PD. Galvanetto and Zaccariotto [30, 31] developed a switching-coupling approach by modifying the stiffness matrix of the finite element zone in 1D, 2D, 3D forms. Zhang and Madenci [36, 37] introduced a 3D FEM-PD coupling strategy using elements and commands native to ANSYS. Liu and Hong [23] introduced interface elements to bridge FE subregions and PD subregions, with two coupling schemes concerning VL-coupling and CT-coupling. The VL-coupling scheme divides the force among all nodes of the element and the CT-coupling scheme distributes the force based on the location of the nodes. However, the aforementioned coupling schemes require the same grid size for both PD and FEM zones, which brings unnecessary computational costs. To reduce the computational cost, Pagani and Carrera [38] introduced a Lagrange multiplier based technique to couple 1D high-order finite elements with 3D PD [39]. The usage of a refined 1D structural theory permits enhanced solutions of almost 3D resolution yet with lower computational cost while 3D PD theory in regions of potential damage.

In the present work, we propose a coupling approach for refined 2D finite element model and 3D PD model. The 2D FEM models employed are established under the framework of Carrera Unified Formulation (CUF) [40]. CUF is a method that solves the elasticity problem by generating hierarchical approximated solution of any accuracy on the basis of fundamental nuclei. It generates any theory of structures from 1D to 3D and allows for the formulation of low- to high-order finite elements. In 2D cases, the displacement components through the thickness are approximated with an arbitrary expansion of the generalized unknowns and through the use of appropriate through-thickness functions. CUF plate theories has also been successfully applied to multilayered structures and multifield analysis [40,41,42]. Herein we extend CUF plate model by coupling it with PD for a refined failure analysis in a global–local manner.

The remainder of this paper has four sections. Section 2 starts with the basics of BB-PD theory. The CUF-based FE-PD coupling scheme is established in Sect. 3 and further verified in Sect. 4. Main conclusions are summarized in Sect. 5.

2 Bond-based peridynamic theory

The Bond-based Peridynamic theory (BB-PD) was introduced by Silling [1]. This theory treats internal forces within a continuous solid as a network of interaction pairs similar to springs (bonds) [2]. Though BB-PD is limited to a fixed Poisson’s ratio, it is widely adopted in PD applications due to its simplicity and computational-efficiency compared with state-based PD (SB-PD). The applicability of BB-PD in modelling material response under both static and dynamic conditions has been proven in many studies [16, 37, 43, 44]. This section provides a brief description of the BB-PD theory.

2.1 BB-PD basics

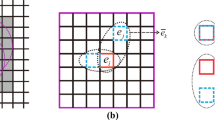
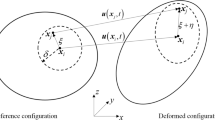
A PD body occupies region \(\mathcal {B}_0\) in the reference configuration and region \(\mathcal {B}_t\) in the deformed configuration at time t (see Fig. 1a). The PD body can be discretized into material particles with the grid spacing of \(\Delta \). Each particle possesses a spherical neighborhood \(\mathcal {H}_{\textbf{x}}\) with the radius of \(\updelta \), known as PD horizon, as shown in Fig. 1b. Within the horizon, central particle generates bonds with its neighbor particles. The PD equation of motion is given by

$$\begin{aligned} \rho (\textbf{x}) \ddot{\textbf{u}}(\textbf{x}, t)=\int _{\mathcal {H}_{\textbf{x}}}\left\{ \underline{\textbf{T}}[\textbf{x}, t]\left\langle \textbf{x}^{\prime }-\textbf{x}\right\rangle -\underline{\textbf{T}}\left[ \textbf{x}^{\prime }, t\right] \left\langle \textbf{x}-\textbf{x}^{\prime }\right\rangle \right\} \textrm{d} V_{\textbf{x}^{\prime }}+\textbf{b}(\textbf{x}, t) \end{aligned}$$
(1)

where \(\rho \) and \(\textbf{u}\) are respectively mass density and displacement vector field of particle \(\textbf{x}\); \(\textbf{b}\) is the body force field. \(\underline{\textbf{T}}\) denotes the force vector state field. \(V_{\textbf{x}^{\prime }}\) is the volume of particle \(\textbf{x}^{\prime }\).

Fig. 1
figure 1

Schematics of bond-based Peridynamics

Full size image

Bond \(\varvec{\upxi }=\textbf{x}^{\prime }-\textbf{x}\) is also known as the reference position vector state \(\underline{\textbf{X}}[\textbf{x}, t]\langle \varvec{\upxi }\rangle \) of particle \(\textbf{x}\) at time t (see Fig. 1). It is mapped to the deformed configuration as the deformation vector state \(\underline{\textbf{Y}}[\textbf{x}, t]\langle \varvec{\upxi }\rangle =\textbf{y}\left( \textbf{x}^{\prime }, t\right) -\textbf{y}(\textbf{x}, t)=\varvec{\upxi }+\varvec{\upeta }\). The displacement vector state \(\varvec{\upeta }\) is written as \(\underline{\textbf{U}}[\textbf{x}, t]\langle \varvec{\upxi }\rangle =\varvec{\upeta }=\textbf{u}\left( \textbf{x}^{\prime }, t\right) -\textbf{u}(\textbf{x}, t)\). The extension scalar state \(\underline{e}\) is defined as \(\underline{e}=\underline{y}-\underline{x}\), where \(\underline{y}=|\underline{\textbf{Y}}|\), \(\underline{x}=|\underline{\textbf{X}}|\). The bond stretch is defined as \(s=\frac{\underline{y} - \underline{x}}{\underline{x}}\). In the case of bond-based PD theory, each bond has its own constitutive relation, independent of the others. The force state is defined as

$$\begin{aligned} \underline{\textbf{T}}=\hat{\textbf{t}}(\underline{\textbf{Y}}\langle \varvec{\upxi }\rangle , \varvec{\upxi }) \end{aligned}$$
(2)

in which \(\hat{\textbf{t}}\) is the force state function. In an elastic-bond-based body, the bond-wise scalar-valued function \(w(\underline{e}, \varvec{\upxi })\) is known as the micropotential. The relation between strain energy density (denoted as \(W=\hat{W}(\underline{\textbf{Y}})\)) and micropotential can be written as

$$\begin{aligned} \hat{W}(\underline{\textbf{Y}})=\int _{\mathcal {H}}\frac{1}{2} \hat{w}(\underline{e}\langle \varvec{\upxi }\rangle , \varvec{\upxi }) \textrm{d} V_{\varvec{\upxi }} \end{aligned}$$
(3)

For a prototype microelastic body, micropotential is given as \(w=c \underline{e}^2 / 2 \xi \), where c denotes bond stiffness expressed as \(c=12 E / \pi \updelta ^4\) with fixed Poisson’s ratio of 0.25 for 3D analysis. According to Ref. [2], the force state function is defined as

$$\begin{aligned} \underline{\hat{\textbf{t}}}(\underline{\textbf{Y}}\langle \varvec{\upxi }\rangle ,\varvec{\upxi })= & {} \underline{t}(\underline{\textbf{Y}}\langle \varvec{\upxi }\rangle , \varvec{\upxi }) \underline{\textbf{M}}\nonumber \\= & {} \frac{1}{2} \hat{w}_{\underline{e}}(\underline{e}\langle \varvec{\upxi }\rangle , \varvec{\upxi }) \underline{\textbf{M}}=\frac{1}{2} {cs} \mu \underline{\textbf{M}} \end{aligned}$$
(4)

where \(\hat{w}_{\underline{e}}\) denotes the partial derivative with respect to \(\underline{e}\). \(\underline{t}\) is the force scalar state and the direction vector state \(\underline{\textbf{M}}\) is defined as \(\underline{\textbf{M}}=\underline{\textbf{Y}}\langle \varvec{\upxi }\rangle /|\underline{\textbf{Y}}\langle \varvec{\upxi }\rangle |\). The pair-wise force is then defined as

$$\begin{aligned} \textbf{f}(\underline{\textbf{Y}}\langle \varvec{\upxi }\rangle , \varvec{\upxi })= & {} f(\underline{\textbf{Y}}\langle \varvec{\upxi }\rangle , \varvec{\upxi }) \underline{\textbf{M}}\nonumber \\= & {} 2 \underline{t}(\underline{\textbf{Y}}\langle \varvec{\upxi }\rangle , \varvec{\upxi }) \underline{\textbf{M}}= {cs} \mu \underline{\textbf{M}} \end{aligned}$$
(5)

To include the bond failure in the formulation, the parameter \(\mu \) is introduced in a history-dependent scalar-valued function form, defined as

$$\begin{aligned} \mu (t, s)= {\left\{ \begin{array}{ll}1, &{} s \le s_0 \\ \beta + \frac{(1 - \beta )(s_1-s)}{s_1-s_0} &{} s_0<s \le s_1 \\ \frac{\beta (s_{\textrm{c}}-s)}{s_{\textrm{c}}-s_1} &{} s_1<s \le s_{\textrm{c}} \\ 0, &{} s > s_{\textrm{c}}\end{array}\right. } \end{aligned}$$
(6)

\(\mu \) is a function of bond stretch and time, with a magnitude of zero when the bond is stretched beyond a predefined critical value of \(s_{\textrm{c}}\). In this study, bonds are postulated to go through elastic deformation, bond decay and failure. Between the elastic limit \(s_0\) and \(s_{\textrm{c}}\), bond degradation is determined based on continuum damage mechanics (CDM), which has shown its effectiveness for nonlocal methods in describing materials such as concretes [45, 46], metals [19], polymers [47] and composites [48, 49]. Herein, bond degradation is modeled by a trilinear damage model as depicted in Fig. 2.

Fig. 2
figure 2

Trilinear damage model

Full size image

Representative points defined by \(s_0\), \(s_1\), \(s_{\textrm{c}}\) and \(\beta \) in this damage model are determined as follows. The area below the softening curve \(W^*\) is generally assumed to be the bond-wise fracture energy. The macro-scale fracture energy \(G_{\textrm{f}}\) is the integral of the work that bonds consume during the softening period according to the development in Ref. [16, 45]. The critical bond stretch can then be obtained as \(s_{\textrm{c}}=\frac{10 \gamma G_{\textrm{f}}}{\pi \updelta ^5 c s_0(1+\gamma \beta )}+s_0\), in which \(\gamma \) is defined as \(\gamma =\frac{s_{\textrm{c}}-s_0}{s_1-s_0}=\frac{3+2 \beta }{2 \beta (1-\beta )}\). \(\beta \) is hereby simplified as the basic damage parameter and varies in different material degradation models. \(s_0\) denotes the ultimate elastic bond stretch, beyond which the bond stiffness starts to decay. Corresponding to the ultimate elastic tension strain in macro scale, \(s_0\) can be approximately determined by \(\sigma _{\textrm{t}} / E\), in which \(\sigma _{\textrm{t}}\) denotes the ultimate strength and E denotes Young’s modulus. The local damage is measured by the index \(\varphi \)

$$\begin{aligned} \varphi (\textbf{x}, t)=1-\frac{\int _{\mathcal {H}_{\textbf{x}}} \mu (t, \varvec{\upxi }, \varvec{\upeta }) \textrm{d} V_{\textbf{x}^{\prime }}}{\int _{\mathcal {H}_{\textbf{x}}} \textrm{d} V_{\textbf{x}^{\prime }}} \end{aligned}$$
(7)

which calculates the percentage of broken bonds within the initial bond family.

2.2 Discretization

To perform a numerical approximation to the peridynamic equations, a PD body is spatially discretized into material particles in the reference configuration. Each particle i possesses a definite volume \(V_i\) and a mass density \(\rho _i\). Within its horizon, each particle i interacts with neighboring particles j in particle set \(\mathcal {F}_i\). The PD equation of motion (Eq. (1)) can be discretized as follows:

$$\begin{aligned} \rho _i \ddot{\textbf{u}}_i^n=\sum _{j \in \mathcal {F}_i} \textbf{f}\left\langle \textbf{u}_j^n-\textbf{u}_i^n, \textbf{x}_j^n-\textbf{x}_i^n\right\rangle V_j+\textbf{b}_i^n \end{aligned}$$
(8)

where \(\textbf{f}\) is given by Eq. (5), subscript n denotes the current time step. After linearization and simplification, Eq. (8) is written as

$$\begin{aligned} \sum _{j \in \mathcal {F}_i} \textbf{C}\left( \textbf{x}_j-\textbf{x}_i\right) \left\langle \textbf{u}_j^n-\textbf{u}_i^n \right\rangle V_j+\textbf{b}_i^n=0 \end{aligned}$$
(9)

where \(\textbf{C}\) is a tensor-valued function named micromodulus. For proportional materials, it is defined as

$$\begin{aligned} \textbf{C}(\xi )=\frac{\partial \textbf{f}}{\partial \varvec{\upeta }}=c \frac{\xi \xi ^{\textrm{T}}}{|\xi |^3} \end{aligned}$$
(10)

Referring to the truss element in finite element method (FEM), multiplying Eq. (9) by \(V_i\) leads to

$$\begin{aligned} \sum _{j \in \mathcal {F}_i} \textbf{C}\left( \textbf{x}_j-\textbf{x}_i\right) \left\langle \textbf{u}_j^n-\textbf{u}_i^n\right\rangle V_j V_i+\textbf{b}_i^n V_i=0 \end{aligned}$$
(11)

Thus, the global equilibrium equation of BB-PD model can also be written into a matrix form as

$$\begin{aligned} \textbf{K}^{\textrm{PD}} \textbf{U}^{\textrm{PD}}=\textbf{F}^{\textrm{PD}} \end{aligned}$$
(12)

where \(\textbf{K}^{\textrm{PD}}\) is the stiffness matrix of PD region. \(\textbf{U}^{\textrm{PD}}\) and \(\textbf{F}^{\textrm{PD}}\) are displacement and force vectors for PD particles. In this study, the computational model is partially discretized with a PD grid and partially with a refined 2D FE mesh.

3 High-order 2D theories based on classical elasticity

Plates are 2D structures in which one dimension, in general the thickness h, is at least one order of magnitude lower than the in-plane dimensions [40]. This permits the reduction of the 3D domains to 2D plates. Carrera Unified Formulation (CUF) integrates all the classical 2D structural theories within one unified formulation and permits the analysis of any plate structure by varying the class of thickness functions and the order of expansion along the thickness. CUF-based 2D FE models can provide 3D-like accuracy with low computational costs. Both CUF theory and 2D CUF-based FE-3D PD coupling technique are elaborated in this section.

3.1 The Carrera unified formulation

The isotropic plate shown in Fig. 3 lays on \(x-y\) plane of a Cartesian reference system (x, y, z). 2D plate model uses the z coordinate for the thickness direction. The expansion of the 2D problem into 3D can be performed through CUF. The 3D displacement field \(\textbf{u}(x, y, z)\) of 2D plate model, within CUF framework, can be expressed as a general expansion of the primary unknowns as

$$\begin{aligned} \textbf{u}(x, y, z)=F_\tau (z) \textbf{u}_\tau (x, y), \quad \tau =1,2, \ldots , M \end{aligned}$$
(13)

where \(F_\tau \) are functions of the thickness coordinate z, \(\textbf{u}_\tau \) is the displacement vector depending on the in-plane coordinates x, y. The repeated indices \(\tau \) imply summation. M is the order of expansion of the model. The main feature of the unified formulation is the ability for arbitrarily choosing the kind of expansion and the number of terms [38]. The choice of the expansion functions depends on different problems and required degree of accuracy. Possible choices include Taylor polynomials, Lagrange polynomials, etc [40].

Fig. 3
figure 3

Schematic of two-dimensional CUF plate model

Full size image

In this study, the through-thickness is approximated with a pattern of Lagrange Points (LPs), which are divided into appropriate Lagrange polynomials. 3D displacement field is the result of an interpolation of the displacements. The Lagrange expansion (LE) has shown to be advantageous since it permits boundary conditions to be applied directly to pure displacement components. Lagrange polynomials of different orders have been introduced to the 2D CUF framework [40]. For instance, if a quadratic interpolation is employed, the Lagrange polynomials for the 2D plates models are:

$$\begin{aligned} F_\tau= & {} \frac{1}{2}\left( \zeta ^2+\zeta \zeta _\tau \right) , \quad \tau =1,3 \end{aligned}$$
(14)
$$\begin{aligned} F_\tau= & {} -\zeta ^2+1, \quad \tau =2 \end{aligned}$$
(15)

where \(\zeta \) varies from -1 to 1, whereas \(\zeta _\tau \) corresponds to the position of the LPs in the natural coordinate. LE models use local expansions of pure displacement variables and can be placed arbitrarily on the expanded direction, which improves the accuracy of the solution in many sophisticated circumstances like those of composite materials and enables the analysis of material behaviors such as plastic deformation and damage.

3.2 CUF-based FE-PD coupling scheme

In 2D CUF-based FE, the plane-wise displacement field \(\textbf{u}_\tau \) is written by FE approximation across the reference surface as

$$\begin{aligned} \textbf{u}_\tau (x, y)=N_i(x, y) \textbf{u}_{\tau i}, \quad i=1,2, \ldots , p \end{aligned}$$
(16)

where \(N_i\) denotes 2D shape function. Subscript i indicates the element node and p stands for the number of nodes per element. \(\textbf{u}_{\tau i}\) is nodal vector of the generalized displacements. Based on Eq. (13) and Eq. (16), the 3D displacement field \(\textbf{u}(x, y, z)\) of 2D plate model can then be written as

$$\begin{aligned} \textbf{u}=N_i F_\tau \textbf{u}_{\tau i} \end{aligned}$$
(17)

For linear elastic static problems, the governing equations can be derived from the principle of virtual work as

$$\begin{aligned} \delta L_{\textrm{int}}=\delta L_{\textrm{ext}} \end{aligned}$$
(18)

where \(L_{\text {int }}\) is the internal work and \(L_{\textrm{ext}}\) is the external work. The internal work is written in terms of stress and strain as

$$\begin{aligned} \delta L_{\textrm{int}}=\int _{\Omega } \int _h \delta \varvec{\upvarepsilon }^{\textrm{T}} \varvec{\upsigma } \textrm{d} z \textrm{ d} \Omega \end{aligned}$$
(19)

where h is the thickness of the plate, \(\Omega \) represents the plate surface. \(\varvec{\upvarepsilon }\) and \(\varvec{\upsigma }\) are 3D strain vector and stress vector, respectively. The internal work can be further rewritten in a compact manner as

$$\begin{aligned} \delta L_{\textrm{int}}=\delta \textbf{u}_{s i}^{\textrm{T}} \textbf{K}^{\tau s i j} \textbf{u}_{\tau j} \end{aligned}$$
(20)

where \(\tau \) and s are associated with the functions that approximate the displacement field and its virtual variation along the plate thickness. i and j deal with the shape functions of the FE model. The matrix \(\textbf{K}^{\tau s i j}\) in Eq. (20) is of size \(3\times 3\), which is the "fundamental necleus (FN)" of the element stiffness matrix of the arbitrarily refined 2D plate theory. For homogeneous isotropic material, the terms of the nucleus of stiffness matrix are

$$\begin{aligned} \begin{aligned} {K}^{\hspace{1pt} \tau \hspace{0.3pt} s \hspace{1pt} i \hspace{0.5pt} j}_{\hspace{0.5pt} x x} \, =&\displaystyle (\lambda \, + 2G) \, \int _{\Omega } N_{i,x} \, N_{j,x} \, \,\textrm{d} \Omega \, \int _h F_{\tau } F_{s} \,\,\textrm{d} z \, \\&+ \, G \, \int _{\Omega } N_i \, N_j \, \,\textrm{d} \Omega \, \int _h F_{\tau ,z} F_{s,z}\,\,\textrm{d} z \, + \\&\displaystyle + \, G \, \int _{\Omega } N_{i, \hspace{1pt} y} \, N_{j, \hspace{1pt} y} \, \,\textrm{d} \Omega \, \int _h F_{\tau } F_{s}\,\,\textrm{d} z \\ {K}^{\hspace{1pt} \tau \hspace{0.3pt} s \hspace{1pt} i \hspace{0.5pt} j}_{\hspace{0.5pt} x y} \, =&\displaystyle \lambda \, \int _{\Omega } N_{i, \hspace{1pt} y} \, N_{j, \hspace{1pt} x} \, \,\textrm{d} \Omega \, \int _h F_{\tau } F_s\,\,\textrm{d} z \, \\&+ \, G \, \int _{\Omega } N_{i, \hspace{1pt} x} \, N_{j, \hspace{1pt} y} \, \,\textrm{d} \Omega \, \int _h F_{\tau } F_{s} \,\,\textrm{d} z \end{aligned} \end{aligned}$$
(21)

where \(\lambda \) and G are Lamé constants. All nine components of FN can be obtained by appropriate index permutation based on Eq. (21). Here, FN functions as a "DNA" structure of any 2D elasticity problem, that is, any plate model can be automatically formulated by expanding the fundamental kernel within the stiffness matrix. After the matrix assembly over the entire FE domain, the equilibrium equation of FE model can be written as

$$\begin{aligned} \textbf{K}^{\textrm{FE}} \textbf{U}^{\textrm{FE}}=\textbf{F}^{\textrm{FE}} \end{aligned}$$
(22)

where \(\textbf{U}^{\textrm{FE}}\) is nodal unknown vector and \(\textbf{F}^{\textrm{FE}}\) is external force vector.

For a better allocation of computing resources, a coupling scheme integrating 3D PD grid and 2D refined FEs within one computational framework is established hereafter. PD is used for critical subregions where damage or fracture might occur while the more efficient refined FEs used for the remainder.

Fig. 4
figure 4

The coupling scheme of refined 2D FEs and 3D PD particles

Full size image

Figure 4 shows a plate in Cartesian reference system, which is divided into high-order 2D FE zone and 3D PD zone. Two components are connected by an interface zone, denoted as \(\mathcal {I}\), where the equilibrium equations of both PD and FE are satisfied simultaneously. Therefore, Eq. (12) and Eq. (22) can be written together in matrix form as

$$\begin{aligned} \textbf{K U}=\textbf{F},\left[ \begin{array}{cc} \textbf{K}^{\textrm{PD}} &{} \textbf{0} \\ \textbf{0} &{} \textbf{K}^{\textrm{FE}} \end{array}\right] \left\{ \begin{array}{l} \textbf{U}^{\textrm{PD}} \\ \textbf{U}^{\textrm{FE}} \end{array}\right\} =\left\{ \begin{array}{l} \textbf{F}^{\textrm{PD}} \\ \textbf{F}^{\textrm{FE}} \end{array}\right\} \end{aligned}$$
(23)

Moreover, the displacement consistency on interface \(\mathcal {I}\) requires a complementary condition for Eq. (23). A displacement constraint is therefore introduced on the boundary of the 3D PD grid and the refined 2D FE mesh, where PD particles and FE nodes have the same displacements. One-to-one correspondence is not required, by virtue of which the size of FE mesh in a coupled form can be chosen flexibly according to the computational needs. By using Lagrange multipliers, the additional condition is given as

$$\begin{aligned} \Pi _k=\lambda _k^{\textrm{T}}\left( \textbf{u}_k^{\textrm{PD}}-\textbf{u}_k^{\textrm{FE}}\right) \end{aligned}$$
(24)

where \(\textbf{u}_k^{\textrm{PD}}\) and \(\textbf{u}_k^{\textrm{FE}}\) are the PD displacement vector and the FE displacement vector of node k on interface \(\mathcal {I}\). \(\lambda _k\) is the three-component vector of Lagrange multipliers. Referring to Eq. (13), Eq. (24) can be rewritten as

$$\begin{aligned} \Pi _k=\lambda _k^{\textrm{T}} \textbf{B}_k \textbf{U}, \quad \textbf{B}_k=\left( \delta _k-F_\tau \left( z_k\right) N_i\left( x_k, y_k\right) \right) \textbf{I} \end{aligned}$$
(25)

where \(\delta _k\) is 1 for PD particle k and null for others. \(\textbf{B}_k\) functions as the fundamental kernel of the coupling matrix. Equation (23) can then be written as

$$\begin{aligned} \left[ \begin{array}{cc} \textbf{K} &{} \textbf{B}^{\textrm{T}} \\ \textbf{B} &{} \textbf{0} \end{array}\right] \left\{ \begin{array}{l} \textbf{U} \\ \lambda \end{array}\right\} =\left\{ \begin{array}{l} \textbf{F} \\ \textbf{0} \end{array}\right\} \end{aligned}$$
(26)

where \(\textbf{B}\) is the final coupling matrix after the assembly of \(\textbf{B}_k\). Solution of Eq. (26) requires solving \(\textbf{U}\) and \(\lambda \). \(\textbf{U}\) denotes displacement vector of PD particles and FE nodes. \(\lambda \) denotes the coupling force vector to be applied on interface nodes/particles, which enables the information exchange across the coupling interface in a strong way.

Fig. 5
figure 5

Flowchart of convergence check

Full size image

3.3 Solution algorithm

The computational domain includes both the refined 2D FEs and 3D PD particles. Within one load step, three main loops are generated over the FE nodes, PD particles and interfacial nodes/particles for computing stiffness matrix regarding to Eq. (23). To guarantee the computational accuracy, a convergence check is hereby introduced to monitor and control the development of force residual and the number of broken bonds [50], as illustrated in Fig. 5.

The present convergence check algorithm contains two inner iterations based on the control of number of broken bonds and residual force. Different from Ref. [50], an adaptive stepsize control is developed according to the number of broken bonds. The trailing load step is halved if the number of broken bonds is larger than the threshold, named broken bond tolerance (BTOL). Once BTOL is satisfied or the prescribed iteration step number is reached, the computation is transferred to another inner iteration with respect to the residual force tolerance (FTOL). According to the computational results, the computational task can be resent to Inner_iteration1 or Inner_iteration2 in case of new bond breakage after Inner_iteration2. Meanwhile, the iteration step number \(n_i\) is still tracked within \(\textrm{n}_{\textrm{max}}\) to prevent infinite loop. For all the computational tasks, \(\textrm{n}_{\textrm{max1}}\) and \(\textrm{n}_{\textrm{max2}}\) are predefined as 10 and 5. To make FTOL consistent and comparable among simulations, forces concerning \({\textrm{F}_\textrm{n2}}\) and \({\textrm{F}_0}\) are rescaled by the peak force indicated from the experimental data. In that case, FTOL takes a ratio form within the range of (0,1). When the rescaled residual force is computed small enough as defined by FTOL, it is assumed that the entire system is energy-conserved, which is in parallel to the case of quasi-static loading.

4 Numerical results

This section aims to demonstrate the efficacy of the proposed computing scheme, concerning the coupling performance and convergence performance. The capabilities of the present computing scheme in modeling linear deformation, material degradation and crack propagation are carefully discussed. Three 3D numerical experiments are carried out, respectively, quasi-static tension tests, wedge splitting tests and L-plate cracking tests.

4.1 Quasi-static tension tests

A \(30 \times 30 \times 12\) plate is discretized by using two computational models with different coupling patterns, referred to as Case (a) and Case (b) as shown in Fig. 6. The test material is Aluminum Alloy 6061(T6) with Young’s modulus of 70 GPa and the Poisson’s ratio of 0.3. Case (a) is discretized into 6 refined 2D nine-node quadrilateral (Q9) elements and 13984 3D PD particles with 487440 bonds generated. In the thickness direction, 2D elements are expanded by three-node quadratic (B3) Lagrange expansion function. In Case (b), FE zone is discretized into 8 refined 2D Q9 elements with 12 B3 expansion elements employed in the thickness direction. PD zone is discretized into 11025 3D particles, with 819817 bonds generated. PD particles are arranged in simple cubic structure with the grid spacing of 0.67 mm (Case (a)) and 0.5 mm (Case (b)). With the left boundary being fixed, the right boundary of the plate is subjected to a uniform displacement tension along x-direction. The total displacement is 1.2 mm to be applied within 20 steps.

Fig. 6
figure 6

Two discretization patterns for quasi-static tension tests (unit: mm)

Full size image

As depicted in Fig. 7, both discretized models can reproduce FE results in a good manner. The horizon sizes are 18.5 mm and 18 mm, accordingly for Case (a) and Case (b), with little discrepancy noticed. In this case, m-ratio, indicating the family size, is not showing obvious influences on the results so that current results are m-convergent as well. According to the displacement cloud charts depicted in Fig. 8, smooth transmission of displacement load from the right sides to the left sides are shown without obvious mismatches. To investigate the effects of FE-PD coupling interface, two discretized models are sliced up. Displacements along x-direction with respect to x and y coordinates curves at the 8th step are illustrated, as shown in Figs. 9, 10 and 11.

As is shown in Fig. 9, displacements of PD particles and FE nodes along x direction shows an overall consistency with each other. The coupling interface permits the displacement continuity between refined FE nodes and PD particles as expected. Through-thickness deformation predicted by CUF-based refined 2D FEs is continuous and smooth as well. According to the zoomed-in window at top left, displacement mismatches with the maximum magnitude of 0.13 mm are notified symmetrically at two interfaces. Similar results are also found in Fig. 10. The maximum displacement mismatch notified in Case (b) is with magnitude of 0.2 mm, which is 50% larger than that from Case (a). In addition, the displacement kink spreads for 5 mm along x-direction in Case (b), while in Case (a) it spreads for 4 mm. That is, with similar horizon sizes, the recovery from the displacement kink in Case (a) is quicker than Case (b). It is highly possible that effects of displacement kink in Case (b) are augmented by y-direction coupling interfaces. Thus, the curve of displacements along x-direction with respect to y-coordinate interfaces is further depicted in Fig. 11. A slight displacement mismatch is noticed with the magnitude of 0.0001 mm. Though the direct influences are small, the augmentation effects caused by coupling interfaces do exist according to the comparison between Case (a) and Case (b). Based on these observations, it is recommended the critical areas such as cracks and shear bands to be placed far from coupling interfaces, at least 6 layers away from coupling interfaces for m=3 case (Case (a)).

Fig. 7
figure 7

Force vs. displacement curves by coupling models compared with FE results

Full size image
Fig. 8
figure 8

x-direction displacement cloud charts of Case (a) and (b)

Full size image
Fig. 9
figure 9

Coupling performance along x direction (Case (a))

Full size image
Fig. 10
figure 10

Coupling performance along x direction (Case (b))

Full size image
Fig. 11
figure 11

Coupling performance along y direction (Case (b))

Full size image

4.2 Wedge splitting tests

Wedge splitting test enables stable crack propagation, which is a suitable method to characterize Mode-I fracture phenomenon [45, 51, 52]. The geometry and the discretized model of wedge splitting tests are illustrated in Fig. 12. By virtue of the versatility of 2D model, PD zone is downsized to a small localized area. FE zone in Fig. 12a is discretized into 54 refined 2D Q9 FEs, with three-node quadratic Lagrange expansion function adopted in the thickness direction. Four PD grids in simple cubic structure with different grid spacings are utilized, respectively, \(\Delta \)x=38 mm, \(\Delta \)x=43.3 mm, \(\Delta \)x=48.4 mm and \(\Delta \)x=63.5 mm for the following simulations. The material used here is quasi-brittle concrete, with Young modulus E=28.3 GPa, Poisson’s ratio \(\nu \)=0.25, density \(\rho =2.5 \times 10^{-6} \,\textrm{kg} / \textrm{mm}^3\), tensile strength \(f_{\textrm{t}}=2.27 \textrm{MPa}\) and fracture energy \(G_{\textrm{f}}=490 \,\textrm{N} / \textrm{m}\). Damage parameter \(\beta \) is defined as 0.1277 [45]. As shown in Fig. 12a, the precracked specimen resting on linear supports is split by two opposite line-wise loads at the pace of \(4 \times 10^{-3}\) mm.

Fig. 12
figure 12

Schematic and discretized model for wedge splitting tests (unit: mm)

Full size image
Fig. 13
figure 13

Effects of FTOL without bond breakage

Full size image
Fig. 14
figure 14

Effects of BTOL

Full size image

To verify the effectiveness of the present convergence algorithm, a series of simulations are carried out using PD grid with \(\Delta \)x=43.3 mm. To minimize the interference factors, simulations without bond breakage are first conducted with different FTOLs. According to Fig. 13, with the decrease of FTOL value from infinity to 0.001, results are converging to one certain curve. Considering that the result of FTOL=0.003 is comparable with that of FTOL = 0.001, FTOL = 0.003 is further utilized to discuss the influence of BTOL. As shown in Fig. 14, with the decrease of BTOL value, the differences among curves are insignificant. Though it seems the computations converge from BTOL=INF to BTOL=50, it is worth noting that bonds start to break when CMOD is about 1.44 mm. Therefore, the influence of BTOL is considered minute at present case when a comparatively ideal FTOL is chosen. Then five simulations with different loading speeds are conducted with FTOL=0.003 and BTOL=20. According to Fig. 15, all five computations show good conformity with each other with similar peak forces, indicating good convergence performance of the present algorithm. Minute differences shown after the peak are considered acceptable.

The influences of PD horizon \(\updelta \) are investigated after establishing the parameters for convergence check algorithm. For the present case, the downward trends of curves are enabled by bond decay. With no bond breakage involved, the effects of PD horizon diminishes at the peaks of these curves. Main function of PD horizon is to increase the family size, corresponding to m, the ratio between the horizon size and the grid spacing. As shown in Fig. 16, with the increase of horizon size, the results converge to one curve. When m-ratio approaches around 2.92 with \(\delta \)=127 mm, m-convergence attains. Within the computational capability, a series of simulations are carried out. Concerning the similarity of resulting curves, peak force vs. m curves are depicted to show the result changes with the increase of m. According to Fig. 17, overall downward trends are noticed with the increase of m-ratio. When m-ratio reaches about 2.92, all four results computed by models with different grid densities under the loading pace of \(2 \times 10^{-3}\) mm show a good conformity with each other. This is further shown in Fig. 18. Though the initial stiffness is overestimated with early force peak, an acceptable agreement can be found among experimental results and simulation results. The final states for the four simulations are recorded in Fig. 20.

Fig. 15
figure 15

Force vs. CMOD curves under different loading step sizes (FTOL=0.003, BTOL=20)

Full size image
Fig. 16
figure 16

Influences of horizon size

Full size image
Fig. 17
figure 17

Influences of family size

Full size image

As the crack initiates, horizon acts as an "effective interaction distance", accounting for the non-locality effects near the crack tip. With the same m-ratio, models with finer grids have smaller horizon sizes. According to Fig. 20, cracks of the four discretized models propagate in a similar symmetrical manner, however, the model with grid spacing of 63.5 mm cracks at a comparatively lower speed than others. Moreover, crack paths of the other three cases are more concentrated and clearly visible [53], which can be explained by non-local averaging effects [35]. Particles farther away with lower degrees of deformation reduces the deformation intensity around the crack tip, thus more bonds are engaged in carrying loads, making those coarsely-discretized models less sensitive to the crack tip than finely-discretized models [19].

Fig. 18
figure 18

Force vs. CMOD curves of wedge splitting tests (\(\updelta \)=2.92\(\Delta \)x)

Full size image
Fig. 19
figure 19

Force vs. CMOD curves of wedge splitting tests computed by different methods

Full size image
Fig. 20
figure 20

Final crack patterns of PD models with different grid spacings of a \(\Delta \)x=38 mm, b \(\Delta \)x=43.3 mm, c \(\Delta \)x=48.4 mm, d \(\Delta \)x=63.5 mm

Full size image
Fig. 21
figure 21

Crack propagation process of specimen with grid spacing of 38 mm a CMOD=1.44 mm, b CMOD=2.06 mm, c CMOD=2.65 mm, d CMOD=3.15 mm, e CMOD=3.69 mm, f CMOD=4.0 mm

Full size image

The crack propagation process of the specimen with grid spacing of 38 mm is recorded in Fig. 21. Corresponding to Fig. 18, crack initiates when CMOD equals 1.44 mm at a slow pace and then propagates faster from CMOD of 3.15 mm to 3.69 mm. At the end of simulation, the crack propagates for around 456 mm as shown in Fig. 21f with comparatively slower propagation speed and lower Phi value than those predicted by Ref. [37]. Furthermore, the force vs. CMOD curve of case \(\Delta x\)=38 mm is taken to compare with the results computed by other models [37, 45, 54], concerning coupled FE-BBPD, coupled FE with ordinary state-based PD (FE-OSBPD) and pure BBPD models, as shown in Fig. 19. The result curve of present method shows a smooth after-peak downward trend without numerical instability. The trilinear damage model exhibits its effectiveness, as also seen in in Yang’s work [45]. In addition, it is noticed that the surface effect is amplified by using a comparatively thin plate (thickness-to-width ratio of 0.16) in present study, leading to a larger bulk elastic modulus among others.

4.3 L-plate cracking tests

L-shape plate is considered for 3D fracture analysis [46, 55,56,57]. The schematic and the discretized model are illustrated in Fig. 22. The L-plate is fully fixed at the bottom and loaded by an upward line-wise displacement at right. The specimen in Fig. 22a is discretized into 34 refined 2D Q9 FEs and 17010 PD particles with grid spacing of 7.2 mm. Refined 2D FEs are expanded with three-node quadratic Lagrange expansion in the thickness direction. Material parameters adopted from Ref. [46] are Young modulus \(E=20\) GPa, Poisson’s ratio \(\nu =0.18\), density \(\rho =2.5 \times 10^{-6} \,\textrm{kg} / \textrm{mm}^3\), tensile strength \(f_{\textrm{t}}=2.5 \textrm{MPa}\) and fracture energy \(G_{\textrm{f}}=0.13 \,\textrm{N} / \textrm{mm}\). Damage parameter \(\beta \) is defined as 0.25 according to Ref. [45, 58]. To determine the convergence criterion for the current displacement loading pace of \(1 \times 10^{-3}\) mm, a convergence check is performed for the accuracy of numerical analysis. Figure 23 depicts the influences of FTOL and BTOL on the results. Horizon size of 19 mm is used for the convergence check.

Fig. 22
figure 22

Schematic diagram and discretized model of L-shape plate (unit: mm)

Full size image

As depicted in Fig. 23, the curve with FTOL=INF and no bond breakage which originally reach the upper bound of experimental results decreases and converges with respect to the decrease in FTOL. When FTOL attains 0.002, numerical convergence is achieved. Then FTOL=0.002 is further utilized to find a proper BTOL. As shown in series of curves from green to yellow, very slight discrepancies are noticed from displacement of 0.35–0.55 mm. It is considered that the broken bond control contributes very little at the present computation. Based on these observations, FTOL of 0.002 and BTOL of 50 are utilized for the following computations.

Fig. 23
figure 23

Convergence check of L-plate cracking tests (with/without bond breakage)

Full size image
Fig. 24
figure 24

Force vs. displacement curves of L-plate tests computed by different methods

Full size image
Fig. 25
figure 25

Force vs. displacement curves of L-plate tests a \(\Delta \)x=9.9 mm, \(\updelta \)=24.5 mm; b \(\Delta \)x=8.3 mm, \(\updelta \)=21 mm; c \(\Delta \)x=7.2 mm, \(\updelta \)=18.4 mm

Full size image
Fig. 26
figure 26

Crack paths of L-plate cracking tests (scaled \(\times 40\)) a \(\Delta \)x=9.9 mm, b \(\Delta \)x=8.3 mm, c \(\Delta \)x=7.2 mm

Full size image

To establish the capability of the present computing model in capturing crack propagation, three different discretization models with different grid spacings are used, respectively, \(\Delta \)x=9.9 mm, \(\Delta \)x=8.3 mm and \(\Delta \)x=7.2 mm. Computational results within the scatter band of experimental data are summarized in Fig. 25. All three sub-figures in Fig. 25 show a good conformity with experimental data, with a little mismatch noticed at the end of curves. It is found that correct results are achieved with small PD horizons with denser grids. Though the horizon sizes are smaller for finely-discretized models, the family sizes quantified by m-ratio are actually larger. The m-ratio used for case \(\Delta \)x=9.9 mm in Fig. 25a ranges from 2.32 to 2.47, while the other two are 2.53\(-\)2.65 for case \(\Delta \)x=8.3 mm and 2.56\(-\)2.70 for case \(\Delta \)x=7.2 mm. Smaller horizon size with bigger m-ratio can contribute to the \(\updelta \)m-convergence [59] to local classical solution. Thus, the model used in Fig. 25c can be considered as an ideal one among the three for describing crack for a fine and localized behavior. Moreover, it is noticed that curves in Fig. 25a, among others, show a different monotonicity with respect to horizon size. As horizon increases, non-local averaging effect, on the one hand, can alleviate the force concentration near the crack tip and prevent crack from breaking too fast. On the other hand, the non-local averaging effect can get more bonds around the crack tip engaged in bearing the load, which can cause a massive bond degradation nearby and bond breakage, leading to a force falling-off. Therefore, the trend in Fig. 25a is reasonable under the cooperation of bond degradation and bond failure. The result curve of case \(\Delta \)x=7.2 mm, \(\updelta \)=18.4 mm is further compared with results computed by pure BBPD [46], phase field (PF) [56] and extended finite element method (XFEM) models [57], as shown in Fig. 24. The coupled CUF-based FE-BBPD model and XFEM model are more effective in reproducing material behaviors for the present case than PF model and pure BBPD model. Furthermore, compared with XFEM, the coupled CUF-based FE-BBPD method is theoretically consistent without special needs to cope with singularity issues for stress fields around the crack tip.

To investigate the crack propagation details, their final crack patterns are recorded in Fig. 26. Three cracks are all localized in fine paths. The finely-discretized model in Fig. 26c shows a more refined crack path with more particle ladders than those of Fig. 26a, b. With refined prediction accuracy, its whole process of crack propagation is further displayed in Fig. 27. As referred to Fig. 25c, after the linear deformation section, no fracture is noticed at curve peak, which indicates that the downward trend of the present curve is due to the effects of bond degradation. With the descending of force value, crack nucleates and propagates in a stable fashion. As the displacement attains 0.8 mm, the whole structure has no force-carrying capacity anymore with the crack length of 158.4 mm. Figure 27d shows the final crack pattern in an integrated form. The angle of crack with respect to -x direction is about \(22^{\circ }\), within the experimental scatter band of \(15^{\circ }\)–\(47^{\circ }\), in line with the results reported in Ref. [46, 56].

Fig. 27
figure 27

Crack propagation process a \(\textrm{u}_\textrm{x}\)=0.2 mm, b \(\textrm{u}_\textrm{x}\)=0.4 mm, c \(\textrm{u}_\textrm{x}\)=0.6 mm, d \(\textrm{u}_\textrm{x}\)=0.8 mm

Full size image

4.4 Computational efficiency

The proposed method was implemented in Microsoft Visual Studio 2022 version 17.6 integrated with Intel Fortran compiler 2023 in Windows 11 system. All the computation tasks discussed above are performed on a personal laptop equipped with 12th Gen Intel(R) Core(TM) i7-12700 H (2.30 GHz). Simulation run times are summarized in Table 1 corresponding to the results depicted in Figs. 15 and  26. The degrees of freedom (DOFs) in FE zone and PD zone, related m-ratio, total CPU time and unit CPU time with respect to each DOF are listed for comparison.

Table 1 Simulation run time
Full size table

For wedge splitting tests, the efficiency of simulations with different loading steps are compared. The unit CPU times of five simulations range from 0.42 s to 0.91 s. Simulations with smaller loading steps consume more CPU time than those with bigger ones because more timesteps are involved [22]. However, as observed from the results of \(\Delta \)u=\(6 \times 10^{-3}\) mm and \(\Delta \)u=\(4 \times 10^{-3}\) mm, an overly large loading step will also cause computational inefficiency because more inner iterations are taken to satisfy convergence thresholds. Compared with Ref. [37] with around \(7.5 \times 10^{5}\) DOFs’ FE zone and Ref. [54] with \(8.5\times 10^{5}\) DOFs’ FE zone, the present study has downsized the FE DOFs effectively by means of CUF. With similar outcomes, CUF has optimized the computing structure by adjusting the mesh accuracy according to practical needs.

In L-plate cracking tests, simulations with finely-discretized PD zones consume more CPU time and more unit CPU time. Therefore, a compromised PD discretization pattern is recommended to provide a reasonable balance between numerical accuracy and computational cost. The present model effectively decreases the DOF number with acceptable results, contributing to an optimized allocation of computing resources. According to the total CPU time reported in Ref. [22], under similar quasi-static loading condition, the unit CPU time is 0.144 s for a 3D SB-PD model by using a HP Z8 G4 workstation with two CPUs (Intel Xeon processor Gold 6154), which is close to that of case \(\Delta \)x=9.9 mm, faster than case \(\Delta \)x=8.3 mm and case \(\Delta \)x=7.2 mm. For the same L-shape test, Cheng et al. [60] reported a total CPU time of 15180 s for a 83667 2D elements’ model by using a workstation with 2 CPUs (Inter Xeon Processor E5-2650v2). Unit CPU time can be computed as around 0.09 s, which is about 1-4 times faster than the results shown in Table 1. However, the present solution is considered economic based on the satisfactory outcomes computed with a personal laptop.

5 Conclusions

This study presents a computational approach to couple peridynamics (PD) and higher-order classical elasticity theory for modelling material fracture in a global–local manner. Main contributions are as follows. A Lagrange multiplier based coupling technique was proposed to glue 3D peridynamic grid with refined 2D finite elements (FEs) based on the Carrera Unified Formulation (CUF), enabling an optimization of PD-FE coupling approach providing satisfactory computational accuracy. An adaptive convergence check algorithm was presented based on the control of number of broken bonds and force residual, whose effectiveness has been examined and discussed in detail. A bond-wise trilinear damage model was implemented within the present computational scheme, showing the compatibility of the present scheme with new constitutive models and its capability in solving practical problems concerning wedge splitting tests and L-plate cracking tests. Compared with other 3D approaches concerning PD in fully-nonlocal manner and other 3D FE-PD coupling schemes, the present computing scheme is able to downsize the total number of degree of freedom (DOF) leading to a reasonable allocation of computing resources. Future work in this area includes mitigating boundary effects by means of peridynamics differential operator for more refined global–local analysis.